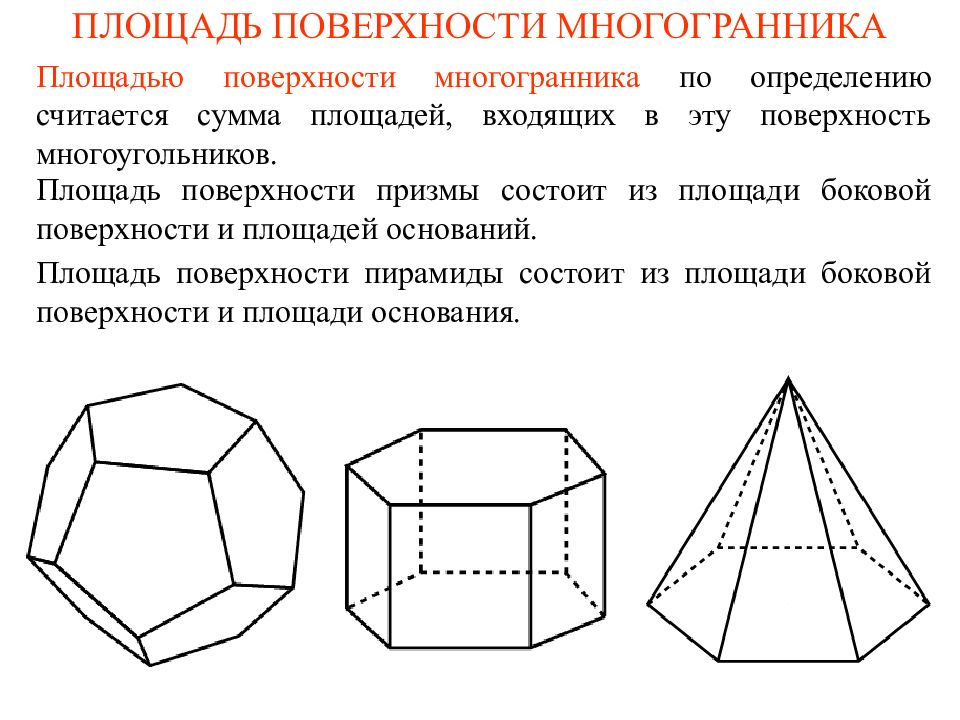
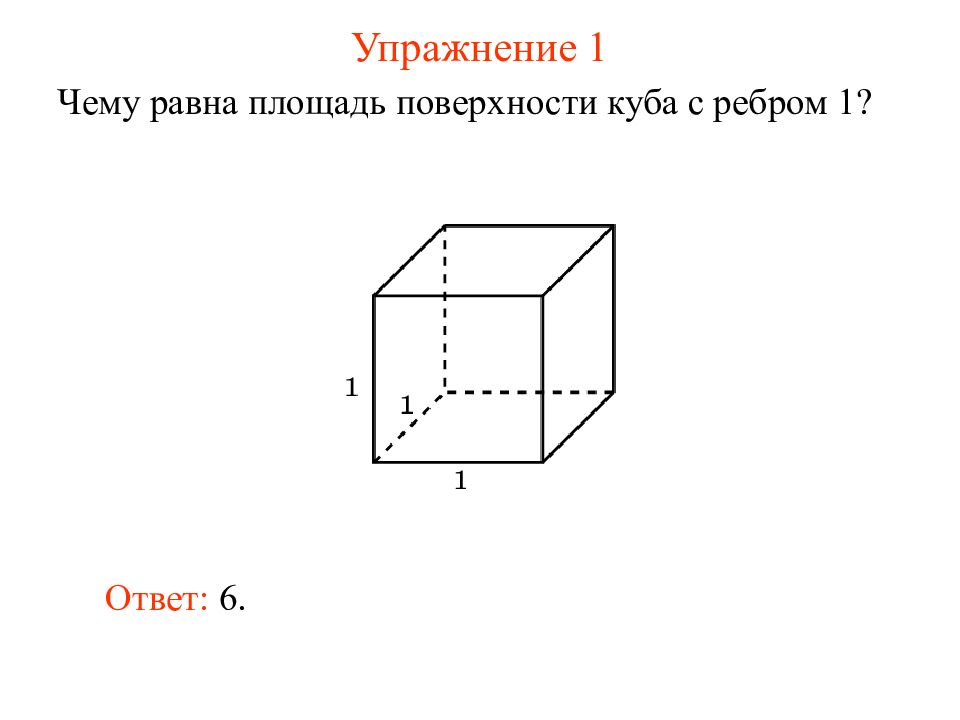
Первый слайд презентации: ПЛОЩАДЬ ПОВЕРХНОСТИ МНОГОГРАННИКА
Площадью поверхности многогранника по определению считается сумма площадей, входящих в эту поверхность многоугольников. Площадь поверхности призмы состоит из площади боковой поверхности и площадей оснований. Площадь поверхности пирамиды состоит из площади боковой поверхности и площади основания.
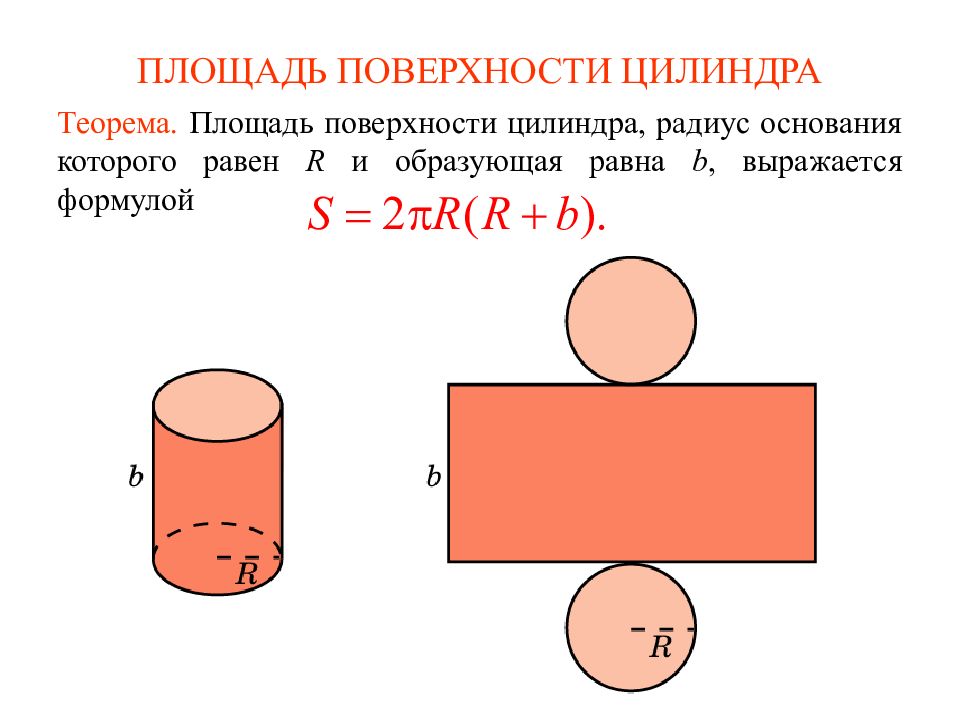
Слайд 2: ПЛОЩАДЬ ПОВЕРХНОСТИ ЦИЛИНДРА
Теорема. Площадь поверхности цилиндра, радиус основания которого равен R и образующая равна b, выражается формулой
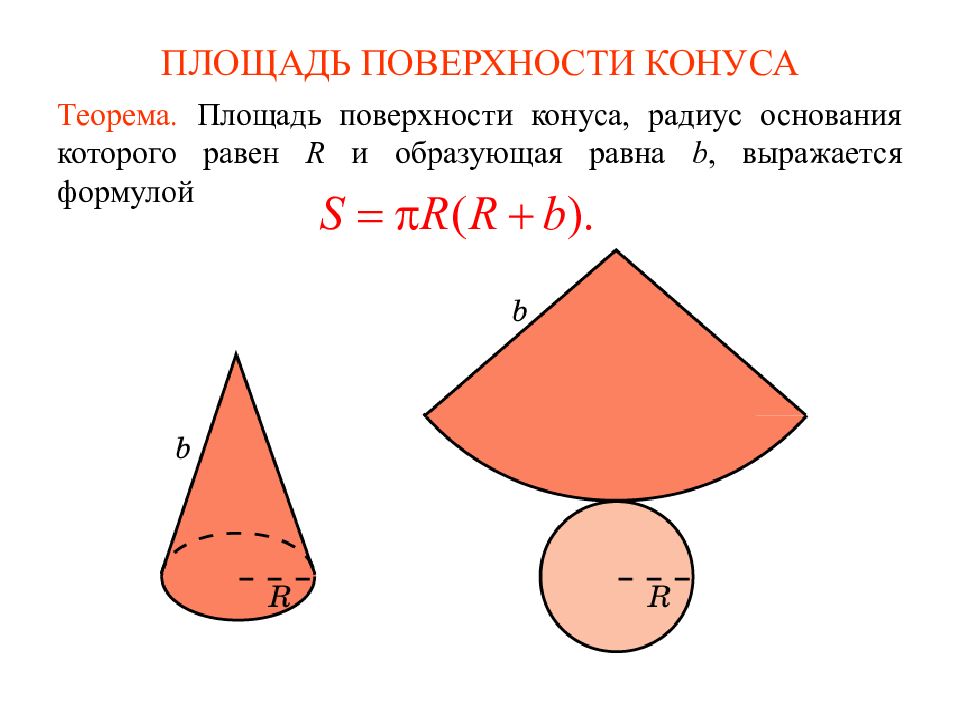
Слайд 3: ПЛОЩАДЬ ПОВЕРХНОСТИ КОНУСА
Теорема. Площадь поверхности конуса, радиус основания которого равен R и образующая равна b, выражается формулой
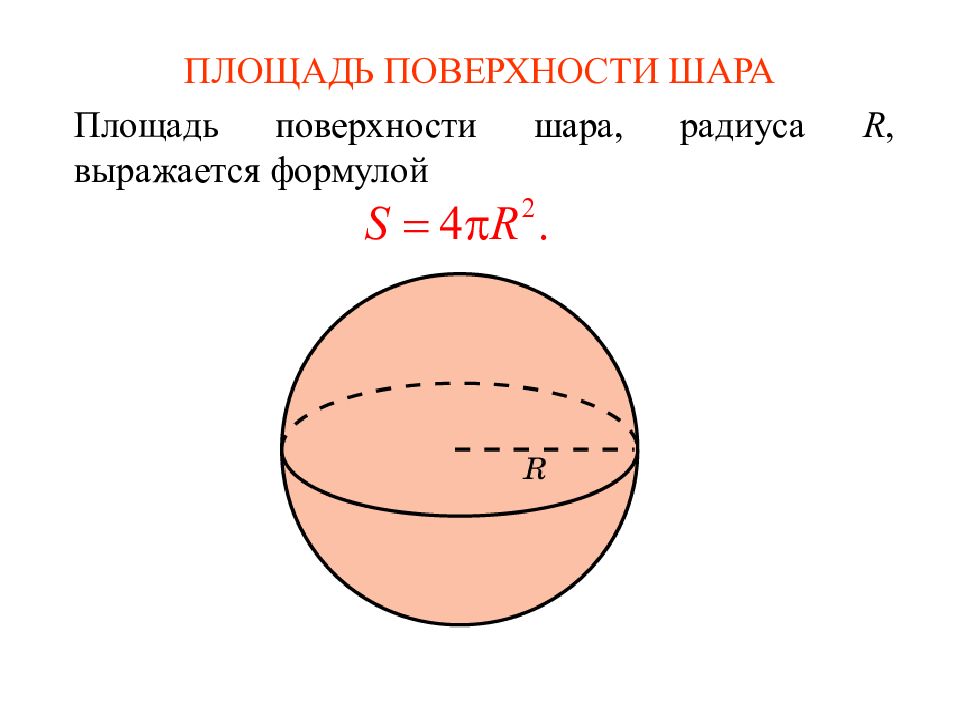
Слайд 4: ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРА
Площадь поверхности шара, радиус а R, выражается формулой
Слайд 6: Упражнение 2
Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Ответ. 22. Решение. Поверхность многогранника состоит из двух квадратов площад и 4, четырех прямоугольников площад и 2 и двух невыпуклых шестиугольников площад и 3. Следовательно, площадь поверхности многогранника равна 22. Упражнение 2
Слайд 7: Упражнение 3
Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Ответ. 22. Решение. Поверхность многогранника состоит из двух квадратов площад и 4, четырех прямоугольников площад и 2, и двух невыпуклых шестиугольников площад и 3. Следовательно, площадь поверхности многогранника равна 22. Упражнение 3
Слайд 8: Упражнение 4
Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Ответ. 22. Решение. Поверхность многогранника состоит из двух квадратов площад и 4, четырех прямоугольников площад и 2 и двух невыпуклых шестиугольников площад и 3. Следовательно, площадь поверхности многогранника равна 22. Упражнение 4
Слайд 9: Упражнение 5
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ. 38. Решение. Поверхность многогранника состоит из квадрат а площад и 9, семи прямоугольников площади которых равны 3, и двух невыпуклых восьми угольников площад и которых равны 4. Следовательно, площадь поверхности многогранника равна 38. Упражнение 5
Слайд 10: Упражнение 6
Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Ответ. 24. Решение. Поверхность многогранника состоит из трех квадратов площад и 4, трех квадратов площад и 1 и трех невыпуклых шестиугольников площад и 3. Следовательно, площадь поверхности многогранника равна 2 4. Упражнение 6
Слайд 11: Упражнение 7
Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Ответ. 92. Решение. Поверхность многогранника состоит из двух квадратов площад и 16, прямоугольника площади 12, трех прямоугольников площади 4, двух прямоугольников площади 8, и двух невыпуклых восьми угольников площад и 10. Следовательно, площадь поверхности многогранника равна 92. Упражнение 7
Слайд 12: Упражнение 8
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ. 48. Упражнение 8
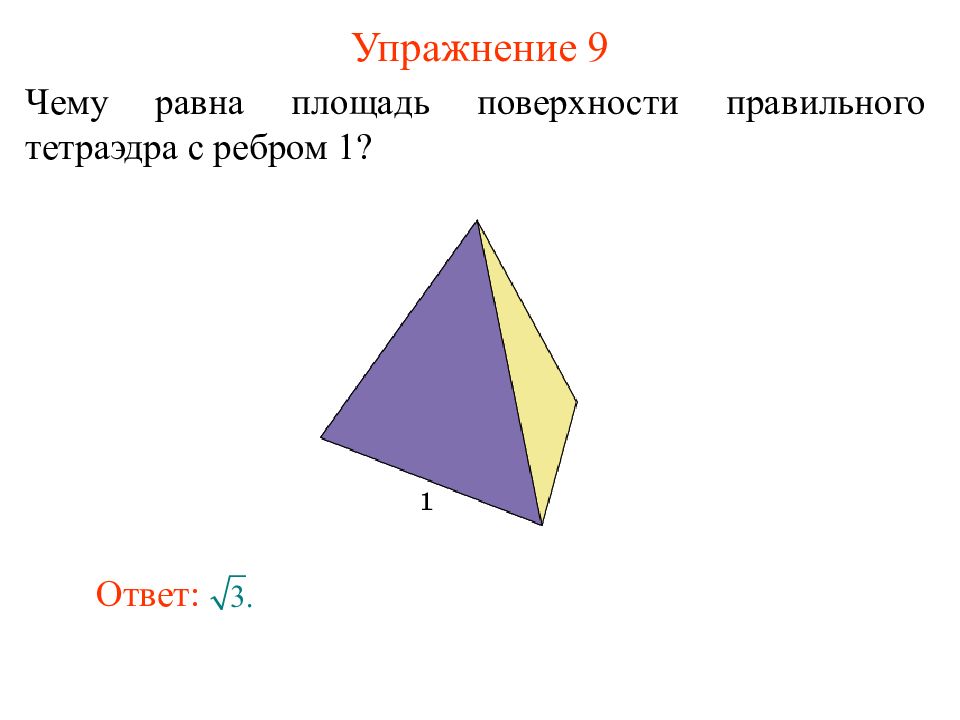
Слайд 13: Упражнение 9
Чему равна площадь поверхности правильного тетраэдра с ребром 1? Ответ:
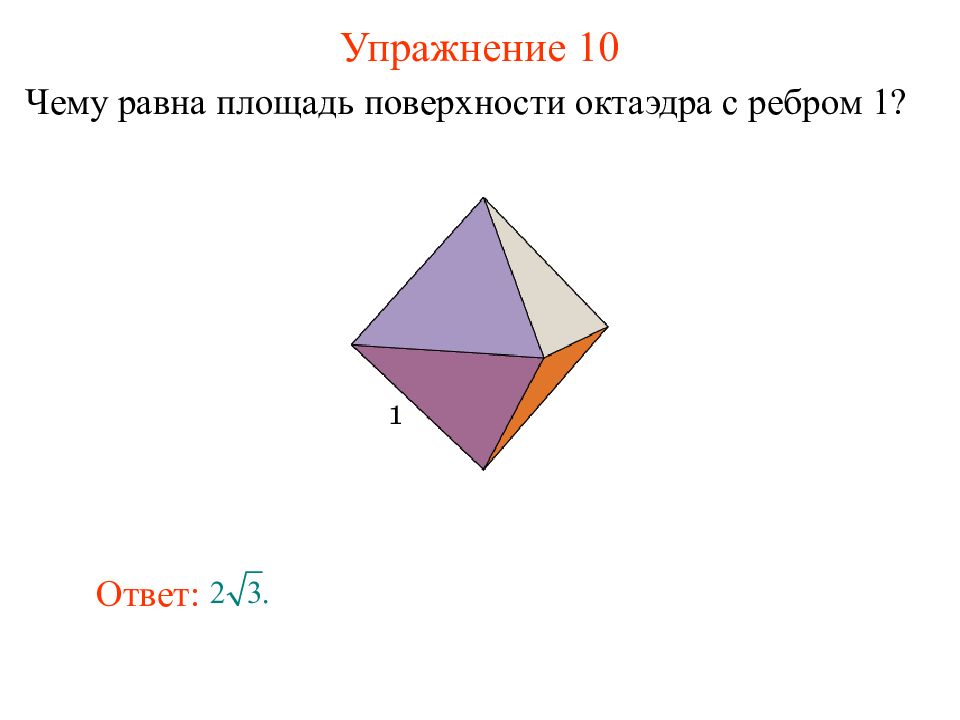
Слайд 14: Упражнение 10
Чему равна площадь поверхности октаэдра с ребром 1? Ответ:
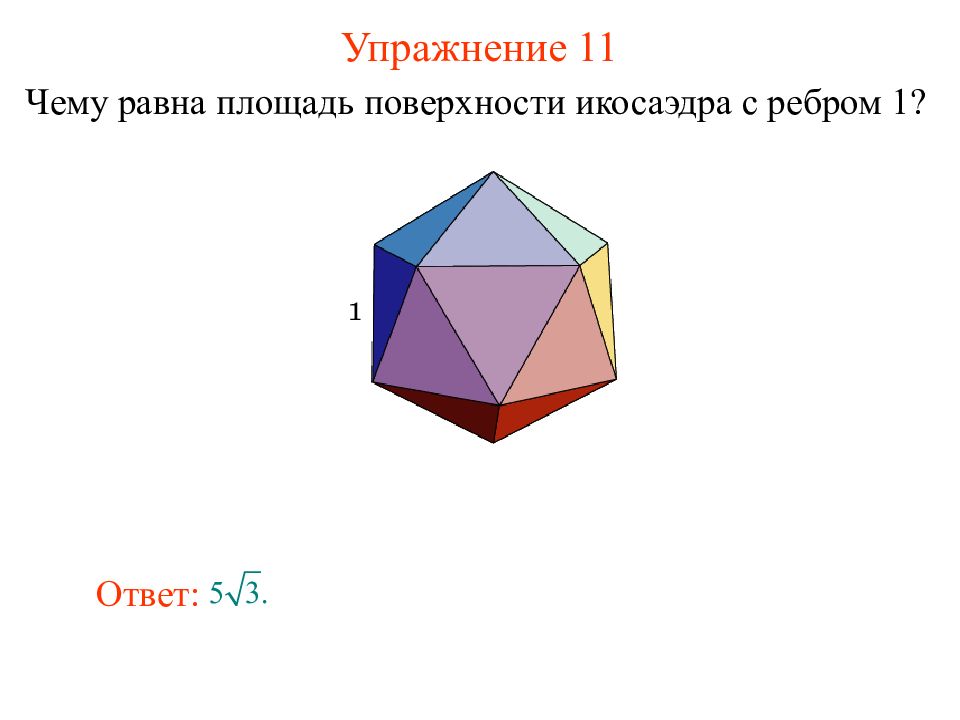
Слайд 15: Упражнение 11
Чему равна площадь поверхности икосаэдра с ребром 1? Ответ:
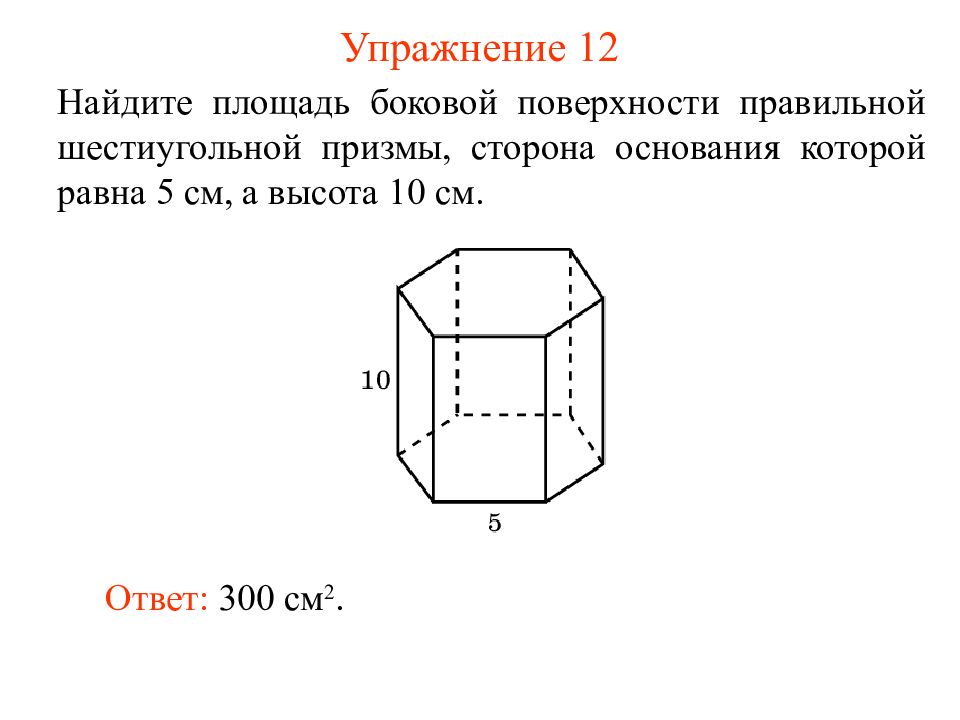
Слайд 16: Упражнение 12
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5 см, а высота 10 см. Ответ: 300 см 2.
Слайд 17: Упражнение 13
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см, высота призмы равна 10 см. Найдите площадь поверхности данной призмы. Ответ: 132 см 2.
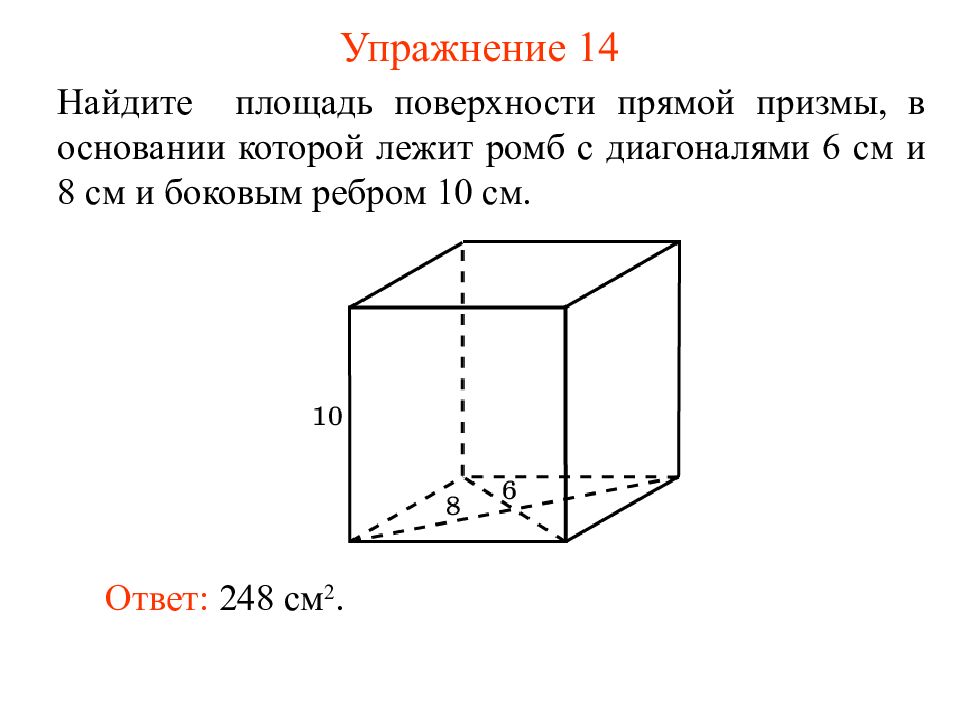
Слайд 18: Упражнение 14
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями 6 см и 8 см и боковым ребром 10 см. Ответ: 248 см 2.
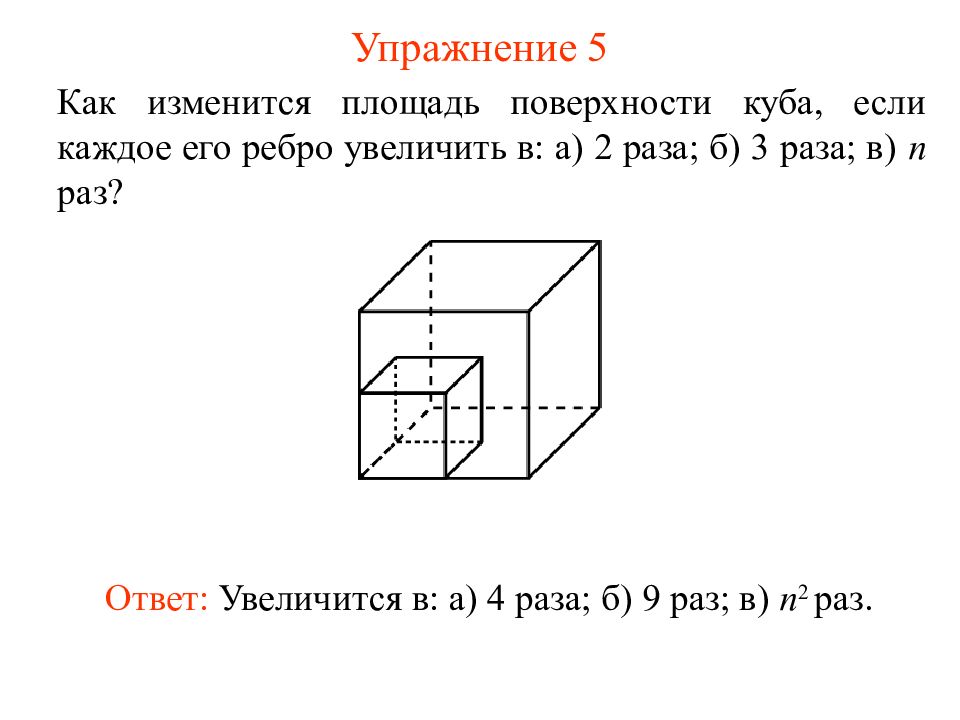
Слайд 19: Упражнение 5
Как изменится площадь поверхности куба, если каждое его ребро увеличить в: а) 2 раза; б) 3 раза; в) n раз? Ответ: Увеличится в: а) 4 раза; б) 9 раз; в) n 2 раз.
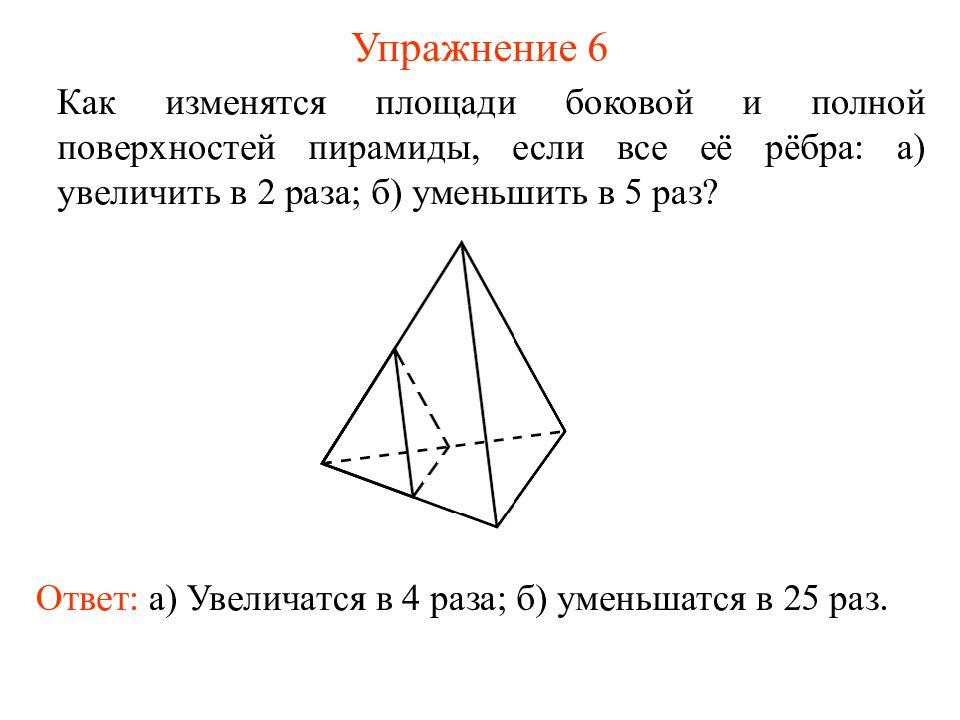
Слайд 20: Упражнение 6
Как изменятся площади боковой и полной поверхностей пирамиды, если все её рёбра: а) увеличить в 2 раза; б) уменьшить в 5 раз? Ответ: а) Увеличатся в 4 раза; б) уменьшатся в 25 раз.
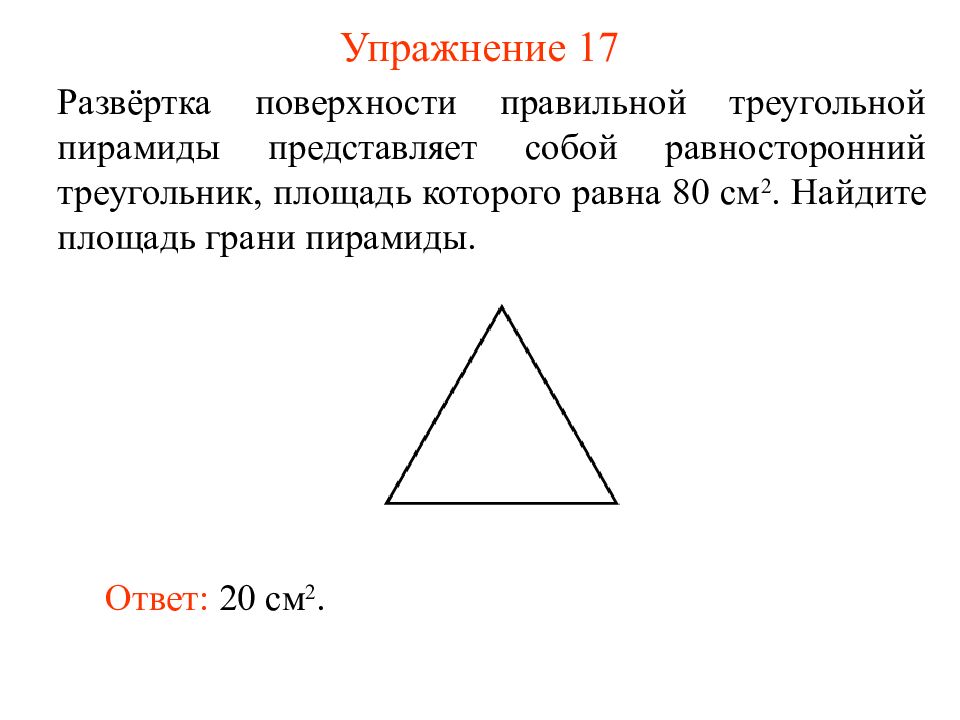
Слайд 21: Упражнение 17
Развёртка поверхности правильной треугольной пирамиды представляет собой равносторонний треугольник, площадь которого равна 80 см 2. Найдите площадь грани пирамиды. Ответ: 20 см 2.
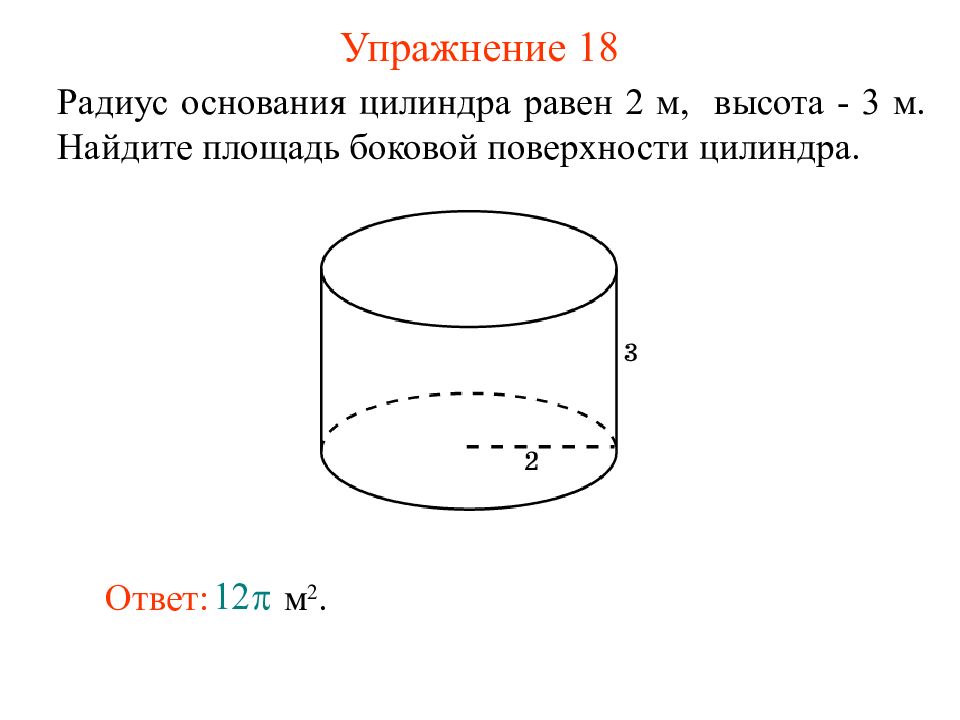
Слайд 22: Упражнение 18
Радиус основания цилиндра равен 2 м, высота - 3 м. Найдите площадь боковой поверхности цилиндра. Ответ: м 2.
Слайд 23: Упражнение 19
Площадь осевого сечения цилиндра равна 4 м 2. Найдите площадь боковой поверхности цилиндра. Ответ: м 2.
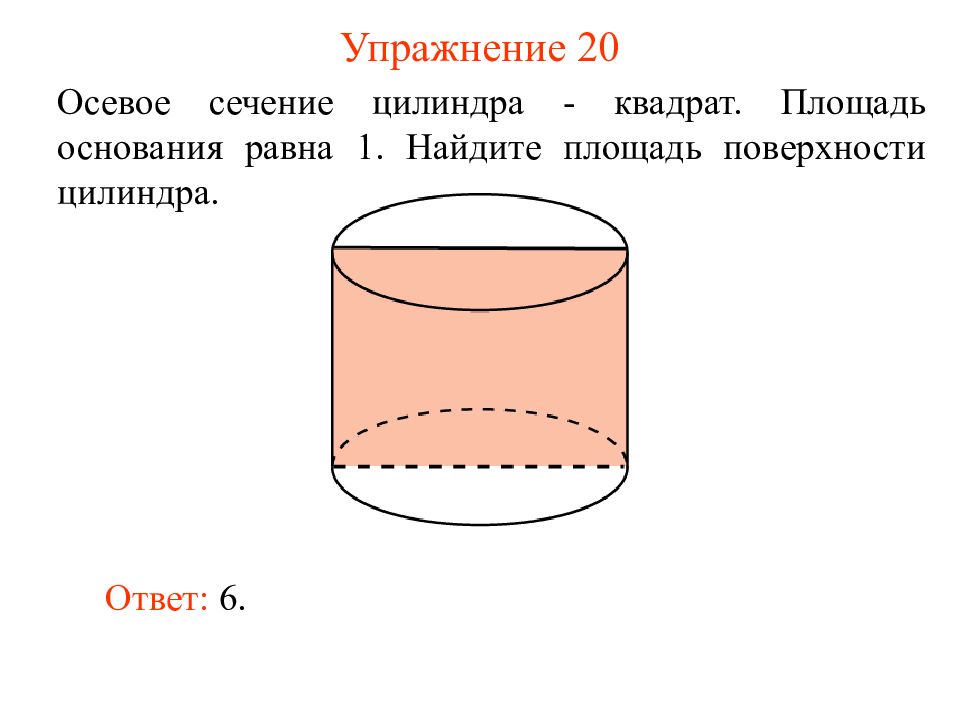
Слайд 24: Упражнение 20
Осевое сечение цилиндра - квадрат. Площадь основания равна 1. Найдите площадь поверхности цилиндра. Ответ: 6.
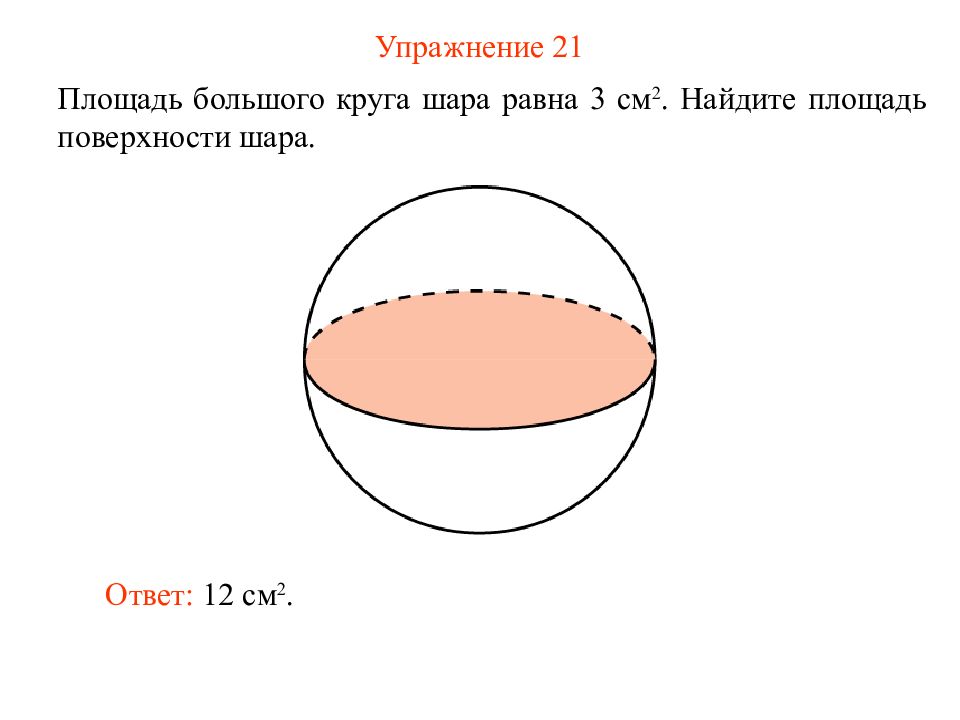
Слайд 25: Упражнение 21
Площадь большого круга шара равна 3 см 2. Найдите площадь поверхности шара. Ответ: 12 см 2.
Слайд 26: Упражнение 22
Как изменится площадь поверхности шара, если увеличить радиус шара в: а) 2 раза; б) 3 раза; в) n раз? Ответ: Увеличится в: а) 4 раза; б) 9 раз; в) n 2 раз.
Слайд 27: Упражнение 23
Площади поверхностей двух шаров относятся как 4 : 9. Найдите отношение их диаметров. Ответ: 2:3.
Последний слайд презентации: ПЛОЩАДЬ ПОВЕРХНОСТИ МНОГОГРАННИКА: Упражнение 24
Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей. Ответ. 10. Решение. Площади поверхностей данных шаров равны и. Их сумма равна. Следовательно, радиус шара, площадь поверхности которого равна этой сумме, равен 10. Упражнение 24