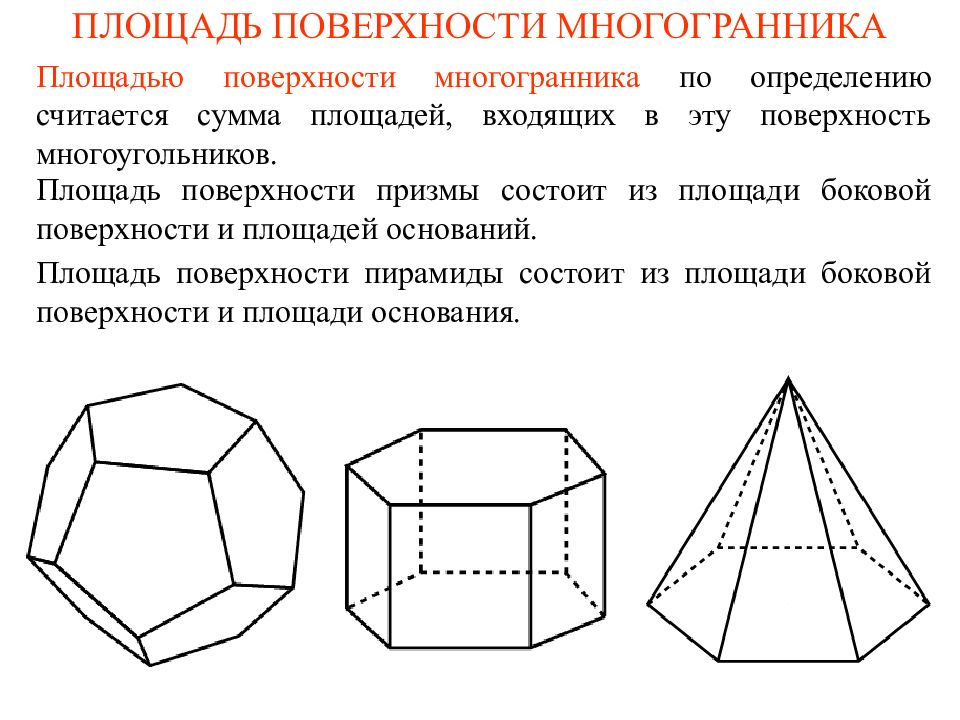
Слайд 3
Какой многогранник называется призмой? Какая призма называется прямой? Какая призма называется правильной? Что называется площадью поверхности призмы? Как вычисляется площадь боковой поверхности прямой призмы ? Как вычислить площадь полной поверхности призмы? Дайте определение угла между прямой и плоскостью Сформулируйте теорему о трех перпендикулярах Геометрическая разминка
Слайд 4
Площадь боковой поверхности прямой призмы Площадь прямоугольного треугольника Площадь правильного треугольника Площадь квадрата Площадь полной поверхности призмы Площадь правильного шестиугольника Теорема Пифагора 1 2 3 4 5 6 7 Установите соответствие
Слайд 5
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 10 и 24. Площадь ее поверхности равна 1680. Найдите высоту призмы. Ответ: 26. 24 10 Решение: Найдем гипотенузы прямоугольного треугольника по теореме Пифагора: с=26 2. S осн. = ½ ab = ½ · 10 · 24 = 120 3. S бок. = Р осн. · h = ( 2 4 + 10 + 26 ) · h = 60 h 4. S пов. = S осн. + S бок. Имеем, 1680 = 120 + 60 h, откуда найдем высоту призмы 60 h = 1680 – 240 60 h = 1560 h = 26. Найди ошибку
Слайд 6
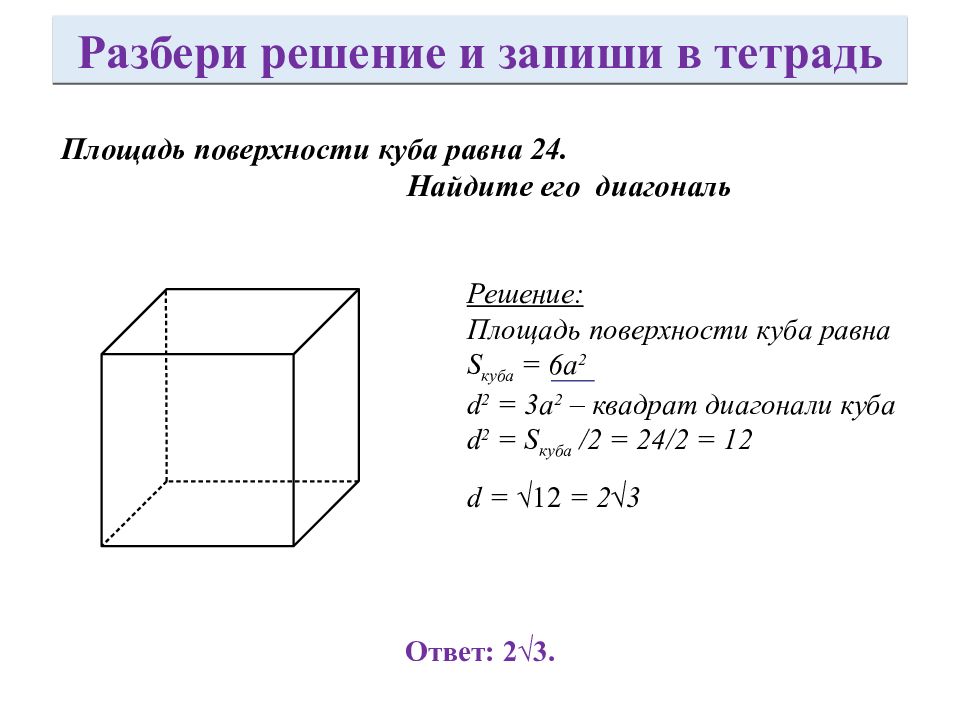
Площадь поверхности куба равна 24. Найдите его диагональ Решение: Площадь поверхности куба равна S куба = 6а 2 d 2 = 3a 2 – квадрат диагонали куба d 2 = S куба /2 = 24 /2 = 12 d = √ 12 = 2√3 Ответ: 2√3. Разбери решение и запиши в тетрадь
Слайд 7
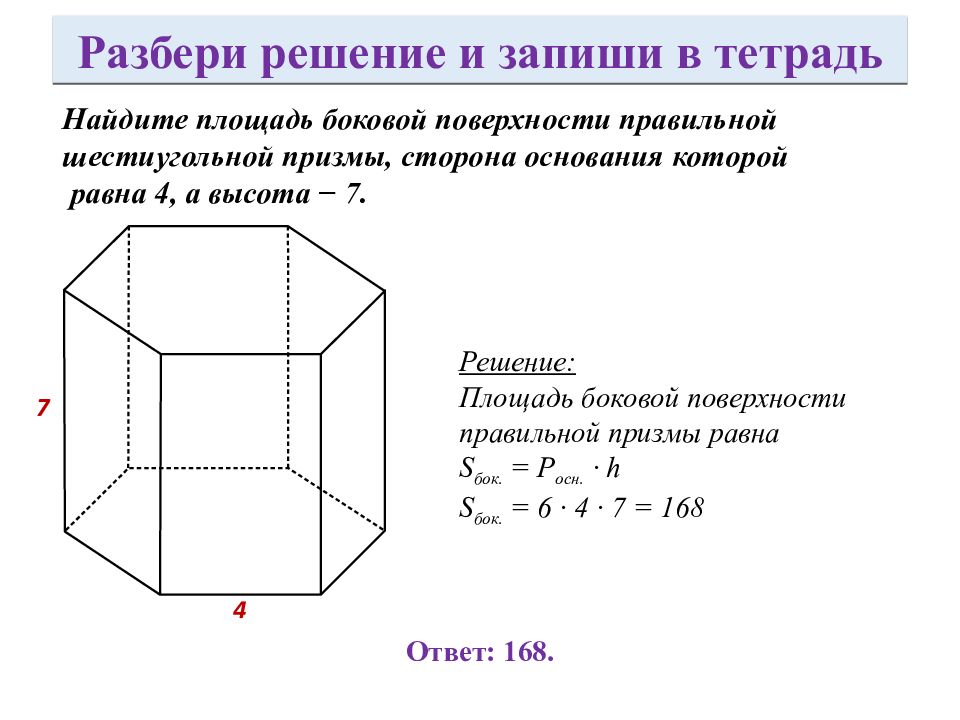
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 4, а высота − 7. Решение: Площадь боковой поверхности правильной призмы равна S бок. = Р осн. · h S бок. = 6 · 4 · 7 = 16 8 Ответ: 168. 7 4 Разбери решение и запиши в тетрадь
Слайд 8
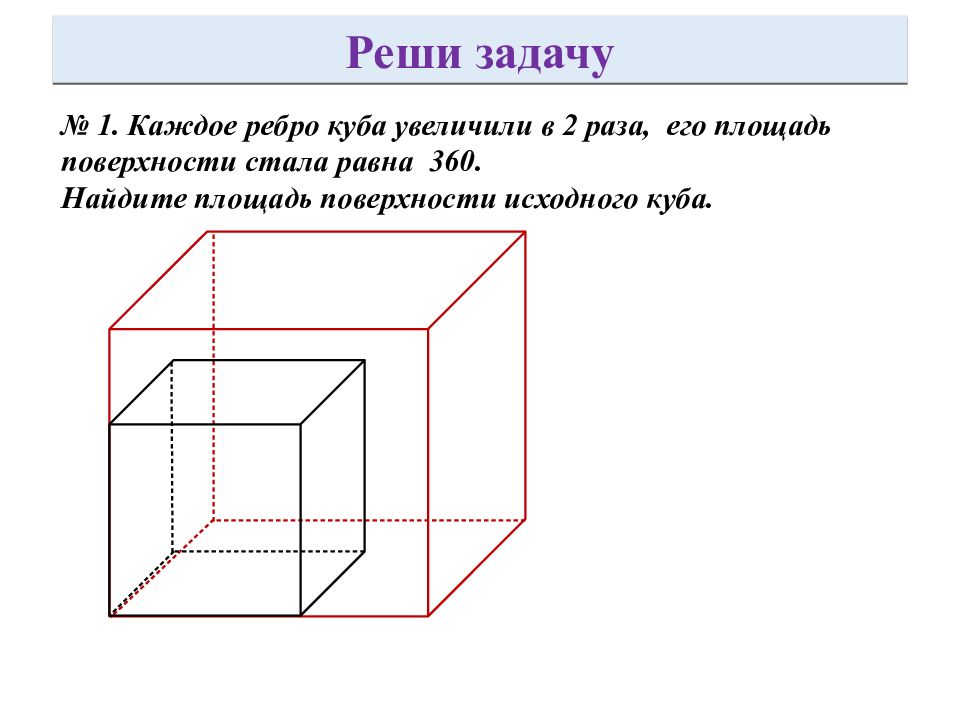
№ 1. Каждое ребро куба увеличили в 2 раза, его площадь поверхности стала равна 360. Найдите площадь поверхности исходного куба. Реши задачу
Слайд 9
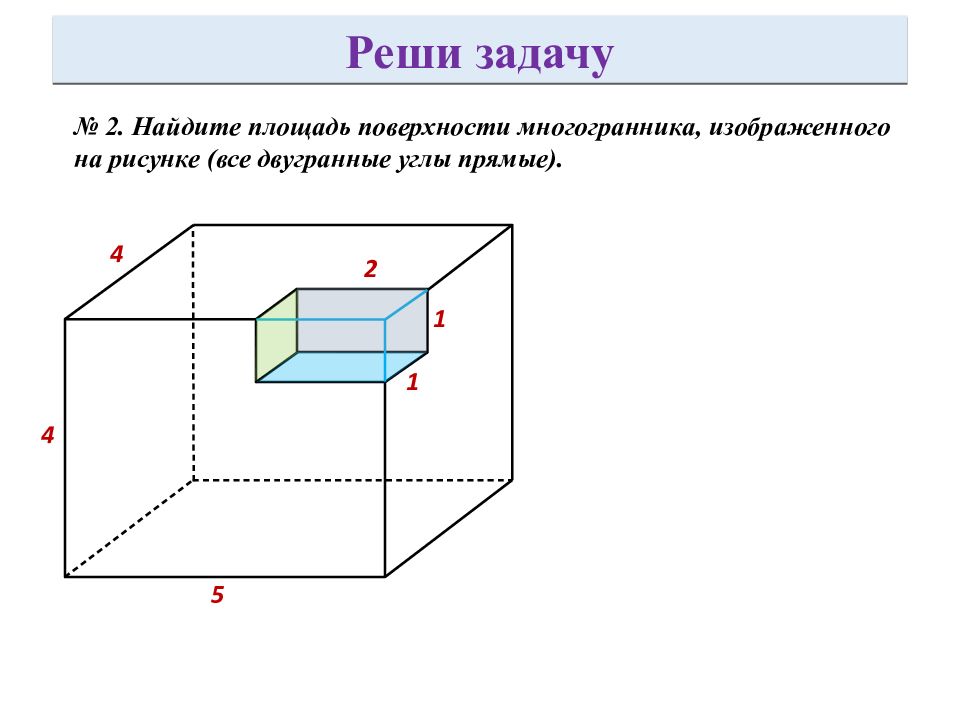
№ 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 5 1 4 2 4 1 Реши задачу
Слайд 10
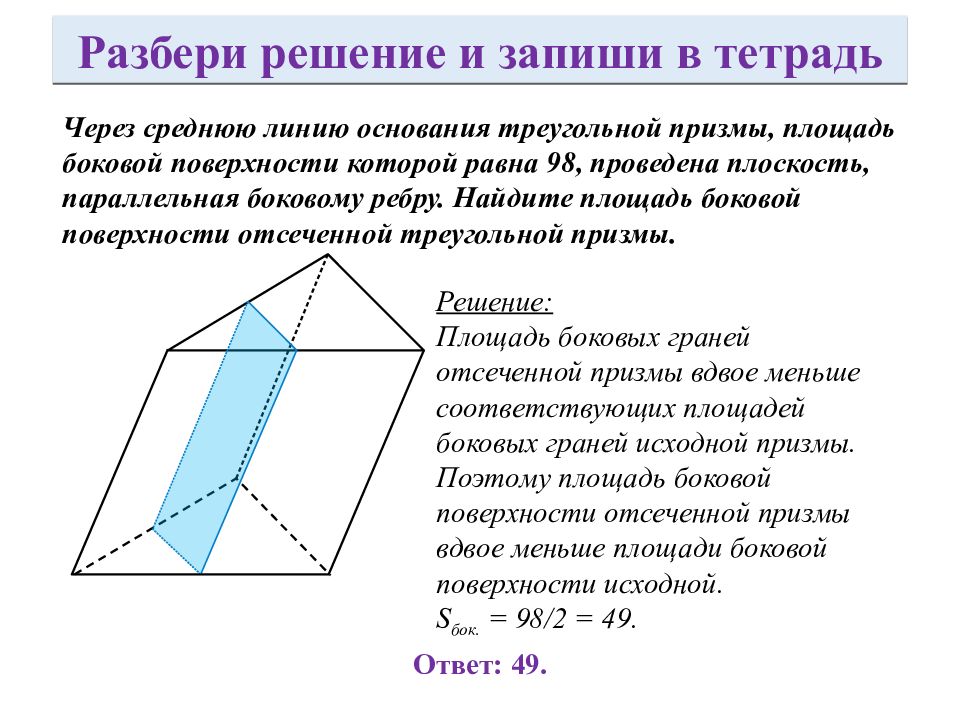
Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 98, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы. Решение: Площадь боковых граней отсеченной призмы вдвое меньше соответствующих площадей боковых граней исходной призмы. Поэтому площадь боковой поверхности отсеченной призмы вдвое меньше площади боковой поверхности исходной. S бок. = 98/2 = 49. Ответ: 49. Разбери решение и запиши в тетрадь
Слайд 11
Реши задачи № 4. В сосуд, имеющий форму правильной треугольной призмы, налили 1100 см 3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 29 см. Чему равен объем детали? Ответ выразите в см 3.
Слайд 12
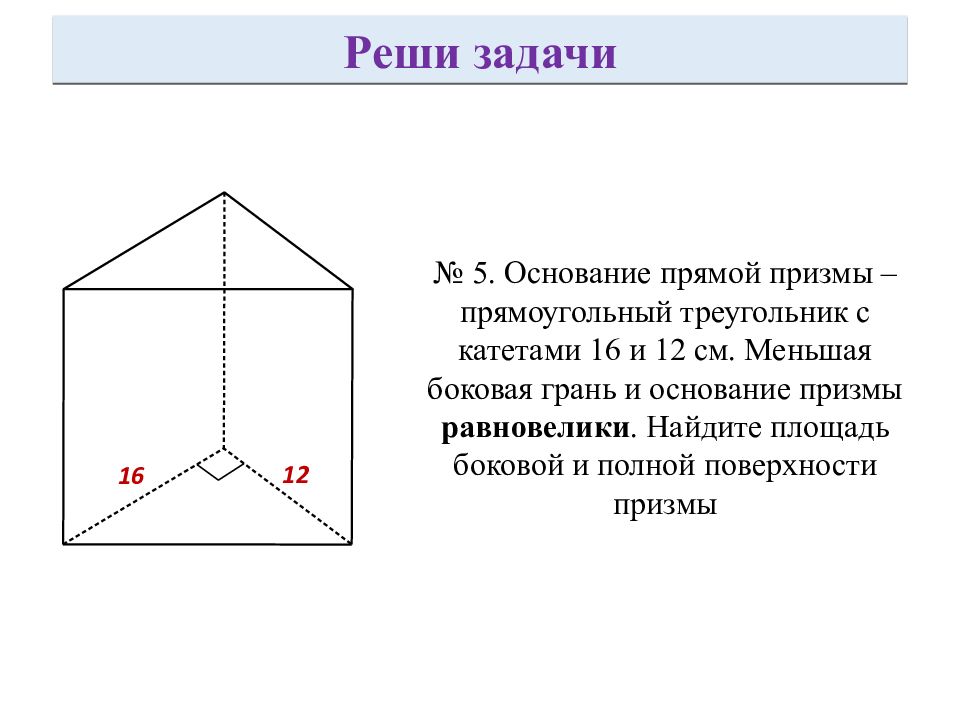
16 12 № 5. Основание прямой призмы – прямоугольный треугольник с катетами 16 и 12 см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы Реши задачи
Последний слайд презентации: Решение задач по теме «Призма»
№ 6. Коллекционер заказал аквариум, имеющий форму правильной шестиугольной призмы. Сколько квадратных метров стекла необходимо для изготовления аквариума, если сторона основания 0,5 м, а высота 1,2 м? Ответ округлите до сотых. Реши задачи