Подготовка к ОГЭ по математике. Окружность.
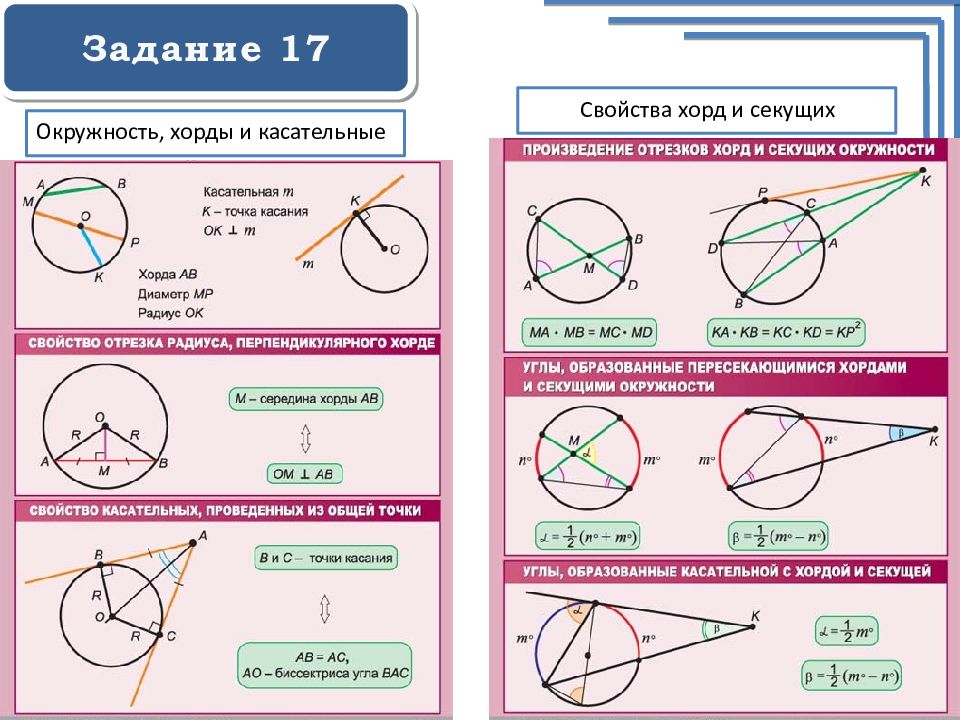
Задание 17 Основные факты по теме «Окружность и круг» Задание № 17 представляет собой задачу, связанную с окружностью и ее элементами. Рассмотрим примеры решения задач по теме «Окружность». • центральный угол равен дуге окружности, на которую он опирается; • вписанный угол окружности равен половине центрального угла и измеряется половиной дуги, на которую он опирается; • вписанный угол, опирающийся на диаметр окружности, равен 90◦; • касательная к окружности перпендикулярна к радиусу этой окружности, проведённому в точку касания; • отрезки касательных, проведённых к окружности из одной точки, равны;
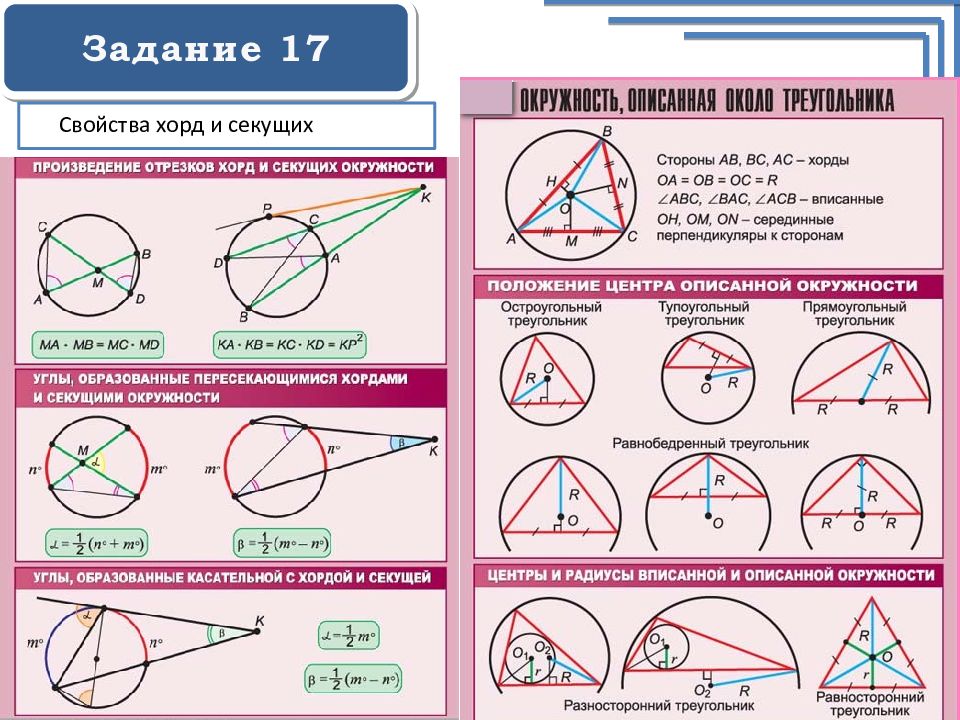
Задание 17 Основные факты по теме «Окружность и круг» • центр окружности, вписанной в угол, лежит на биссектрисе этого угла; • угол между двумя секущими к окружности, пересекающимися внутри окружности, равен полусумме дуг, высекаемых на окружности вертикальными углами, образованными этими секущими; • угол между двумя секущими к окружности, пересекающимися вне окружности, равен полуразности дуг, высекаемых на окружности углом, образованным этими секущими; • две окружности имеют ровно две общие точки (пересекаются в двух точках) в том и только том случае, если расстояние между их центрами меньше суммы радиусов этих окружностей, но больше разности большего и меньшего радиусов; • две окружности имеют ровно одну общую точку (касаются) в том и только том случае, если расстояние между их центрами равно сумме радиусов этих окружностей (внешнее касание) либо равно разности большего и меньшего радиусов этих окружностей (внутреннее касание); • формула длины окружности, где r —радиус окружности; • формула площади круга, где r —радиус круга.
Задание 17 Основные факты по теме «Окружность и круг»
Задание 17 Основные факты по теме «Окружность и круг»
Задание 17 Окружность, хорды и касательные Свойства хорд и секущих
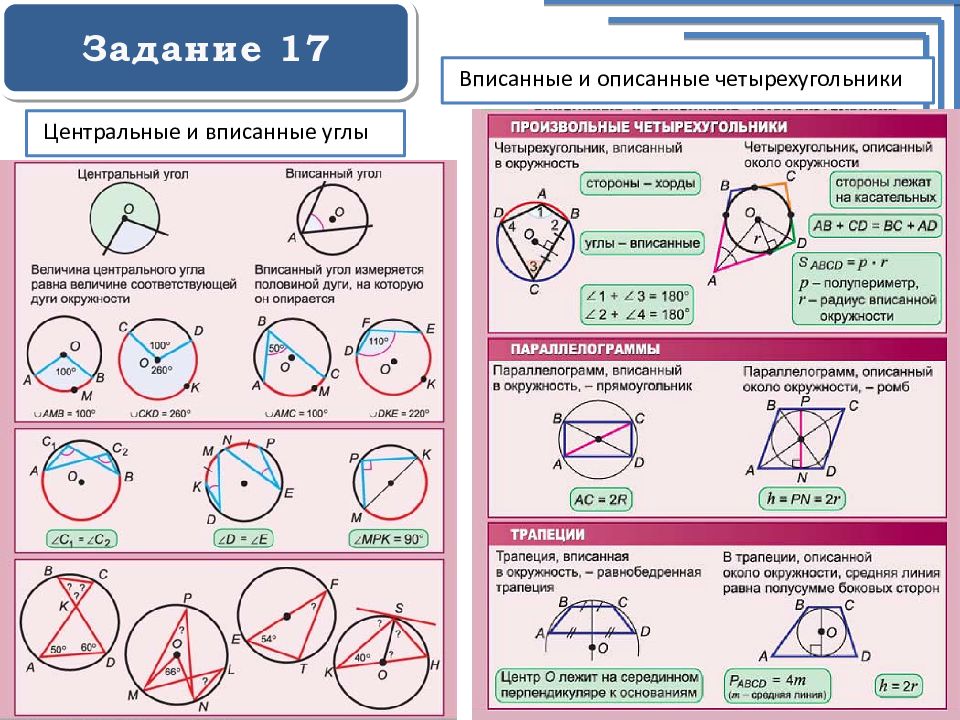
Задание 17 Центральные и вписанные углы Вписанные и описанные четырехугольники
Задание 17 Свойства хорд и секущих
Задание 17
Задание 17
Задание 17 Пример 1. Окружность пересекает стороны угла величиной 33 ◦с вершиной C в точках A, E, D и B, как показано на рисунке. Найдите угол ADB, если угол EAD равен 22◦. Ответ дайте в градусах. Решение. Рассмотрим треугольник ACD. Угол ADB является для него внешним при вершине D, значит, он равен сумме двух других углов треугольника, не смежных с ним: Ответ: 55. Пример 2. Точки А, В, С и D, последовательно расположенные на окружности в указанном порядке, делят ее на четыре дуги, градусные меры которых относятся как 1:2:7:8 (дуга АВ – наименьшая). Найдите градусную меру дуги В D, содержащей точку С.
Задание 17 Пример 3. Решение. Рассмотрим треугольник ВОС. ВО=ОС= R, следовательно, треугольник ВОС равнобедренный, ∠ОСВ = ∠ОВС = ∠ АО D = ∠ ВОС (как вертикальные), ∠ АО D = ∠ ВОС= 180 – 38*2=180-76=104. Ответ: 104.
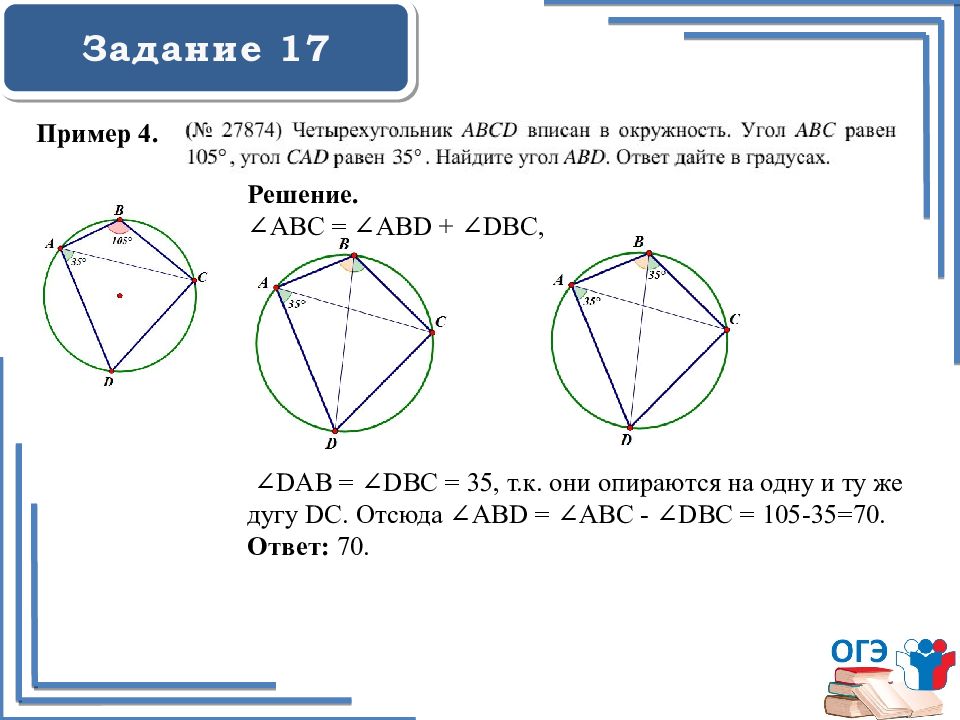
Задание 17 Пример 4. Решение. ∠АВС = ∠АВ D + ∠ D ВС, ∠ D АВ = ∠ D ВС = 35, т.к. они опираются на одну и ту же дугу D С. Отсюда ∠АВ D = ∠АВС - ∠ D ВС = 105-35=70. Ответ: 70.
Задание 17 Пример 5 Решение. Чтобы решить эту задачу нам нужно вспомнить два факта: 1. Вписанный угол, который опирается на диаметр, равен. И наоборот, если вписанный угол равен, то он опирается на диаметр. Следовательно, гипотенуза АВ прямоугольного треугольника АВС является диаметром описанной около треугольника окружности, то есть 2. центр описанной около прямоугольного треугольника окружности совпадает с серединой гипотенузы. Найдем по теореме Пифагора гипотенузу АВ Отсюда АВ = 5, тогда R=2,5. Ответ: 2,5.
Задание 17 Пример 6 Решение. ∠ NMB опирается на дугу NB. Найдем величину этой дуги. ∠ NBA опирается на дугу NA. Вписанный угол равен половине величины дуги, на которую он опирается, следовательно, NA = 36*2= 72. АВ – диаметр окружности, поэтому градусная мера дуги ANB равна 180. отсюда дуга NB =180 – 72 = 108. Тогда ∠ MNB = 108 : 2 = 54. Ответ: 54.
