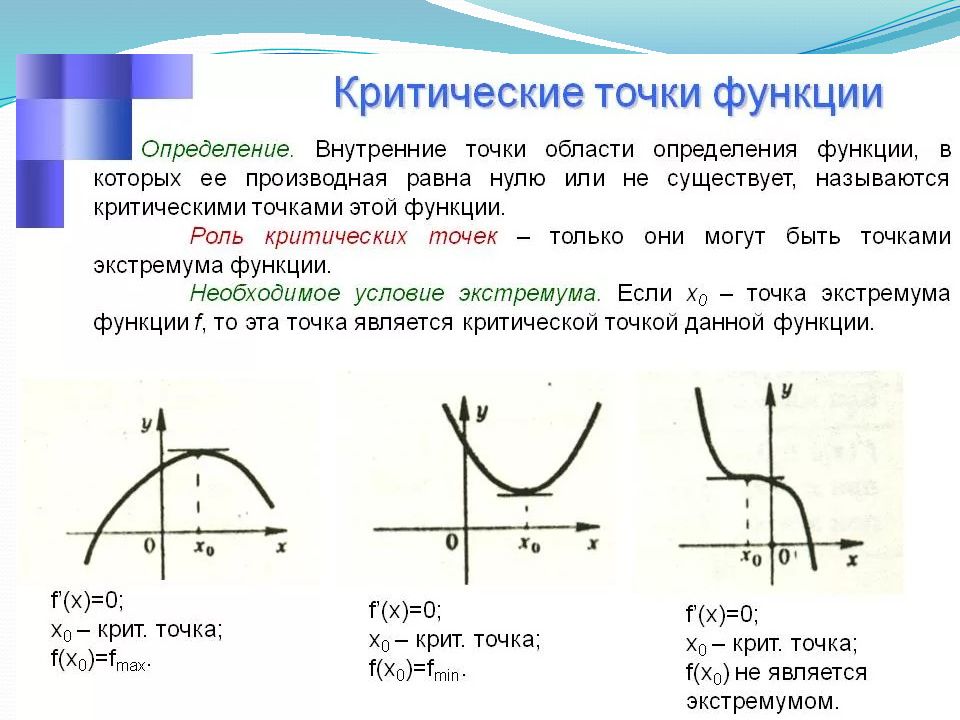
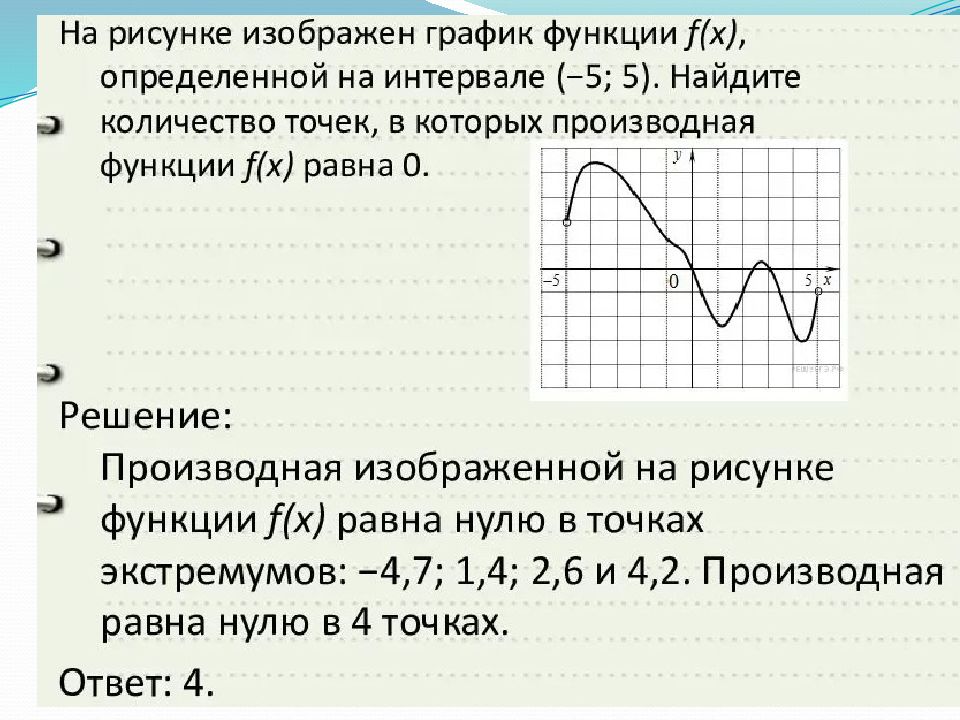
Слайд 2
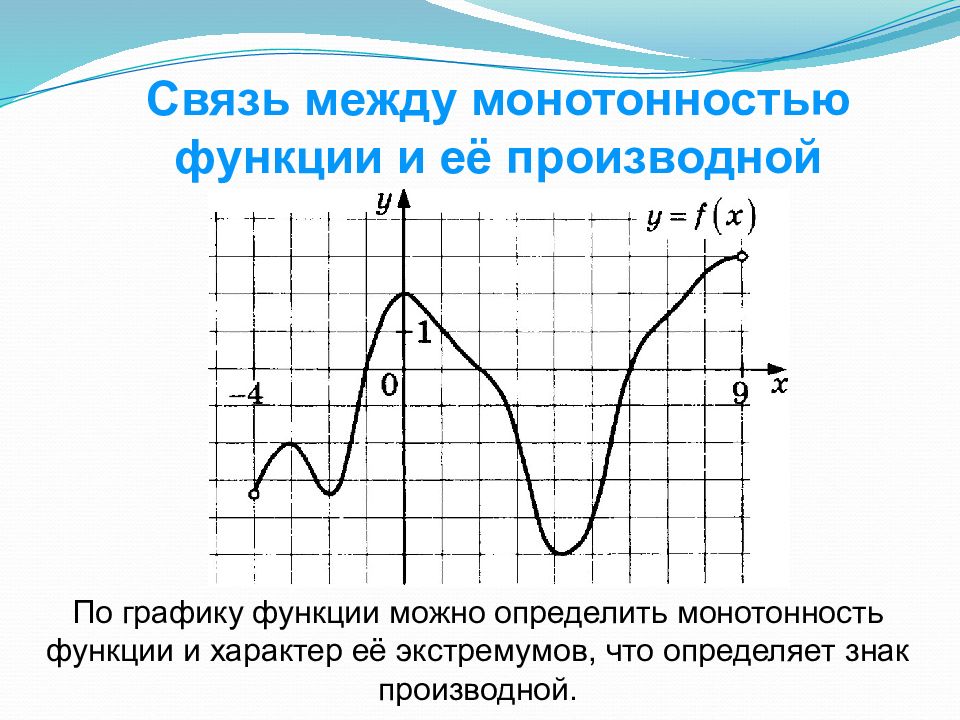
Связь между монотонностью функции и её производной По графику функции можно определить монотонность функции и характер её экстремумов, что определяет знак производной.
Слайд 3
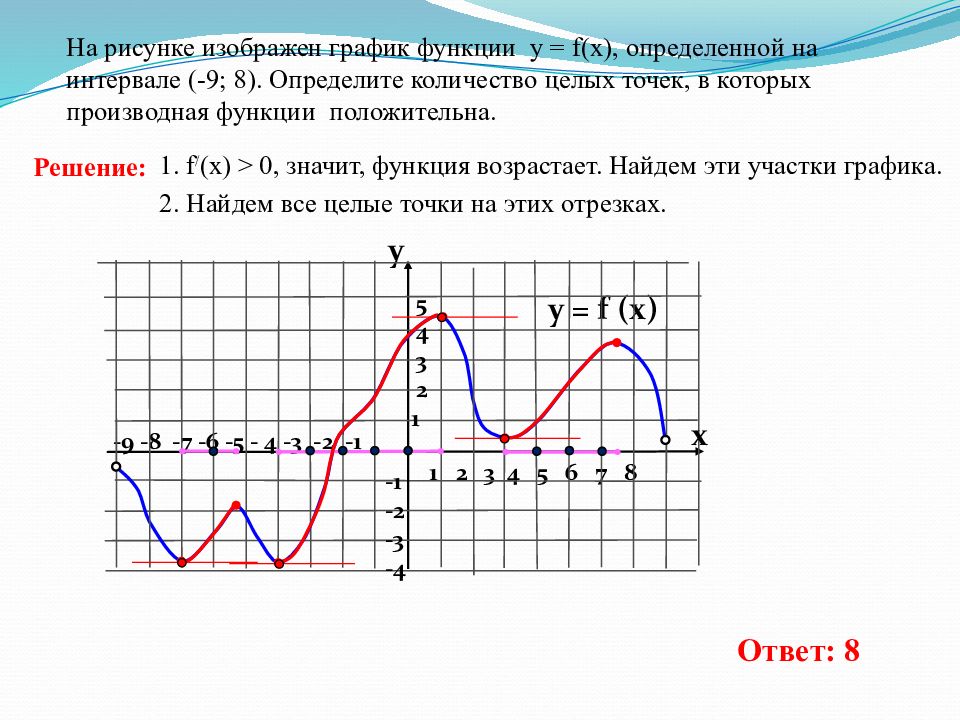
-9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 На рисунке изображен график функции у = f(x), определенной на интервале (-9; 8). Определите количество целых точек, в которых производная функции положительна. y = f (x) y x 5 4 3 2 1 -1 -2 -3 -4 1. f / (x) > 0, значит, функция возрастает. Найдем эти участки графика. 2. Найдем все целые точки на этих отрезках. Ответ: 8 Решение:
Слайд 4
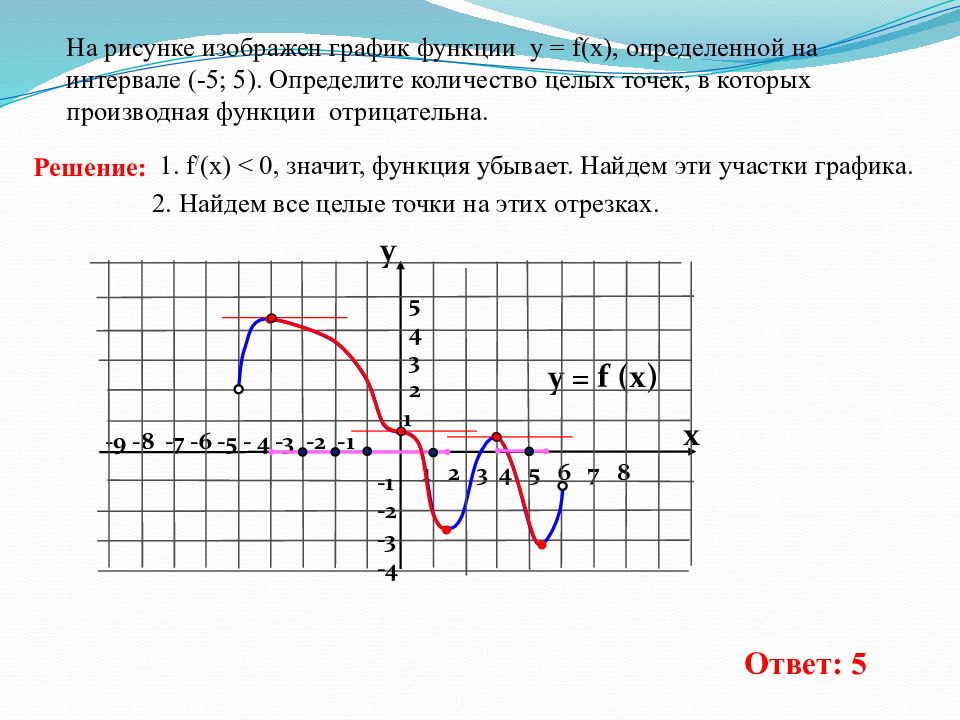
-9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 На рисунке изображен график функции у = f(x), определенной на интервале (-5; 5). Определите количество целых точек, в которых производная функции отрицательна. y = f (x) y x 5 4 3 2 1 -1 -2 -3 -4 1. f / (x) < 0, значит, функция убывает. Найдем эти участки графика. 2. Найдем все целые точки на этих отрезках. Ответ: 5 Решение:
Слайд 5
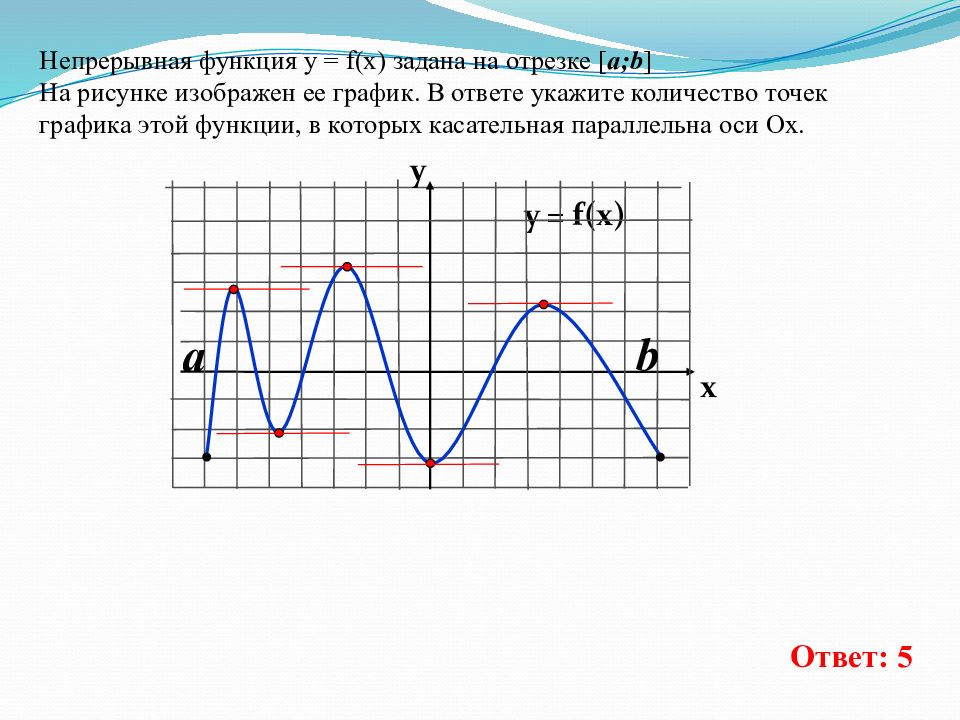
Непрерывная функция у = f(x) задана на отрезке [ a;b ] На рисунке изображен ее график. В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох. y = f(x) y x Ответ: 5 a b
Слайд 8
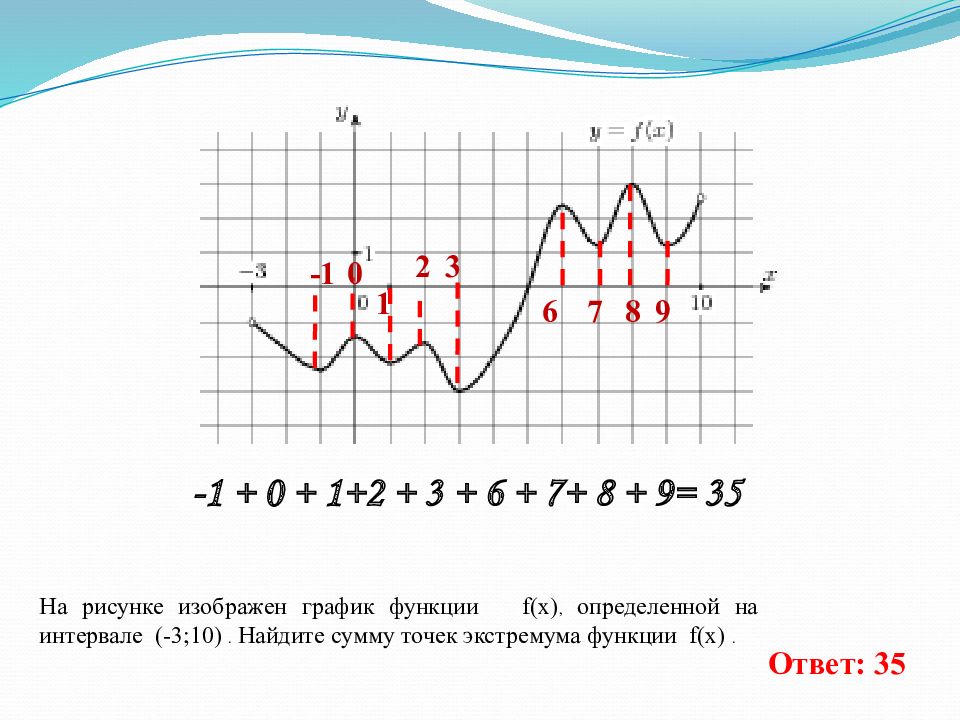
На рисунке изображен график функции f(x), определенной на интервале (-3;10). Найдите сумму точек экстремума функции f(x). -1 0 1 3 6 7 8 9 -1 + 0 + 1+2 + 3 + 6 + 7+ 8 + 9= 35 Ответ: 35 2
Слайд 9
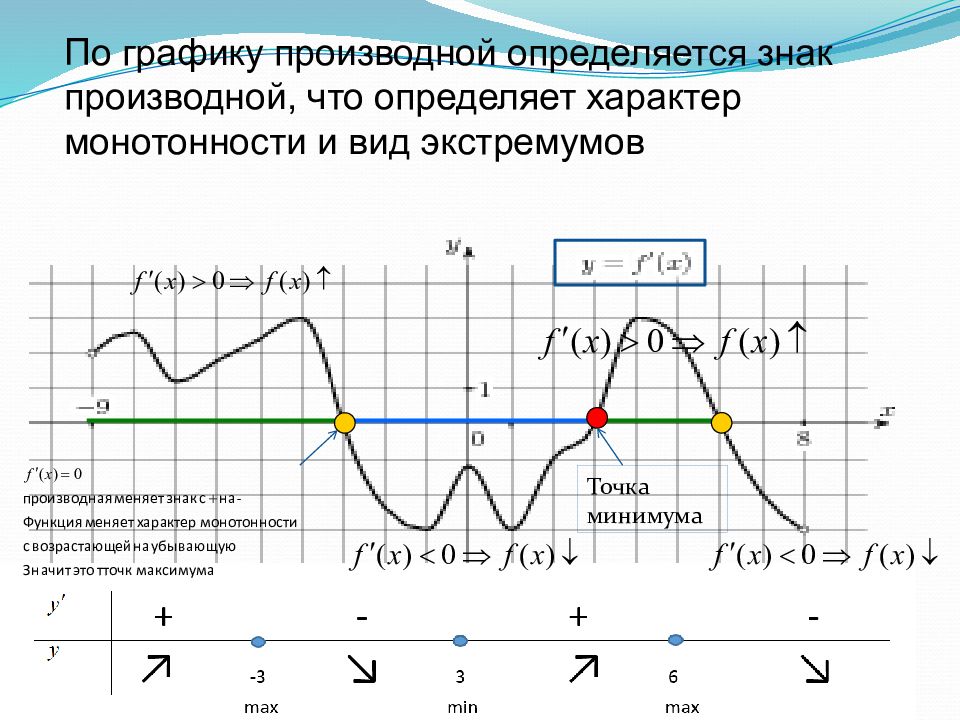
По графику производной определяется знак производной, что определяет характер монотонности и вид экстремумов Точка минимума
Слайд 10
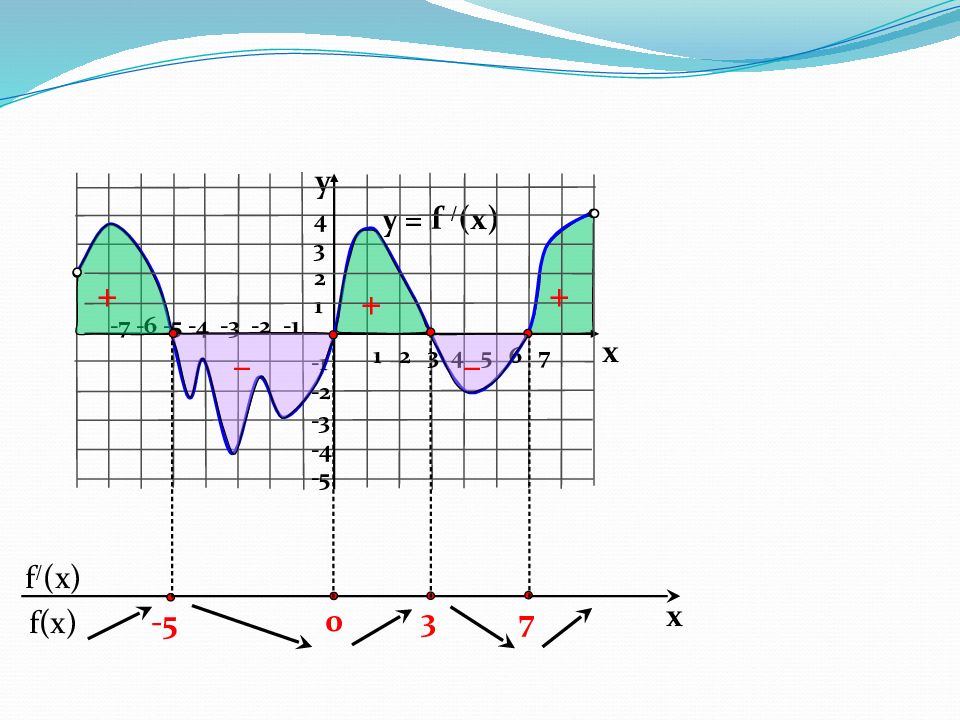
f(x) f / (x) x y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x 7 3 0 -5 + – – + +
Слайд 11
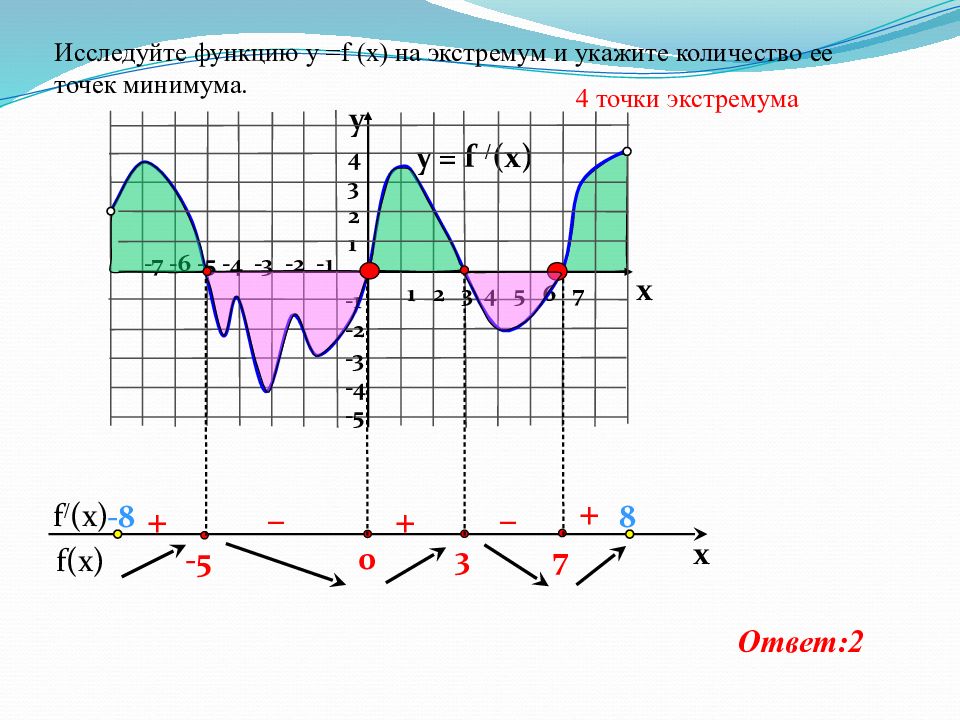
f(x) f / (x) x y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x 7 3 0 -5 + – – + + Исследуйте функцию у = f (x) на экстремум и укажите количество ее точек минимума. 4 точки экстремума Ответ:2 - 8 8
Слайд 12
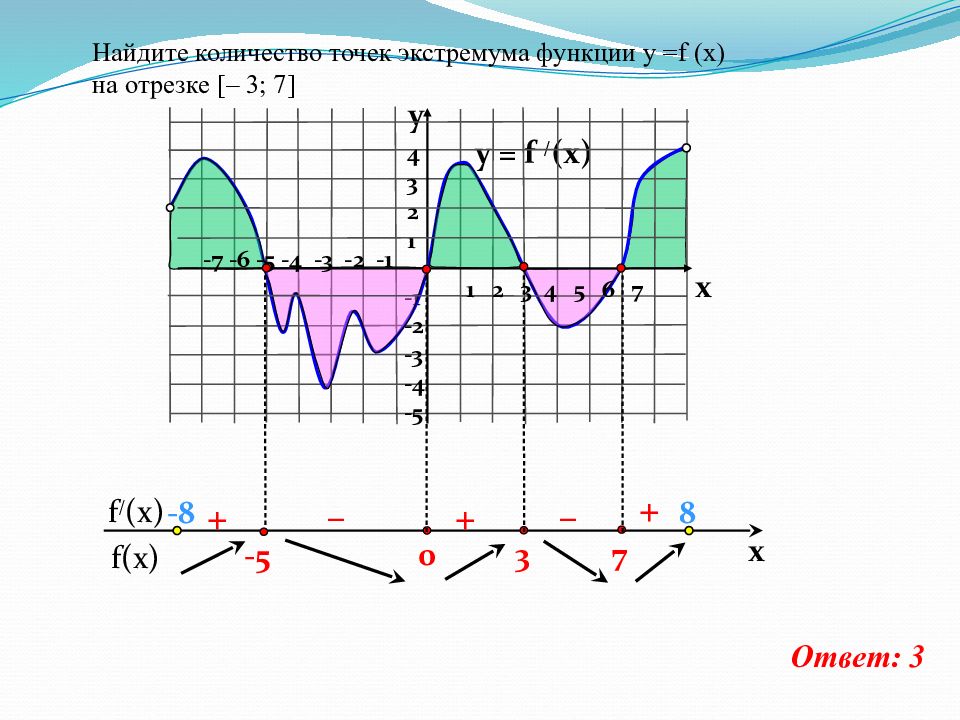
f(x) f / (x) x y = f / (x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + Найдите количество точек экстремума функции у = f (x) на отрезке [ – 3; 7 ] Ответ: 3 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -5 - 8 8 7 3 0
Слайд 13
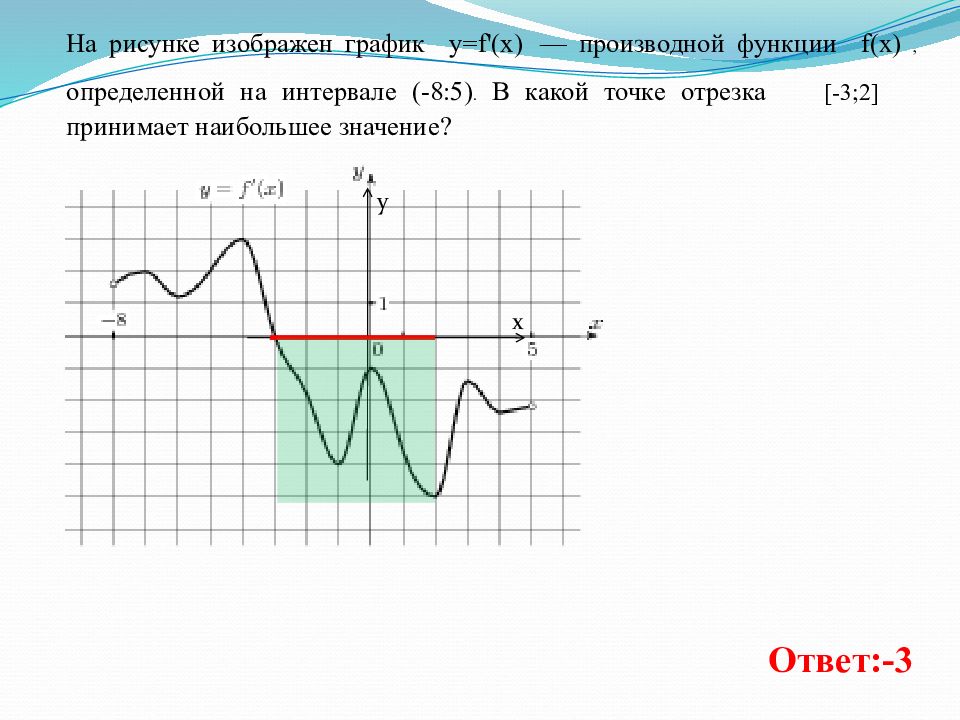
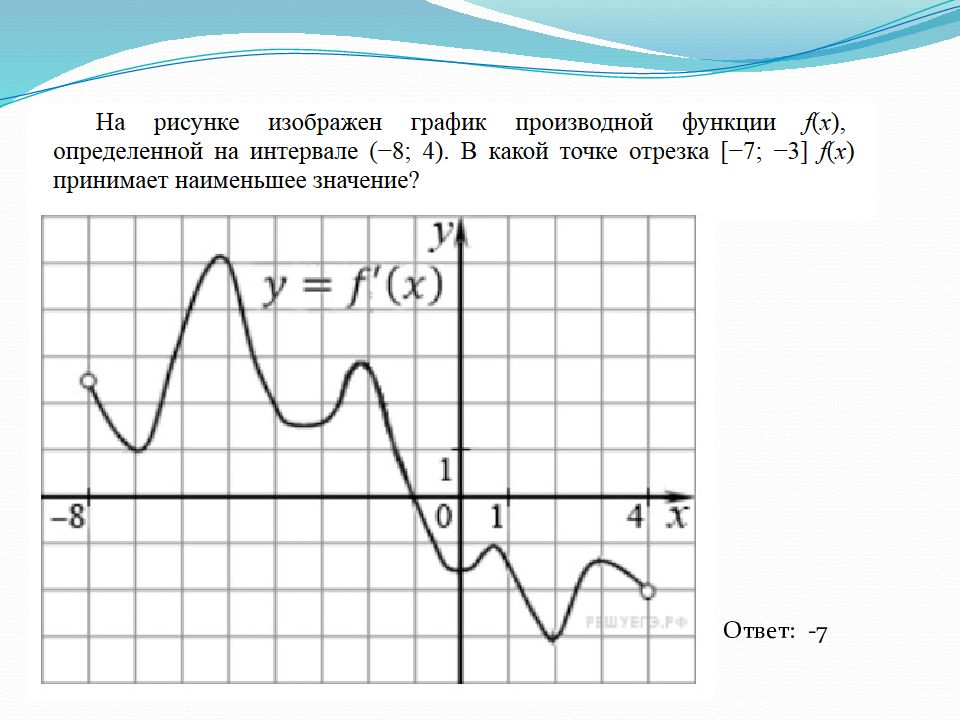
На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (-8:5). В какой точке отрезка [-3;2] принимает наибольшее значение? х у Ответ:-3
Слайд 15
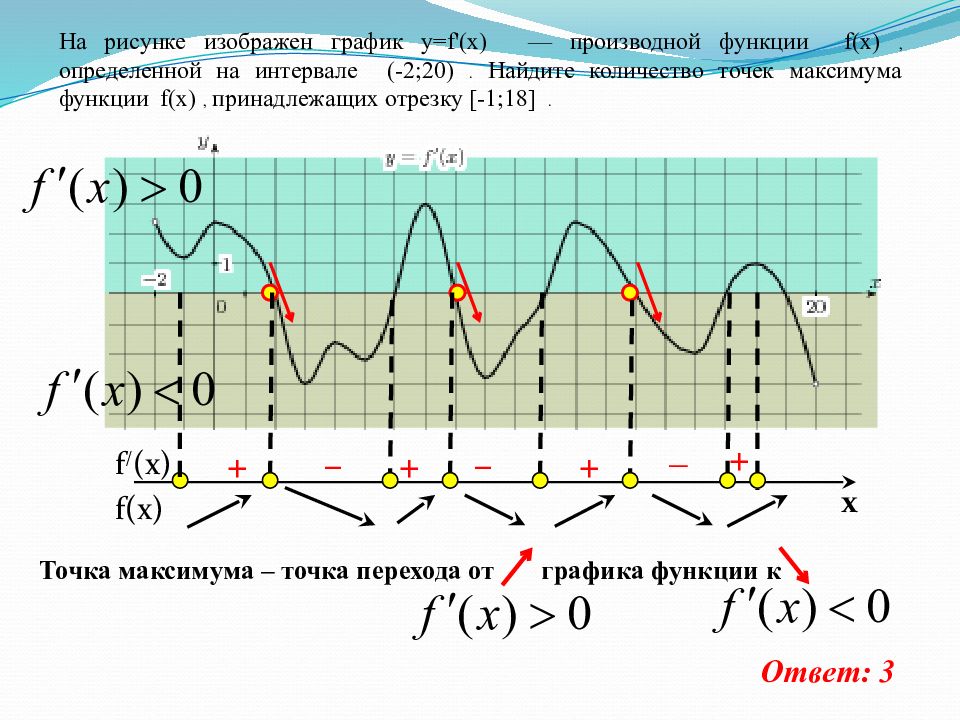
На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (-2;20). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-1;18]. Точка максимума – точка перехода от графика функции к Ответ: 3 f(x) f / (x) x _ – – + + + +
Слайд 16
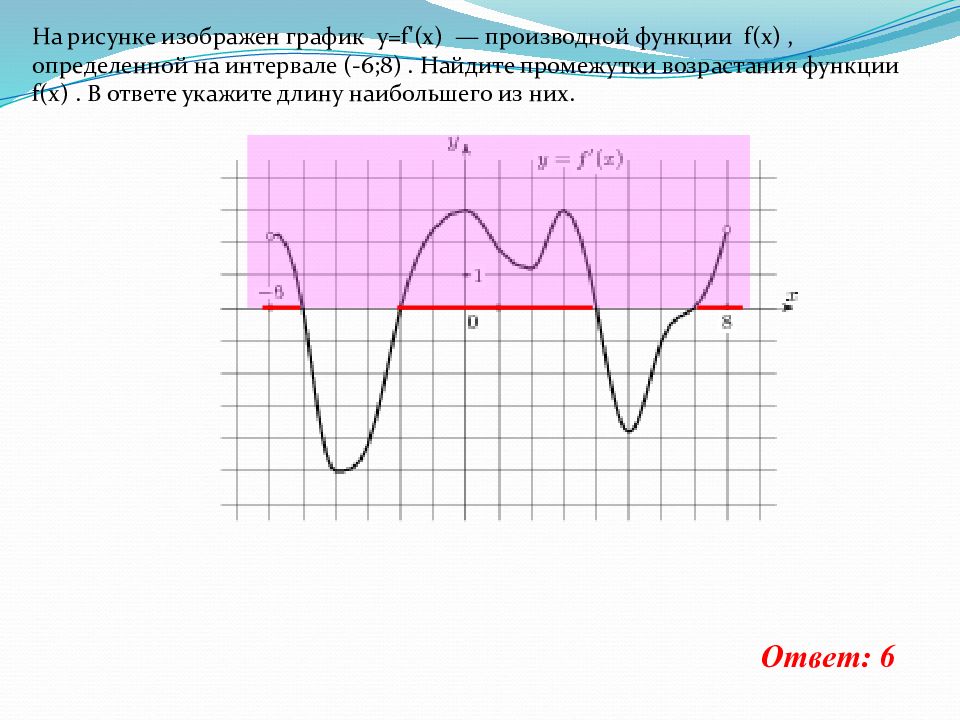
Ответ: 6 На рисунке изображен график y = f '( x ) — производной функции f ( x ), определенной на интервале (-6;8). Найдите промежутки возрастания функции f ( x ). В ответе укажите длину наибольшего из них.
Слайд 17
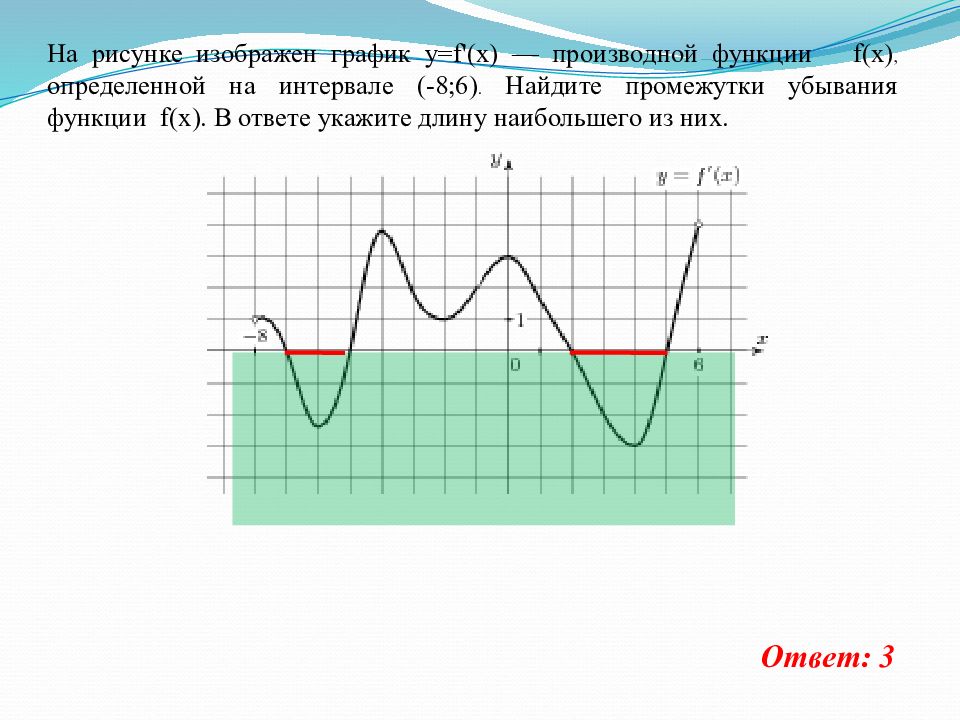
На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (-8;6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них. Ответ: 3
Слайд 18
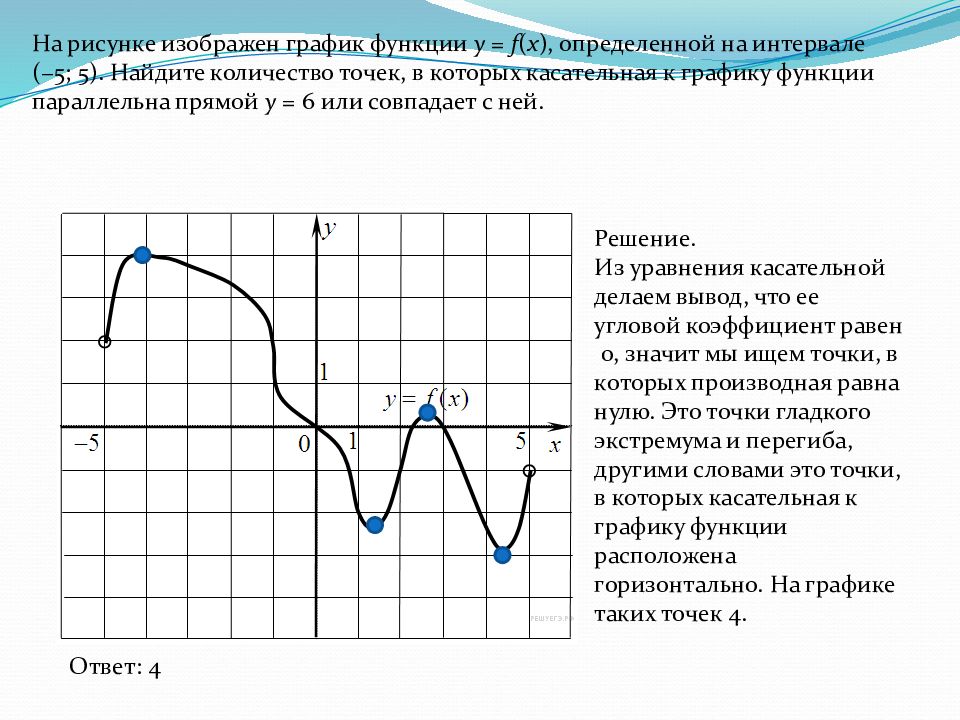
На рисунке изображен график функции y = f ( x ), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней. Ответ: 4 Решение. Из уравнения касательной делаем вывод, что ее угловой коэффициент равен 0, значит мы ищем точки, в которых производная равна нулю. Это точки гладкого экстремума и перегиба, другими словами это точки, в которых касательная к графику функции расположена горизонтально. На графике таких точек 4.
Слайд 19
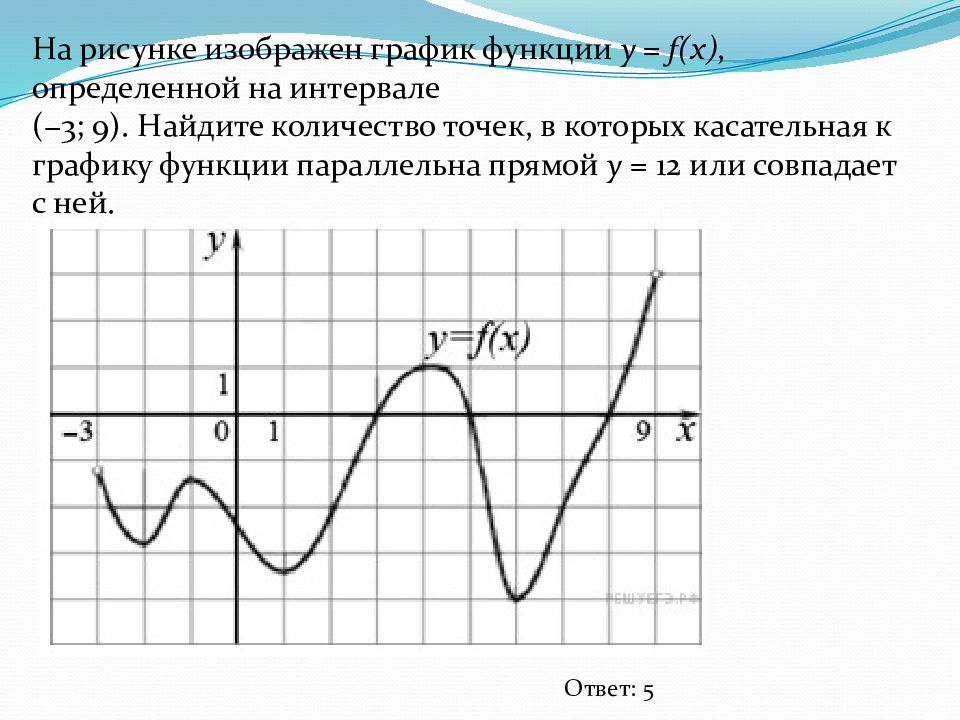
На рисунке изображен график функции y = f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 12 или совпадает с ней. Ответ: 5
Слайд 20
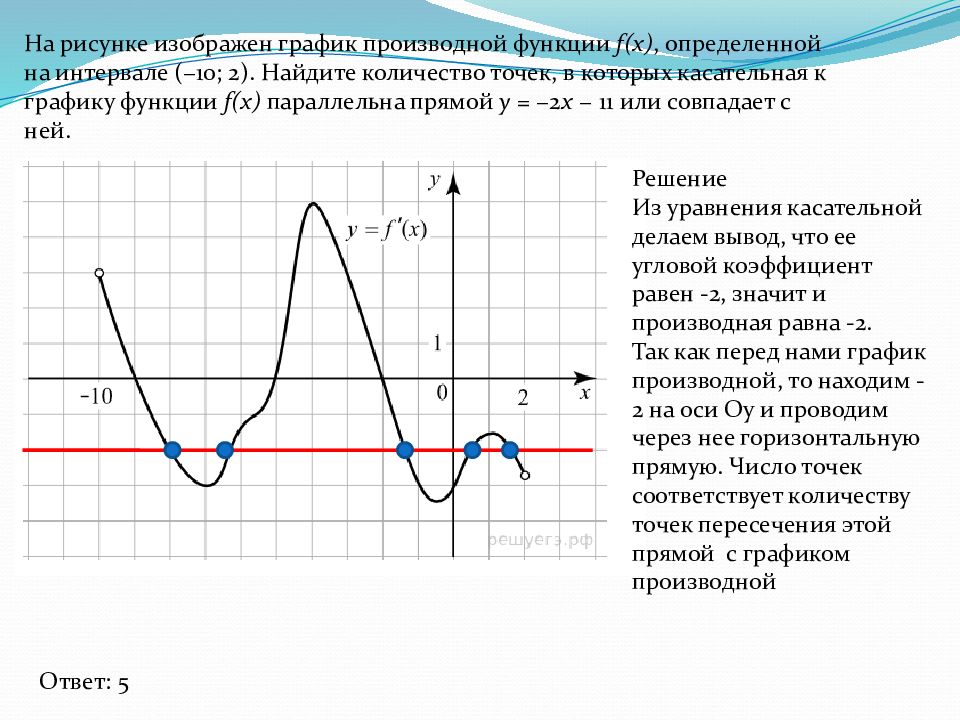
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2 x − 11 или совпадает с ней. Ответ: 5 Решение Из уравнения касательной делаем вывод, что ее угловой коэффициент равен -2, значит и производная равна -2. Так как перед нами график производной, то находим -2 на оси Оу и проводим через нее горизонтальную прямую. Число точек соответствует количеству точек пересечения этой прямой с графиком производной
Слайд 21
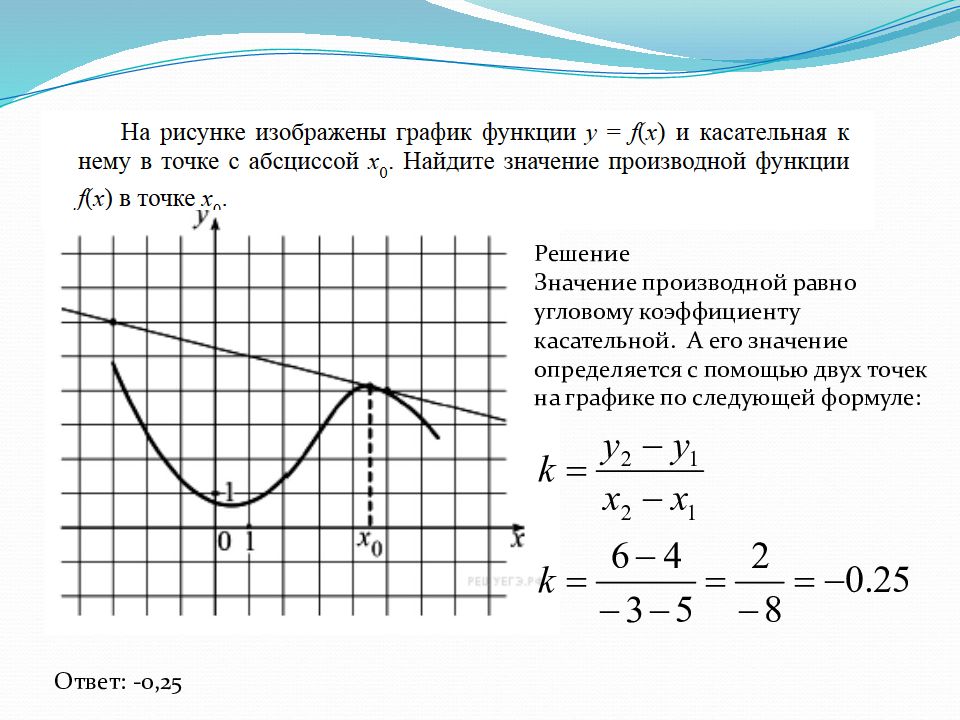
Ответ: -0,25 Решение Значение производной равно угловому коэффициенту касательной. А его значение определяется с помощью двух точек на графике по следующей формуле: