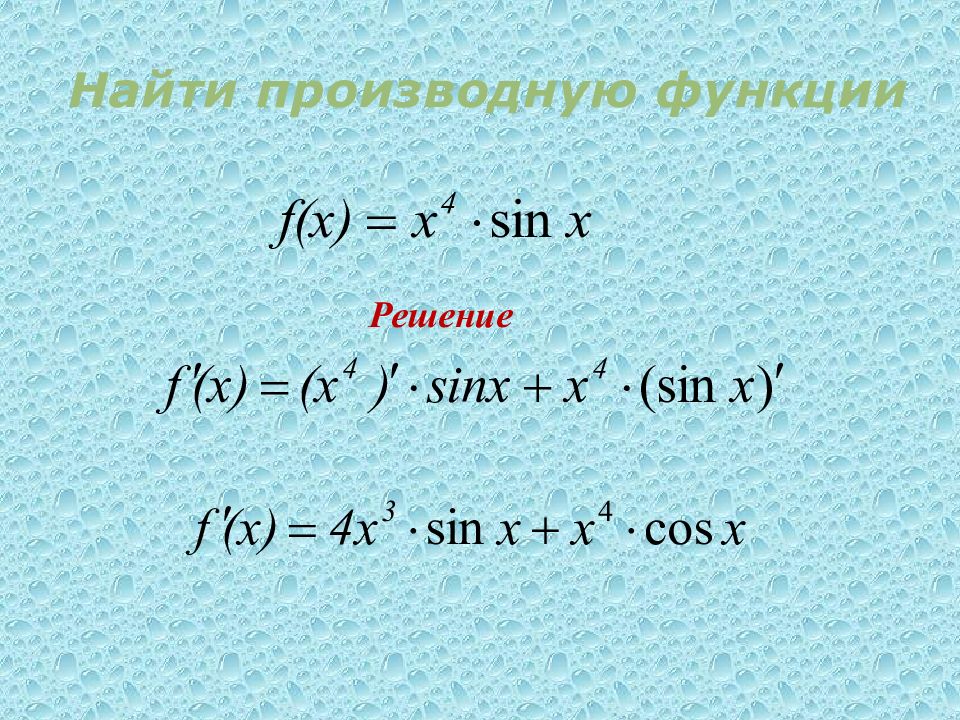Слайд 2: Определение
Производной функции в данной точке называется предел отношения приращения функции к приращению аргумента при условии,что приращение аргумента стремится к нулю 2
Слайд 5: НАЙДИТЕ ПРОИЗВОДНУЮ
2 ответ 3 ответ 5) 4 ответ 5 ответ 1 ответ 4) 3) 2) 1)
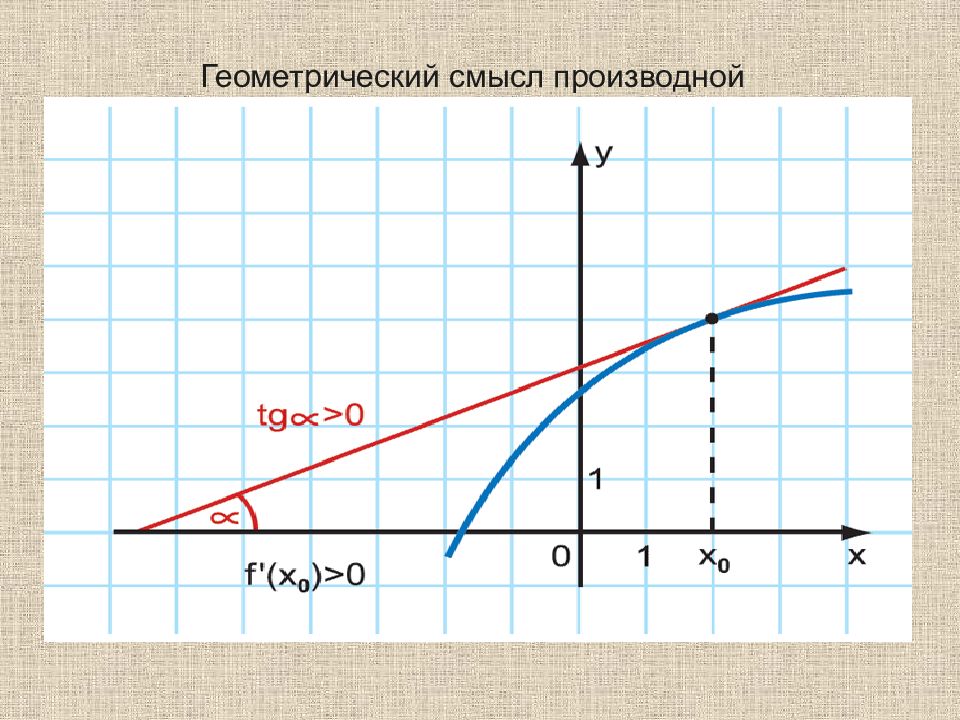
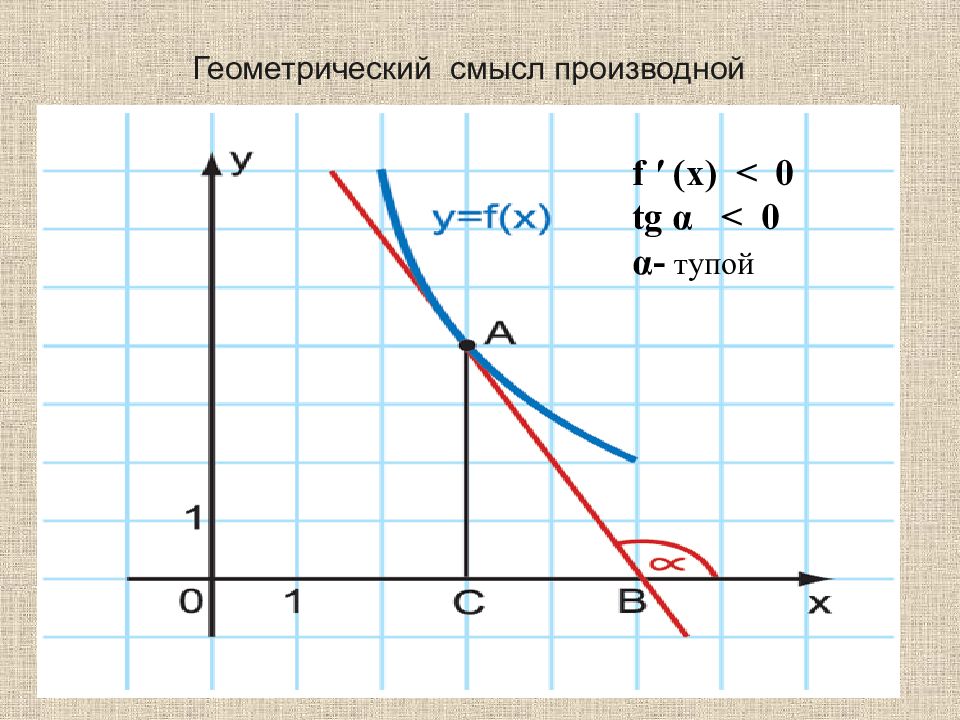
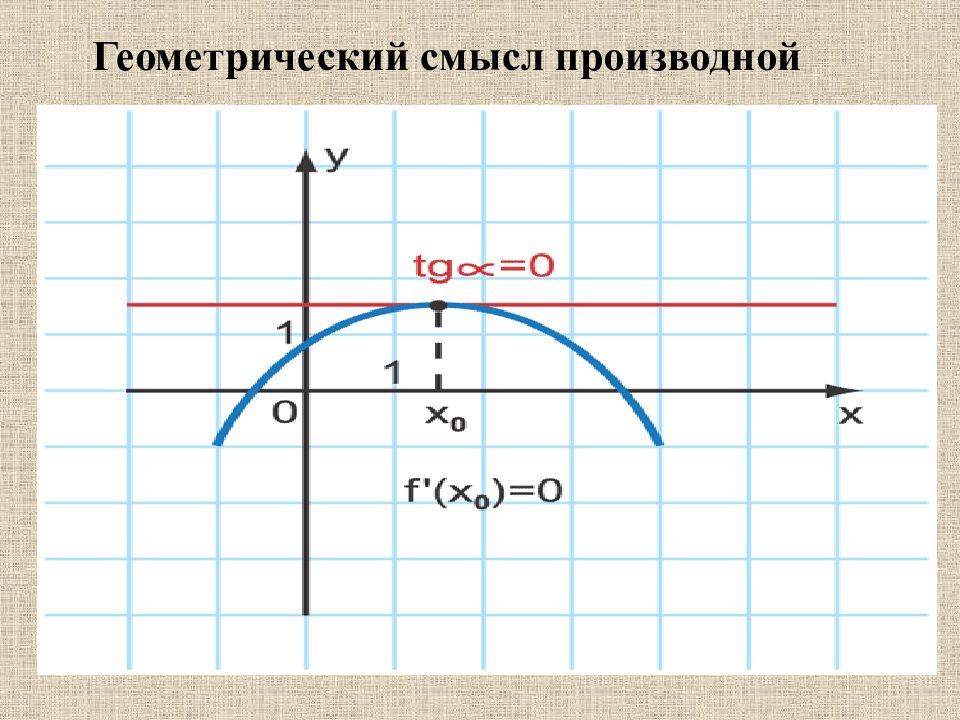
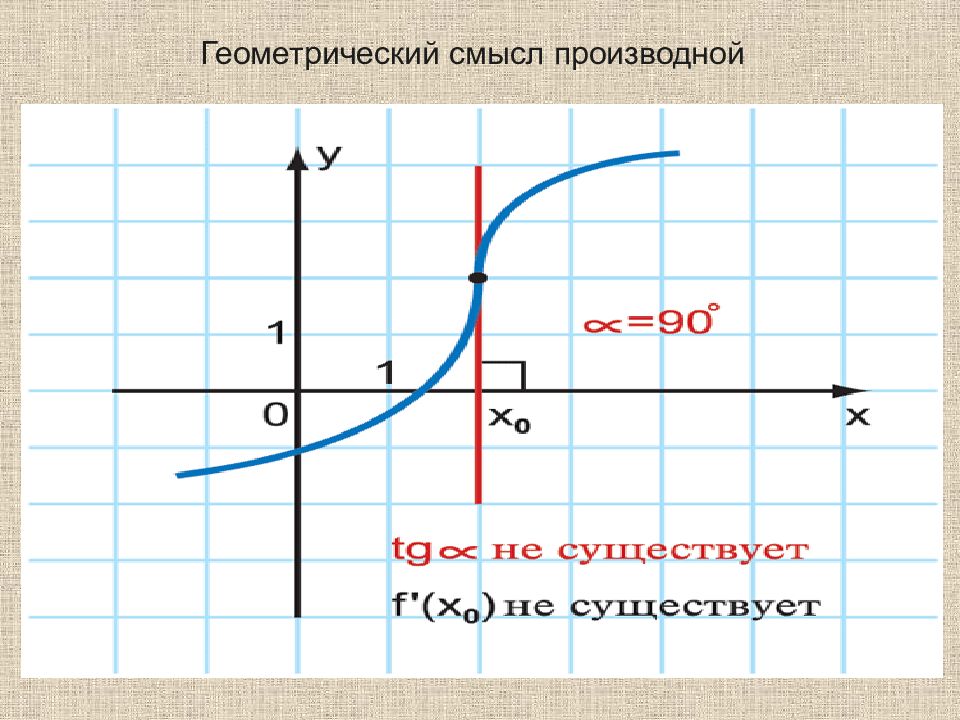
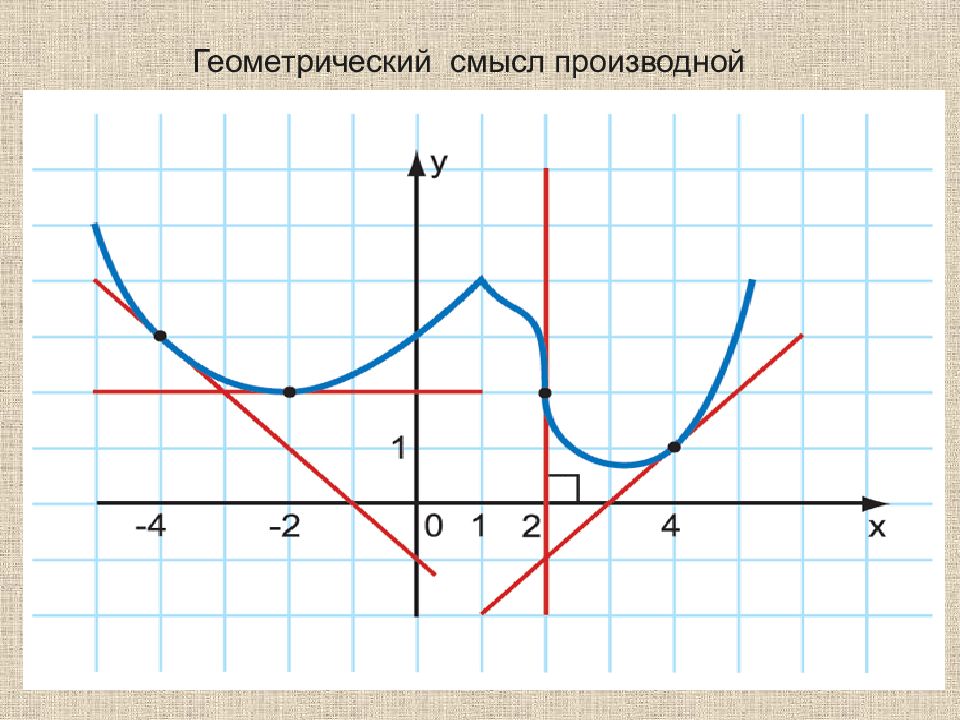
Слайд 13: Геометрический смысл производной
13 Геометрический смысл производной Геометрический смысл производной состоит в том, что значение производной функции y = f (x) в точке x равно угловому коэффициенту касательной к графику функции в точке с абсциссой x.