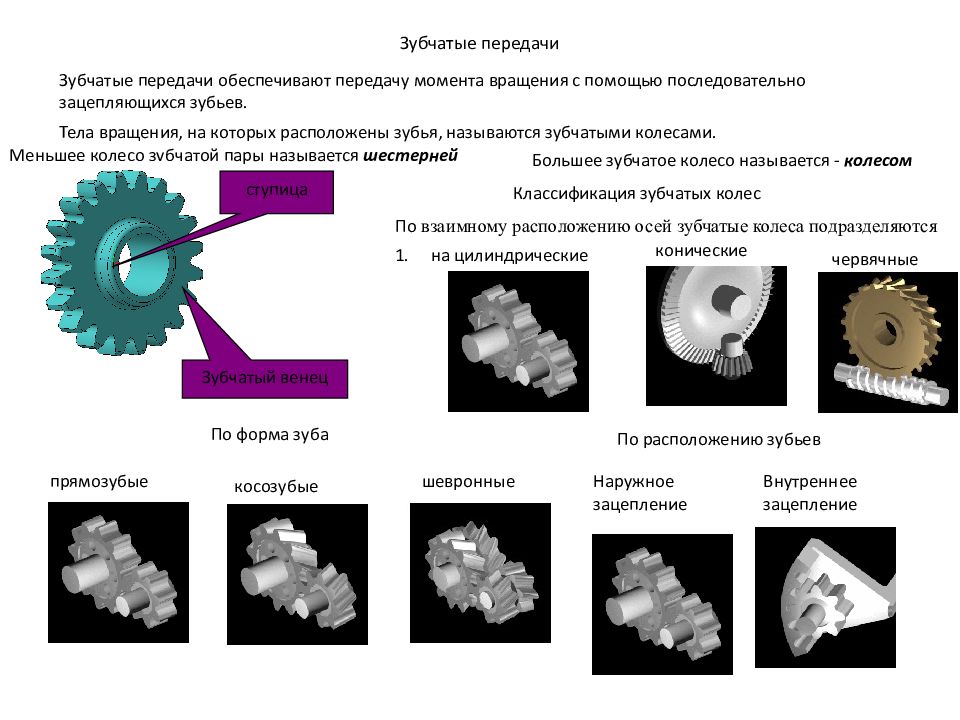
Первый слайд презентации: Пример расчета цилиндрической косозубой передачи
Слайд 2
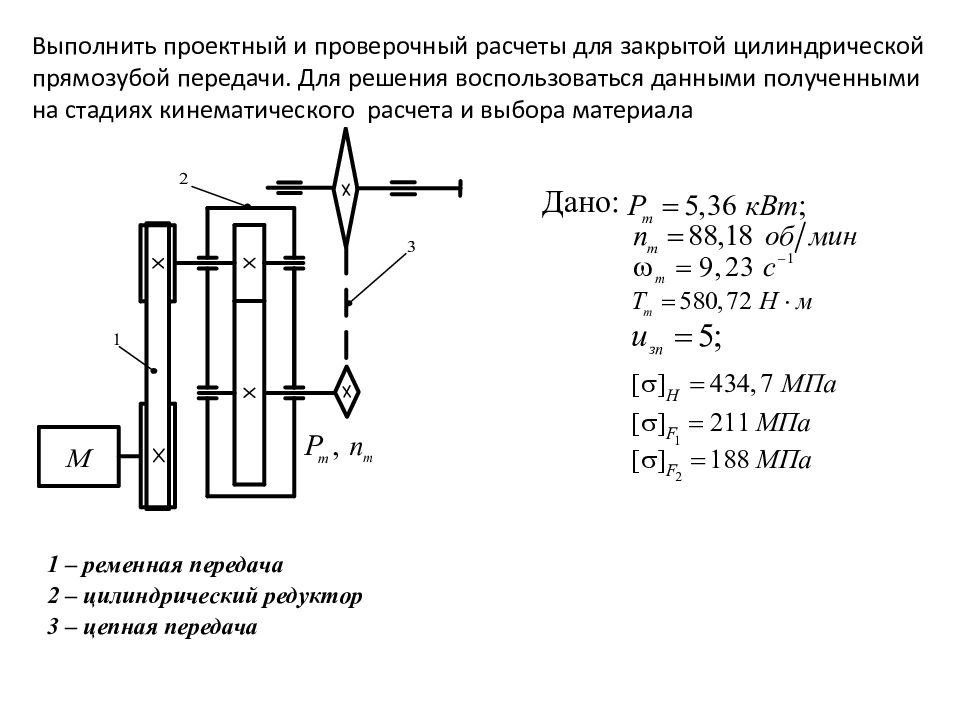
Выполнить проектный и проверочный расчеты для закрытой цилиндрической прямозубой передачи. Для решения воспользоваться данными полученными на стадиях кинематического расчета и выбора материала 1 – ременная передача 2 – цилиндрический редуктор 3 – цепная передача Дано:
Слайд 3
Определяем межосевое расстояние передачи: где K а – вспомогательный коэффициент для косозубых и шевронных передач K а = 43 для прямозубых передач K а = 49,5 K H – коэффициент неравномерности нагрузки по длине зуба. для прирабатывающихся зубьев при твердости < 350 HB K H = 1, при твердости > 350 HB определяется по таблице а – коэффициент ширины венца колеса а = b 2 / а W : для симметрично расположенной прямозубой и косозубой передачи относительно опор а = 0,25 0,4, для шевронной а = 0,4 0,8; в открытой передаче для шестерни, расположенной консольно относительно опор а = 0,2 0,25 ; Расположение шестерни относительно опор Твердость, НВ 0,2 0,4 0,6 0,8 1,2 1,6 Консольное, опоры шарикоподшипники 350 > 350 1,08 1,2 1,17 1,44 1,28 Консольное, опоры роликоподшипники 350 > 350 1,06 1,11 1,12 1,25 1,19 1,45 1,27 Симметричное 350 > 350 1,01 1,01 1,02 1,02 1,03 1,04 1,04 1,07 1,07 1,16 1,11 1,26 Несимметричное 350 > 350 1,03 1,06 1,05 1,12 1,07 1,2 1,12 1,29 1,19 1,48 1,28 Проектный расчет
Слайд 4
Полученное значение межосевого расстояния округляют до ближайшего стандартного значения а W, мм : 200 Вычисляют модуль зацепления: для закрытых передач при твердостях колес HB 350 для открытых передач Полученное значение модуля m округляют до стандартного m (мм) из ряда чисел: при твердости колеса и шестерни соответственно HB 350 и HRC > 45 при твердостях колес HRC 45 3
Слайд 5
В силовых зубчатых передачах при твердости колес 350 НВ принимаем m 1 мм ; при твердости одного из колес 45 HRC, принять m 1,5 мм. В открытых зубчатых передачах расчетное значение модуля m увеличить на 30 % из-за повышенного изнашивания зубьев. Угол наклона зубьев для косозубых передач: ширина венца колеса b 2 = a a W = 0,3·200 = 60 мм. Тогда Для косозубых колес угол наклона зубьев должен находиться в диапазоне 816, для шевронных - 2540 Суммарное число зубьев шестерни и колеса. Число зубьев шестерни зуба зуб
Слайд 6
Число зубьев колеса Вычисляют фактическое передаточное число и ф и его отклонение и от заданного и : Определяют действительную величину угла наклона зубьев для косозубых и шевронных передач Проверяют фактическое межосевое расстояние:
Слайд 7
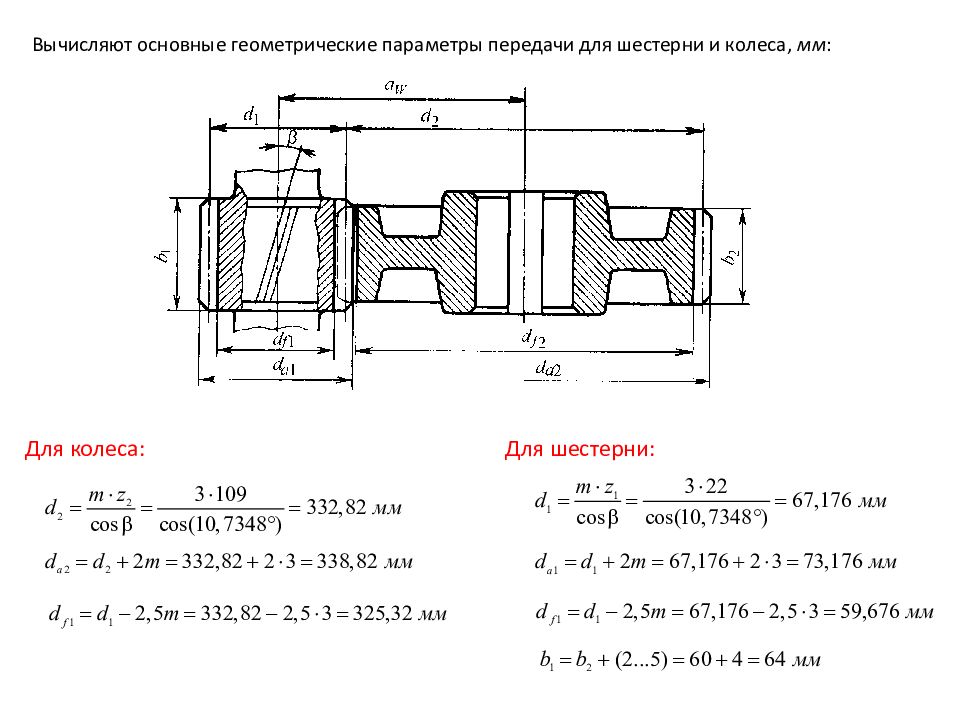
Вычисляют основные геометрические параметры передачи для шестерни и колеса, мм : Для шестерни: Для колеса:
Слайд 8
Проверочный расчет Проверяем межосевое расстояние Диаметр заготовки шестерни Ширина заготовки шестерни Диаметр заготовки колеса Ширина заготовки колеса
Слайд 9
Проверяем выполнение условия по контактной прочности H [ ] H где K – вспомогательный коэффициент, для косозубых и шевронных передач K = 376 для прямозубых K = 436 ; F t – окружная сила в зацеплении, Н ; K H коэффициент, учитывающий распределение нагрузки между зубьями. д ля прямозубых K H = 1, для косозубых и шевронных K H выбирается в зависимости от окружной скорости колес V = 2 d 2 / (2 10 3 ), м/с и степени точности передачи ;
Слайд 10
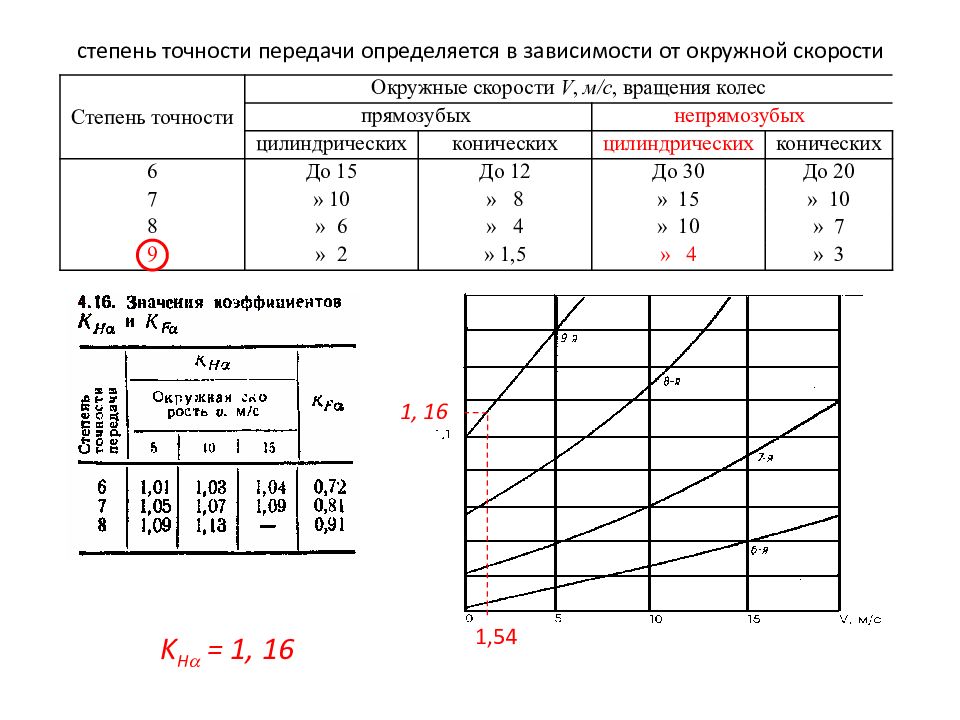
степень точности передачи определяется в зависимости от окружной скорости Степень точности Окружные скорости V, м/с, вращения колес прямозубых непрямозубых цилиндрических конических цилиндрических конических 6 До 15 До 12 До 30 До 20 7 » 10 » 8 » 15 » 10 8 » 6 » 4 » 10 » 7 9 » 2 » 1,5 » 4 » 3 1,54 K H = 1, 16 1, 16
Слайд 11
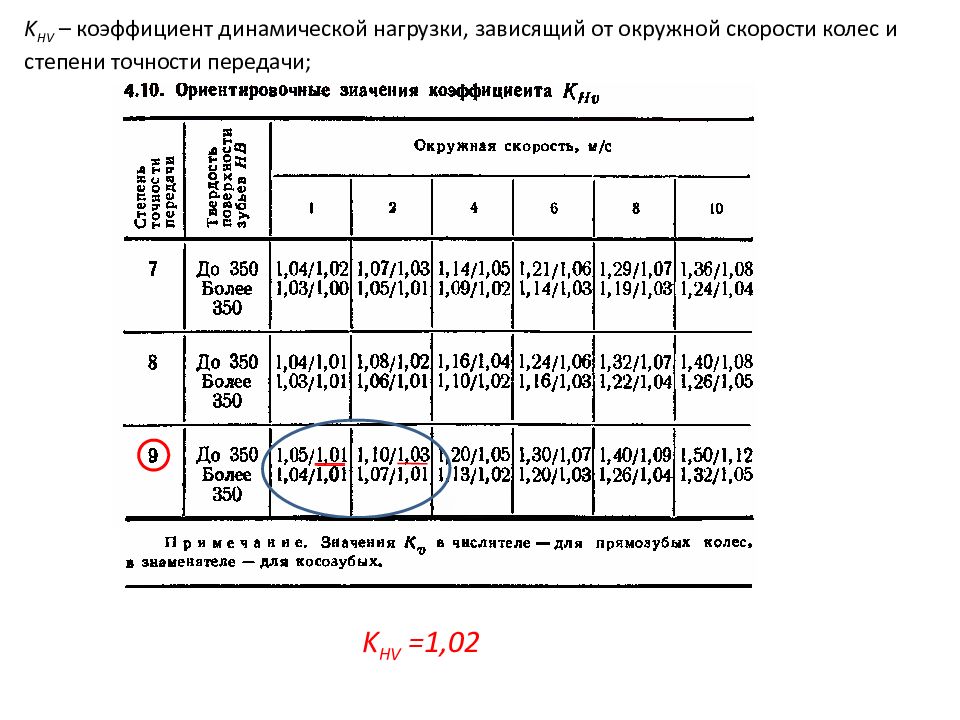
K HV – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи; K HV =1,02
Слайд 12
Далее проверяем выполнение условия изгибной прочности зубьев шестерни и колеса K F коэффициент, учитывающий распределение нагрузки между зубьями. для прямозубых K F = 1, для косозубых и шевронных K F зависит от степени точности передачи, определяемой по таблице. Степень точности 6 7 8 9 Коэффициент K F 0,72 0,81 0,91 1,0
Слайд 13
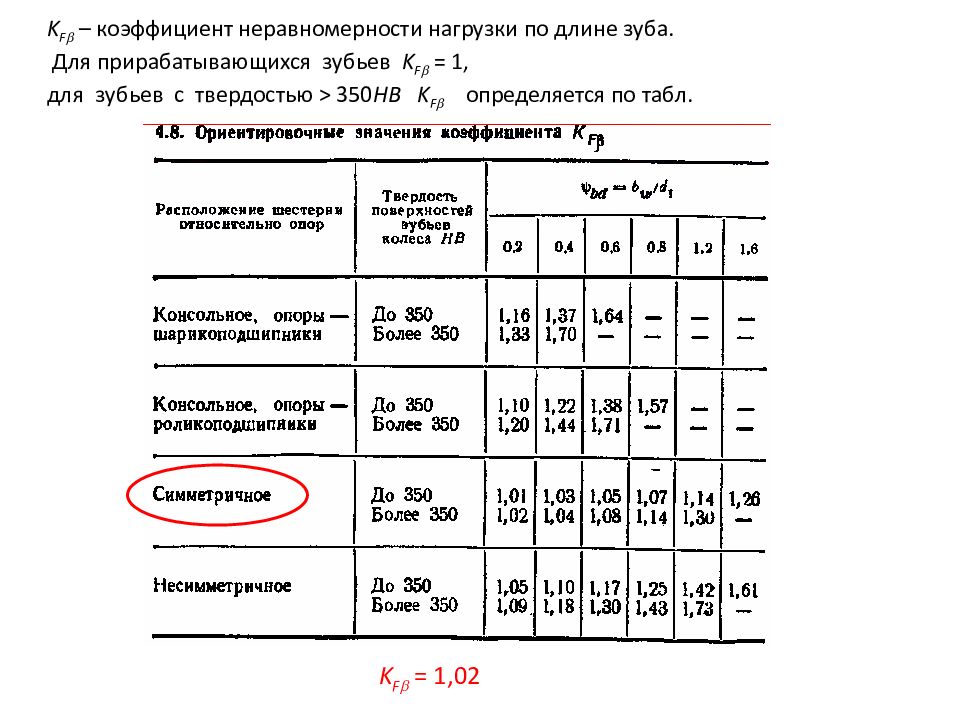
K F – коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев K F = 1, для зубьев с твердостью > 350 НВ K F определяется по табл. K F = 1,02
Слайд 14
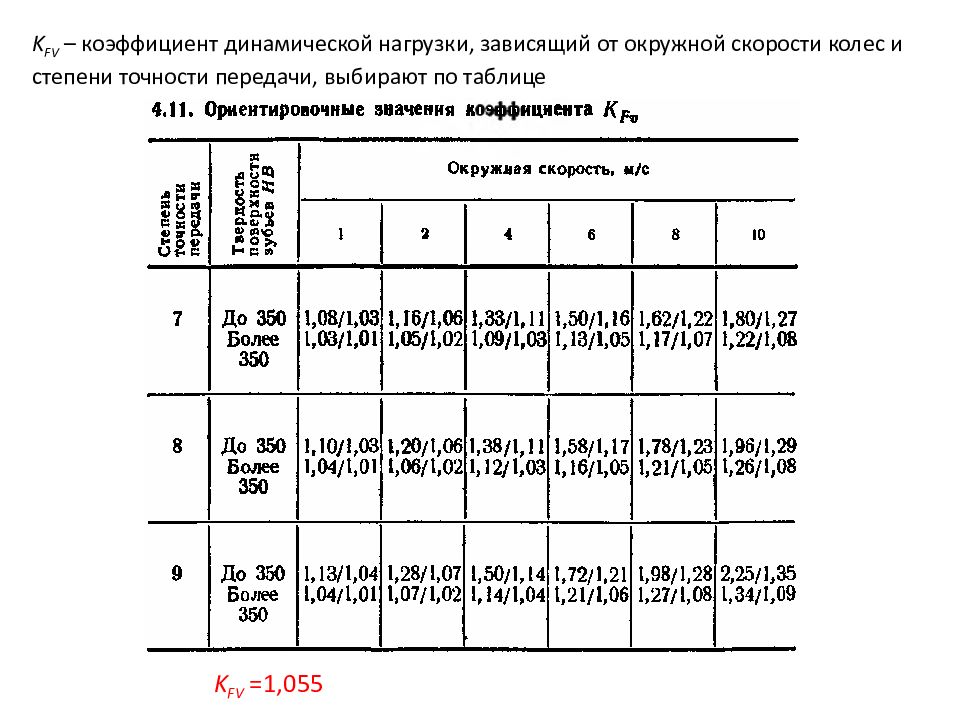
K FV – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи, выбирают по таблице K FV =1,055
Слайд 15
коэффициент формы зуба шестерни и колеса. Для прямозубых колес определяют по таблице в зависимости от числа зубьев шестерни Z 1 и колеса Z 2. Для косозубых и шевронных – в зависимости от эквивалентного числа зубьев шестерни Z V 1 = Z 1 / c os 3 и колеса Z V 2 = Z 2 / c os 3 Y – коэффициент, учитывающий наклон зуба, для прямозубых колес Y = 1 для косозубых Y = 1 /140 =1-