Первый слайд презентации: Производная
Слайд 2: Происхождение производной
В конце 17 века в Европе образовались две крупные математические школы. Главой одной из них был Готфрид Вильгельм фон Лейбниц. Его ученики и сотрудники – Лопиталь, братья Бернулли, Эйлер жили и творили на континенте. Вторая школа, возглавляемая Исааком Ньютоном, состояла из английских и шотландских ученых. Обе школы создали новые мощные алгоритмы, приведшие по сути к одним и тем же результатам – к созданию дифференциального и интегрального исчисления.
Слайд 4: Происхождение производной
Ряд задач дифференциального исчисления был решен еще в древности. Такие задачи можно найти у Евклида и у Архимеда, однако основное понятие – понятие производной функции – возникло только в17 веке в связи с необходимостью решить ряд задач из физики, механики и математики, в первую очередь следующих двух: определение скорости прямолинейного неравномерного движения и построения касательной к произвольной плоской кривой. Первую задачу: о связи скорости и пути прямолинейно и неравномерно движущейся точки впервые решил Ньютон. Он пришел к формуле :
Слайд 6
Ньютон пришел к понятию производной, исходя из вопросов механики. Свои результаты в этой области он изложил в трактате «Метод флюксий и бесконечных рядов». Написана работа была в 60-е годы 17 века, однако опубликована после смерти Ньютона. Ньютон не заботился о том, чтобы своевременно знакомить математическую общественность со своими работами. Флюксией называлась производная функции – флюэнты. Флюэнтой таже в дальнейшем называлась первообразная функция.
Слайд 7
В подходе Лейбница к математическому анализу были некоторые особенности. Лейбниц мыслил высший анализ не кинематически, как Ньютон, а алгебраически. Он шел к своему открытию от анализа бесконечно малых величин и теории бесконечных рядов. В 1675 году Лейбниц завершает свой вариант математического анализа, тщательно продумывает его символику и терминологию, отражающую существо дела. Почти все его нововведения укоренились в науке и только термин «интеграл» ввёл Якоб Бернулли (1690), сам Лейбниц вначале называл его просто суммой.
Слайд 9
По мере развития анализа выяснилось, что символика Лейбница, в отличие от ньютоновской, отлично подходит для обозначения многократного дифференцирования, частных производных и т. д. На пользу школе Лейбница шла и его открытость, массовая популяризация новых идей, что Ньютон делал крайне неохотно.
Слайд 10
Работы Лейбница по математике многочисленны и разнообразны. В 1666 году он написал первое сочинение: «О комбинаторном искусстве». Сейчас комбинаторика и теория вероятности одна из обязательных тем математики в школе.
Слайд 11
В1672 году Лейбниц изобретает собственную конструкцию арифмометра, гораздо лучше паскалевской — он умел выполнять умножение, деление и извлечение корней. Предложенные им ступенчатый валик и подвижная каретка легли в основу всех последующих арифмометров. Лейбниц также описал двоичную систему счисления с цифрами 0 и 1, на которой основана современная компьютерная техника.
Слайд 12
Производной функции у = f(x), заданной на некотором интервале ( a; b), в некоторой точке х этого интервала называют предел отношения приращения функции в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю. f ′(x) = lim ∆ f ∆ x ∆ x →0
Слайд 14: Таблица производных
f (x) f ′(x) f (x) f ′(x) C 0 √ x 1/(2 √ x) kx + b k e x e x x 2 2x a x a x lna x n nx n–1 tg x 1/cos 2 x 1/x – 1/x 2 ctg x – 1/sin 2 x sin x cos x ln x 1/x cos x – sin x log a x 1/(x lna )
Слайд 15: Правила нахождения производной
1. Если функции u(x) и v(x) имеют в точке х производные, то их сумма u(x) + v(x) также имеет в этой точке производную, причем ( u + v )′ = u′ + v′ 2. Если функция u(x) имеет в точке х производную и С – данное число, то функция С ∙ u(x) также имеет в этой точке производную, причем (С u )′ = С∙ u′
Слайд 16: Правила нахождения производной
3. Если функции u(x) и v(x) имеют в точке х производные, то их произведение u(x) ∙ v(x) также имеет в этой точке производную, причем ( u ∙ v )′ = u′∙v + u∙v′ 4. Если функция v(x) имеет в точке х производную и v(x) ≠ 0, то функция также имеет в этой точке производную, причем v(x) 1 v 2 v′ = – v 1 ( ) ′
Слайд 17: Правила нахождения производной
5. Если функции u(x) и v(x) имеют в точке х производные и v(x) ≠ 0, то функция также имеет в этой точке производную, причем v(x) u(x) v 2 u′v – uv′ = ( ) v u ′ 6.Производная сложной функции (f(g(x)))′ = f′(g(x))∙g′(x)
Слайд 20
“ При изучении наук примеры не менее поучительны, нежели правила” “Примеры учат больше, чем теория”. И. Ньютон М. Ломоносов
Слайд 24
Правильный ответ Правильный ответ Правильный ответ Правильный ответ Правильный ответ Найдите производные функций:
Слайд 25
Найдите производную функции(устно): а) у = 6х 5 – 7х 3 + 2х 2 – 5, у / = 30 х 4 – 21х 2 + 4х, б) у = (4 – 5х) 7, у / = 7·( – 5)·(4 – 5х) 6 = – 35·(4 – 5х) 6 в) у = 8 + 3 cos х, у / = 8 – 3 sin х г) у = 4 sin х – 6 lnx, у / = 4 cos х – 6/ х Правильный ответ Правильный ответ Правильный ответ Правильный ответ
Слайд 26: Найдите производную функции(устно):
Правильный ответ Правильный ответ Правильный ответ Правильный ответ
Слайд 29
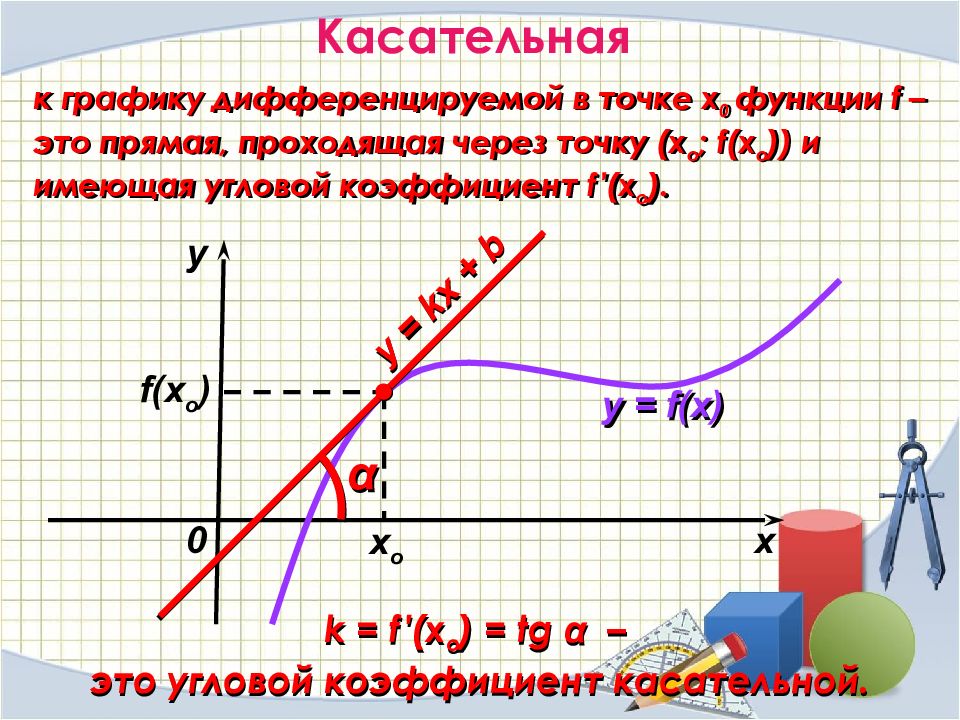
k = f ′(x o ) = tg α – это угловой коэффициент касательной. f(x o ) Касательная к графику дифференцируемой в точке х 0 функции f – это прямая, проходящая через точку (х о ; f(x о )) и имеющая угловой коэффициент f ′ (х о ). х у х о y = kx + b α y = f(x) 0
Слайд 30
Общий вид уравнения касательной y = f ′(x o )(x – x o ) + f(x o ) Алгоритм составления уравнения касательной 1 о Находим значение функции в точке х о : f(x o ). 2 о Дифференцируем функцию: f′(x). 3 о Находим значение производной в точке х о : f′(x o ). 4 о Подставляем эти данные в общее уравнения касательной: y = f′(x o )(x – x o ) + f(x o ).
Слайд 31
Одна из основных задач исследования функции – это нахождение промежутков её возрастания и убывания. Признак возрастания функции: Если f´(x)>0 в каждой точке интервала I, то функция f возрастает на I. Признак убывания функции: Если f´(x)<0 в каждой точке интервала I, то функция f убывает на I.
Слайд 32: Алгоритм решения неравенств методом интервалов:
Выделить функцию y=f(x). Найти область определения функции D ( f). Указать промежутки непрерывности. Найти нули функции, решив уравнение f(x)=0. Определить знак функции между её нулями в области определения.
Слайд 33
Решите неравенство: 1. 2x+5≠0, х ≠-2,5 2. f(x)=0, если x 1 = 8, x 2 = -2 3. Ответ: X 8 -2 -2,5
Слайд 34: Алгоритм нахождения промежутков возрастания (убывания) функции y=f(x) :
Найти производную функции f ´ (x). Решить уравнение f´ (x) =0. Найти знак производной на каждом интервале. Согласно признаку возрастания (убывания) функции, найти промежутки возрастания и убывания.
Слайд 35
Найдите промежутки возрастания и убывания функции: 1. 2. f´(x)=0, если 3. Ответ: X 1 0 f´(x) f (x)
Слайд 36
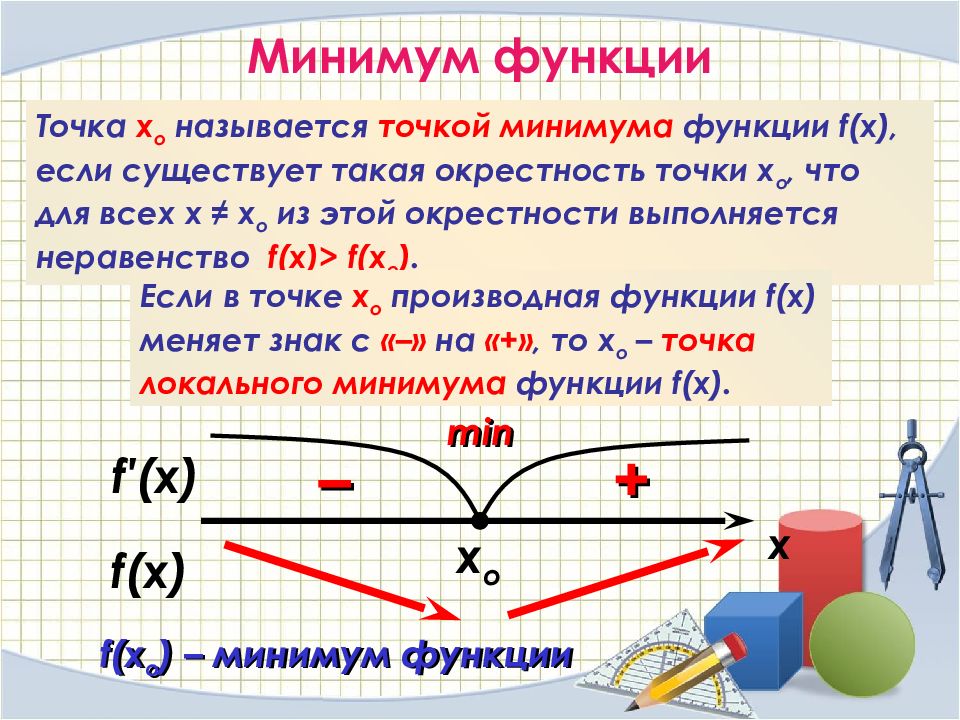
f ′(x) x o Минимум функции Точка х о называется точкой минимума функции f(x), если существует такая окрестность точки х о, что для всех х ≠ х о из этой окрестности выполняется неравенство f(x)> f(x o ). Если в точке х о производная функции f(x) меняет знак с «–» на «+», то х о – точка локального минимума функции f(x). f (x) – + x min f (x о ) – минимум функции
Слайд 37
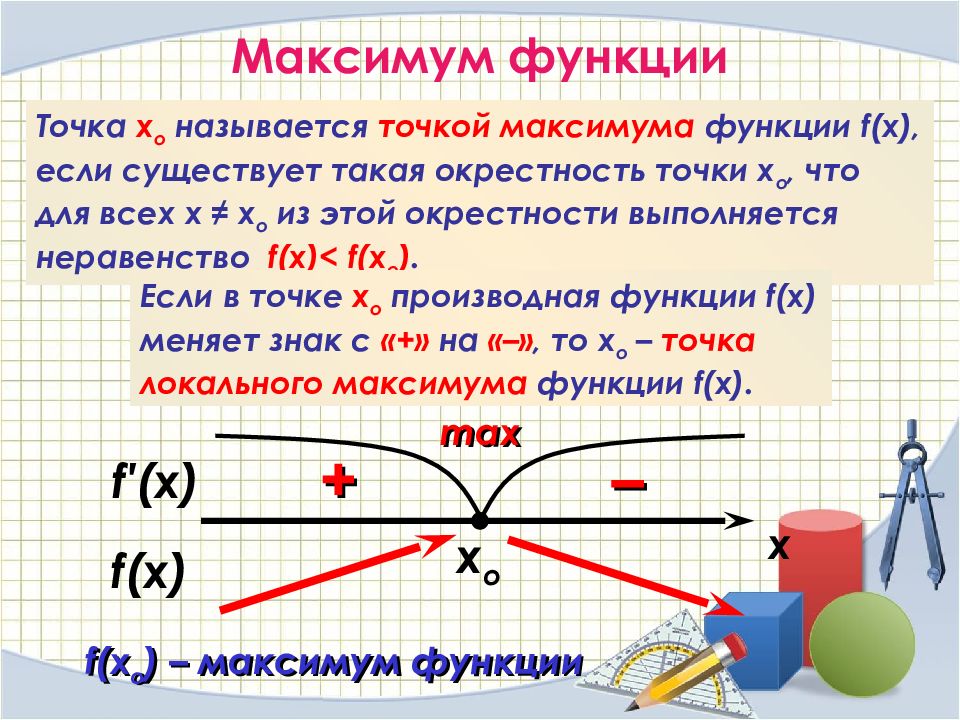
x o Максимум функции Точка х о называется точкой максимума функции f(x), если существует такая окрестность точки х о, что для всех х ≠ х о из этой окрестности выполняется неравенство f(x)< f(x o ). Если в точке х о производная функции f(x) меняет знак с «+» на «–», то х о – точка локального максимума функции f(x). f ′(x) f (x) + – x max f (x о ) – максимум функции
Слайд 38
Алгоритм исследования функции на монотонность 1 о Дифференцируем функцию: f′(x). 2 о Находим критические точки из уравнения: f′(x) = 0. 3 о Решаем неравенства: f′(x) > 0 и f′(x) < 0. 4 о Полученные данные изображаем на схеме: 5 o a) Промежутки возрастания: (– ∞; х 1 ] ; [x 2 ; x 3 ]. б) Промежутки убывания: [x 1 ; x 2 ] ; [x 3 ; + ∞). f ′(x) x 2 f (x) – + x + – x 1 x 3
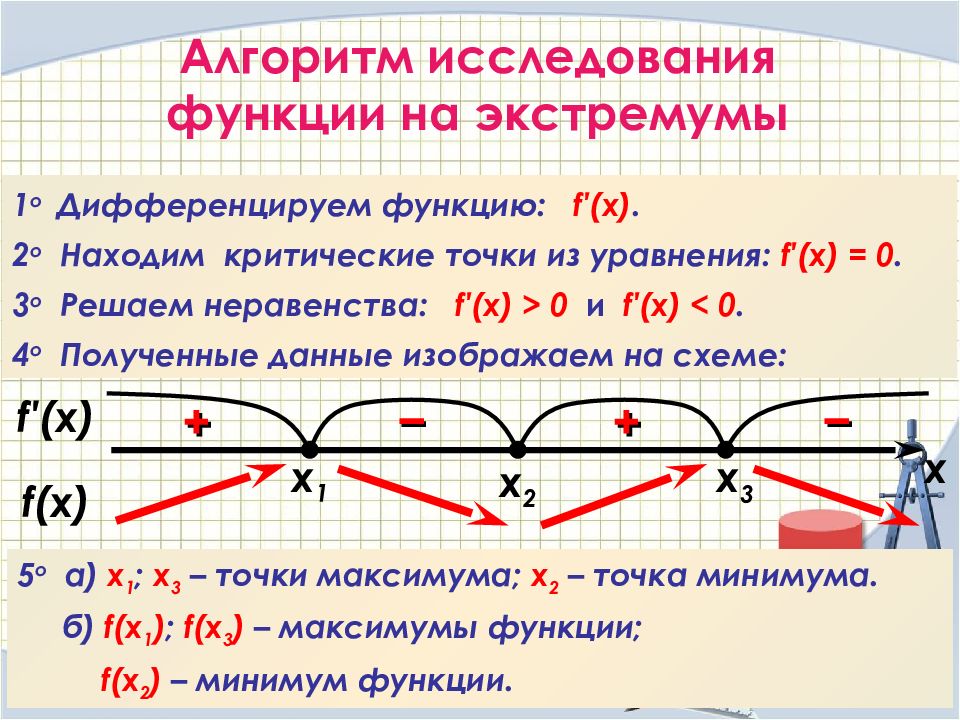
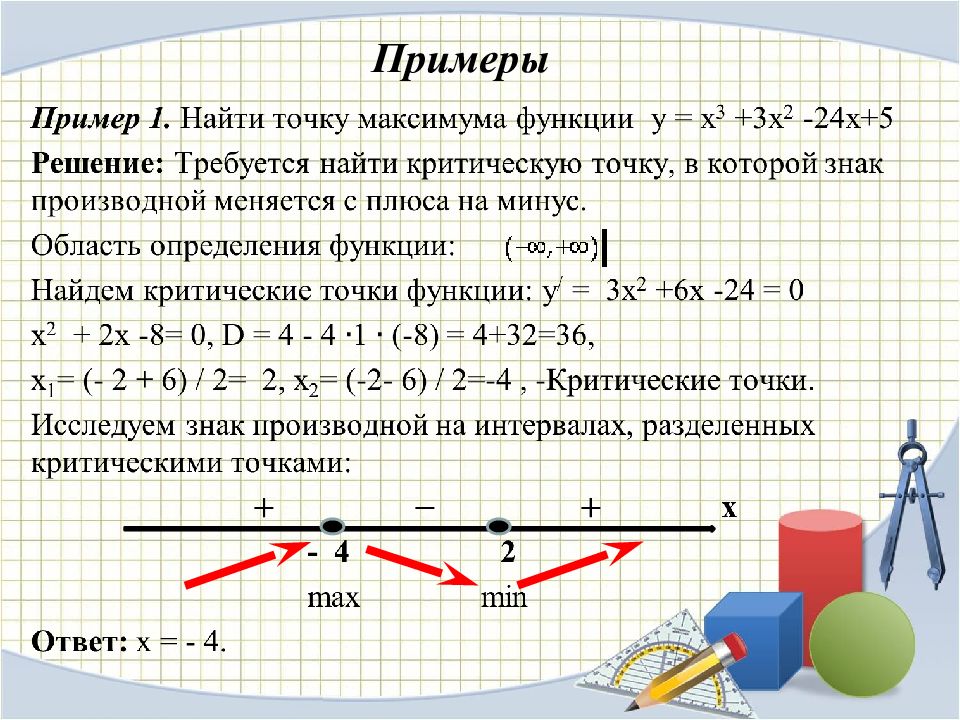
Слайд 39
Алгоритм исследования функции на экстремумы 1 о Дифференцируем функцию: f′(x). 2 о Находим критические точки из уравнения: f′(x) = 0. 3 о Решаем неравенства: f′(x) > 0 и f′(x) < 0. 4 о Полученные данные изображаем на схеме: 5 o a) х 1 ; x 3 – точки максимума; x 2 – точка минимума. б) f(x 1 ) ; f(x 3 ) – максимумы функции; f(x 2 ) – минимум функции. f ′(x) x 2 f (x) – + x + – x 1 x 3