Производные высших порядков Производные от функций, заданных параметрически Дифференциал функции Геометрический смысл дифференциала Основные теоремы о дифференциалах Применение дифференциала в приближенных вычислениях Некоторые теоремы о дифференцируемых функциях Правило Лопиталя 1
Итак: Производной n – ого порядка (или n – ой производной) называется производная от производной n -1 - ого порядка. Производная функции есть также функция от x и называется производной первого порядка. Если функция дифференцируема, то ее производная называется производной второго порядка и обозначается: Производная от производной второго порядка, если она существует называется производной третьего порядка и обозначается: Итак: 2
- производная пятого порядка. Начиная от производной 4 порядка, производные обозначаются римскими цифрами или цифрами в скобках: Вычислить производную n – ого порядка от функции: 3
Производная первого порядка от этой функции находится по формуле: Пусть функция y = f(x) задана параметрически уравнениями: Найдем производную второго порядка: Аналогично получаем: и т. д. 4
Вычислить производную 3 – ого порядка от функции: 5
Пусть функция y = f(x) имеет в некоторой точке х отличную от нуля производную, следовательно существует предел: где при По теореме о связи функции, ее предела и бесконечно малой функции Таким образом, приращение функции представляет собой сумму двух слагаемых: и, являющимися бесконечно малыми при. При этом первое слагаемое есть бесконечно – малая одного порядка с, так как: 6
Второе слагаемое есть бесконечно малая функция более высокого порядка по сравнению с, так как: Поэтому первое слагаемое называют главной частью приращения функции. Дифференциалом функции y = f(x) в точке х называется главная часть ее приращения: Найдем дифференциал независимой переменной, то есть функции : Дифференциал независимой переменной равен приращению этой переменной Поэтому: Дифференциал функции равен произведению производной функции на дифференциал независимой переменной 7
Проведем к графику функции y = f(x) в точке М( x, y) касательную y 0 х х f(x ) x + Δ x М М 1 f(x+ Δ x ) Рассмотрим ординату касательной для точки x + Δ x. α Согласно геометрическому смыслу производной, B A Из прямоугольного треугольника A ВМ имеем: Дифференциал функции y = f(x) в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получает приращение Δ x. 8
Теорема 1 Дифференциал суммы, разности, произведения и частного двух дифференцируемых функций находится по формулам: Теорема 2 Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента. dy du Это свойство дифференциала называют инвариантностью (неизменностью) формы дифференциала. 9
Как известно, приращение функции можно представить в виде: dy Отбрасывая бесконечно малую более высокого порядка, чем, получим приближенной равенство: Это равенство позволяет с большой точностью вычислять приращение любой дифференцируемой функции. Подставим в равенство выражения для приращения и дифференциала функции: Формула позволяет приближенно вычислять значение функции в точке x 0 + Δ x, зная значение функции в точке x 0. 0 0 0 10
Вычислить приближенно: Рассмотрим функцию: Так как то 11
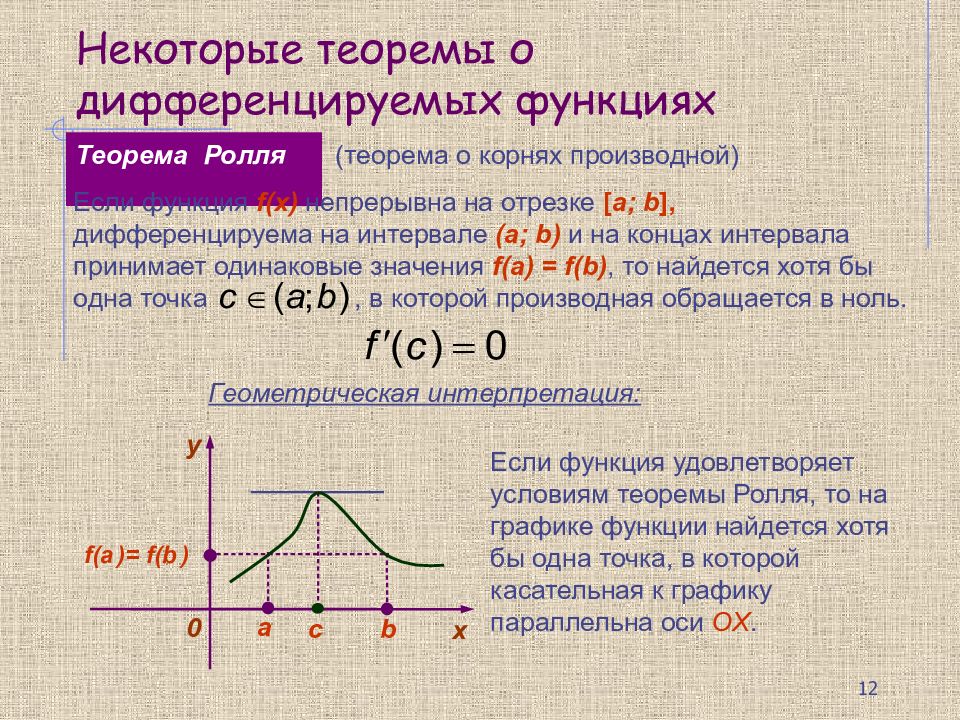
Теорема Ролля Геометрическая интерпретация: Если функция f(x) непрерывна на отрезке [ a; b ], дифференцируема на интервале (a; b) и на концах интервала принимает одинаковые значения f(a) = f(b), то найдется хотя бы одна точка, в которой производная обращается в ноль. y 0 х а f( а ) = f(b ) с b Если функция удовлетворяет условиям теоремы Ролля, то на графике функции найдется хотя бы одна точка, в которой касательная к графику параллельна оси OX. (теорема о корнях производной) 12
Теорема Коши Если функции f(x) и g(x) непрерывны на отрезке [ a; b ], дифференцируемы на интервале (a; b), причем для ,то найдется холя бы одна точка, такая, что выполняется равенство: (теорема об отношении приращений) Теорема Лагранжа (теорема о конечных приращениях) Если функция f(x) непрерывна на отрезке [ a; b ], дифференцируема на интервале (a; b),то найдется хотя бы одна точка, в которой выполняется равенство: y 0 х а с b А В На графике функции найдется хотя бы одна точка, в которой касательная параллельна хорде AB 13
Теорема Рассмотрим способ раскрытия неопределенностей вида и , который основан на применении производной. Пусть функции f(x) и g(x) непрерывны и дифференцируемы в окрестности точки x 0 и обращаются в ноль в этой точке: . Если существует предел то Теорема справедлива также в случае, если 14
15
Обозначим: Прологарифмируем равенство: 16
