Первый слайд презентации: Производственные функции
Слайд 2: ПФ
функциональная зависимость между количеством используемых в производстве ресурсов и объемом выпускаемой продукции
производитель из всего множества планов производства выбирает тот, который принесет ему максимальную прибыль.
Слайд 4: Гипотезы
Гипотеза Н1 ( гипотеза измеримости ): каждый ресурс является количественно измеримым. Гипотеза H2 ( гипотеза однородности ): каждая точка пространства Rn+ может быть отождествлена с некоторым планом производства, (все ресурсы могут использоваться в количестве, измеряемом любым неотрицательным действительным числом). Гипотеза Н 3 ( гипотеза однозначности ): при одинаковых затратах ресурсов производитель выпускает одно и то же количество продукции.
Слайд 5: пространство ресурсов
- множество n-мерных векторов с неотрицательными координатами точки этого множества – планы производства по ресурсам.
Линейная Кобба-Дугласа Леонтьева …
Слайд 7: Поверхность (линия) уровня
– множество значений аргумента, в которых функция принимает одно и то же значение Геометрически линия уровня (уровень) функции двух переменных - плоская кривая, получаемая при пересечении графика этой функции плоскостью, параллельной координатной плоскости XOY Z=C, где C=const Изобразить поверхность на плоскости можно, проектируя линии уровня на плоскость XOY. Семейство полученных кривых задается уравнениями вида F(x,y)=C
Слайд 9: Частные производные
Частная производная функции в точке по переменной - обыкновенная производная функции одной переменной при фиксированных значениях других переменных - она характеризует скорость изменения ФНП в направлении данной координатной оси при фиксированных значениях других координат.
Слайд 10: Предельный продукт
=предельная эффективность ресурса, =предельная производительность ресурса, =предельная отдача ресурса при плане
Слайд 11: средний продукт
средний продукт первого ресурса (средняя производительность ресурса, средняя отдача ресурса) - отношение объема выпущенной продукции к количеству затраченного переменного ресурса
Слайд 12: Производственная функция (ПФ) типа Кобба – Дугласа где Q – объем производства, a 0 > 0, 0 < a < 1, 0 < b < 1 K – капитал, L – рабочая сила,
Пример : ПФ небольшого цеха, изготавливающего рамы для картин, имеет вид: где x 1 – отработанные человеко-часы, x 2 – отработанные машино-часы, q – число изготовленных рам. Найти количество продукции при плане x * = (64, 81).
Слайд 13: ПРИМЕР:
Вычислим частные производные ПФ, т.е. первый и второй предельный продукты ( предельную отдачу первого и второго ресурса) для плана x *=(64, 81): значение 3 / 4 первого предельного продукта означает, что при увеличении затрат первого ресурса на единицу и неизменных затратах второго выпуск продукции увеличится примерно на 3/4 ед. Каков экономический смысл второго предельного продукта?
Слайд 14: Уровень ПФ – изокванта
Построить изокванту, проходящую через точку х * затраты первого и второго ресурсов для всех планов производства, обеспечивающих выпуск 96 единиц продукции, связаны уравнением: Графиком полученной функции в пространстве ресурсов является изокванта, соответствующая выпуску 96 единиц продукции
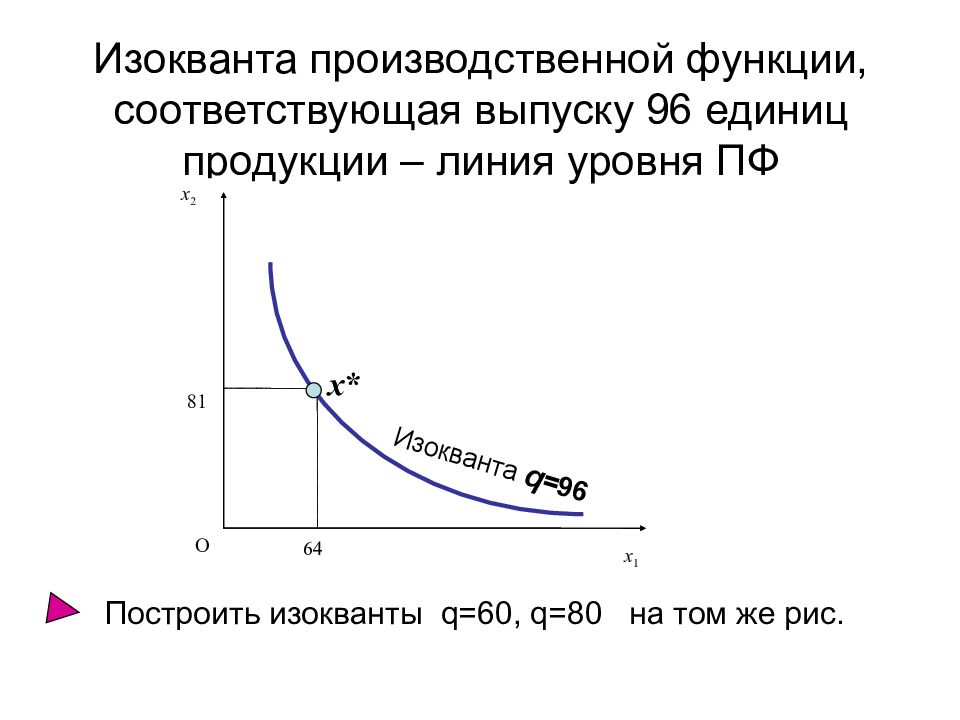
Слайд 15: Изокванта производственной функции, соответствующая выпуску 96 единиц продукции – линия уровня ПФ
x 1 x 2 64 O 81 x * q =96 x 1 x 2 64 O 81 x * Изокванта q =96 Построить изокванты q=60, q=80 на том же рис.
Слайд 16: Градиент
Градиент ФНП в точке – вектор, координаты которого равны частным производным функции в этой точке Градиент указывает направление и величину максимальной скорости возрастания функции в точке
Слайд 17: Свойства градиента
Градиент функции в точке перпендикулярен (ортогонален) поверхности уровня, проходящей через данную точку. Если приращения аргумента достаточно малы, функция возрастает (убывает) только для тех из них, которые составляют острый (тупой) угол с градиентом Функция практически не меняется для приращений, ортогональных градиенту. Градиент ПФ называют вектором предельного продукта
Слайд 18: Экономическая область ПФ
область, в которой увеличение затрат любого ресурса не приводит к уменьшению выпуска продукции. План ( ) лежит в экономической области ПФ
Слайд 19: Закон убывающей отдачи ресурса
если последовательное равномерное увеличение затрат этого ресурса при фиксированных значениях остальных приводит к последовательно уменьшающемуся приросту выпуска продукции. Теорема. Для того, чтобы в некоторой области выполнялся Закон убывающей отдачи ресурса, необходимо и достаточно, чтобы в этой области вторая частная производная ПФ по соответствующей переменной была отрицательна:
Слайд 20: Коэффициенты эластичности выпуска по затратам ресурсов
определяются следующими формулами : Коэффициенты эластичности равны отношению предельной отдачи ресурса к средней отдаче ресурса: Экономический смысл : коэффициент эластичности выпуска по затратам первого ресурса показывает, на сколько примерно процентов изменится выпуск продукции, если затраты первого ресурса увеличить на 1%.
Слайд 21: Эффект масштаба
- объем выпускаемой продукции при плане ( ). При увеличении затрат ресурсов в k раз ( k > 1) выпуск составит выпуск продукции увеличился эффект от расширения масштабов производства тоже в k раз постоянный более, чем в k раз менее, чем в k раз возрастающий убывающий
Слайд 22: Однородные функции
Функция нескольких переменных называется однородной порядка m, если для всех х из некоторой области Х Если ПФ является однородной порядка m, то при m =1 ПФ обладает постоянным ; при m >1 ПФ обладает возрастающим при m <1 ПФ обладает убывающим эффектом масштаба
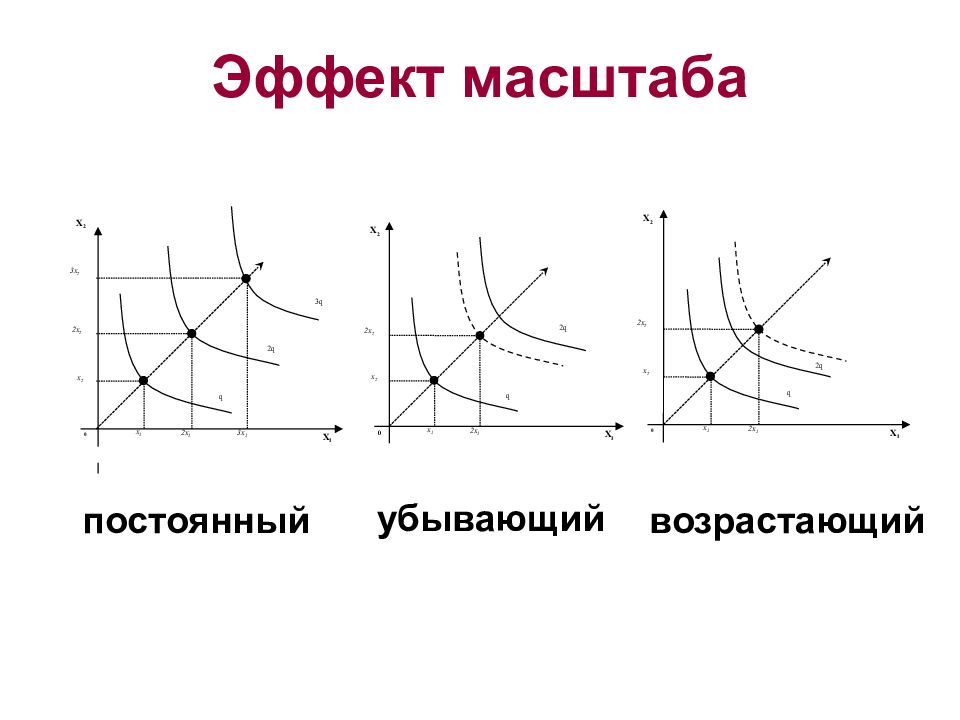
Слайд 23: Эффект масштаба
0 X 1 X 2 q 2q 3q x 1 2x 1 3x 1 x 2 2x 2 3x 2 0 X 1 X 2 q 2q x 1 2x 1 x 2 2x 2 0 X 1 X 2 q 2q x 1 2x 1 x 2 2x 2 убывающий возрастающий постоянный
Слайд 25: Планирование производства
Долговременное Long-run возможны изменения всех ресурсов Все ресурсы переменные Эффект от расширения масштаба производства Кратковременное short-run Есть ограничения на ресурсы Ресурсы постоянные и переменные Закон убывающей отдачи переменного ресурса
Слайд 26: Приращение ФНП
функция f ( x, y ) имеет в точке М 0 непрерывные частные производные, то по известным приращениям аргументов Δ x, Δ y, приближенно вычислим полное приращение функции
Слайд 27: Дифференциал ФНП
полным дифференциалом функции называется линейная по приращениям аргументов часть приращения функции
Слайд 29: Предельная норма технологического замещения второго ресурса первым
Экономический смысл предельной нормы замещения - это примерное количество второго ресурса, которое можно сэкономить, увеличив затраты первого ресурса на 1 единицу, при этом объем выпуска не изменится. MRTS – marginal rate of technical substitution.
Слайд 30: Геометрический смысл предельной нормы замещения второго ресурса первым:
численно равна тангенсу угла наклона касательной к изокванте в точке ( x 1, x 2 ), взятому с обратным знаком. мы будем рассматривать тангенс смежного острого угла, поскольку тангенсы этих углов отличаются только знаком.
Слайд 31: Основные свойства
численно равна тангенсу острого угла наклона касательной к изокванте в точке ( x 1, x 2 ).
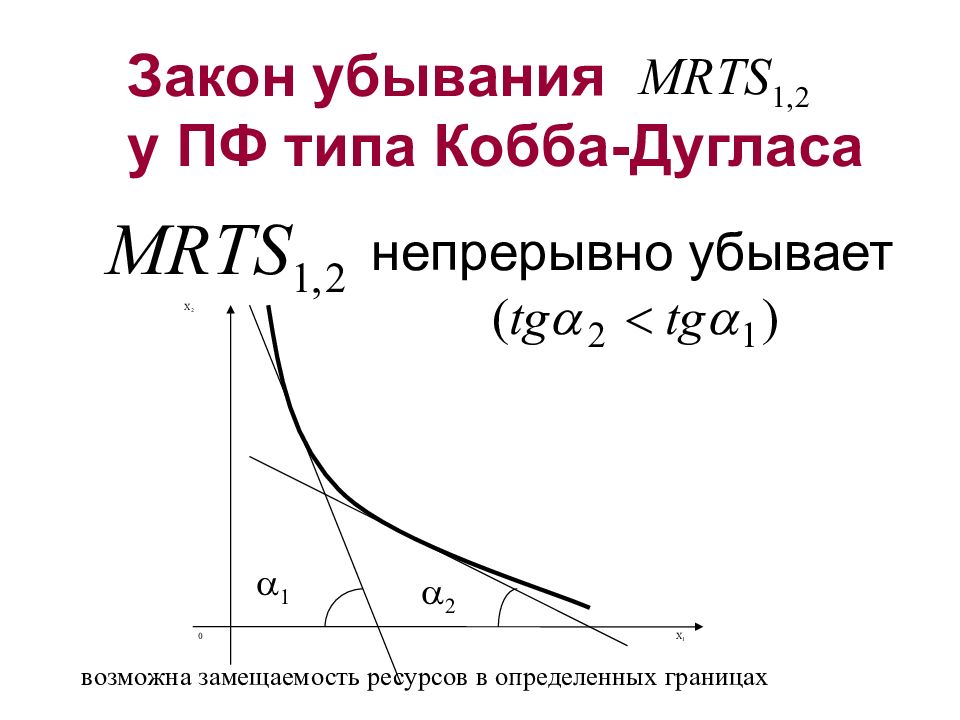
Слайд 32: Закон убывания у ПФ типа Кобба-Дугласа
непрерывно убывает 1 X 2 X 1 0 2 возможна замещаемость ресурсов в определенных границах
Слайд 33: Линейная производственная функция
применяется при моделировании таких производственных процессов, где выпуск однородной продукции является результатом одновременного функционирования нескольких технологий, выпуск линейно зависит от затрат, ресурсы полностью взаимозаменяемы, т. е. для выпуска достаточно наличия хотя бы одного ресурса. 0 X 2 X 1 a 1 a 2 (a 1,a 2 )
Слайд 34: ПРИМЕРЫ применения линейной ПФ:
производство однотипных деталей рабочими различных разрядов, выемка грунта рабочими или экскаваторами, выручка дистрибьюторов однородного товара, сегмент рынка, крупная отрасль, народное хозяйство в целом.
Слайд 35: Ресурсы
x = ( x 1, x 2,..., x n ) - план по затратам переменных ресурсов вектор w = ( w 1, w 2,..., w n ) задает цены переменных ресурсов. Стоимость переменных ресурсов = переменные издержки стоимость затраченных постоянных ресурсов С 0 = постоянные издержки, G ( x ) = общая стоимость затраченных ресурсов = общие издержки переменные постоянные
Слайд 36: Изокоста
- множество планов производства с одинаковыми переменными издержками Уравнение изокосты Семейство изокост на плоскости – множество отрезков параллельных прямых с нормалью Угол наклона изокосты к оси О x 1 определяется отношением цен на ресурсы: tg = – w 1 / w 2.