Первый слайд презентации
ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ Уфа-2017 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Уфимский государственный авиационный технический университет » Кафедра Управления в социальных и экономических системах Доцент каф. УСиЭС к.э.н. Орешников Владимир Владимирович
Слайд 2
Организационные вопросы Сверить расписание Список группы, телефон старосты, ящик группы За пропуски – дополнительное задание на допуск к экзамену Правила внутреннего распорядка Данный курс лекций является лишь базовой основой для изучения дисциплины. Надеюсь, что будите благоразумны и прочитаете еще хотя бы пару книг. Вместе с лекциями будет высланы: Различные материалы по дисциплине Требования к выполнению контрольной работы (заочники полные) Критерии выполнения и защиты контрольной работы (заочники полные) Перечень вопросов для подготовки к экзамену Критерии оценки на экзамене Список рекомендованной литературы (библиотека УГАТУ ждет Вас ) Voresh@mail.ru 892731 8 6940 ГМУ УГАТУ vk.com/ gmu_usatu
Слайд 3
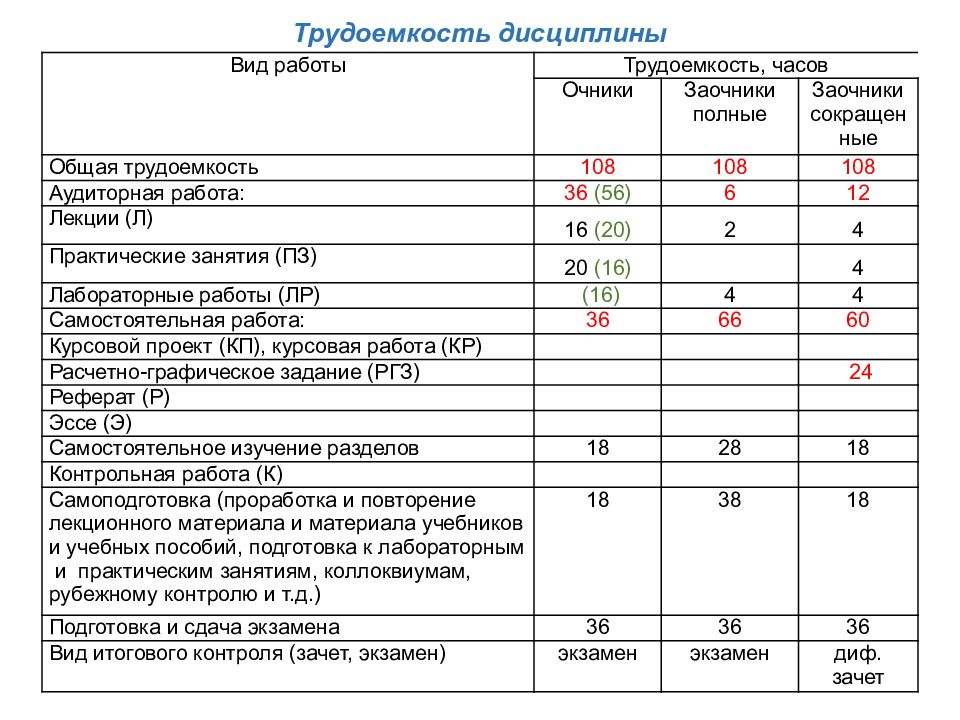
Трудоемкость дисциплины Вид работы Трудоемкость, часов Очники Заочники полные Заочники сокращенные Общая трудоемкость 108 108 108 Аудиторная работа: 36 (56) 6 12 Лекции (Л) 16 (20) 2 4 Практические занятия (ПЗ) 20 (16) 4 Лабораторные работы (ЛР) (16) 4 4 Самостоятельная работа: 36 66 60 Курсовой проект (КП), курсовая работа (КР) Расчетно-графическое задание (РГЗ) 24 Реферат (Р) Эссе (Э) Самостоятельное изучение разделов 18 28 18 Контрольная работа (К) Самоподготовка (проработка и повторение лекционного материала и материала учебников и учебных пособий, подготовка к лабораторным и практическим занятиям, коллоквиумам, рубежному контролю и т.д.) 18 38 18 Подготовка и сдача экзамена 36 36 36 Вид итогового контроля (зачет, экзамен) экзамен экзамен диф. зачет
Слайд 4
Структура курса 1 Сущность математического моделирования социально-экономических процессов 2 Модели и методы линейного программирования 3 Система национальных счетов 4 Вероятностно-статистические модели социально-экономических процессов 5 Особенности моделирования различных сфер 6 Имитационное моделирование социально-экономических процессов
Слайд 5
Методические рекомендации РГР ВНИМАНИЕ! РГР защищается. Заказал и не можешь понять что написано? Готовься к повторной защите. Теория (5-7 страниц, уникальность > 50%) Задача об использовании ресурсов; Задача использования мощностей ; Задача о составлении рациона; Задача о раскрое материалов; Регрессия. Пояснение по решению первой задачи смотрите в методических указаниях к практическим и лабораторным работам, к остальным задачам – в приложении 2.
Слайд 6
Экзамен (очники) Экзамен проводится в письменном виде. Экзаменационный билет включает один теоретический вопрос, блок из 4 тестовых заданий и практическое задание. Выполнение каждого задания оценивается по пятибалльной шкале. Время на выполнение всех заданий составляет 45 минут. Лекциями, формулами, телефоном и т.д. пользоваться нельзя. Остальные подробности на консультации. В тестовые задания включают 4 варианта ответа, правильным из которых является лишь один. За правильный ответ на 4 тестовых вопроса по данному заданию выставляется оценка «отлично», на 3 тестовых вопроса – оценка «хорошо», на 2 тестовых вопроса – оценка «удовлетворительно», менее, чем 2 ответа – оценка «неудовлетворительно». Итоговая оценка определяется как средняя за три представленных задания. Кроме того студент заслуживает оценки «не удовлетворительно» в случае, если за любое из заданий он получил оценку «неудовлетворительно» вне зависимости от суммарного числа баллов. Балльно -рейтинговая система Сумма баллов Числовой эквивалент 91 – 100 5 «отлично» 74 – 90 4 «хорошо» 61 – 73 3 «удовлетворительно» 0-60 2 «неудовлетворительно»
Слайд 7
Дифференцированный зачет (заочники) Зачет проводится в письменном виде. Билет включает: блок из тестовых заданий (последний вопрос открытый) Практическое задание Время на выполнение всех заданий составляет 45 минут. Выполнение каждого задания оценивается по пятибалльной шкале. Итоговая оценка определяется как средняя за три представленных задания. Кроме того студент заслуживает оценки «не удовлетворительно» в случае, если за любое из заданий он получил оценку «неудовлетворительно» вне зависимости от суммарного числа баллов.
Слайд 8
Рекомендуемая литература Учебники по эконометрике, статистике Книги по работе с Екселем и статистикой Основная литература. Орлова, Е. В. Эконометрическое моделирование и прогнозирование : [учебное пособие для бакалавров и магистров всех форм обучения по напр. 080100 "Экономика"] / Е. В. Орлова ; ФГБОУ ВПО УГАТУ.— Уфа : УГАТУ, 2013.— 250 с. Математическое моделирование экономических процессов и систем : [учебное пособие для студентов, обучающихся по специальностям "Мировая экономика", "Финансы и кредит", "Бухгалтерский учет, анализ и аудит"] / О. А. Волгина [и др.].— Москва : КноРус, 2011.— 200 с. Дополнительная литература Высшая математика для экономического бакалавриата : учебник и практикум : [учебник для студентов высших учебных заведений, обучающихся по специальности "Математические методы в экономике" и другим экономическим специальностям] / Н. Ш. Кремер [и др.] ; под ред. Н. Ш. Кремера.— 4-е изд., перераб. и доп. — Москва : Юрайт, 2012.— 909 с. Общий курс высшей математики для экономистов : [учебник для студентов высших учебных заведений, обучающихся по экономическим специальностям] / Б. М. Рудык [и др.] ; под общ. ред. В. И. Ермакова.— Москва : Инфра-М, 2010.— 656 с.
Слайд 9
Лекция 1 Сущность математического моделирования социально-экономических процессов
Слайд 10
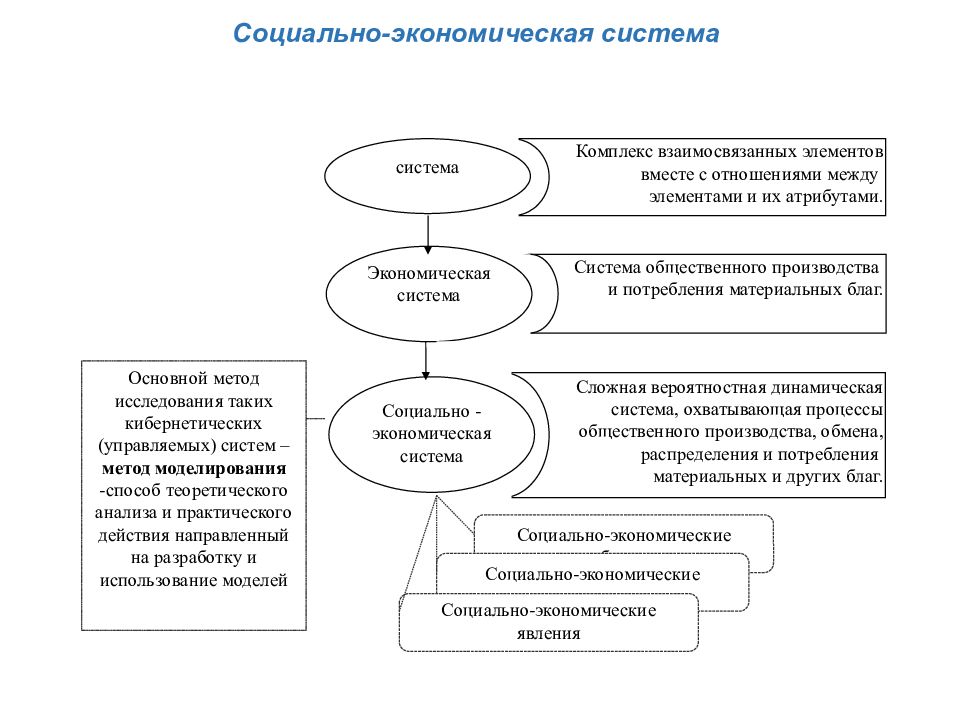
Система общественного производства и потребления материальных благ. Экономическая система Комплекс взаимосвязанных элементов вместе с отношениями между элементами и их атрибутами. система Сложная вероятностная динамическая система, охватывающая процессы общественного производства, обмена, распределения и потребления материальных и других благ. Социально -экономическая система Основной метод исследования таких кибернетических (управляемых) систем – метод моделирования -способ теоретического анализа и практического действия направленный на разработку и использование моделей Социально-экономические объекты Социально-экономические процессы Социально-экономические явления Социально-экономическая система
Слайд 11
Свойства социально-экономической системы эмерджентность ( интегративность ) – проявление свойства целостности системы, т.е. наличия у экономической системы таких свойств, которые не присущи ни одному из составляющих систему элементов; Сложность Целостность иерархичность массовость: закономерности процессов не обнаруживаются на основании небольшого числа наблюдений, поэтому моделирование должно опираться на массовые наблюдения; динамичность случайность: экономические явления и процессы носят в основном вероятностный характер, и для их изучения необходимо применение экономико-математических моделей на базе теории вероятностей и математической статистики; активная реакция на появляющиеся новые факторы открытость
Слайд 12
Ранг целей Функция целей Постановка целей Главная Интегральная Повышение уровня и качества жизни населения на основе постиндустриальной экономики; благополучие физическое и духовное здоровье людей Подцели – цели первого порядка Социальная Социальная и территориальная справедливость, цивилизованный образ жизни Демографическая Расширенное воспроизводство здоровых людей Экономическая Переход всех регионов на постиндустриальный уровень Экологическая Экологическое равновесие, благоприятная для жизни природная среда Политическая Целостность федеративного государства Культурная Расцвет национальной и региональной культуры, искусства, науки, образования Цели стратегии регионального развития У СЭС много подсистем, много субъектов и много целей
Слайд 13
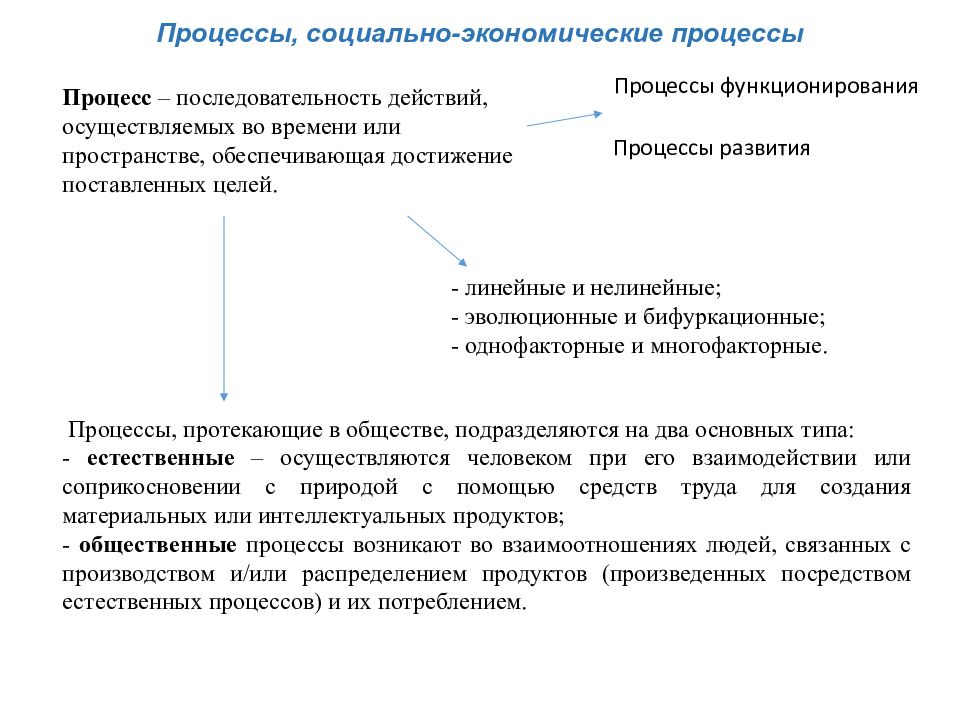
Процессы, социально-экономические процессы Процесс – последовательность действий, осуществляемых во времени или пространстве, обеспечивающая достижение поставленных целей. Процессы функционирования Процессы развития - линейные и нелинейные; - эволюционные и бифуркационные ; - однофакторные и многофакторные. Процессы, протекающие в обществе, подразделяются на два основных типа: - естественные – осуществляются человеком при его взаимодействии или соприкосновении с природой с помощью средств труда для создания материальных или интеллектуальных продуктов; - общественные процессы возникают во взаимоотношениях людей, связанных с производством и/или распределением продуктов (произведенных посредством естественных процессов) и их потреблением.
Слайд 15
Свойства социально-экономических процессов Многомереность. Социальные процессы являются чрезвычайно сложными, что существенно затрудняет их понимание и объяснение. Постижение природы социальных процессов возможно через использование междисциплинарных под-ходов, позволяющих отобразить многослойный характер общественной жизни. Динамизм. Неравномерность Многовекторность ( поливариантность ).
Слайд 16
Уровни СЭП (1) Макропроцессы осуществляются на уровне мирового сообщества, на- циональных государств, регионов, этнических групп. По времени они относятся к наиболее продолжительным. Сюда относятся процессы гло-бализации, мировые социальные движения, процессы секуляризации и т.п. (2) Мезопроцессы охватывают большие группы, сообщества, ассоциации – напр., процессы образования политических партий, формирование национальной бюрократии и т.п. (3) Микропроцессы протекают в повседневной жизни людей – в малых группах, семьях, школах, кружках и т.п.
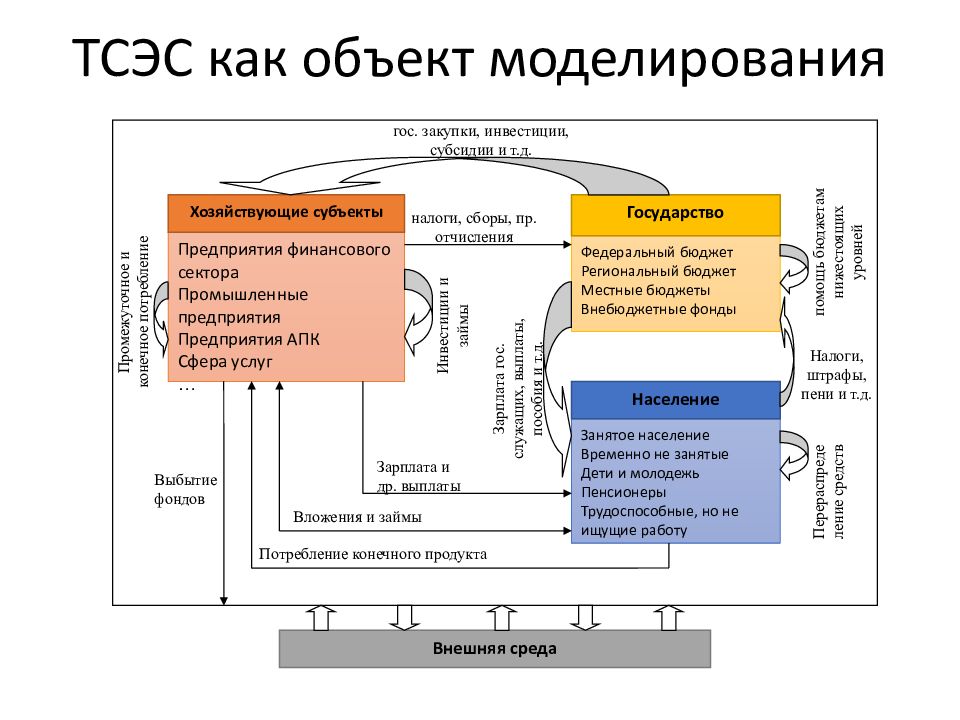
Слайд 17: ТСЭС как объект моделирования
Федеральный бюджет Региональный бюджет Местные бюджеты Внебюджетные фонды Государство Занятое население Временно не занятые Дети и молодежь Пенсионеры Трудоспособные, но не ищущие работу Население Предприятия финансового сектора Промышленные предприятия Предприятия АПК Сфера услуг … Хозяйствующие субъекты налоги, сборы, пр. отчисления помощь бюджетам нижестоящих уровней Зарплата гос. служащих, выплаты, пособия и т.д. Перераспреде ление средств гос. закупки, инвестиции, субсидии и т.д. Зарплата и др. выплаты Потребление конечного продукта Выбытие фондов Промежуточное и конечное потребление Налоги, штрафы, пени и т.д. Вложения и займы Инвестиции и займы Внешняя среда
Слайд 18
Прогнозирование и планирование Различаются следующие периоды прогнозирования : краткосрочный (1-5 лет); среднесрочный (5-10 лет); долгосрочный (15-20 лет); сверхсрочный (50-100 лет). По масштабу прогнозы делятся на личные, на уровне предприятия (организации), местные, региональные, отраслевые, страновые, мировые (глобальные). Плани́рование — оптимальное распределение ресурсов для достижения поставленных целей, деятельность (совокупность процессов), связанных с постановкой целей (задач) и действий в будущем. Постановка целей и задач Составление программы действий (проектирования) Вариантное составление программы (вариантное проектирование) Выявление необходимых ресурсов и их источников Определение непосредственных исполнителей и доведение планов до них Фиксация результатов планирования в материальном виде, например, в виде проекта, карты боевых действий, приказа в письменной форме и т. п.
Слайд 19
Предвидение Сценарий Предсказательная фаза Предуказательная фаза Целевая программа
Слайд 20
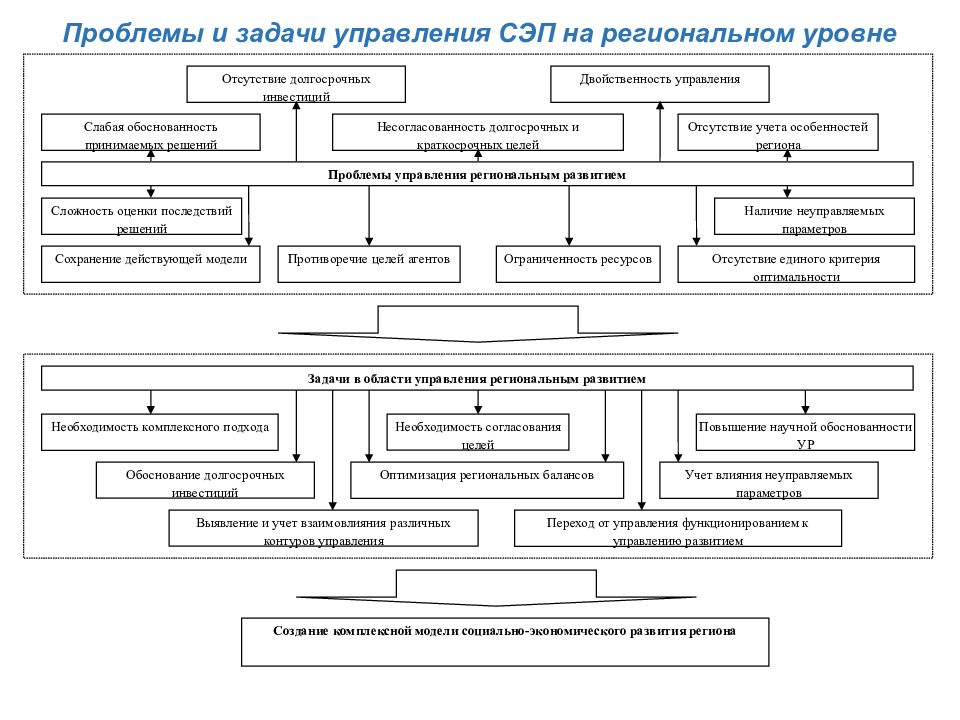
Проблемы и задачи управления СЭП на региональном уровне Создание комплексной модели социально-экономического развития региона Выявление и учет взаимовлияния различных контуров управления Переход от управления функционированием к управлению развитием Оптимизация региональных балансов Обоснование долгосрочных инвестиций Необходимость комплексного подхода Учет влияния неуправляемых параметров Повышение научной обоснованности УР Задачи в области управления региональным развитием Необходимость согласования целей Проблемы управления региональным развитием Слабая обоснованность принимаемых решений Несогласованность долгосрочных и краткосрочных целей Сохранение действующей модели Отсутствие долгосрочных инвестиций Сложность оценки последствий решений Ограниченность ресурсов Двойственность управления Отсутствие учета особенностей региона Наличие неуправляемых параметров Противоречие целей агентов Отсутствие единого критерия оптимальности
Слайд 21
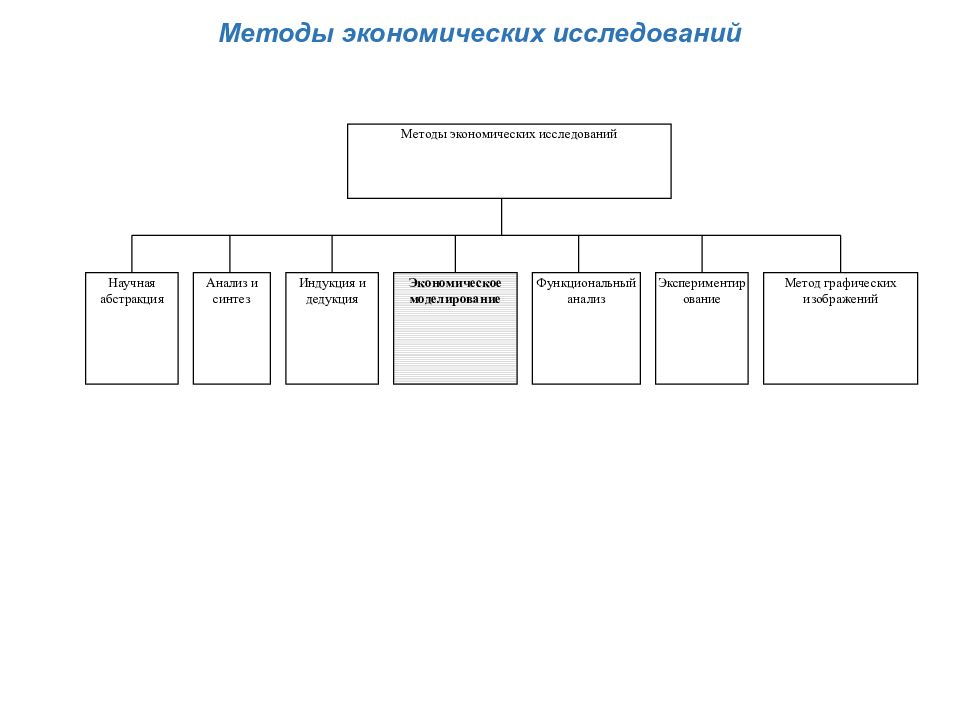
Методы экономических исследований Научная абстракция Анализ и синтез Индукция и дедукция Экономическое моделирование Функциональный анализ Экспериментирование Метод графических изображений Методы экономических исследований
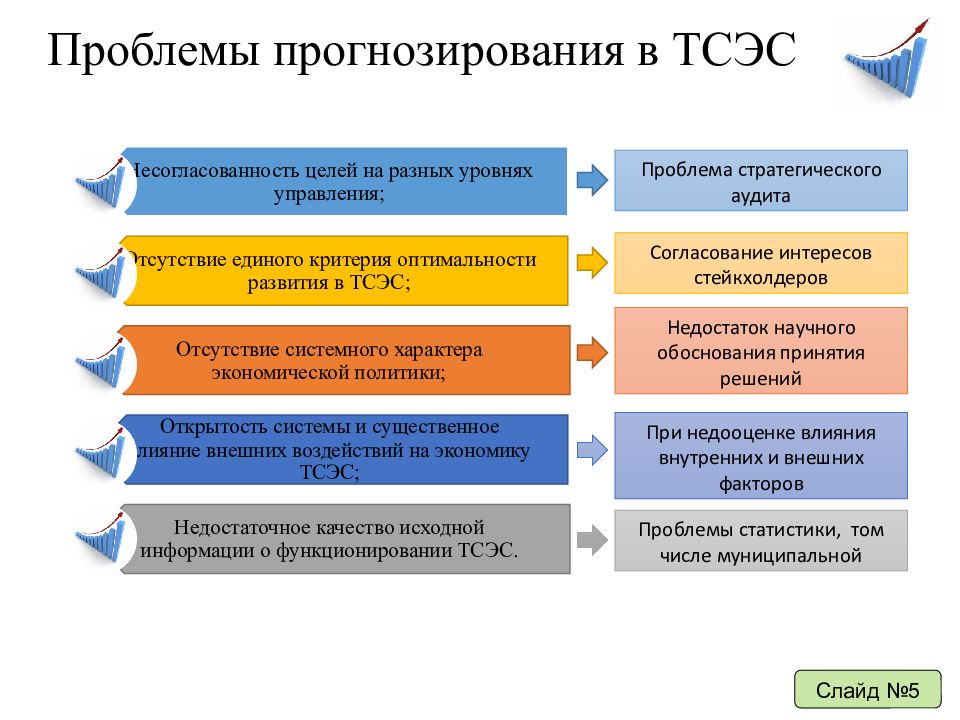
Слайд 22: Проблемы прогнозирования в ТСЭС
Слайд №5 Проблема стратегического аудита Согласование интересов стейкхолдеров Недостаток научного обоснования принятия решений При недооценке влияния внутренних и внешних факторов Проблемы статистики, том числе муниципальной
Слайд 23
Прогнозирование и планирование Прогнозирование - предсказание будущего с помощью научных методов.
Слайд 24
Понятие модели и моделирования Модели́рование — построение и исследование моделей реально существующих объектов, процессов или явлений с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих исследователя. Модель (фр. modèle, от лат. modulus — «мера, аналог, образец») — это система, исследование которой служит средством для получения информации о другой системе, это упрощённое представление реального устройства и/или протекающих в нём процессов, явлений. Процесс моделирования включает три элемента: субъект (исследователь), объект исследования, модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта. Математическая модель — это математическое представление реальности. Является частным случаем понятия модели, как системы, исследование которой позволяет получать информацию о некоторой другой системе. Процесс построения и изучения математических моделей называется математическим моделированием.
Слайд 25
Виды моделирования Информационное моделирование Компьютерное моделирование Математическое моделирование Математико-картографическое моделирование Молекулярное моделирование Цифровое моделирование Логическое моделирование Педагогическое моделирование Психологическое моделирование Статистическое моделирование Структурное моделирование Физическое моделирование Экономико-математическое моделирование Имитационное моделирование Эволюционное моделирование Графическое и геометрическое моделирование Натурное моделирование ЭКОНОМИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ – текстовое и математическое описание исследуемого социально-экономического объекта, отражающее основные закономерности в абстрактном виде с помощью математических соотношений.
Слайд 26
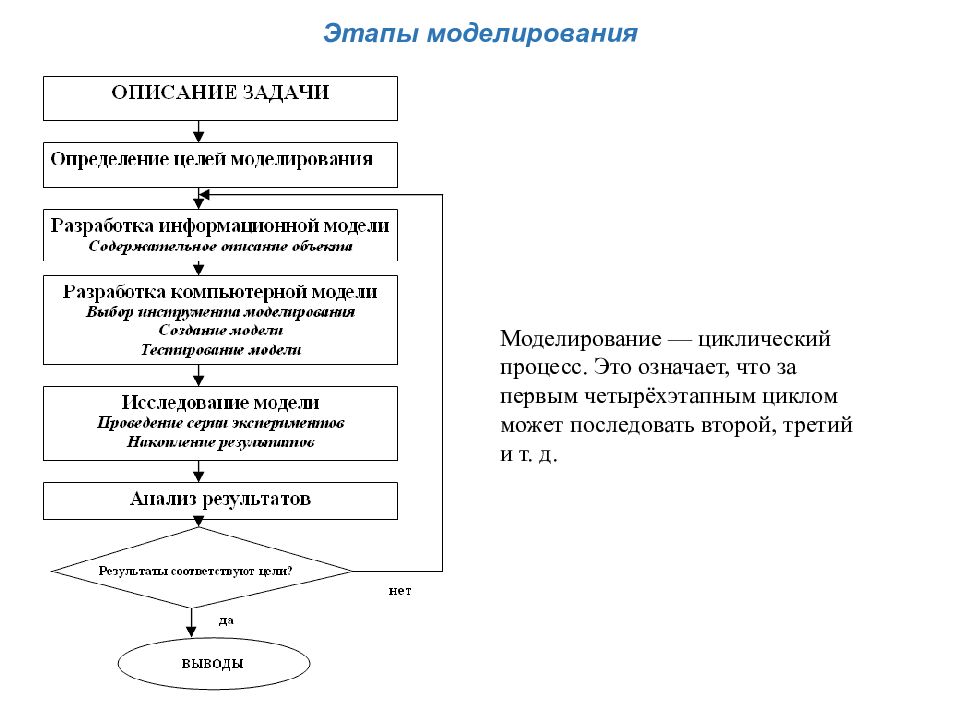
Этапы моделирования Первый этап построения модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обусловливаются тем, что модель отображает (воспроизводит, имитирует) какие-либо существенные черты объекта-оригинала. Вопрос о необходимой и достаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, модель утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от исследования других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации. На втором этапе модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о её «поведении». Конечным результатом этого этапа является множество (совокупность) знаний о модели. На третьем этапе осуществляется перенос знаний с модели на оригинал — формирование множества знаний. Одновременно происходит переход с «языка» модели на «язык» оригинала. Процесс переноса знаний проводится по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели. Четвёртый этап — практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им. Моделирование — циклический процесс. Это означает, что за первым четырёхэтапным циклом может последовать второй, третий и т. д.
Слайд 27
Требования к моделям адекватность, то есть соответствие модели исходной реальной системе и учет, прежде всего, наиболее важных качеств, связей и характеристик. Оценить адекватность выбранной модели, особенно, например, на начальной стадии проектирования, когда вид создаваемой системы ещё неизвестен, очень сложно. В такой ситуации часто полагаются на опыт предшествующих разработок или применяют определённые методы, например, метод последовательных приближений ; точность, то есть степень совпадения полученных в процессе моделирования результатов с заранее установленными, желаемыми. Здесь важной задачей является оценка потребной точности результатов и имеющейся точности исходных данных, согласование их как между собой, так и с точностью используемой модели; универсальность, то есть применимость модели к анализу ряда однотипных систем в одном или нескольких режимах функционирования. Это позволяет расширить область применимости модели для решения большего круга задач; целесообразная экономичность, то есть точность получаемых результатов и общность решения задачи должны увязываться с затратами на моделирование. И удачный выбор модели, как показывает практика, — результат компромисса между отпущенными ресурсами и особенностями используемой модели; и др.
Слайд 28
История применения мат. аппарата для решения задач управления Здесь много информации, на которую не хочется тратить время аудиторных занятий. Почитайте самостоятельно. основатель классической школы политической экономии Вильям Петти (1623 – 1687) «Политическая арифметика» В качестве исторически первой модели общественного производства называют экономическую таблицу Франсуа Кене (1694 – 1774) Родоначальником математической школы считается французский ученый Антуан Огюст Курно (1801 – 1877). В 1838 г. вышла его книга «Исследование математических принципов теории богатства» Видными представителями математической школы являются Г. Госсен (1810 – 1859) в Германии, В. Джевонс (1835 – 1882) в Англии, Л. Вальрас (1834 – 1910) в Швейцарии, Г. Кассель (1866 – 1944) в Швеции, Ф. Эджворд (1845 – 1926) в Англии, В. Парето (1848 – 1923) в Италии, В. Дмитриев)1868 – 1913) в России. 1909 г. Митчерлих предложил нелинейную производственную функцию В 1928 г. Чарльз Кобб и Пол Дуглас на основе данных по обрабатывающей промышленности США за период 1899 – 1922 гг. В 1932 г. Джон фон Нейман изложил основы многосекторной модели расширяющейся экономики
Слайд 29
В 1931 г. было создано международное эконометрическое общество, видным представителем и активным деятелем которого был норвежский ученый Рагнар Фриш (1895 – 1973) Р. Солоу. В статье, опубликованной в 1956 году, он предложил простую модель, которая привела к появлению многочисленных исследований в области неоклассических моделей роста. В 1936 г. Василий Васильевич Леонтьев опубликовал основы метода (модели) «затраты – выпуск». Леонил Вительевич Канторовича «Математические методы организации и планирования производства» (Ленинград, 1939г.) В. В. Новожилов, В. С. Немчинов…
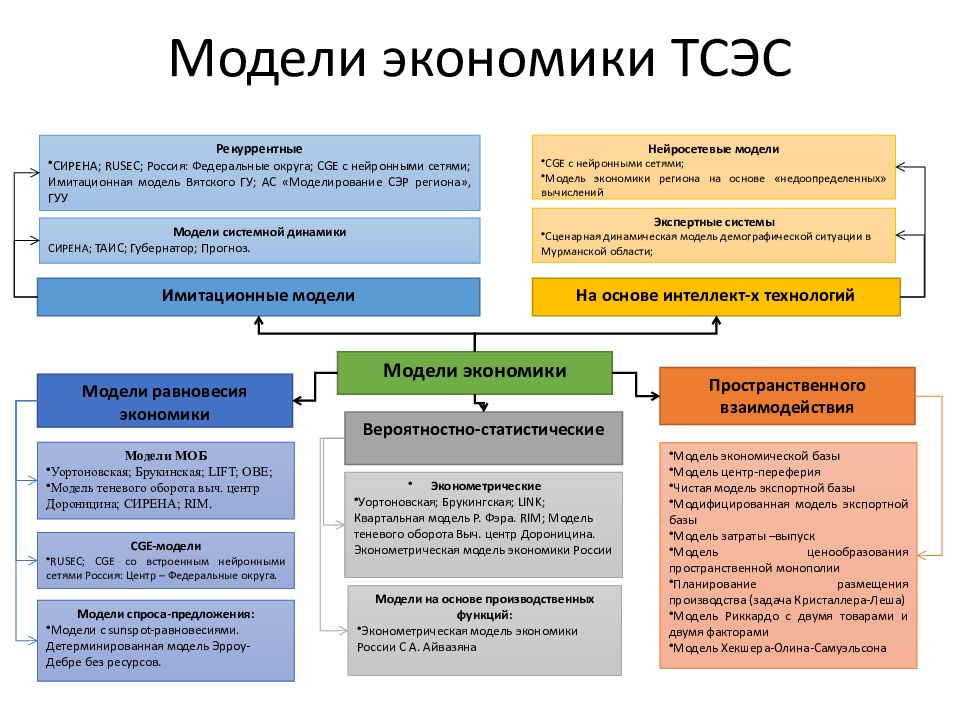
Слайд 32: Модели экономики ТСЭС
Модели экономики Модели равновесия экономики Модели МОБ Уортоновская; Брукинская; LIFT ; OBE ; Модель теневого оборота выч. центр Дороницина; СИРЕНА; RIM. CGE- модели RUSEC ; CGE со встроенным нейронными сетями Россия: Центр – Федеральные округа. Модели спроса-предложения: Модели с sunspot -равновесиями. Детерминированная модель Эрроу-Дебре без ресурсов. Вероятностно-статистические Эконометрические Уортоновская; Брукингская; LINK ; Квартальная модель Р. Фэра. RIM ; Модель теневого оборота Выч. центр Дороницина. Эконометрическая модель экономики России Модели на основе производственных функций: Эконометрическая модель экономики России С А. Айвазяна Пространственного взаимодействия Модель экономической базы Модель центр-переферия Чистая модель экспортной базы Модифицированная модель экспортной базы Модель затраты –выпуск Модель ценообразования пространственной монополии Планирование размещения производства (задача Кристаллера-Леша) Модель Риккардо с двумя товарами и двумя факторами Модель Хекшера-Олина-Самуэльсона Имитационные модели Рекуррентные СИРЕНА; RUSEC ; Россия: Федеральные округа; CGE с нейронными сетями; Имитационная модель Вятского ГУ; АС «Моделирование СЭР региона», ГУУ Модели системной динамики СИРЕНА; ТАИС; Губернатор; Прогноз. На основе интеллект-х технологий Экспертные системы Сценарная динамическая модель демографической ситуации в Мурманской области; Нейросетевые модели CGE с нейронными сетями; Модель экономики региона на основе « недоопределенных » вычислений
Слайд 33: Модели общеэкономического равновесия
Модели общеэкономического равновесия Балансовые модели CGE -модели баланс между имеющимися ресурсами (трудовыми, материальными, финансовыми) и потребностями в них вычислимые модели общего равновесия, где экономика в моделях представляют собой систему уравнений, решением которой является общее экономическое равновесие
Слайд 34: Вероятностно-статистические модели
Традиционные методы в рамках эконометрического подхода Методы анализа и прогноза временных рядов (множество методов и алгоритмов сглаживания рядов) Методы прогнозирования на основе факторных регрессионных моделей (совокупность методов отражения принципа максимального правдоподобия, а также их адаптационные настройки) Прогнозирование на основе собственно эконометрических методов и моделей (методы решения систем одновременных уравнений) Общий вид функциональных соотношений эконометрической модели
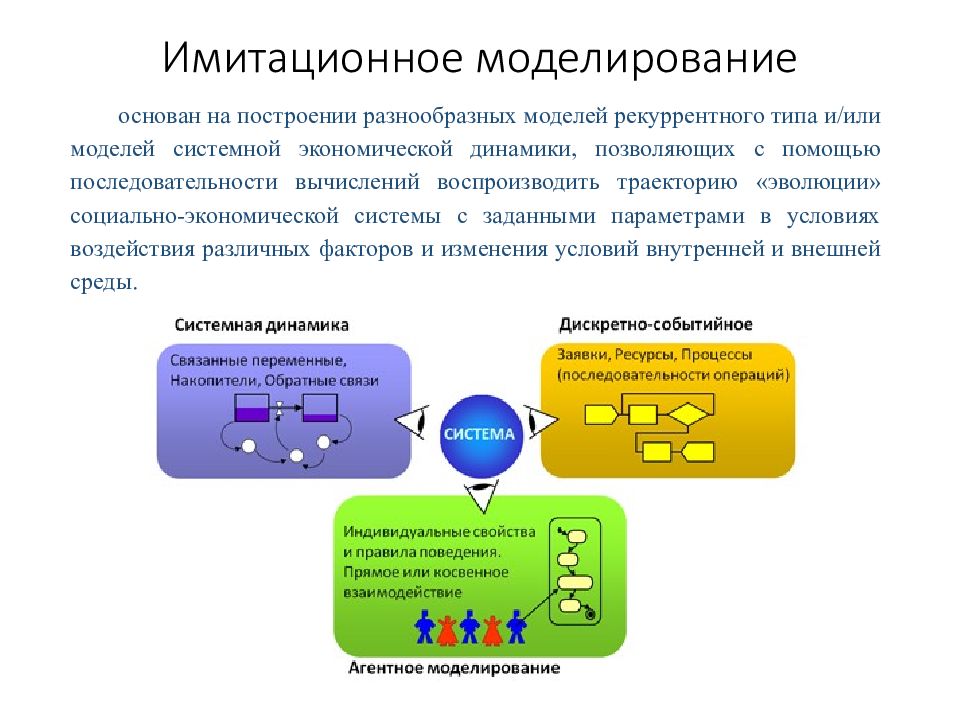
Слайд 35: Имитационное моделирование
основан на построении разнообразных моделей рекуррентного типа и/или моделей системной экономической динамики, позволяющих с помощью последовательности вычислений воспроизводить траекторию «эволюции» социально-экономической системы с заданными параметрами в условиях воздействия различных факторов и изменения условий внутренней и внешней среды.
Слайд 36
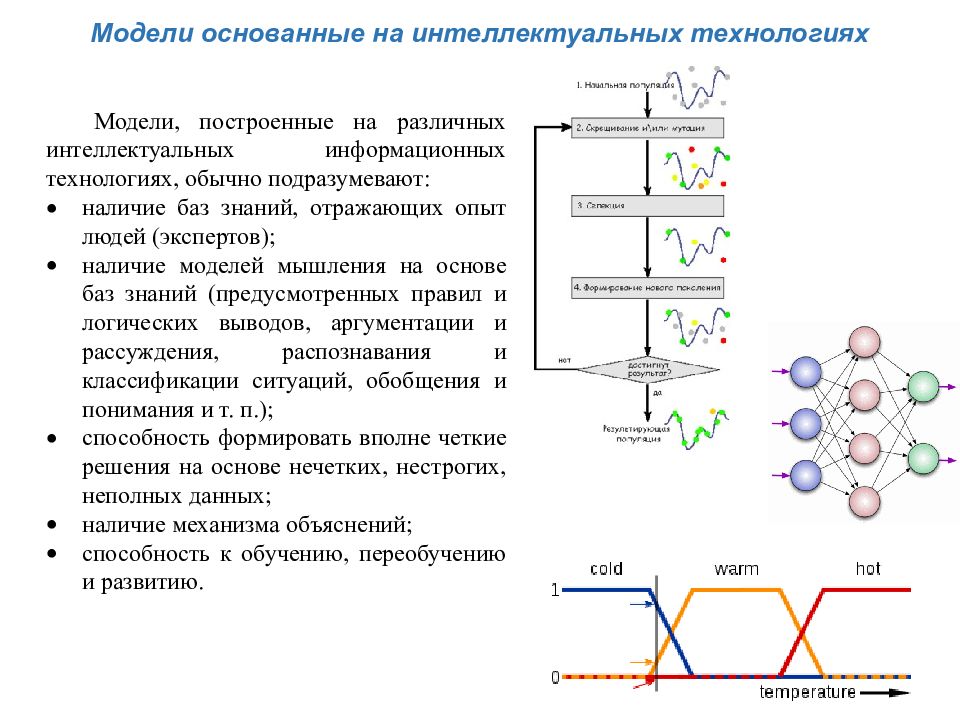
Модели основанные на интеллектуальных технологиях Модели, построенные на различных интеллектуальных информационных технологиях, обычно подразумевают: наличие баз знаний, отражающих опыт людей (экспертов); наличие моделей мышления на основе баз знаний (предусмотренных правил и логических выводов, аргументации и рассуждения, распознавания и классификации ситуаций, обобщения и понимания и т. п.); способность формировать вполне четкие решения на основе нечетких, нестрогих, неполных данных; наличие механизма объяснений; способность к обучению, переобучению и развитию.
Слайд 37: Сценарии развития
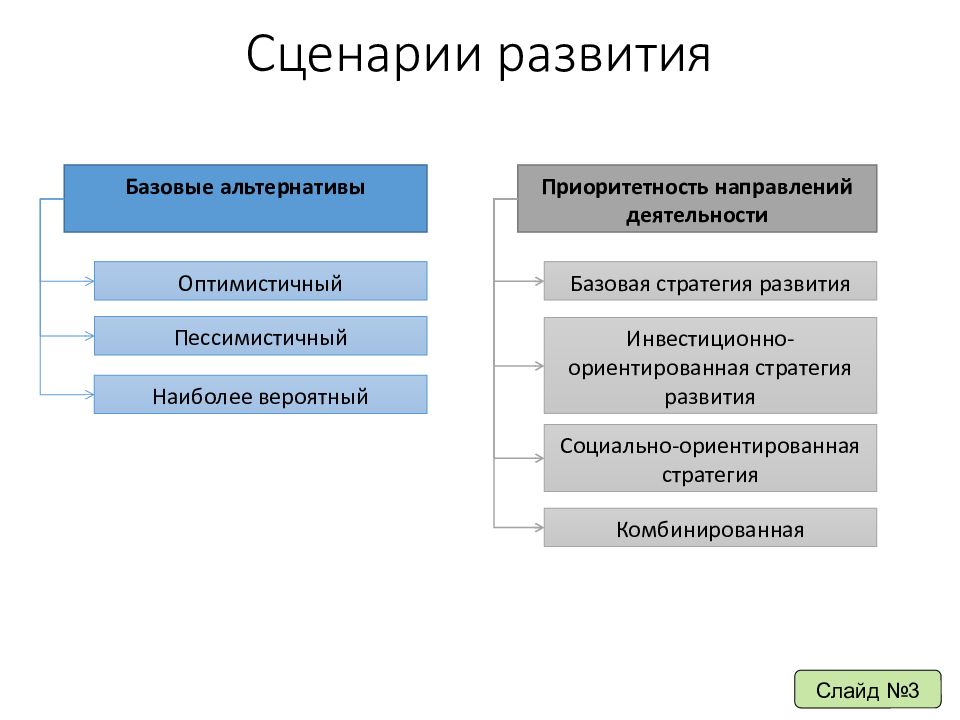
Слайд №3 Базовые альтернативы Приоритетность направлений деятельности Оптимистичный Пессимистичный Наиболее вероятный Базовая стратегия развития Инвестиционно-ориентированная стратегия развития Социально-ориентированная стратегия Комбинированная
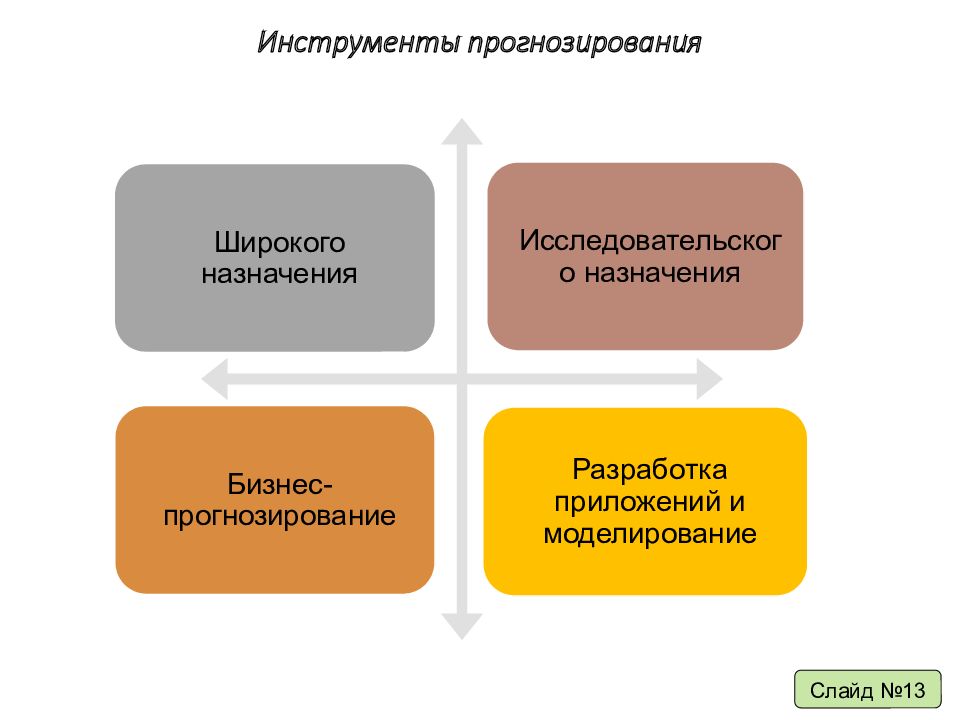
Слайд 39: Программные продукты широкого назначения
Область применения: создания документов имеющих табличное представление (в том числе, без расчетов); создание различных видов графиков, диаграмм и других иллюстративных материалов; элементарные расчеты; специфические расчеты с применением математических и статистических функций; используется в бухгалтерском учете для оформления документов, расчётов и создания диаграмм. Имеет в себе соответствующие функции; используется в качестве базы данных; используется в качестве формы для представления обработанных данных. Слайд №14 Отсутствует узкая специализация, возможность использования в различных видах деятельности. Microsoft Office : Excel Пакет OpenOffice.org: Электронная таблица
Слайд 40
Microsoft Excel Функция Описание Функция НОРМ.СТ.РАСП Возвращает стандартное нормальное интегральное распределение. Функция ПИРСОН Возвращает коэффициент корреляции Пирсона. Функция ПРЕДСКАЗ Возвращает значение линейного тренда. Функция ПРОЦЕНТРАНГ.ИСКЛ Возвращает ранг значения в наборе данных как процентное содержание в наборе данных (от 0 до 1, не включая эти числа). Функция ПУАССОН.РАСП Возвращает распределение Пуассона. Функция КОРРЕЛ Возвращает коэффициент корреляции между двумя множествами данных. Функция КОВАРИАЦИЯ.В Возвращает ковариацию для выборки, то есть среднее произведений отклонений для каждой пары точек данных в двух наборах данных. Функция ЛИНЕЙН Возвращает параметры линейного тренда. Функция СТЬЮДЕНТ.ОБР Возвращает t-значение распределения Стьюдента как функцию вероятности и числа степеней свободы. Функция ФИШЕР Возвращает преобразование Фишера. Функция ХИ2.ТЕСТ Возвращает тест на независимость. Функция ДИСП.В Оценивает дисперсию по выборке. Активация надстроек Регрессия Поиск решения Слайд №15
Слайд 41
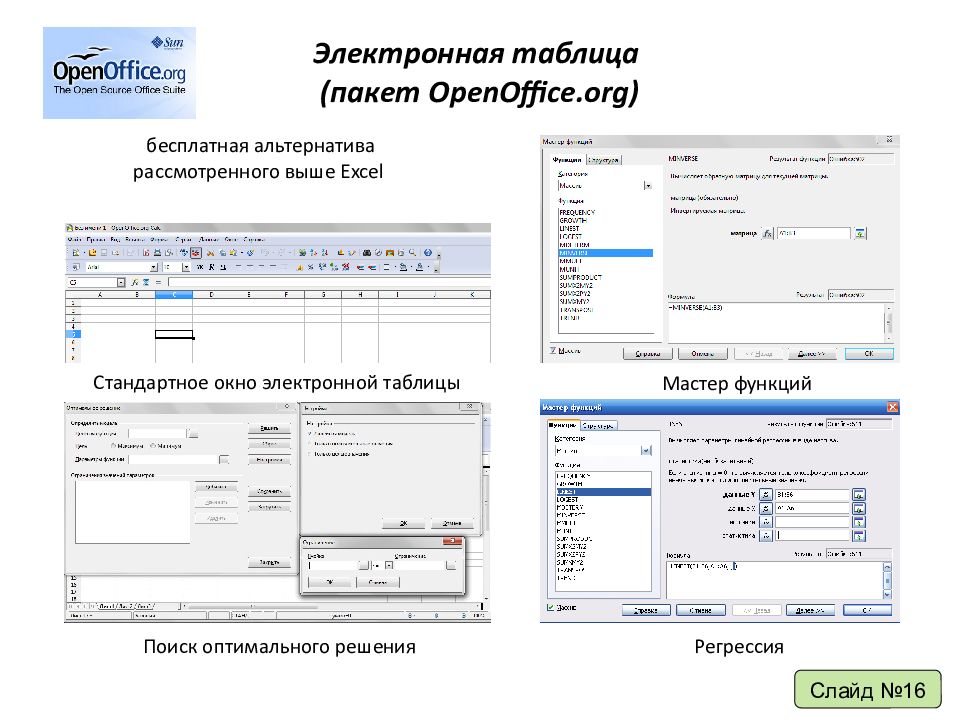
Электронная таблица (пакет OpenOffice.org) Стандартное окно электронной таблицы Мастер функций Поиск оптимального решения Слайд №16 бесплатная альтернатива рассмотренного выше Excel Регрессия
Слайд 42
Программные продукты исследовательского назначения Слайд №17 Основное назначение – научно-исследовательская работа. Требуется математическое образование Широкий спектр регрессионных, нейросетевых и других моделей
Слайд 43
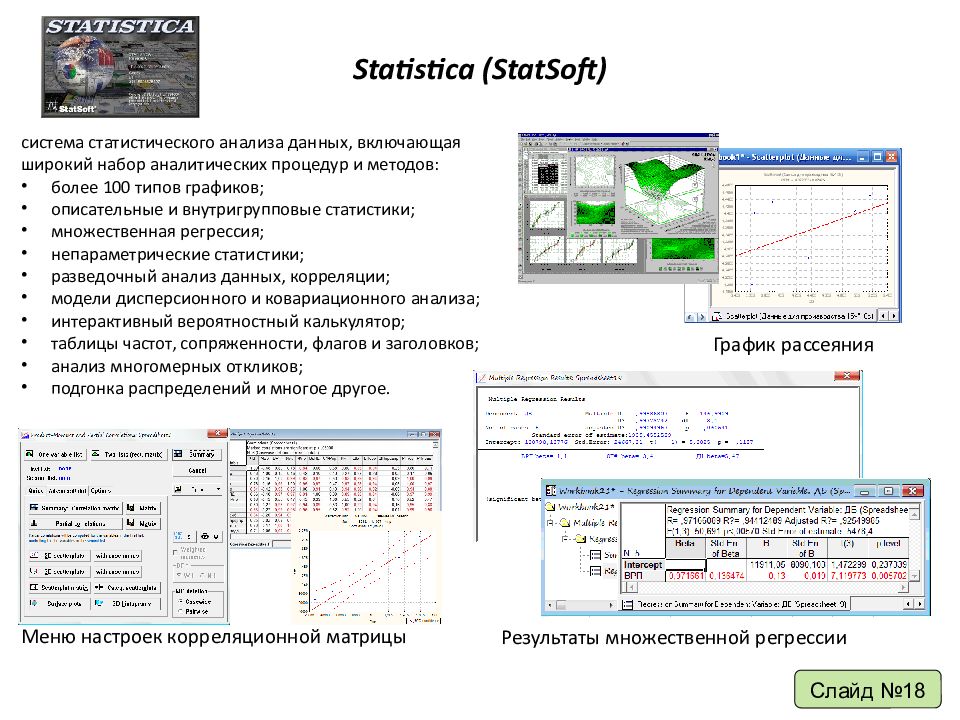
Statistica ( StatSoft) система статистического анализа данных, включающая широкий набор аналитических процедур и методов: более 100 типов графиков; описательные и внутригрупповые статистики; множественная регрессия; непараметрические статистики; разведочный анализ данных, корреляции; модели дисперсионного и ковариационного анализа; интерактивный вероятностный калькулятор; таблицы частот, сопряженности, флагов и заголовков; анализ многомерных откликов; подгонка распределений и многое другое. График рассеяния Меню настроек корреляционной матрицы Результаты множественной регрессии Слайд №18
Слайд 44
«Statistical Package for the Social Sciences» (SPSS) «статистический пакет для социальных наук» Известен также под названием PASW (Predictive Analytics SoftWare) Statistics. Основные возможности: сбор и хранение данных; работа с переменными разных типов; частотность признаков, таблицы, графики, таблицы сопряжённости, диаграммы; первичная описательная статистика; маркетинговые исследования и анализ полученных данных этих исследований. Отчет о корреляции Инструменты анализа Отчет о регрессии Слайд №19
Слайд 45
E-views Области применения Eviews : моделирование; анализ научной информации и оценивание; финансовый анализ; макроэкономическое прогнозирование; прогнозирование состояния рынков. Отчет о регрессии Корреляционная матрица и поле корреляции Окна с данными Слайд №20
Слайд 46
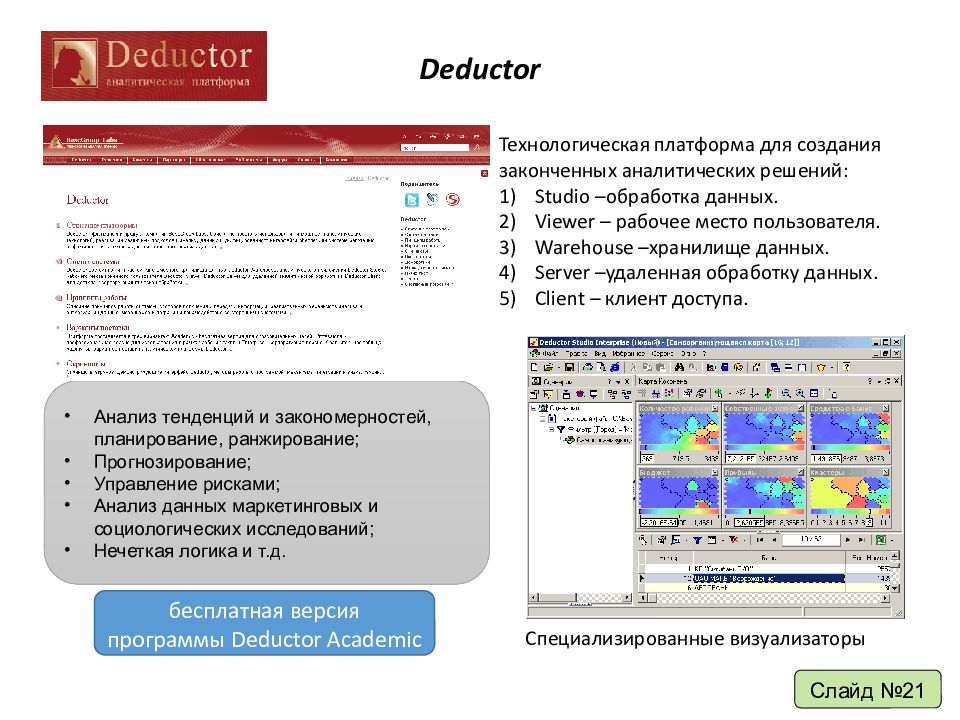
Deductor Анализ тенденций и закономерностей, планирование, ранжирование; Прогнозирование; Управление рисками; Анализ данных маркетинговых и социологических исследований; Нечеткая логика и т.д. Технологическая платформа для создания законченных аналитических решений: Studio –обработка данных. Viewer – рабочее место пользователя. Warehouse –хранилище данных. Server –удаленная обработку данных. Client – клиент доступа. бесплатная версия программы Deductor Academic Специализированные визуализаторы Слайд №21
Слайд 47
Gretl GNU Regression, Econometrics and Time-series Library авторегрессия скользящего среднего (ARMA), авторегрессия интегрированного скользящего среднего (ARIMA), обобщённая авторегрессия условной гетероскедастичности (GARCH), векторная авторегрессия (VAR), векторная модель коррекции ошибок (VECM) и др. http://gretl.sourceforge.net/ Примеры использования www.kufel.torun.pl/ru/ Интерфейс программы Gretl Слайд №22
Слайд 49
Maple предназначена для символьных вычислений, хотя имеет ряд средств и для численного решения дифференциальных уравнений и нахождения интегралов. www.maplesoft.com интерфейс программы Слайд №24
Слайд 50
Другие программные продукты исследовательского назначения Слайд №25 Включает более 20 различных программных продуктов, объединенных друг с другом «средствами доставки информации» - Information Delivery System (иногда обозначается как SAS/IDS) Направление - социологические исследования Система SAS SYSTAT Алгоритмы анализа шкал опросников (анализ внутреннего постоянства, многомерное шкалирование, классический и логит -анализ пунктов шкалы); Описательная и непараметрическая статистика, корреляция, кластерный анализ, проверка многомерных гипотез для общей линейной модели и таблицы сопряженности. SciLab Пакет прикладных математических программ для инженерных (технических) и научных расчётов, по своей сути является бесплатным аналогом инструмента Matlab STATA базовые статистические методы ; линейные и обобщенные линейные модели; панельные/повторные данные; непараметрические методы; многомерные методы; кластерный анализ…
Слайд 51
Другие программные продукты исследовательского назначения Слайд №26 STADIA STATGRAPHICS МГУ им. М. В. Ломоносова совместно с НПО «Информатика и компьютеры» описательная статистика, дисперсионный, корреляционный и спектральный анализ, сглаживание, прогнозирование, простая, нелинейная регрессия, проверка различных гипотез, анализ временных рядов, многомерные (факторный, кластерный, дискриминантный анализ и др.) и непараметрические методы анализа, методы контроля качества, анализ и замена пропущенных значений. более чем 250 статистических процедур, которые используются в бизнесе, экономике, маркетинге, социологии, психологии, производстве и других сферах MINITAB регрессионный анализ; работа с выборками; построение графиков; многомерный анализ, факторный анализ, кластерный анализ, анализ соответствий, непараметрический анализ; временные ряды и прогнозирование; статистическое управление процессами; системный анализ измерений…
Слайд 52
Программы бизнес-прогнозирования Слайд №27 Прикладное значение, используются для целей бизнес-планирования и бизнес-прогнозирования. Project Expert ForecastPro Специализированная программа для прогнозирования в области бизнеса. Планирование инвестиционных решений и мониторинг получаемых результатов
Слайд 53
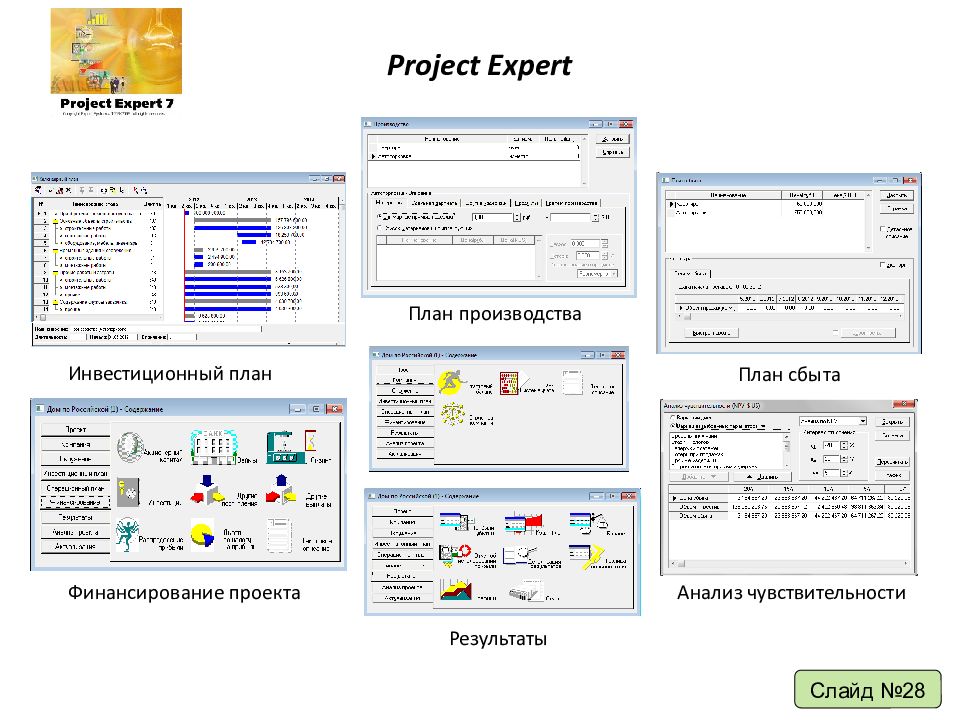
Project Expert Инвестиционный план План сбыта План производства Финансирование проекта Результаты Анализ чувствительности Слайд №28
Слайд 54
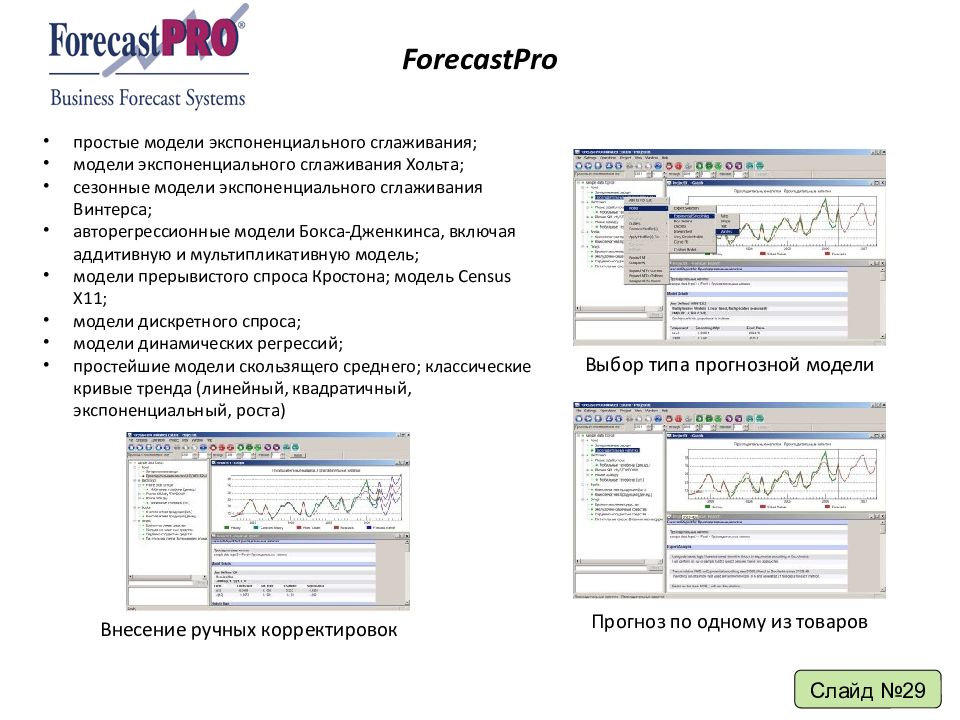
ForecastPro простые модели экспоненциального сглаживания; модели экспоненциального сглаживания Хольта; сезонные модели экспоненциального сглаживания Винтерса; авторегрессионные модели Бокса-Дженкинса, включая аддитивную и мультипликативную модель; модели прерывистого спроса Кростона; модель Census X11; модели дискретного спроса; модели динамических регрессий; простейшие модели скользящего среднего; классические кривые тренда (линейный, квадратичный, экспоненциальный, роста) Выбор типа прогнозной модели Прогноз по одному из товаров Внесение ручных корректировок Слайд №29
Слайд 55
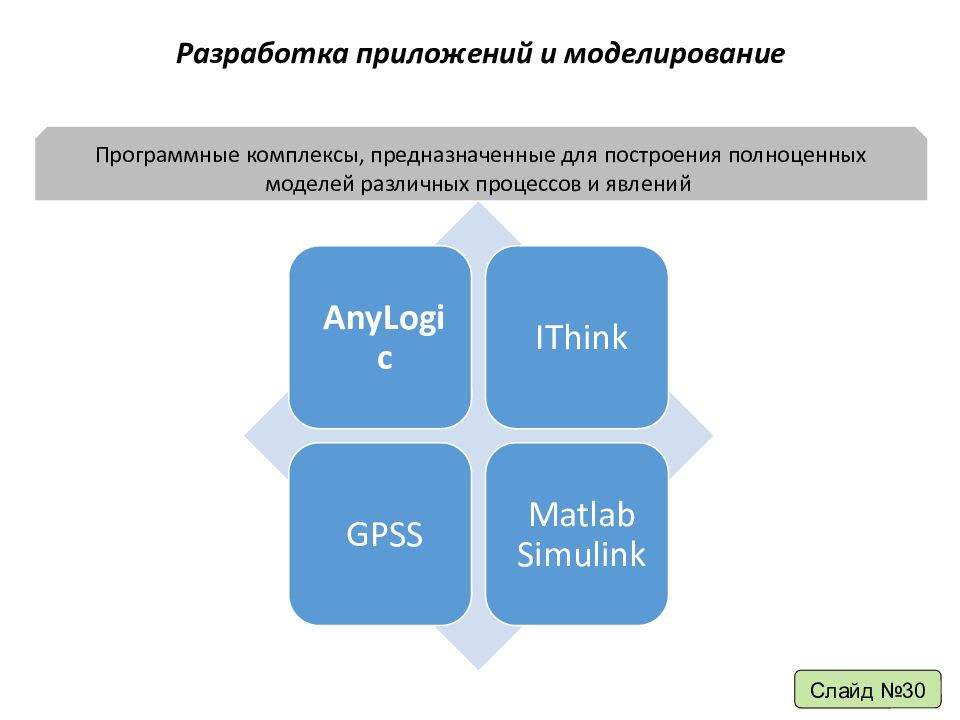
Разработка приложений и моделирование Слайд №30 Программные комплексы, предназначенные для построения полноценных моделей различных процессов и явлений
Слайд 56
AnyLogic Составные элементы AnyLogic системная динамика - Диаграмма потоков и накопителей (Stock & Flow Diagrams); в агентных моделях - Карты состояний (Statecharts) для определения поведения агентов; в дискретно-событийном моделировании - Процессные диаграммы (Process flowcharts). блок-схемы (аction charts), применяемые в дискретно-событийном моделировании (маршрутизация звонков) и агентном моделировании (для логики решений агента) Слайд №31 информация о программе, примеры реализованных моделей представлены на сайте компании www.xjtek.ru/anylogic/overview/
Слайд 57
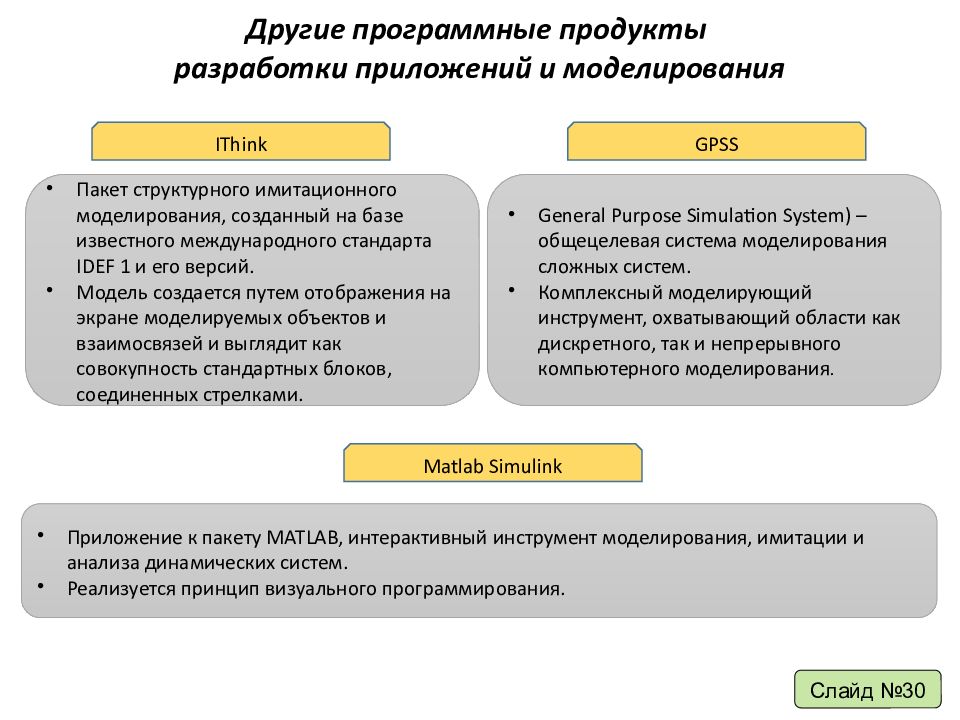
Другие программные продукты р азработки приложений и моделирования Слайд №30 Matlab Simulink Приложение к пакету MATLAB, интерактивный инструмент моделирования, имитации и анализа динамических систем. Реализуется принцип визуального программирования. GPSS General Purpose Simulation System ) – общецелевая система моделирования сложных систем. Комплексный моделирующий инструмент, охватывающий области как дискретного, так и непрерывного компьютерного моделирования. IThink Пакет структурного имитационного моделирования, созданный на базе известного международного стандарта IDEF 1 и его версий. Модель создается путем отображения на экране моделируемых объектов и взаимосвязей и выглядит как совокупность стандартных блоков, соединенных стрелками.
Слайд 59
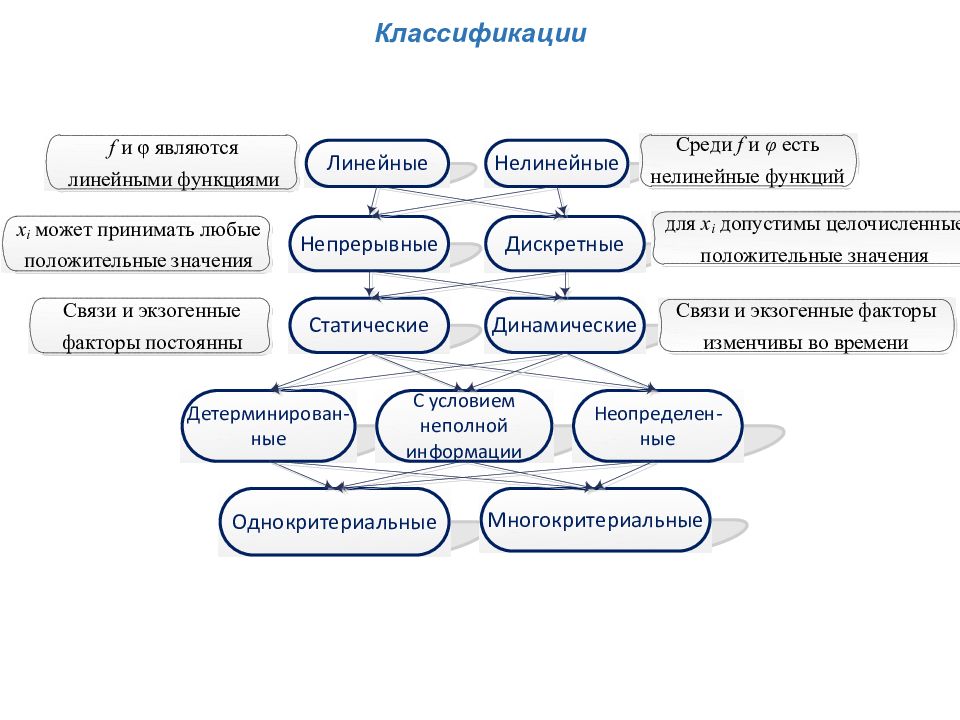
Оптимизационные задачи ОПТИМИЗАЦИОННАЯ ЗАДАЧА в математической интерпретации является задачей определения экстремума n переменных при некоторых ограничениях, т.е. задачей на условный экстремум. В основу классификации закладываются вид и свойства входящих в модель функции, ограничений, параметров и переменных, такие как: Характер взаимосвязи между переменными ; Характер изменения переменных ; Зависимость параметров и функций от времени; Степень полноты данных; Количество критериев оптимизации.
Слайд 62
Задача об использовании ресурсов Задача об использовании ресурсов (задача планирования производства, задача оптимального распределения ресурсов). Дано: Для изготовления n видов продукций P 1, P 2,…, P n используется ресурсы S 1, S 2,…, S m, запас которых ограничен - b 1, b 2,…, b m. Норма затрат ресурсов на изготовление единицы продукций (технологический коэффициент) - a ij, то есть это число единиц ресурса S i затрачиваемого на изготовление единицы продукции P j. Обозначим так же c j - прибыль от реализации единицы продукции P j.. В планируемый период все показатели предполагаются постоянными. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Вид ресурса Запас, ед Расход ресурса на ед. продукции P 1 P 2 … P n S 1 b 1 a 11 a 12 … a 1n S 2 b 2 a 21 a 22 … a 2n … … … … … … S m b m a m1 a m2 … a mn Прибыль от ед. продукции, руб c 1 c 2 … c n Найти такое решение системы ограничений, при котором функция F = с 1 х 1 + с 2 х 2 +...+ с n х n, принимает максимальное значение
Слайд 63
Найти такое решение системы ограничений, при котором функция F = с 1 х 1 + с 2 х 2 +...+ с n х n, принимает максимальное значение
Слайд 64
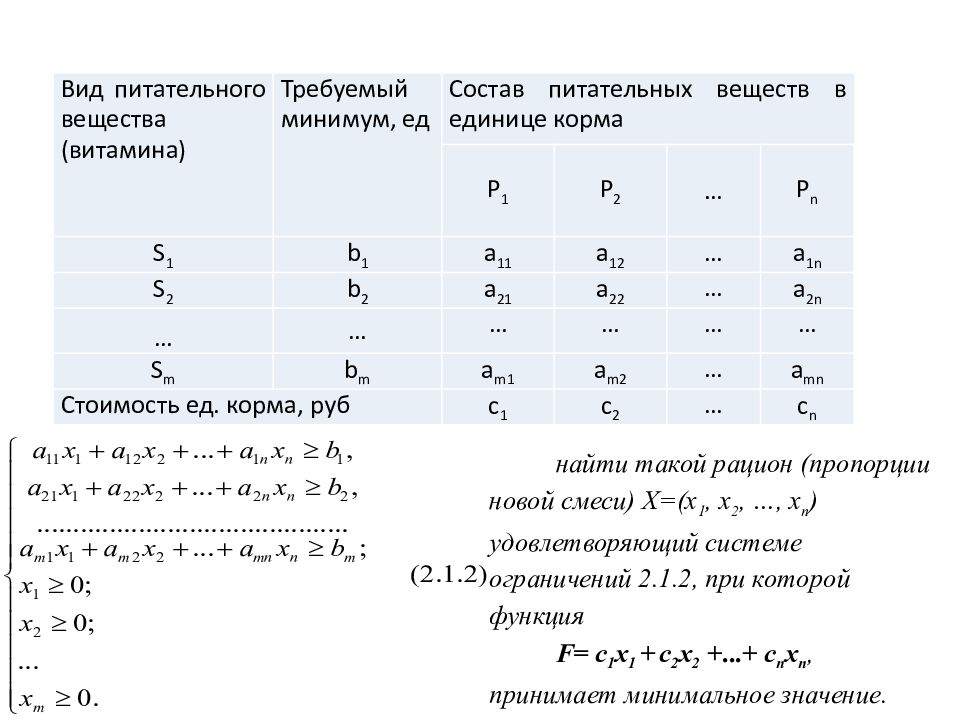
Задача о составлении рациона Из существующих n видов ингредиентов (корма P 1, P 2,…, P n ), содержащие питательные элементы S i (витамины S 1, S 2,…, S m ) требуется синтезировать новый продукт (рацион) с наименьшей стоимостью. При этом содержание питательных веществ в новом суточном рационе должно быть не менее b i соответственно по каждому виду. Известны содержания питательных элементов в единице j -го вида исходного ингредиента (корма) – a ij и стоимость единицы i -го вида корма – c j. Вид питательного вещества (витамина) Требуемый минимум, ед Состав питательных веществ в единице корма P 1 P 2 … P n S 1 b 1 a 11 a 12 … a 1n S 2 b 2 a 21 a 22 … a 2n … … … … … … S m b m a m1 a m2 … a mn Стоимость ед. корма, руб c 1 c 2 … c n (задача о диете, задача о смесях) найти такой рацион (пропорции новой смеси) X =( x 1, x 2, …, x n ) удовлетворяющий системе ограничений 2.1.2, при которой функция F = с 1 х 1 + с 2 х 2 +...+ с n х n, принимает минимальное значение.
Слайд 65
Вид питательного вещества (витамина) Требуемый минимум, ед Состав питательных веществ в единице корма P 1 P 2 … P n S 1 b 1 a 11 a 12 … a 1n S 2 b 2 a 21 a 22 … a 2n … … … … … … S m b m a m1 a m2 … a mn Стоимость ед. корма, руб c 1 c 2 … c n найти такой рацион (пропорции новой смеси) X =( x 1, x 2, …, x n ) удовлетворяющий системе ограничений 2.1.2, при которой функция F = с 1 х 1 + с 2 х 2 +...+ с n х n, принимает минимальное значение.
Слайд 66
Задача об использовании мощностей ( задача о загрузке оборудования) Предприятию задан план производства продукции по времени и номенклатуре. Требуется за время Т на производственных линиях (станках) S 1, S 2,..., S m выпустить N 1, N 2,…, N n единиц продукции Р 1, Р 2,.., Р n. Для каждого станка известны производительность а ij (т.е. число единиц продукции P j, которое можно произвести на станке S i ) и затраты b ij на изготовление продукции P j на станке S i в единицу времени. Необходимо составить такой план работы станков (эффективно распределить производство продукции между станками), чтобы затраты на производство всей продукции были наименьшими. Продукт P 1 Продукт P 2 … Продукт P n Линия S 1 b 11 / a 11 b 12 / a 12 b 1n / a 1n Линия S 2 b 21 / a 21 b 2 2 / a 2 2 b 2n / a 2n … Линия S m b m1 / a m1 b m2 / a m2 b mn / a mn Кол-во N 1 N 2 … N n Обозначим x ij - время, в течение которого станок S i за нят изготовлением продукции P j Так как время работы каждого станка ограничено и не превышает Т, то справедливы неравенства: Для выполнения плана по номенклатуре необходимо, чтобы выполнялись следующие равенства: (3.2) Кроме того x ij >= 0 Затраты на производство всей продукции выразятся функцией: F = b 11 x 11 + b 12 x 12 +...+ b mn x mn Экономико-математическая модель задачи: Найти такое решение X =( x 11, x 12, …, x mk ) удовлетворяющее системам (3.1) и (3.2) и условию неотрицательности переменных, при ко тором функция затрат принимает минимальное значение.
Слайд 67
Задача об использовании мощностей ( задача о загрузке оборудования) Предприятию задан план производства продукции по времени и номенклатуре. Требуется за время Т на производственных линиях (станках) S 1, S 2,..., S m выпустить N 1, N 2,…, N n единиц продукции Р 1, Р 2,.., Р n. Для каждого станка известны производительность а ij (т.е. число единиц продукции P j, которое можно произвести на станке S i ) и затраты b ij на изготовление продукции P j на станке S i в единицу времени. Необходимо составить такой план работы станков (эффективно распределить производство продукции между станками), чтобы затраты на производство всей продукции были наименьшими.
Слайд 68
Задача об использовании мощностей ( задача о загрузке оборудования) Продукт P 1 Продукт P 2 … Продукт P n Линия S 1 b 11 / a 11 b 12 / a 12 b 1n / a 1n Линия S 2 b 21 / a 21 b 2 2 / a 2 2 b 2n / a 2n … Линия S m b m1 / a m1 b m2 / a m2 b mn / a mn Кол-во N 1 N 2 … N n
Слайд 69
Задача об использовании мощностей ( задача о загрузке оборудования) Обозначим x ij - время, в течение которого станок S i за нят изготовлением продукции P j Так как время работы каждого станка ограничено и не превышает Т, то справедливы неравенства: Кроме того x ij >= 0 Затраты на производство всей продукции выразятся функцией: F = b 11 x 11 + b 12 x 12 +...+ b mn x mn Экономико-математическая модель задачи: Найти такое решение X =( x 11, x 12, …, x mk ) удовлетворяющее системам (3.1) и (3.2) и условию неотрицательности переменных, при ко тором функция затрат принимает минимальное значение.
Слайд 70
Задача о раскрое материала (о распиле) На раскрой (распил, обработку) поступает материал одного образца в количестве а единиц. Требуется изготовить из него l разных комплектующих изделий в количествах, пропорциональных числам b 1, b 2,... b l (условие комплектности). Каждая единица материала может быть раскроена п различными способами, причем использование j -го способа дает а jk единиц k -го изделия. Необходимо найти план раскроя, обеспечивающий максимальное число комплектов. Способ раскроя j Число получаемых комплектов 1 2 … l 1 2 n a 11 а 21 … а n1 a 12 а 22 … а n2 … … … … a 1l а 2 l … а nl Обозначим x j — число единиц материала, раскраиваемых j -м способом, и x - число изготовляемых комплектов изделий. Так как общее количество материала равно сумме его единиц, раскраиваемых различными способами, то Требование комплектности выразится уравнениями Очевидно, что x j >= 0 Экономико-математическая модель задачи: найти такое решение Х=(х 1, x 2,..., x п ), удовлетворяющее системе уравнений и условию, при котором функция F = x принимает максимальное значение.
Слайд 71
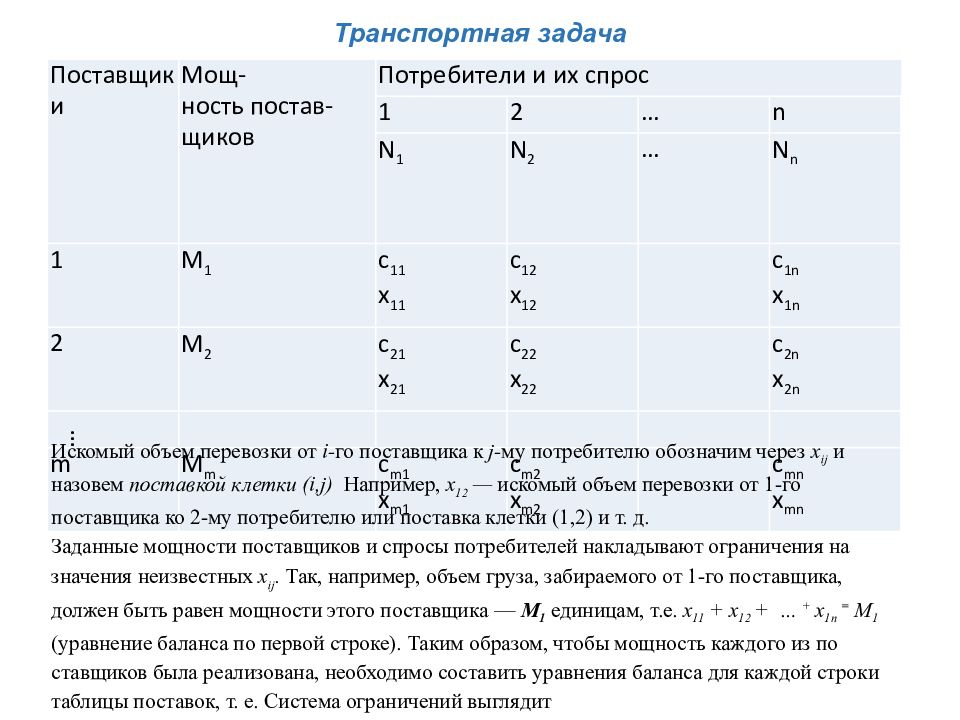
Транспортная задача Пусть некое предприятие решило оптимизировать свои систематические транспортные расходы по поставке груза в собственные каналы распределения. В структуру предприятия входят m поставщиков и n потребителей. Обозначим через: M i - мощность поставщиков, N j - спросы потребителей, c ij - коэффициенты затрат на перевозку единицы груза для каждой пары "поставщик - потребитель". Найти объемы перевозок для каждой пары так, чтобы: мощности всех поставщиков были реализованы; спросы всех потребителей удовлетворены; суммарные затраты на перевозку были минимальны
Слайд 72
Транспортная задача Поставщики Мощ- ность постав- щиков Потребители и их спрос 1 2 … n N 1 N 2 … N n 1 M 1 c 11 x 11 c 12 x 12 c 1n x 1n 2 M 2 c 21 x 21 c 22 x 22 c 2n x 2n … m M m c m1 x m1 c m2 x m2 c mn x mn Искомый объем перевозки от i - го поставщика к j - му потребителю обозначим через х ij и назовем поставкой клетки ( i, j ) Например, х 12 — искомый объем перевозки от 1-го поставщика ко 2-му потребителю или поставка клетки (1,2) и т. д. Заданные мощности поставщиков и спросы потребителей накладывают ограничения на значения неизвестных х ij. Так, например, объем груза, забираемого от 1-го поставщика, должен быть равен мощности этого поставщика — M 1 единицам, т.е. х 11 + х 12 + … + х 1 n = M 1 (уравнение баланса по первой строке). Таким образом, чтобы мощность каждого из поставщиков была реализована, необходимо составить уравнения баланса для каждой строки таблицы поставок, т. е. Система ограничений выглядит
Слайд 73
Транспортная задача - уравнение баланса по строкам; - уравнение баланса по столбцам. для любых x ij >=0. Линейная функция: на множестве неотрицательных (допустимых) решений системы ограничений найти такое решение Х= (х 11, x 12, …, x ij,..., х mn ), при котором значение линейной функции минимально. Особенности экономико-математической модели транс портной задачи: система ограничений есть система уравнений (т.е. транспорт ная задача задана в канонической форм e ); коэффициенты при переменных системы ограничений равны единице или нулю; каждая переменная входит в систему ограничений два раза. , то такая задача называется закрытой. Иначе – открытой. Если
Слайд 75: Стандартная форма
Первая стандартная форма задачи линейного программирования имеет вид
Слайд 76: Стандартная форма
Вторая стандартная форма задачи линейного программирования имеет вид
Слайд 77: Каноническая форма
Канонической формой задачи линейного программирования называется задача вида
Слайд 78: Правила приведения
Рассмотрим теперь те приёмы, которые позволяют произвольные формы задач линейного программирования приводить к указанным выше стандартным формам. 1. Превращение max в min и наоборот. Если целевая функция в задаче линейного программирования задана в виде то, умножая её на (- 1), приведем её к виду так как смена знака приводит к смене min на max. Аналогично можно заменить max на min. ,
Слайд 79: Правила приведения
2. Смена знака неравенства. Если ограничение задано в виде то, умножая на (-1), получим: Аналогично, неравенство вида больше либо равно можно превратить в неравенство вида меньше либо равно.
Слайд 80: Правила приведения
3. Превращение равенства в систему неравенств. Если ограничение задано в виде то его можно заменить эквивалентной системой двух неравенств или такой же системой неравенств со знаками больше либо равно. Указанные выше приемы позволяют приводить задачи линейного программирования к стандартной форме.
Слайд 81: Правила приведения
4. Превращение неравенств в равенства. Для приведения задачи к канонической форме, где все ограничения имеют вид равенств, вводят дополнительные переменные, которые тоже считаются неотрицательными и записывают исходную задачу в виде
Слайд 82: Правила приведения
То есть в неравенстве со знаком меньше либо равно добавляют дополнительную неотрицательную переменную, а из неравенства со знаком больше либо равно вычитают дополнительную переменную. В целевую функцию эти дополнительные переменные включают с коэффициентом 0, т.е. фактически они в целевой функции отсутствуют. Получив решение задачи в канонической форме, для получения решения исходной задачи надо просто выбросить из решения значения введенных дополнительных переменных.
Слайд 83
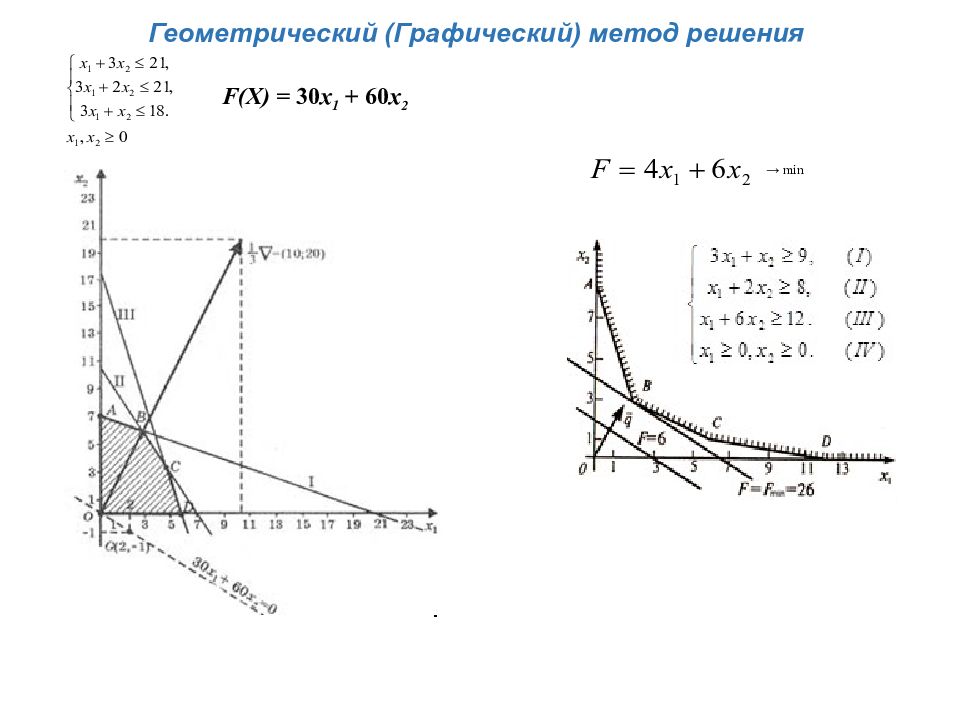
Геометрический (Графический) метод решения F ( X ) = 30 x 1 + 60 х 2 → min
Слайд 84
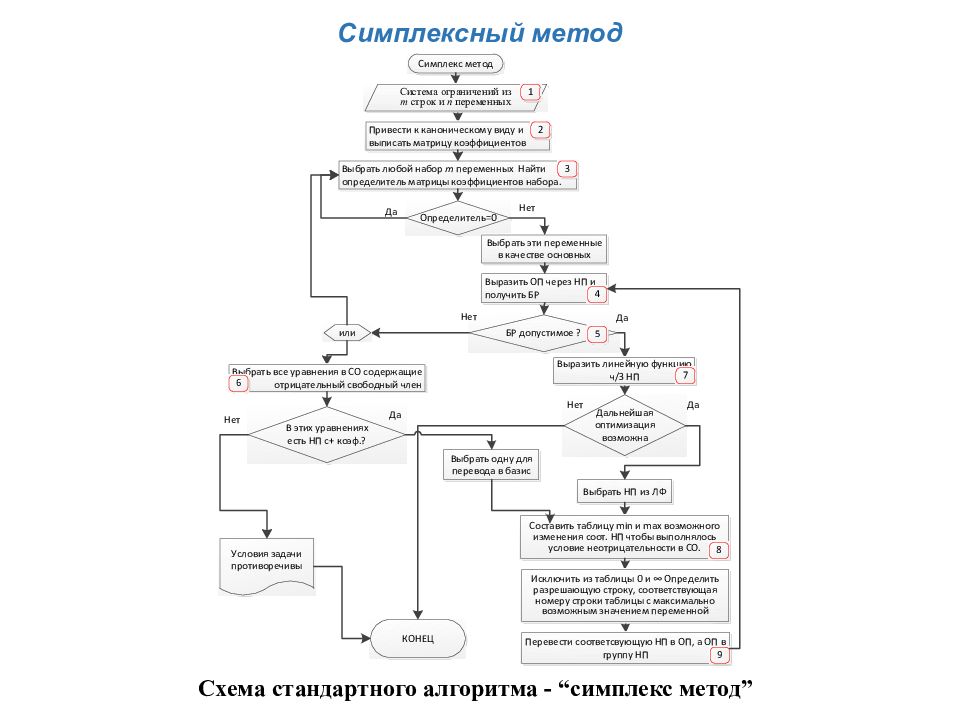
Общая задача линейного программирования решается симплексным методом Симплекс (лат. simplex - простой) – простейший выпуклый многогранник в n- мерном пространстве с n+1 вершиной (например, тетраэдр в 3-мерном пространстве)
Слайд 85
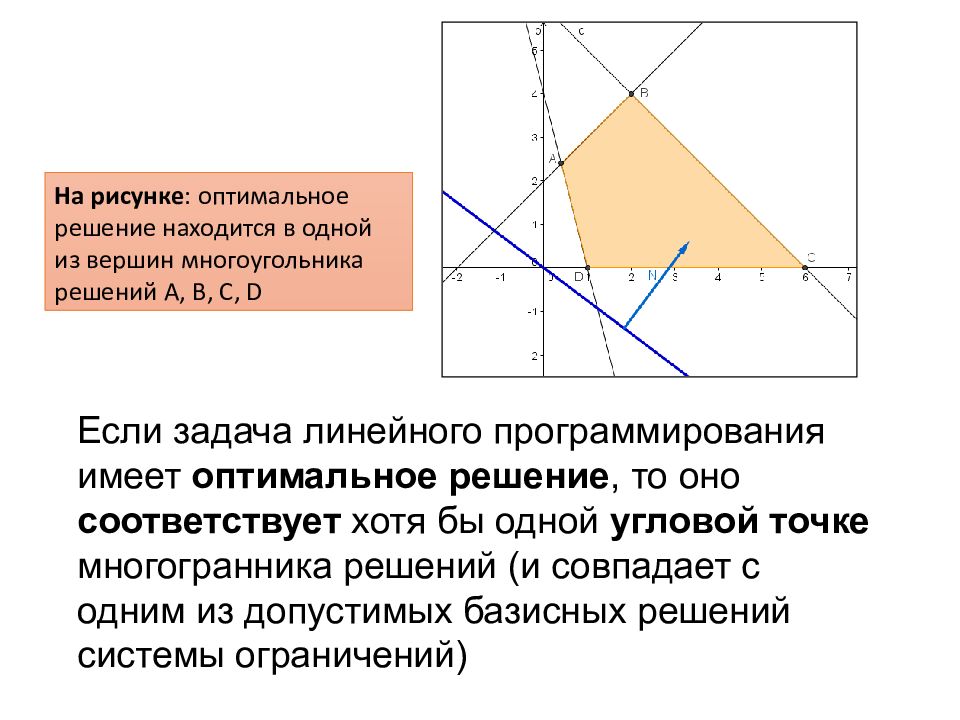
Если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений (и совпадает с одним из допустимых базисных решений системы ограничений) На рисунке : оптимальное решение находится в одной из вершин многоугольника решений А, В, С, D
Слайд 86
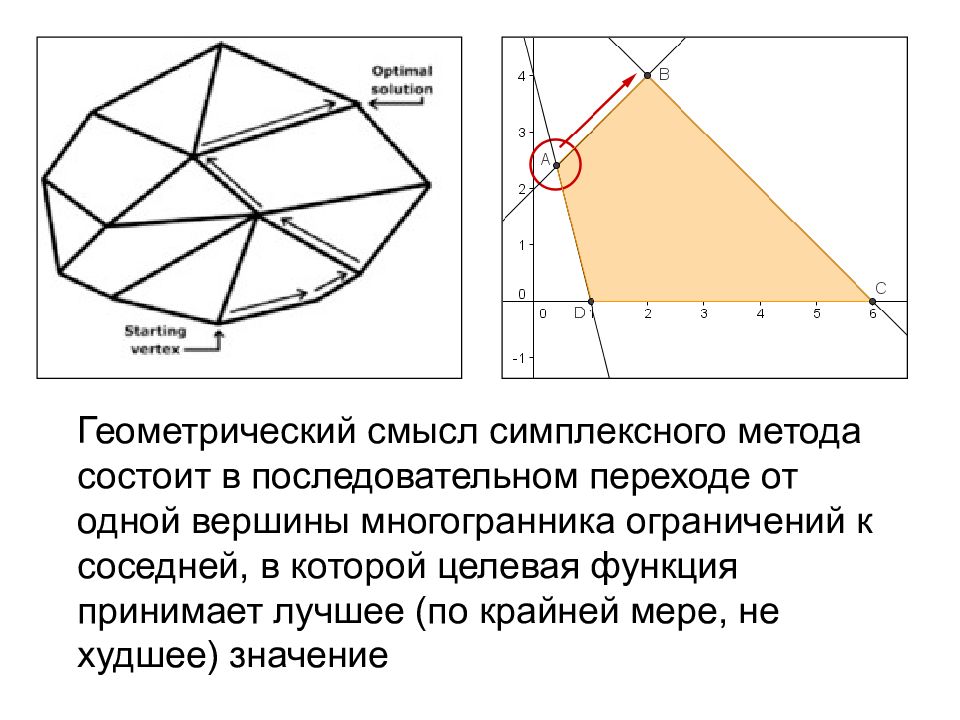
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (по крайней мере, не худшее) значение
Слайд 87
Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г. Джордж Бернард Данциг (1914-2005) – американский математик, разработал симплексный алгоритм, считается основоположником методов линейного программирования Леонид Витальевич Канторович (1912-1986) – советский математик и экономист, лауреат Нобелевской премии по экономике 1975 года «за вклад в теорию оптимального распределения ресурсов». Один из создателей линейного программирования Идеи симплексного метода были разработаны в 1939 г. российским ученым Л.В.Канторовичем
Слайд 89
Симплексный метод позволяет решить любую задачу линейного программирования В настоящее время он используется для компьютерных расчетов На практиках рассмотрим решение задачи линейного программирования в MS Excel
Слайд 90
Двойственная задача Задаче ЛП соответствует другая задача, называемая двойственной или сопряженной по отношению к исходной. Теория двойственности полезна для проведения качественных исследований задач линейного программирования. Пусть имеются две задачи линейного программирования обладающие следующими особенностями: В одной задаче ищут максимум линейной функции, в другой — минимум ; Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений в другой; Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида "<=", а в задаче минимизации — все неравенства вида ">=";
Слайд 91
Двойственная задача 4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу: 5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче; 6. Условия неотрицательности переменных имеются в обеих задачах, то эти задачи линейного программирования, обладающие указанными свойствами, называются симметричными взаимно двойственными задачами.
Слайд 100
Система национальных счетов (СНС) – совокупность статистических макроэкономических показателей, характеризующих состояние экономики страны СНС была разработана группой американских ученых, c отрудников NBER (National Bureau of Economic Research) в конце 20-х годов ХХ века под руководством Саймона Кузнеца Саймон Кузнец, лауреат Нобелевской премии 1968 г.
Слайд 101
Понятие СНС Система национальных счетов (СНС) представляет систему взаимосвязанных статистических показателей, построенную в виде определенного набора счетов и таблиц, характеризующих результаты экономической деятельности страны. Для учета результатов труда в отраслях производства услуг используются следующие понятия: Продукты – результаты труда, имеющие материально-вещественную форму (включая энергию). Услуги – результаты деятельности, удовлетворяющие определенные, личные и общественные потребности, но не воплощающиеся в материально-вещественной форме. Товары – продукты и услуги, предназначенные для продажи на рынке по цене, покрывающей их издержки.
Слайд 102
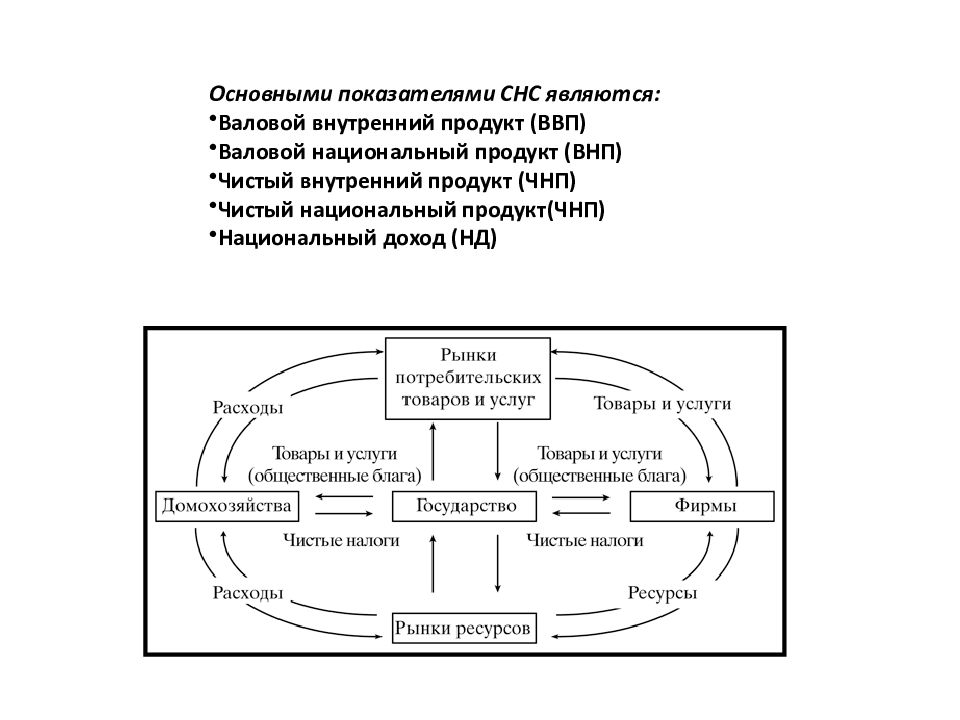
Основными показателями СНС являются: Валовой внутренний продукт (ВВП) Валовой национальный продукт (ВНП) Чистый внутренний продукт (ЧНП) Чистый национальный продукт(ЧНП) Национальный доход (НД)
Слайд 103
счет товаров и услуг; счет производства ; счет образования доходов; счет распределения первичных доходов; счет вторичного распределения доходов; счет использования располагаемого дохода ; счет операций с капиталом счет производства; счет образования доходов; элементы счета использования располагаемого дохода; элементы счета операций с капиталом СНС включает Каждый счет СНС состоит из двух сторон: ресурсов и использования (сумма записей в ресурсах равна сумме записей в использовании). Различают следующие группы счетов: Счета для секторов экономики Счета для отраслей экономики Счета для отдельных экономических операций Счета для экономики в целом (консолидированные счета)
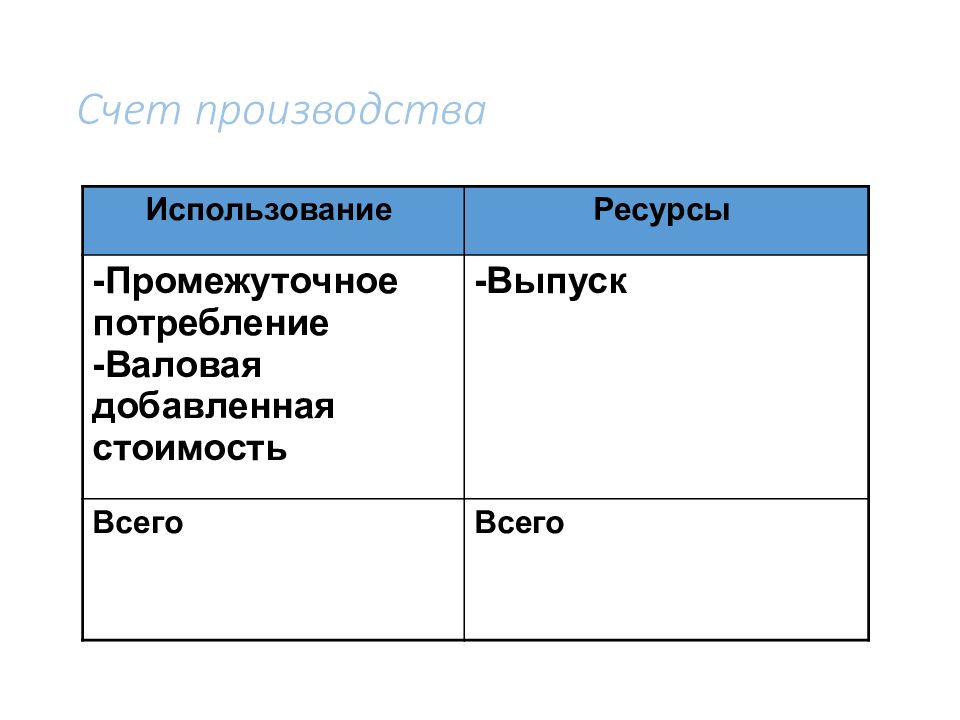
Слайд 104: Счет производства
Использование Ресурсы -Промежуточное потребление -Валовая добавленная стоимость -Выпуск Всего Всего
Слайд 105: Сектора национальной экономики
нефинансовых корпораций; финансовых корпораций; государственного управления; домашних хозяйств; некоммерческих организаций, обслуживающих домашние хозяйства.
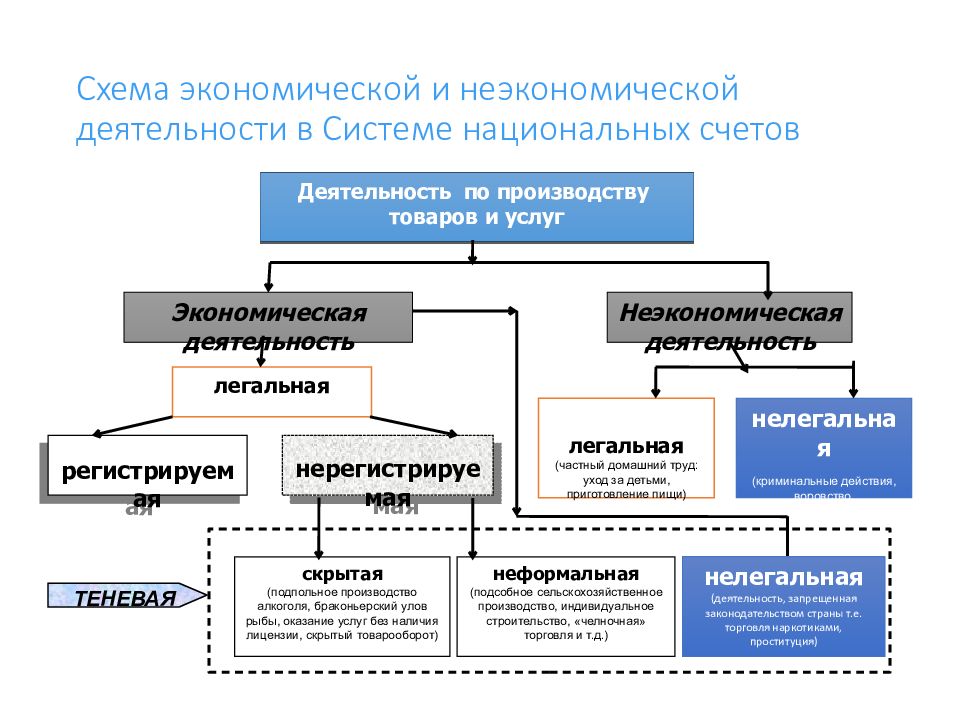
Слайд 106: Схема экономической и неэкономической деятельности в Системе национальных счетов
регистрируемая Деятельность по производству товаров и услуг нерегистрируемая Экономическая деятельность легальная Неэкономическая деятельность легальная (частный домашний труд: уход за детьми, приготовление пищи) нелегальная (криминальные действия, воровство, мошенничество) скрытая (подпольное производство алкоголя, браконьерский улов рыбы, оказание услуг без наличия лицензии, скрытый товарооборот) неформальная (подсобное сельскохозяйственное производство, индивидуальное строительство, «челночная» торговля и т.д.) нелегальная (деятельность, запрещенная законодательством страны т.е. торговля наркотиками, проституция) ТЕНЕВАЯ Схема экономической и неэкономической деятельности в Системе национальных счетов
Слайд 107: Схема расчета Валового регионального продукта производственным методом
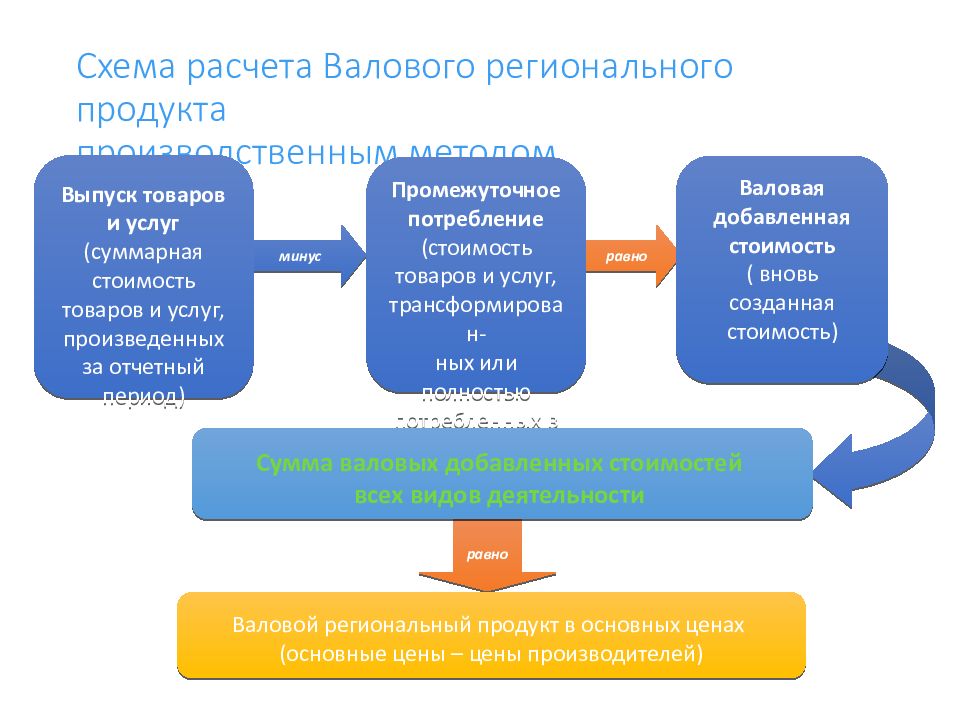
равно минус Схема расчета Валового регионального продукта производственным методом Выпуск товаров и услуг (суммарная стоимость товаров и услуг, произведенных за отчетный период) Промежуточное потребление (стоимость товаров и услуг, трансформирован - ных или полностью потребленных в процессе производства) равно Сумма валовых добавленных стоимостей всех видов деятельности Валовой региональный продукт в основных ценах (основные цены – цены производителей) Валовая добавленная стоимость ( вновь созданная стоимость)
Слайд 108: Схема расчета Валового регионального продукта производственным методом
Налоги на продукты (налоги, взимаемые пропорционально количеству или стоимости товаров и услуг - НДС, акцизы, налог с продаж) Субсидии на продукты (субсидии, выплачиваемые государством предприятиям-производителям обычно за единицу произведенного товара) Валовой региональный продукт в рыночных ценах (аналог Валового внутреннего продукта России) плюс минус равно Валовой региональный продукт в основных ценах (основные цены – цены производителей) Схема расчета Валового регионального продукта производственным методом
Слайд 109
Взаимосвязь показателей ИСПОЛЬЗОВАНИЕ РЕСУРСЫ 1. Счёт производства Промежуточное потребление (ПП) Валовой выпуск в основных ценах (ВВ) Чистые налоги на продукты (ЧНП) БАЛАНСИ-РУЮЩАЯ СТАТЬЯ Валовой внутренний продукт в рыночных ценах (ВВП) ВВП = ВВ – ПП + ЧНП 2. Счёт образования доходов Оплата труда (ОТ) ВВП в рыночных ценах Чистые налоги на производство (включая налоги на продукты) и импорт (ЧНПИ) БАЛАНСИ-РУЮЩАЯ СТАТЬЯ Валовая прибыль экономики/Валовые смешанные доходы (ВПЭ) ВПЭ= ВВП - ОТ - ЧНПИ 3. Счёт распределения первичных доходов Доходы от собственности, переданные «остальному миру» ВПЭ ОТ ЧНПИ Доходы от собственности, полученные от «остального мира» БАЛАНСИ-РУЮЩАЯ СТАТЬЯ Сальдо первичных доходов (валовой национальный доход) (ВНД) ВНД = ВПЭ + ОТ + ЧНПИ + Сальдо доходов от собственности
Слайд 110
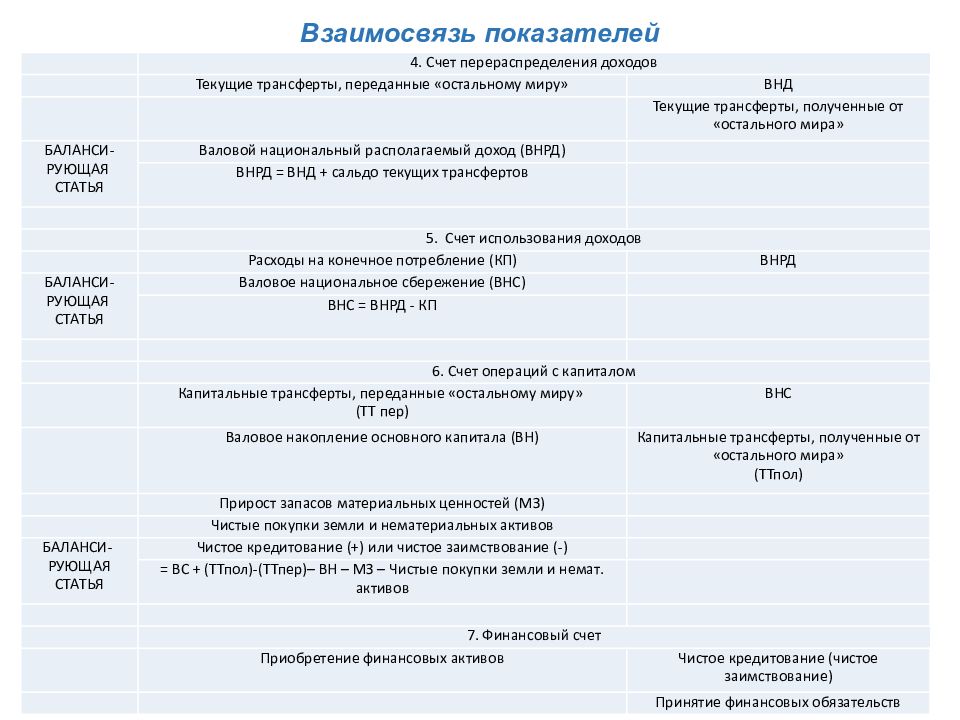
Взаимосвязь показателей 4. Счет перераспределения доходов Текущие трансферты, переданные «остальному миру» ВНД Текущие трансферты, полученные от «остального мира» БАЛАНСИ-РУЮЩАЯ СТАТЬЯ Валовой национальный располагаемый доход (ВНРД) ВНРД = ВНД + сальдо текущих трансфертов 5. Счет использования доходов Расходы на конечное потребление (КП) ВНРД БАЛАНСИ-РУЮЩАЯ СТАТЬЯ Валовое национальное сбережение (ВНС) ВНС = ВНРД - КП 6. Счет операций с капиталом Капитальные трансферты, переданные «остальному миру» (ТТ пер) ВНС Валовое накопление основного капитала (ВН) Капитальные трансферты, полученные от «остального мира» ( ТТпол ) Прирост запасов материальных ценностей (МЗ) Чистые покупки земли и нематериальных активов БАЛАНСИ- РУЮЩАЯ СТАТЬЯ Чистое кредитование (+) или чистое заимствование (-) = ВС + (ТТпол)-(ТТпер)– ВН – МЗ – Чистые покупки земли и немат. активов 7. Финансовый счет Приобретение финансовых активов Чистое кредитование (чистое заимствование) Принятие финансовых обязательств
Слайд 111
Регион как объект моделирования А. Г. Гранберг : «Регион – это определенная территория, отличающаяся от других территорий по ряду признаков и обладающая некоторой целостностью, взаимосвязанностью составляющих её элементов» При всем разнообразии экономических агентов региона следует выделить три основных типа: Домохозяйства – домашние хозяйства (индивиды и их семьи), которые с одной стороны являются поставщиками на рынке ресурсов, с другой – потребителями товаров и услуг. Предприятия – это хозяйствующие субъекты, выполняющие функции производства товаров и предоставления услуг. Как и домохозяйства, они являются как объектами спроса, так и объектами предложения. Агент «государство» с одной стороны также выступает в качестве представителя / потребителя товаров и услуг, а с другой прямо или косвенно может вмешиваться и контролировать этот кругооборот ресурсов. Экономические агенты — субъекты экономических отношений, принимающие участие в производстве, распределении, обмене и потреблении экономических благ. Отличительная черта экономических агентов — принятие и реализация самостоятельных решений в сфере хозяйственной деятельности.
Слайд 112
Укрупненная схема региона Федеральный бюджет Региональный бюджет Местные бюджеты Внебюджетные фонды Государство Занятое население Временно не занятые Дети и молодежь Пенсионеры Трудоспособные, но не ищущие работу Население Предприятия финансового сектора Промышленные предприятия Предприятия АПК Сфера услуг … Хозяйствующие субъекты налоги, сборы, пр. отчисления помощь бюджетам нижестоящих уровней Зарплата гос. служащих, выплаты, пособия и т.д. Перераспределение средств гос. закупки, инвестиции, субсидии и т.д. Зарплата и др. выплаты Потребление конечного продукта Выбытие фондов Промежуточное и конечное потребление Налоги, штрафы, пени и т.д. Вложения и займы Инвестиции и займы Внешняя среда
Слайд 113
Лекция 4 Вероятностно-статистические модели социально-экономических процессов (2 пары)
Слайд 114: Временные ряды
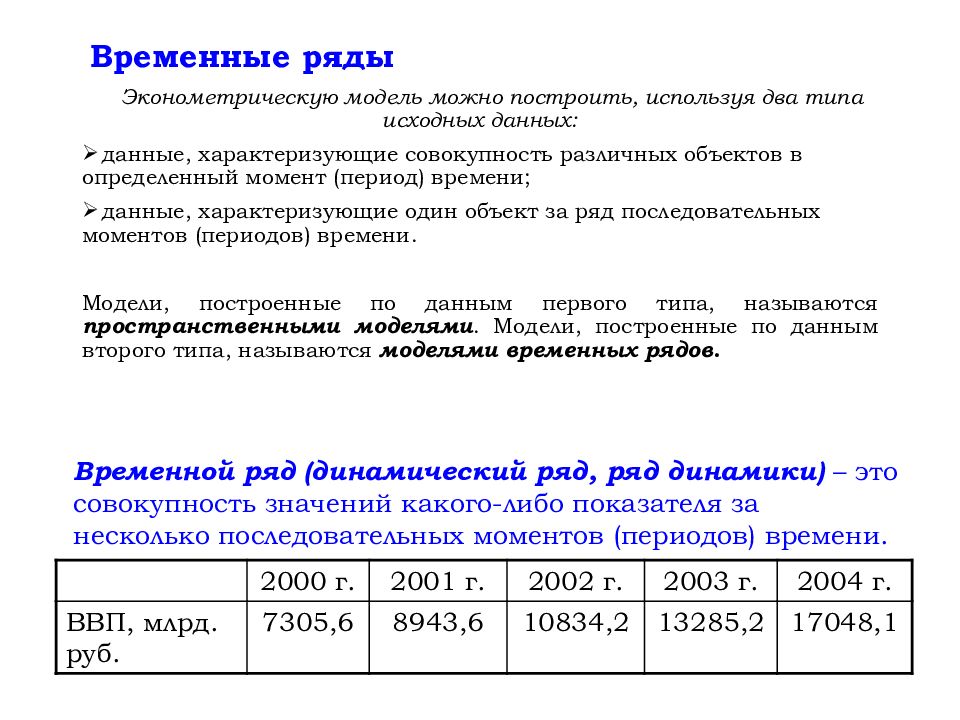
Эконометрическую модель можно построить, используя два типа исходных данных: данные, характеризующие совокупность различных объектов в определенный момент (период) времени; данные, характеризующие один объект за ряд последовательных моментов (периодов) времени. Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные по данным второго типа, называются моделями временных рядов. 2000 г. 2001 г. 2002 г. 2003 г. 2004 г. ВВП, млрд. руб. 7305,6 8943,6 10834,2 13285,2 17048,1 Временной ряд (динамический ряд, ряд динамики) – это совокупность значений какого-либо показателя за несколько последовательных моментов (периодов) времени.
Слайд 115: Три составляющие временного ряда
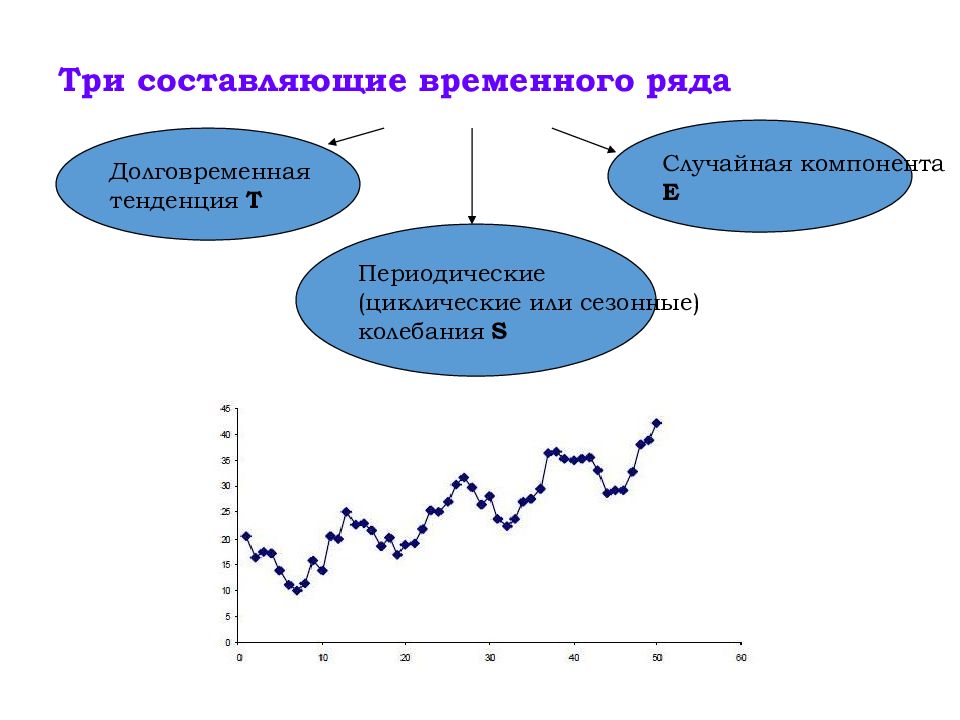
Долговременная тенденция Т Периодические (циклические или сезонные) колебания S Случайная компонента Е
Слайд 116: Модели временного ряда:
Основная задача эконометрического исследования временного ряда: выявление и количественное выражение его компонент (тенденции, периодичности, случайной компоненты) в целях их использования для прогнозирования будущих значений ряда. 1) аддитивная 2) мультипликативная 3) смешанная
Слайд 117: Автокорреляция уровней временного ряда –
это корреляционная зависимость между последовательными уровнями временного ряда. Измеряется с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями ряда, сдвинутыми на несколько шагов назад во времени:
Слайд 118: τ – величина сдвига во времени, или лаг
Например, лаг τ=1 означает, что ряд сдвинут на один период (момент) назад и т.д. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. τ=1 = > τ= 2 = >
Слайд 119: Свойства коэффициента автокорреляции:
характеризует тесноту только линейной связи текущего и предыдущего уровней ряда, поэтому по данному коэффициенту можно судить о наличии линейной или близкой к линейной тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию, коэффициент автокорреляции может приближаться к нулю; по знаку коэффициента автокорреляции нельзя судить о возрастающей или убывающей тенденции в уровнях ряда.
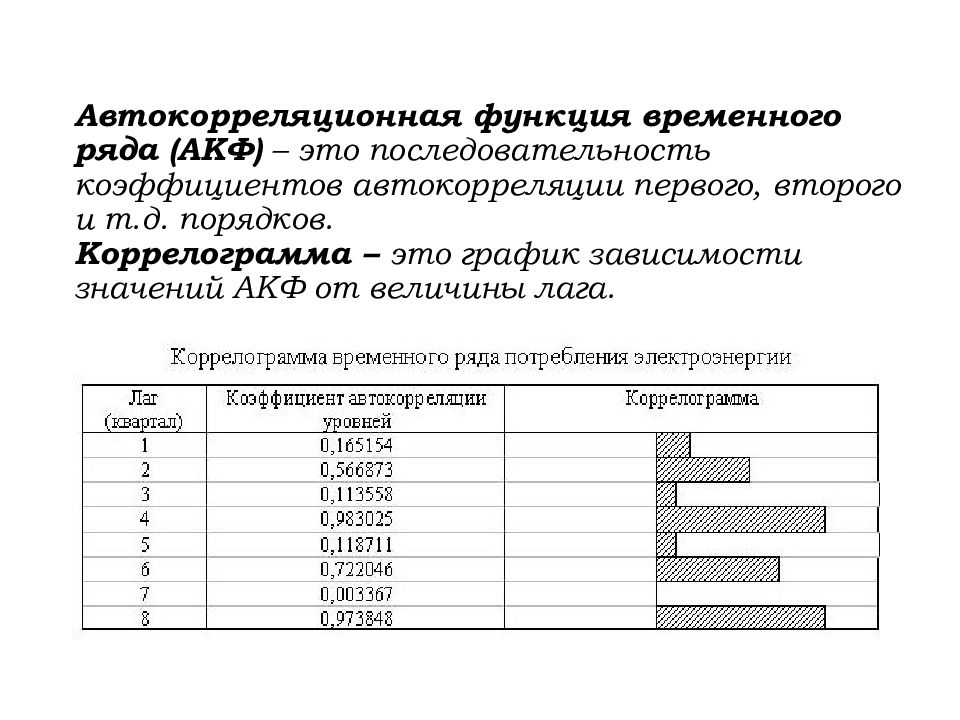
Слайд 120: Автокорреляционная функция временного ряда (АКФ) – это последовательность коэффициентов автокорреляции первого, второго и т.д. порядков. Коррелограмма – это график зависимости значений АКФ от величины лага
Слайд 121: Спецификация модели
121 Спецификация модели Уравнение множественной регрессии Цель множественной регрессии: Построить модель с большим числом факторов, определив влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый фактор. Спецификация модели включает в себя два круга вопросов : - отбор факторов ; - выбор вида уравнения регрессии.
Слайд 122: 1 Отбор факторов
122 1 Отбор факторов Требования к включаемым факторам: количественно измеримы ; не должны находиться в точной функциональной связи или быть сильно коррелированы. Пример y - себестоимость единицы продукции x – заработная плата работника z – производительность труда
Слайд 123: Два этапа отбора факторов:
123 Два этапа отбора факторов: исходя из сущности проблемы; на основе корреляционной матрицы и - статистики параметров регрессии 1) Проверка парной корреляции. Принцип исключения факторов: Если две переменные явно коллинеарны ( ), то одну из них исключаем. Включаем фактор, имеющий наименьшую тесноту связи с другими факторами 2) Оценка мультиколлинеарности факторов (когда более, чем два фактора связаны между собой линейной зависимостью): Проверка гипотезы H 0 : R – матрица коэффициентов корреляции. Чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов
Слайд 124: Пути преодоления сильной межфакторной корреляции
124 Пути преодоления сильной межфакторной корреляции Исключение одного или нескольких факторов Преобразование факторов для уменьшения корреляции между ними Переход к первым разностям Переход к линейным комбинациям (метод главных компонент) Переход к совмещенным уравнениям регрессии Переход к уравнениям приведенной формы
Слайд 125: Моделирование тенденции временного ряда
Аналитическое выравнивание – это построение аналитической функции, характеризующей зависимость уровней ряда от времени, т.е. построение тренда: линейный тренд экспоненциальный тренд гипербола тренд в форме степенной функции
Слайд 126: Для определения вида тенденции применяются следующие методы:
– качественный анализ изучаемого процесса; – построение и визуальный анализ графика зависимости уровней ряда от времени; – расчет и анализ показателей динамики временного ряда (абсолютные приросты, темпы роста и др.); – метод перебора, при котором строятся тренды различного вида с последующим выбором наилучшего на основании значения скорректированного коэффициента детерминации.
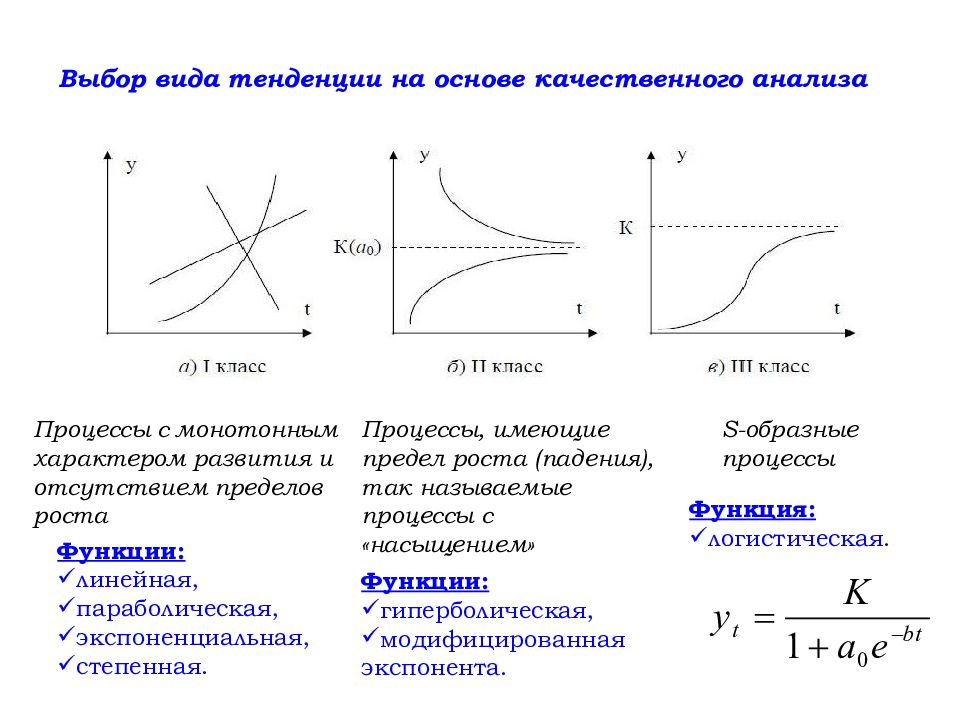
Слайд 127: Выбор вида тенденции на основе качественного анализа
Процессы с монотонным характером развития и отсутствием пределов роста Функции: линейная, параболическая, экспоненциальная, степенная. Процессы, имеющие предел роста (падения), так называемые процессы с «насыщением» Функции: гиперболическая, модифицированная экспонента. S-образные процессы Функция: логистическая.
Слайд 128: Моделирование периодических колебаний
Построение аддитивной и мультипликативной моделей сводится к расчету значений T, S, E для каждого уровня ряда. Процесс построения модели включает в себя следующие этапы: 1. Выравнивание исходного ряда методом скользящей средней. 2. Расчет значений периодической компоненты S. 3. Устранение периодической компоненты из исходных уровней ряда и получение выравненных данных (Т+Е) в аддитивной или (Т•Е) в мультипликативной модели. 4. Аналитическое выравнивание уровней ряда и расчет значений Т с использованием полученного уравнения тренда. 5. Расчет полученных по модели значений (Т+ S ) или (Т• S ). 6. Расчет абсолютных и/или относительных ошибок.
Слайд 129: Парная регрессия и корреляция в эконометрических исследованиях. Смысл и оценка параметров
часть значения у, которая объяснена уравнением регрессии необъясненная часть значения у (или возмущение)
Слайд 130: Экономический смысл
Невключение объясняющих переменных в уравнение. На самом деле на переменную Y влияет не только переменная X, но и ряд других переменных, которые не учтены в модели по следующим причинам: мы знаем, что другая переменная влияет, но не можем ее учесть, потому как не знаем, как измерить (психологический фактор, например); существуют факторы, которые мы знаем, как измерить, но влияние их на Y так слабо, что их не стоит учитывать; существенные переменные, но из-за отсутствия опыта или знаний мы их таковыми не считаем. Неправильная функциональная спецификация. Функциональное соотношение между Y и Х может быть определено неправильно. Например, мы предположили линейную зависимость, а она может быть более сложной. Ошибки наблюдений и измерений.
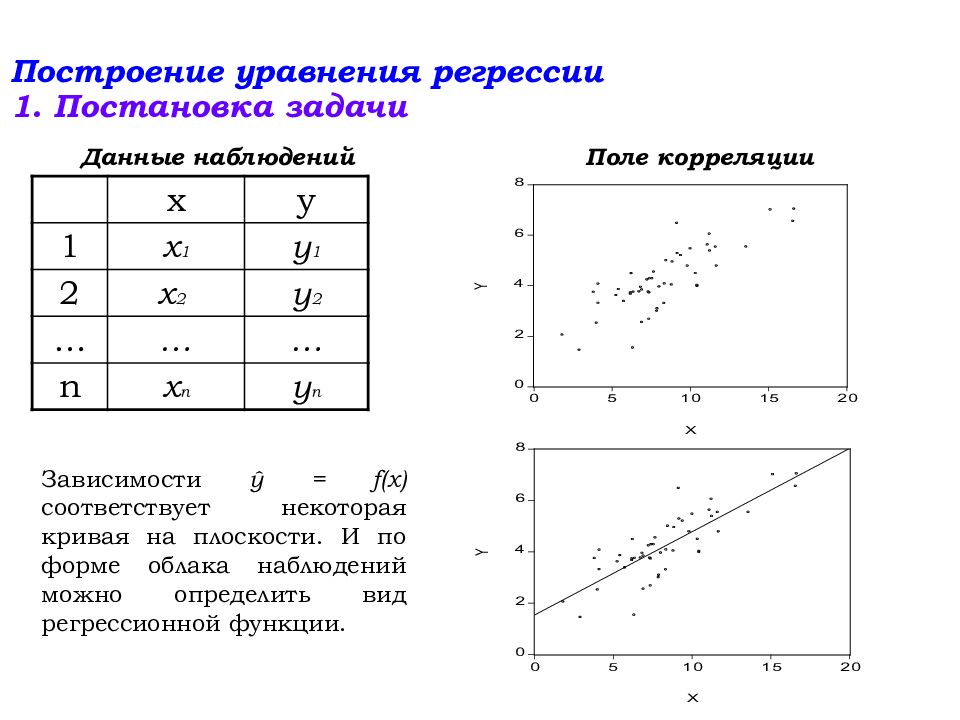
Слайд 131: Построение уравнения регрессии 1. Постановка задачи
x y 1 x 1 y 1 2 x 2 y 2 … … … n x n y n Данные наблюдений Поле корреляции Зависимости ŷ = f(x) соответствует некоторая кривая на плоскости. И по форме облака наблюдений можно определить вид регрессионной функции.
Слайд 134: Парная линейная регрессионная модель
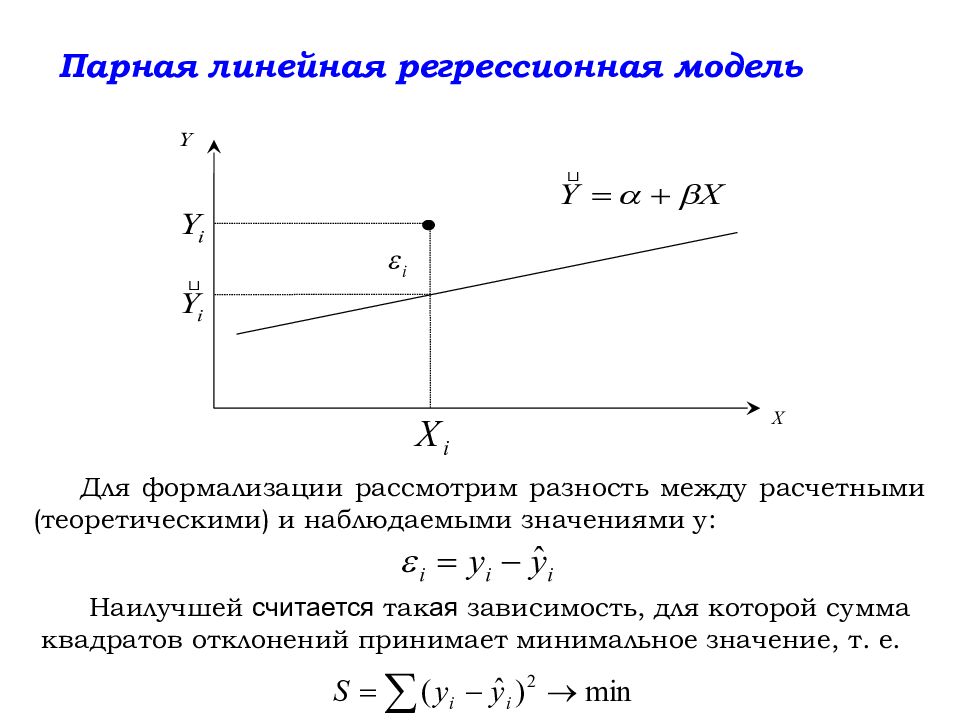
Для формализации рассмотрим разность между расчетными (теоретическими) и наблюдаемыми значениями у: Наилучшей считается так ая зависимость, для которой сумма квадратов отклонений принимает минимальное значение, т. е.
Слайд 135: 2. Спецификация модели
В парной регрессии выбор вида аналитической зависимости может быть осуществлен тремя методами: – графическим (на основе анализа поля корреляции); – аналитическим (на основе изучения теоретической природы связи между исследуемыми признаками); – экспериментальным (построение нескольких моделей различного вида с выбором наилучшей, согласно применяемому критерию качества).
Слайд 136: 3. Оценка параметров модели 3.1. Оценка параметров линейной парной регрессии – метод наименьших квадратов (МНК)
или Отсюда получаем систему уравнений: Разделим оба уравнения на n : Подставляем во второе уравнение:
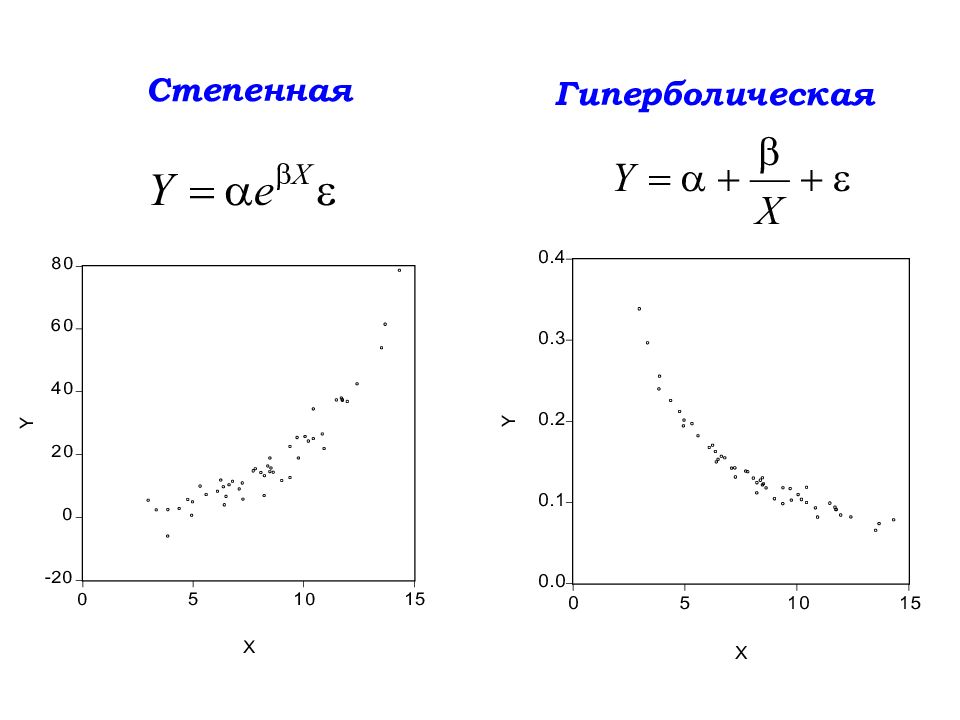
Слайд 137: 3.2. Оценка параметров нелинейных моделей
Зависимость Формула Линеаризующее преобразование Зависимость между параметрами Гиперболическая y1=y X=1/x а1=а b 1= b Логарифмическая y1=y X=ln x а1=а b 1= b Экспоненциальная Y = ln y х1=х а1=а b 1= b Степенная Y = ln y ( Y = lg y ) X = ln x ( X = lg x ) ln a=C ( lg a=C ) b1=b Показательная Y = ln y ( Y = lg y ) х1=х ln a=C ( lg a=C ) ln b=B ( lg b=B )
Слайд 138: Оценка параметров внутренне нелинейных моделей:
1. Задаются некоторые «правдоподобные» начальные (исходные) значения параметров а и b. 2. Вычисляются теоретические значения ŷi = f(xi) с использованием этих значений параметров. 3. Вычисляются остатки еi = ŷi – yi и сумма квадратов остатков S. 4. Вносятся изменения в одну или более оценку параметров. 5. Вычисляются новые теоретические значения ŷi, остатки еi и S. 6. Если произошло уменьшение S, то новые значения оценок используются в качестве новой отправной точки. 7. Шаги 4, 5 и 6 повторяются до тех пор, пока не будет достигнута ситуация, когда величину S невозможно будет улучшить (в пределах заданной точности). 8. Полученные на последнем шаге значения параметров а и b являются оценками параметров нелинейного уравнения регрессии. Оценка параметров внутренне нелинейных моделей:
Слайд 139: 4. Проверка качества уравнения регрессии
Н 0 : уравнение статистически не значимо yi = ŷi + εi D(y) = D(ŷ) + D(ε) полная (общая) сумма квадратов отклонений = сумма квадратов отклонений, объясненная регрессией + (остаточная) сумма квадратов отклонений, не объясненная регрессией
Слайд 140: F- критерий Фишера:
где m – число независимых переменных в уравнении регрессии (для парной регрессии m = 1); n – число единиц совокупности. Если F факт > F табл, то Н 0 о случайной природе связи отклоняется и признается статистическая значимость и надежность уравнения. Если F факт < F табл, то Н 0 не отклоняется и признается статистическая незначимость уравнения регрессии.
Слайд 141
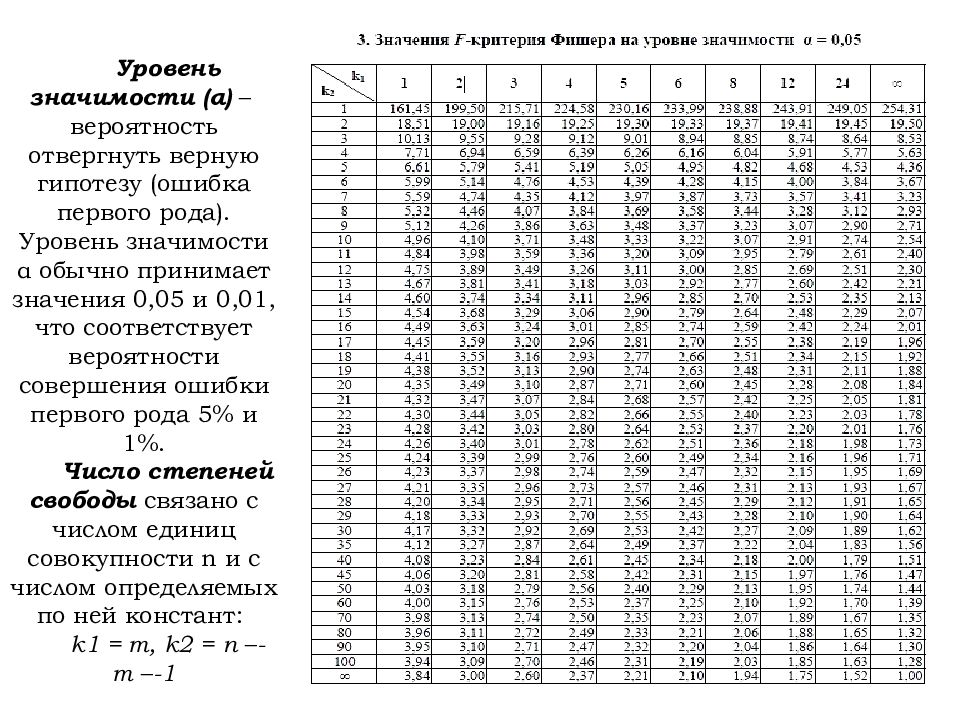
Уровень значимости ( α ) – вероятность отвергнуть верную гипотезу (ошибка первого рода). Уровень значимости α обычно принимает значения 0,05 и 0,01, что соответствует вероятности совершения ошибки первого рода 5% и 1%. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант: k1 = m, k2 = n - m -1
Слайд 142: t-критерий Стьюдента
Н 0 : а=0; b =0 Стандартные ошибки параметров регрессии и коэффициента корреляции: Данный критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом « Student » (Студент).
Слайд 144: Оценка значимости параметров уравнения и коэффициента корреляции проводится путем сопоставления их значений с величиной случайной ошибки:
Если t факт > t табл, то Н 0 отклоняется, т.е. a, b, r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если t факт < t табл, то Н 0 не отклоняется и признается случайная природа формирования a, b, r.
Слайд 145: Доверительные интервалы – это пределы, в которых лежит точное значение определяемого показателя с заданной вероятностью
Доверительные интервалы для параметров a и b уравнения линейной регрессии определяются соотношениями: ;
Слайд 146: Точечный и интервальный прогноз по уравнению линейной регрессии
Точечный прогноз заключается в получении прогнозного значения у, которое определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения х. Интервальный прогноз заключается в построении доверительного интервала прогноза. При построении доверительного интервала прогноза используется стандартная ошибка прогноза : Строится доверительный интервал прогноза :
Слайд 148
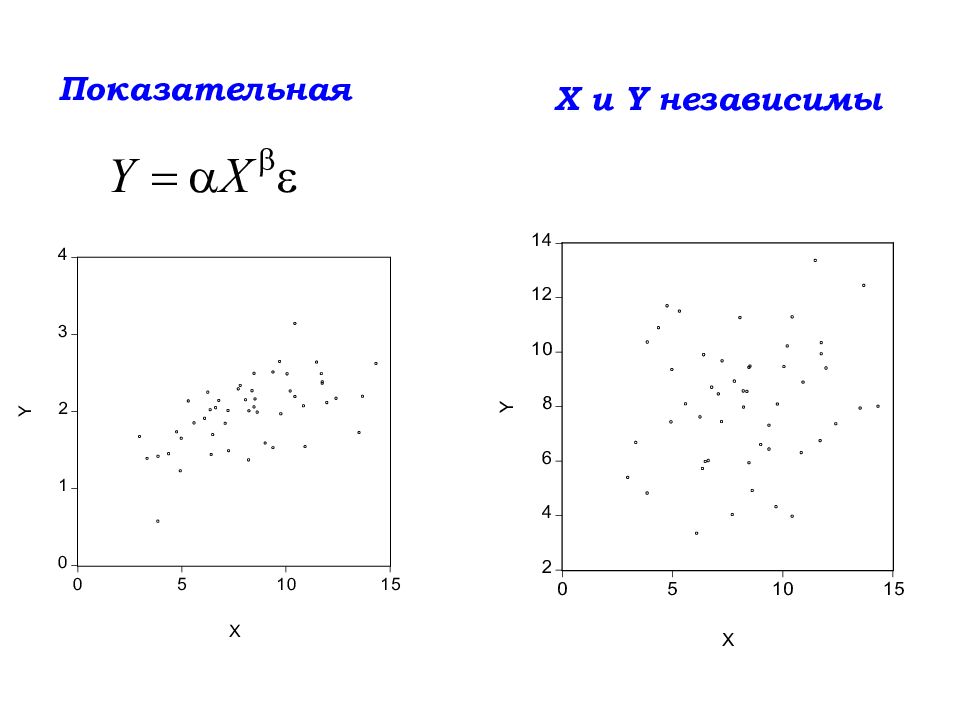
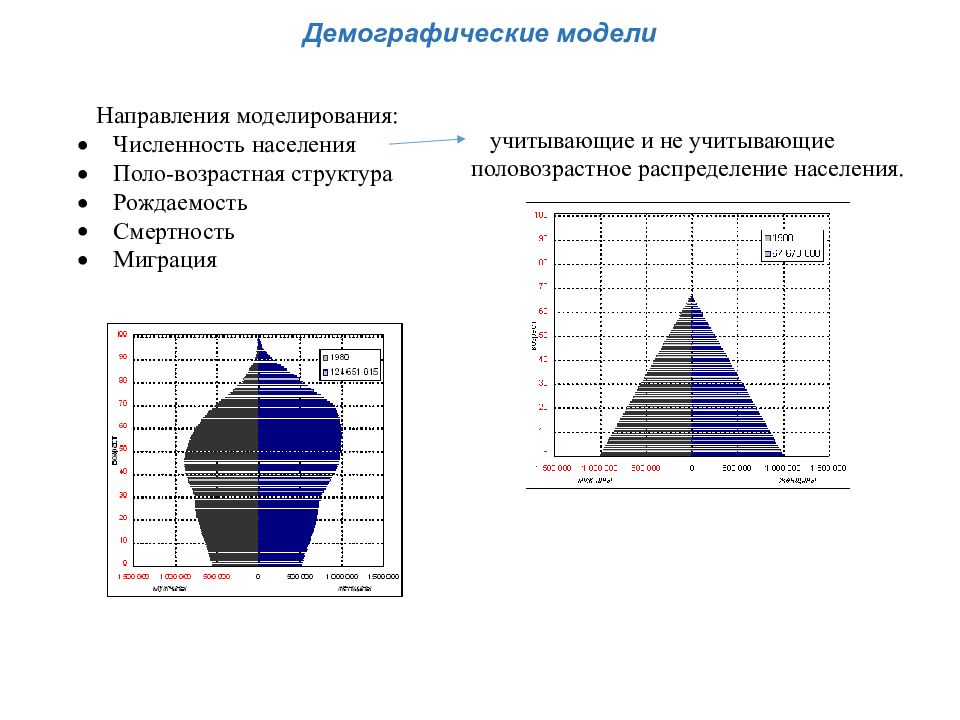
Демографические модели Направления моделирования: Численность населения Поло-возрастная структура Рождаемость Смертность Миграция учитывающие и не учитывающие половозрастное распределение населения.
Слайд 149
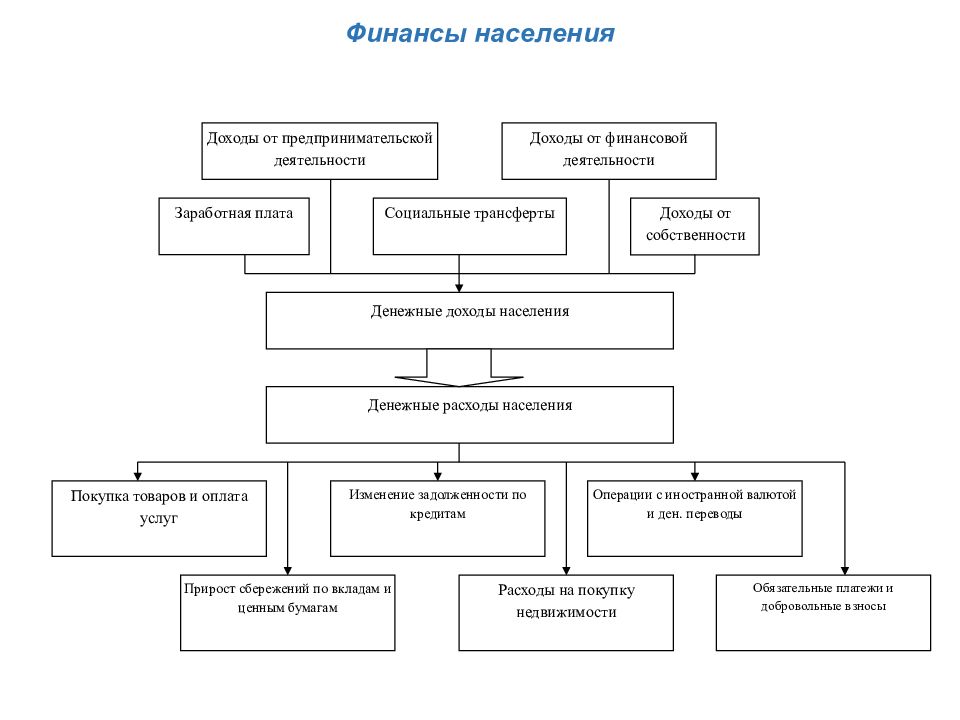
Финансы населения Социальные трансферты Заработная плата Доходы от предпринимательской деятельности Доходы от собственности Доходы от финансовой деятельности Покупка товаров и оплата услуг Операции с иностранной валютой и ден. переводы Обязательные платежи и добровольные взносы Прирост сбережений по вкладам и ценным бумагам Расходы на покупку недвижимости Изменение задолженности по кредитам Денежные доходы населения Денежные расходы населения
Слайд 150
Финансы населения Средняя склонность к потреблению (АРС) выражается отношением потребляемой части национального дохода ко всему национальному доходу: Средняя склонность к потреблению (АРС) = (потребление: национальный доход) х 100. (1) Предельная склонность к потреблению (МРС) выражается отношением изменения (прироста) потребления к тому изменению (приросту) дохода, которое его вызвало: Предельная склонность к потреблению (МРС) = (изменение в потреблении/изменение в доходе)*100. (2) Функции Предельная склонность к потреблению (МРС) Средняя склонность к потреблению (АРС) Пропорциональность потребления (С) и располагаемого дохода (Дi) Краткосрочного периода постоянная падает с ростом Д непропорциональная Долгосрочного периода постоянная постоянная пропорциональная Подоходная падает с ростом располагаемого дохода (Д) падает с ростом Д непропорциональная Средняя склонность к сбережению (APS ) выражается отношением сберегаемой части национального дохода ко всему национальному доходу: Средняя склонность к сбережению (APS)=(сбережение: национальный доход) х 100. (4) Предельная склонность к сбережению (MPS) выражается отношением любого изменения в сбережениях к тому изменению в доходе, которое его вызвало: Предельная склонность к сбережению (MPS) = (изменение в сбережении: изменение в доходе) х 100. (5)
Слайд 151
Производство Производственная функция (также функция производства ) — экономико-математическая количественная зависимость между величинами выпуска (количество продукции) и факторами производства, такими как затраты ресурсов, уровень технологий.
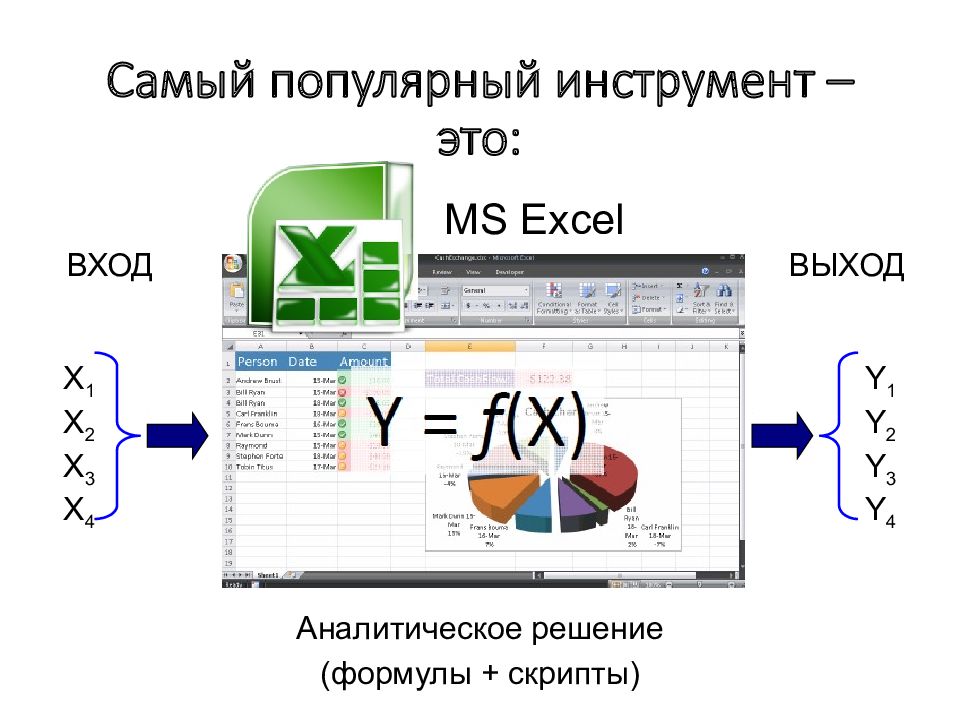
Слайд 157: Самый популярный инструмент – это:
MS Excel Аналитическое решение (формулы + скрипты) ВХОД ВЫХОД X 1 X 2 X 3 X 4 Y 1 Y 2 Y 3 Y 4
Слайд 158: Однако…
• Аналитическое решение можно найти, если • Обозримое количество параметров • Линейное поведение • Зависимости понятны, легко построить модель • А если это не так: • Параметров много • Нелинейные, неочевидные зависимости • Время, причинно - следственные связи • Антиинтуитивное поведение • Неопределённость – стохастическая система
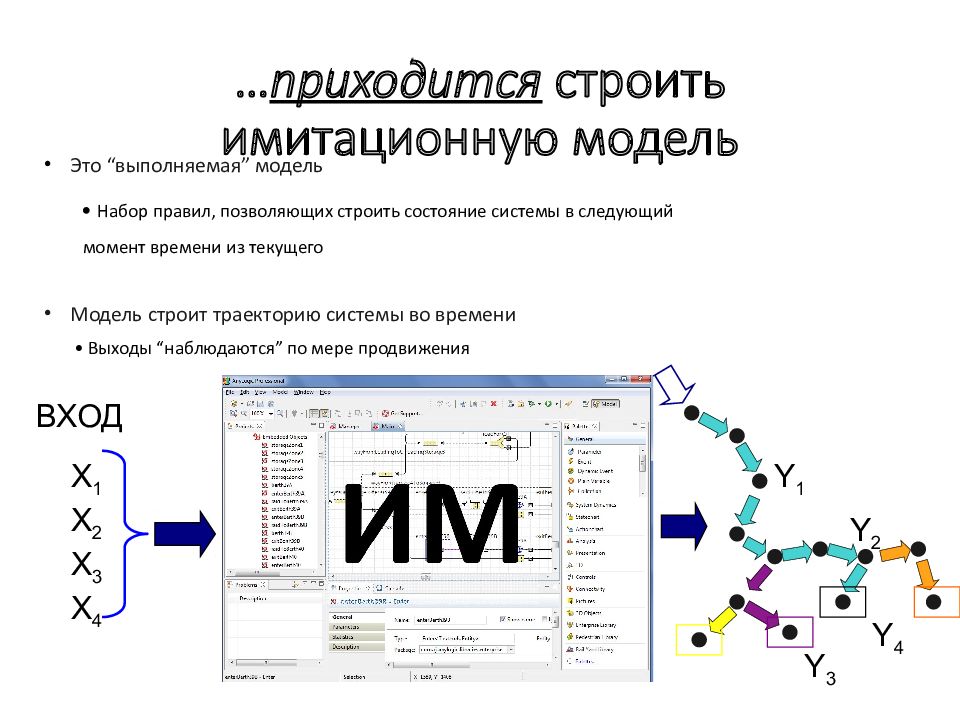
Слайд 159: приходится строить имитационную модель
Это “выполняемая” модель • Набор правил, позволяющих строить состояние системы в следующий момент времени из текущего Модель строит траекторию системы во времени • Выходы “наблюдаются” по мере продвижения ВХОД X 1 X 2 X 3 X 4 Y 1 Y 2 Y 3 Y 4
Слайд 160: Чем ещё хороша имитация:
Любая величина доступна для измерения в любое время • Если, конечно, она находится не ниже уровня абстракции Вы можете наглядно увидеть динамику системы • Имитационная модель – фактически интерактивная игра с графическим интерфейсом, часто 3D • В этом смысле по своей убедительности ИМ существенно превосходят любые “чёрные ящики” с аналитикой, тот же Excel
Слайд 161: Где применяется ИМ?
Агрегаты, глобальные причинные зависимости, динамика обратных связей, … Отдельные объекты, точные размеры, расстояния, скорости, времена, … Рынок и конкуренция Высокий уровень абстракции [меньше деталей макро уровень стратегический уровень ] Средний уровень абстракции [средняя детальность мезо-уровень тактический уровень ] Низкий уровень абстракции [больше деталей микро уровень оперативный уровень ] Социальные системы Управление активами Экосистемы Динамика персонала Экономика здравоохранения Энергетические сети Управление активами Цепочки поставок Перевозки Бизнес-процессы Больница Система обслуживания Производство Склад Военные действия Движение пешеходов Транспорт: микро-модели Системы управления Компьютерные системы
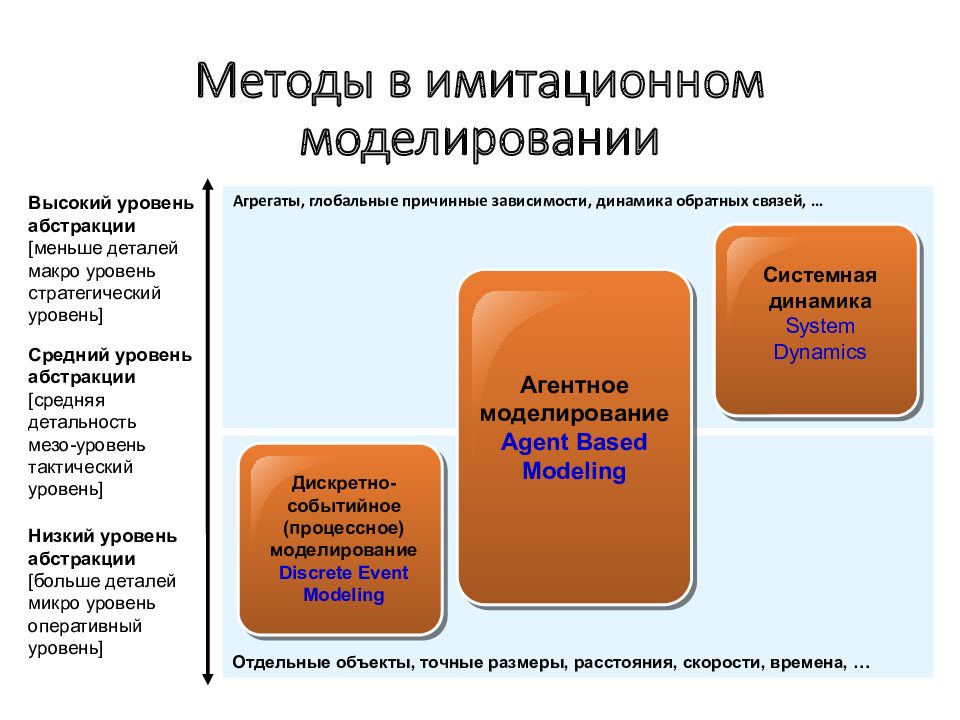
Слайд 162: Методы в имитационном моделировании
Агрегаты, глобальные причинные зависимости, динамика обратных связей, … Отдельные объекты, точные размеры, расстояния, скорости, времена, … Дискретно-событийное (процессное) моделирование Discrete Event Modeling Агентное моделирование Agent Based Modeling Системная динамика System Dynamics Высокий уровень абстракции [меньше деталей макро уровень стратегический уровень ] Средний уровень абстракции [средняя детальность мезо-уровень тактический уровень ] Низкий уровень абстракции [больше деталей микро уровень оперативный уровень ]
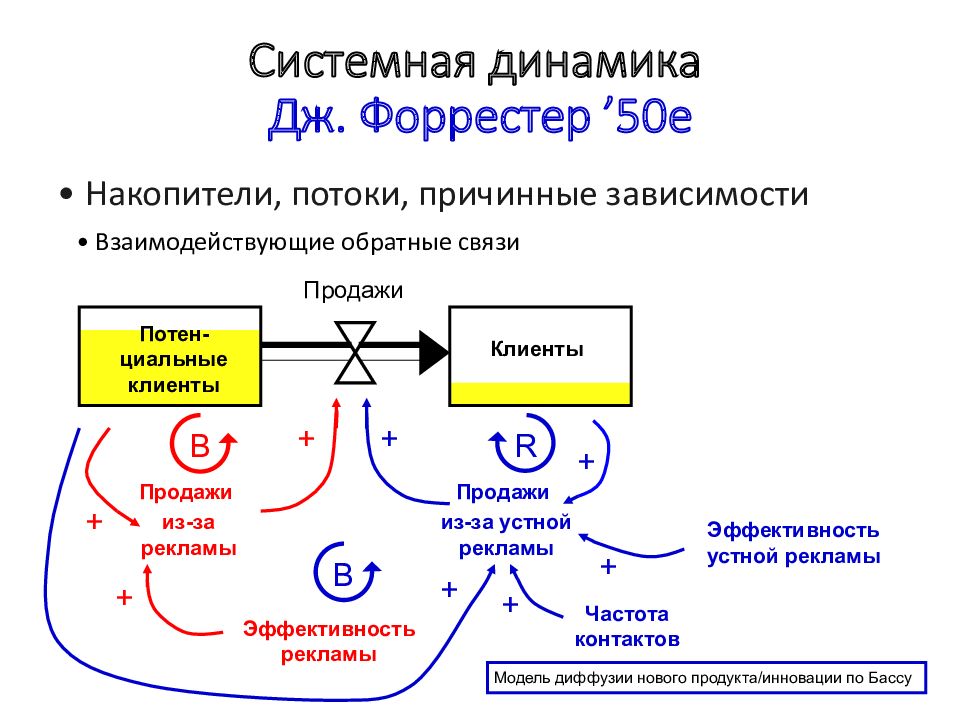
Слайд 163: Системная динамика Дж. Форрестер ’50е
• Накопители, потоки, причинные зависимости • Взаимодействующие обратные связи Продажи Потен-циальные клиенты Клиенты Продажи из-за рекламы Эффективность рекламы Продажи из-за устной рекламы Частота контактов Эффективность устной рекламы Модель диффузии нового продукта/инновации по Бассу + + + + + + + + R B B
Слайд 164: Системная динамика Дж. Форрестер ’50е
• Накопители, потоки, причинные зависимости • Взаимодействующие обратные связи Системная динамика Дж. Форрестер ’50е d( Потенциальные клиенты)/dt = - Продажи d (клиенты)/dt = Продажи Продажи = Продажи из-за рекламы + Продажи из-за устной рекламы Продажи из-за рекламы = Эффективность рекламы * Потенциальные клиенты Продажи из-за устной рекламы = Частота контактов * Эффективность устной рекламы * П отенциальные клиенты * Клиенты / ( Потенциальные клиенты + Клиенты ) Эквивалентная математическая модель: Модель диффузии нового продукта/инновации по Бассу
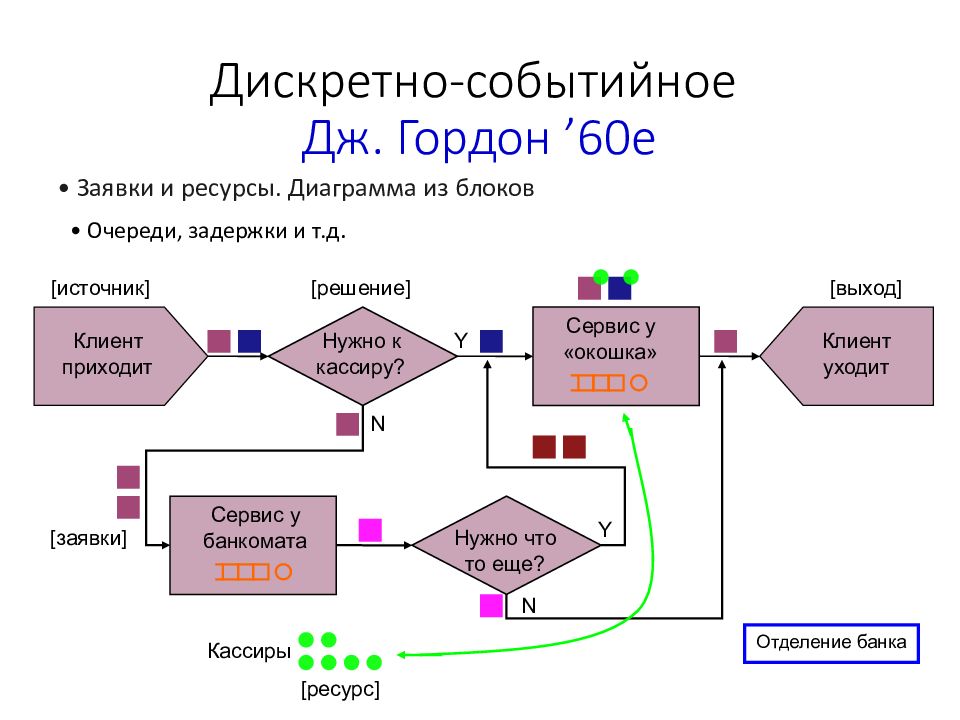
Слайд 165: Дискретно - событийное Дж. Гордон ’60е
• Заявки и ресурсы. Диаграмма из блоков • Очереди, задержки и т.д. [ источник ] Клиент приходит Нужно к кассиру? [ решение ] [ выход ] Сервис у «окошка» Сервис у банкомата Нужно что то еще? [ заявки ] Клиент уходит Y Y N N Кассиры [ ресурс ] Отделение банка
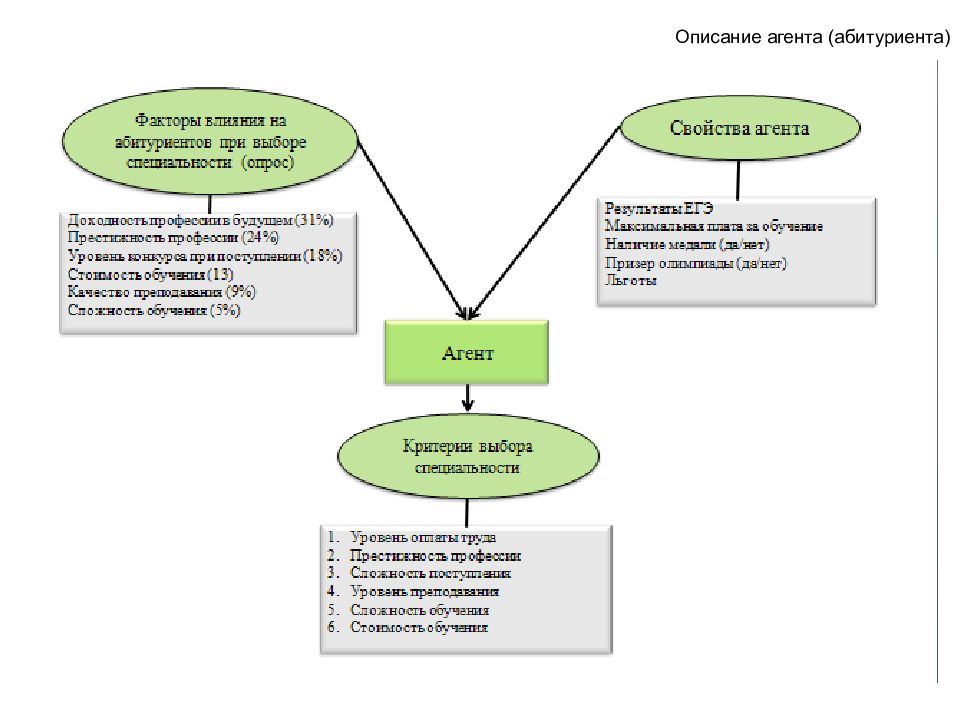
Слайд 166: Агентное моделирование
Описываем отдельные объекты и их локальные правила поведения. Иногда – модель среды СРЕДА Поведение агента Ребёнок Нет семьи Семья Пожилой
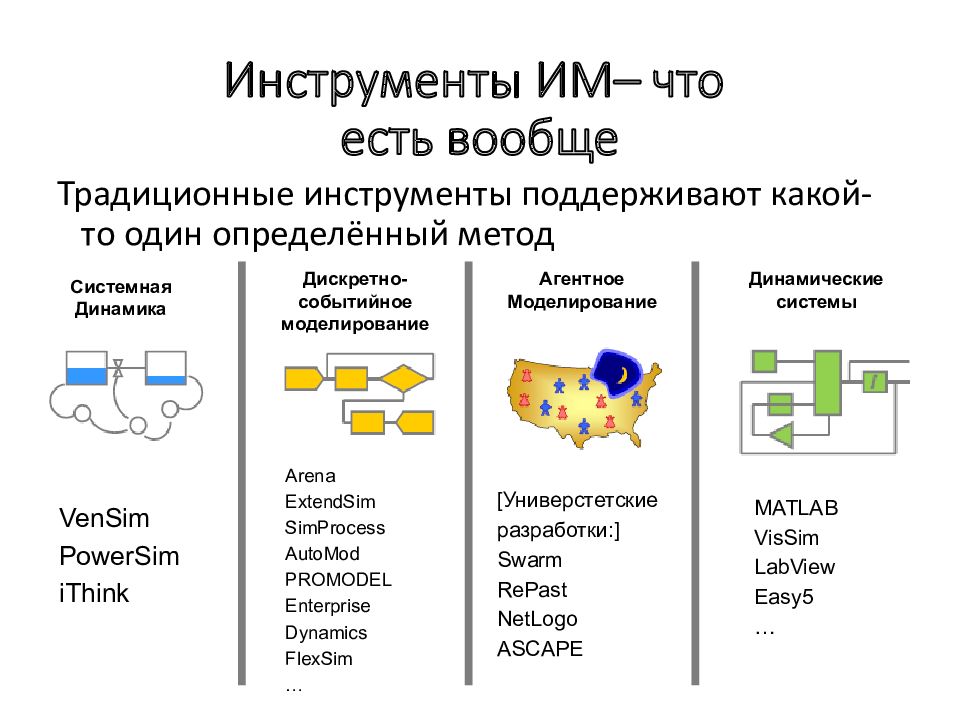
Слайд 167: Инструменты ИМ– что есть вообще
Традиционные инструменты поддерживают какой-то один определённый метод Дискретно - событийное моделирование Динамические системы Агентное Моделирование Системная Динамика VenSim PowerSim iThink Arena ExtendSim SimProcess AutoMod PROMODEL Enterprise Dynamics FlexSim … MATLAB VisSim LabView Easy5 … [Универстетские разработки:] Swarm RePast NetLogo ASCAPE
Слайд 168: AnyLogic –многоподходный инструмент ИМ
Легко менять и выбирать подходящий уровень абстракции Можно переключаться между подходами Можно смешивать разные подходы в одной модели Всё это на гибкой ОО платформе Агентное Моделирование Системная Динамика Динамические системы Дискретно - событийное моделирование
Слайд 169: Как используются имитационные модели?
Встроены в процесс оперативного управления • Модель полностью встроена в процесс производства, логистики, бизнес- процесс, запускается автоматически, может быть “не видна” явно Запускаются периодически при принятии решений • Модель запускается вручную, скажем, при планировании на квартал Оценка и сравнение сценариев планируемых изменений • Модель – инструмент планирования модернизации, оценки новых проектов, оптимизации будущей стратегии Для анимации / демонстрации предлагаемого проекта • Иллюстрирует работу объекта, который предлагается создать, используется как дополнительный аргумент в пользу данного решения Для тренировки и обучения • Позволяет персоналу лучше понять работу системы, обучиться принятию решений. Часть используется для “управленческих игр”
Слайд 170
Меню и панели инструментов Редактирование (Отменить,Повторить, Вырезать, Скопировать, Вставить, Удалить) Стандартная (Создать, Открыть модель, Сохранить модель, Сохранить все модели) Быстрый доступ к основным командам Набор видимых панелей инструментов изменяется в зависимости от текущего рабочего вида Рисование (100%, Отдалить, Масштаб, Приблизить, Отобразить/скрыть сетку, …) Построение (Построить модель, Построить все, Отладка, Запуск)
Слайд 171: Пользовательский интерфейс
Меню и панели инструментов. «Быстрые» клавиши к основным командам Графический редактор Панель Палитра. Элементы разбиты по группам, отображаемым на разных вкладках Свойства Выбранного элемента Панель Ошибки. Отображает ошибки и помогает их локализовать Панель Проекты. Навигацияпо моделям Двойной щелчок Щелчок
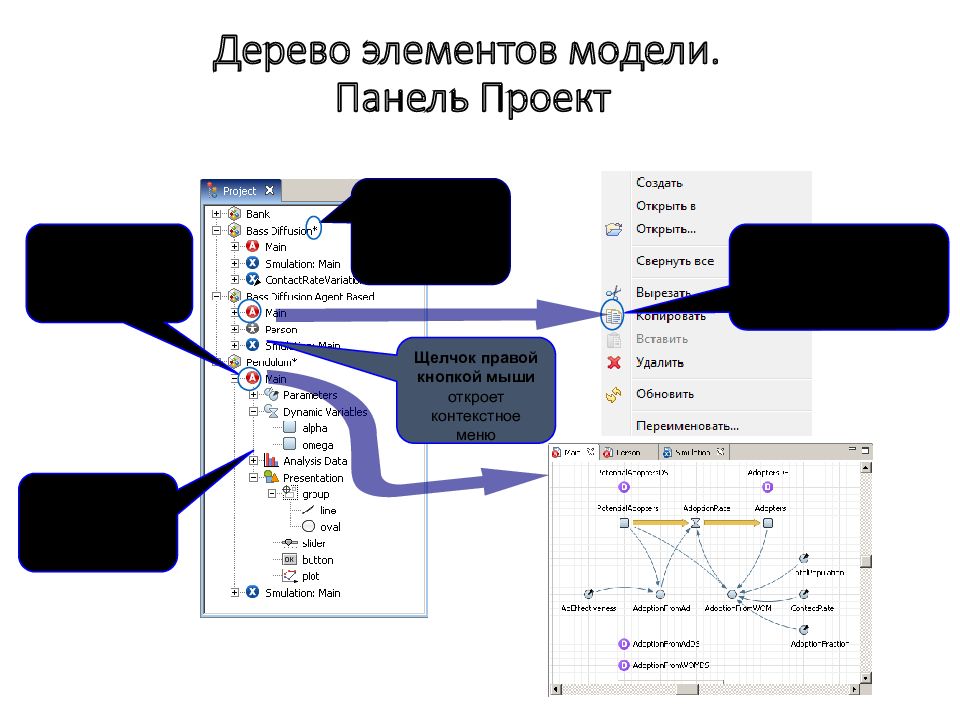
Слайд 172: Дерево элементов модели. Панель Проект
Модели с несохраненными изменениями помечаются звездочками Двойной щелчок откроет редактор и/или свойства элемента Все элементы модели структурированы иерархически Копируйте элементы дерева с помощью команд Копировать/Вырезать и Вставить Щелчок правой кнопкой мыши откроет контекстное меню
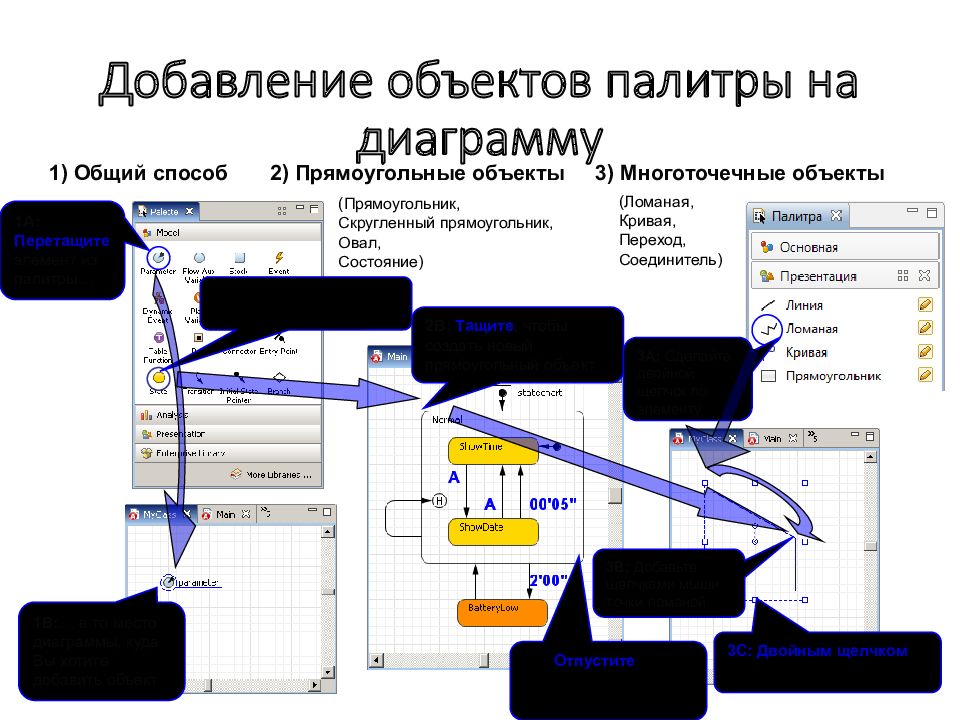
Слайд 173: Добавление объектов палитры на диаграмму
1) Общий способ 1A: Перетащите элемент из палитры… 2B: Тащите, чтобы создать новый прямоугольный объект 1B: … в то место диаграммы, куда Вы хотите добавить объект 3C: Двойным щелчком завершите рисование 2) Прямоугольные объекты 3) Многоточечные объекты ( Прямоугольник, Скругленный прямоугольник, Овал, Состояние) ( Ломаная, Кривая, Переход, Соединитель) 3В: Добавьте щелчками мыши точки ломаной 2C: Отпустите кнопку, чтобы завершить операцию 2A: Сделайте двойной щелчок по элементу 3A: Сделайте двойной щелчок по элементу
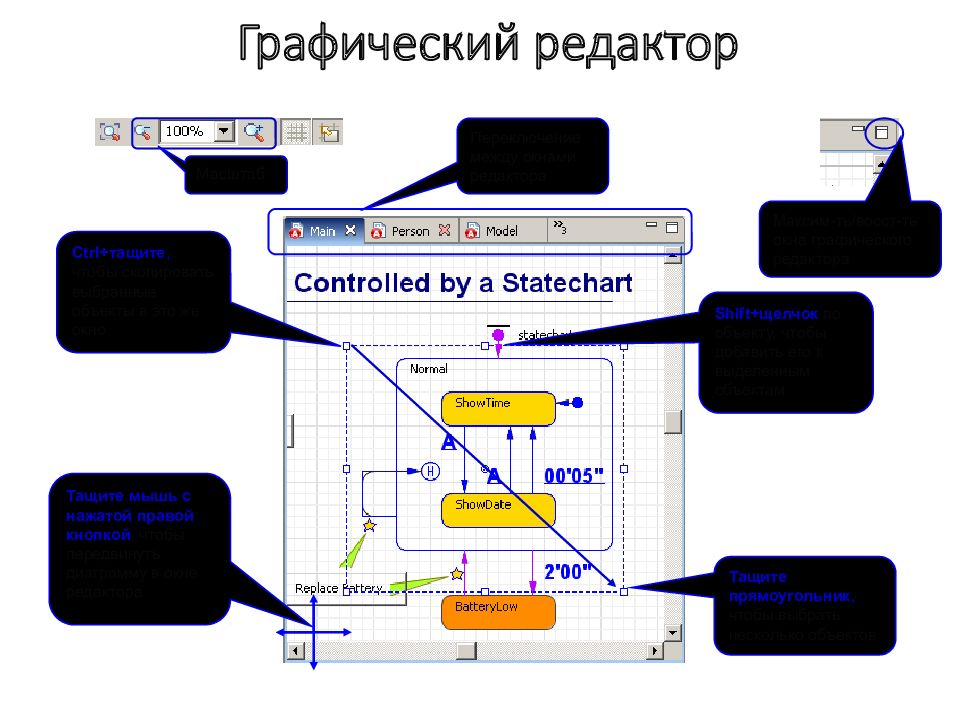
Слайд 174: Графический редактор
Масштаб Переключение между окнами редактора Максим-ть/восст-ть окна графического редактора Тащите прямоугольник, чтобы выбрать несколько объектов Shift+щелчок по объекту, чтобы добавить его к выделенным объектам Ctrl+тащите, чтобы скопировать выбранные объекты в это же окно Тащите мышь с нажатой правой кнопкой, чтобы передвинуть диаграмму в окне редактора
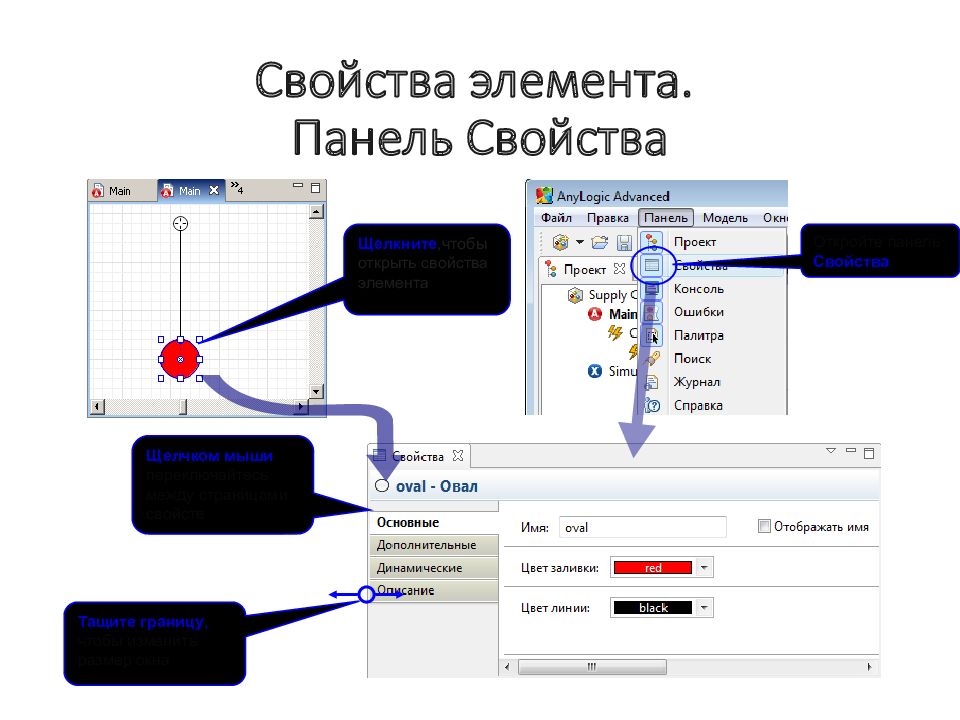
Слайд 175: Свойства элемента. Панель Свойства
Щелкните,чтобы открыть свойства элемента Откройте панель Свойства Щелчком мыши переключайтесь между страницами свойств Тащите границу, чтобы изменить размер окна
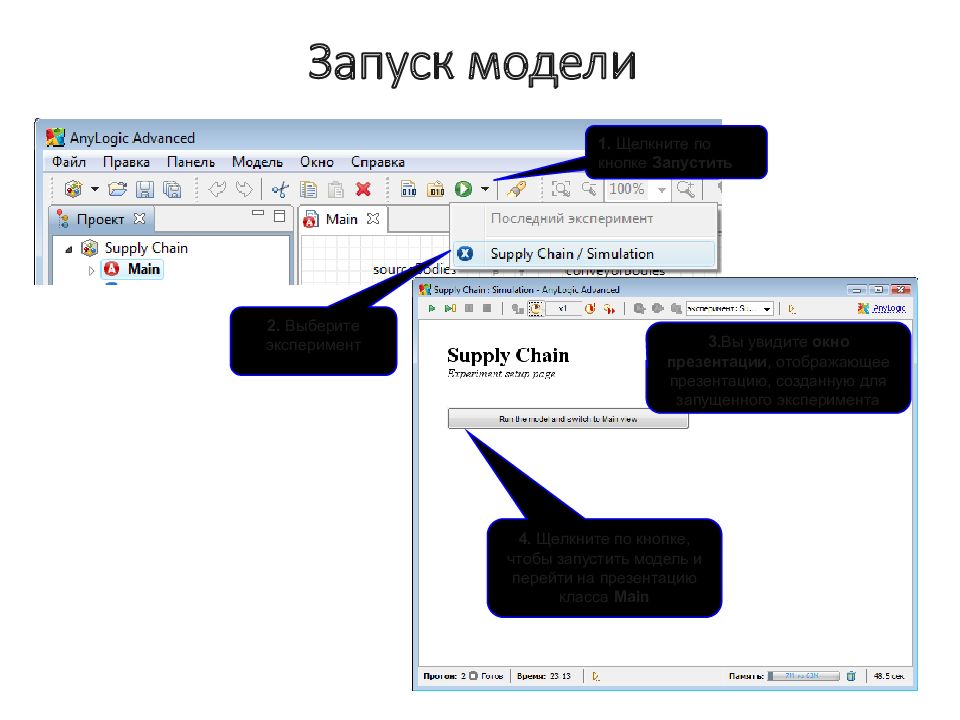
Слайд 176: Запуск модели
2. Выберите эксперимент 1. Щелкните по кнопке Запустить 3. Вы увидите окно презентации, отображающее презентацию, созданную для запущенного эксперимента 4. Щелкните по кнопке, чтобы запустить модель и перейти на презентацию класса Main
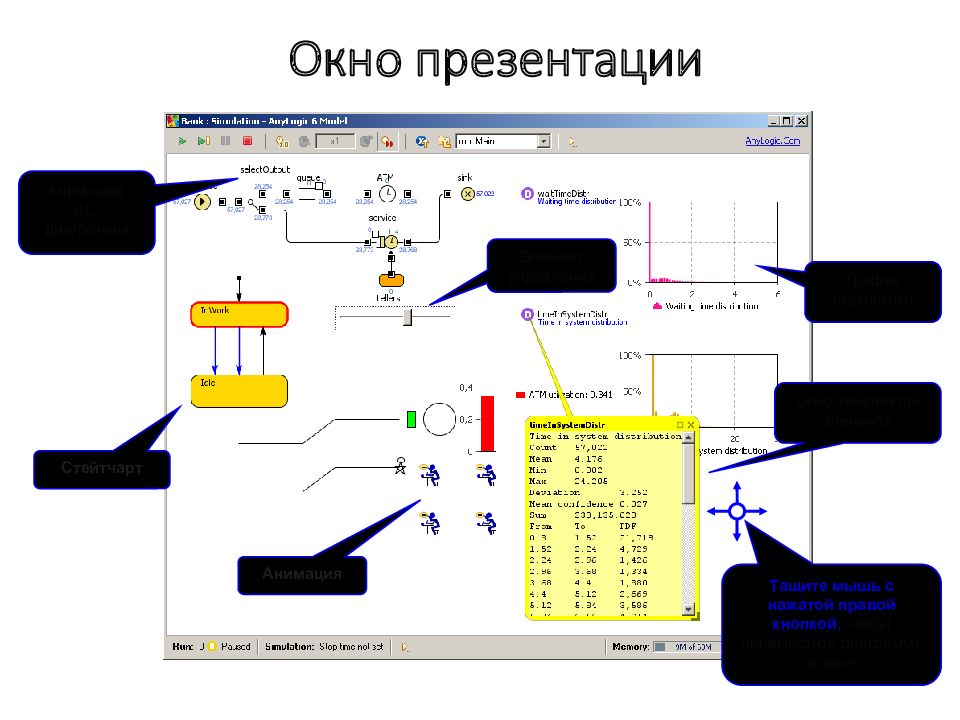
Слайд 177: Окно презентации
График статистики Окно «инспекта» элемента Тащите мышь с нажатой правой кнопкой, чтобы переместить диаграмму в окне Стейтчарт Анимация Анимация ДС- диаграммы Элемент управления
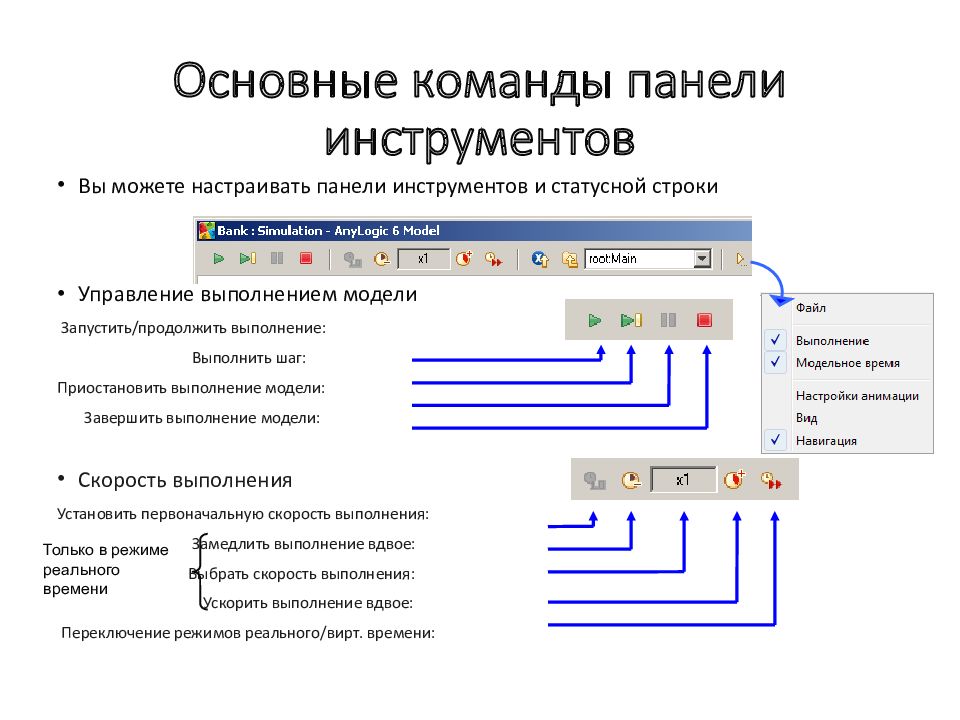
Слайд 178: Основные команды панели инструментов
Вы можете настраивать панели инструментов и статусной строки Управление выполнением модели Запустить/продолжить выполнение: Выполнить шаг: Приостановить выполнение модели: Завершить выполнение модели: Скорость выполнения Установить первоначальную скорость выполнения: Замедлить выполнение вдвое: Выбрать скорость выполнения: Ускорить выполнение вдвое: Переключение режимов реального/вирт. времени: Только в режиме реального времени
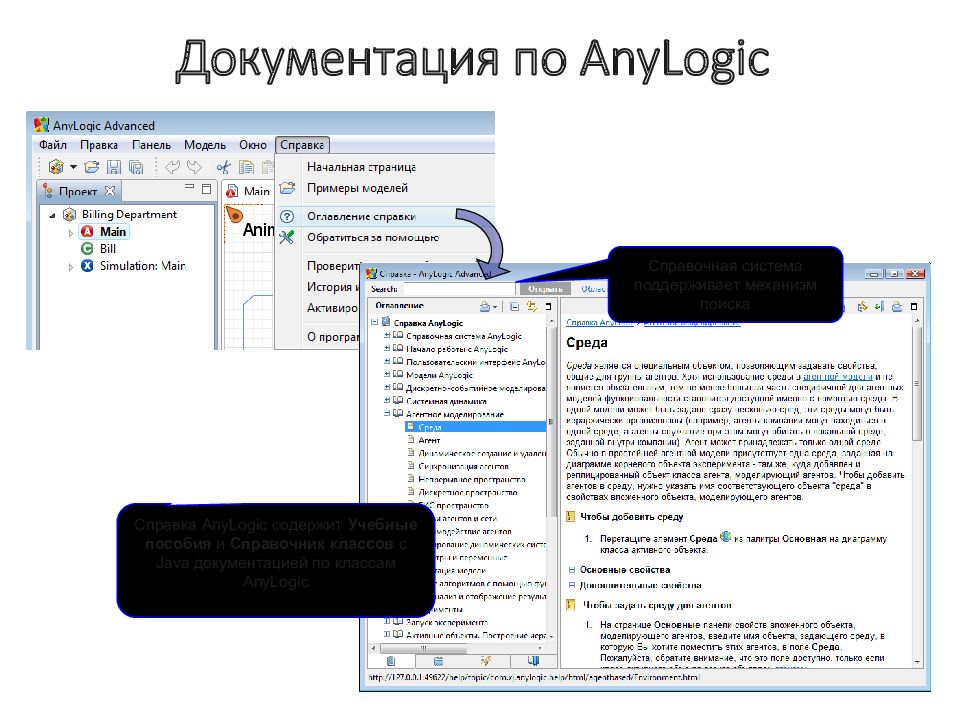
Слайд 179: Документация по AnyLogic
Справка Any L ogic содержит Учебные пособия и Справочник классов с Java документацией по классам Any L ogic Справочная система поддерживает механизм поиска
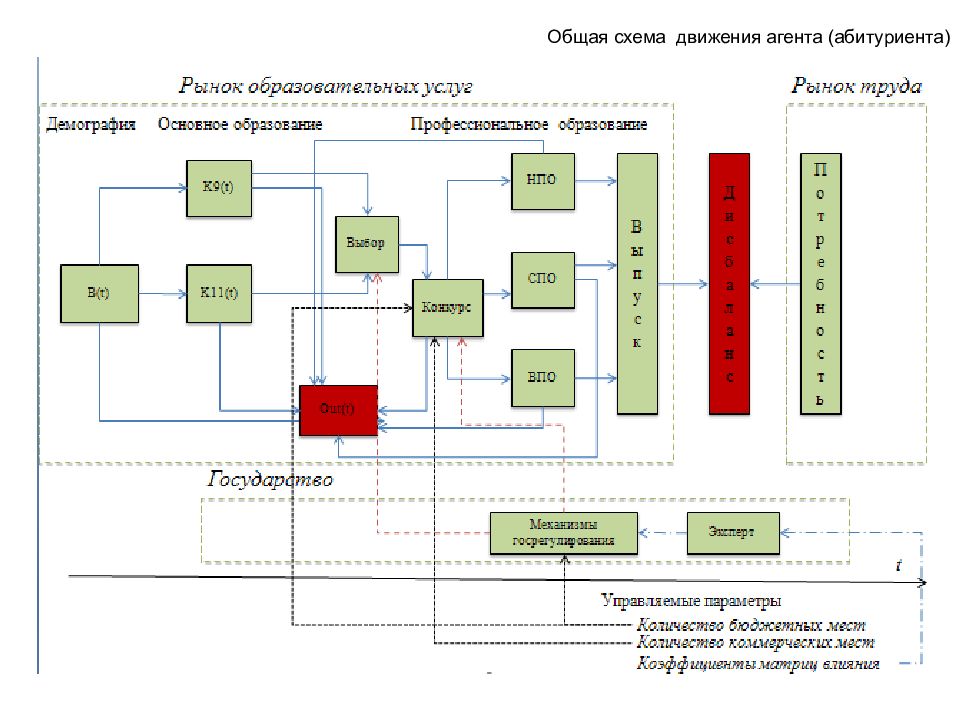
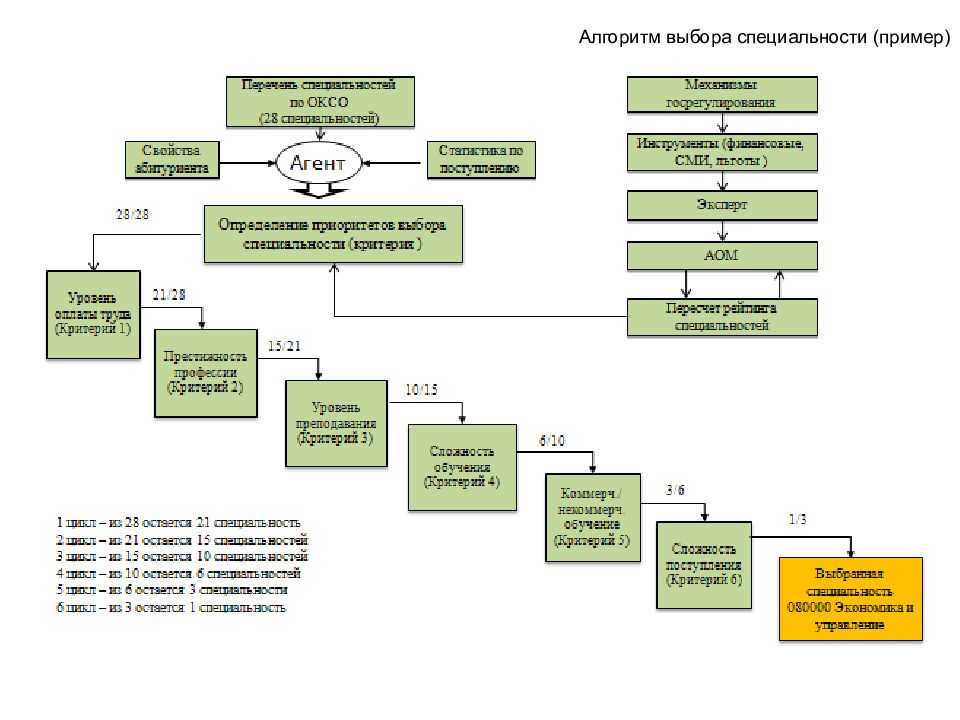
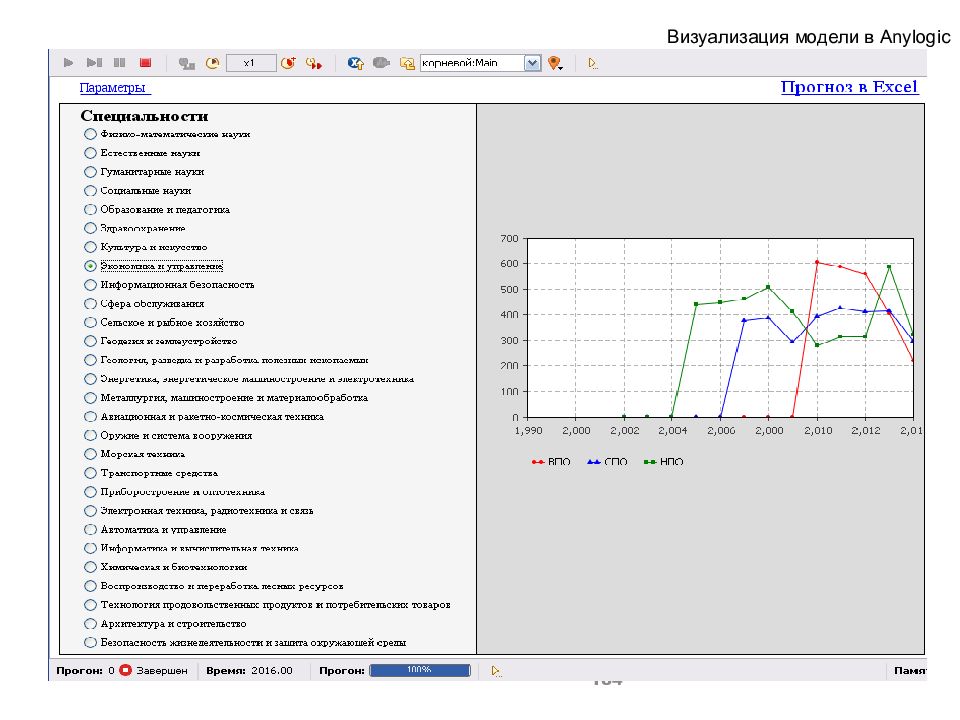
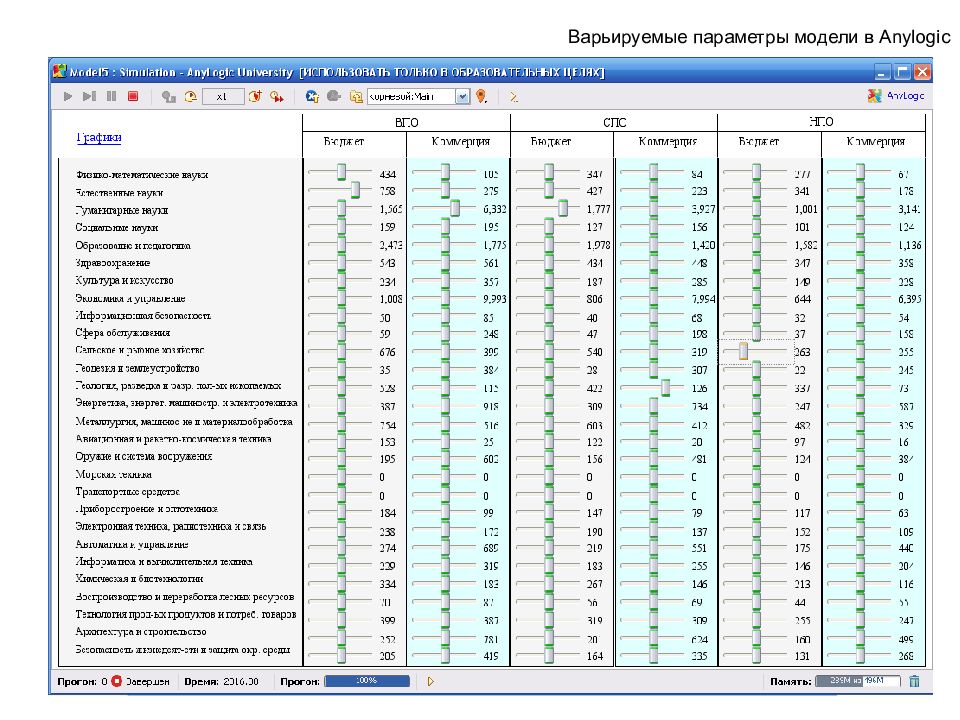
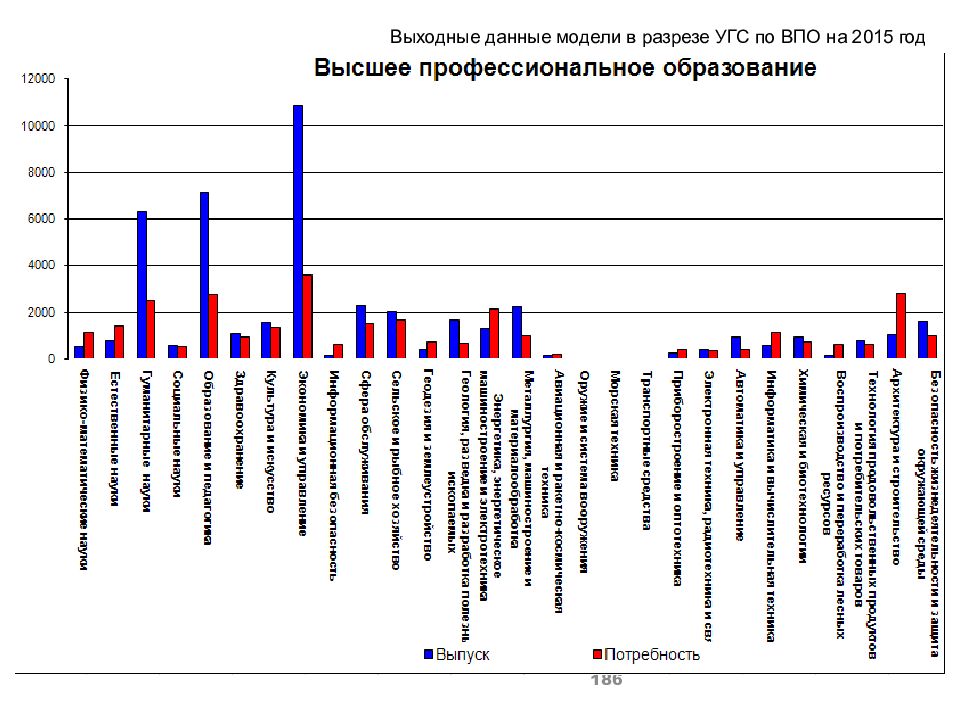
Слайд 180: Инструментарий имитационного моделирования профессионально-квалификационного дисбаланса рынков труда и образовательных услуг
Последний слайд презентации: ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ
Практические занятия № занятия № раздела Тема Кол-во часов 1 1 Обзор программных продуктов используемых для моделирования социально-экономических процессов 2 2 2 Составление и решение задач линейного программирования 2 3 3 Формирование логической модели региональной социально-экономической системы 2 4 4 Использование корреляционно-регрессионных методов при анализе временных рядов 2 5 4 Оценка качества математической модели социально-экономической системы 2 Математическая формализация логической модели: 6 5 - производственной сферы региона 2 7 5 - домохозяйств региона 2 8 5 -формирования и использования консолидированного бюджета региона 2 9 5 Формирование комплексной модели социально-экономической системы региона 2 10 6 Использование агент-ориентированных моделей в исследовании социально-экономических процессов 2