РАБОТА. ЭНЕРГИЯ Работа силы. Мощность Элементарная работа dA силы на элементарном перемещении : скалярное произведение длина элементарного пути Можно представить dA в виде проекция dr на направление вектора проекция ds на направление вектора проекция силы на направление пути (касательной к траектории). В декартовых координатах скалярное произведение можно представить как
РАБОТА. ЭНЕРГИЯ Работа силы. Мощность Работой силы при перемещении материальной точки из точки (1) в точку (2) называется: Точное значение А: Полная работа приближённо: Интеграл от вектора берётся вдоль траектории (по линии) – линейный интеграл. Траектория разбивается на малые участки. На каждом участке F s ~const и.
РАБОТА. ЭНЕРГИЯ Работа силы. Мощность Мощность характеризует быстроту с которой совершается работа: Размерность работы: [ A ]=[ F ] L = MLT -2 * L = ML 2 T -2 Единица измерения работы в системе СИ: Дж = кг*м 2 /сек 2 Размерность мощности: [ P ]=[ A ] T -1 == ML 2 T -3 Вт=кг*м 2 /сек 3 Единица измерения мощности в системе СИ:
Работа силы тяготения. Работа силы Кулона РАБОТА. ЭНЕРГИЯ Закон тяготения Две материальные точки притягиваются с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними и направленной по соединяющей их прямой. м³/(кг с²) притяжение В векторной форме Закон Кулона Два точечных заряда взаимодействуют с силой прямо пропорциональной произведению зарядов и обратно пропорциональной квадрату расстояния между ними. Сила направлена по прямой, соединяющей заряды. Н·м 2 /Кл 2 q 1 и q 2 - алгебраические величины – знак – притяжение или отталкивание
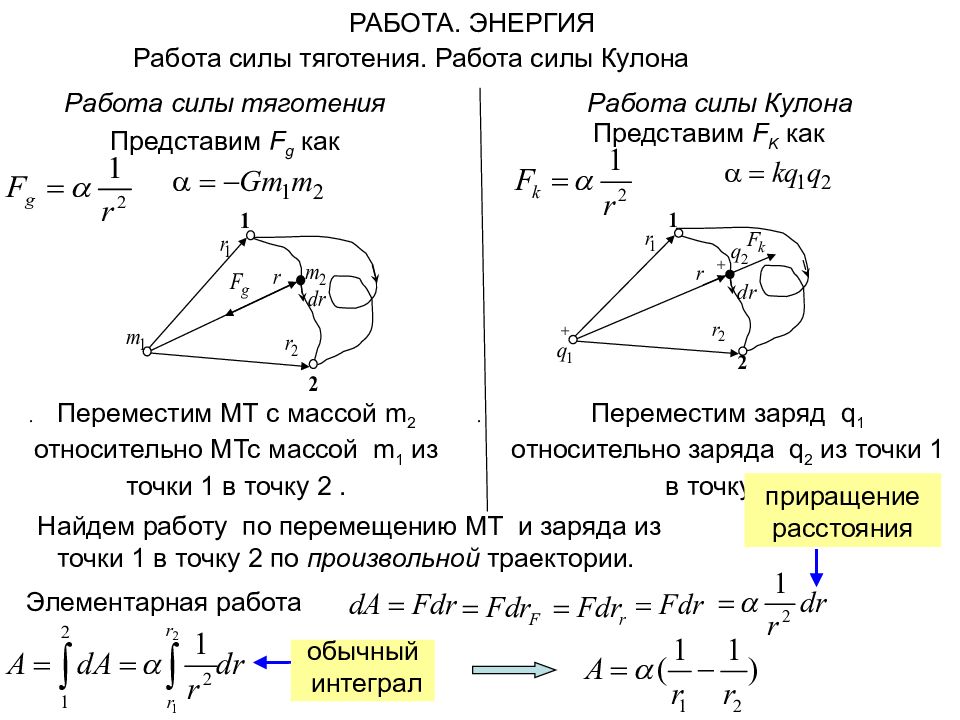
Работа силы тяготения. Работа силы Кулона РАБОТА. ЭНЕРГИЯ Работа силы тяготения . Представим F g как Переместим МТ с массой m 2 относительно МТс массой m 1 из точки 1 в точку 2. Работа силы Кулона Представим F K как . Переместим заряд q 1 относительно заряда q 2 из точки 1 в точку 2. Найдем работу по перемещению МТ и заряда из точки 1 в точку 2 по произвольной траектории. Элементарная работа приращение расстояния обычный интеграл
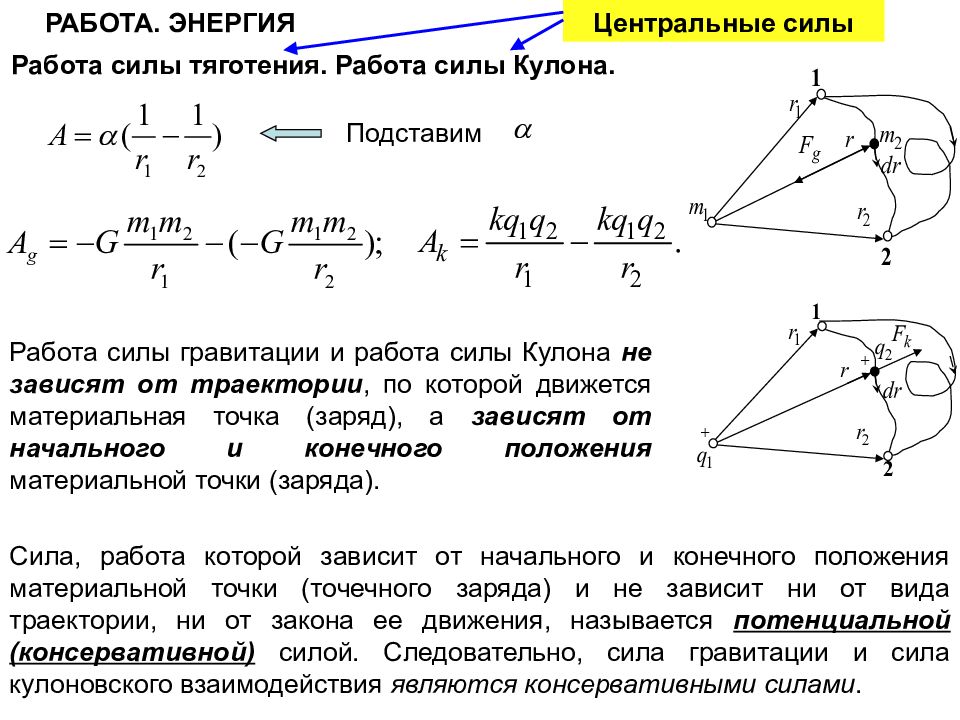
Работа силы тяготения. Работа силы Кулона. РАБОТА. ЭНЕРГИЯ Подставим Работа силы гравитации и работа силы Кулона не зависят от траектории, по которой движется материальная точка (заряд), а зависят от начального и конечного положения материальной точки (заряда). Сила, работа которой зависит от начального и конечного положения материальной точки (точечного заряда) и не зависит ни от вида траектории, ни от закона ее движения, называется потенциальной (консервативной) силой. Следовательно, сила гравитации и сила кулоновского взаимодействия являются консервативными силами. Центральные силы
Работа силы тяжести (работа в однородном поле) РАБОТА. ЭНЕРГИЯ На поверхности Земли Вблизи поверхности Земли h<<R Сила тяжести F т не зависит от координат однородное силовое поле. сила тяжести Найдём работу по перемещению МТ из точки 1 в точку 2 по произвольной траектории. Элементарная работа силы тяжести на элементарном перемещении Не зависит от траектории, определяется только начальной и конечной координатой Сила тяжести – консервативная сила
РАБОТА. ЭНЕРГИЯ Работа силы упругости При r = 0 пружина не деформирована Пружина с закрепленным концом. даёт положение тела относительно положения равновесия сила упругости, приложенная к телу со стороны пружины, направлена к положению равновесия. Небольшие деформации Закон Гука: коэффициент упругости (жёсткости ) Элементарная работа силы упругости: Работа силы упругости по перемещению материальной точки из положения 1 ( ) в положение 2 ( ): Упругая сила - консервативная
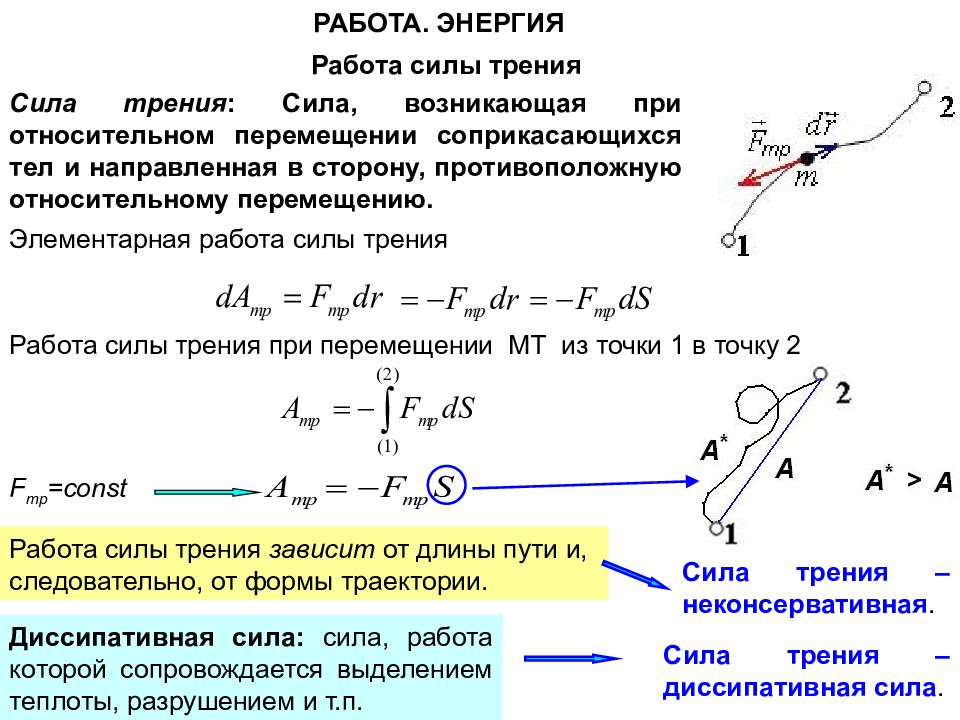
РАБОТА. ЭНЕРГИЯ Работа силы трения Сила трения : Сила, возникающая при относительном перемещении соприкасающихся тел и направленная в сторону, противоположную относительному перемещению. Элементарная работа силы трения Работа силы трения при перемещении МТ из точки 1 в точку 2 F тр =const Работа силы трения зависит от длины пути и, следовательно, от формы траектории. Сила трения – неконсервативная. Диссипативная сила: сила, работа которой сопровождается выделением теплоты, разрушением и т.п. Сила трения – диссипативная сила.
Механическая энергия и закон её сохранения РАБОТА. ЭНЕРГИЯ Важнейшее понятие в физике - энергия. Механика – механическая энергия. Тепловая, электрическая, ядерная энергия. Энергия любого вида имеет размерность работы и тесно связана с понятием работы. Зачем водится понятие энергии? Закон сохранения энергии. Позволяет решать задачи, не входя в детали конкретного механизма. Пример. mgh=mv2/2 →. Скорость не зависит от формы траектории. Отсекаются все идеи, как увеличить скорость, изменяя форму склона. Пример : превращение энергии поднятой плотиной воды в электричество Пример: солнечная батарея - цена в энерг единицах.
Механическая энергия : потенциальная и кинетическая. Механическая энергия и закон её сохранения РАБОТА. ЭНЕРГИЯ Кинетическая энергия связана со скоростью их движения тел (м.т.). Потенциальная энергия связана со взаимным расположением взаимодействующих тел (материальных точек).
Механическая энергия и закон её сохранения РАБОТА. ЭНЕРГИЯ Поле силы. Потенциальная энергия. Поле сил – свойство пространства, которое заключается в том, что на помещенное в него тело действует сила, закономерно изменяющаяся от точки к точке пространства. Сила – результат взаимодействия пары тел. В ряде случаев случаях удобно не говорить о втором теле, а считать силу свойством пространства Примеры Околосолнечное пространство - гравитационное поле. Околоземное пространство - сила тяжести свойство околоземного пространства тела в околоземном пространстве - в поле силы тяжести – однородное поле. Важный случай силового поля – потенциальное поле. Потенциальное поле это поле консервативных ( потенциальных) сил.
Механическая энергия и закон её сохранения Поле силы. Потенциальная энергия. Примеры потенциальных полей и работы сил этих полей. Гравитационное поле: Электростатическое поле: Поле силы тяжести: A T =mgh 1 -mgh 2. Работа упругой силы: Работа консервативной силы: A кс = W п1 - W п2 разность значений функции, зависящая от относительного положения взаимодействующих тел (или от координат тела в потенциальном поле). Работа консервативной силы Работа сил потенциальных полей = Обозначим эти значения функции W п1 и W п2 и назовем их потенциальными энергиями взаимодействия.
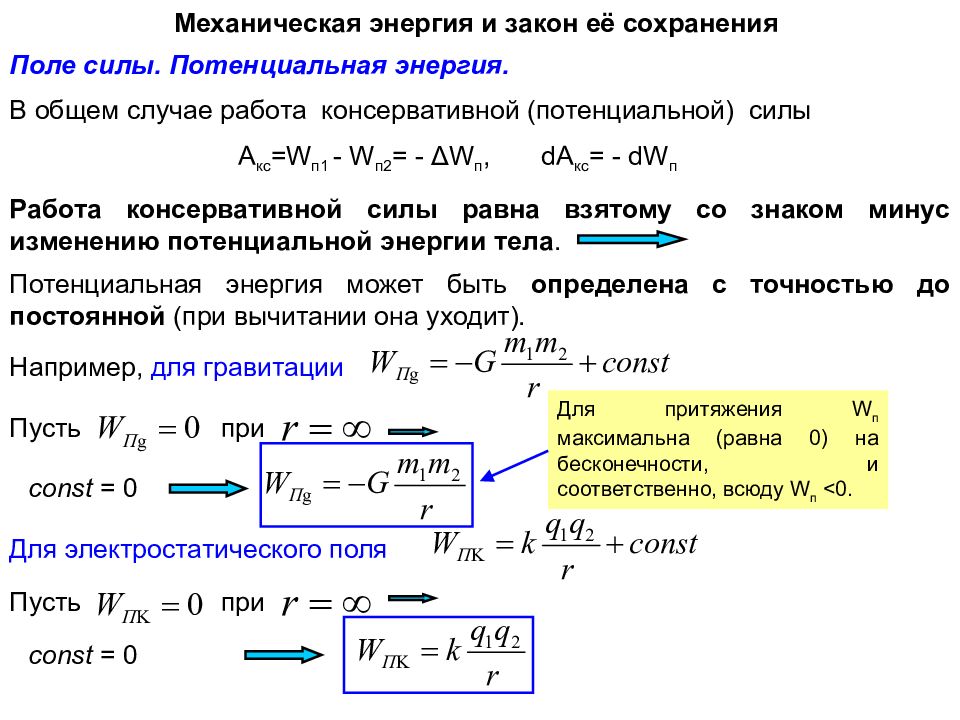
Механическая энергия и закон её сохранения Поле силы. Потенциальная энергия. В общем случае работа консервативной (потенциальной) силы A кс = W п1 - W п2 = - Δ W п, dA кс = - dW п Работа консервативной силы равна взятому со знаком минус изменению потенциальной энергии тела. Потенциальная энергия может быть определена с точностью до постоянной (при вычитании она уходит). Например, для гравитации Пусть при Для электростатического поля Для притяжения W п максимальна (равна 0) на бесконечности, и соответственно, всюду W п <0. Пусть при const = 0 const = 0
Механическая энергия и закон её сохранения Поле силы. Потенциальная энергия. Для поля силы тяжести : W П T = mgh + const Пусть W П T =0 при h =0 Для силы упругости Пусть при r = 0 Резюме: Потенциальная энергия есть величина относительная. Потенциальная энергия системы в данном ее положении численно равна работе, которую совершают действующие на систему консервативные силы при перемещении системы из этого положения в то, где потенциальная энергия условно принимается равной нулю. W П T = mgh
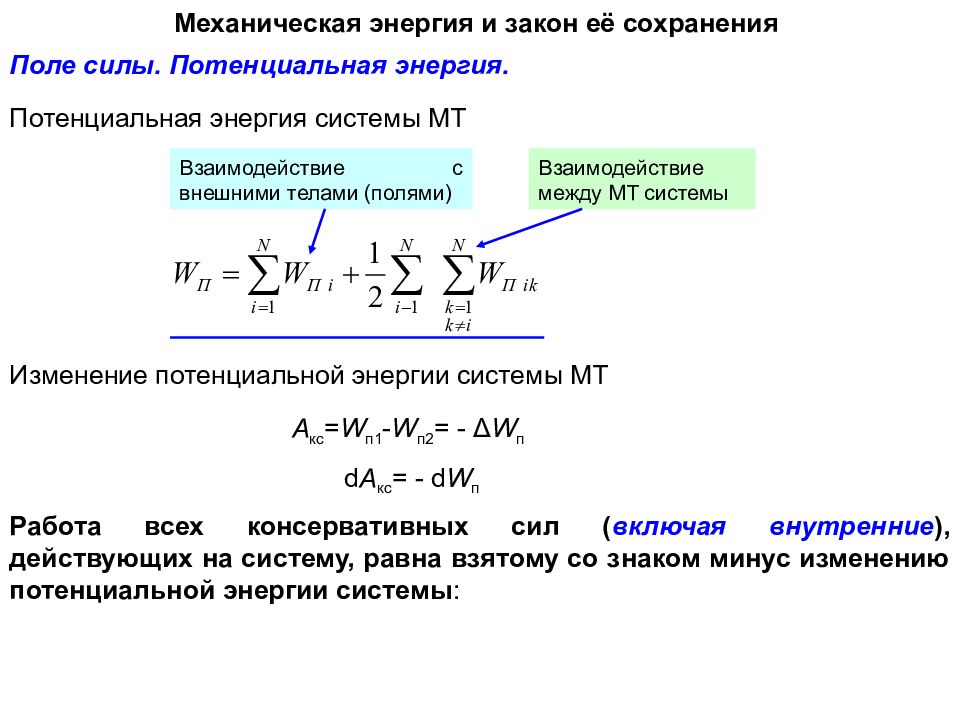
Потенциальная энергия - часть механической энергии системы, зависящая от взаимного расположения материальных точек, составляющих эту систему, и от их положения во внешнем силовом поле. Поле силы. Потенциальная энергия. Пример Для системы материальных точек: W пik – потенциальная энергия взаимодействия i -й МТ с k -й МТ. – потенц. энергия взаимодействия i -й МТ со всеми МТ системы. – полная потенциальная энергия взаимодействия МТ друг с другом -потенц. энергия взаимодействия i -й МТ с внешними телами (полями). – полная потенциальная энергия взаимодействия системы с внешними телами (полями) – полная потенциальная энергия системы МТ
Механическая энергия и закон её сохранения Поле силы. Потенциальная энергия. Взаимодействие с внешними телами (полями) Взаимодействие между МТ системы Работа всех консервативных сил ( включая внутренние ), действующих на систему, равна взятому со знаком минус изменению потенциальной энергии системы : Потенциальная энергия системы МТ Изменение потенциальной энергии системы МТ A кс = W п1 - W п2 = - Δ W п d A кс = - d W п
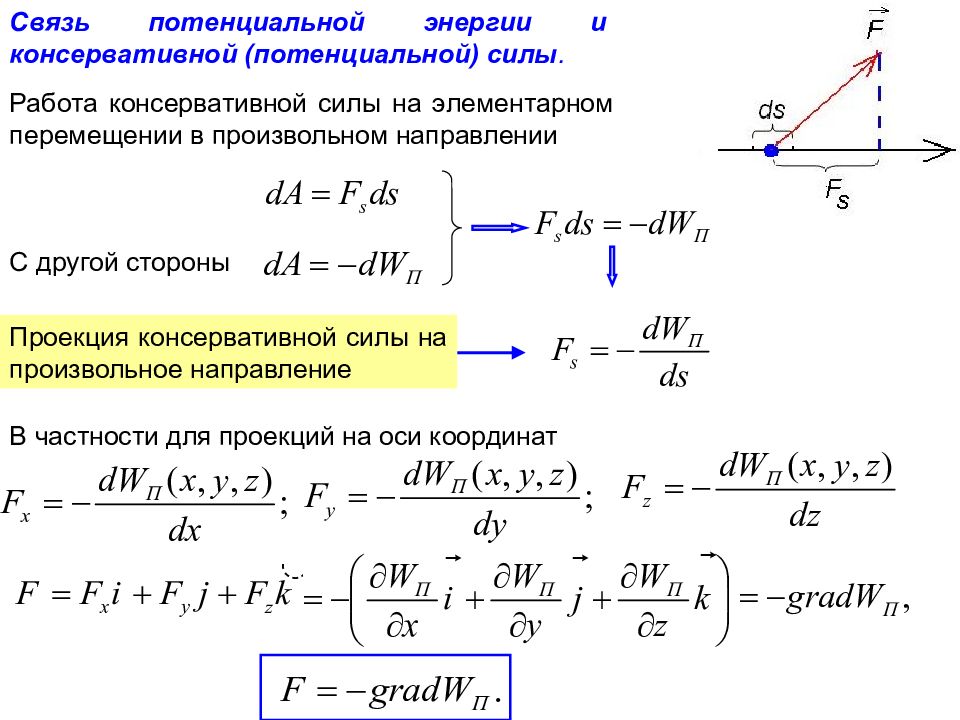
Связь потенциальной энергии и консервативной (потенциальной) силы. С другой стороны Проекция консервативной силы на произвольное направление В частности для проекций на оси координат Работа консервативной силы на элементарном перемещении в произвольном направлении
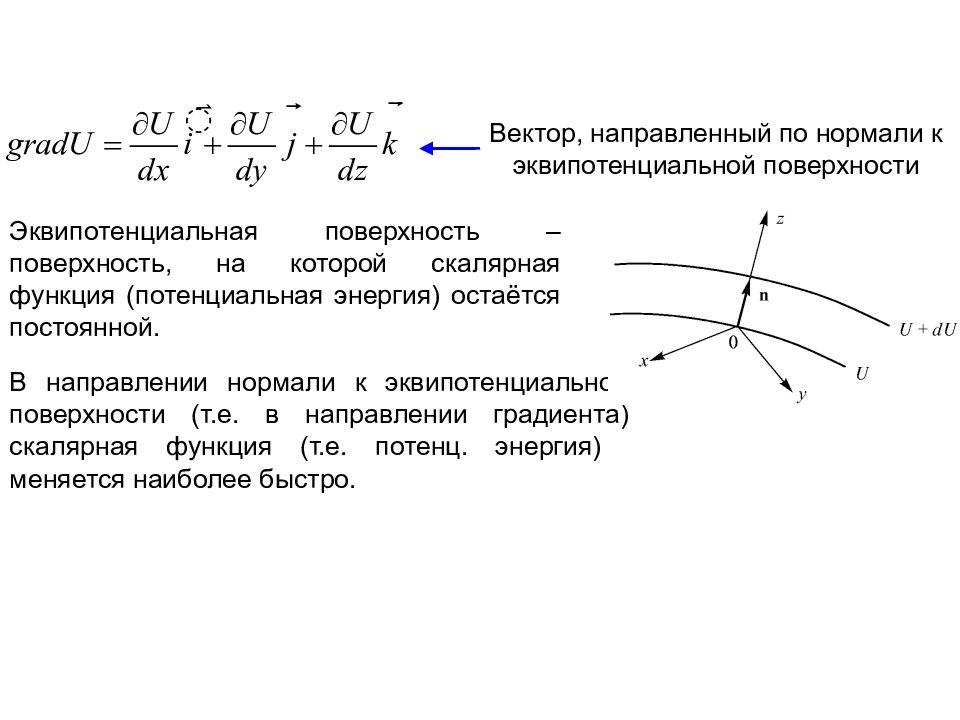
Вектор, направленный по нормали к эквипотенциальной поверхности Эквипотенциальная поверхность – поверхность, на которой скалярная функция (потенциальная энергия) остаётся постоянной. В направлении нормали к эквипотенциальной поверхности (т.е. в направлении градиента) скалярная функция (т.е. потенц. энергия) меняется наиболее быстро.
Механическая энергия и закон её сохранения Связь потенциальной энергии и консервативной (потенциальной) силы. Консервативная сила, действующая на материальную точку, равна минус градиенту потенциальной энергии и направлена в сторону уменьшения потенциальной энергии по нормали к эквипотенциальной поверхности Пример : сила тяжести, эквипотенциальная поверхность - горизонтальная поверхность - сила направлена вниз (по нормали). Пример: центральная сила (точечные заряды, гравитация) эквипотенциальная поверхность – сфера: r = c o nst
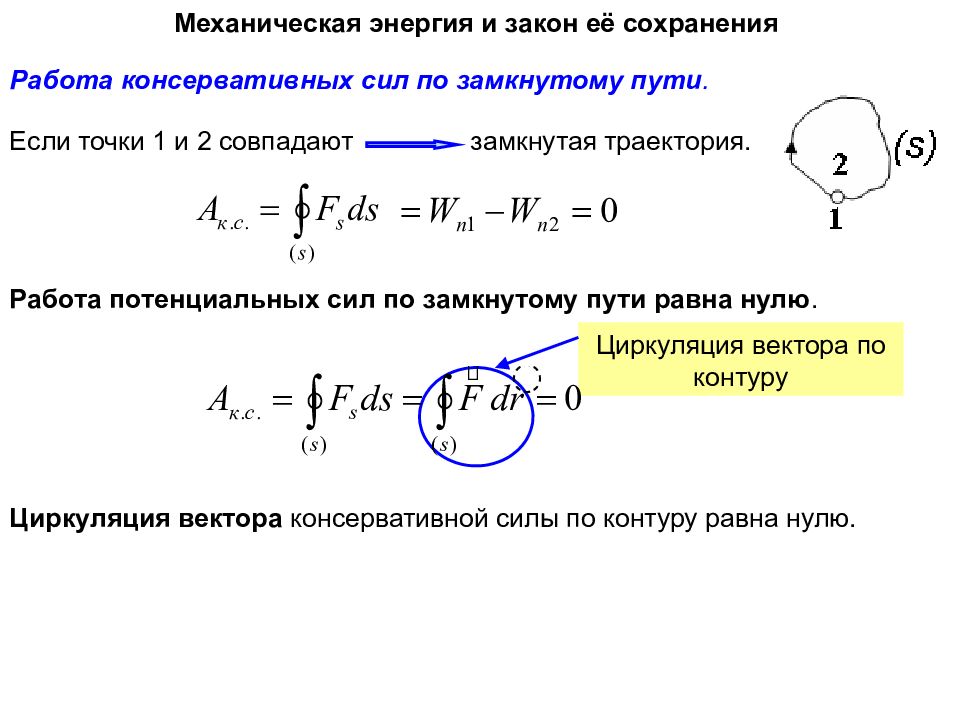
Работа консервативных сил по замкнутому пути. Механическая энергия и закон её сохранения Если точки 1 и 2 совпадают замкнутая траектория. Работа потенциальных сил по замкнутому пути равна нулю. Циркуляция вектора консервативной силы по контуру равна нулю. Циркуляция вектора по контуру
Механическая энергия и закон её сохранения Кинетическая энергия Кинетическая энергия материальной точки Пусть – результирующая всех сил, действующих на материальную точку. Элементарная работа результирующей силы - проекция на направление вектора скорости, т.е. тангенциальная составляющая отвечающая за изменение величины скорости. Работа при перемещении МТ из точки 1 в точку 2 обычный интеграл
Механическая энергия и закон её сохранения Кинетическая энергия Кинетическая энергия материальной точки Назовём кинетической энергией МТ. Изменение кинетической энергии МТ равно работе результирующей всех сил, действующих на МТ ( теорема об изменении кинетической энергии МТ ). В дифференциальной форме. Кинетическая энергия определена с точностью до постоянной. При этом const = 0 и. В данной системе отсчёта удобно, что бы было при. Работа результирующей всех сил при перемещении МТ из точки 1 в точку 2:
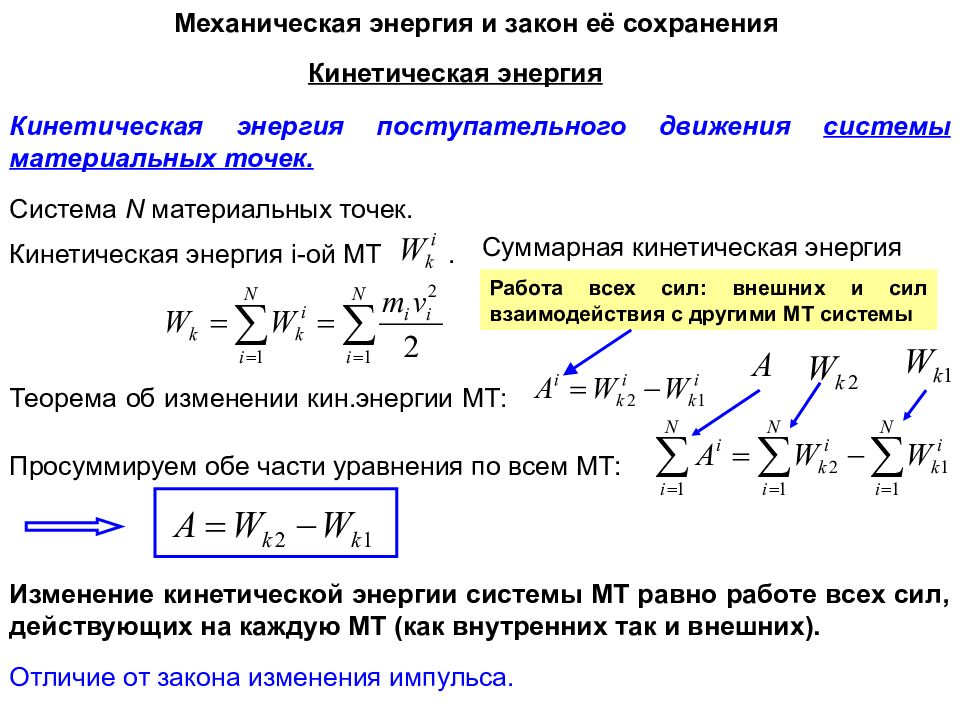
Механическая энергия и закон её сохранения Кинетическая энергия Кинетическая энергия поступательного движения системы материальных точек. Система N материальных точек. Суммарная кинетическая энергия Теорема об изменении кин.энергии МТ: Кинетическая энергия i -ой МТ. Просуммируем обе части уравнения по всем МТ: Изменение кинетической энергии системы МТ равно работе всех сил, действующих на каждую МТ (как внутренних так и внешних). Отличие от закона изменения импульса. Работа всех сил: внешних и сил взаимодействия с другими МТ системы
Кинетическая энергия поступательного и вращательного движения абсолютно твёрдого тела Механическая энергия и закон её сохранения Кинетическая энергия Поступательное движение АТТ. Разобьём тело массой m на кусочки с массами, которые можно считать материальными точками. .
Кинетическая энергия вращательного движения абсолютно твёрдого тела АТТ вращается вокруг неподвижной оси z Разобьём тело на маленькие фрагменты. Кинетическая энергия тела равна сумме кинетических энергий его фрагментов
A= = W k 2 - W k 1 = ΔW k Работа при вращательном движении АТТ вращается вокруг неподвижной оси z Докажем, что Результирующий момент сил, действующих на тело, относительно оси z. Пределы интегрирования 1 и 2 соответствуют состояниям АТТ в моменты времени t 1 и t 2, когда f меняется от f 1 до f 2, а w от w 1 до w 2. - элементарное угловое перемещение (вектор, направленный также как и ). =A
Закон сохранения полной механической энергии Полная механическая энергия системы = сумма кинетических энергий тел, входящих в систему сумма потенциальных энергий, обусловленных их взаимодействием друг с другом и внешними телами (полями) +
Закон сохранения полной механической энергии A – работа всех сил, приложенных к МТ системы Теорема об изменении кинетической энергии для системы МТ По определению потенциальной энергии
Закон сохранения полной механической энергии Внешние неконсервативные силы, например, мускульная сила, силы со стороны каких-либо механизмов и т.п. В системе с одними только консервативными силами полная механическая энергия остаётся постоянной. Что такое неконсервативные силы? Силы трения (диссипативные силы), действующие между телами системы.
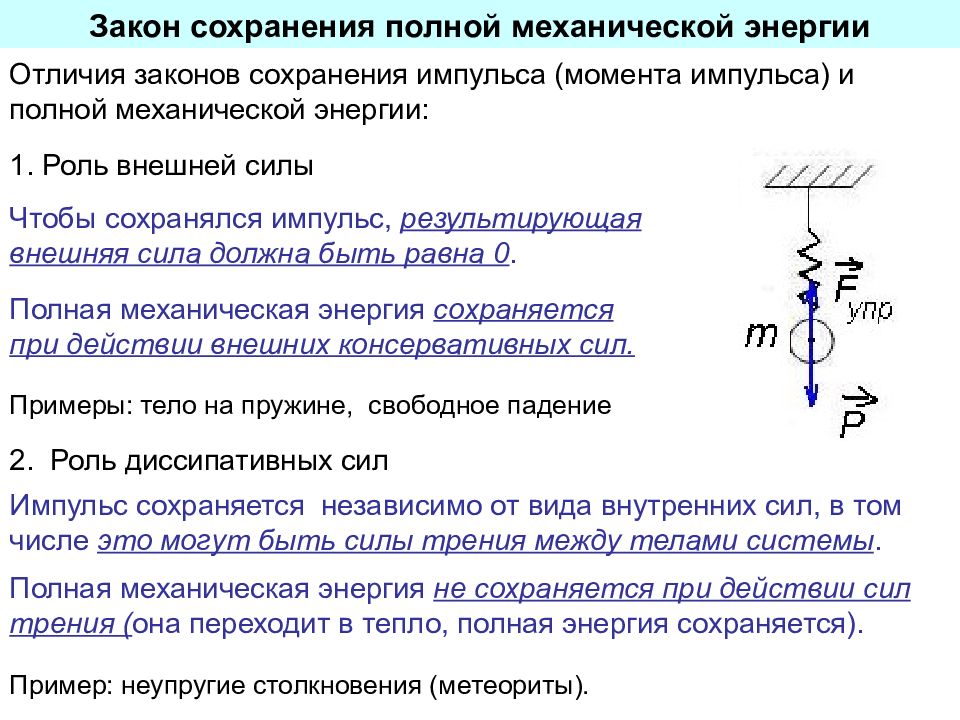
Закон сохранения полной механической энергии Отличия законов сохранения импульса (момента импульса) и полной механической энергии: Чтобы сохранялся импульс, результирующая внешняя сила должна быть равна 0. Полная механическая энергия сохраняется при действии внешних консервативных сил. Примеры: тело на пружине, 1. Роль внешней силы 2. Роль диссипативных сил Импульс сохраняется независимо от вида внутренних сил, в том числе это могут быть силы трения между телами системы. Полная механическая энергия не сохраняется при действии сил трения ( она переходит в тепло, полная энергия сохраняется). Пример: неупругие столкновения (метеориты). свободное падение
Закон сохранения полной механической энергии В системе с одними только консервативными силами полная механическая энергия остаётся постоянной. В замкнутой (не действуют внешние силы) системе с одними только консервативными силами полная механическая энергия остаётся постоянной.
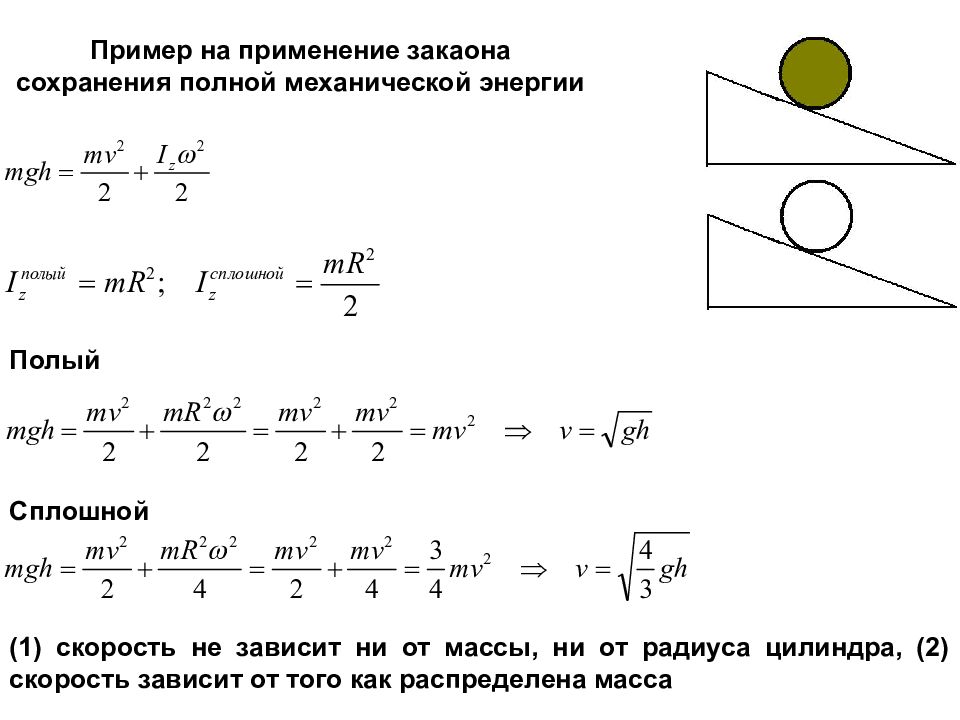
Полый Сплошной (1) скорость не зависит ни от массы, ни от радиуса цилиндра, (2) скорость зависит от того как распределена масса Пример на применение закаона сохранения полной механической энергии
Согласно теореме Нётер (Эмми Нётер), закон сохранения механической энергии является следствием однородности времени. закон сохранения импульса — однородности пространства, закон сохранения момента импульса — изотропности пространства. Закон сохранения полной механической энергии
Закон сохранения и превращения энергии Диссипативные силы: механическая энергия системы тел уменьшается внутренняя энергии тел увеличивается (нагрев при трении) на ту же величину. Виды энергии: механическая, внутренняя, электрическая, магнитная, ядерная и др. Энергия не исчезает бесследно и не возникает из ничего, она превращается из одного вида энергии в другой, либо передается от одних тел к другим в эквивалентном количестве. При этом суммарное количество энергии остается постоянным. Следствие закона сохранения и превращения энергии - невозможность создания «вечного двигателя».
Вопросы к коллоквиуму. Кинематика материальной точки. Кинематика вращательного движения. Законы Ньютона. Принцип относительности Галилея. Второй закон Ньютона. Движение центра инерции. Третий закон Ньютона. Закон изменения и сохранения импульса. Момент импульса. Момент силы. Связь между ними. Момент инерции. Моменты инерции тонкостенного кольца и сплошного цилиндра. Теорема Штейнера. Основное уравнение динамики вращательного движения. Работа силы. Мощность. Работа силы тяготения. Работа сил Кулона. Работа силы тяжести. Работа силы упругости. Поле силы. Потенциальная энергия. Связь поля силы с потенциальной энергией. Кинетическая энергия (мат. точки, системы мат. точек, кинетическая энергия поступательного и вращательного движения АТТ). Работа при вращательном движении. Полная механическая энергия. Закон изменения и сохранения полной механической энергии.
2. Заряд любого тела или частицы кратен элементарному заряду e 3. Выполняется закон сохранения заряда в электрически изолированной системе: алгебраическая сумма зарядов электрически изолированной системы есть величина постоянная. 4. Имеет место инвариантность заряда : заряд системы инвариантен относительно системы отсчета, т. е. во всех инерциальных системах отсчета заряд одинаковый. ЗАКОН КУЛОНА ОСНОВНЫЕ ПОСТУЛАТЫ. 1. В природе существуют 2 типа зарядов – положительные "+" и отрицательные " ".
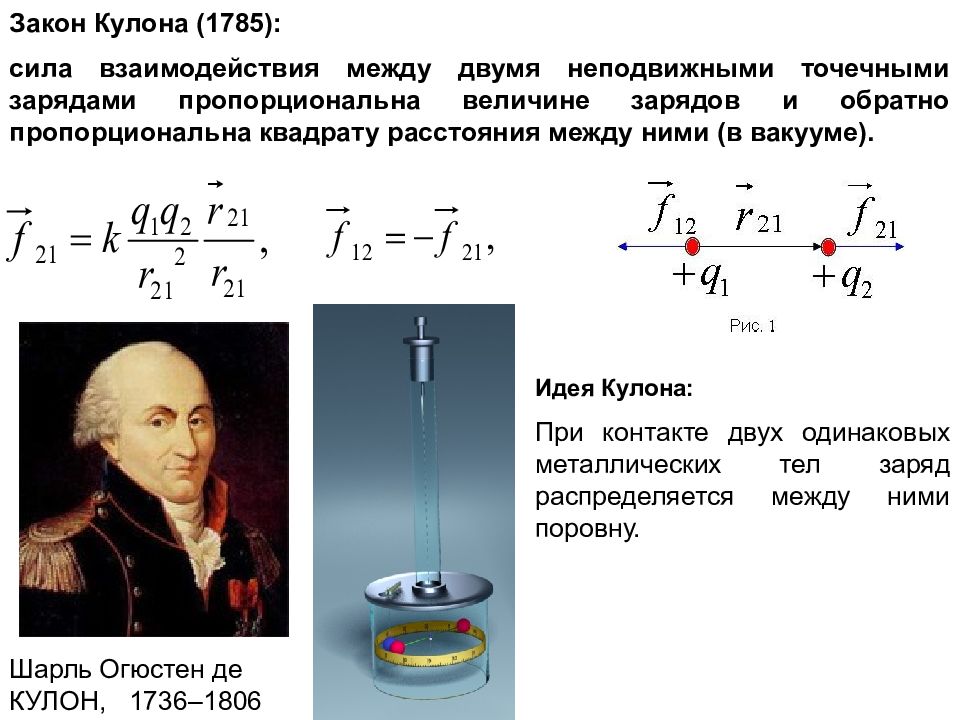
Шарль Огюстен де КУЛОН, 1736–1806 Закон Кулона (1785): сила взаимодействия между двумя неподвижными точечными зарядами пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния между ними (в вакууме). Идея Кулона: При контакте двух одинаковых металлических тел заряд распределяется между ними поровну.
k = 1 Система СИ: Основная электрическая единица: ампер. Единица заряда: Кулон = Ампер·сек Закон Кулона в системе СИ: электрическая постоянная. Пример: q 1 =q 2 =1K, r 12 =1 м f ~10 10 Н~10 9 кГ (!!) Кулон – это очень большой заряд.
ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ В ВАКУУМЕ Принцип суперпозиции электрических полей Система N неподвижных точечных зарядов : , пробный заряд Напряженность – силовая характеристика поля, равная силе, действующей на пробный заряд, помещенный в данную точку поля, деленной на величину этого заряда. Напряженность поля точечного заряда:
ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ В ВАКУУМЕ Принцип суперпозиции электрических полей Принцип суперпозиции для напряженности: напряженность поля, создаваемого системой точечных зарядов в данной точке, равна векторной сумме напряженностей полей, создаваемых каждым из зарядов системы в отдельности в этой точке.
Принцип суперпозиции электрических полей Потенциал электрического поля. Найдём потенциальную энергию взаимодействия пробного заряда с полем, создаваемым системой зарядов.
Принцип суперпозиции электрических полей Потенциал электрического поля. Потенциал поля, создаваемый системой точечных зарядов в данной точке, равен потенциальной энергии взаимодействия пробного заряда со всеми зарядами, деленной на величину пробного заряда. потенциал поля точечного заряда Потенциал поля, создаваемого системой точечных зарядов в данной точке, равен алгебраической сумме потенциалов, создаваемых каждым зарядом в отдельности в данной точке.
Принцип суперпозиции электрических полей Потенциал электрического поля. Разность потенциалов – величина, равная работе сил поля по перемещению пробного заряда из одной точки в другую, деленной на величину этого заряда. Потенциал в данной точке поля равен работе сил поля по перемещению пробного заряда из данной точки поля на бесконечность, деленной на величину этого заряда.
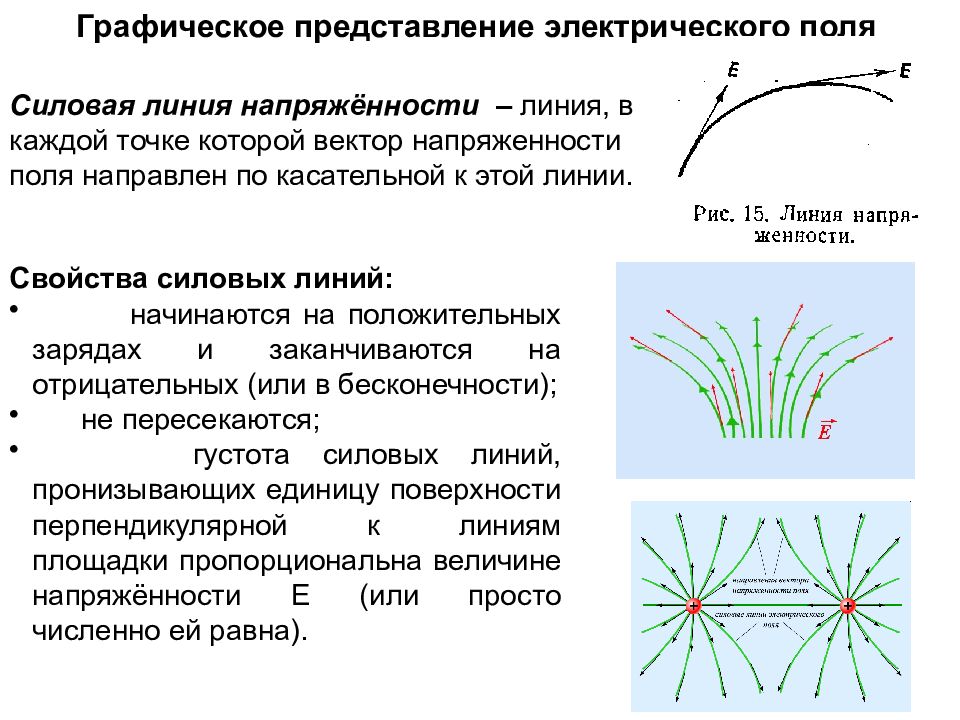
Графическое представление электрического поля Силовая линия напряжённости – линия, в каждой точке которой вектор напряженности поля направлен по касательной к этой линии. Свойства силовых линий: начинаются на положительных зарядах и заканчиваются на отрицательных (или в бесконечности); не пересекаются; густота силовых линий, пронизывающих единицу поверхности перпендикулярной к линиям площадки пропорциональна величине напряжённости Е (или просто численно ей равна).
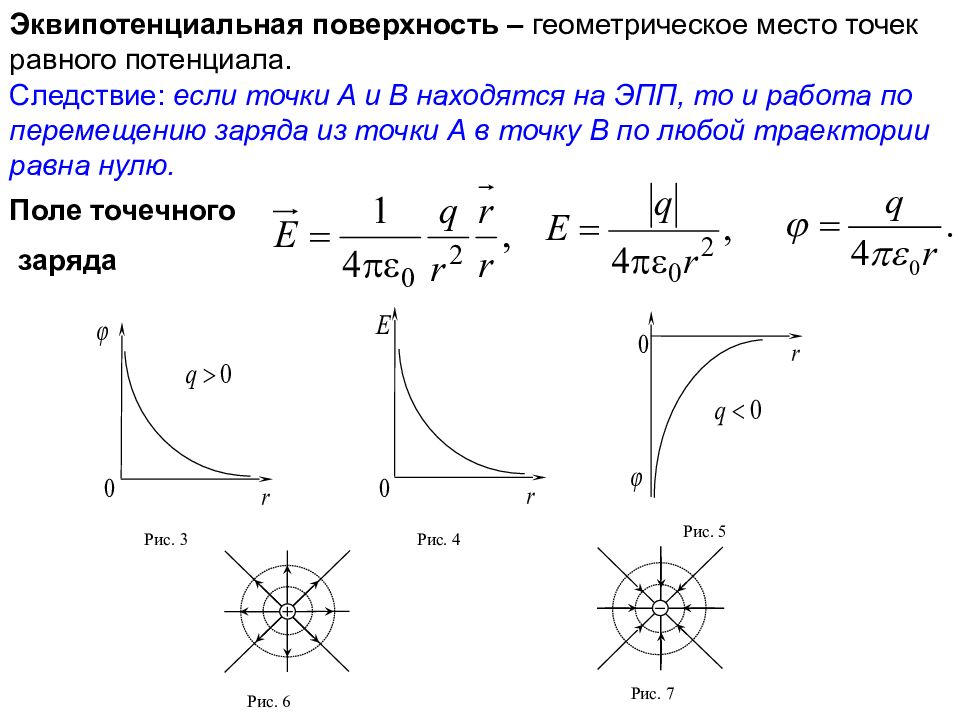
Эквипотенциальная поверхность – геометрическое место точек равного потенциала. Следствие: если точки A и B находятся на ЭПП, то и работа по перемещению заряда из точки А в точку В по любой траектории равна нулю. Поле точечного заряда Рис. 3 Рис. 4 Рис. 5 Рис. 6 Рис. 7
Связь между напряженностью электростатического поля и потенциалом Разность потенциалов как интеграл от напряженности электростатического поля. Рис. 8 Рис. 9 Напряженность поля как градиент потенциала.
