Гармонические колебания пружинного маятника (гармонический осциллятор)
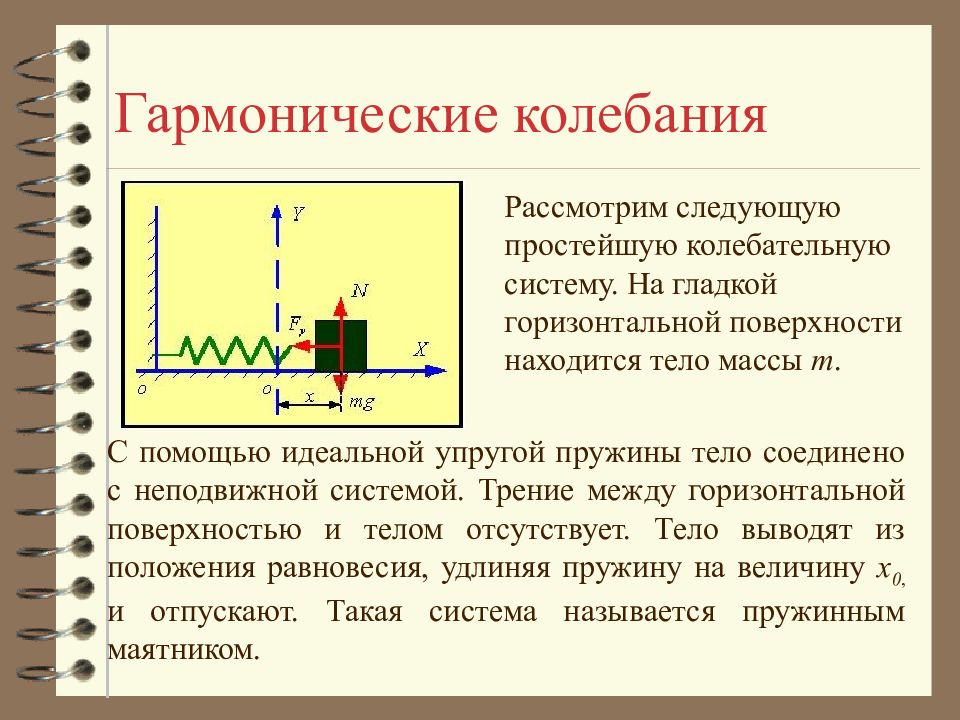
Рассмотрим следующую простейшую колебательную систему. На гладкой горизонтальной поверхности находится тело массы m. С помощью идеальной упругой пружины тело соединено с неподвижной системой. Трение между горизонтальной поверхностью и телом отсутствует. Тело выводят из положения равновесия, удлиняя пружину на величину x 0, и отпускают. Такая система называется пружинным маятником.
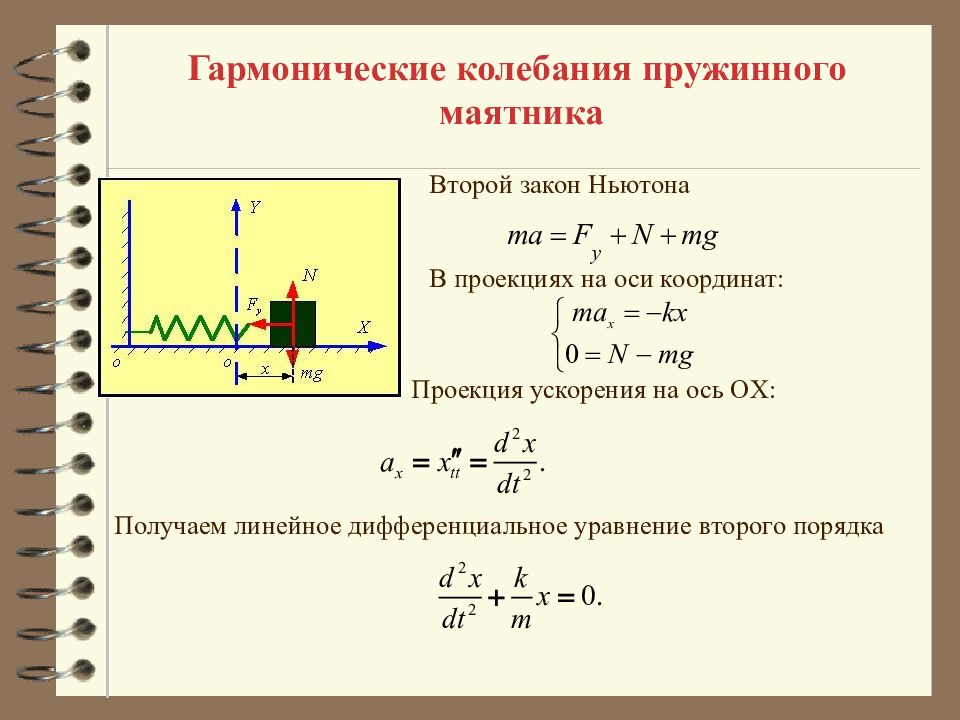
Гармонические колебания пружинного маятника Второй закон Ньютона В проекциях на оси координат: Проекция ускорения на ось OX: Получаем линейное дифференциальное уравнение второго порядка
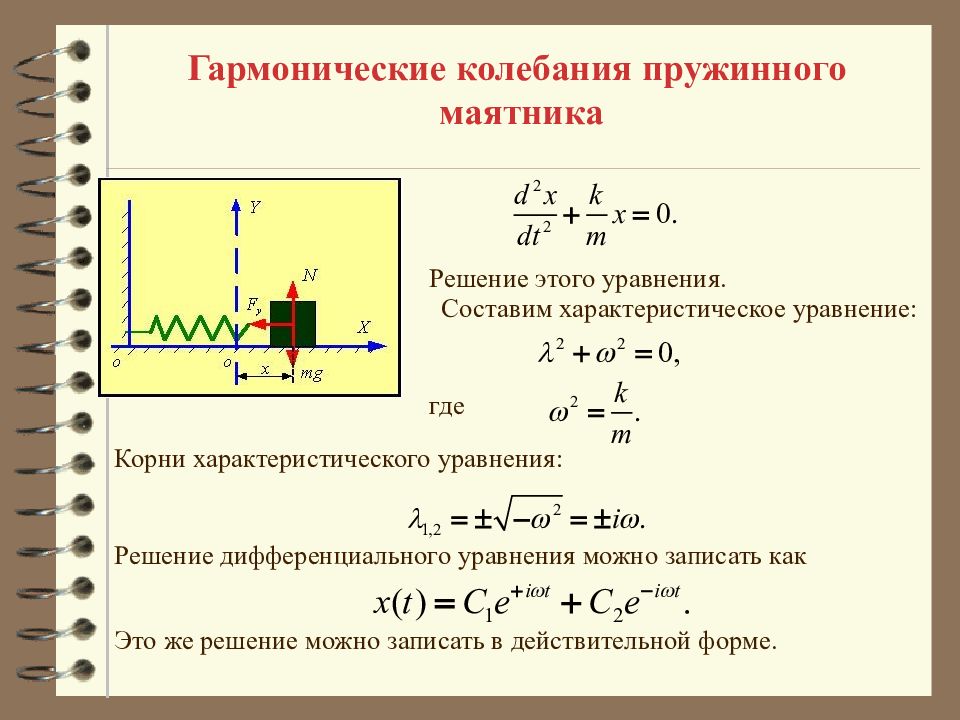
Гармонические колебания пружинного маятника где Решение этого уравнения. Составим характеристическое уравнение : Корни характеристического уравнения: Решение дифференциального уравнения можно записать как Это же решение можно записать в действительной форме.
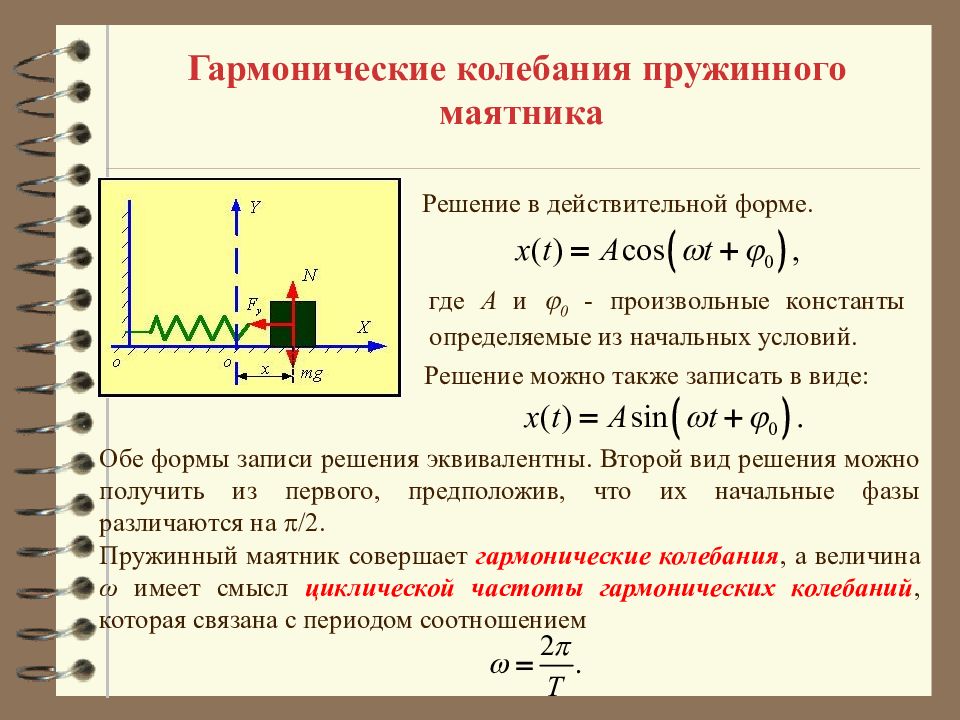
Гармонические колебания пружинного маятника где А и 0 - произвольные константы определяемые из начальных условий. Решение можно также записать в виде : Обе формы записи решения эквивалентны. Второй вид решения можно получить из первого, предположив, что их начальные фазы различаются на /2. Пружинный маятник совершает гармонические колебания, а величина ω имеет смысл циклической частоты гармонических колебаний, которая связана с периодом соотношением Решение в действительной форме.
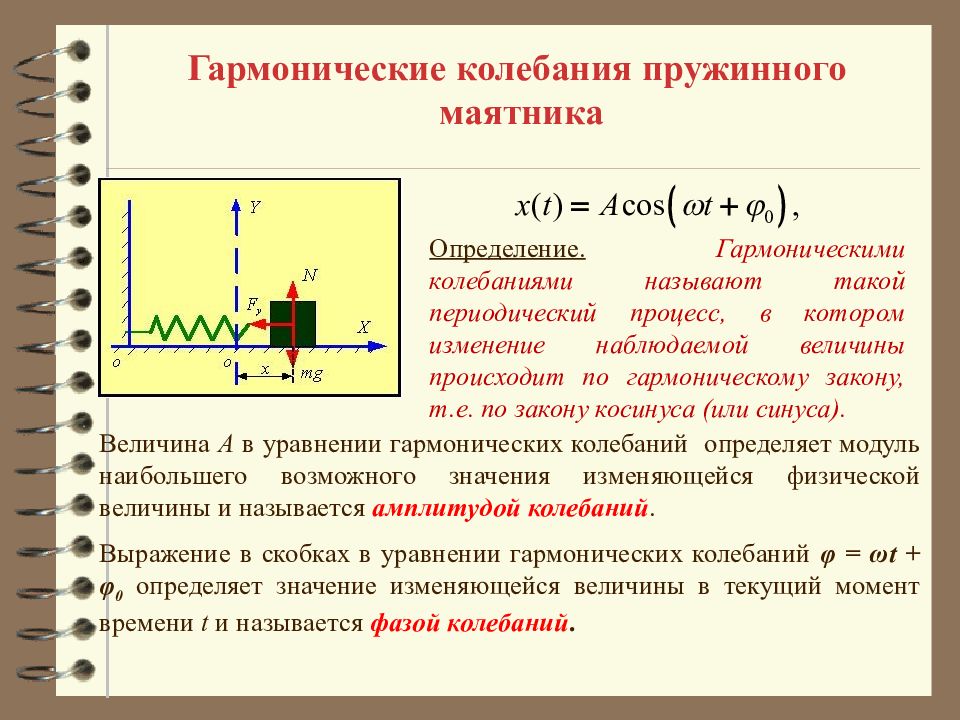
Гармонические колебания пружинного маятника Определение. Гармоническими колебаниями называют такой периодический процесс, в котором изменение наблюдаемой величины происходит по гармоническому закону, т.е. по закону косинуса (или синуса). Величина A в уравнении гармонических колебаний определяет модуль наибольшего возможного значения изменяющейся физической величины и называется амплитудой колебаний. Выражение в скобках в уравнении гармонических колебаний φ = ω t + φ 0 определяет значение изменяющейся величины в текущий момент времени t и называется фазой колебаний.
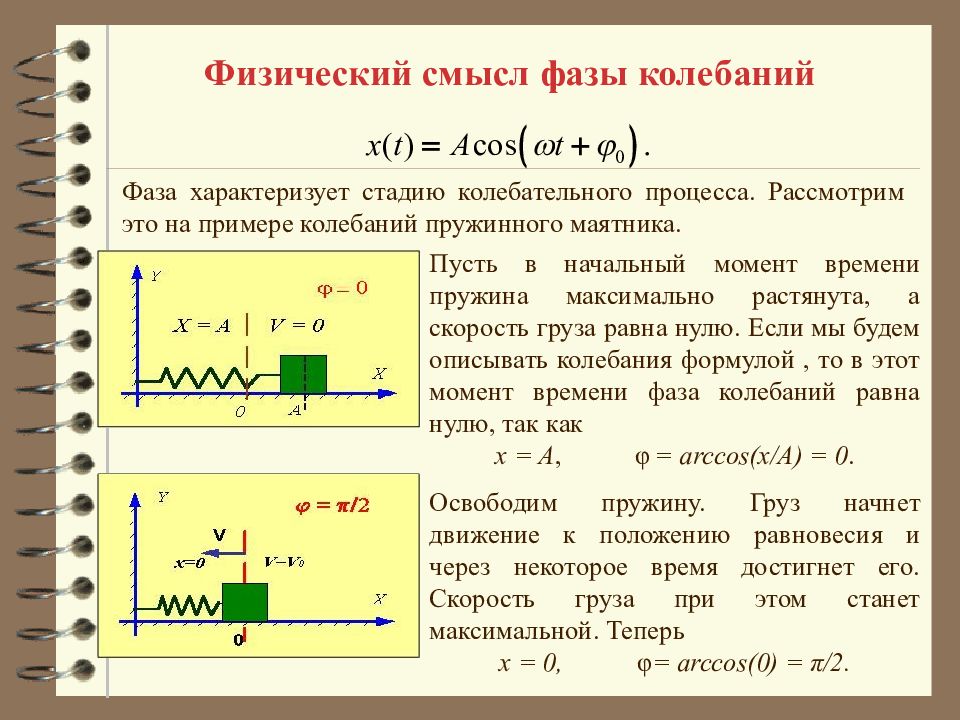
Физический смысл фазы колебаний Фаза характеризует стадию колебательного процесса. Рассмотрим это на примере колебаний пружинного маятника. Пусть в начальный момент времени пружина максимально растянута, а скорость груза равна нулю. Если мы будем описывать колебания формулой, то в этот момент времени фаза колебаний равна нулю, так как x = A, φ = arccos ( x / A ) = 0. Освободим пружину. Груз начнет движение к положению равновесия и через некоторое время достигнет его. Скорость груза при этом станет максимальной. Теперь x = 0, φ = arccos (0) = π /2.
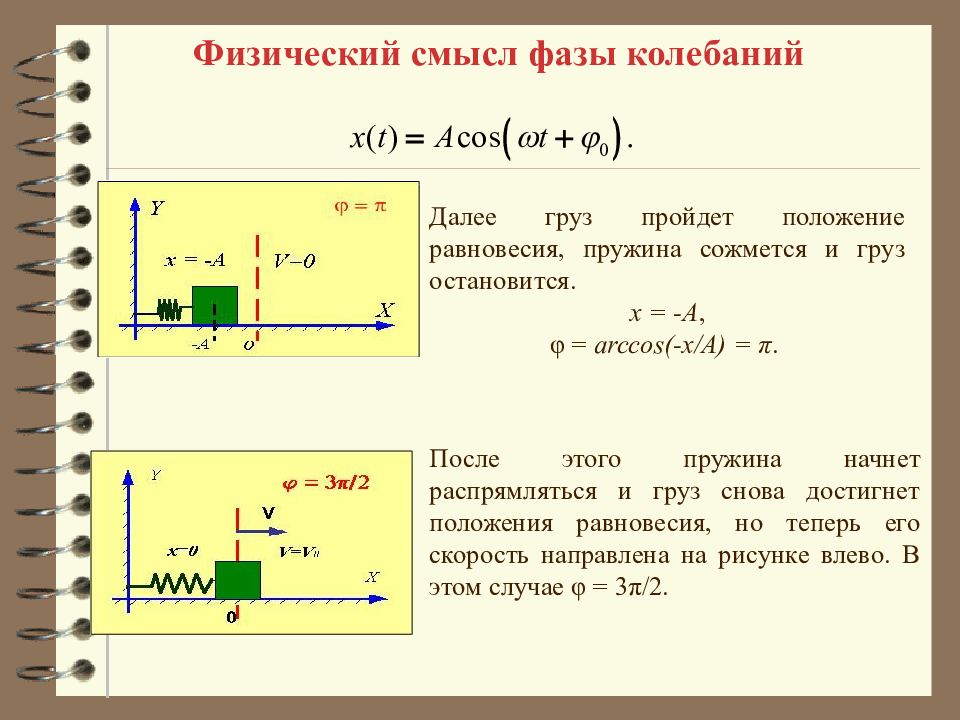
Физический смысл фазы колебаний Далее груз пройдет положение равновесия, пружина сожмется и груз остановится. x = - A, φ = arccos (- x / A ) = π. После этого пружина начнет распрямляться и груз снова достигнет положения равновесия, но теперь его скорость направлена на рисунке влево. В этом случае φ = 3π/2.
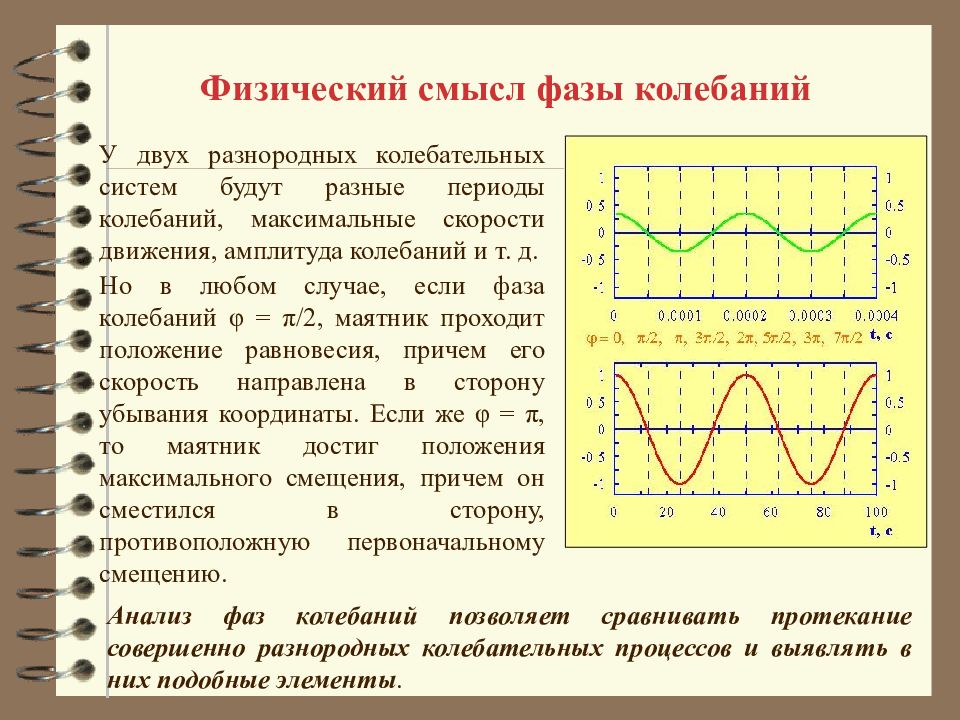
Физический смысл фазы колебаний У двух разнородных колебательных систем будут разные периоды колебаний, максимальные скорости движения, амплитуда колебаний и т. д. Но в любом случае, если фаза колебаний φ = π/2, маятник проходит положение равновесия, причем его скорость направлена в сторону убывания координаты. Если же φ = π, то маятник достиг положения максимального смещения, причем он сместился в сторону, противоположную первоначальному смещению. Анализ фаз колебаний позволяет сравнивать протекание совершенно разнородных колебательных процессов и выявлять в них подобные элементы.
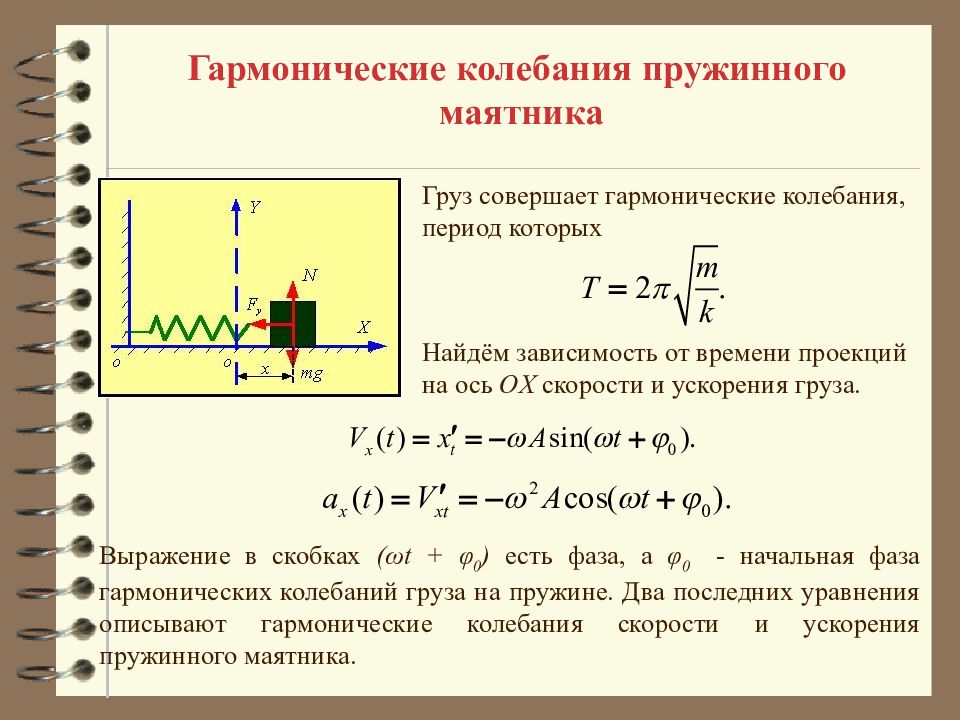
Гармонические колебания пружинного маятника Найдём зависимость от времени проекций на ось OX скорости и ускорения груза. Выражение в скобках (ω t + φ 0 ) есть фаза, а φ 0 - начальная фаза гармонических колебаний груза на пружине. Два последних уравнения описывают гармонические колебания скорости и ускорения пружинного маятника. Груз совершает гармонические колебания, период которых
Изменения энергии при гармонических колебаниях
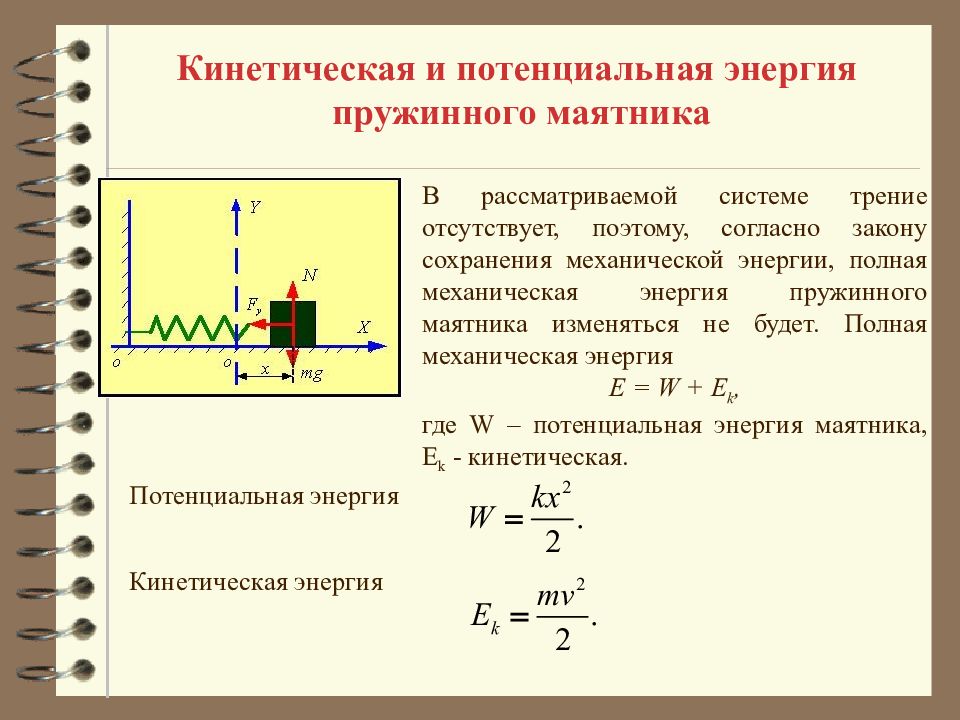
Кинетическая и потенциальная энергия пружинного маятника Потенциальная энергия В рассматриваемой системе трение отсутствует, поэтому, согласно закону сохранения механической энергии, полная механическая энергия пружинного маятника изменяться не будет. Полная механическая энергия E = W + E k, где W – потенциальная энергия маятника, E k - кинетическая. Кинетическая энергия
Кинетическая и потенциальная энергия пружинного маятника Потенциальная энергия Пусть колебания начались, когда груз был смещен из положения равновесия на максимальное расстояние вправо. Тогда при t = 0 x = A и начальная фаза φ 0 = 0. В момент времени t = 0 скорость груза равна нулю и, следовательно, его кинетическая энергия тоже равна нулю. Поэтому полная механическая энергия груза в этот момент времени равна его потенциальной энергии
Кинетическая и потенциальная энергия пружинного маятника Преобразуем выражение для потенциальной энергии груза. Для этого используем формулу из тригонометрии: Таким образом, потенциальная энергия груза всегда положительна и совершает гармонические колебания с частотой Ω = 2ω.
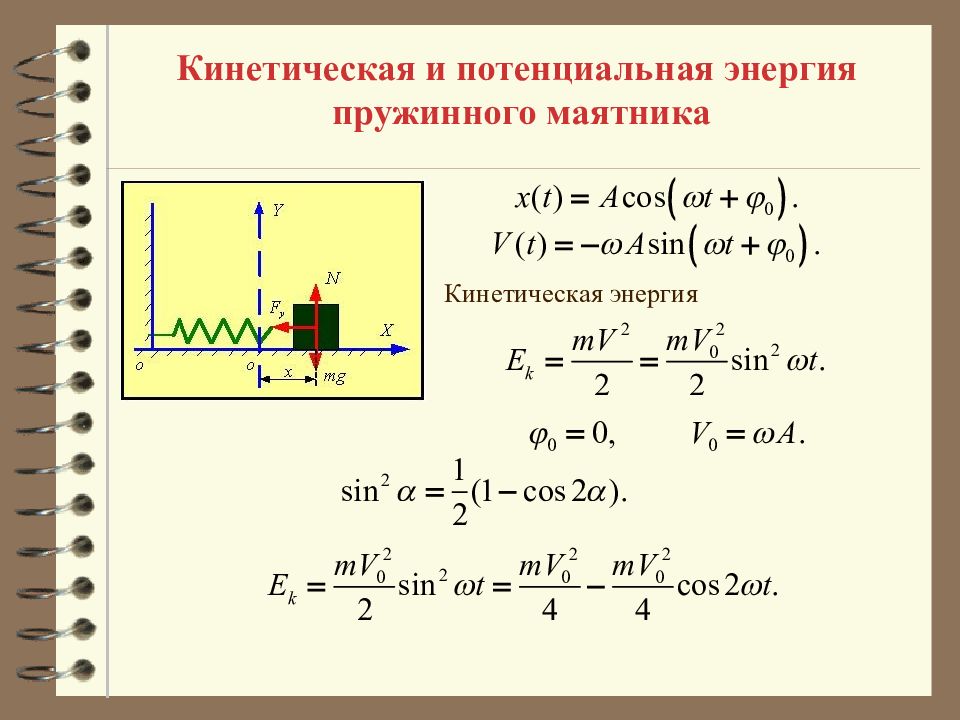
Кинетическая и потенциальная энергия пружинного маятника Кинетическая энергия
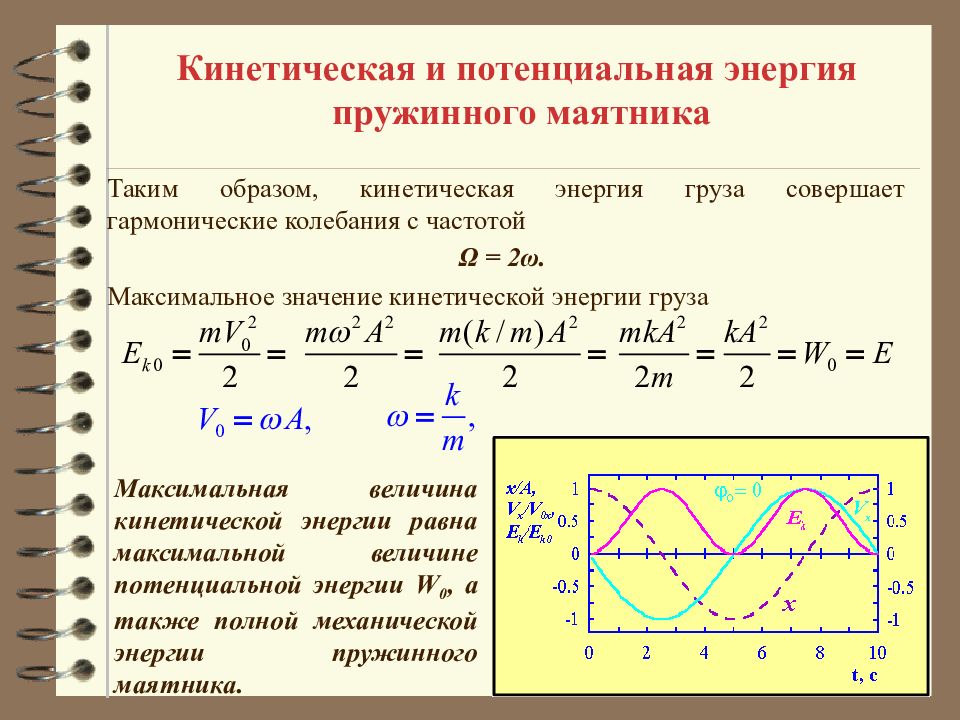
Кинетическая и потенциальная энергия пружинного маятника Максимальная величина кинетической энергии равна максимальной величине потенциальной энергии W 0, а также полной механической энергии пружинного маятника. Таким образом, кинетическая энергия груза совершает гармонические колебания с частотой Ω = 2ω. Максимальное значение кинетической энергии груза
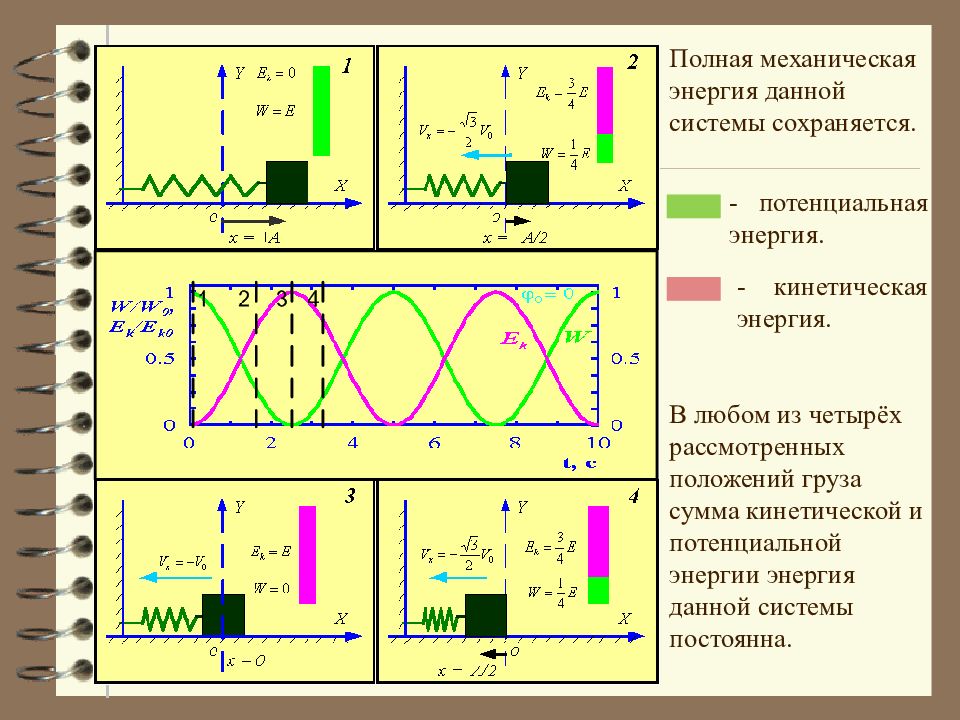
Кинетическая и потенциальная энергия пружинного маятника В рассматриваемой системе отсутствует трение, поэтому в любой момент времени сумма кинетической и потенциальной энергии груза должна быть неизменной и равной полной механической энергии. Полная механическая энергия данной системы сохраняется.
Полная механическая энергия данной системы сохраняется. - потенциальная энергия. - кинетическая энергия. В любом из четырёх рассмотренных положений груза сумма кинетической и потенциальной энергии энергия данной системы постоянна.
Условия возникновения гармонических колебаний
Условия возникновения гармонических колебаний Рассмотрим механическую систему вблизи положения устойчивого равновесия, в котором потенциальная энергия системы достигает минимума. Пусть возможно движение тела только вдоль одной координаты. Положение равновесия находится в точке с координатой x 0. При смещении тела из положения равновесия потенциальная энергия тела увеличивается. Возникает сила, действующая на тело: dx > 0, dW > 0, следовательно, F x < 0. Сила направлена к положению равновесия.
Условия возникновения гармонических колебаний Вблизи положения устойчивого равновесия могут возникнуть колебания. Чтобы эти колебания были гармоническими, проекция «возвращающей» силы на ось OX должна линейно зависеть от смещения тела из положения равновесия x = x – x 0. Такая зависимость силы от смещения возможна, если потенциальная энергия тела зависит от координаты как W(x) = Ax 2, где A – произвольный постоянный коэффициент. В этом случае действительно возникает «возвращающая» сила, пропорциональная смещению из положения равновесия.
Условия возникновения гармонических колебаний В то же время любую произвольную зависимость потенциальной энергии от координаты можно приближенно представить в виде полинома В этом случае зависимость проекции силы от координаты Если величина смещения из положения равновесия мала, то x 2 << x, а остальные слагаемые, содержащие еще более высокие степени x еще меньше, поэтому приближенно выражение для силы можно записать как
Условия возникновения гармонических колебаний Постоянная величина A 1 не влияет на характер колебаний, так как действует одинаково во всех точках оси OX. При выполнении условия малости смещения тела из положения устойчивого равновесия «возвращающая» сила пропорциональна смещению, и колебания можно считать гармоническими. Силы, направленные к положению равновесия, величина которых прямо пропорциональна смещению тела из положения равновесия называют квазиупругими. Если в системе действуют квазиупругие силы (независимо от природы этих сил), то в ней возможны гармонические колебания.
