Решение задания №17 Подготовка к ЕГЭ по информатике
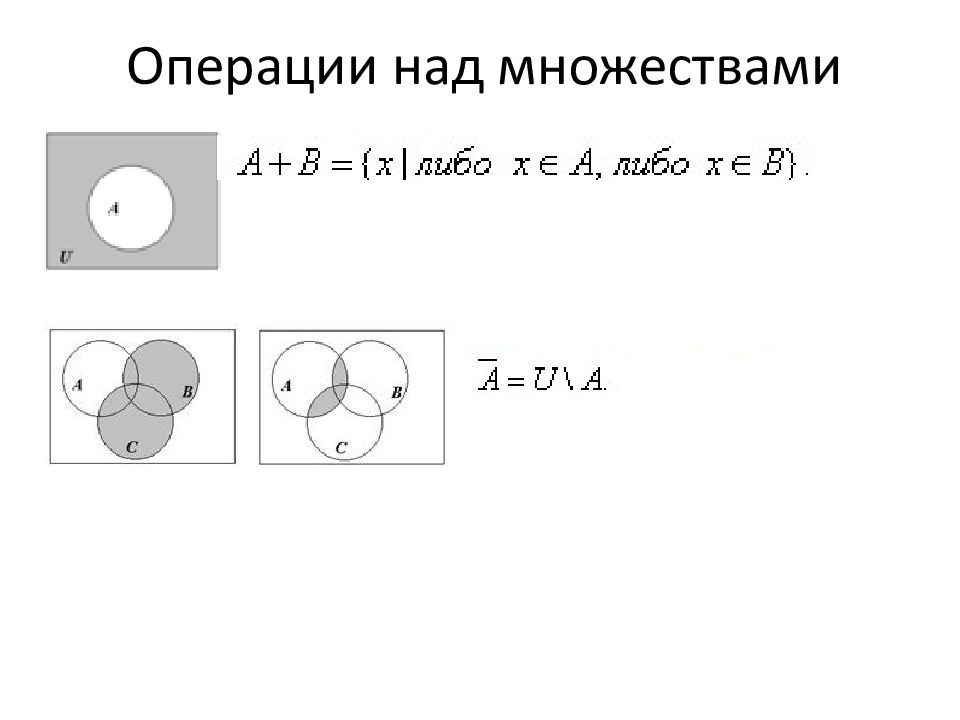
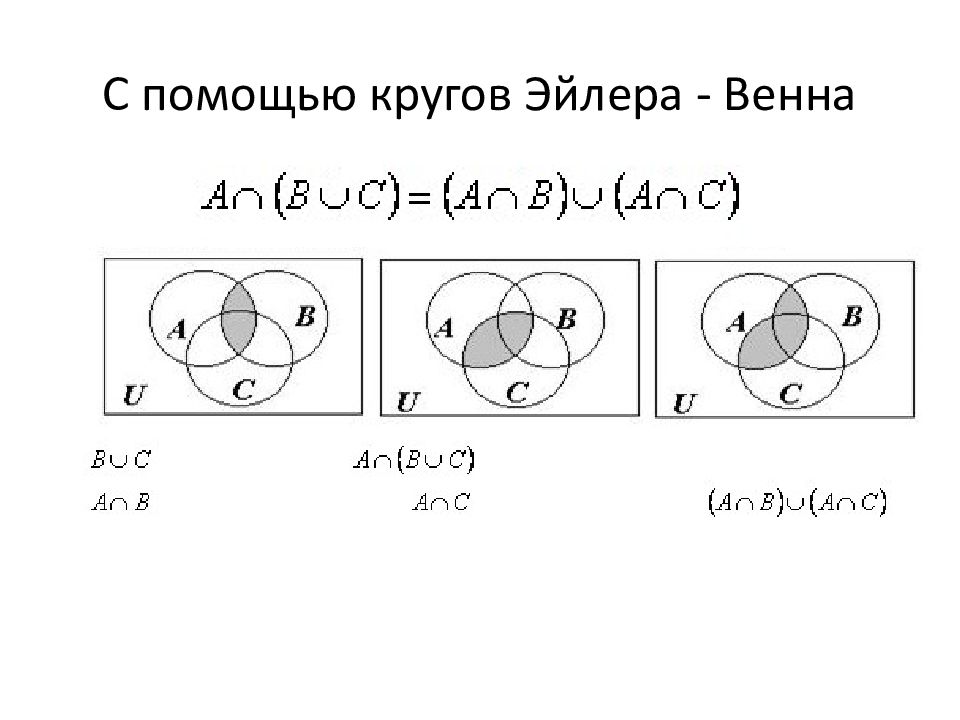
Умение осуществлять поиск информации в сети Интернет Задание относится к П - повышенному, отводится на него 2 мин Использование метода кругов Эйлера при решении задач (Операции над множествами)
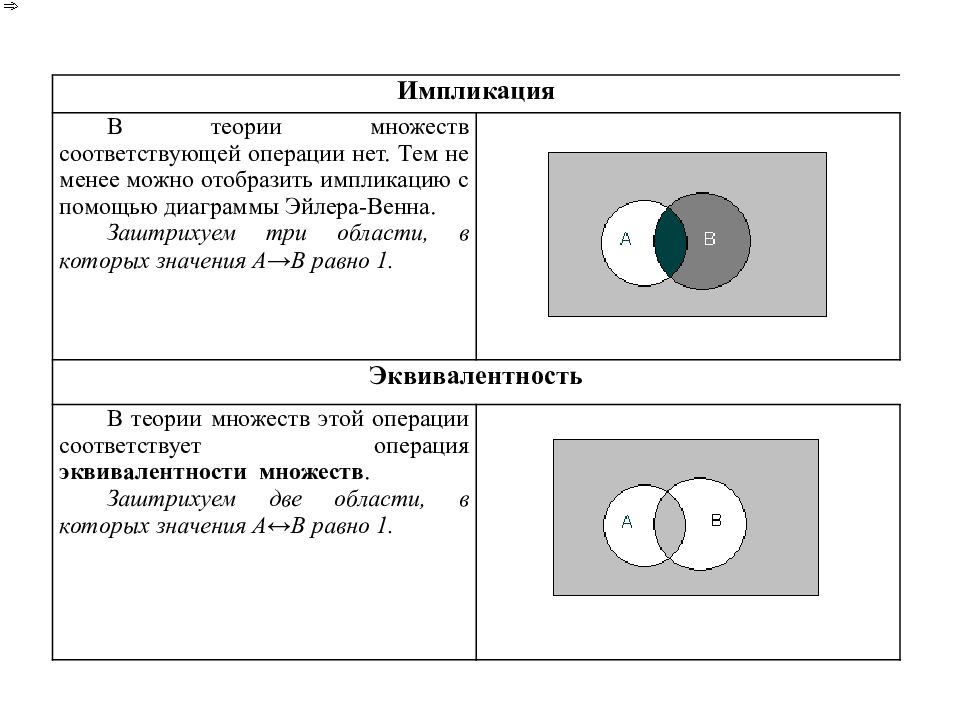
Импликация В теории множеств соответствующей операции нет. Тем не менее можно отобразить импликацию с помощью диаграммы Эйлера-Венна. Заштрихуем три области, в которых значения А → В равно 1. Эквивалентность В теории множеств этой операции соответствует операция эквивалентности множеств. Заштрихуем две области, в которых значения А ↔ В равно 1.
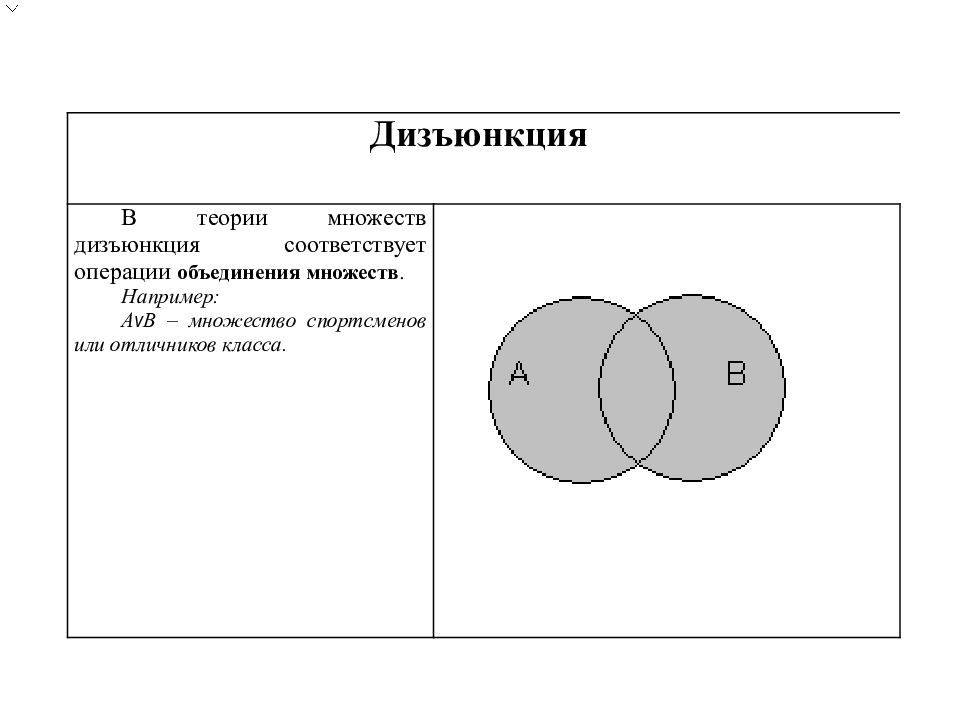
Дизъюнкция В теории множеств дизъюнкция соответствует операции объединения множеств. Например: А v В – множество спортсменов или отличников класса.
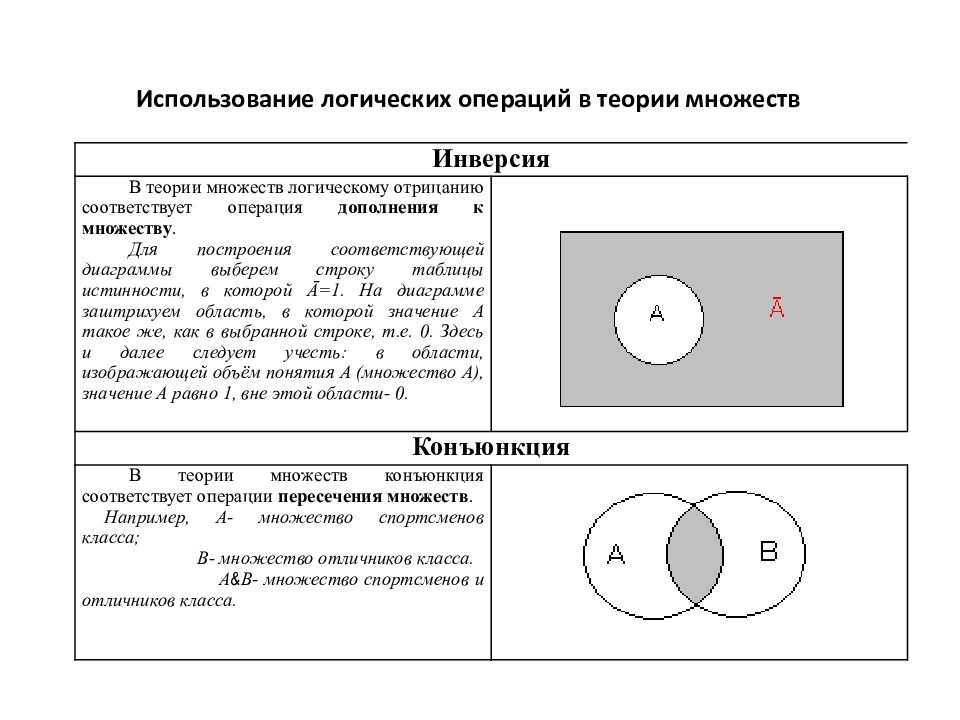
Инверсия В теории множеств логическому отрицанию соответствует операция дополнения к множеству. Для построения соответствующей диаграммы выберем строку таблицы истинности, в которой Ā=1. На диаграмме заштрихуем область, в которой значение А такое же, как в выбранной строке, т.е. 0. Здесь и далее следует учесть: в области, изображающей объём понятия А (множество А), значение А равно 1, вне этой области- 0. Конъюнкция В теории множеств конъюнкция соответствует операции пересечения множеств. Например, А- множество спортсменов класса; В- множество отличников класса. А & В- множество спортсменов и отличников класса. Использование логических операций в теории множеств
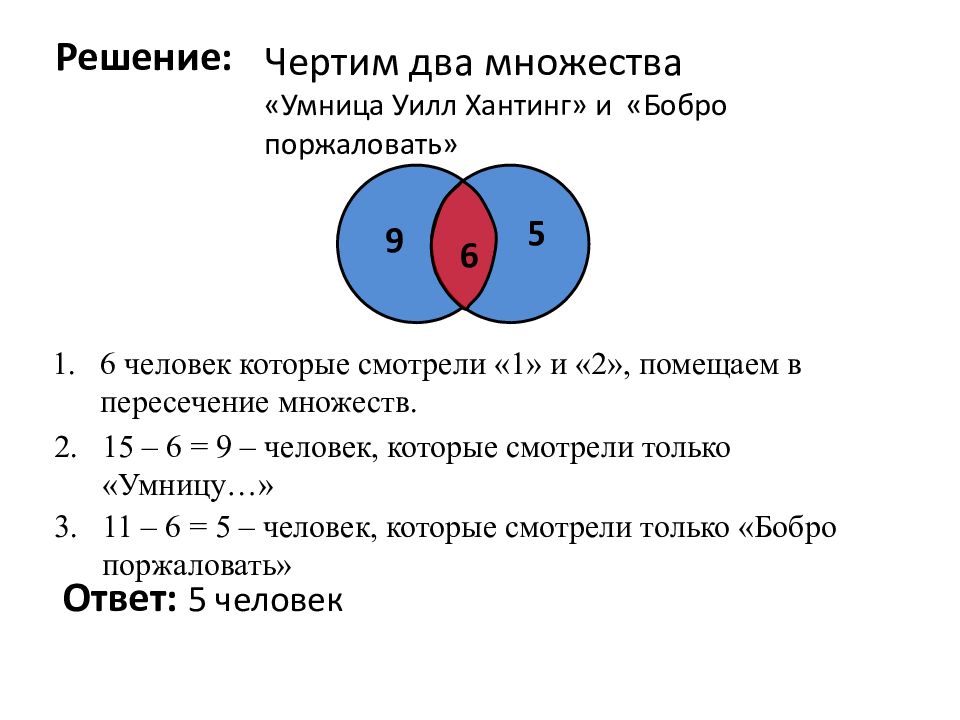
Условия: Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Умница Уилл Хантинг » и « Бобро поржаловать », из них 6 смотрели и «Умницу…» и « Бобро поржаловать ». Сколько человек смотрели только фильм « Бобро поржаловать »?
Решение: 9 5 Ответ: 5 человек 6 человек которые смотрели «1» и «2», помещаем в пересечение множеств. 2. 15 – 6 = 9 – человек, которые смотрели только «Умницу…» 3. 11 – 6 = 5 – человек, которые смотрели только « Бобро поржаловать » Чертим два множества «Умница Уилл Хантинг » и « Бобро поржаловать » 6
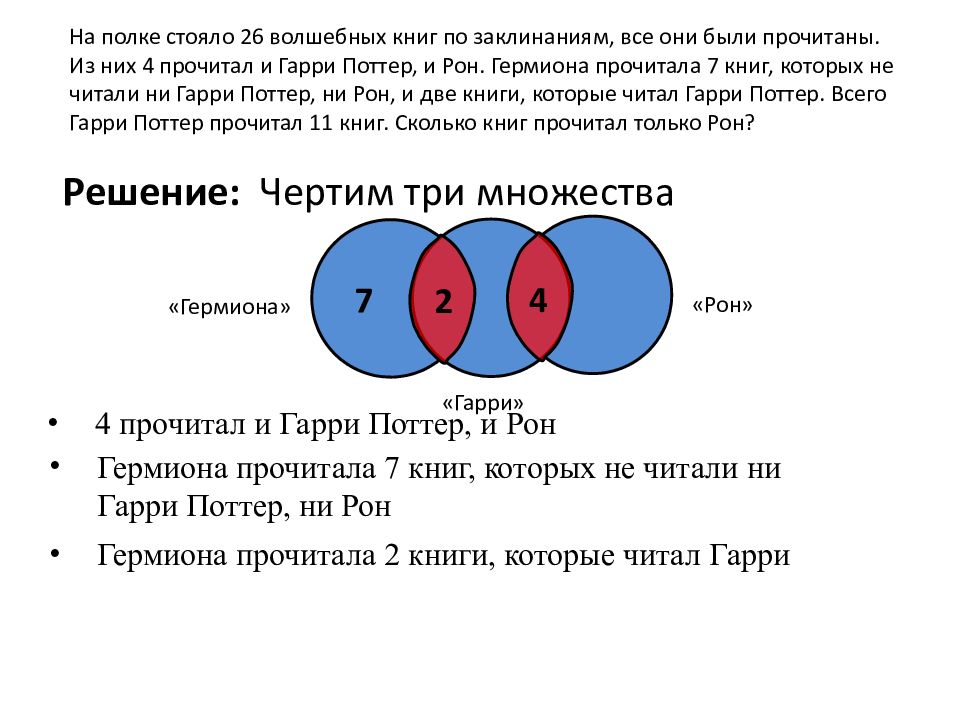
Условия: На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон ?
Решение: « Гермиона » «Гарри» 7 4 прочитал и Гарри Поттер, и Рон Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон Гермиона прочитала 2 книги, которые читал Гарри Чертим три множества « Рон » 2 4 На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон ?
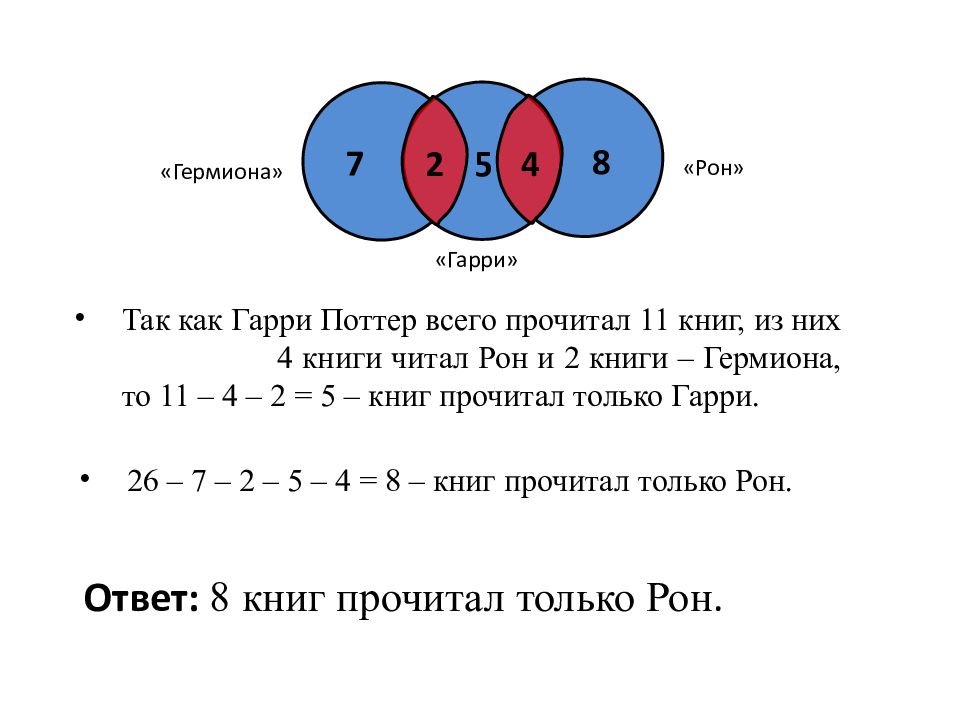
« Гермиона » «Гарри» 7 « Рон » Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон. 5 8 Ответ: 8 книг прочитал только Рон. 2 4
Условия: Какое количество страниц (в сотнях тысяч) будет найдено по запросу Подкова & Наковальня?
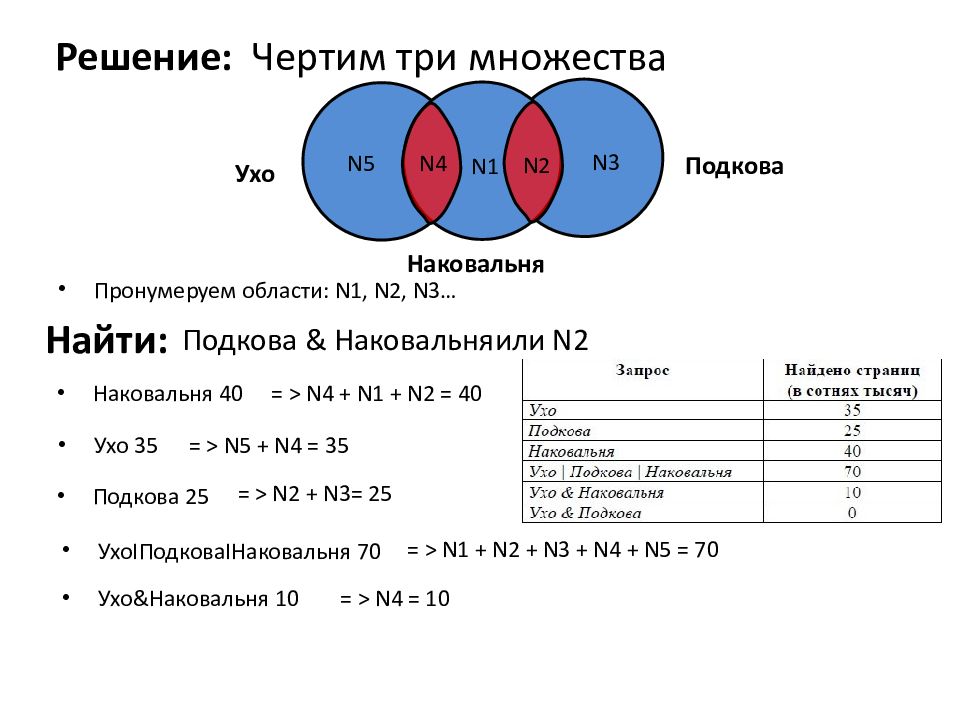
Решение: Чертим три множества Ухо Подкова Наковальня Пронумеруем области: N1, N2, N3 … N 5 N 1 N 3 Наковальня 40 = > N4 + N1 + N2 = 40 Ухо 35 = > N 5 + N 4 = 35 Подкова 25 = > N 2 + N 3 = 25 Ухо I Подкова I Наковальня 70 = > N1 + N2 + N3 + N4 + N5 = 70 Ухо & Наковальня 10 = > N4 = 10 N 4 Найти: Подкова & Наковальня или N2 N 2
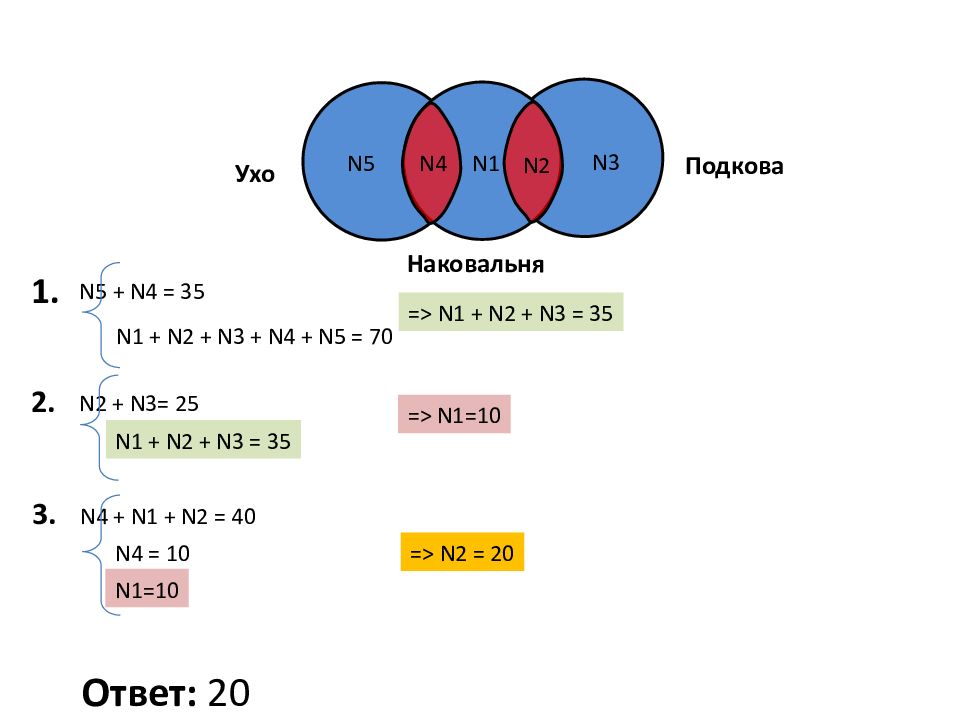
N 5 + N 4 = 35 N1 + N2 + N3 + N4 + N5 = 70 = > N1 + N2 + N3 = 35 N 2 + N 3 = 25 N1 + N2 + N3 = 35 = > N1=10 N4 + N1 + N2 = 40 N4 = 10 N1=10 = > N2 = 20 Ответ: 20 1. 2. 3. Ухо Подкова Наковальня N 5 N 1 N 3 N 4 N 2
http://www.lvf2004.com/dop_t2r2part2.html http://infoegehelp.ru/index.php?option=com_content&view=article&id=457&Itemid=77 http://4ege.ru/informatika/5643-demoversiya-ege-po-informatike-2015.html
