Приведены результаты 25 измерений напряжения (в вольтах) в бытовой сети. Все измерения были сделаны в дневное время, в случайно (бессистемно) выбранные моменты времени. 225 В, 227 В, 225 В, 228 В, 225 В, 228 В, 218 В, 217 В, 218 В, 220 В, 223 В, 225 В, 216 В, 222 В, 224 В, 220 В, 218 В, 221 В, 220 В, 216 В, 214 В, 219 В, 231 В, 228 В, 227 В.
Слайд 4: Колебания напряжения в бытовых электрических сетях
Во время измерения напряжения последняя цифра все время изменяется в пределах двух-трех единиц. Поэтому приходиться брать среднее значение этих быстро меняющихся показаний вольтметра. В России номинальное напряжение в бытовых сетях 220 В. Как вы видите, реальное напряжение может отличаться от 220 В. Обычно напряжение либо немного выше этого значения, либо ниже. Это зависит от дополнительно включенных электроприборов. Моменты включения электроприборов является случайными и приводят к случайной изменчивости напряжения Электрические приборы в России рассчитаны на напряжение 220 В. При небольших отклонениях напряжения от 220 В они работают исправно, а при значительных колебаниях напряжения могут прийти в негодность.
Слайд 5: Колебания напряжения в бытовых электрических сетях
225 В, 227 В, 225 В, 228 В, 225 В, 228 В, 218 В, 217 В, 218 В, 220 В, 223 В, 225 В, 216 В, 222 В, 224 В, 220 В, 218 В, 221 В, 220 В, 216 В, 214 В, 219 В, 231 В, 228 В, 227 В. 1.Какое самое большое напряжение было зафиксировано в период наблюдения? 2.Какое самое маленькое напряжение было зафиксировано? 3. Каков размах значений напряжения? 4. Какова медиана и мода напряжения? 5. Каково среднее значение напряжения?
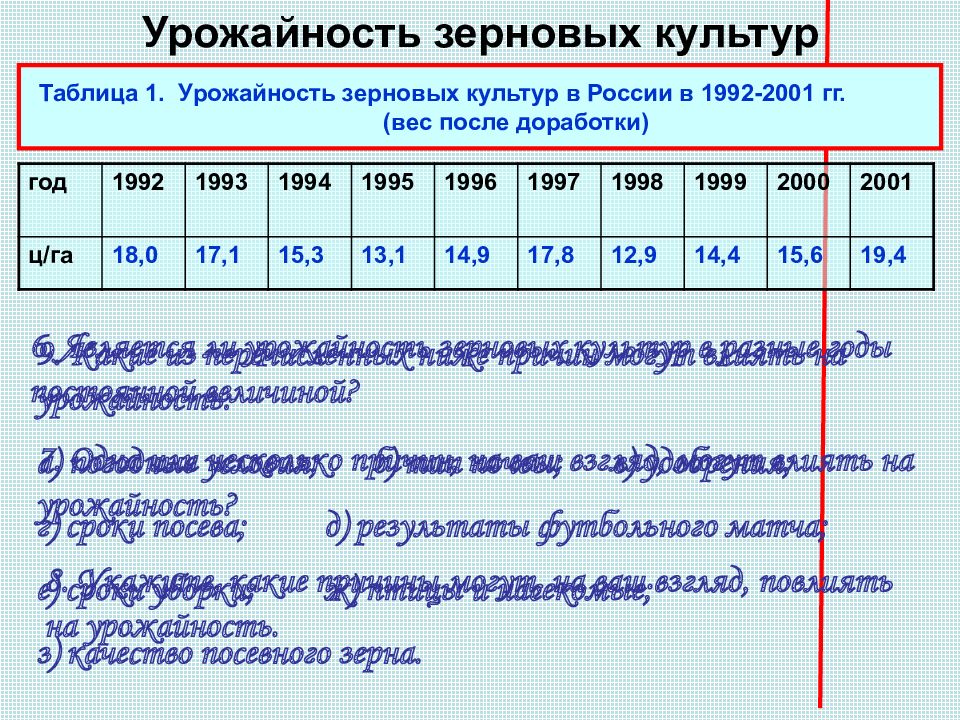
Слайд 6: Урожайность зерновых культур
Таблица 1. Урожайность зерновых культур в России в 1992-2001 гг. (вес после доработки) год 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 ц/га 18,0 17,1 15,3 13,1 14,9 17,8 12,9 14,4 15,6 19,4 6. Является ли урожайность зерновых культур в разные годы постоянной величиной? 7. Одна или несколько причин, на ваш взгляд, могут влиять на урожайность? 8. Укажите, какие причины могут, на ваш взгляд, повлиять на урожайность. 9. Какие из перечисленных ниже причин могут влиять на урожайность: а) погодные условия; б) тип почвы; в) удобрения; г) сроки посева; д) результаты футбольного матча; е) сроки уборки; ж) птицы и насекомые; з) качество посевного зерна.
Слайд 7
Как видно из таблицы 1, урожайность зерновых культур – изменчивая величина. Ее значение зависит от многих причин, главное из которых – погодные условия и деятельность человека (удобрения, выбор посевного материала и сроков сева, совершенство уборочной техники). Можно ли найти в этой изменчивости закономерности? Для этого следует провести анализ данных в таблице. Некоторые этапы этого анализа сформулированы в следующих упражнениях.
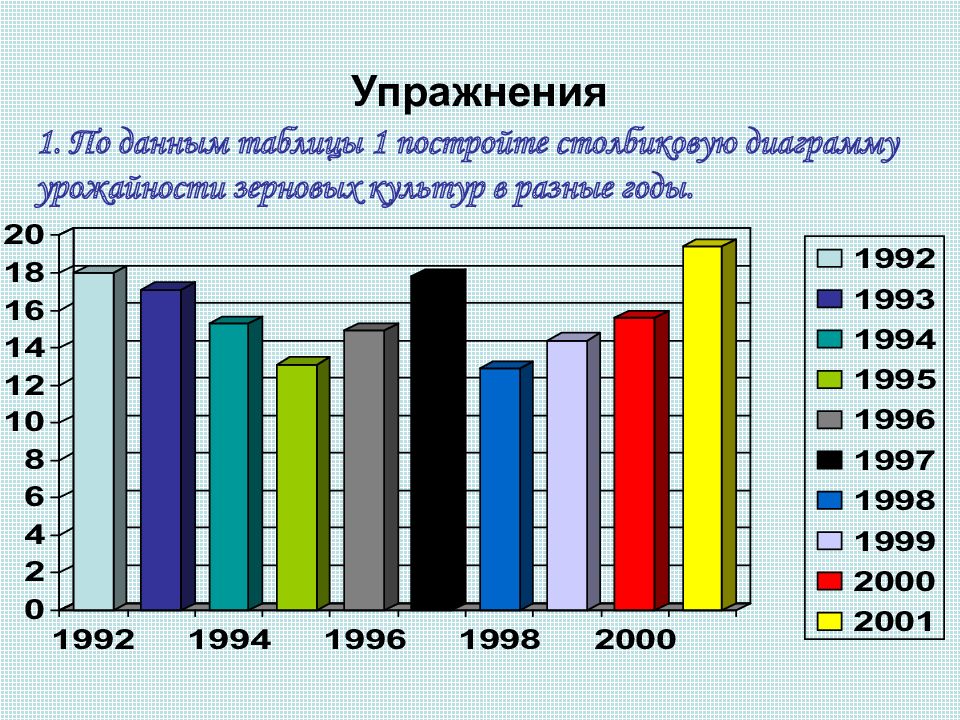
Слайд 8: Упражнения
1. По данным таблицы 1 постройте столбиковую диаграмму урожайности зерновых культур в разные годы.
Слайд 9: Упражнения
год 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 ц/га 18,0 17,1 15,3 13,1 14,9 17,8 12,9 14,4 15,6 19,4 2. Упорядочите данные таблицы 1 в порядке возрастания. 12,9; 13,1; 14,4; 14,9; 15,3; 15,6; 17,1; 17.8; 18,0; 19,4 3. Вычислите средние урожайности зерновых в периоды 1992-1996 и 1997-2001 гг. Сравните между собой полученные результаты.
Слайд 10: Упражнения
4. Составьте таблицу отклонений ежегодной урожайности в 1992-1996 и в 1997-2001 гг. от средних показателей за соответствующие пять лет. 5. Составьте таблицу квадратов отклонений ежегодной урожайности в 1992-1996 и 1997-2001 гг. от средних показателей за соответствующие пять лет. 6. Что больше подвержено изменчивости: средняя урожайность за пять последовательных лет или урожайность в отдельные годы?
Слайд 11
год Урожайность, ц/га Отклонение от среднего Квадрат отклонения 1992 18,0 18,0-15,68=2,32 5,3824 1993 17,1 17,1-15,68=1,42 2,0164 1994 15,3 15,3-15,68=-0,38 0,1444 1995 13,1 13,1-15,68=-2,58 6,6564 1996 14,9 14,9-15,68=-0,78 0,6084 1997 17,8 17,8-16,02=1,78 3,1684 1998 12,9 12,9-16,02=-3,12 9,7344 1999 14,4 14,4-16,02=-1,62 2,6244 2000 15,6 15,6-16,02=-0,42 0,1764 2001 19,4 19,4-16,02=3,38 11,4244
Слайд 12: Массовое производство
На обертке шоколадного батончика написано, что его масса 50 граммов. Это – номинальная масса или номинальный вес. Ребята купили десять батончиков и взвесили их. Они получили следующие 10 значений (в граммах) : 49,1; 50,0; 49,7; 50,5; 48,1; 50,3; 49,7; 51,6; 49,8; 50,1. Только один батончик весил в точности 50 г. Некоторые батончики весили больше, другие – меньше. В ряде случаев отклонения превышали 1,5 г. Чтобы понять, всегда ли наблюдается такое явление, ребята купили и взвесили еще одну партию из десяти батончиков. Вот такие значения (в граммах) они получили для второй партии: 49,7; 48,8; 51,4; 49,1; 49,6; 50,9; 48,5; 52,0; 50,7; 50,6.
Слайд 13: Массовое производство
7. Найдите наибольший и наименьший вес взвешенных шоколадных батончиков в первой партии. 49,1; 50,0; 49,7; 50,5; 48,1; 50,3; 49,7; 51,6; 49,8; 50,1. 8. Найдите наибольшее абсолютное отклонение от номинального веса батончиков в первой партии. 9. Найдите средний вес шоколадного батончика в первой партии. Убедитесь, что он мало отличается от 50 г. 10. Найдите средний вес батончика во второй партии. 49,7; 48,8; 51,4; 49,1; 49,6; 50,9; 48,5; 52,0; 50,7; 50,6. 11. Убедитесь, что средние веса батончиков в первой и второй партиях мало отличается друг от друга и от номинального веса.
Слайд 14: Массовое производство
12. Сколько в каждой партии батончиков, вес которых превышает 50 г. Сколько таких батончиков в обеих партиях? Какую долю и какой процент они составляют? 49,1; 50,0; 49,7; 50,5; 48,1; 50,3; 49,7; 51,6; 49,8; 50,1. 49,7; 48,8; 51,4; 49,1; 49,6; 50,9; 48,5; 52,0; 50,7; 50,6. 13. Вес батончика, который вы покупаете, может быть больше или меньше номинального. Можно ли считать, что шансы этих событий равны, если судить по результатам наших взвешиваний?
Слайд 15
Ситуация, с которой столкнулись ребята, часто встречается при массовом производстве различных изделий. Если отклонение размера, массы или иной характеристики изделия не сильно отличается от заданного стандарта, т.е. находится в пределах установленной нормы (допуска), то такое изделие считается годным. Такие изделия идут в продажу или дальнейшее производство. Изделия, для которых отклонения превышают допуск, считают бракованными. Для разных изделий допуски разные. ВЫВОД: Многие величины подвержены случайной изменчивости.
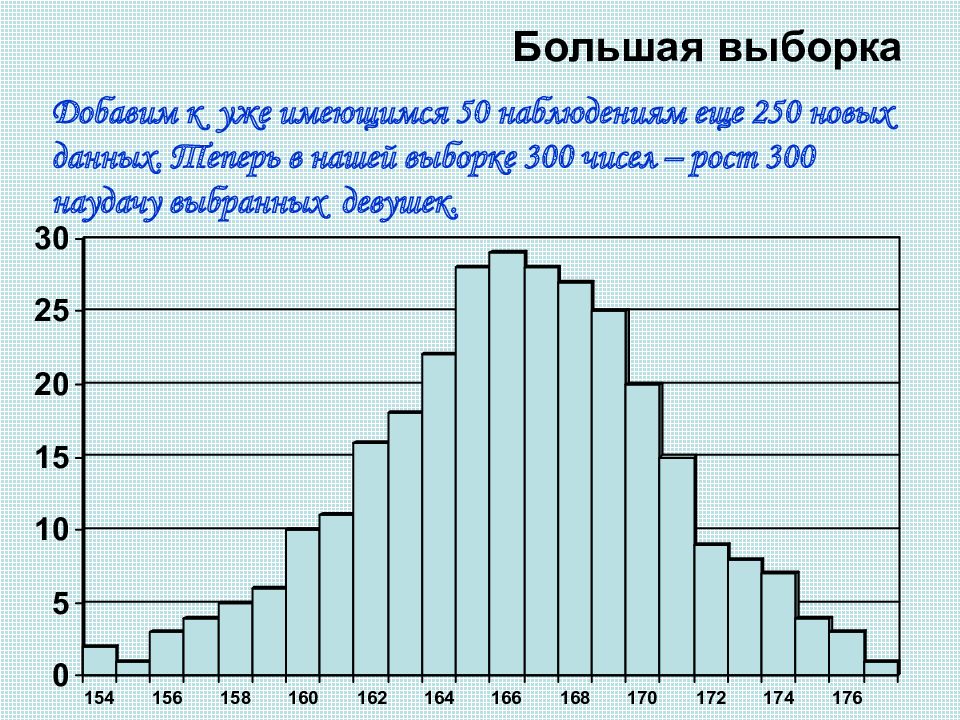
Слайд 16: Рост человека
Невозможно заранее предсказать рост незнакомого человека. Для исследователя эта величина случайная. Но если измерить рост многих людей (тоже выбранных случайно), то станет видна закономерность. Чтобы в этом убедиться, мы последовательно обсудим данные о росте человека по малому, среднему и большому числу наблюдений.
Слайд 17: Малая выборка
В таблице приведен рост (в сантиметрах) десяти случайно выбранных девушек. 164 170 160 163 170 171 166 169 166 165 Из таблицы видно, что рост человека изменчив. В этой таблице рост колеблется около 166 см. Найдем среднее значение, медиану и размах Среднее значение = 166,4 см, медиана = 166 см, размах = 11 см.
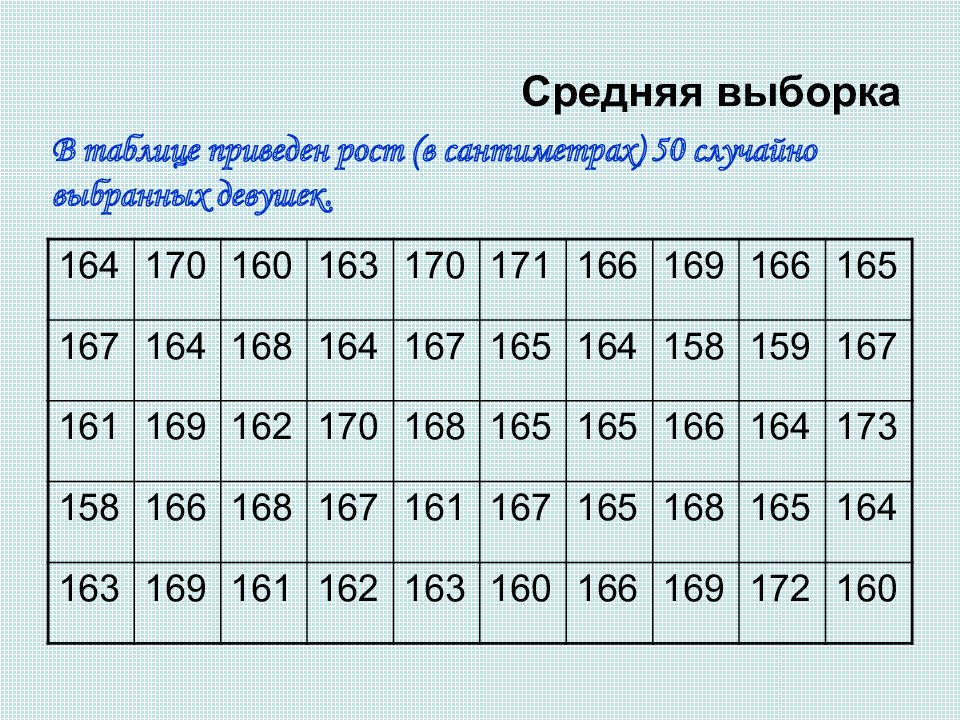
Слайд 18: Средняя выборка
В таблице приведен рост (в сантиметрах) 50 случайно выбранных девушек. 164 170 160 163 170 171 166 169 166 165 167 164 168 164 167 165 164 158 159 167 161 169 162 170 168 165 165 166 164 173 158 166 168 167 161 167 165 168 165 164 163 169 161 162 163 160 166 169 172 160
Слайд 19
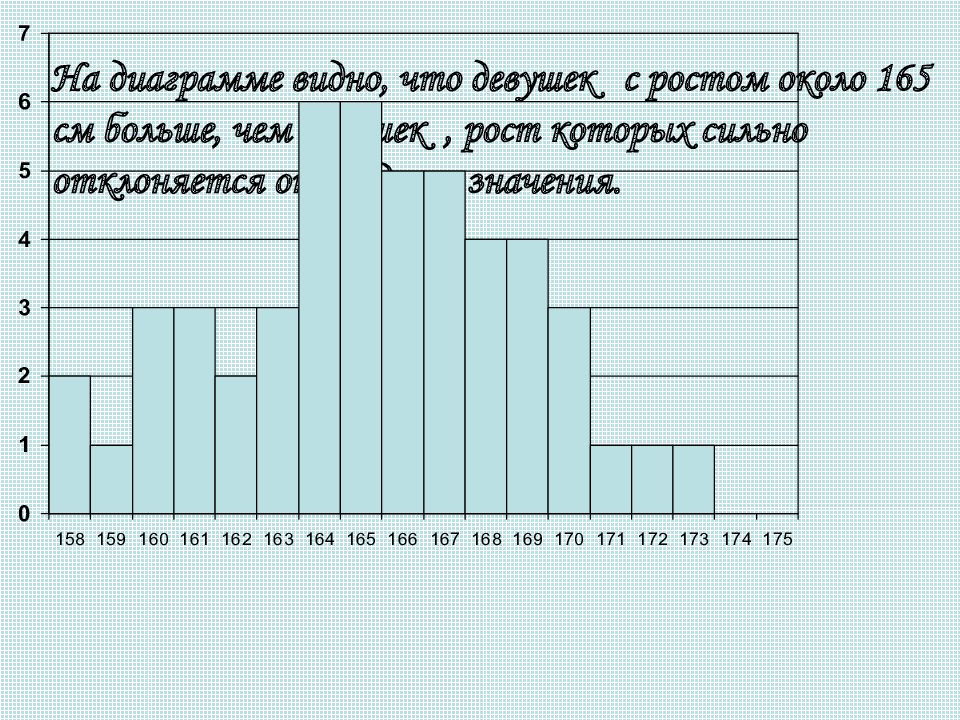
Среднее значение роста в этой выборке равно 165,3 см, а медиана – 165 см. Эти значения мало отличаются от тех, что были получены для первых двух выборок. А вот размах колебаний роста увеличился до 15см. Это естественно. Чем больше человек мы случайно выбираем, тем больше шансы, что среди них попадутся более высокие и более низкие люди. Поэтому размах значений роста может увеличиваться, а среднее значение роста остается практически неизменным. Трудно изучать эту совокупность чисел, читая в таблице одно число за другим. Лучше представить этот набор чисел наглядно, например в виде столбиковой диаграммы. По оси абсцисс будем откладывать рост, начиная с наименьшего значения 158 см, с шагом 1 см. Высота столбика будет показывать, сколько в выборке девушек с заданным ростом.
Слайд 20
На диаграмме видно, что девушек с ростом около 165 см больше, чем девушек, рост которых сильно отклоняется от среднего значения.