Первый слайд презентации: Тема 4. Режимы течения жидкости. Число Рейнольдса
Слайд 2: Режимы движения жидкости в трубах
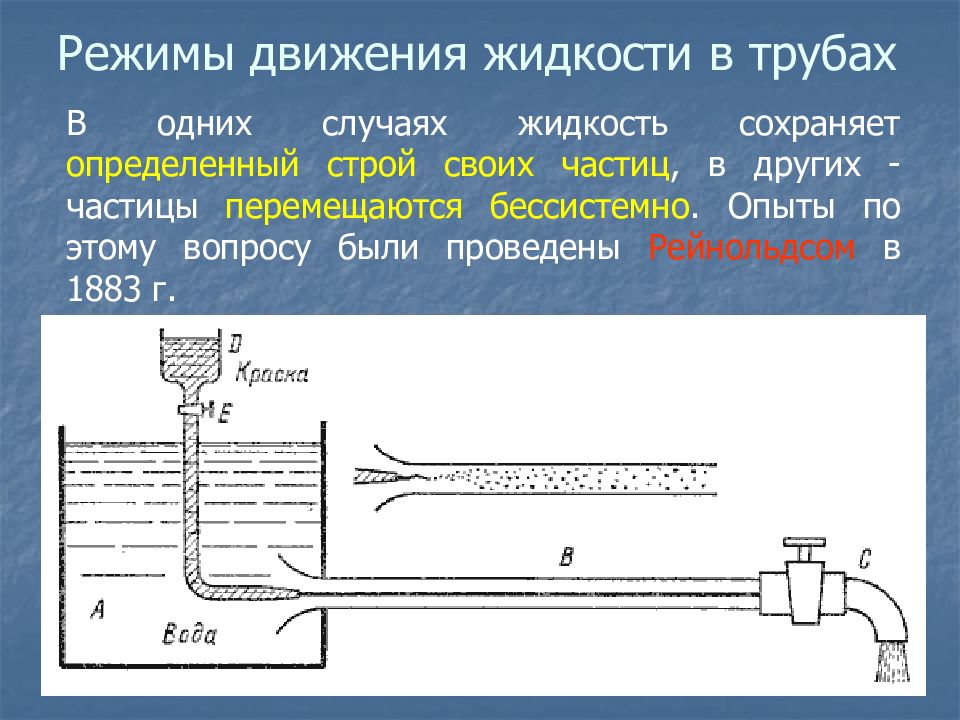
В одних случаях жидкость сохраняет определенный строй своих частиц, в других - частицы перемещаются бессистемно. Опыты по этому вопросу были проведены Рейнольдсом в 1883 г.
Слайд 3: Опыты Рейнольдса
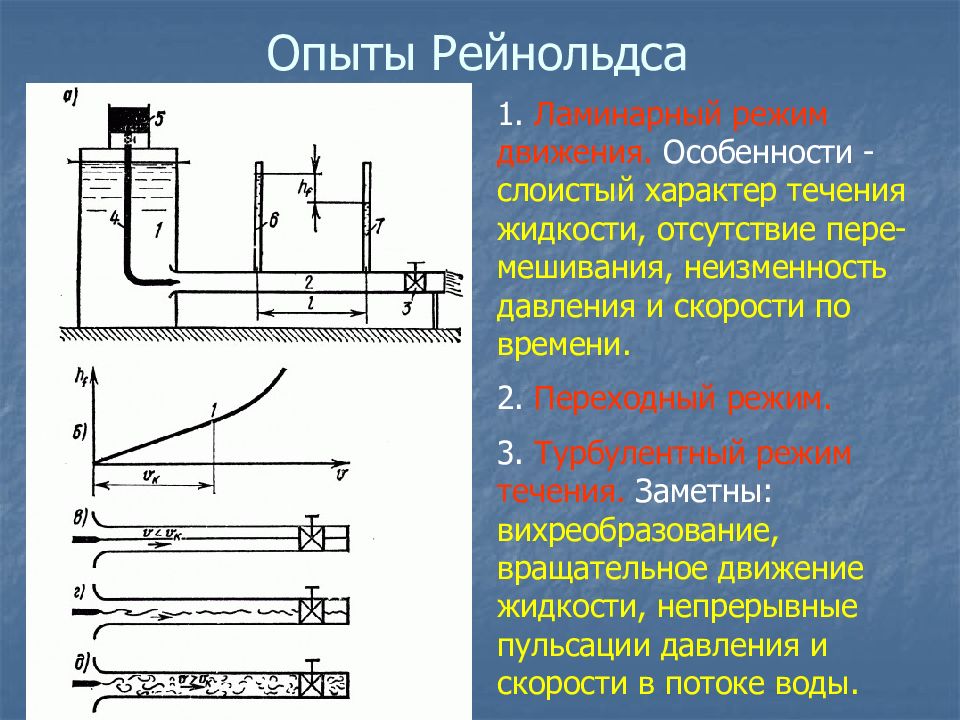
1. Ламинарный режим движения. Особенности - слоистый характер течения жидкости, отсутствие пере-мешивания, неизменность давления и скорости по времени. 2. Переходный режим. 3. Турбулентный режим течения. Заметны: вихреобразование, вращательное движение жидкости, непрерывные пульсации давления и скорости в потоке воды.
Слайд 4
1. Ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости. 2. Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.
Слайд 5
Примеры ламинарного и турбулентного течений Пламя Турбулентное течение в трубе Турбулентное и ламинарное обтекание Турбулентное течение за соплами
Слайд 6
3. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической V кр. Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы d. 4. Входящий в эту формулу безразмерный коэффициент k одинаков для всех жидкостей и газов, а также для любых диаметров труб. Этот коэффициент называется критическим числом Рейнольдса Re кр и определяется следующим образом:
Слайд 7
5. Критерий подобия Рейнольдса (число Рейнольдса) позволяет судить о режиме течения жидкости в трубе. При Re < Re кр =2320 течение является ламинарным ; 2320 < Re < 3800…4200 - переходная область ; Re > 3800…4200 течение турбулентное. Зависимости справедливы только для круглых труб. Число Рейнольдса: Эпюры скоростей в трубе: а) ламинарный режим; б) турбулентный
Слайд 8: Физический смысл числа Рейнольдса
Число (критерий) Рейнольдса) Re - мера отношения силы инерции к силе трения - динамический коэффициент вязкости - кинематический коэффициент вязкости При увеличении скорости растут силы инерции. Силы трения при этом больше сил инерции и до некоторых пор выпрямляют траектории струек При некоторой скорости v кр : Сила инерции F и > силы трения F тр, поток становится турбулентным
Слайд 9: Распределение скоростей в ламинарном и турбулентном потоке
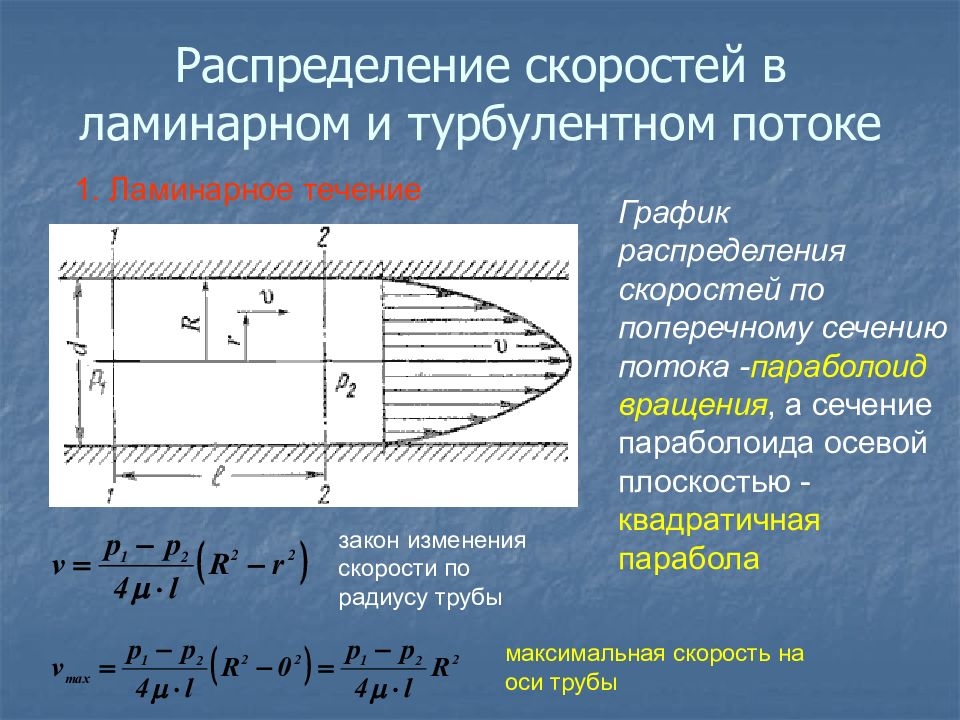
1. Ламинарное течение График распределения скоростей по поперечному сечению потока - параболоид вращения, а сечение параболоида осевой плоскостью - квадратичная парабола закон изменения скорости по радиусу трубы максимальная скорость на оси трубы
Слайд 10
Средняя скорость Объемный расход Потеря давления в трубопроводе Для использования в уравнении Бернулли перейдем к потерям напора: - потери напора пропорциональны средней скорости - коэффициент Кориолиса
Слайд 11
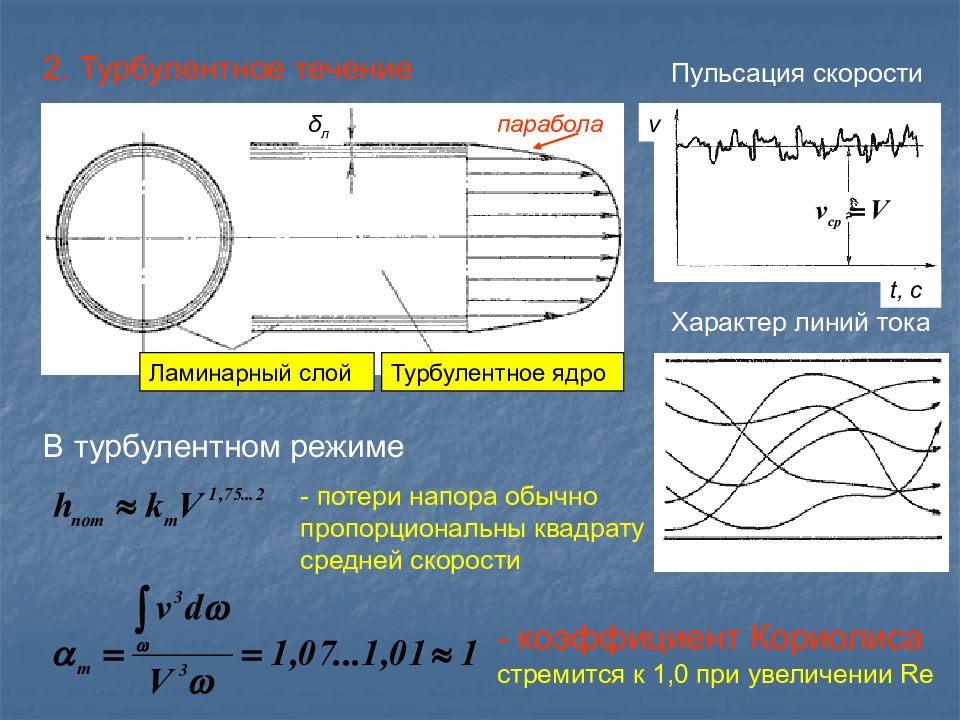
2. Турбулентное течение Пульсация скорости Характер линий тока В турбулентном режиме Ламинарный слой Турбулентное ядро δ л v t, c парабола - потери напора обычно пропорциональны квадрату средней скорости - коэффициент Кориолиса стремится к 1,0 при увеличении Re
Слайд 12: Кавитация
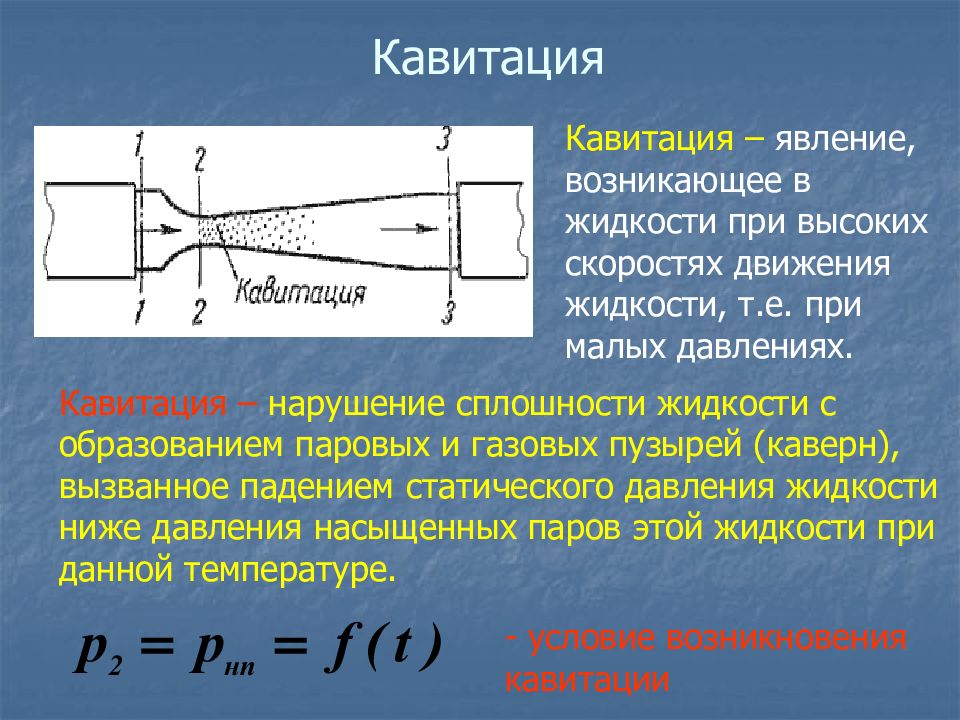
Кавитация – явление, возникающее в жидкости при высоких скоростях движения жидкости, т.е. при малых давлениях. Кавитация – нарушение сплошности жидкости с образованием паровых и газовых пузырей (каверн), вызванное падением статического давления жидкости ниже давления насыщенных паров этой жидкости при данной температуре. - условие возникновения кавитации
Слайд 13: Сущность кавитации
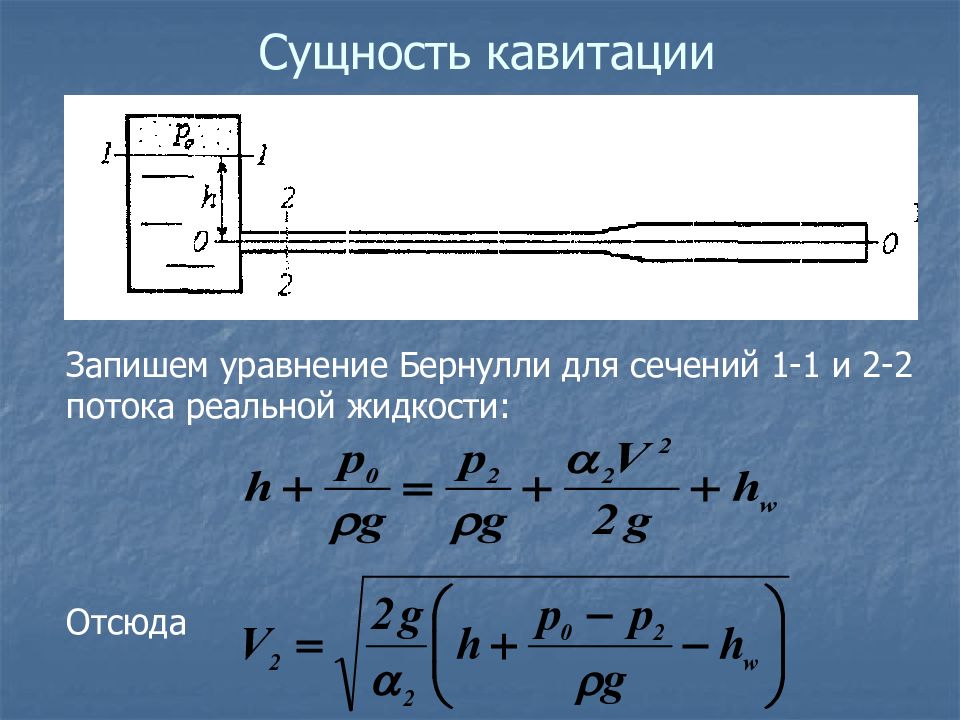
Запишем уравнение Бернулли для сечений 1-1 и 2-2 потока реальной жидкости: Отсюда
Слайд 14
Скорость максимальна при минимально возможном давлении р 2 = р нп : - максимальная скорость истечения В жидкости наступает кипение – выделение пузырьков пара по всему объему. Поток превращается в двухфазный (пар + жидкость), его сплошность нарушается – кавитация Кавитация полностью нарушает процесс транспортировки жидкости.
Слайд 15: Стадии кавитации
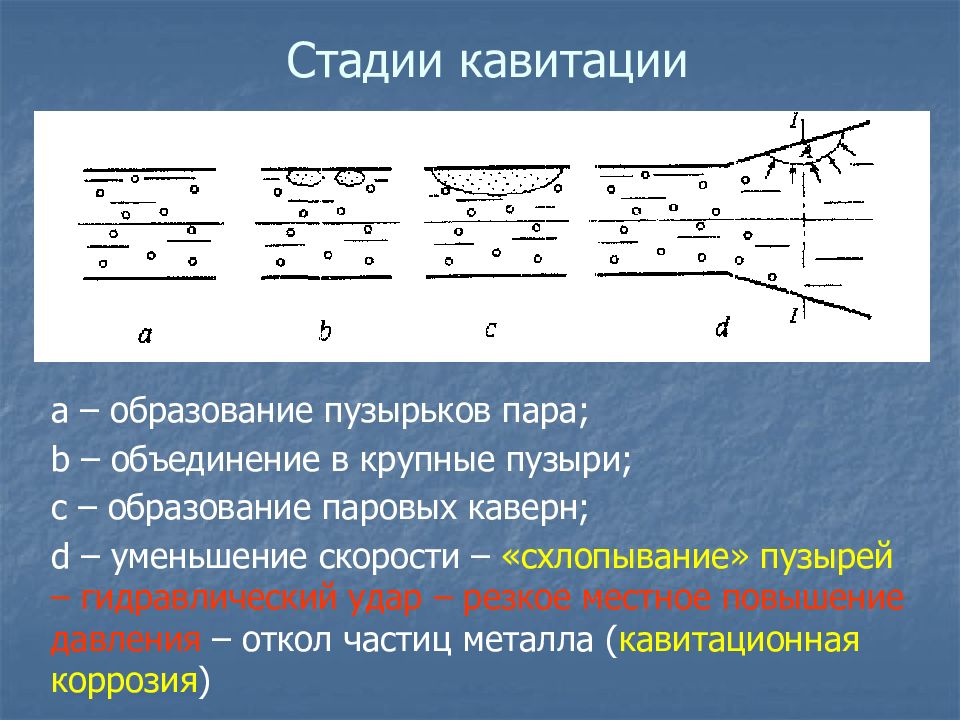
а – образование пузырьков пара; b – объединение в крупные пузыри; c – образование паровых каверн; d – уменьшение скорости – «схлопывание» пузырей – гидравлический удар – резкое местное повышение давления – откол частиц металла ( кавитационная коррозия )
Слайд 17: Борьба с кавитацией
Возникает в гидромашинах, кранах, вентилях, гребных винтах, всасывающих трубопроводах насосов и т.д. Меры борьбы с кавитацией: снижение скорости жидкости в трубопроводе; уменьшение перепадов диаметров трубопровода; повышение рабочего давления в гидросистемах (наддув баков сжатым газом); установка всасывающего отверстия насоса не выше допускаемой высоты всасывания (из паспорта насоса); применение кавитационно-стойких материалов.
Слайд 18: Тема 5. Гидравлические сопротивления
Слайд 19: Гидравлические сопротивления в уравнении Бернулли
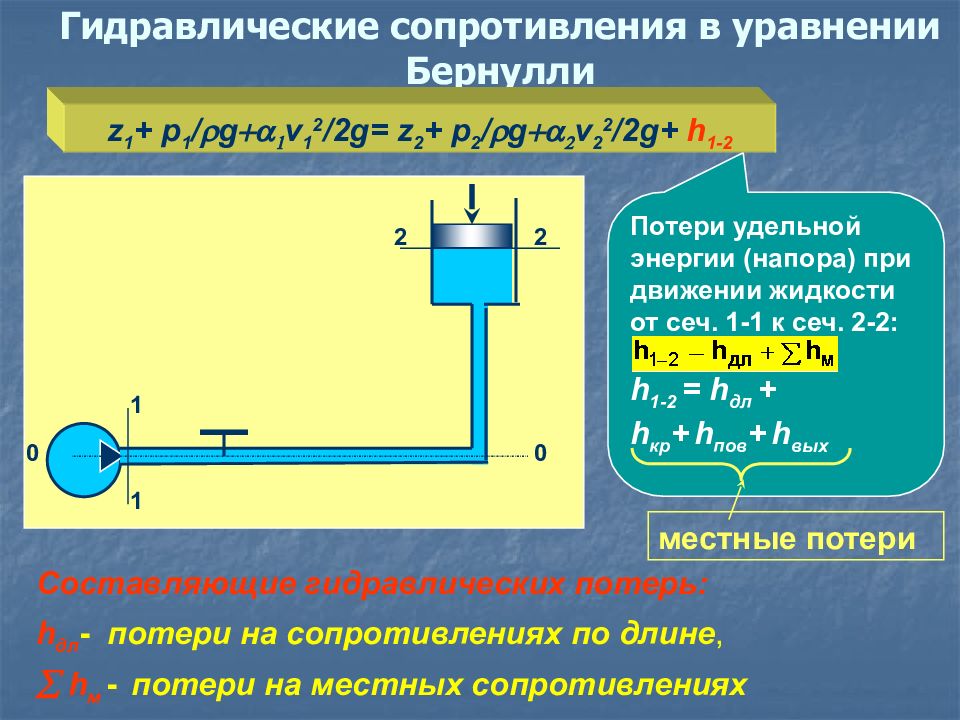
0 0 1 1 2 2 Потери удельной энергии (напора) при движении жидкости от сеч. 1-1 к сеч. 2-2: h 1-2 = h дл + h кр + h пов + h вых Гидравлические сопротивления в уравнении Бернулли Составляющие гидравлических потерь: h дл - потери на cопротивлениях по длине, å h м - потери на местных сопротивлениях местные потери z 1 + p 1 / r g +a 1 v 1 2 /2g= z 2 + p 2 / r g +a 2 v 2 2 /2g+ h 1-2
Слайд 20
В одних случаях потери напора распределяются по длине трубопровода - это линейные (путевые) потери ; В других - потери сосредоточены на очень коротких участках, длиной которых можно пренебречь - потери на местных гидравлических сопротивлениях (местные потери) : вентили, закругления, сужения, расширения и т.д., - потери на деформацию потока. Источником потерь во всех случаях является вязкость жидкости, т.е. потери возникают только в реальной жидкости, в идеальной потерь нет. Потери напора по длине и в местных гидравлических сопротивлениях сильно зависят от режима движения жидкости.
Слайд 21: Физическая природа гидравлических сопротивлений
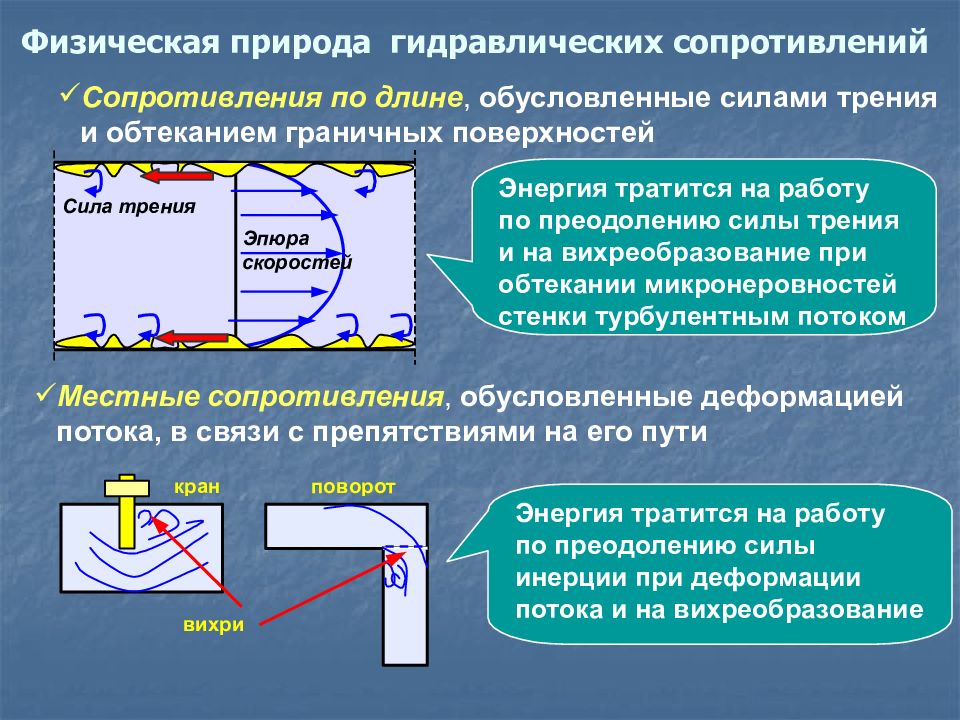
Местные сопротивления, обусловленные деформацией потока, в связи с препятствиями на его пути Сопротивления по длине, обусловленные силами трения и обтеканием граничных поверхностей Энергия тратится на работу по преодолению силы трения и на вихреобразование при обтекании микронеровностей стенки турбулентным потоком Энергия тратится на работу по преодолению силы инерции при деформации потока и на вихреобразование
Слайд 22: Потери по длине. Формула Дарси-Вейсбаха
Формула Дарси-Вейсбаха для трубы постоянного сечения l - коэффициент гидравлического трения, зависит от режима течения и состояния поверхности трубопровода l, d – длина и диаметр трубопровода V – средняя скорость движения
Слайд 23: Местные потери. Формула Вейсбаха
Потери напора V – средняя скорость потока перед препятствием. Иначе - обязательно оговаривается. x (кси) (иногда ζ (дзета) ) - коэффициент местного сопротивления, зависит от его вида, размера и конструктивного выполнения. Потери давления
Слайд 24: Определение коэффициентов местных сопротивлений
Формула Вейсбаха Коэффициент в основном берется из справочной литературы, кроме случаев: внезапное расширение потока; внезапное сужение; диффузор и конфузор (плавное расширение/сужение); резкий и плавный поворот русла (колено/отвод). Во всех случаях - только для турбулентного режима течения.
Слайд 25: Коэффициент сопротивления при внезапном расширении потока
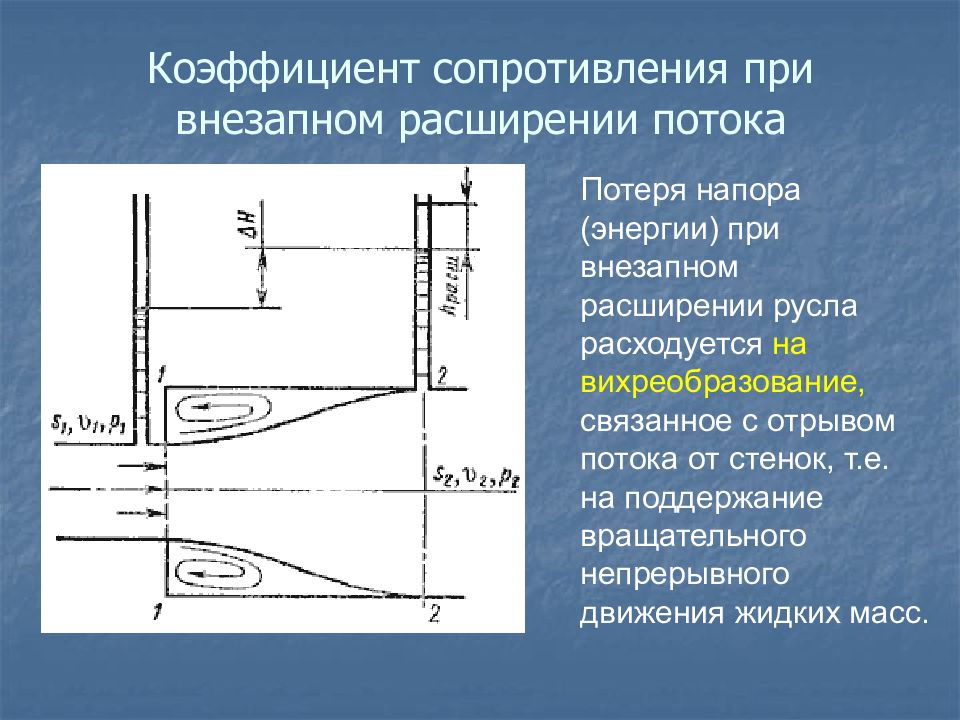
Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс.
Слайд 26
Рассмотрим два сечения потока: 1-1 и 2-2. Допущения: а) поток турбулентный ( = 1 ); б) напряжения трения = 0. Уравнение Бернулли для сечений 1-1 и 2-2: Из теоремы об изменении количества движения Учитывая, что и разделив на ,
Слайд 27
получаем: или , то есть - теорема Борда (1766) Теорема Борда - потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей
Слайд 28
Частный случай: при ( расширение из трубы в бассейн) - полная потеря напора Из уравнения неразрывности и
Слайд 29: Коэффициент сопротивления при плавном расширении русла (диффузор)
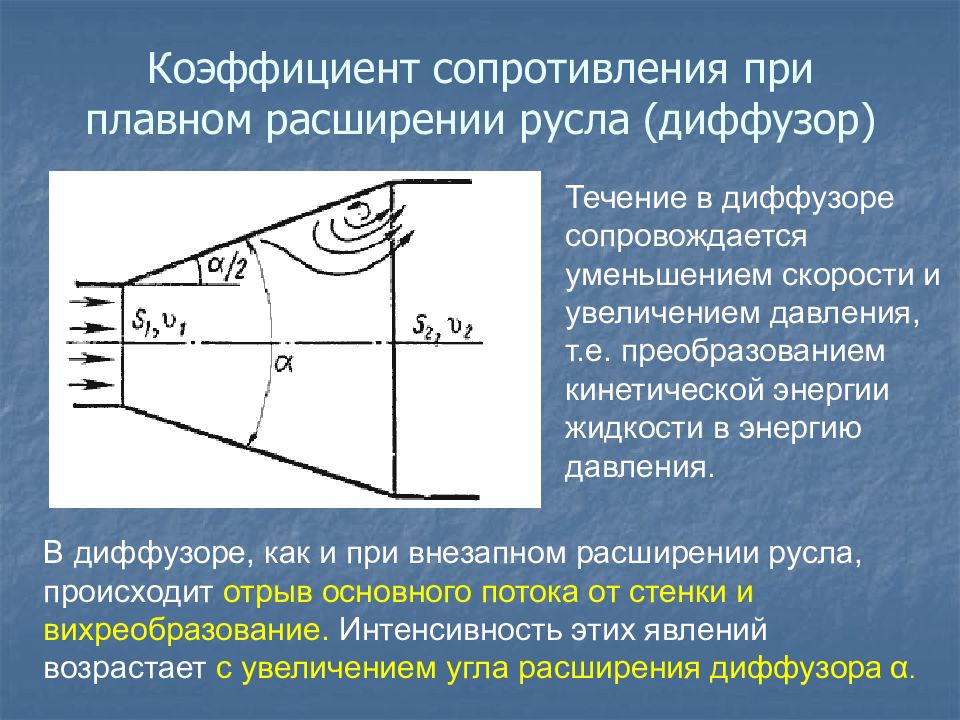
Течение в диффузоре сопровождается уменьшением скорости и увеличением давления, т.е. преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразование. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.
Слайд 30
Кроме того, в диффузоре имеются и обычные потери на трение, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых: h тр и h расш - потери напора на трение и расширение (вихреобразование). Без вывода: где n = S 2 /S 1 = ( r 2 /r 1 ) 2 - степень расширения диффузора; k - коэффициент смягчения (отн. уступа). При = 5…20° k = sin .
Слайд 31
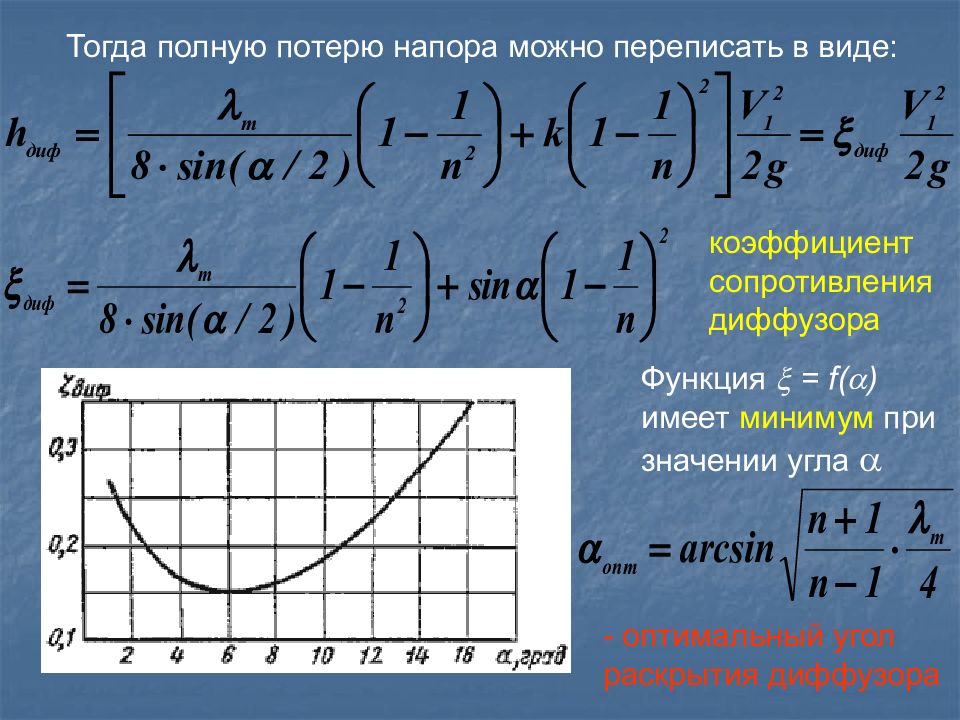
Тогда полную потерю напора можно переписать в виде: коэффициент сопротивления диффузора Функция = f( ) имеет минимум при значении угла - оптимальный угол раскрытия диффузора
Слайд 32: Коэффициент сопротивления при внезапном и плавном сужении русла
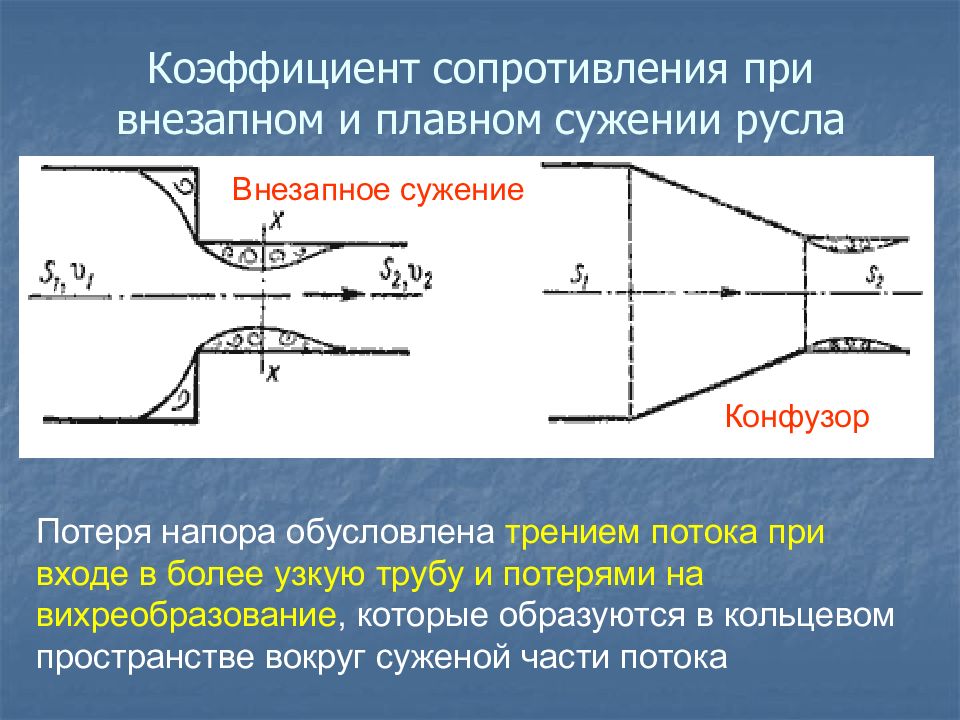
Потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока Конфузор Внезапное сужение
Слайд 33
Полная потеря напора определится по формуле: Коэффициент сопротивления сужения суж определяется по полуэмпирической формуле И.Е. Идельчика: где n = S 1 /S 2 При выходе трубы из резервуара больших размеров (когда можно считать, что S 2 /S 1 = 0 ), а также при отсутствии закругления входного угла, коэффициент сопротивления суж = 0,5.
Слайд 34
Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение где коэффициент сопротивления конфузора определяется по формуле где n = S 1 /S 2 - степень сужения Внимание! При сужении русла потери напора относятся к скорости за препятствием V 2 !
Слайд 35: Внезапный и плавный поворот потока
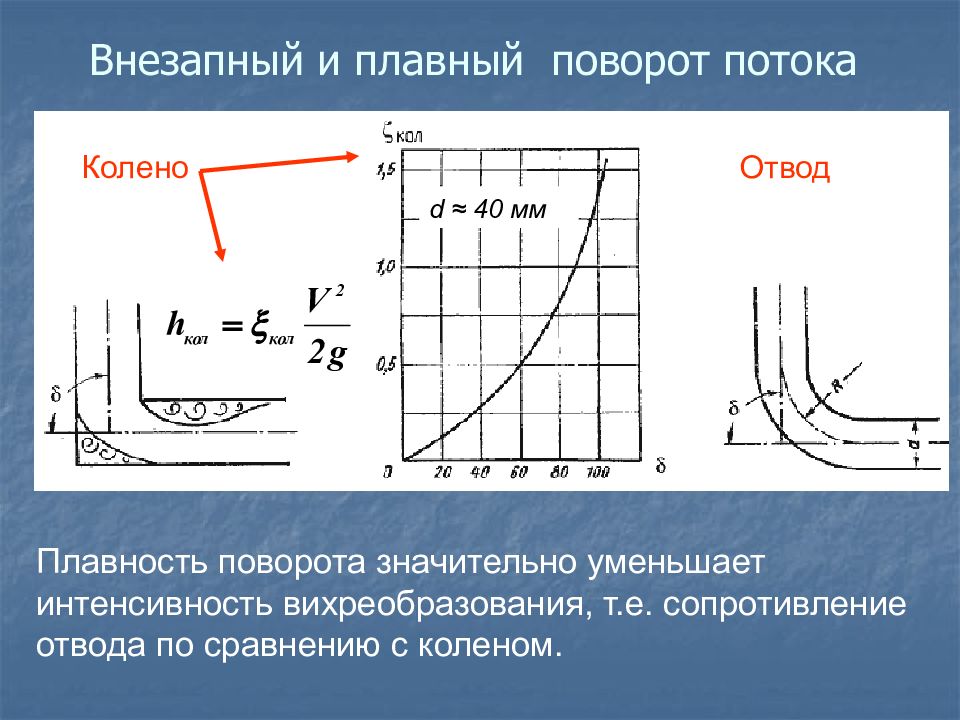
Плавность поворота значительно уменьшает интенсивность вихреобразования, т.е. сопротивление отвода по сравнению с коленом. Колено Отвод d ≈ 40 мм
Слайд 36
Коэффициент сопротивления отвода отв зависит от отношения R / d, угла δ, и формы поперечного сечения трубы. Для отводов круглого сечения с углом δ= 90° и R/d > 1 при турбулентном течении можно воспользоваться эмпирической формулой: Для углов δ 70° коэффициент сопротивления При δ > 100°
Слайд 37: Справочные коэффициенты местных потерь
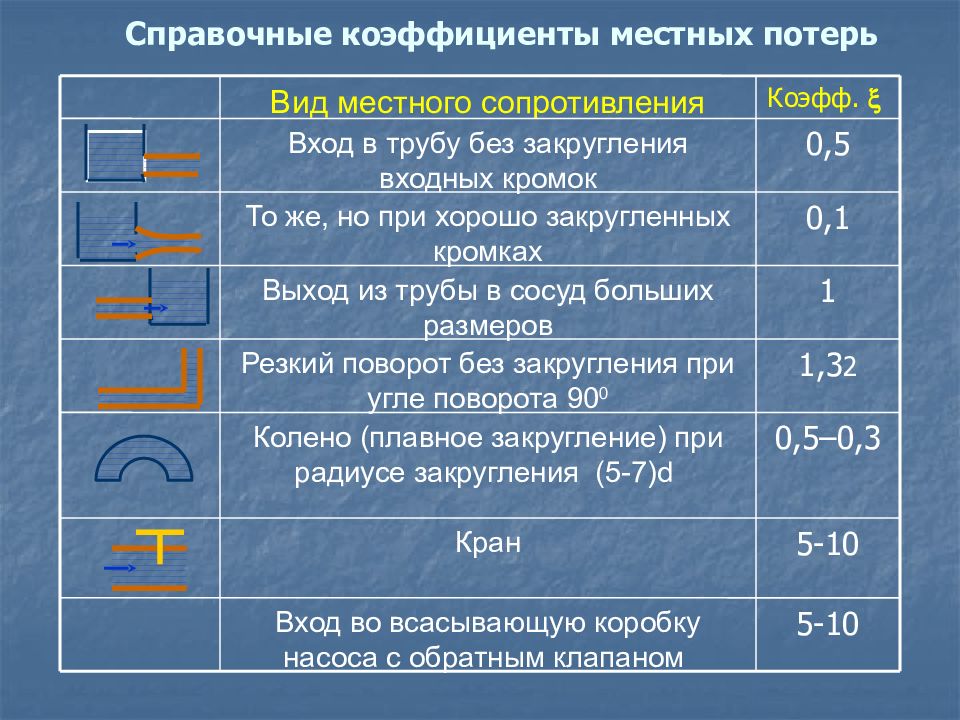
5-10 Вход во всасывающую коробку насоса с обратным клапаном 5-10 Кран 0,5–0,3 Колено (плавное закругление) при радиусе закругления (5-7)d 1,3 2 Резкий поворот без закругления при угле поворота 90 0 1 Выход из трубы в сосуд больших размеров 0,1 То же, но при хорошо закругленных кромках 0,5 Вход в трубу без закругления входных кромок Коэфф. x Вид местного сопротивления
Слайд 38: Зависимость коэффициента местных потерь от Re
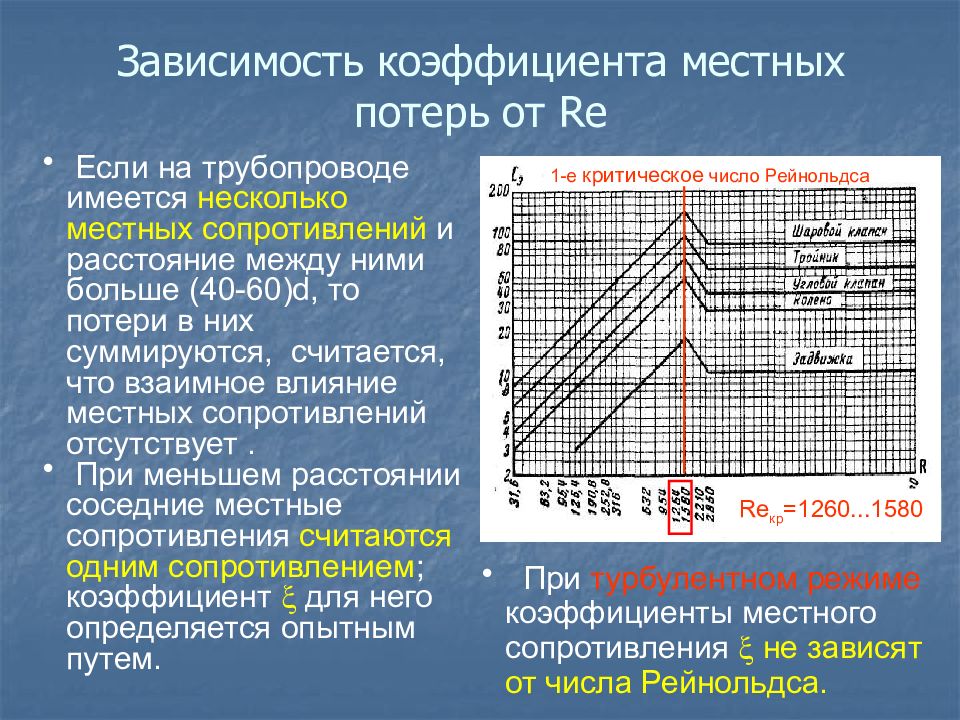
Если на трубопроводе имеется несколько местных сопротивлений и расстояние между ними больше (40-60) d, то потери в них суммируются, считается, что взаимное влияние местных сопротивлений отсутствует. При меньшем расстоянии соседние местные сопротивления считаются одним сопротивлением ; коэффициент для него определяется опытным путем. При турбулентном режиме коэффициенты местного сопротивления не зависят от числа Рейнольдса. 1-е критическое число Рейнольдса Re кр =1260...1580
Слайд 39: Определение потерь по длине (потерь на трение)
Формула Дарси-Вейсбаха l - коэффициент гидравлического трения. Зависит от режима течения (числа Рейнольдса) и состояния поверхности трубопровода (ее эквивалентной шероховатости) Определение коэффициента гидравлического трения λ для каждого конкретного случая - одна из самых сложных задач гидравлики
Слайд 40: Коэффициент гидравлического трения
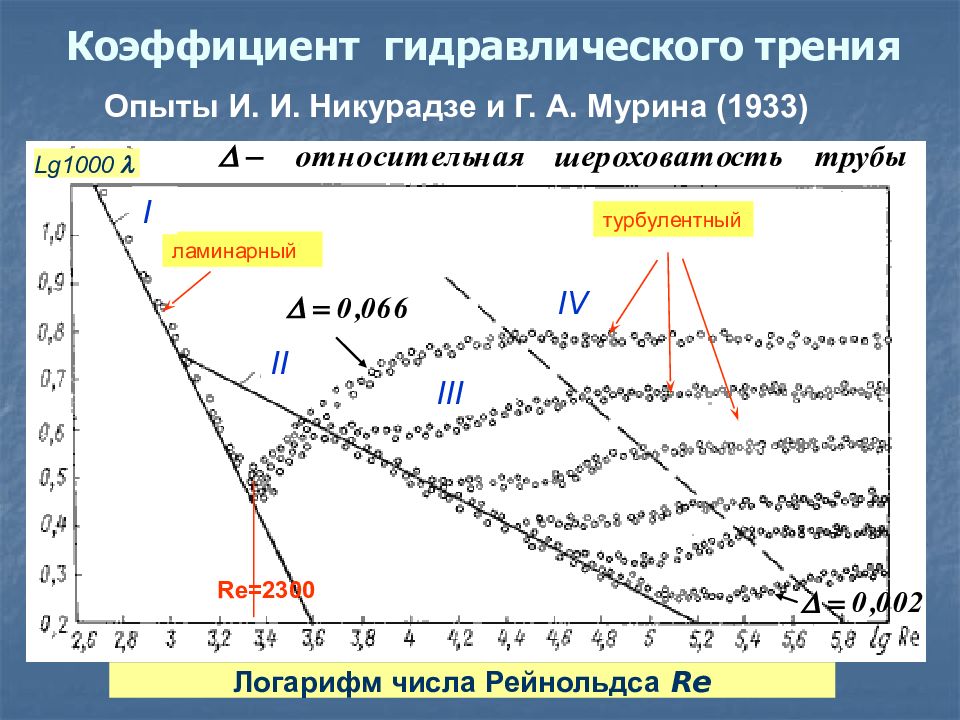
Опыты И. И. Никурадзе и Г. А. Мурина (1933) Логарифм числа Рейнольдса Re Re=2300 L g1000 l ламинарный турбулентный Re=2300 I II III IV
Слайд 41: Участок I - ламинарный режим ( =2)
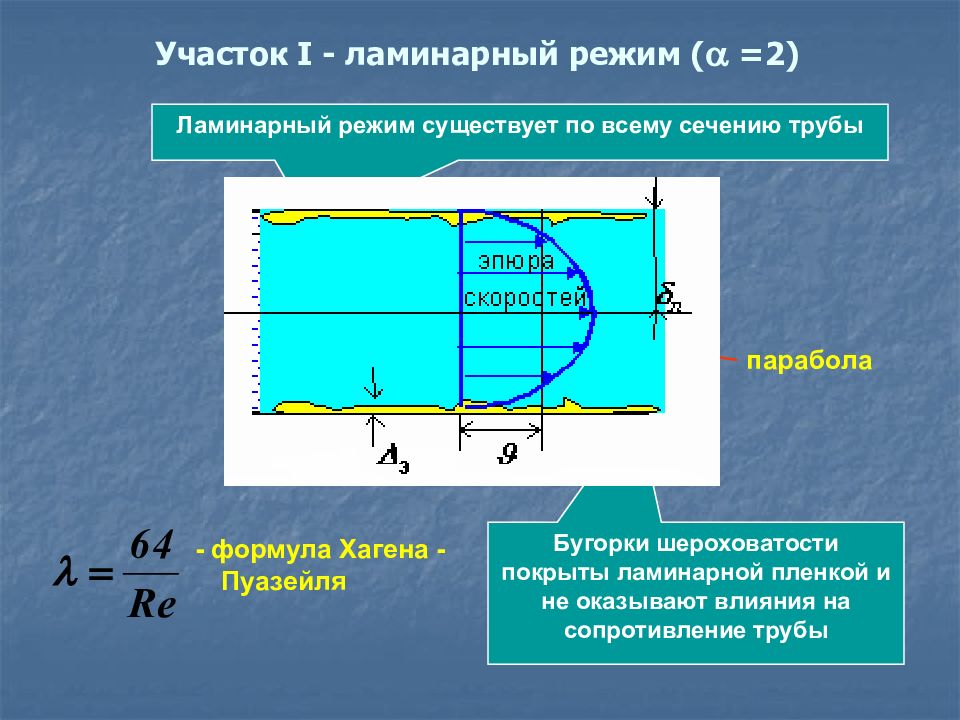
Бугорки шероховатости покрыты ламинарной пленкой и не оказывают влияния на сопротивление трубы Ламинарный режим существует по всему сечению трубы - формула Хагена - Пуазейля парабола V
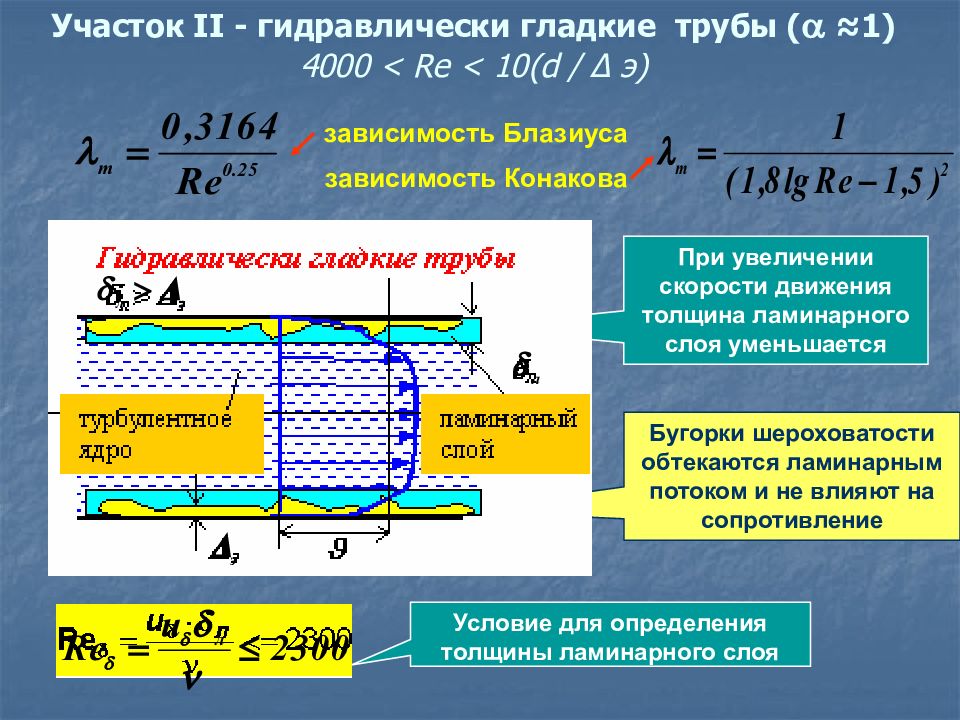
Слайд 42: Участок II - гидравлически гладкие трубы ( ≈ 1) 4000 < Re < 10(d / Δ э)
При увеличении скорости движения толщина ламинарного слоя уменьшается Бугорки шероховатости обтекаются ламинарным потоком и не влияют на сопротивление зависимость Блазиуса зависимость Конакова Гидравлически гладкие трубы V Условие для определения толщины ламинарного слоя
Слайд 43: Участок III - гидравлически шероховатые трубы
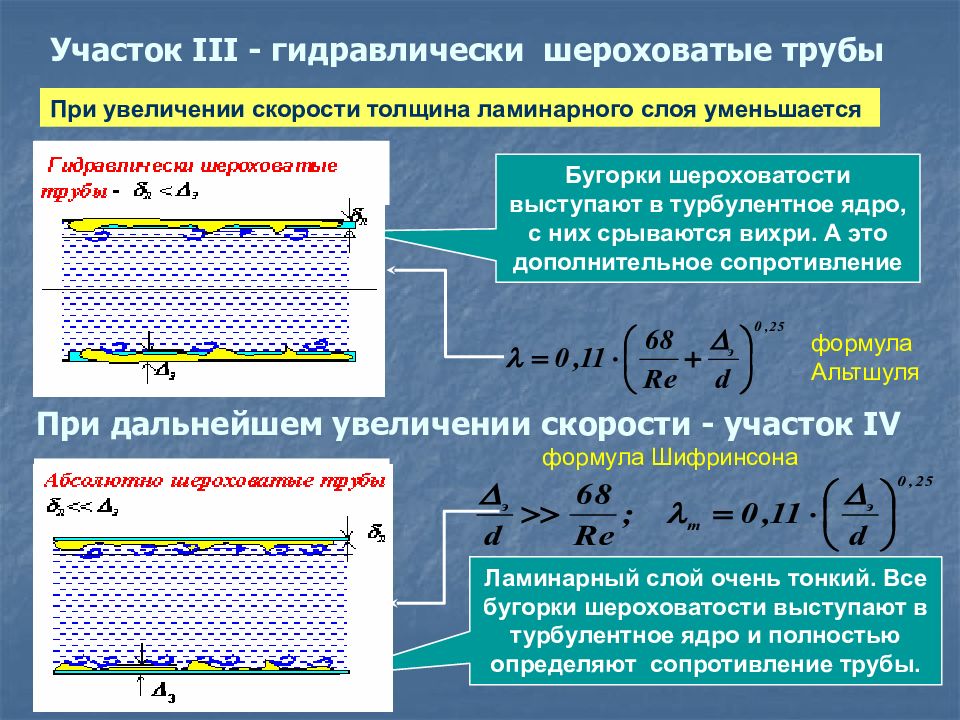
Бугорки шероховатости выступают в турбулентное ядро, с них срываются вихри. А это дополнительное сопротивление Ламинарный слой очень тонкий. Все бугорки шероховатости выступают в турбулентное ядро и полностью определяют сопротивление трубы. При увеличении скорости толщина ламинарного слоя уменьшается Абсолютно шероховатые трубы δ л << Δ э формула Альтшуля формула Шифринсона Гидравлически шероховатые трубы δ л < Δ э При дальнейшем увеличении скорости - участок IV
Слайд 44: Характерные значения эквивалентной шероховатости Δ э для труб из различных материалов (в мм)
Стекло 0 Трубы, тянутые из латуни, свинца, меди 0…0,002 Высококачественные бесшовные стальные трубы 0,06…0,2 Стальные трубы 0,1…0,5 Чугунные асфальтированные трубы 0,1…0,2 Чугунные трубы 0,2…1,0 Эквивалентной шероховатостью Δ э называется такая равномерная зернистая шероховатость («шероховатость Никурадзе»), которая дает одинаковую с естественной шероховатостью данной трубы величину λ. Для определения Δ э не нужно производить каких-либо обмеров шероховатости - ее определяют путем гидравлических испытаний.
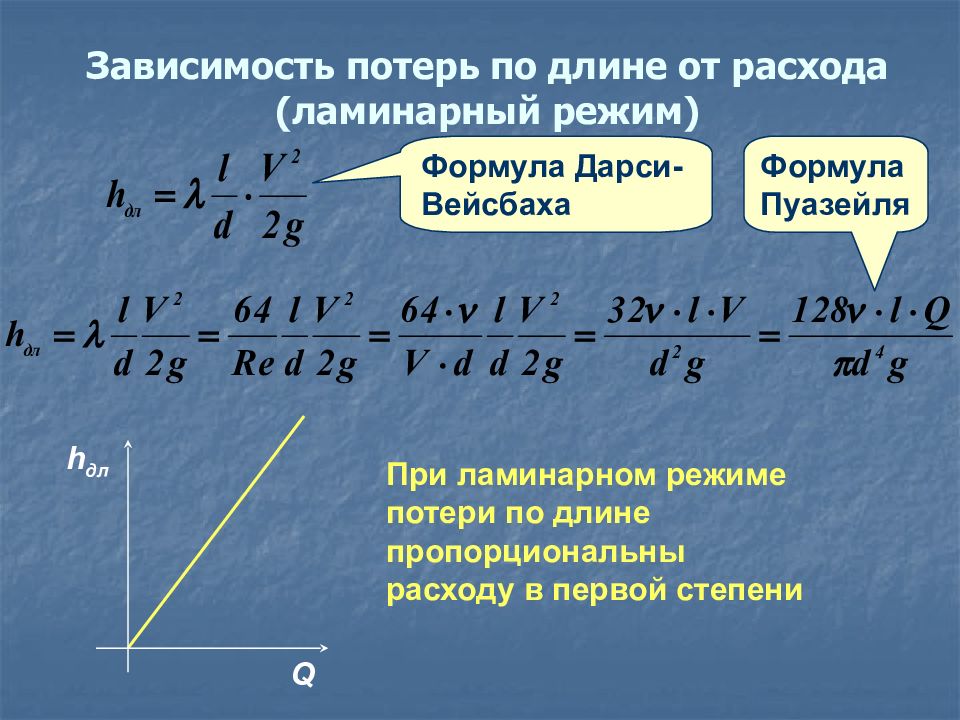
Слайд 45: Зависимость потерь по длине от расхода (ламинарный режим)
Формула Дарси-Вейсбаха Зависимость потерь по длине от расхода (ламинарный режим) Формула Пуазейля h дл Q При ламинарном режиме потери по длине пропорциональны расходу в первой степени
Слайд 46: Зависимость потерь по длине от расхода (турбулентный режим)
Формула Дарси-Вейсбаха Зависимость потерь по длине от расхода (турбулентный режим) h дл Q При турбулентном режиме потери по длине пропорциональны Q 1.75 (зона III – зона доквадратичного сопротивления) и Q 2 (зона IV – зона квадратичного сопротивления) Гидравлически гладкие трубы Абсолютно шероховатые трубы Q 0
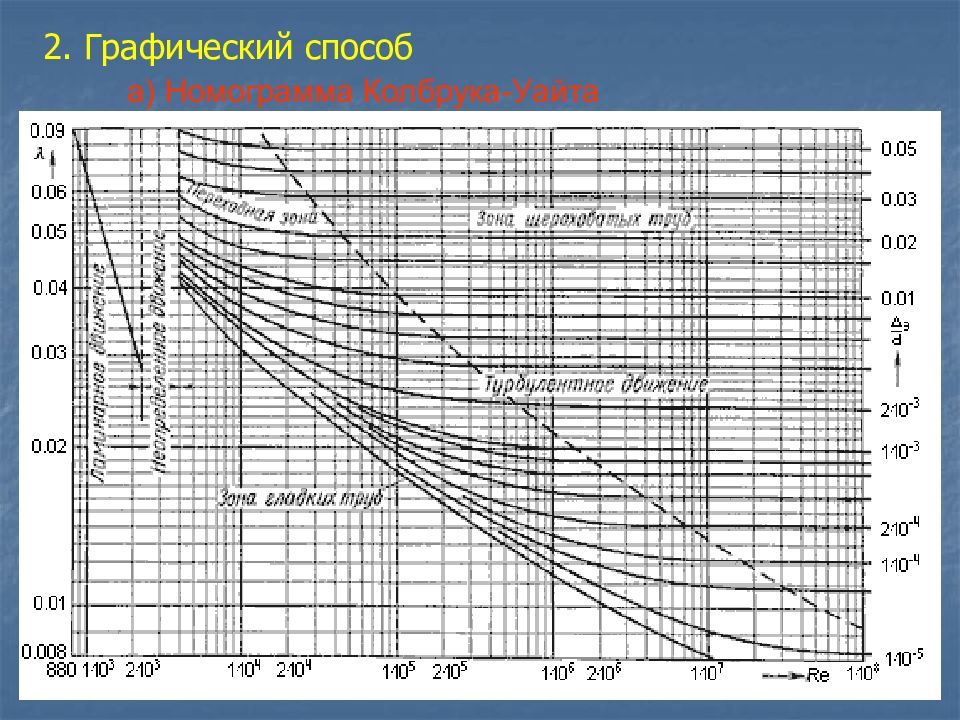
Слайд 49
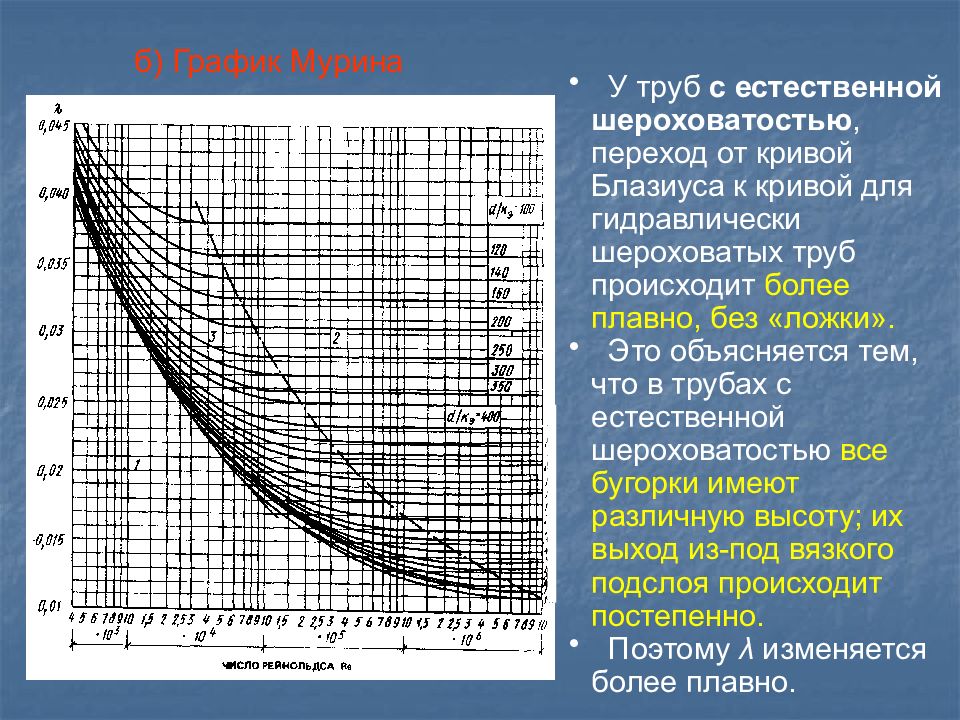
б) График Мурина У труб с естественной шероховатостью, переход от кривой Блазиуса к кривой для гидравлически шероховатых труб происходит более плавно, без «ложки». Это объясняется тем, что в трубах с естественной шероховатостью все бугорки имеют различную высоту; их выход из-под вязкого подслоя происходит постепенно. Поэтому λ изменяется более плавно.
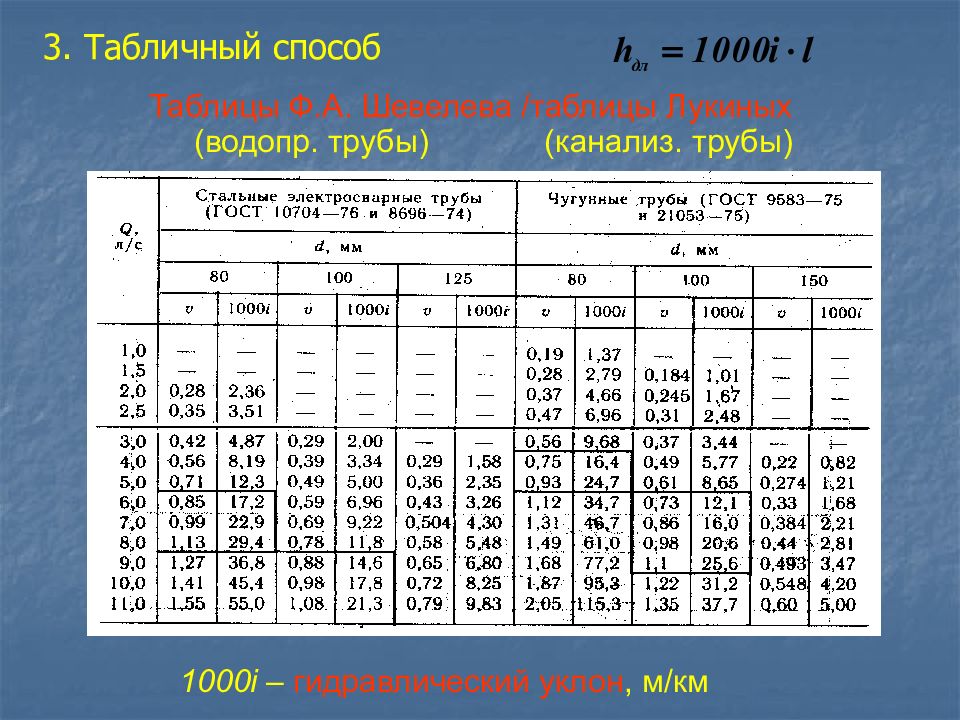
Слайд 50
3. Табличный способ Таблицы Ф.А. Шевелева /таблицы Лукиных (водопр. трубы) (канализ. трубы) 1000 i – гидравлический уклон, м/км