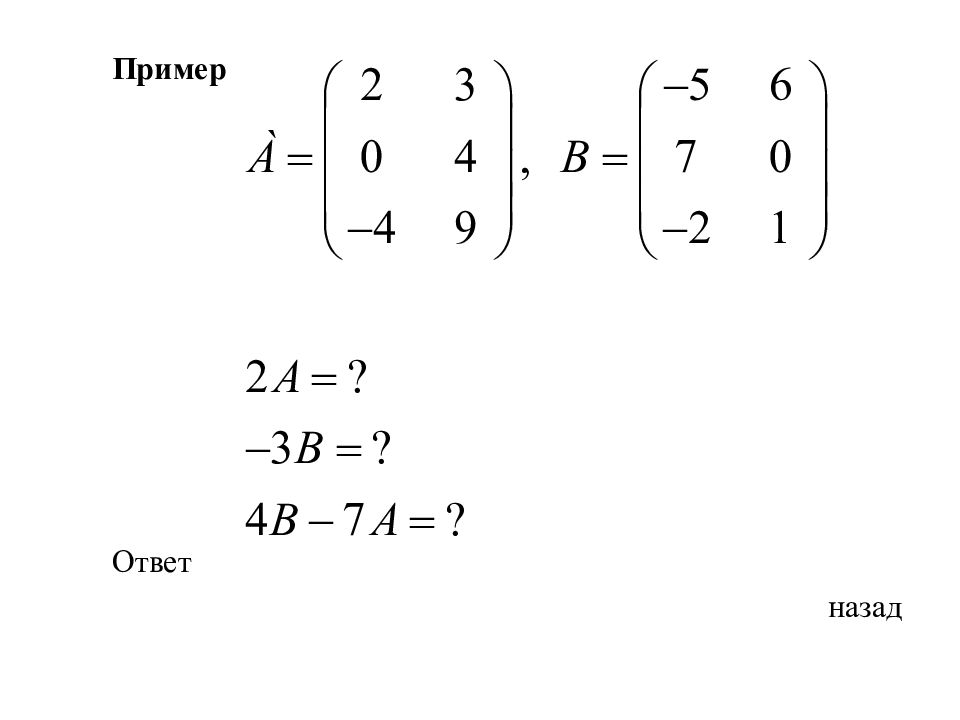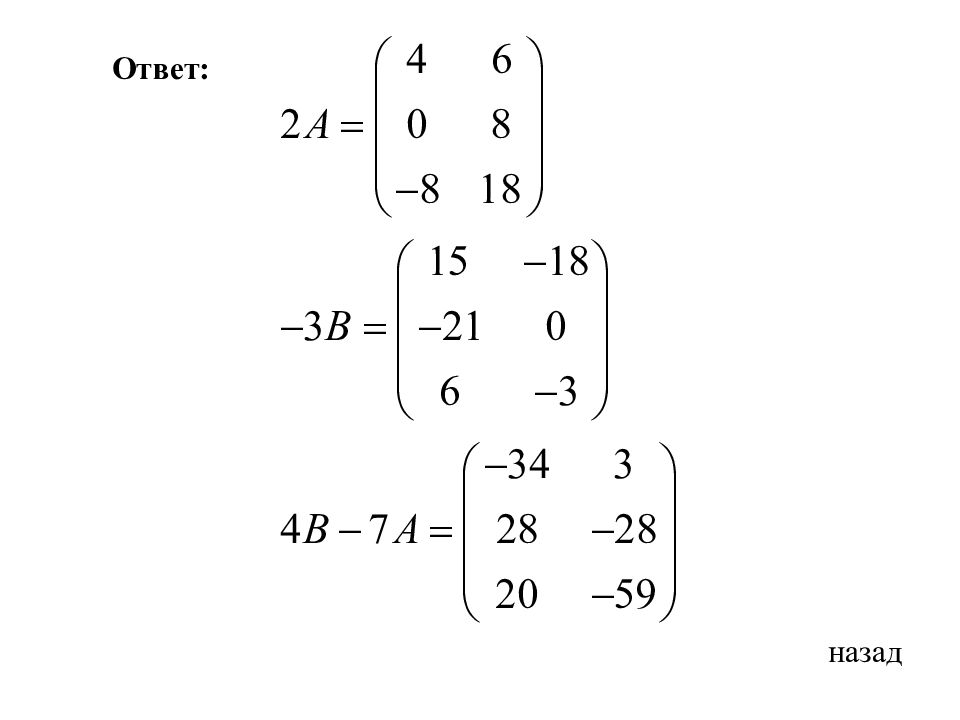Тема 1. «Матрицы и действия над ними» Основные понятия: Определение матрицы Виды матриц Действия над матрицами Перестановочные матрицы завершить
1. Определение матрицы Прямоугольная таблица чисел вида называется матрицей. - элементы матрицы. Размер матрицы Главная диагональ матрицы Побочная диагональ матрицы назад
2. Виды матриц Прямоугольная Квадратная Нулевая Единичная Диагональная Симметричная Вырожденная Равные Треугольная Квазитреугольная (ступенчатая или трапециевидная) Матрица-строка или строчная матрица Матрица-столбец или столбцевая матриц назад
Матрица называется прямоугольн ой, если количество ее строк не совпадает с количеством столбцов : Матрица называется квадратной, если количество ее строк совпадает с количеством столбцов : назад
Матрица называется нулевой, если все ее элементы нулевые : Квадратная матрица называется единичной, если элементы по главной диагонали единицы, а остальные элементы нулевые : назад
Квадратная матрица называется диагональной, если элементы по главной диагонали отличны от нуля, а остальные элементы нулевые : Квадратная матрица называется симметричной, если относительно главной диагонали для всех ее элементов выполняется условие : назад
Квадратная матрица называется вырожденной, если ее определитель равен нулю. Матрицы А и В (одинаковых размерностей) называются равными, если : назад
Квадратные матрицы вида или называются треугольными. назад
Прямоугольная матрица вида называется квазитреугольной (ступенчатая или трапециевидная) назад
Матрица, состоящая из одной строки называется матрицей-строкой или строчной матрицей. Матрица, состоящая из одного столбца называется матрицей-столбцом или столбцевой матрицей назад
назад
Суммой (разностью) двух матриц одинаковой размерности называется матрица, элементы которой равны сумме (разности) соответствующих элементов матриц слагаемых. Например : Пример назад
Пример Ответ назад
Произведением матрицы на число называется матрица, полученная из данной умножением всех ее элементов на число. Например : Пример назад
Линейные операции обладают следующими свойствами :
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, т ранспонированной относительно данной. Например : Свойства назад
Умножение матриц определяется для согласованных матриц. Произведением матрицы на матрицу называется матрица, для которой, т.е. каждый элемент матрицы С равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В. Например Свойства назад
Например : Пример назад
В случае, когда АВ=ВА, матрицы А и В называют перестановочными или коммутативными. Пример 1. Найти все перестановочные матрицы к матрице Пример 2. Найти все перестановочные матрицы к матрице назад
Ответ: назад
Пример Ответ назад
Ответ: назад
Свойства операции транспонирования : назад
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В: Например: назад
Пример Ответ назад
Ответ: назад
Свойства операции умножение матриц: 1. Свойство сочетательности или ассоциативности 2. Свойство распределительности (дистрибутивности) справа и слева относительно сложения матриц назад
Решение (Пример 1) : 1) общий вид всех перестановочных матриц 2) Применим определение перестановочных матриц AB=BA :
Получаем: 3) По определению равных матриц 4) Общий вид всех перестановочных матриц 5) Проверка назад
Ответ: или или назад
Спасибо за внимание! (Тема следующей лекции «Определители»)
