Матрицы. Основные понятия. Действия над матрицами Элементарные преобразования матриц Определитель матрицы. Определители второго порядка Определители третьего порядка Разложение определителя Свойства определителей Обратная матрица 1
Матрицей называется прямоугольная таблица, составленная из каких – либо элементов и имеющая m строк и n столбцов. Элементами матрицы могут быть числа, алгебраические выражения, функции и т.д. Матрицы обозначаются заглавными буквами латинского алфавита, элементы матрицы – теми же маленькими буквами. Размерность матрицы обозначается: количество строк количество столбцов 2
Если, то матрица называется прямоугольн ой. Любое число (скаляр) можно представить как матрицу первого порядка, размерностью. Если, то матрица называется квадратной ( n - ного порядка). Матрица типа называется матриц а -строк а: Матрица типа называется матрица-столбец : 3
Квадратная матриц а называется единичной, если ее элементы, расположенные на главной диагонали, равны единице, остальные – нулю (обозначается буквой Е ): Если все элементы квадратной матрицы равны нулю, то она называется нуль-матрицей и обозначается символом 0. 4
Равенство матриц Сложение (вычитание) матриц Сумма и разность матриц существуют только для матриц одинакового размера, при этом соответствующие элементы матриц складываются или вычитаются. Матрицы равны, если они имеют одинаковую размерность и их соответствующие элементы равны. 5
Умножение матрицы на число Найти значение выражения: При умножении матрицы A на число k получается матрица того же размера, при этом каждый элемент матрицы A умножается на k. 6
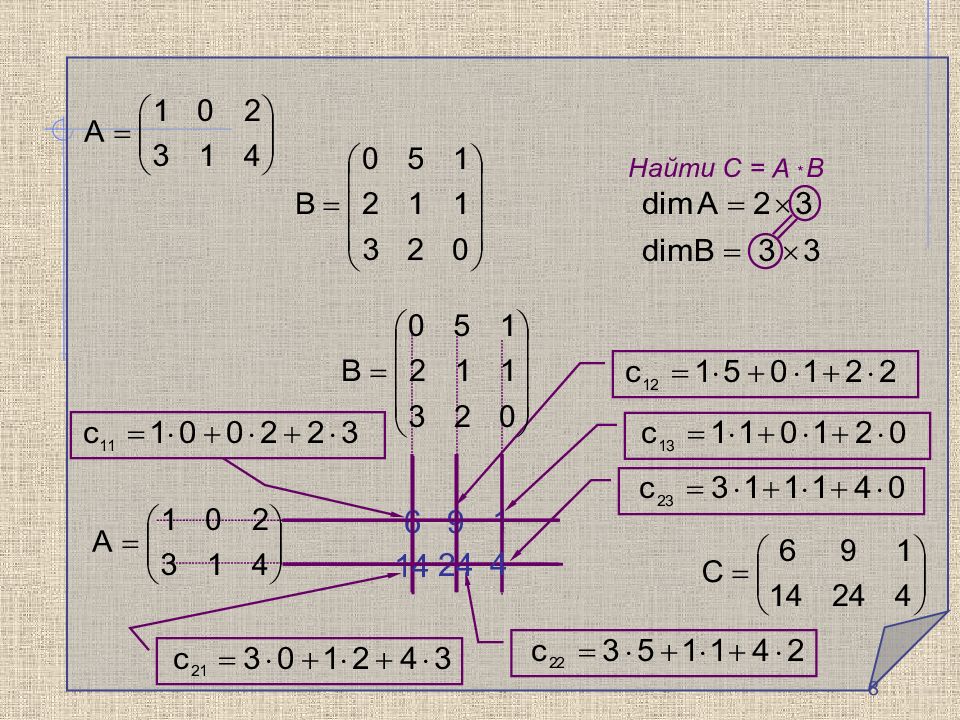
Умножение матриц Произведение матриц A * B определено только тогда, когда число столбцов матрицы А равно числу строк матрицы В, в противном случае произведение не существует. Произведением матрицы A размера с элементами a ij на матрицу B размера с элементами b jq называется матрица C р азмера с элементами: 7
Найти С = A * B 6 9 1 14 24 4 8
Свойства операции произведения матриц : 1) 2) 3) 4) В общем случае для произведения матриц не действует переместительный закон: иногда АВ существует, а ВА не имеет смысла. В случае, когда АВ = ВА, матрицы А и В называются коммутативными. 5) Единичная матрица является коммутативной для любой квадратной матрицы того же порядка : 6) Для двух квадратных матриц А и В одного порядка произведение определителей равно определителю произведения. 9
10 Транспонирование матрицы Под этой операцией понимают переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.
11 Отбрасывание нулевой строки (столбца) Умножение всех элементов строки (столбца) на число, не равное нулю Изменение порядка строк (столбцов) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число Транспонирование Две матрицы называются эквивалентными, если одна получается из другой с помощью конечного числа элементарных преобразований.
12 Матрица А называется ступенчатой, если она имеет следующий вид: С помощью элементарных преобразований любую матрицу можно привести к ступенчатому виду
Для каждой квадратной матрицы n - ного порядка существует определитель n - ного порядка, элементы которого равны соответствующим элементам матрицы. Определитель любой единичной матрицы равен единице. Если определитель матрицы равен нулю, то матрица называется вырожденной, в противном случае матрица невырожденная. 13 Определитель матрицы.
Определителем n – ого порядка называется число: 14
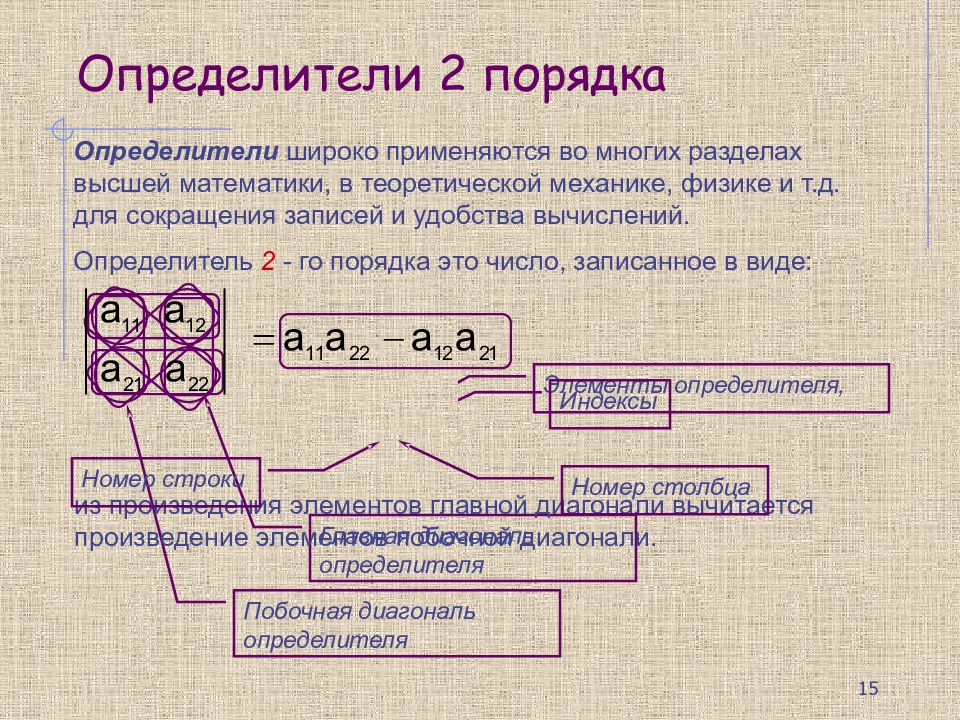
Определители широко применяются в о многих разделах высшей математики, в теоретической механике, физике и т.д. для сокращения записей и удобства вычислений. Определитель 2 - го порядка это число, записанное в виде: a i j Элементы определителя, Главная диагональ определителя Побочная диагональ определителя Индексы из произведения элементов главной диагонали вычитается произведение элементов побочной диагонали. Номер строки Номер столбца 15
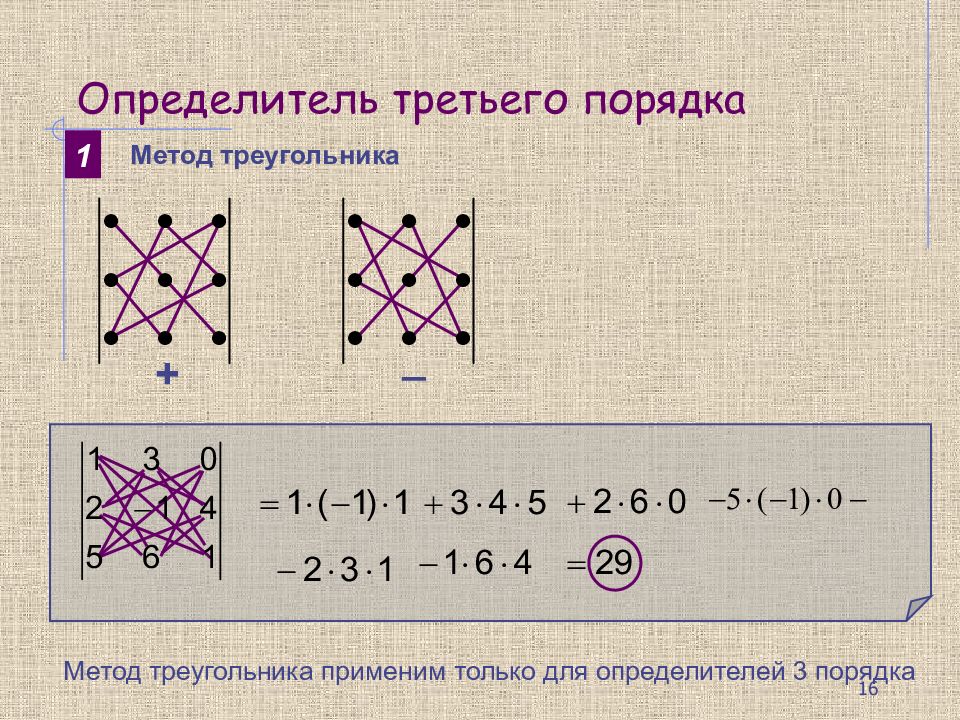
1 Метод треугольника + _ Метод треугольника применим только для определителей 3 порядка 16
2 Метод Саррюса Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии: Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс». Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус : 17
Минором M ij элемента определителя a ij называется определитель, полученный после вычеркивания из исходного строки и столбца, на пересечении которых стоит этот элемент. Алгебраическое дополнение A ij элемента – это минор этого элемента, взятый со знаком (+), если сумма номеров строки и столбца, на которых находится элемент – четная, и со знаком (-), если эта сумма – нечетная. 18
Величина определителя равна сумме произведений элементов какой – либо строки (столбца) определителя на их алгебраические дополнения: Разложение определителя по элементам i – ой строки Разложение определителя по элементам j – ого столбца 19
Свойства определителя : Величина определителя равна нулю, если элементы какого - либо столбца или строки равны нулю : Величина определителя равна нулю, если соответствующие элементы двух строк (столбцов) равны 20
Определитель меняет знак, если поменять местами строки (столбцы) : Определитель увеличивается в k раз, если элементы какого - либо столбца (строки) увеличить в k раз : Определитель не меняется при замене строк соответствующими столбцами: 21
Определитель не меняется, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель Если определитель имеет так называемый треугольный вид, то он вычисляется как произведение чисел, стоящих на главной диагонали: 22
Выберем 1 столбец и превратим второй и третий элементы в нули К элементам 2 строки прибавим элементы 1 строки, умноженные на (-2) К элементам 3 строки прибавим элементы 1 строки Разложим определитель по элементам 1 столбца Также, используя свойства, можно привести определитель к треугольному виду и вычислить по последнему свойству. Пример вычисления определителя при помощи свойств 23
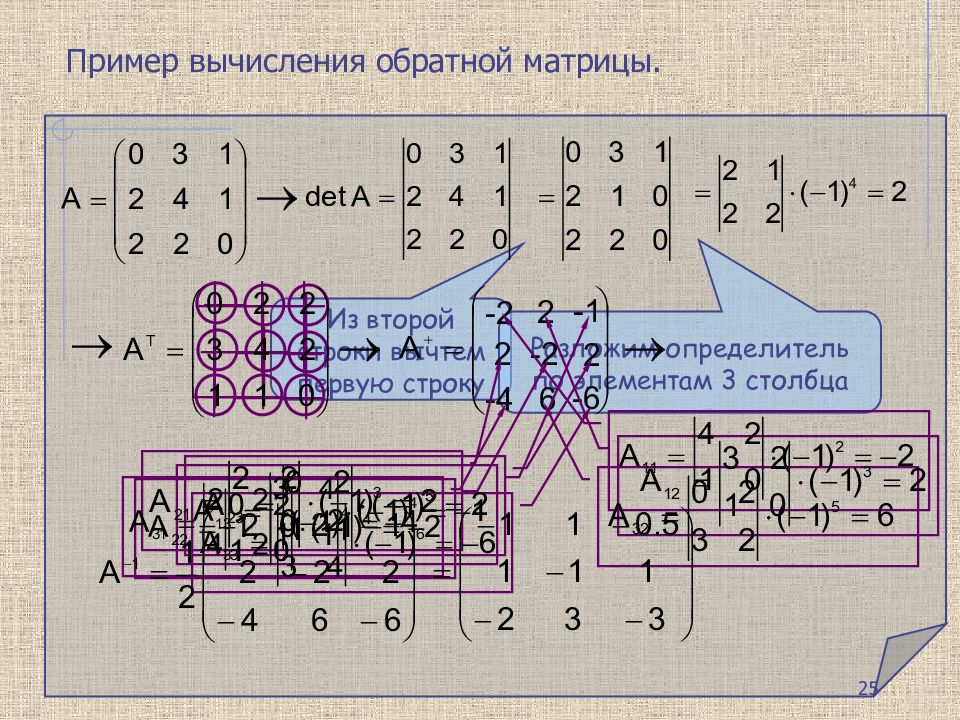
О братная матрица обозначается символом А -1. Таким образом, согласно определению : АА -1 =А -1 А=Е. Обратной матрицей по отношению к данной невырожденной квадратной матрице A n - ного порядка, называется матрица, которая, будучи умноженной как слева, так и справа на данную матрицу, дает единичную матрицу. Если определитель матрицы равен нулю, то обратная матрица не существует Транспонированная матрица получается из матрицы А путем замены строк соответствующими столбцами Присоединенная матрица получается путем замены каждого элемента матрицы А т на его алгебраическое дополнение 24 Обратная матрица
Из второй строки вычтем первую строку Разложим определитель по элементам 3 столбца -2 2 -1 2 -2 2 -4 6 -6 25 Пример вычисления обратной матрицы.
