Первый слайд презентации: Теоретико-игровые модели Принятия решений в конфликтных ситуациях
Игрой называется упрощённая формализованная модель конфликтной ситуации, а конфликтующие стороны называются игроками. 1 Однократный розыгрыш игры от начала до конца называется партией. Партия состоит из ходов, а под ходом понимается выбор из множества возможных альтернатив. Результатом партии являются платежи (выигрыши, проигрыши игроков). Ситуация называется конфликтной, если в ней сталкиваются интересы двух или более сторон, преследующих различные, в частном случае противоположные, цели. личные случайные Игра, включающая личные ходы, называется стратегической. Игра, состоящая из одних случайных ходов, называется азартной и такие игры в теории игр ( ТИ ) не рассматриваются.
2 Исход каждой партии оценивается платежом, определяющим выигрыш (проигрыш) каждого игрока. Игра n - лиц может быть описана следующим образом G = { A 1, …, A n, H ( A 1, …, A n )}, где A i – стратегия i игрока, H – платёж по игре. Основная задача теории игр ( ТИ ) : нахождение оптимальных стратегий игроков в стратегических играх.
Вершины дерева – это ситуации или состояния, которые возможны в процессе игры. Корень дерева – начальная ситуация (начало игры). Концевые вершины – это конечные состояния игры, взвешенные платежами. Дуги – возможные переходы из состояния под действием определённой стратегии. В класс информации объединяются все те вершины ДИ, в которых игроку, делающему личный ход, доступна одна и та же информация. Если в ДИ все классы информации содержат по одной вершине, то это игра с полной информацией, а в противном случае это игра с неполной информацией. Игровая модель для двух лиц (парная антагонистическая игра) с нулевой суммой Игрок A обладает множеством стратегий A 1,…, A n 4 Игрок B обладает множеством стратегий B 1,…, B m
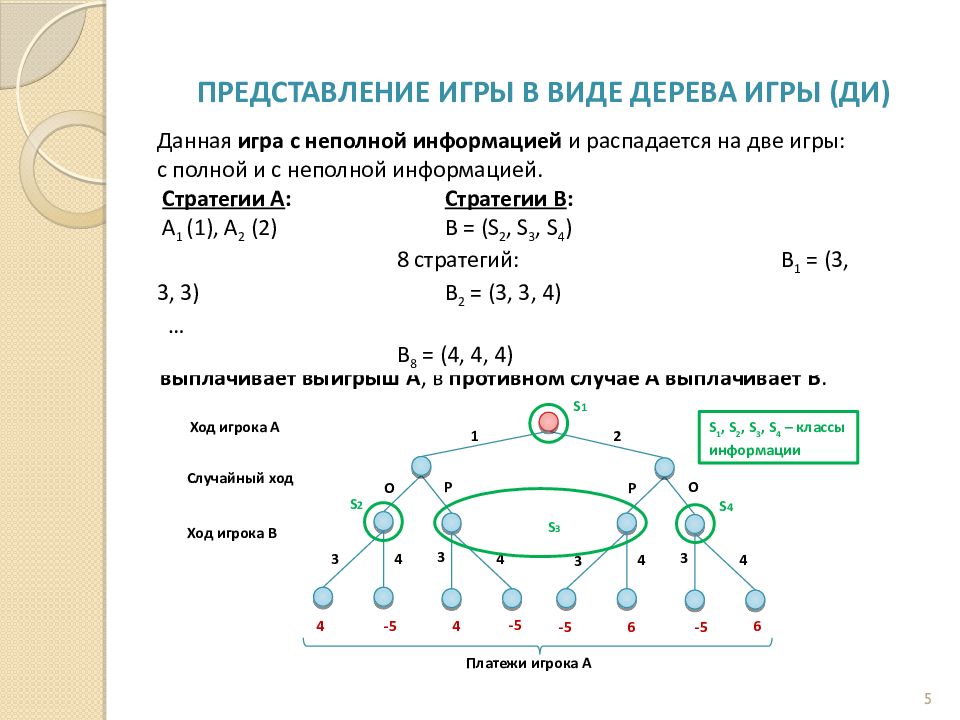
Слайд 5: Представление игры в виде дерева ИГРЫ ( ДИ )
Пример: Два игрока A и B. 1 ход (личный): А выбирает цифру 1 или 2. 2 ход (случайный): Если орел (О), то А сообщает о своём выборе В. Если решка ( Р ), А не сообщает о своём выборе В. 3 ход (личный): В выбирает цифру 3 или 4. Итог: Суммируются выборы игроков А и В, и если сумма чётная, то В выплачивает выигрыш А, в противном случае А выплачивает В. 5 -5 4 4 Ход игрока А Ход игрока B 1 2 3 4 Платежи игрока А Случайный ход 3 4 - 5 6 -5 -5 3 4 3 4 6 О Р Р О S 1 S 3 S 2 S 4 S 1, S 2, S 3, S 4 – классы информации Данная игра с неполной информацией и распадается на две игры: с полной и с неполной информацией. Стратегии А : Стратегии В : A 1 (1), A 2 (2) B = ( S 2, S 3, S 4 ) 8 стратегий : B 1 = (3, 3, 3) B 2 = (3, 3, 4) … B 8 = (4, 4, 4)
6 1) Поиск путём полного перебора: поиск “в глубину”; поиск “в ширину”; комбинированные методы поиска. 2) Сокращённый перебор: точная оценка с получением оптимального решения; эвристическая оценка без гарантии получения оптимального решения. Опр. 1: Алгоритм поиска решения называется допустимым, если он гарантирует нахождение оптимального решения. Опр. 2: Допустимый алгоритм называется оптимальным, если при поиске решения оценивается минимальное число вершин ДИ. Оценка алгоритма – это оценка временных ресурсов, требуемых для оценки вершин ДИ.
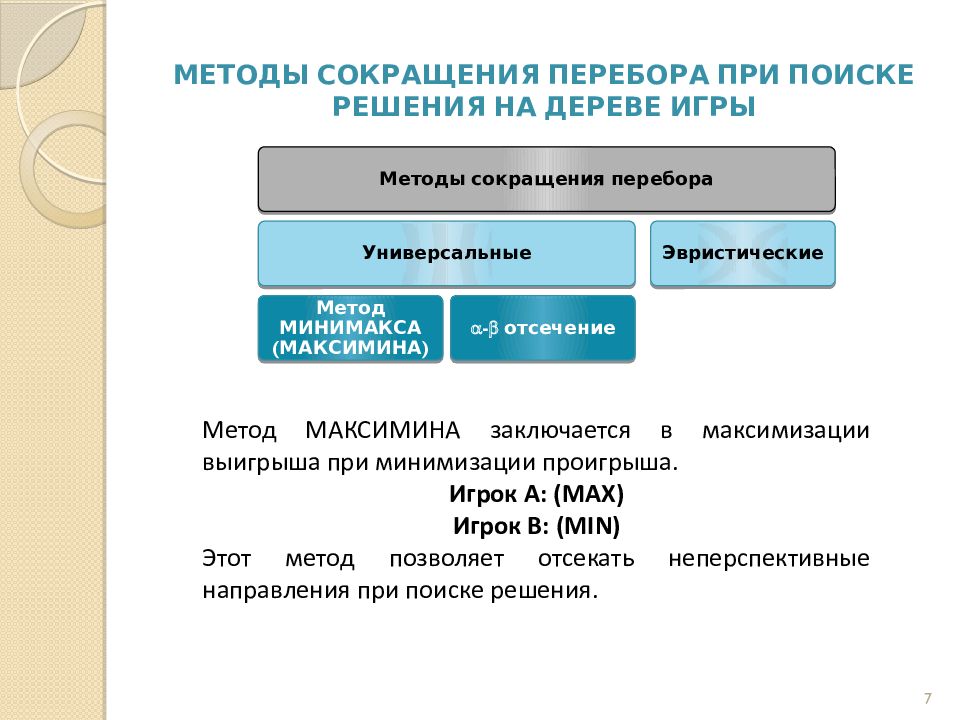
Слайд 7: Методы сокращения перебора при поиске решения на дереве игры
7 Методы сокращения перебора Универсальные - отсечение Эвристические Метод МИНИМАКСА (МАКСИМИНА) Метод МАКСИМИНА заключается в максимизации выигрыша при минимизации проигрыша. Игрок А: ( MAX ) Игрок В: ( MIN ) Этот метод позволяет отсекать неперспективные направления при поиске решения.
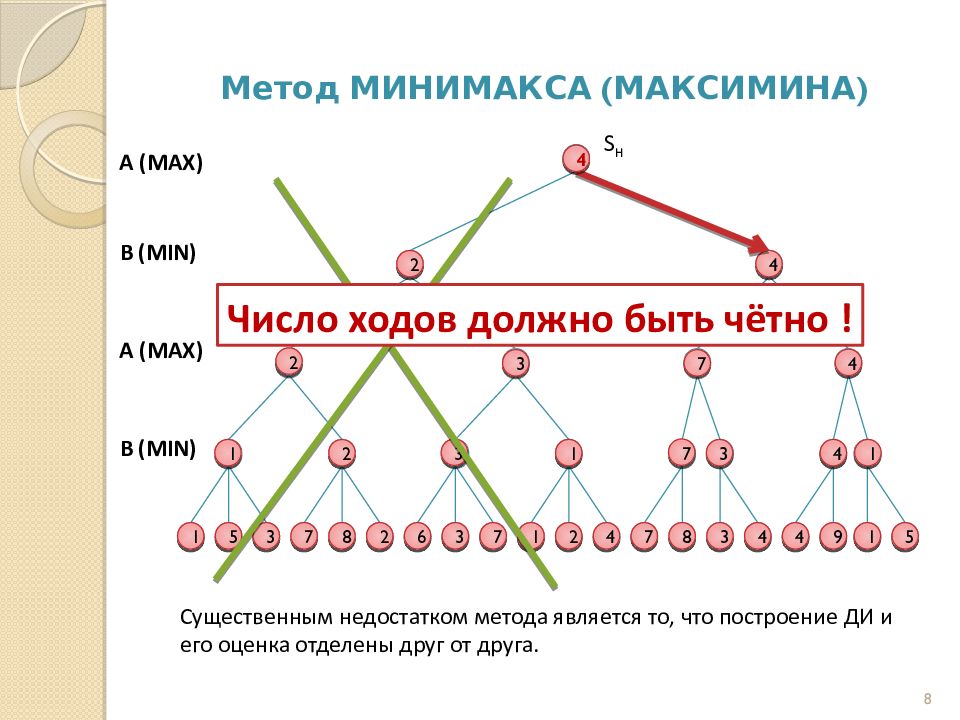
Последний слайд презентации: Теоретико-игровые модели Принятия решений в конфликтных ситуациях: Метод МИНИМАКСА (МАКСИМИНА)
8 S H А ( MAX ) А ( MAX ) B ( MIN ) B ( MIN ) 1 5 3 7 8 2 6 3 7 1 2 4 7 8 3 4 4 9 1 5 1 2 3 1 7 3 4 1 2 3 7 4 2 4 4 Число ходов должно быть чётно ! Существенным недостатком метода является то, что построение ДИ и его оценка отделены друг от друга.