Первый слайд презентации
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ Курс читает: к.т.н., доцент Журавлев Илья Александрович
Слайд 2: План курса
1.Комплексные числа (напоминание). 2.Общие сведения о системах управления. 3. Математические модели. 4. Типовые динамические звенья. 5. Структурные схемы. 6. Анализ систем автоматического управления 2
Слайд 4
Теория автоматического управления (ТАУ) : 1.Принцип управления (как нужно управлять). 2.Математические модели. 3.Устойчивость работы. 4.Качество управления. 4
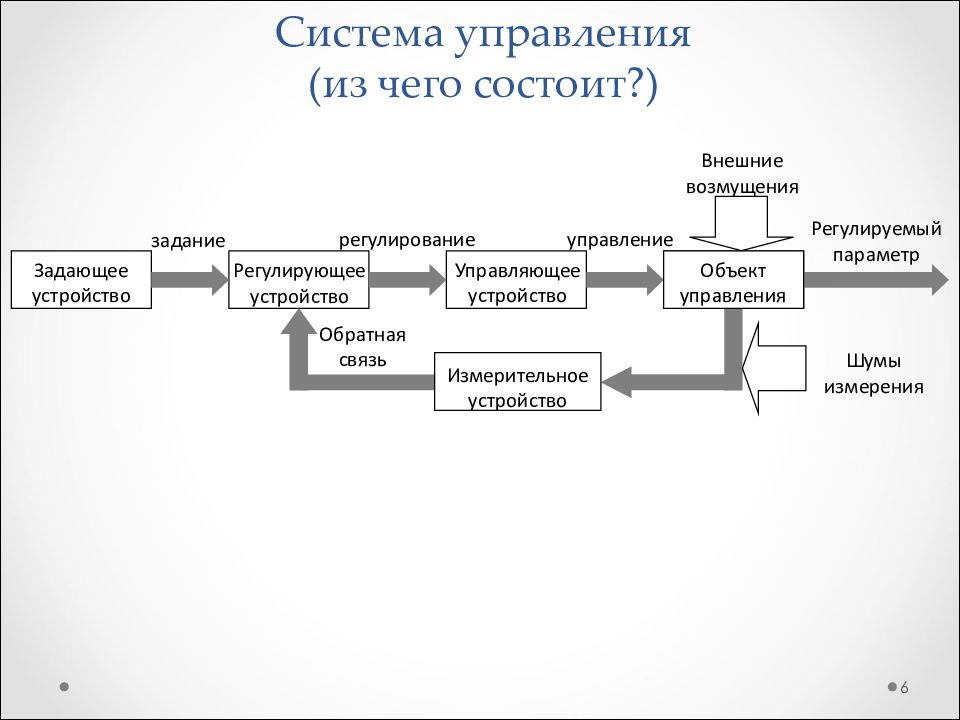
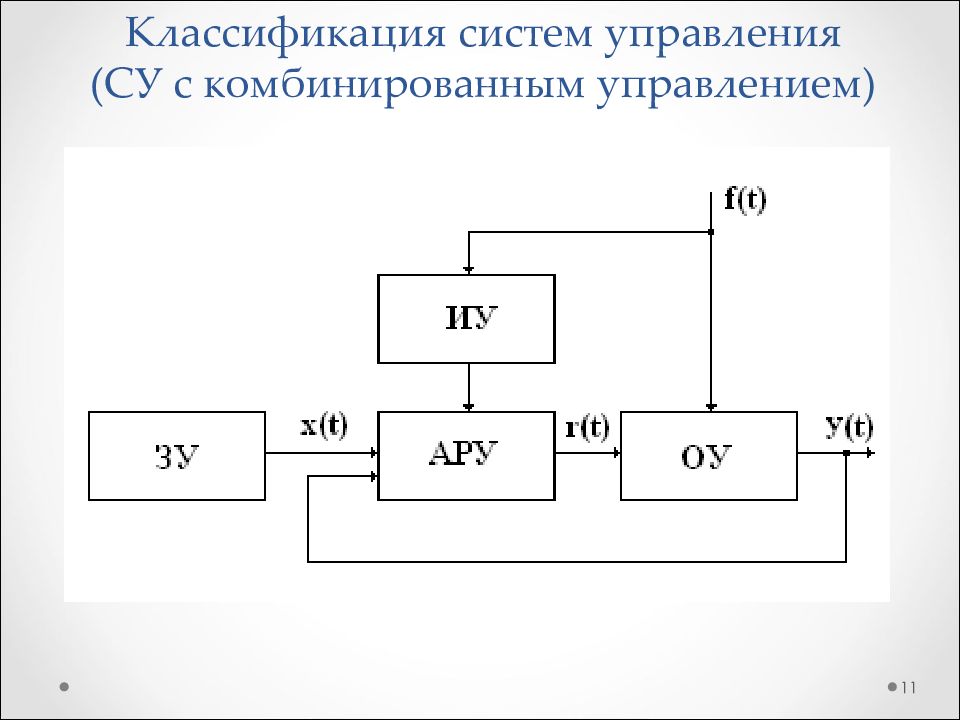
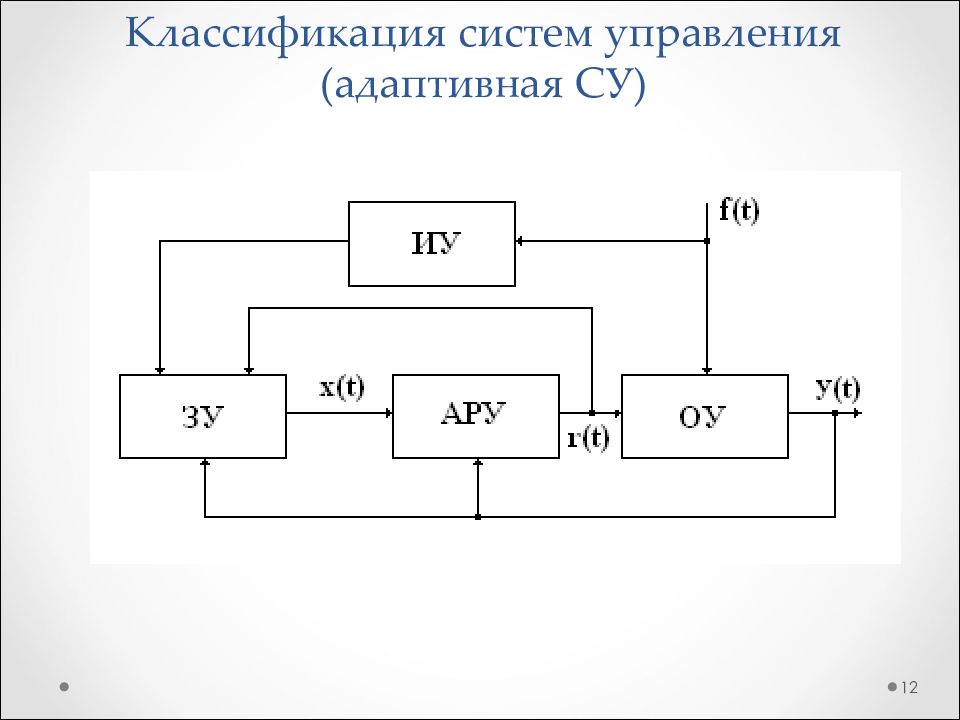
6 Задающее устройство Регулирующее устройство Управляющее устройство Объект управления Измерительное устройство Внешние возмущения регулирование управление задание Шумы измерения Обратная связь Регулируемый параметр
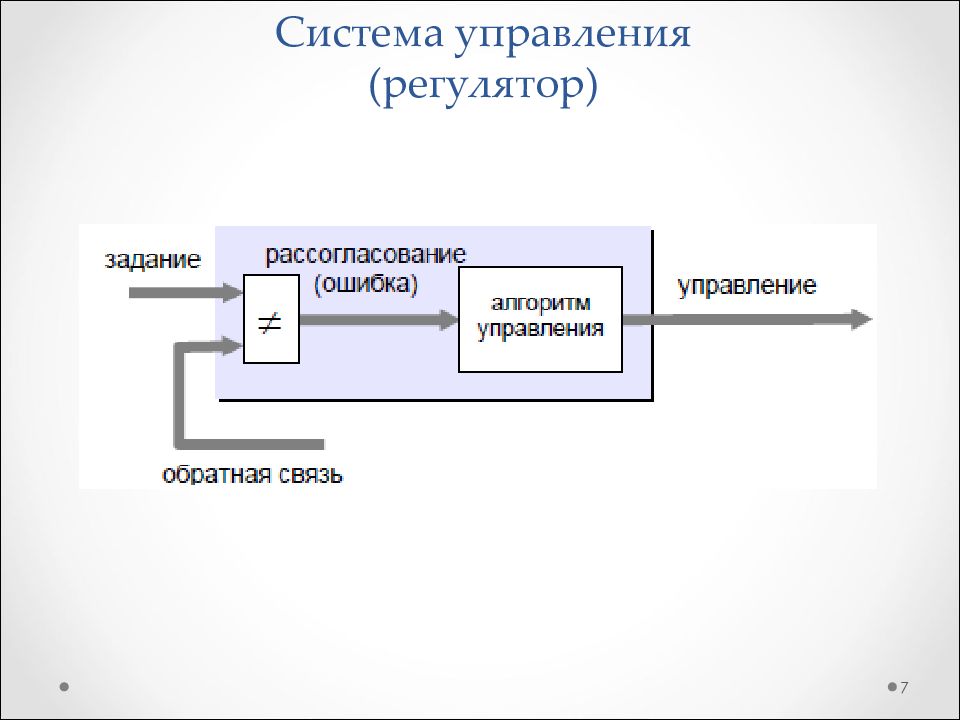
8 Задающее устройство Задающее воздействие Регулирующее устройство Регулирование Управляющее устройство Управление Объект управления Регулируемый параметр Измерительное устройство Сравнивающее устройство
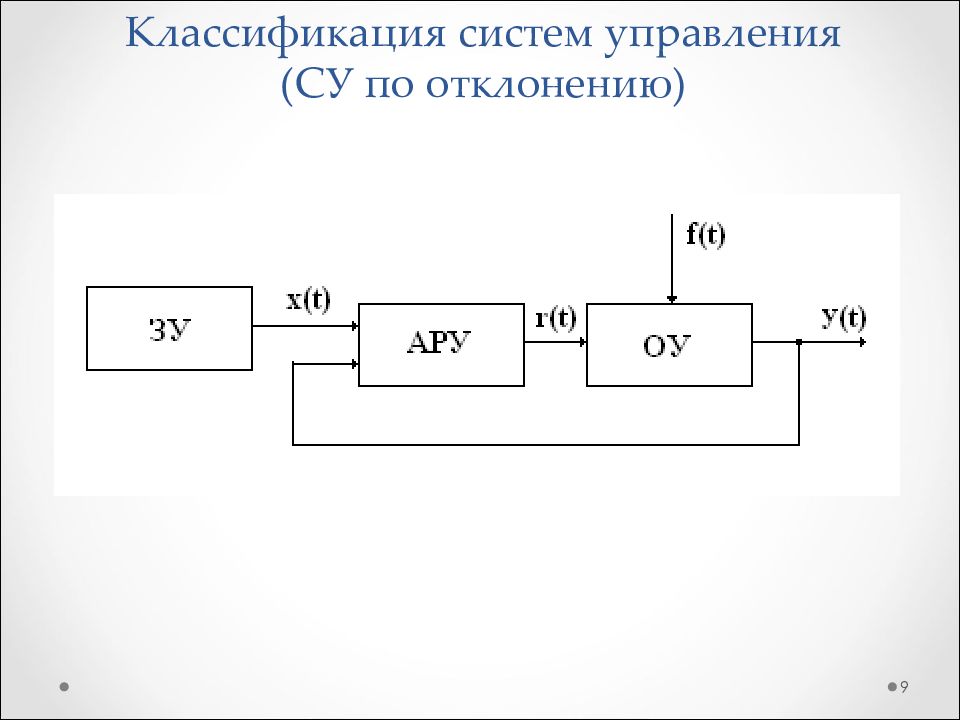
Слайд 13: Классификация систем управления (Уровень автоматизации)
13 Системы управления Автоматические Автоматизированные
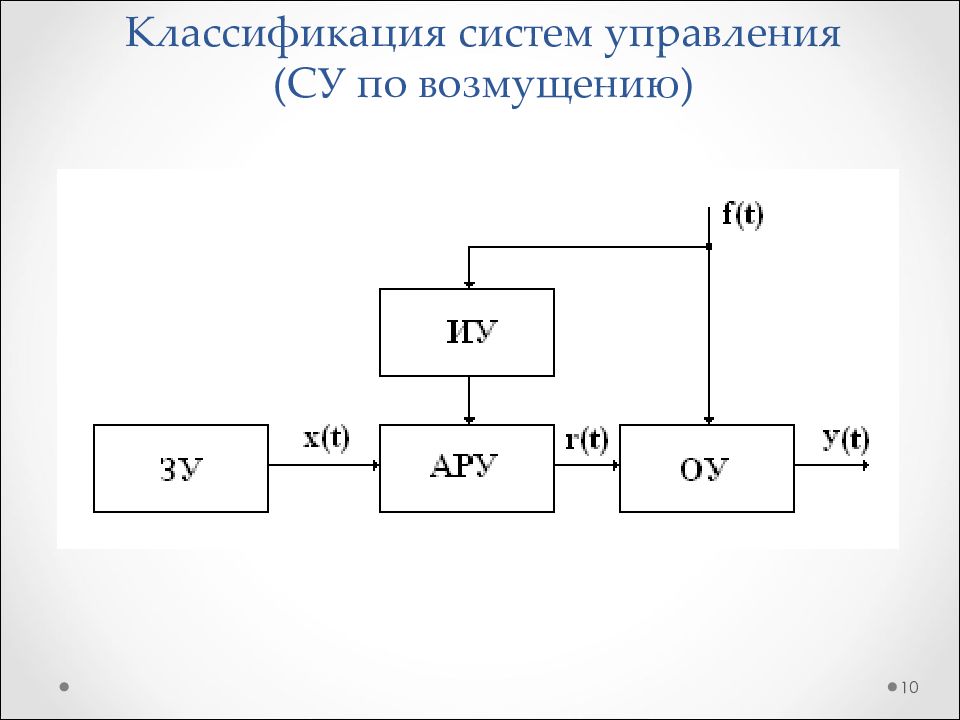
Слайд 14: Классификация систем управления (Задачи систем управления)
14 Системы управления Стабилизация Программное управление Слежение
Слайд 15: Классификация систем управления (По количеству входов и выходов)
15 Системы управления Одномерные Многомерные
Слайд 16: Классификация систем управления (Характер сигналов системы)
16 Системы управления Непрерывные Дискретные Непрерывно-дискретные
Слайд 17: Классификация систем управления (Характер сигналов системы)
17 Системы Автоматического управления (САУ) Автоматического регулирования (САР)
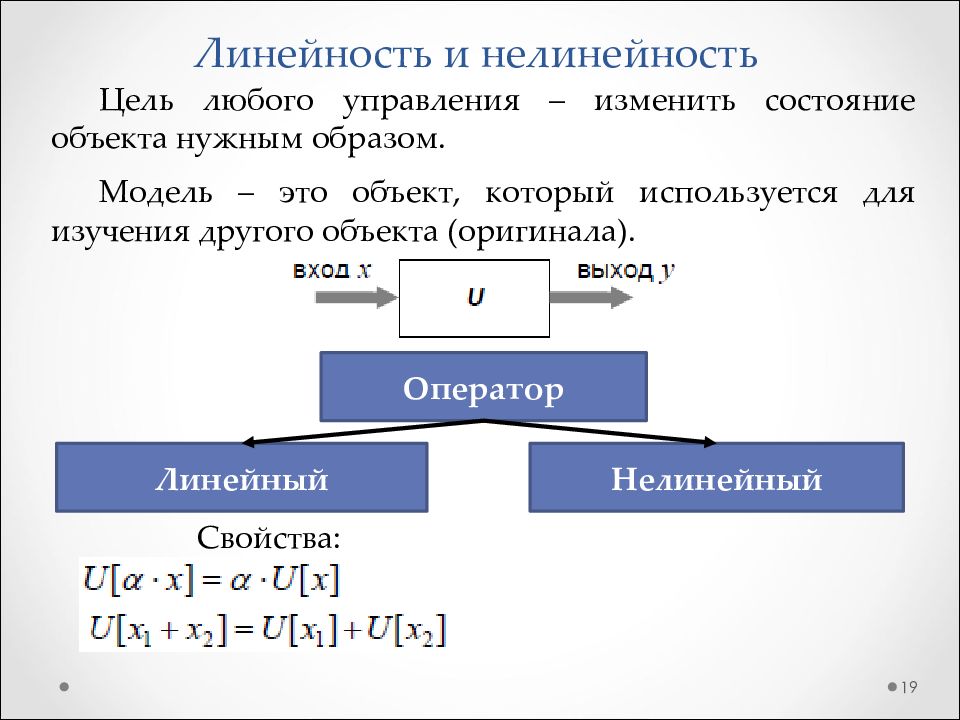
Слайд 19: Линейность и нелинейность
19 Цель любого управления – изменить состояние объекта нужным образом. Модель – это объект, который используется для изучения другого объекта (оригинала). Оператор Линейный Нелинейный Свойства:
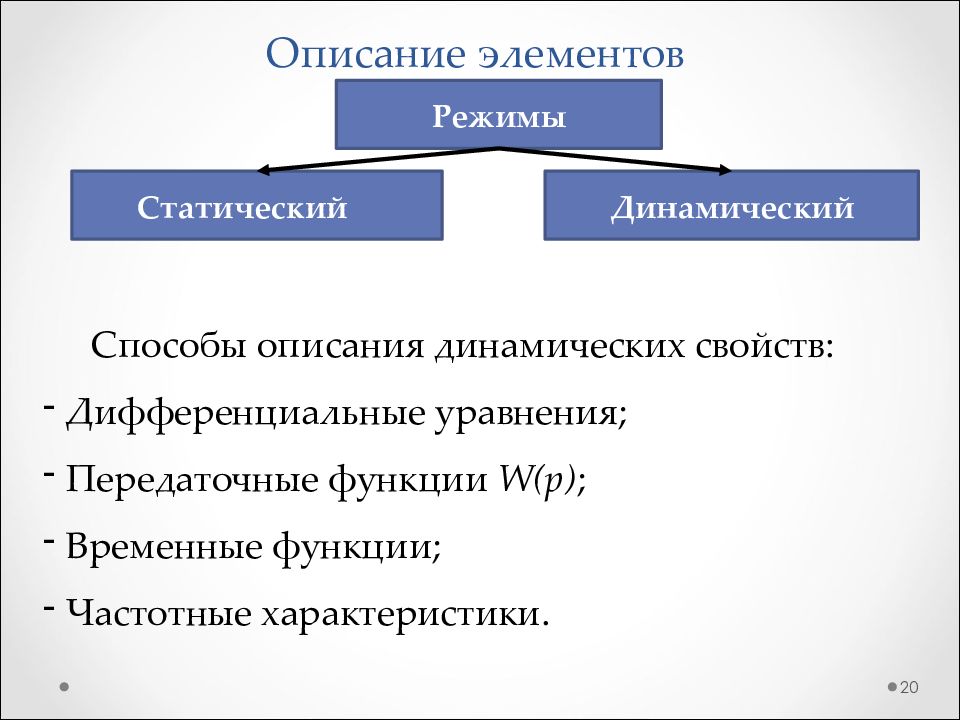
Слайд 20: Описание элементов
20 Способы описания динамических свойств: Дифференциальные уравнения; Передаточные функции W(p) ; Временные функции; Частотные характеристики. Режимы Статический Динамический
Слайд 21: Дифференциальные уравнения
21 Здесь: y(t) – временная функция выходного сигнала; x ( t ) – временная функция входного сигнала; y ( j ) (t) – j- я производная функции y(t) ; x ( j ) (t) – j- я производная функции x(t) ; a m, b m – постоянные коэффициенты уравнения при соответствующих переменных.
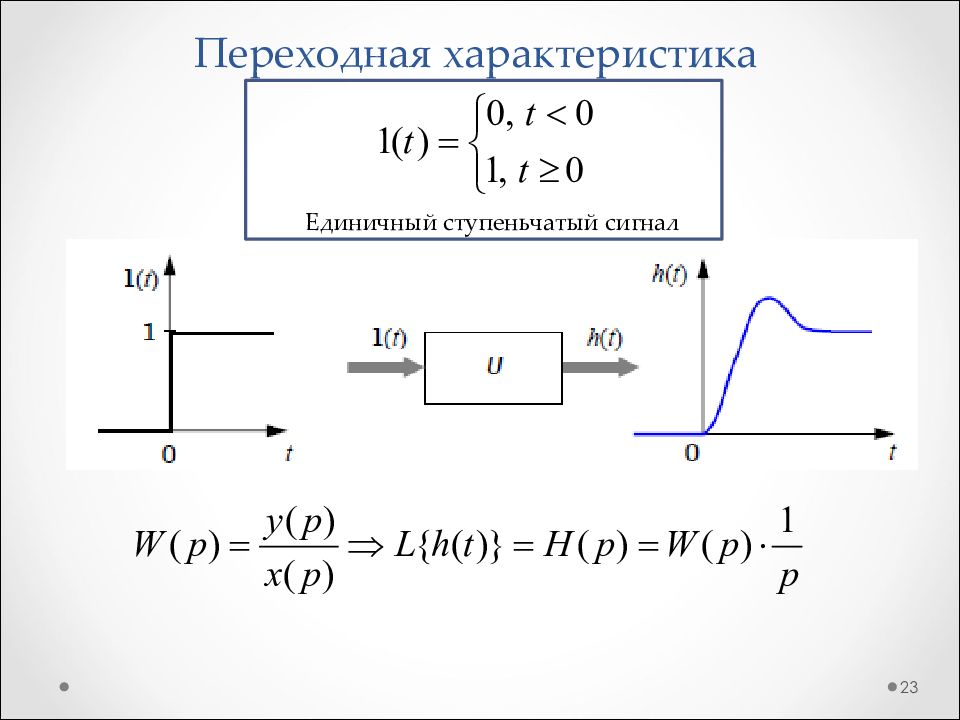
Слайд 22: Передаточная функция
22 Передаточная функция W ( p ) есть отношение выходного сигнала к входному сигналу, представленное в операторной форме: Заменим d/dt на оператор Лапласа – p и получим:
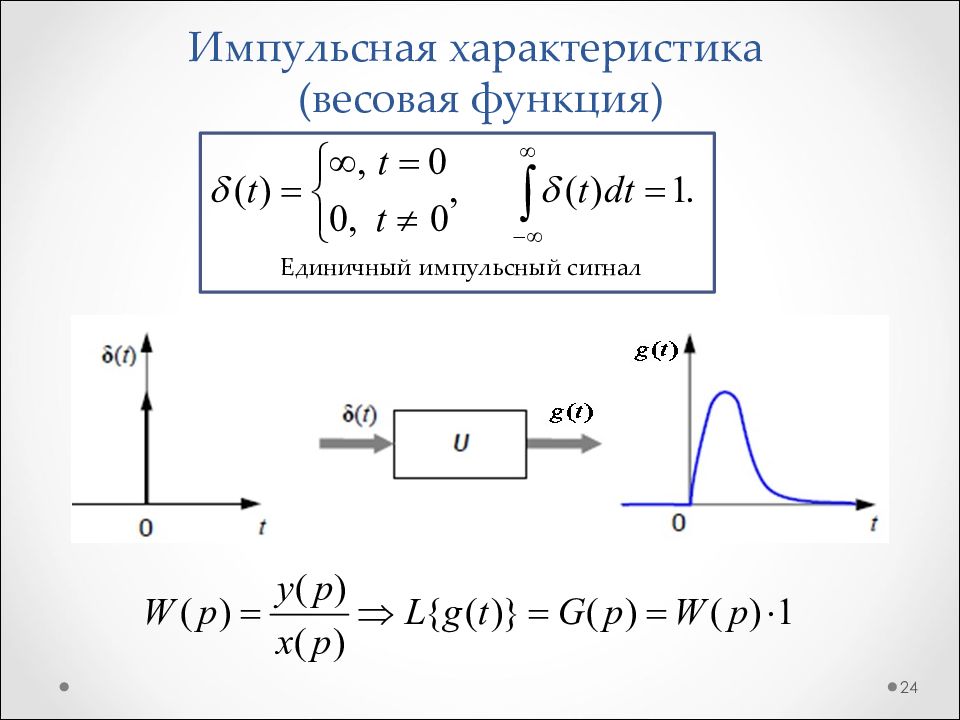
Слайд 24: Импульсная характеристика (весовая функция)
24 Единичный импульсный сигнал
Слайд 25: Разложение дроби на сумму элементарных дробей
25 Имеем рациональную дробь R ( x ) вида: где степени m>n. Дробь такого вида можно представить, притом единственным образом, в виде суммы элементарных дробей: где A, B, C — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.
Слайд 26: Таблица оригиналов и изображений (обратное / прямое преобразование Лапласа)
26
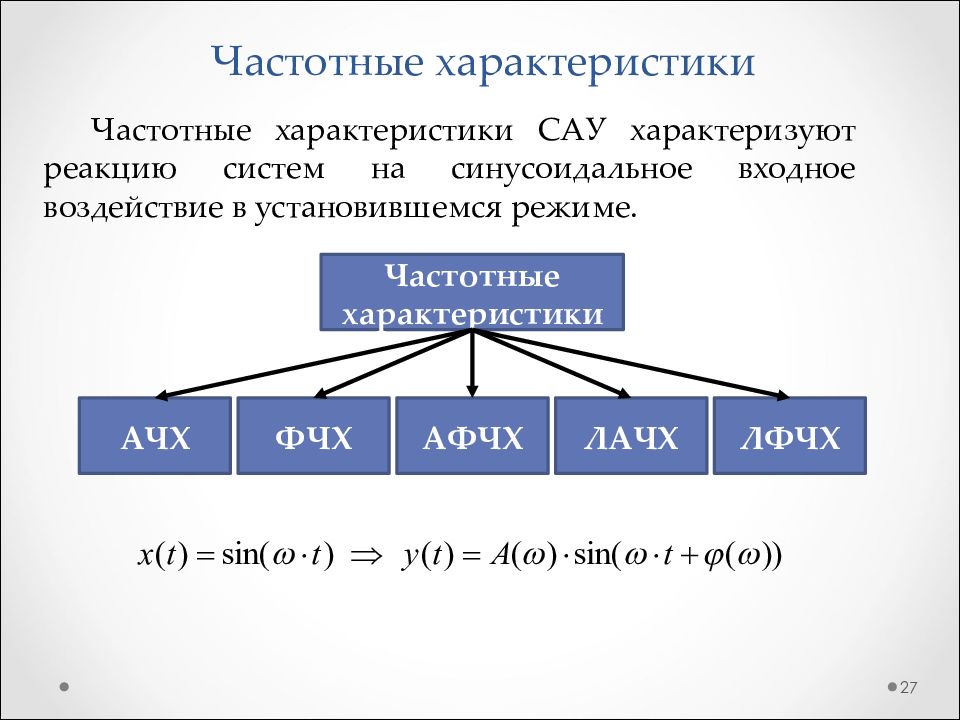
Слайд 27: Частотные характеристики
27 Частотные характеристики САУ характеризуют реакцию систем на синусоидальное входное воздействие в установившемся режиме. Частотные характеристики АЧХ АФЧХ ФЧХ ЛАЧХ ЛФЧХ
Слайд 28: Частотные характеристики
28 Зная передаточную функцию W(p), можно получить амплитудно-фазовую частотную характеристику, путем замены оператора Лапласа – p, на мнимое число – jw. - АФЧХ - АЧХ - ФЧХ где -
Слайд 29: Логарифмические частотные характеристики
29 - ось ординат - ось абсцисс ЛАЧХ - ось ординат - ось абсцисс ЛФЧХ (Дб) (Декада) (Декада) Свойства: 1) 2) Асимптотические ЛАЧХ
Слайд 31: Усилитель
31 - Передаточная функция - Переходная характеристика - Импульсная характеристика - АЧХ - ФЧХ, ЛФЧХ - ЛАЧХ
Слайд 32: Апериодическое звено
32 - Передаточная функция - Переходная характеристика - Импульсная характеристика - АФЧХ - ЛАЧХ
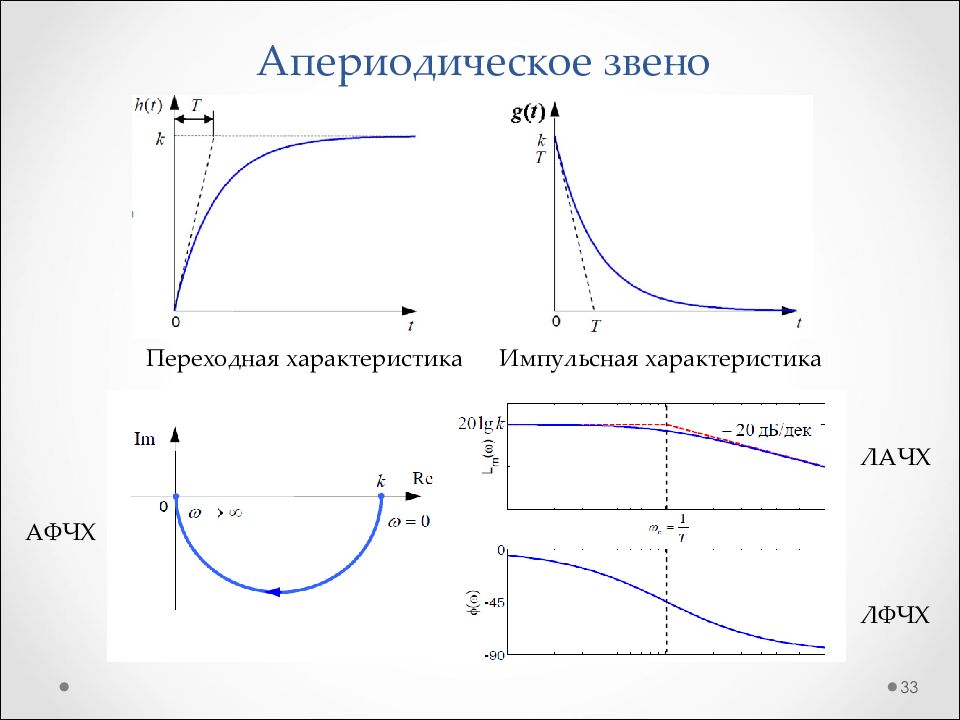
Слайд 33: Апериодическое звено
33 Переходная характеристика Импульсная характеристика АФЧХ ЛАЧХ ЛФЧХ
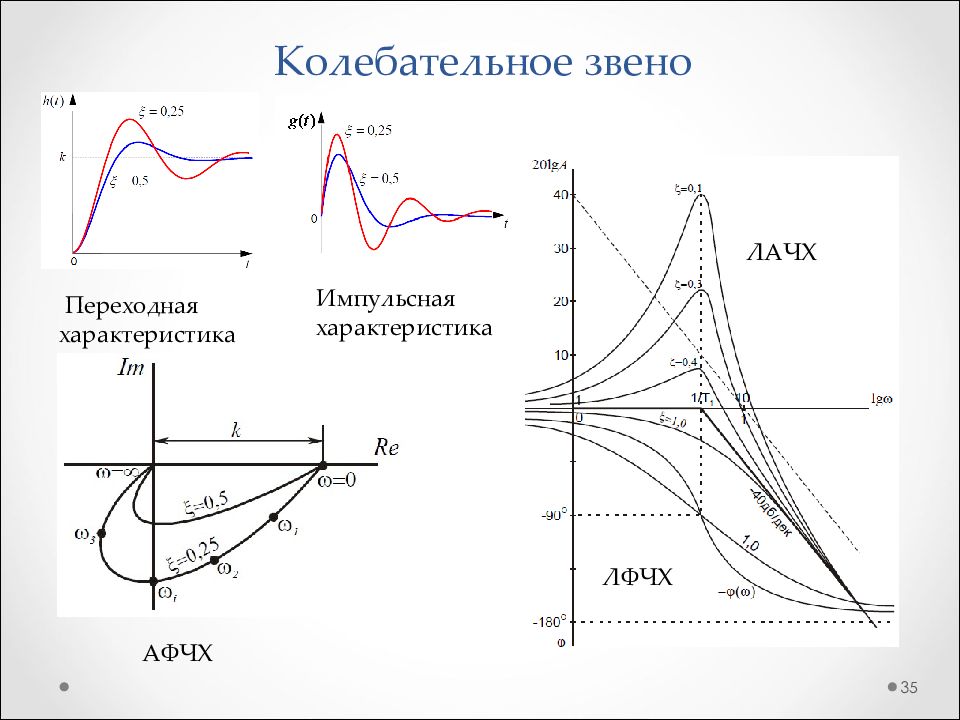
Слайд 35: Колебательное звено
35 Переходная характеристика Импульсная характеристика АФЧХ ЛАЧХ ЛФЧХ
Слайд 36: Интегрирующее звено
36 - Передаточная функция - Переходная характеристика - Импульсная характеристика - АФЧХ - ЛАЧХ
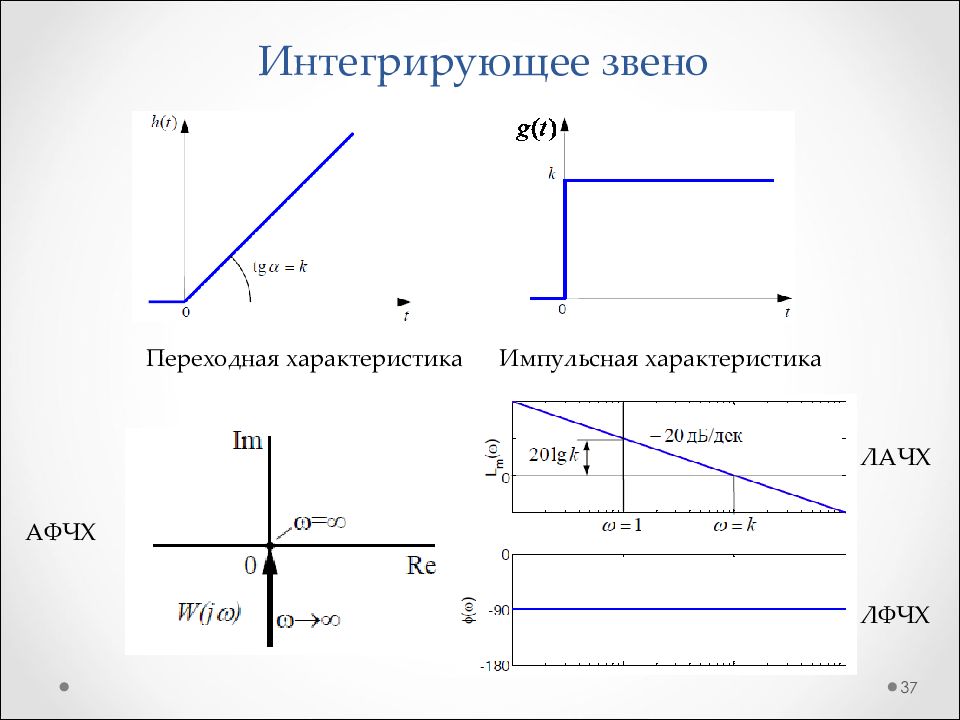
Слайд 37: Интегрирующее звено
37 Переходная характеристика Импульсная характеристика АФЧХ ЛАЧХ ЛФЧХ
Слайд 38: Идеально дифференцирующее звено
38 - Передаточная функция - Переходная характеристика - Импульсная характеристика - АФЧХ - ЛАЧХ Физически не реализуемое, так как звено реагирует не на изменение самой входной величины, а на изменение ее производной, то есть на тенденцию развития событий.
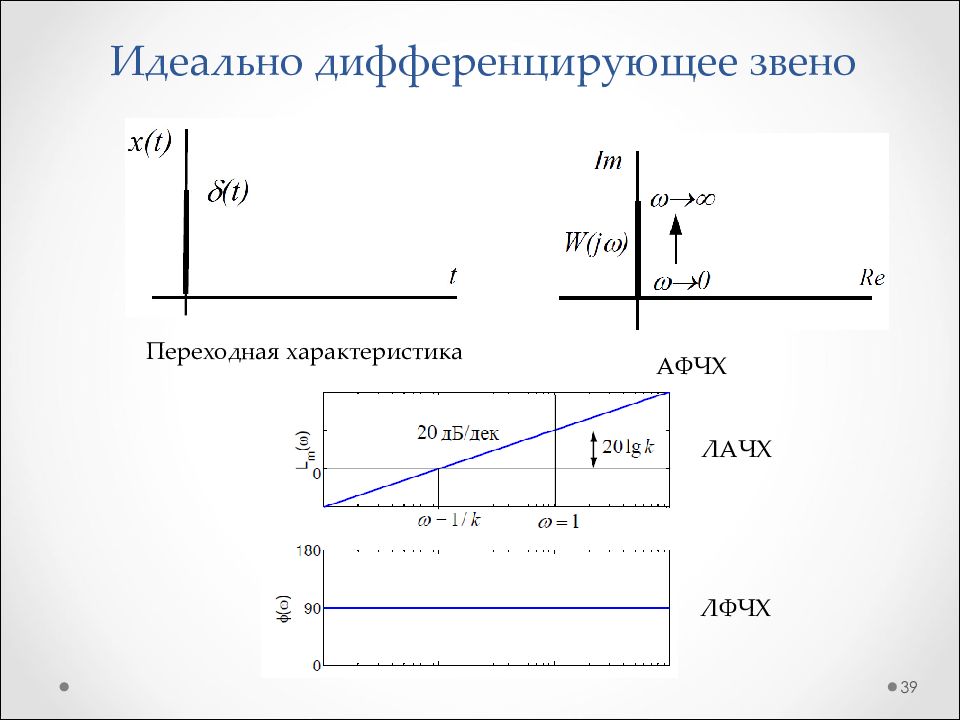
Слайд 39: Идеально дифференцирующее звено
39 Переходная характеристика АФЧХ ЛАЧХ ЛФЧХ
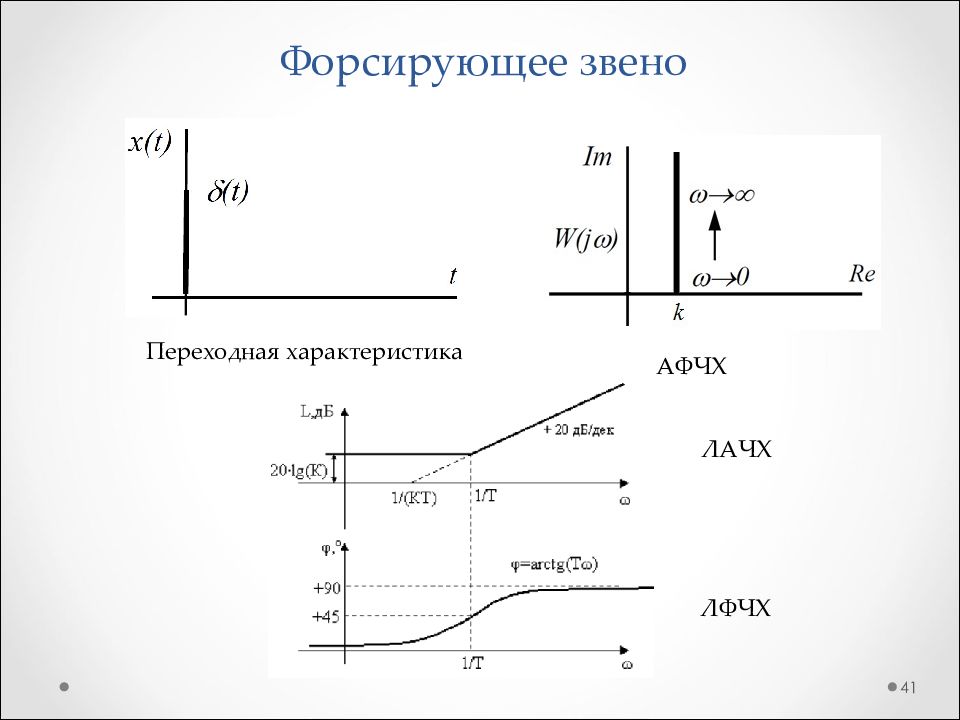
Слайд 40: Форсирующее звено
40 - Передаточная функция - Переходная характеристика Физически не реализуемое - АФЧХ - ЛАЧХ
Слайд 42: Построение ЛАЧХ
42 Рассмотрим звено второго порядка с передаточной функцией: 1)Представим данную передаточную функцию в виде произведения 2)Согласно первому свойству ЛАЧХ, получим: 3)Определяем сопрягающие частоты. Частоты на, которых «подключаются» соответствующие звенья.
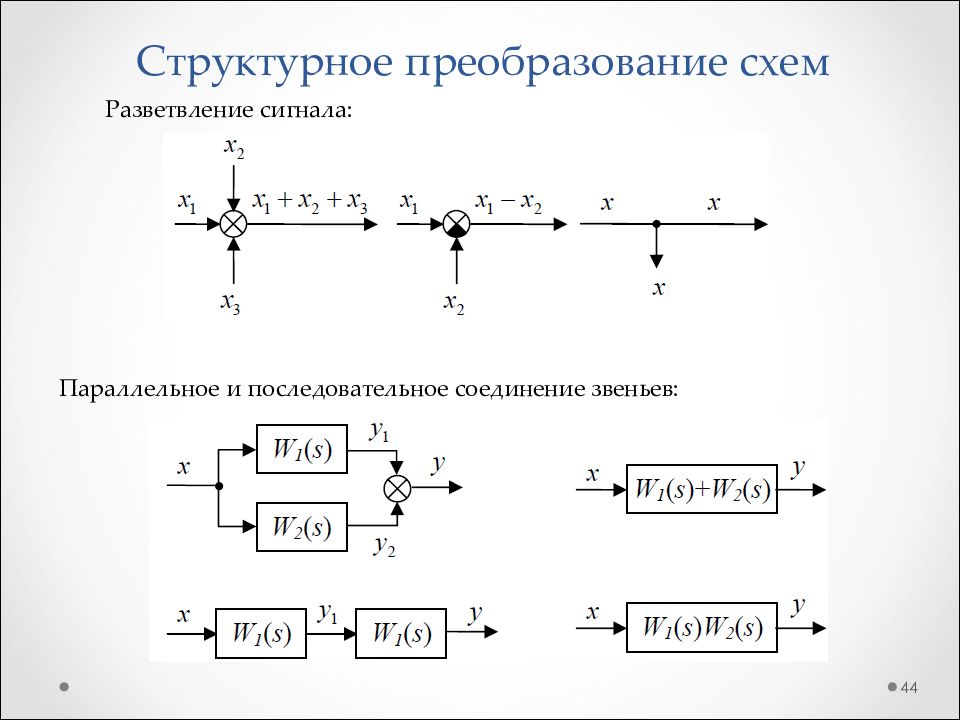
Слайд 44: Структурное преобразование схем
44 Разветвление сигнала: Параллельное и последовательное соединение звеньев:
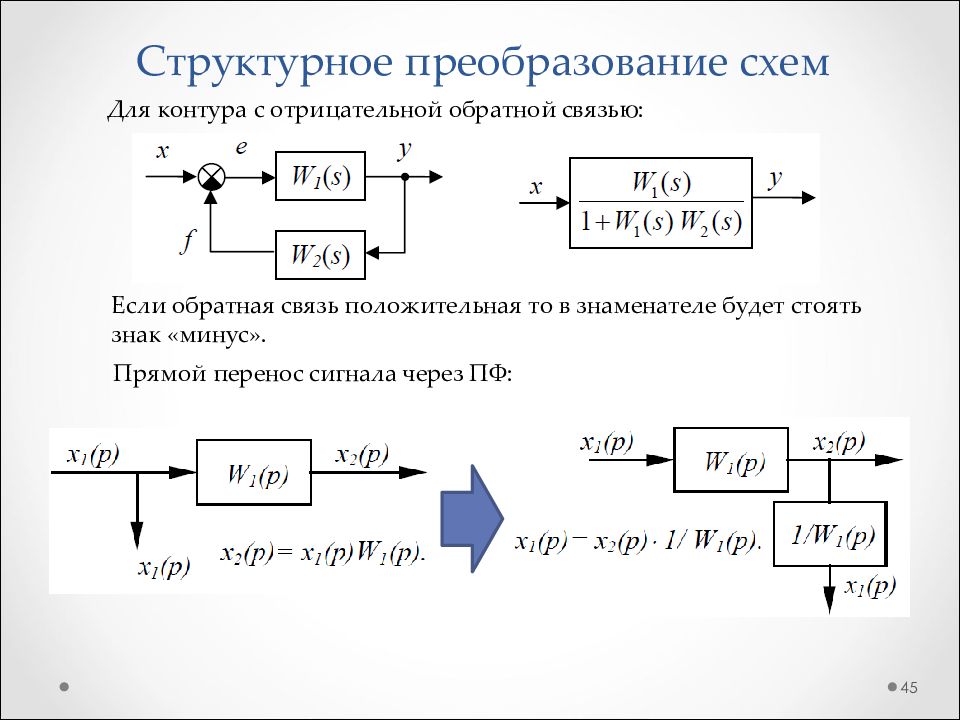
Слайд 45: Структурное преобразование схем
45 Для контура с отрицательной обратной связью: Если обратная связь положительная то в знаменателе будет стоять знак «минус». Прямой перенос сигнала через ПФ:
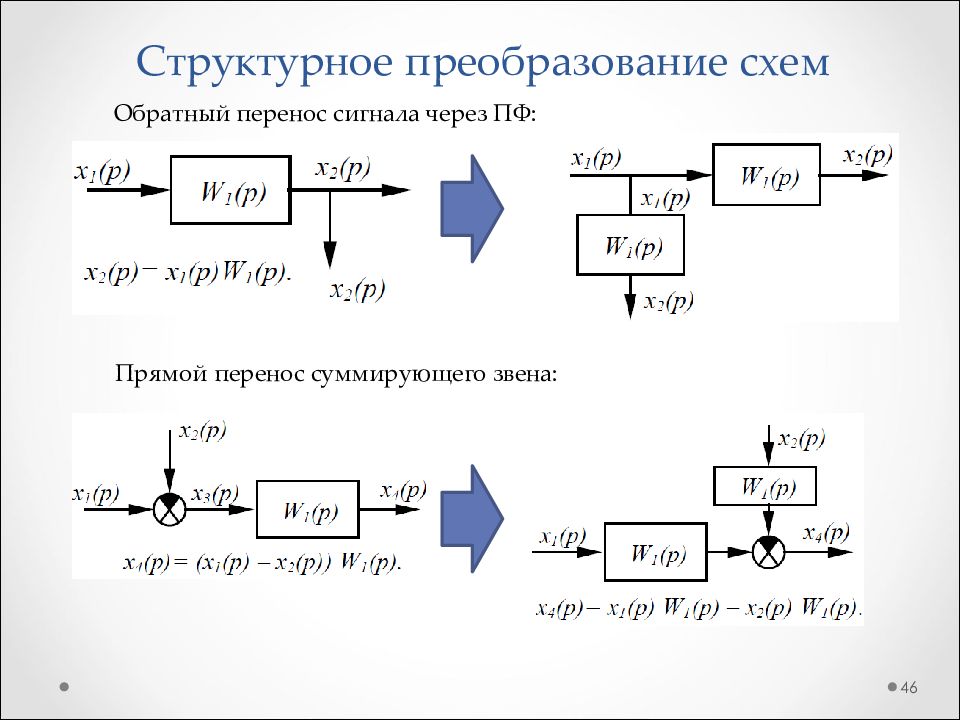
Слайд 46: Структурное преобразование схем
46 Прямой перенос суммирующего звена: Обратный перенос сигнала через ПФ:
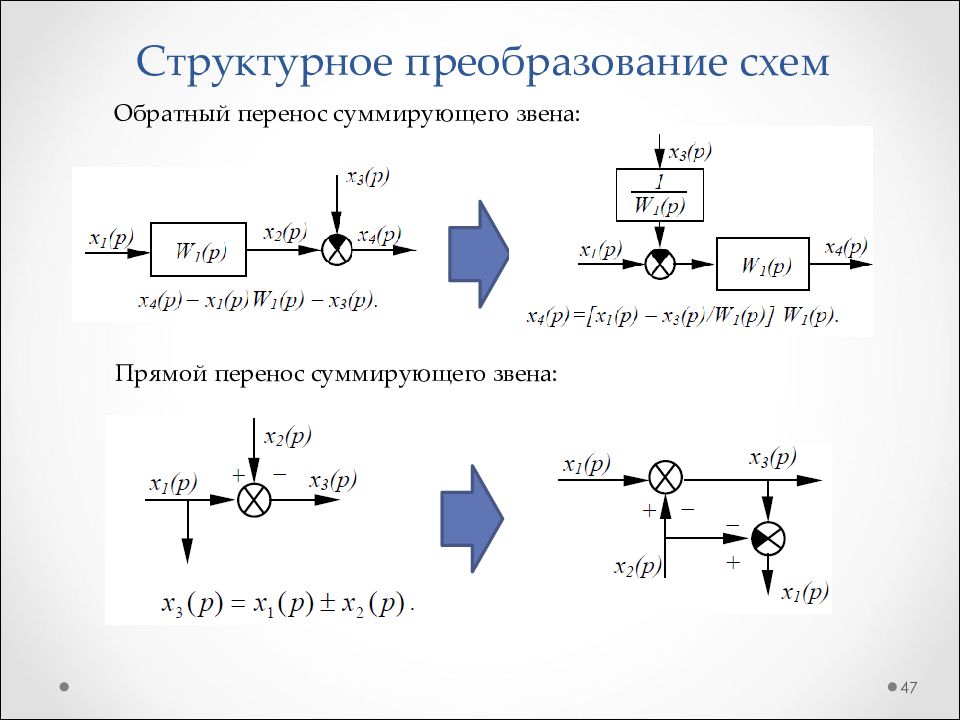
Слайд 47: Структурное преобразование схем
47 Прямой перенос суммирующего звена: Обратный перенос суммирующего звена:
Слайд 48: Передаточные функции систем
48 Передаточная функция по возмущающему воздействию: Передаточная функция по управлению Передаточная функция по рассогласованию:
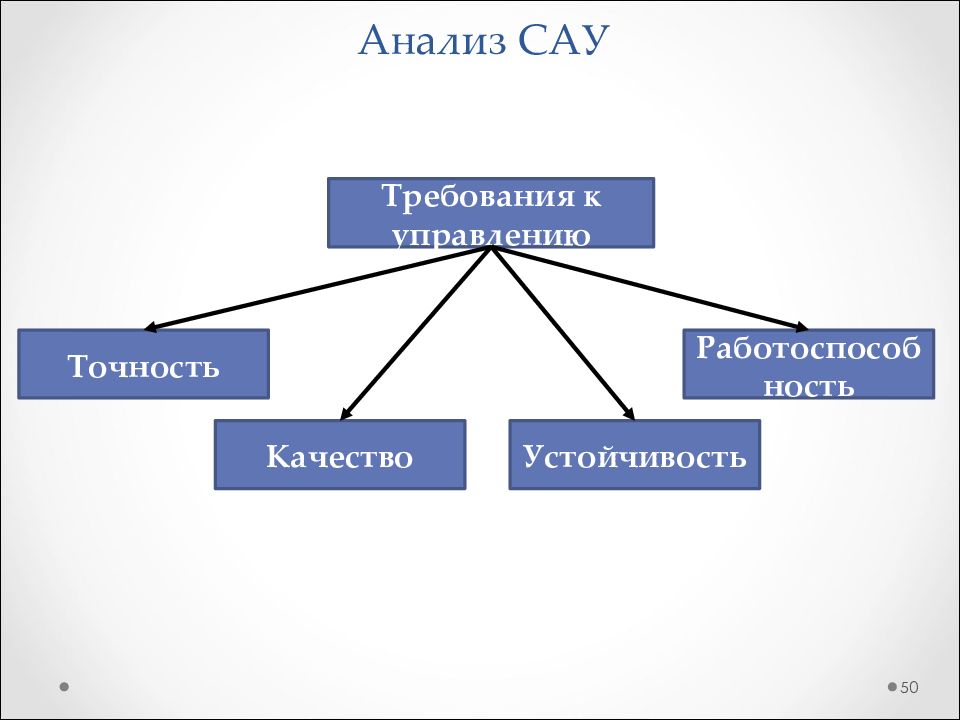
Слайд 50: Анализ САУ
50 Требования к управлению Точность Качество Устойчивость Работоспособность
Слайд 51: Критерии устойчивости (критерий Гурвица)
51 Пример для полинома пятого порядка ( n=5 ): Все корни полинома Δ( s) имеют отрицательные вещественные части тогда и только тогда, когда все n главных миноров матрицы H n (определителей Гурвица) положительны. Характеристическое уравнение замкнутой САУ: