1 3. Основы автоматики и системы автоматического управления (ОА и САУ) 1.5. Анализ одномерных САУ.
2 Содержание раздела 1.5 ОА и САУ 1.5. Анализ одномерных САУ. 2-4 1.5.1. Динамическая устойчивость САУ. 5- 20 1.5.2. Критерий устойчивости Гурвица. 2 1 - 31 1.5.3. Критерий устойчивости Михайлова. З 2 - 41 1.5.4. Критерий устойчивости Найквиста. 42 - 47 1.5.5. Логарифмический критерий устойчивости. 48 - 54 1.5.6. Качество САУ. 55 - 65 1.5.7. Точность САУ. 66 - 76 1.5.8. Инвариантность САУ. 77 - 96 1.5.9. Качество переходного процесса. 97 - 136 1.5.10. Чувствительность систем управления. 137-153
3 1.5. Анализ одномерных САУ ( c одной выходной величиной y ( t ) ) определяет 5 их основны х свойств: 1. Устойчивость САУ – собственное свойство САУ возвращаться в начальное (нулевое) установившееся состояние после исчезновения внешних воздействий выведших САУ из этого начального (нулевого) состояния, что определяет работоспособность САУ; 2. Точность САУ – измеряется величиной ошибки управления e ( t ) = g ( t ) – y ( t ) в установившихся режимах работы ;
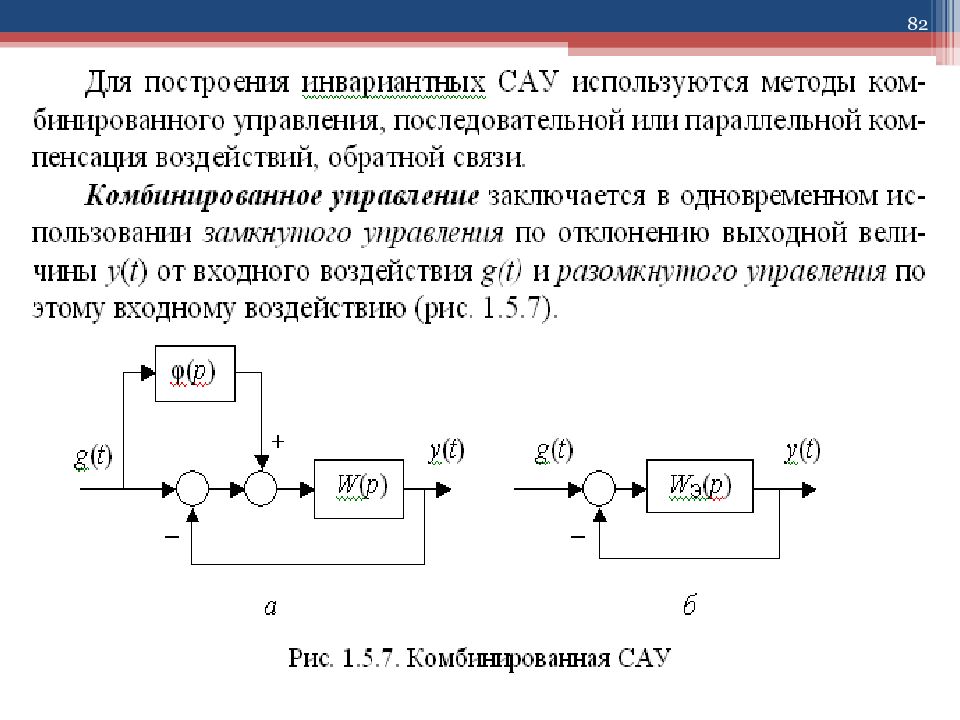
4 1.5. Анализ одномерных САУ c одной выходной величиной y ( t ) определяет 5 их основны х свойств: 3. Инвариантность САУ – определяется независимостью выходной величины y ( t ) от вариаций возмущающих воздействий f ( t ) и ковариантностью (близостью) y ( t ) к задающему воздействию y ( t )≈ g ( t ). 4. Качество переходных процессов в САУ – определяется степенью близости переходного процесса управляемой выходной величины y(t) к единичному входному воздействию g(t)= 1[ t ] или f(t )=1[ t ]. 5. Робастность САУ – это малая чувствительность (грубость) САУ к малым отклонениям (вариациям) собственных параметров САУ в процессе работы.
5 1.5.1. Динамическая устойчивость САУ Изменение внешних воздействий g(t) и f(t) вызывает процесс перехода выходной величины y(t) САУ в другое установившееся состояние: где: (1.5.1) y C ( t ) – собственное (свободное) движение в виде суммы экспонент – переходная составляющая процесса y пер ( t ); y B ( t ) – вынужденное установившееся движение y уст ( t ), определяемое из уравнения САУ при t =∞ ; – постоянные интегрирования; – корни характеристического уравнения замкнутой САУ: (1.5.2)
6 1.5.1. Динамическая у стойчивость САУ При исчезновении внешних воздействий в САУ возникает только переходной процесс собственного (свободного) движения y C ( t ) к ну левому равновесию, т. е. переходная составляющая y пер ( t ).
7 1.5.1. Динамическая у стойчивость САУ Динамической устойчивостью или устойчивостью по начальным условиям (по Ляпунову) называется собственное свойство САУ возвращаться в состояние начального ( нулевого ) равновесия после затухания свободных движений, вызванных ненулевыми условиями, т. е. внешними входными воздействиями.
8 1.5.1. Динамическая у стойчивость САУ Динамическая устойчивость САУ определяется по виду переходного процесса собственного ( свободного ) движения САУ к состоянию начального (нулевого) равновесия, зависящего только от собственных свойств САУ, т. е. от корней p i = α i ± jβ i характеристического уравнения (1.5.2).
9 1.5.1. Динамическая у стойчивость САУ Корни p i =α i ± jβ i характеристического уравнения САУ определяют тип переходного процесса свободного движения САУ : 1) затухающий апериодический, если все действительные корни отрицательные ; 2) затухающий колебательный, если все действительные корни и вещественные части всех комплексно-сопряженных корней отрицательные ; 3) расходящийся апериодический, если из действительных корней хотя бы один имеет положительное значение ; 4) расходящийся колебательный, если хотя бы один из комплексно-сопряженных корней имеет положительную вещественную часть ; 5) незатухающий колебательный, если хотя бы один из комплексно-сопряженных корней имеет нулевую вещественную часть.
10 Работоспособны только САУ типа 1 и 2 с затухающими переходными процессами, обладающие динамической устойчивостью, о которой можно судить по расположению корней характеристического уравнения на комплексной плоскости корней – в устойчивых САУ все корни располагаются в левой полуплоскости. Такие САУ называются статическими, поскольку они имеют ошибку в установившихся (статических) режимах работы.
11 Граница устойчивости САУ проходит по оси мнимых чисел комплексной плоскости корней характеристического уравнения (1.5.2). Поэтому при проектировании САУ расчетные значения корней характеристического уравнения САУ должны располагаться слева от мнимой оси на некотором расстоянии, определяющим запас устойчивости САУ.
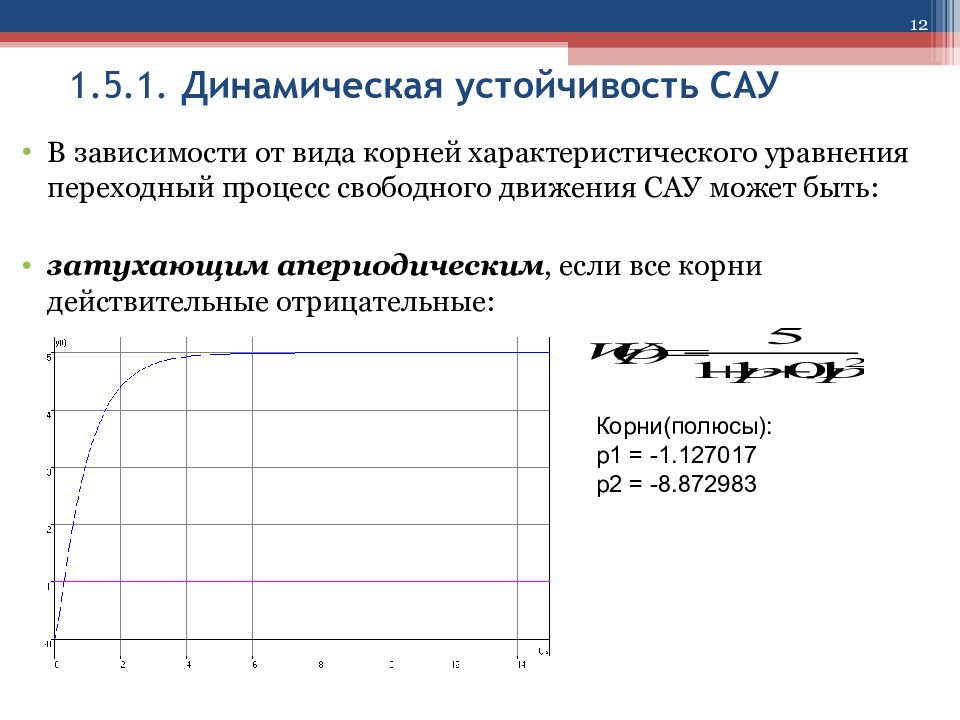
12 1.5.1. Динамическая устойчивость САУ В зависимости от вида корней характеристического уравнения переходный процесс свободного движения САУ может быть: затухающим апериодическим, если все корни действительные отрицательные: Корни(полюсы): p1 = -1.127017 p2 = -8.872983
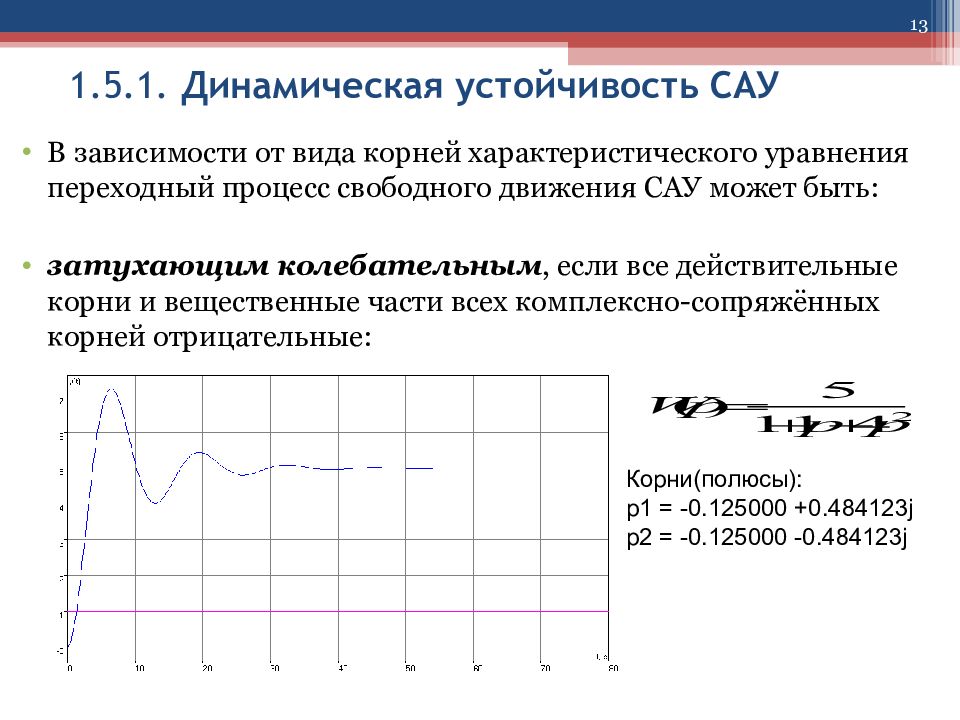
13 1.5.1. Динамическая устойчивость САУ В зависимости от вида корней характеристического уравнения переходный процесс свободного движения САУ может быть: затухающим колебательным, если все действительные корни и вещественные части всех комплексно-сопряжённых корней отрицательные: Корни(полюсы): p1 = -0.125000 +0.484123j p2 = -0.125000 -0.484123j
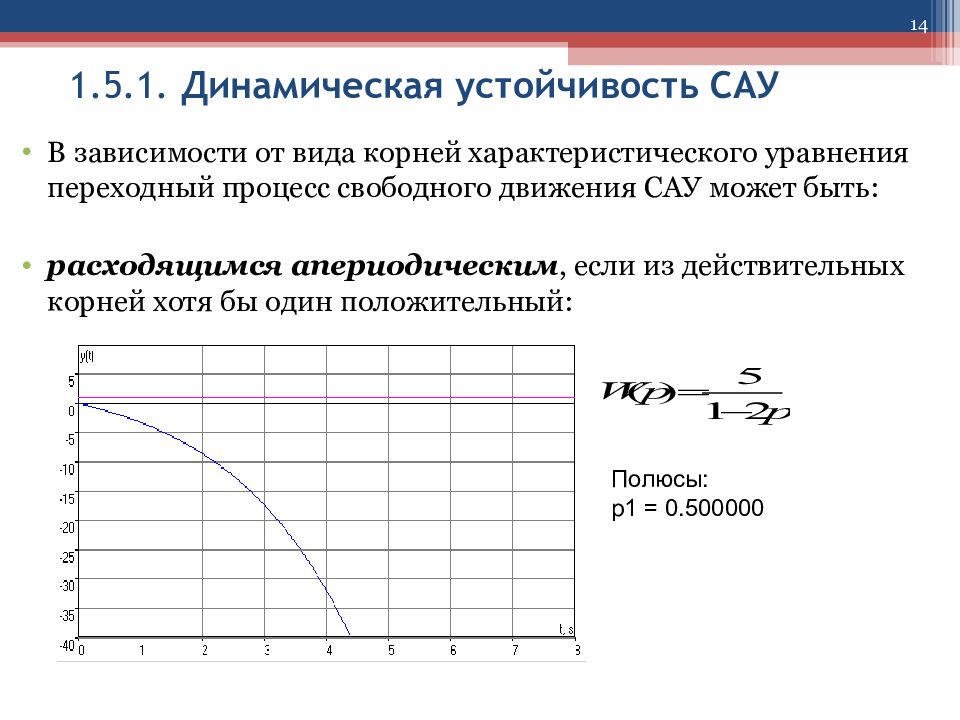
14 1.5.1. Динамическая устойчивость САУ В зависимости от вида корней характеристического уравнения переходный процесс свободного движения САУ может быть: расходящимся апериодическим, если из действительных корней хотя бы один положительный: Полюсы: p1 = 0.500000
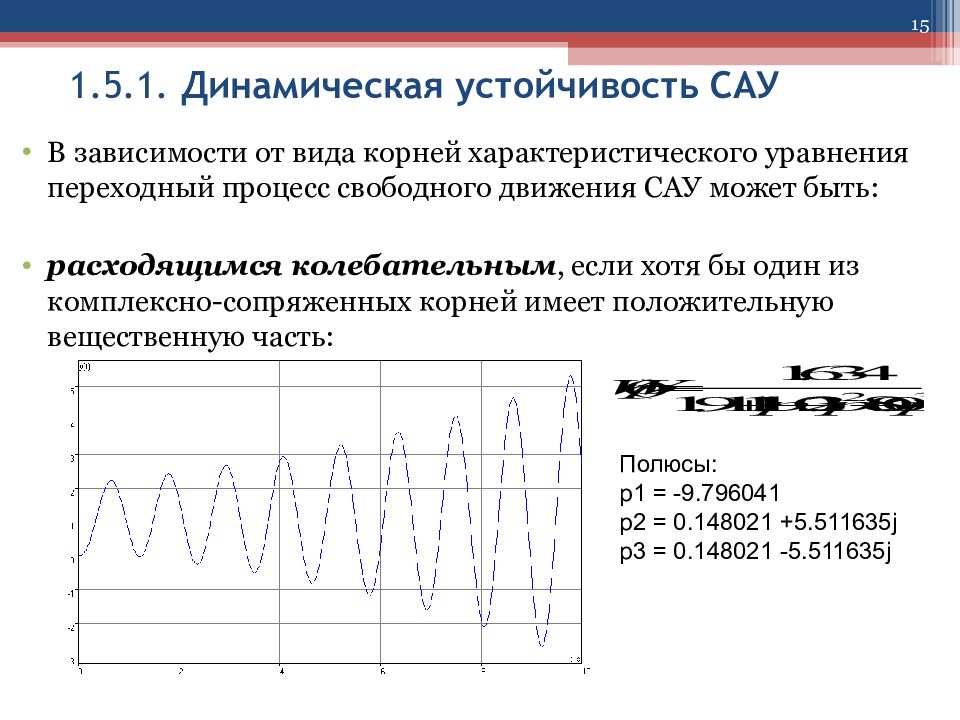
15 1.5.1. Динамическая устойчивость САУ В зависимости от вида корней характеристического уравнения переходный процесс свободного движения САУ может быть: расходящимся колебательным, если хотя бы один из комплексно-сопряженных корней имеет положительную вещественную часть: Полюсы: p1 = -9.796041 p2 = 0.148021 +5.511635j p3 = 0.148021 -5.511635j
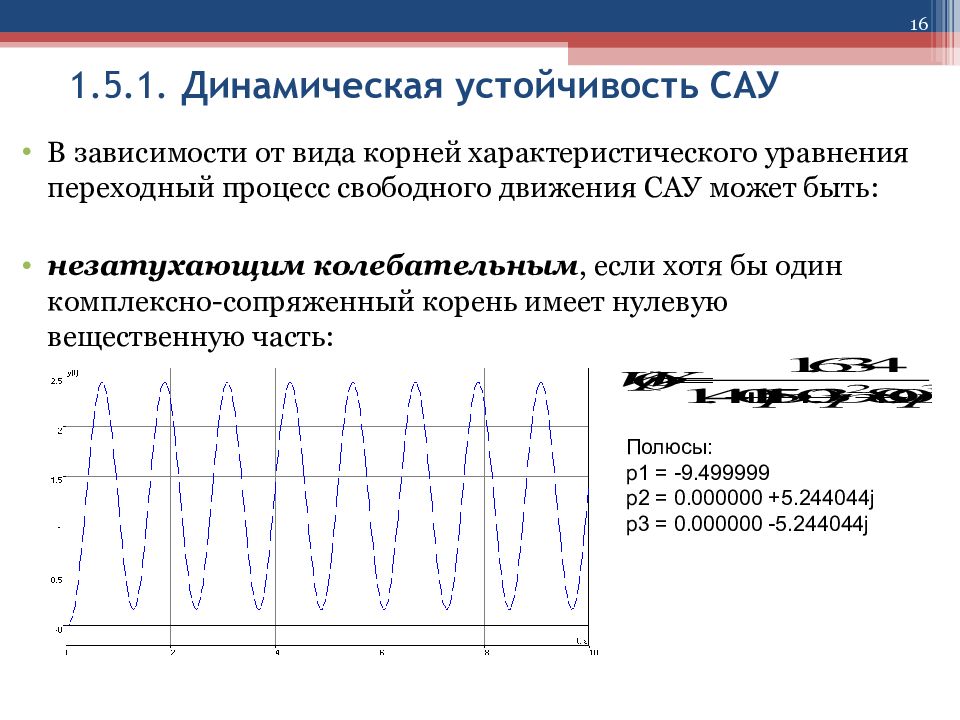
16 1.5.1. Динамическая устойчивость САУ В зависимости от вида корней характеристического уравнения переходный процесс свободного движения САУ может быть: незатухающим колебательным, если хотя бы один комплексно-сопряженный корень имеет нулевую вещественную часть: Полюсы: p1 = -9.499999 p2 = 0.000000 +5.244044j p3 = 0.000000 -5.244044j
17 1.5.1. Динамическая у стойчивость САУ В астатических ( не статических ) САУ установившаяся ошибка отсутствует. В их характеристическом уравнении отсутствует свободный член, что ведет к бесконечному увеличению выходной величины y(t) (например, углового перемещения вала двигателя) и имеется один или несколько нулевых действительных корней, расположенных в начале координат (в нулевой точке) комплексной плоскости корней характеристического уравнения. Из-за нулевых корней астатические САУ неустойчивы по управляемой величине y(t), но устойчивы по её первой производной (по скорости изменения ) dy(t)/dt. Поэтому астатические САУ называют нейтрально устойчивыми по управляемой величине y(t), которая может принимать любые установившиеся значения.
18 1.5.1. Динамическая у стойчивость САУ В структурно неустойчивых САУ изменением их параметров нельзя достичь устойчивости без изменения структуры. Например, замкнутый контур с положительной обратной связью структурно неустойчив, поскольку в характеристическом уравнении САУ имеется отрицательный свободный член, который дает положительный корень в характеристическом уравнении и бесконечно возрастающий переходный процесс в САУ.
19 1.5.1. Динамическая у стойчивость САУ Для оценки устойчивости САУ по коэффициентам характеристического уравнения, без вычисления корней характеристического уравнения и без решения дифференциального уравнения переходного процесса, разработаны алгебраические (аналитические) и частотные (геометрические) критерии устойчивости САУ.
20
21 1.5.2. Критерий устойчивости Гурвица Для оценки устойчивости замкнутой САУ по коэффициентам её характеристического уравнения вида (1.5.2) без поиска его корней были разработаны алгебраические критерии устойчивости Рауса, Гурвица, Шур-Кона, Льенара-Шипара, Джури-Бланшара, которые различаются только по форме. Например, Раус в 1877 г. предложил критерий устойчивости в алгоритмической форме, а Гурвиц в 1895 г. – в практически более удобной определительной форме.
22 1.5.2. Критерий устойчивости Гурвица Критерий устойчивости Гурвица формулируется так: для устойчивости САУ необходимо и достаточно, чтобы при a 0 > 0 все диагональные определители матрицы Гурвица, сформированные из коэффициентов характеристического уравнения, были положительны. Для неустойчивой САУ определитель Гурвица имеет отрицательное значение, а на границе устойчивости САУ – равен нулю.
23 1.5.2. Критерий устойчивости Гурвица Матрица Гурвица формируется из коэффициентов характеристического уравнения следующим образом:
24 1.5.2. Критерий устойчивости Гурвица Диагональные определители матрицы Гурвица ( n × n ):
25 1.5.2. Критерий устойчивости Гурвица С использованием критерия Гурвица и других алгебраических (аналитических) и частотных (геометрических) критериев устойчивости можно строить границы устойчивости и выделять области устойчивости в пространстве коэффициентов характеристического уравнения или параметров САУ.
26 1.5.2. Критерий устойчивости Гурвица К недостаткам критерия Гурвица относится трудность вычисления аналитической связи между параметрами и устойчивостью в САУ выше пятого порядка ( n > 5) из-за того, что одни и те же параметры САУ одновременно входят в несколько коэффициентов характеристического уравнения. В таких случаях можно использовать алгебраические критерии Рауса, Льенара-Шипара, Шур-Кона с расчетами на ЭВМ с применением пакетов прикладных программ.
27 1.5.2. Критерий устойчивости Гурвица Пример. Исслед уем по критерию Гурвица устойчивость замкнутой САУ с единичной обратной связью, если её ОФП в разомкнутом состоянии имеет вид: Разомкнутая САУ неустойчива из-за бесконечного возрастания выходной величины, поскольку характеристическое уравнение имеет нулевой корень р 0 = 0.
28 1.5.2. Критерий устойчивости Гурвица Пример. Передаточная функция САУ в замкнутом состоянии запишется в виде: Характеристическое уравнение замкнутой САУ имеет вид:
29 1.5.2. Критерий устойчивости Гурвица Пример. Составим определители Гурвица по выражениям:
30 1.5.2. Критерий устойчивости Гурвица Пример. Из полученных определителей Гурвица условие устойчивости замкнутой САУ определяется вторым неравенством Δ 2, которое можно записать в виде: Неравенство выражает условие отсутствия нулевых и правых корней в характеристическом уравнении замкнутой САУ и позволяет исследовать устойчивость САУ в трёхмерном пространстве параметров K, Т1, Т2. 1.5.2. Критерий устойчивости Гурвица
31
32 Для исследования устойчивости САУ с высоким порядком характеристического уравнения разработаны частотные (геометрические) критерии устойчивости, позволяющие судить об устойчивости САУ по геометрическому виду их частотных характеристик. К частотны м критери ям устойчивости относятся критерий Михайлова, критерий Найквиста, логарифмический критерий.
33 Характеристическое уравнение замкнутой САУ (1.5.2) можно представить в виде: D(p)=a 0 p n + a 1 p n-1 +…+ a n-1 p+ a n = =a 0 (p–p 1 )(p–p 2 )(p–p n )=0, где p 1, p 2,..., p n – корни характеристического уравнения. Заменив p=jω, получим характеристический вектор D(j )=D()e j() ( 1.5.12 ) в виде произведения n векторов-сомножителей, аргументы которых суммируются: 1.5.3. Критерий устойчивости Михайлова
34 1.5.3. Критерий устойчивости Михайлова При изменении частоты ω от 0 до бесконечности каждый вектор-сомножитель ( jω - p i ) в (1.5.12) повернется на угол π /2 против часовой стрелки, если корень p i левый. Вектор D(jω) повернется на угол n π /2 против часовой стрелки, если все n корней левые. Если хотя бы один из n корней правый или нулевой, то угол поворота D(jω) будет меньше nπ/2, что укажет на неустойчивость САУ. Для устойчивых САУ n- го порядка конец вектора D(jω) по (1.5.12) при изменении ω от 0 до бесконечности описывает на комплексной плоскости годографы, названные кривыми Михайлова, которые имеют вид расходящихся спиралей, начинающихся на вещественной полуоси при ω= 0 (рис. 1.5.1).
35 1.5.3. Критерий устойчивости Михайлова
36 1.5.3. Критерий устойчивости Михайлова имеет три формулировки:
37 1.5.3. Критерий устойчивости Михайлова
38 1.5.3. Критерий устойчивости Михайлова
39
40
41
42
43
44
45
46
47
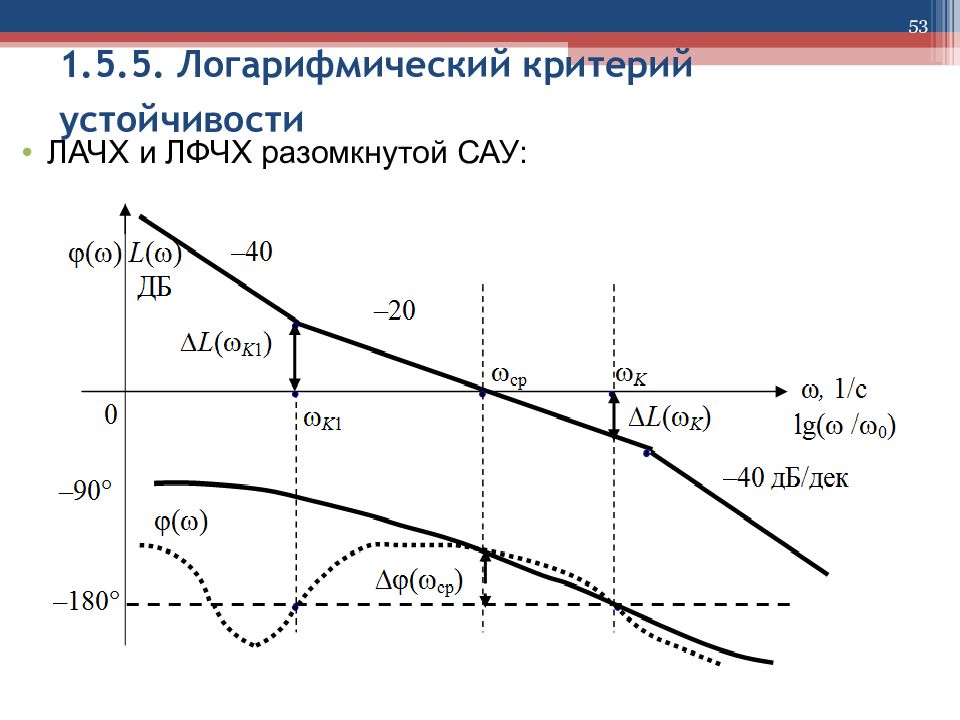
48 1.5.5. Логарифмический критерий устойчивости Логарифмический критерий устойчивости формулируется так: для устойчивости замкнутой САУ необходимо и достаточно, чтобы в ее разомкнутой цепи запаздывание по фазе φ ( ω ср ) не достигало минус 180º на частоте среза ЛАЧХ при L ( ω ср ) = 20lg A ( ω ср ) = 0 или чтобы при фазовом запаздывании ( k ) = – 180º величина ЛАЧХ была бы меньше нуля L ( k ) = 20lg A ( ω К ) < 0.
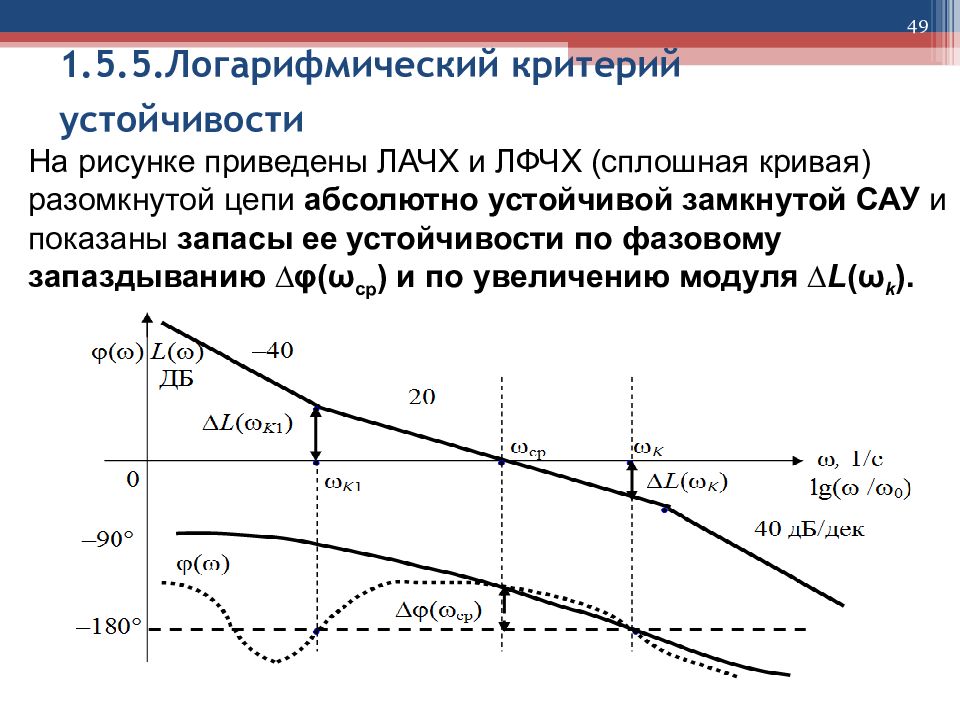
49 1.5.5. Логарифмический критерий устойчивости На рисунке приведены ЛАЧХ и ЛФЧХ (сплошная кривая) разомкнутой цепи абсолютно устойчивой замкнутой САУ и показаны запасы ее устойчивости по фазовому запаздыванию ∆φ(ω ср ) и по увеличению модуля ∆ L (ω k ).
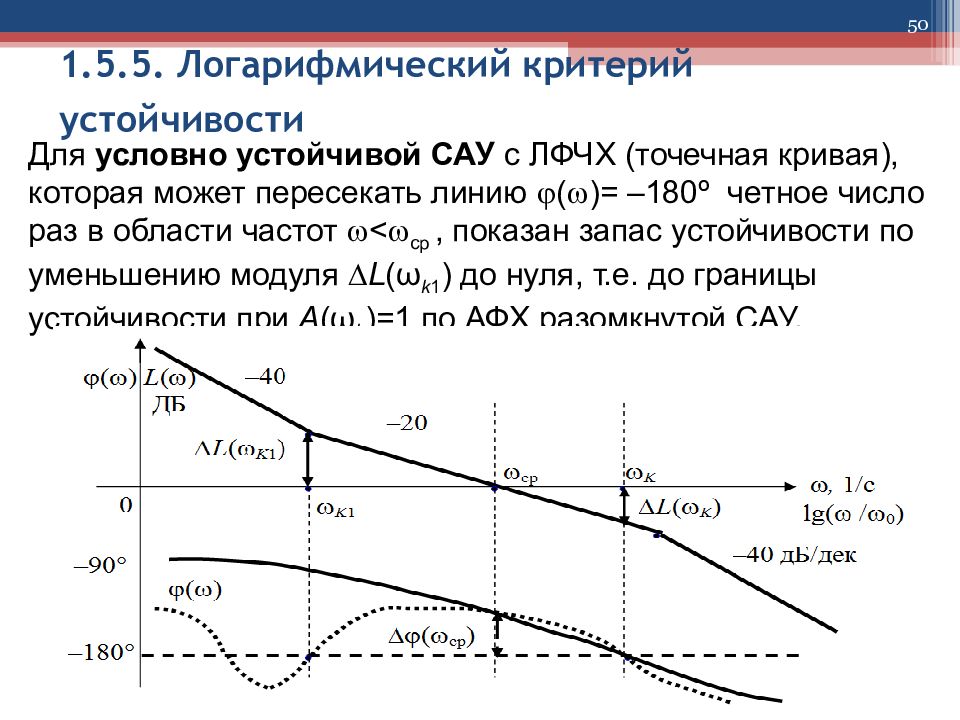
50 1.5.5. Логарифмический критерий устойчивости Для условно устойчивой САУ с ЛФЧХ (точечная кривая), которая может пересекать линию ( ) = – 180º четное число раз в области частот < ср, показан запас устойчивости по уменьшению модуля ∆ L (ω k 1 ) до нуля, т.е. до границы устойчивости при A (ω k ) = 1 по АФХ разомкнутой САУ.
51 1.5.5. Логарифмический критерий устойчивости Пример. Определить устойчивость замкнутой САУ с использованием логарифмического критерия устойчивости, если передаточная функция её разомкнутой цепи имеет вид: Видно, что разомкнутая САУ состоит из трёх типовых звеньев с единичными коэффициентами передачи – интегрирующего с постоянной времени Ти= 1 /K и двух апериодических (инерционных) первого порядка с постоянными времени Т1 и Т2. Выражения для ЛАЧХ и ЛФЧХ разомкнутой САУ запишутся :
52 1.5.5. Логарифмический критерий устойчивости По заданным формулам строим ЛАЧХ и ЛФЧХ. Из L (ω) = 0 находим частоту среза ω ср и по ЛФЧХ определяем устойчивость САУ по [–φ(ω ср )]<[–180º] и запас устойчивости по фазе ∆φ(ω ср ). Для частоты ω k при φ(ω k ) = – 180º по ЛАЧХ для этой частоты определяем запас устойчивости ∆ L (ω k ) по уменьшению модуля коэффициента передачи САУ А (ω k ) до 1 при L (ω k ) = 0.
53 1.5.5. Логарифмический критерий устойчивости ЛАЧХ и ЛФЧХ разомкнутой САУ:
54
55 1.5.6. Качество САУ Качество САУ оценивается по четырем критериям качества (1,2,3,4). Критерии точности САУ определяются по установившейся ошибке управления e ( t )= g ( t )– y ( t ) при t = ∞, приходящейся на единицу типового внешнего воздействия. При g ( t )= A ∙1[ t ], G ( p )= A / p получим добротность по положению K A = e ( t )/ A ; при g ( t )= Vt, G( p )= V / p 2 получим добротность по скорости K V = e ( t )/ V ; при g ( t )= at 2 / 2, G ( p )= a / p 3 получим добротность по ускорению K a =e(t)/a.
56 1.5.6. Качество САУ Качество САУ оценивается по четырем критериям качества (1,2,3,4). 2. Критерии устойчивости САУ определяются по запасу устойчивости, который ограничивает возможность повышения точности САУ за счет увеличения коэффициента передачи, что приближает САУ к границе устойчивости.
57 1.5.6. Качество САУ Качество САУ оценивается по четырем критериям качества (1,2,3,4). 3. Критерии качества переходных процессов определяются по показателям формы переходного процесса y ( t ) при отработке единичного ступенчатого задающего g ( t ) или возмущающего f ( t ) воздействия, характеризующих величину перерегулирования, время затухания переходного процесса, количество колебаний и другие показатели.
58 1.5.6. Качество САУ Качество САУ оценивается по четырем критериям качества (1,2,3,4). 4. Комплексные критерии качества САУ определяются по показателям обобщённых свойств САУ, одновременно учитывающих точность и динамические свойства. К таким комплексным критериям относятся частотные, корневые и интегральные оценки качества процесса управления.
59 1.5.6. Качество САУ Оценки качества САУ можно получить по расчетным или экспериментально полученным переходным или частотным характеристикам с использованием прямых или косвенных методов расчета. Прямые методы расчетов оценивают качество САУ непосредственно по графикам переходных процессов. Косвенные методы расчетов оценивают качество переходных процессов в САУ по определенным частотным, корневым или интегральным показателям, связанным с параметрами САУ без расчетов и построения переходных процессов.
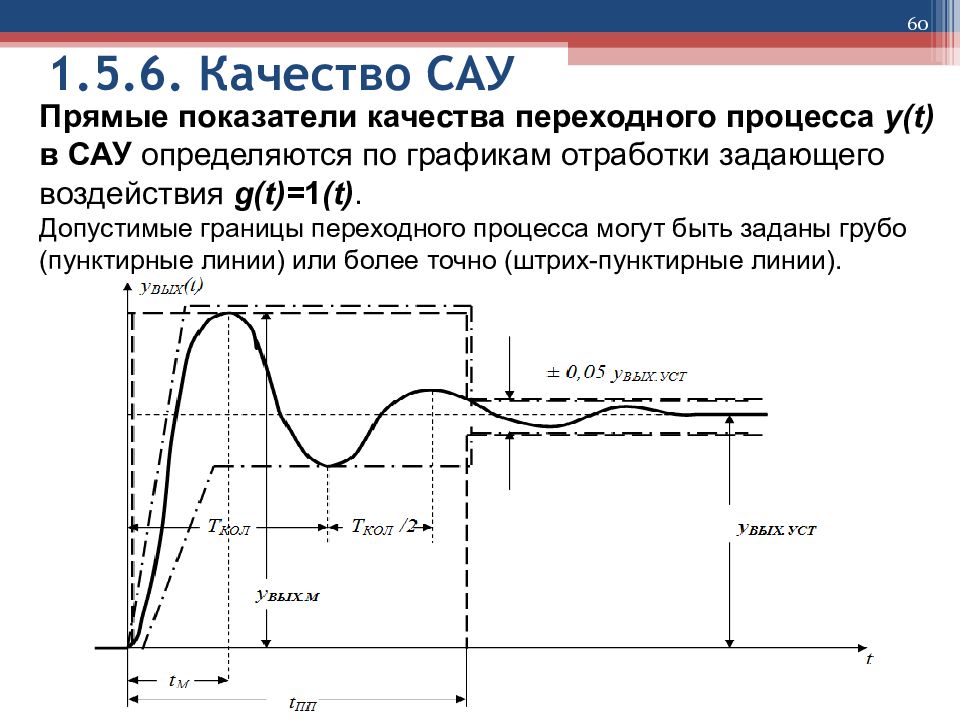
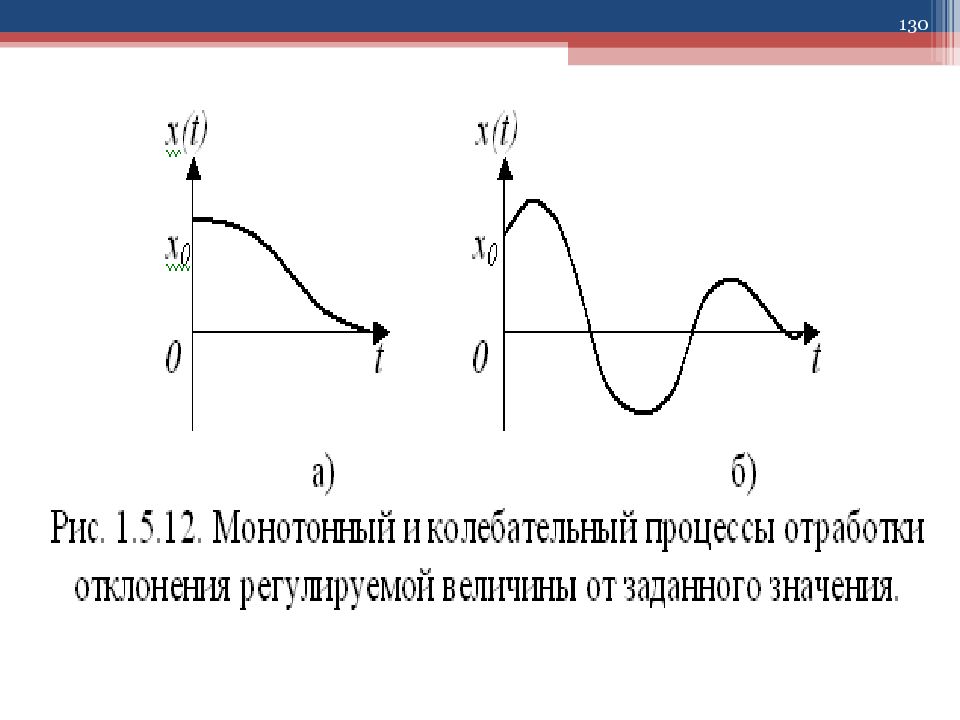
60 1.5.6. Качество САУ Прямые показатели качества переходного процесса y ( t ) в САУ определяются по графикам отработки задающего воздействия g ( t )= 1 ( t ). Допустимые границы переходного процесса могут быть заданы грубо (пунктирные линии) или более точно (штрих-пунктирные линии).
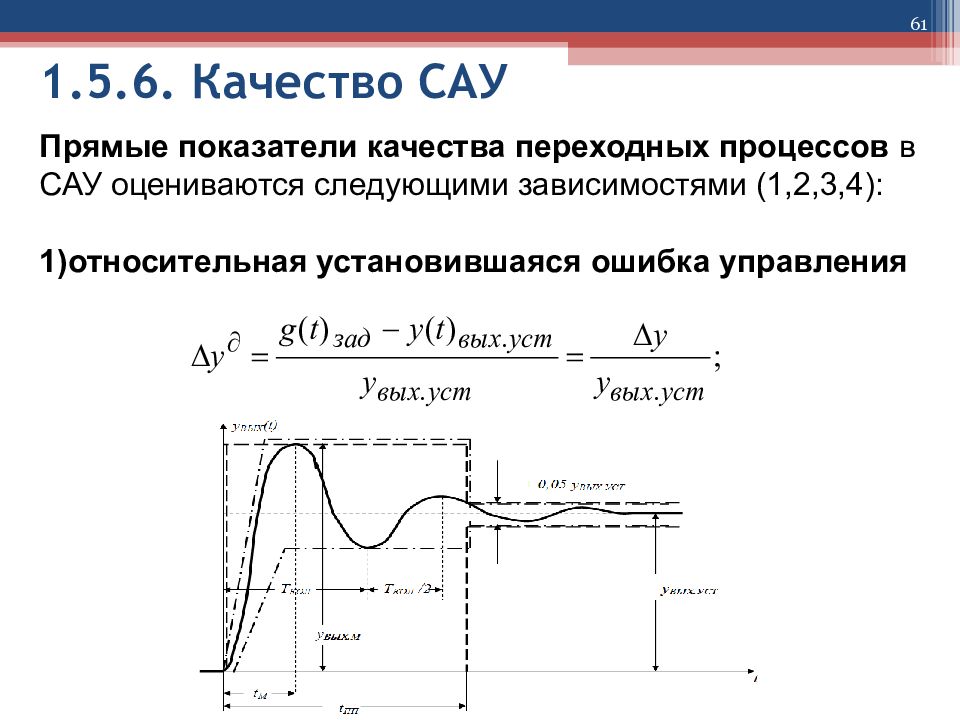
61 1.5.6. Качество САУ Прямые показатели качества переходных процессов в САУ оцениваются следующими зависимостями (1,2,3,4) : относительная установившаяся ошибка управления
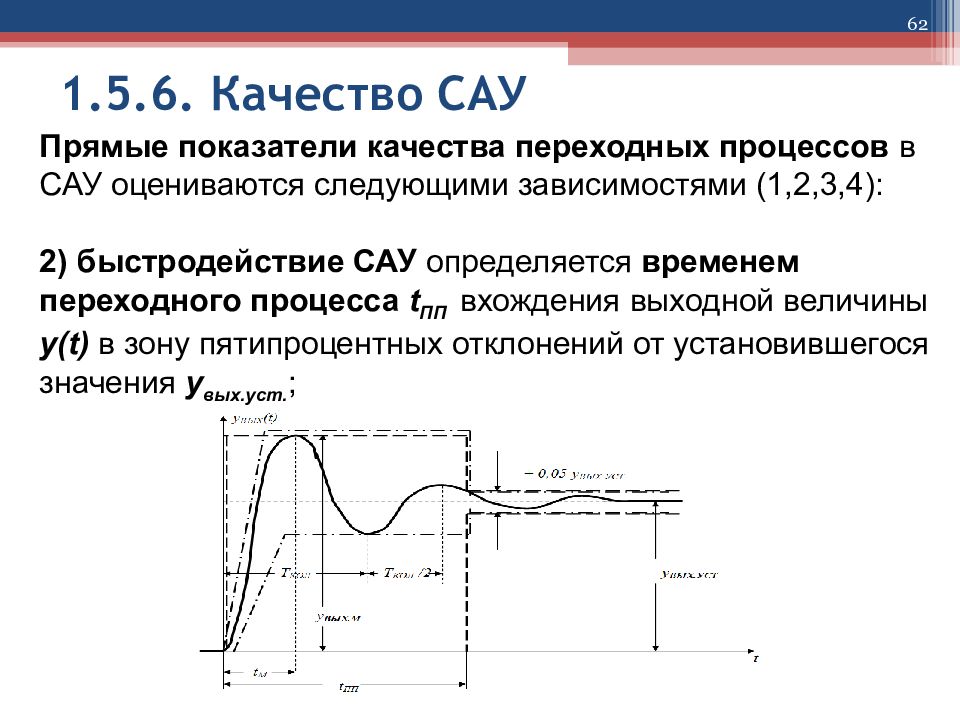
62 1.5.6. Качество САУ Прямые показатели качества переходных процессов в САУ оцениваются следующими зависимостями (1,2,3,4) : 2) быстродействие САУ определяется временем переходного процесса t ПП вхождения выходной величины y ( t ) в зону пятипроцентных отклонений от установившегося значения y вых.уст. ;
63 1.5.6. Качество САУ Прямые показатели качества переходных процессов в САУ оцениваются следующими зависимостями (1,2,3,4) : 3) относительная величина перерегулирования σ характеризует запас устойчивости САУ, который считается достаточным, если перерегулирование не превышает 0,1 – 0,3, редко до 0,5 – 0,7
64 1.5.6. Качество САУ Прямые показатели качества переходных процессов в САУ оцениваются следующими зависимостями (1,2,3,4) : 4) число колебаний управляемой величины y ( t ) также характеризует запас устойчивости САУ, обычно допускается 1–2 колебания, редко – до 4-х.
65
66 1.5.7. Точность САУ Точность САУ при отработке типовых воздействий определяется по величине установившейся ошибки е уст, вычисляемой по теореме о конечном значении функции ошибки:
67 1.5.7. Точность САУ где полученные в разделе 1.4 «ОФП замкнутых САУ» : Ф е (p) – ОФП по ошибке; Ф fi (p) – ОФП по i -му возмущающему воздействию; W(p) – ОФП прямого канала САУ; H i (p) – ОФП канала влияния на выходную величину i -го возмущающего воздействия; W OC (p) – ОФП цепи обратной связи; G(p) и F i (p) – изображения по Лапласу задающего и возмущающих типовых воздействий.
68 1.5.7. САУ ЗАДАННОЙ ТОЧНОСТИ я на выходе замкнутой САУ будет
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
