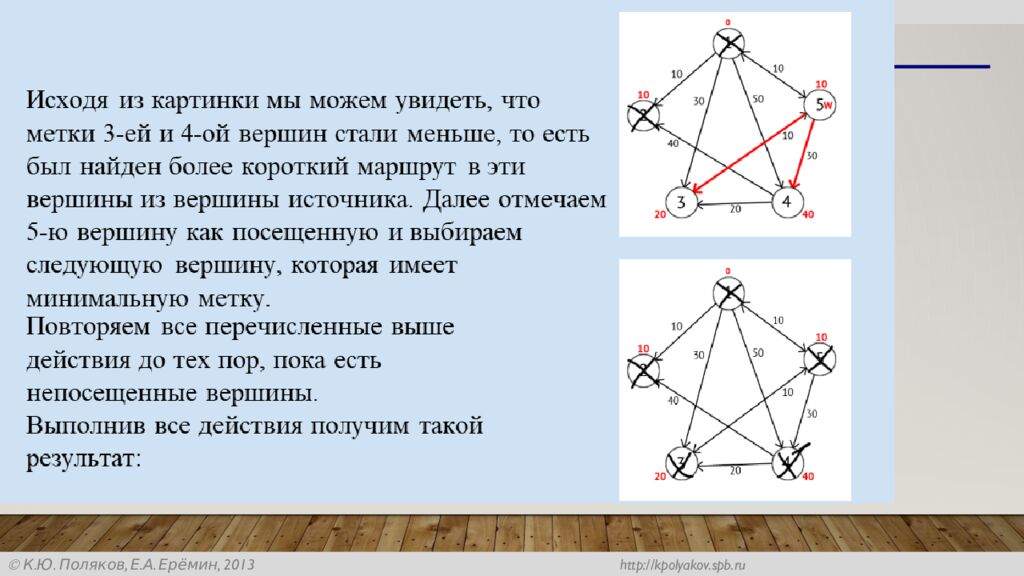
Слайд 2: Проверка ДЗ
Слайд 3: Проверка ДЗ
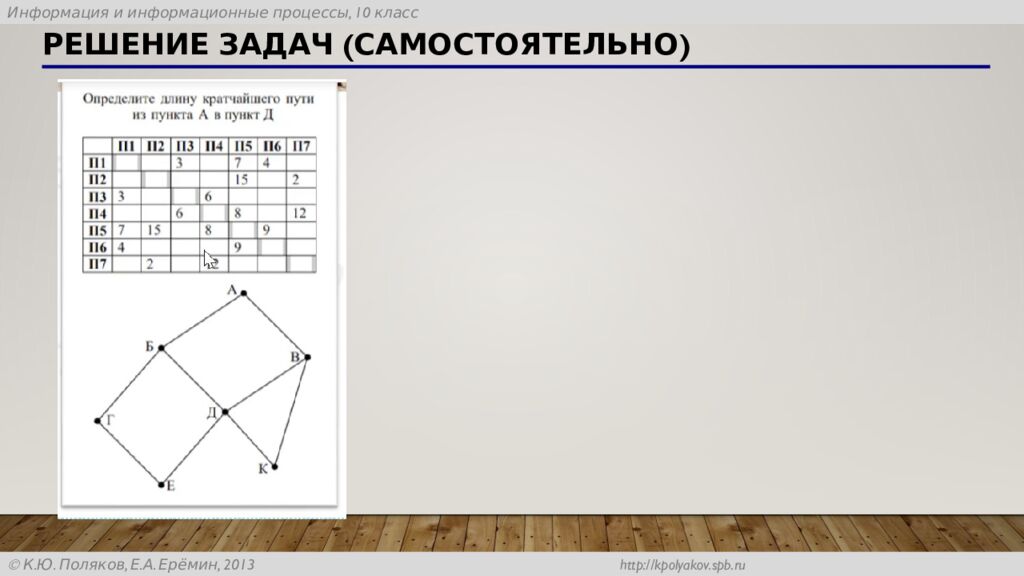
точка Возможные вершины Связи 1 A D E 5 3 6 3 2 B C F G 3 3 4 2 7 2 3 B C F G 2 3 5 3 7 2 4 A D E 2 3 6 3 5 B C F G 1 2 3 3 6 3 6 B C F G 1 2 4 2 5 3 7 A D E Ответ 26
Слайд 4: Проверка ДЗ
1 А DCB 1+4+4=9 2 ACB 5+4=9 3 ACB ADB 3+2=5 1+1=2 4 ACB AEB 2+2=4 3+2=5 Минимальная стоимость перевозки из A в B равна 2 ( таблица 3)
Слайд 5: Видео «Сопоставление графа и весовой матрицы»:
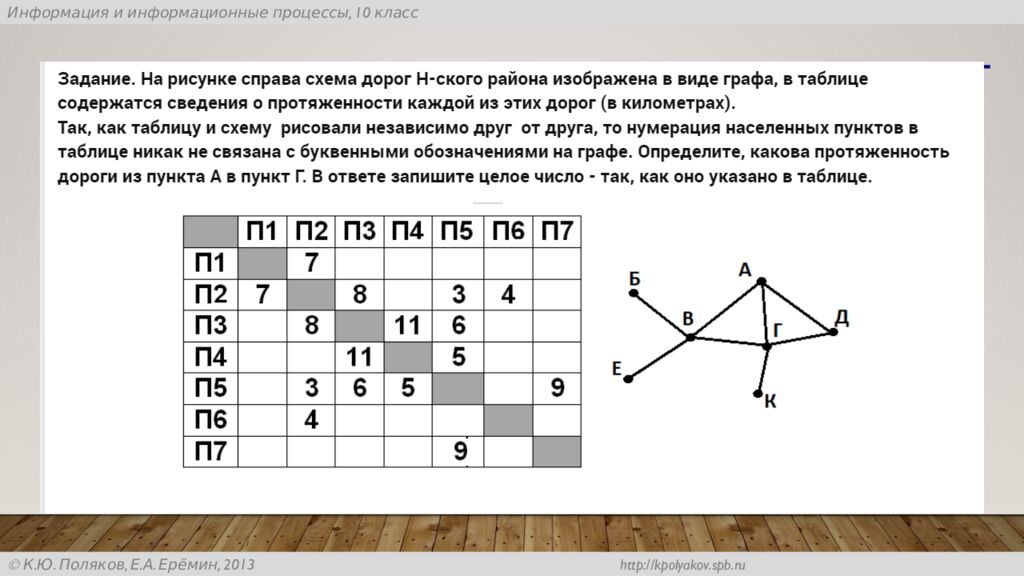
https://uchebnik.mos.ru/material_view/atomic_objects/9309814?menuReferrer=catalogue Граф Таблица А -3 П5 Б – 4 П4 В – 3 П7 Г – 4 п3 Д – 5 П6 Е – 3 П1 Ж – 2 П2 Ответ ЕЖГБАДВ
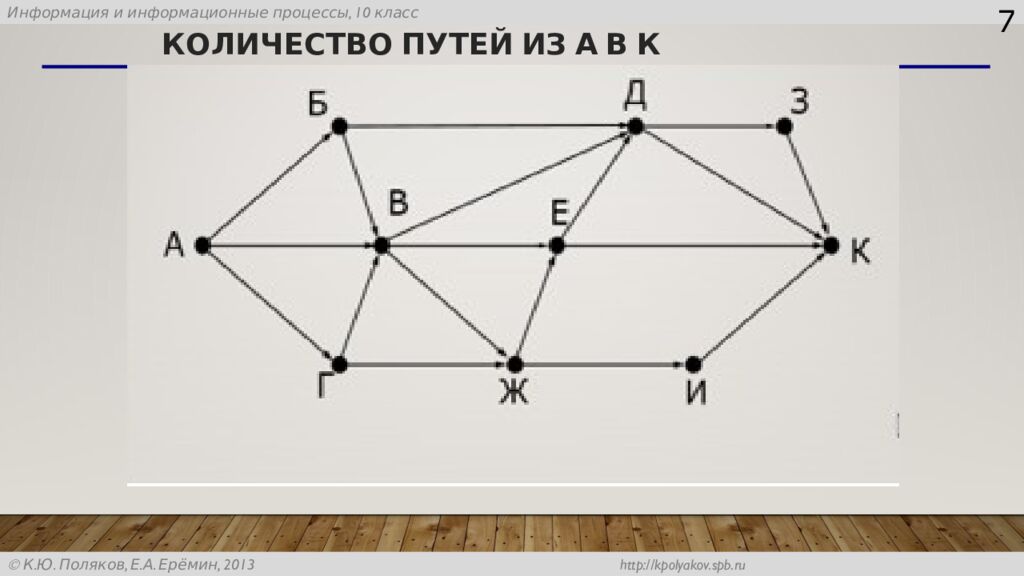
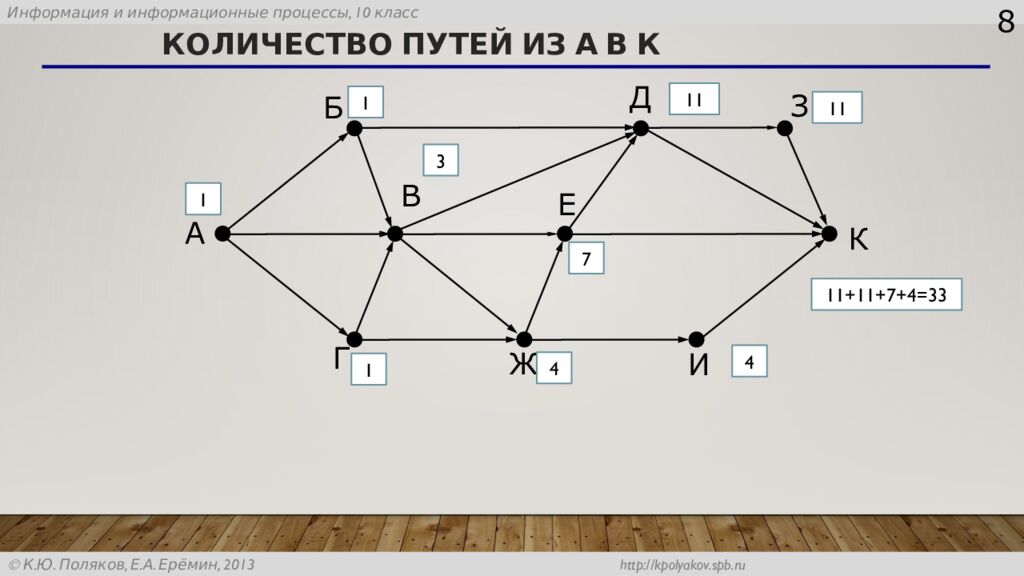
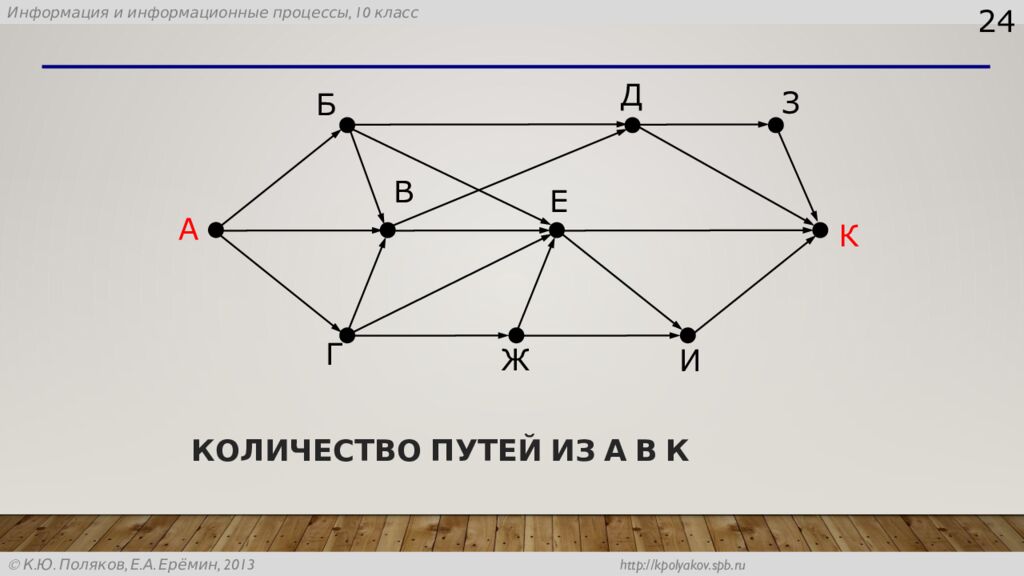
Слайд 8: Количество путей из А в К
8 А Б B Г Д Е Ж З И К 1 7 1 1 3 4 11 11 4 11+11+7+4=33
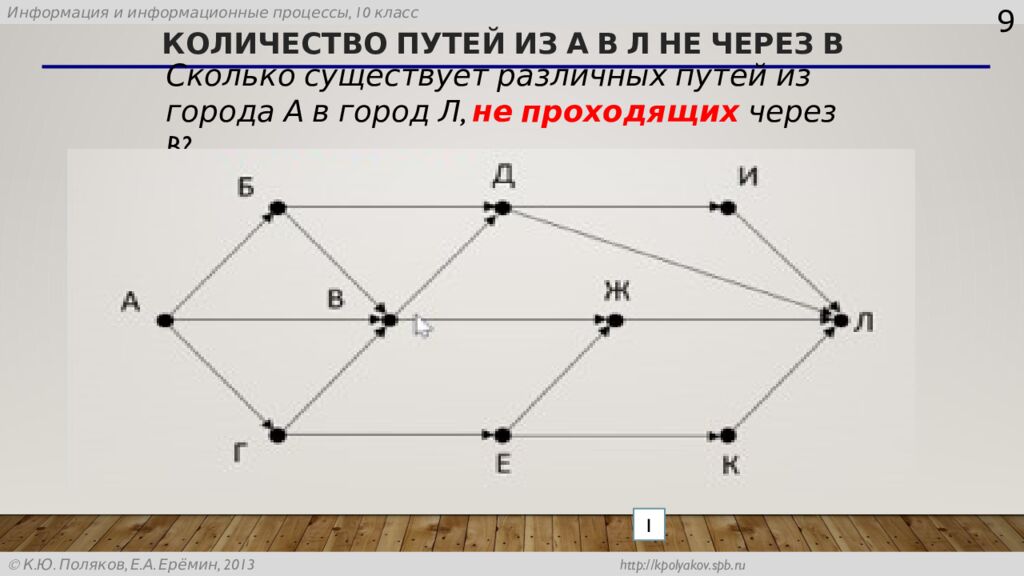
Слайд 9: Количество путей из А в Л не через В
9 Сколько существует различных путей из города А в город Л, не проходящих через B ? 1
Слайд 10: Количество путей из А в Л не через В
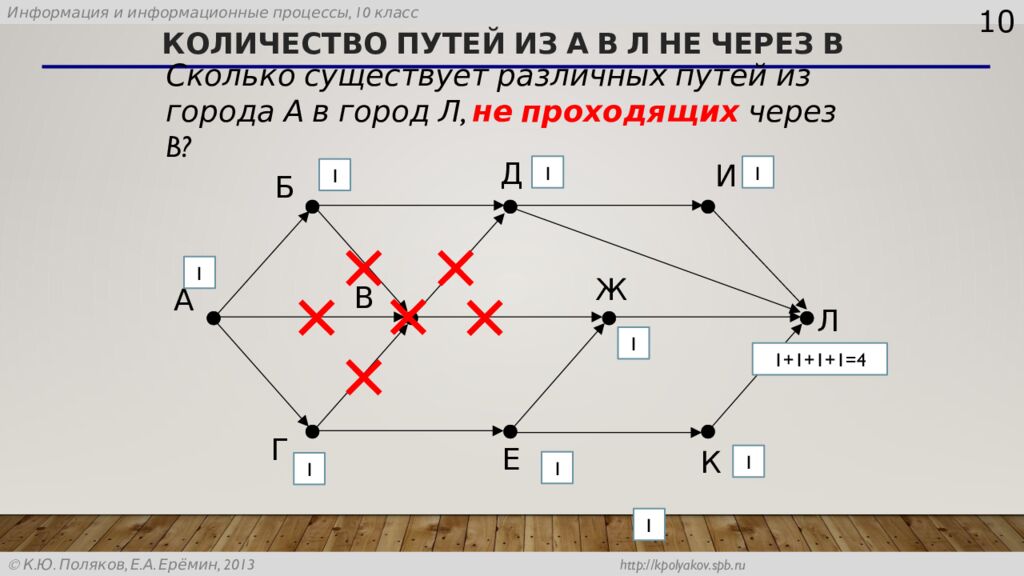
10 А Б В Г Д Е Ж И К Л Сколько существует различных путей из города А в город Л, не проходящих через B ? 1 1 1 1 1 1 1 1 1 1+1+1+1=4
Слайд 11: Количество путей из А в Л через Д
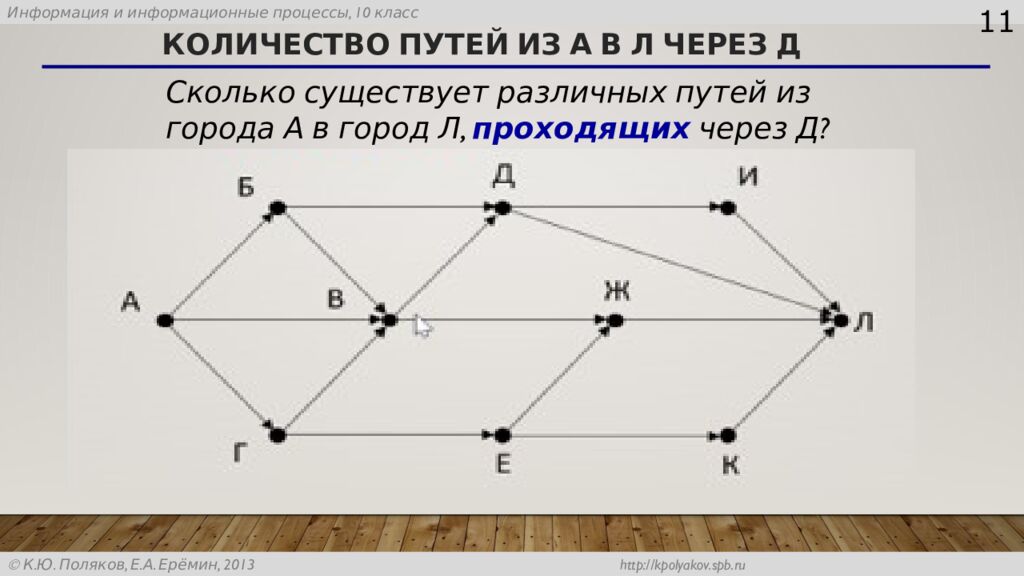
11 Сколько существует различных путей из города А в город Л, проходящих через Д?
Слайд 12: Количество путей из А в Л через Д
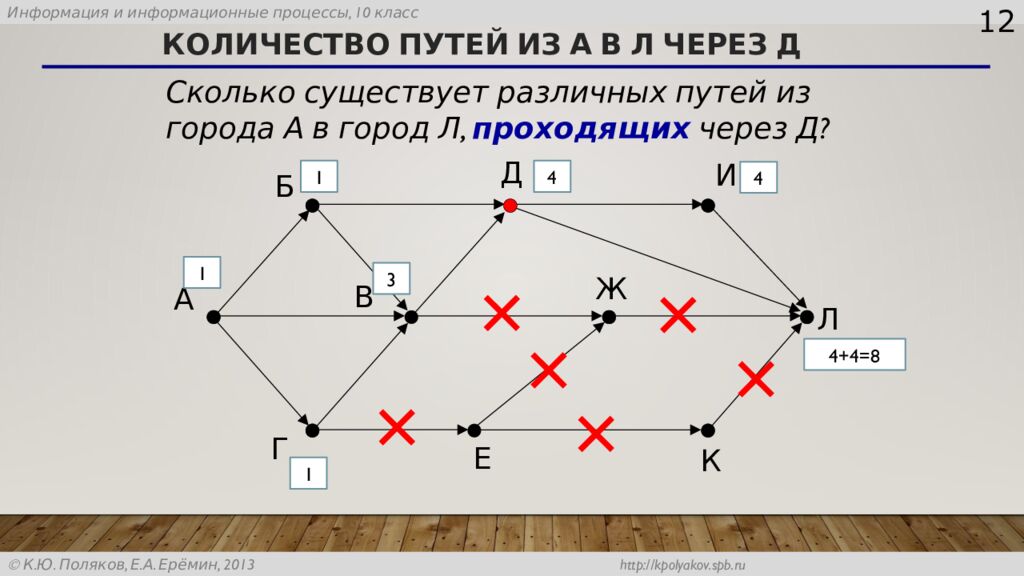
12 А Б В Г Д Е Ж И К Л Сколько существует различных путей из города А в город Л, проходящих через Д? 1 1 1 3 4 4 4+4=8
Слайд 13: подсчёт количества путей в графе с «обязательной» и «избегаемой» вершинами
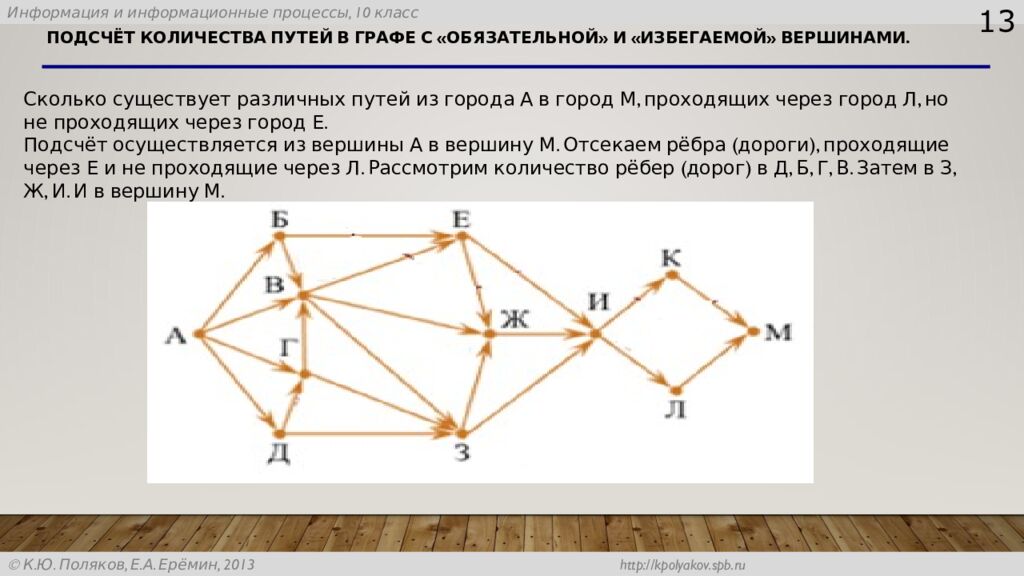
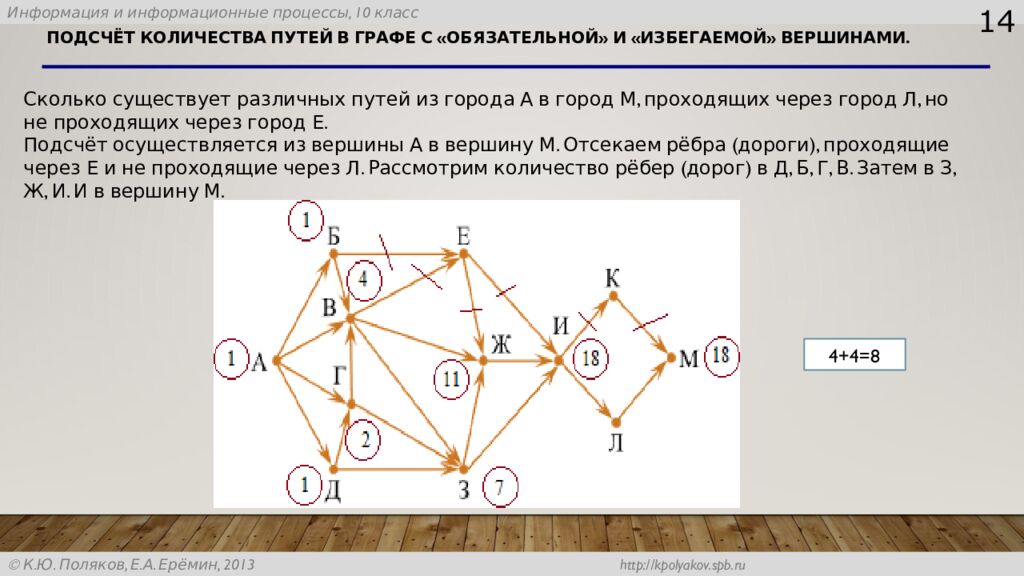
13 Сколько существует различных путей из города А в город М, проходящих через город Л, но не проходящих через город Е. Подсчёт осуществляется из вершины А в вершину М. Отсекаем рёбра (дороги), проходящие через Е и не проходящие через Л. Рассмотрим количество рёбер (дорог) в Д, Б, Г, В. Затем в З, Ж, И. И в вершину М.
Слайд 14: подсчёт количества путей в графе с «обязательной» и «избегаемой» вершинами
14 Сколько существует различных путей из города А в город М, проходящих через город Л, но не проходящих через город Е. Подсчёт осуществляется из вершины А в вершину М. Отсекаем рёбра (дороги), проходящие через Е и не проходящие через Л. Рассмотрим количество рёбер (дорог) в Д, Б, Г, В. Затем в З, Ж, И. И в вершину М. 4+4=8
Слайд 15: Решение задач
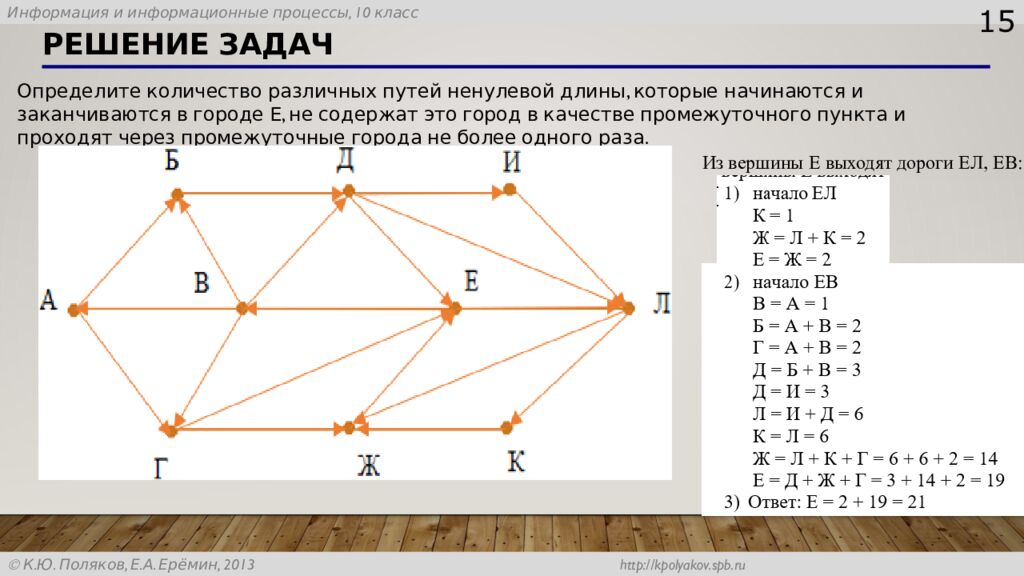
15 Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат это город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза. Решение задач Из вершины Е выходят дороги ЕЛ, ЕВ:
Слайд 21: Домашнее задание
Повторить теоретический материал. Решить задания на слайдах 22-25