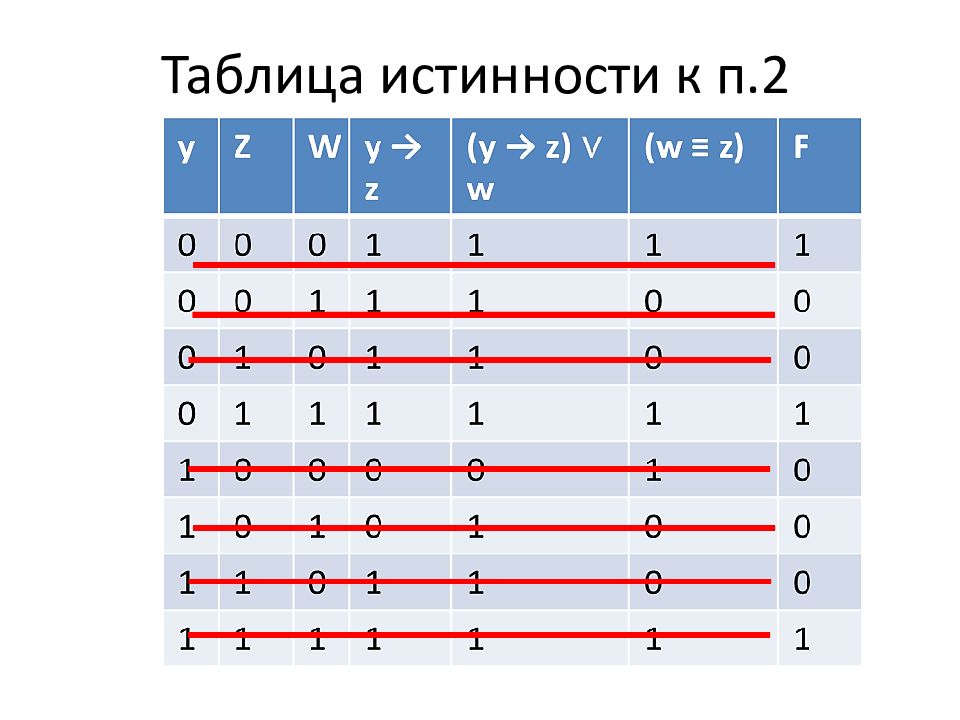
Слайд 2: Логическая функция F задаётся выражением (( y → z) ∨ (¬x ∧ w)) ≡ (w ≡ z )
Перем. 1 Перем. 2 Перем. 3 Перем. 4 Функция F 1 0 0 1 0 0 0 1 1 0 1 1 1) Рассмотрим вторую строку таблицы. Только 1 переменная равна 1, когда остальные равны нулю. Проверим поочередно каждую из них. (приравняем к 1) При х=1 функция истинна, значит можем точно определит перем.4 – х. Х Y Z W 2) Рассмотрим первую строку. Известно, что х=0, тогда можно упростить выражение: ((y → z) ∨ w) ≡ (w ≡ z). Построим таблицу истинности для этого выражения. Из нее получим, что y=0, z=1, w=1. Из этого делаем вывод, что переменная 3 – Y. 3) Оставшиеся переменные w и z соответствуют 1 и 2 столбикам, то есть они разные согласно строке 3. Таким образом вторая часть выражения будет равняться 0, а значит первая тоже должна быть равна 0: (y → z) ∨ (¬x ∧ w). Отсюда следует: y=1, z=0, w=1, x=1.
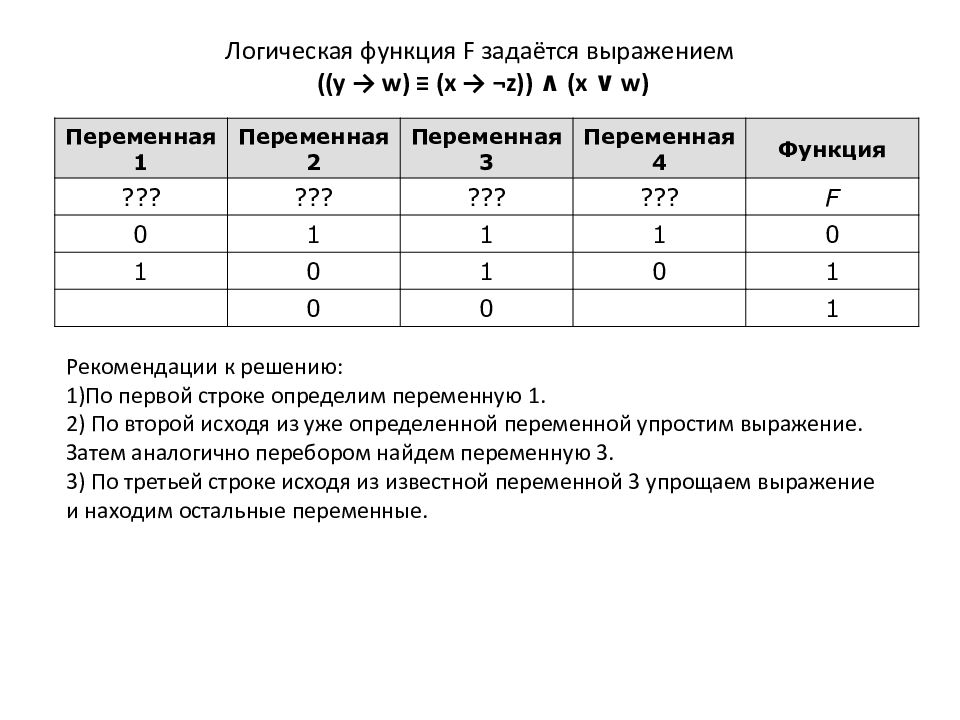
Слайд 4: Логическая функция F задаётся выражением (( y → w) ≡ (x → ¬z)) ∧ (x ∨ w )
Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция ??? ??? ??? ??? F 0 1 1 1 0 1 0 1 0 1 0 0 1 Рекомендации к решению: 1)По первой строке определим переменную 1. 2) По второй исходя из уже определенной переменной упростим выражение. Затем аналогично перебором найдем переменную 3. 3) По третьей строке исходя из известной переменной 3 упрощаем выражение и находим остальные переменные.
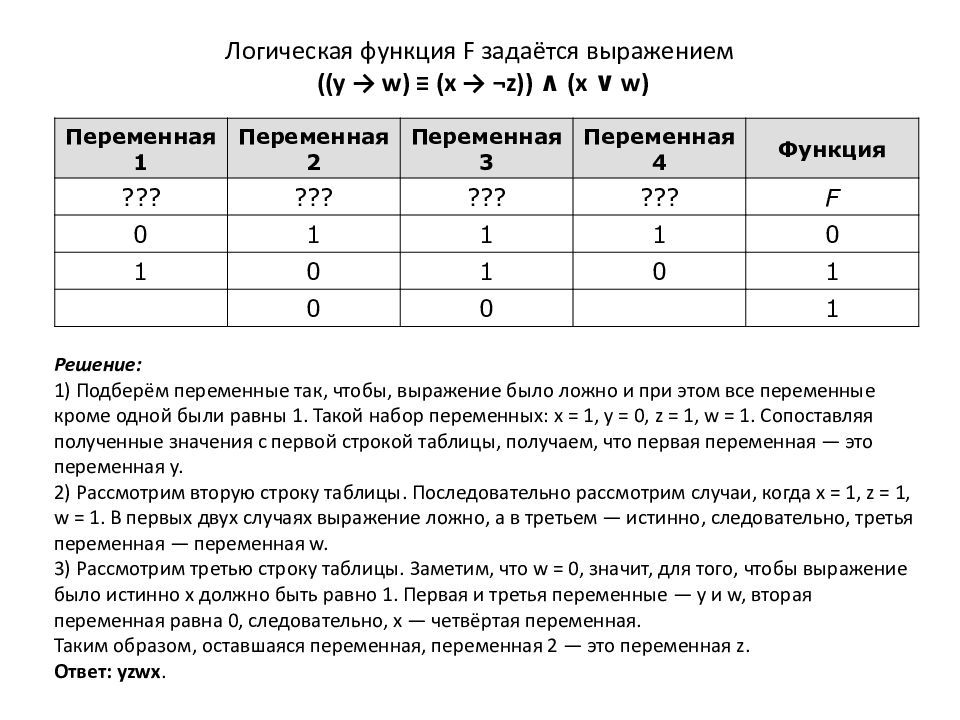
Слайд 5: Логическая функция F задаётся выражением (( y → w) ≡ (x → ¬z)) ∧ (x ∨ w )
Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция ??? ??? ??? ??? F 0 1 1 1 0 1 0 1 0 1 0 0 1 Решение : 1) Подберём переменные так, чтобы, выражение было ложно и при этом все переменные кроме одной были равны 1. Такой набор переменных: x = 1, y = 0, z = 1, w = 1. Сопоставляя полученные значения с первой строкой таблицы, получаем, что первая переменная — это переменная y. 2) Рассмотрим вторую строку таблицы. Последовательно рассмотрим случаи, когда x = 1, z = 1, w = 1. В первых двух случаях выражение ложно, а в третьем — истинно, следовательно, третья переменная — переменная w. 3) Рассмотрим третью строку таблицы. Заметим, что w = 0, значит, для того, чтобы выражение было истинно x должно быть равно 1. Первая и третья переменные — y и w, вторая переменная равна 0, следовательно, x — четвёртая переменная. Таким образом, оставшаяся переменная, переменная 2 — это переменная z. Ответ: yzwx.
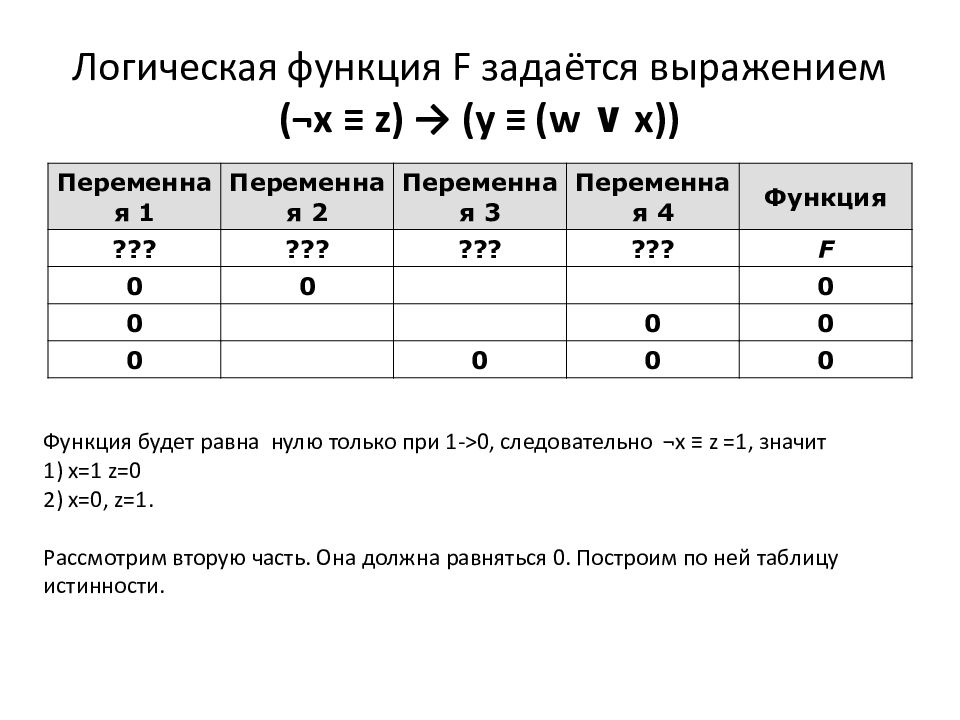
Слайд 6: Логическая функция F задаётся выражением (¬x ≡ z) → (y ≡ (w ∨ x ))
Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция ??? ??? ??? ??? F 0 0 0 0 0 0 0 0 0 0 Функция будет равна нулю только при 1- > 0, следовательно ¬ x ≡ z =1, значит 1) х=1 z=0 2) x=0, z=1. Рассмотрим вторую часть. Она должна равняться 0. Построим по ней таблицу истинности.
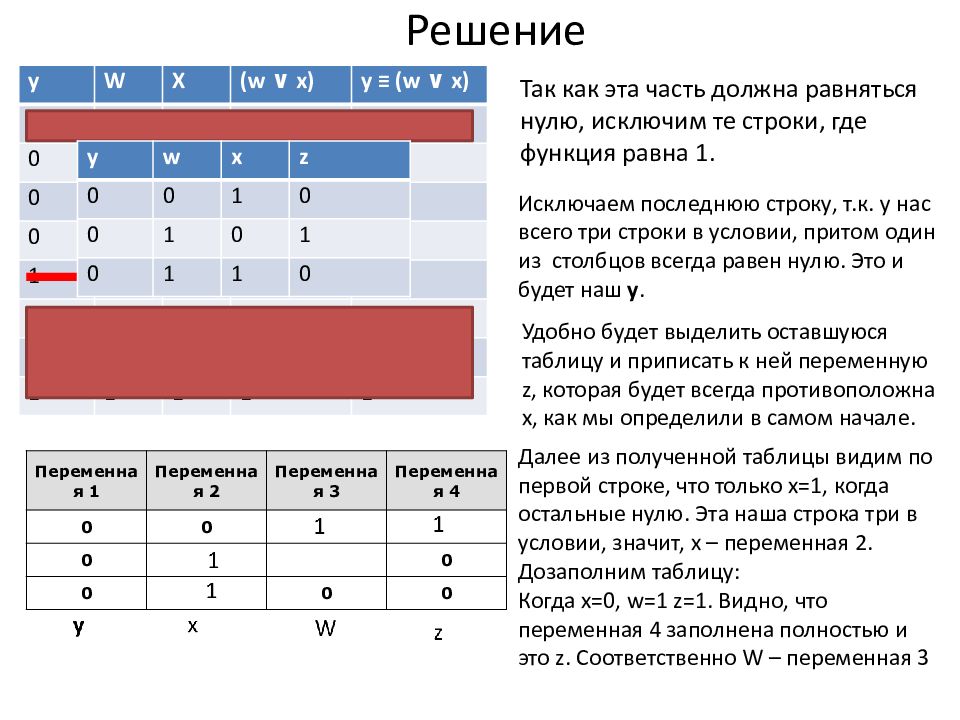
Слайд 7: Решение
Исключаем последнюю строку, т.к. у нас всего три строки в условии, притом один из столбцов всегда равен нулю. Это и будет наш y. Переменная 1 Переменная 2 Переменная 3 Переменная 4 0 0 0 0 0 0 0 y W X (w ∨ x) y ≡ (w ∨ x) 0 0 0 0 1 0 0 1 1 0 0 1 0 1 0 0 1 1 1 0 1 0 0 0 0 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 Так как эта часть должна равняться нулю, исключим те строки, где функция равна 1. Удобно будет выделить оставшуюся таблицу и приписать к ней переменную z, которая будет всегда противоположна х, как мы определили в самом начале. y w x z 0 0 1 0 0 1 0 1 0 1 1 0 Далее из полученной таблицы видим по первой строке, что только х=1, когда остальные нулю. Эта наша строка три в условии, значит, х – переменная 2. Дозаполним таблицу: Когда х=0, w=1 z=1. Видно, что переменная 4 заполнена полностью и это z. Соответственно W – переменная 3
Слайд 8: Условие Фано
Условие Фано : для того, чтобы сообщение, записанное с помощью неравномерного по длине кода, однозначно раскодировалось, достаточно, чтобы никакой код не был началом другого (более длинного) кода. Обратное условие Фано также является достаточным условием однозначного декодирования неравномерного кода. В нём требуется, чтобы никакой код не был окончанием другого (более длинного) кода.
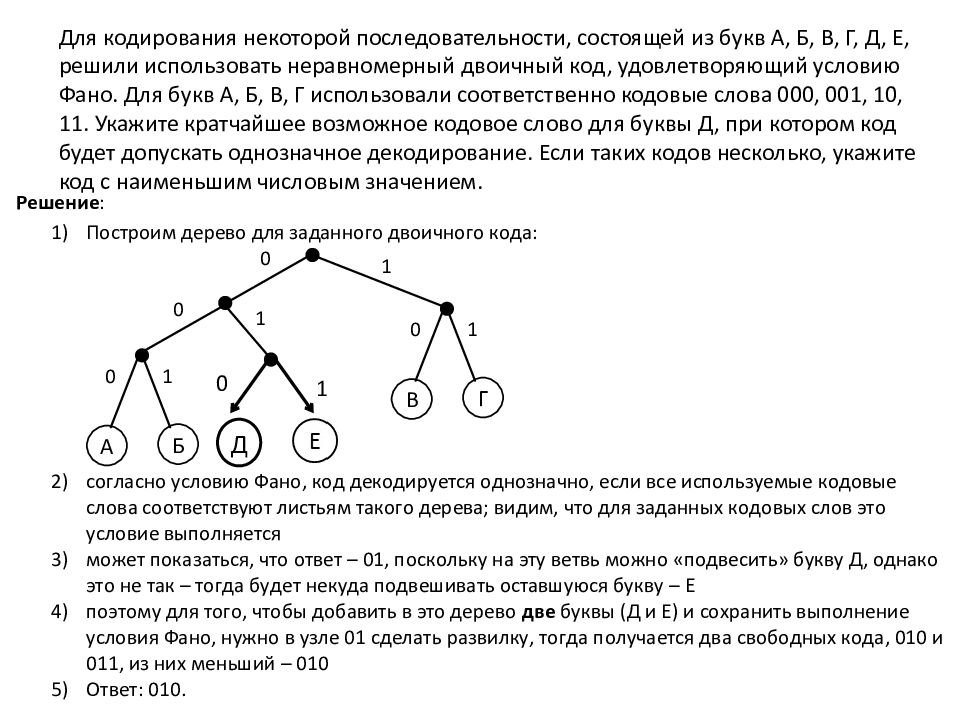
Слайд 9: Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением
0 1 Д
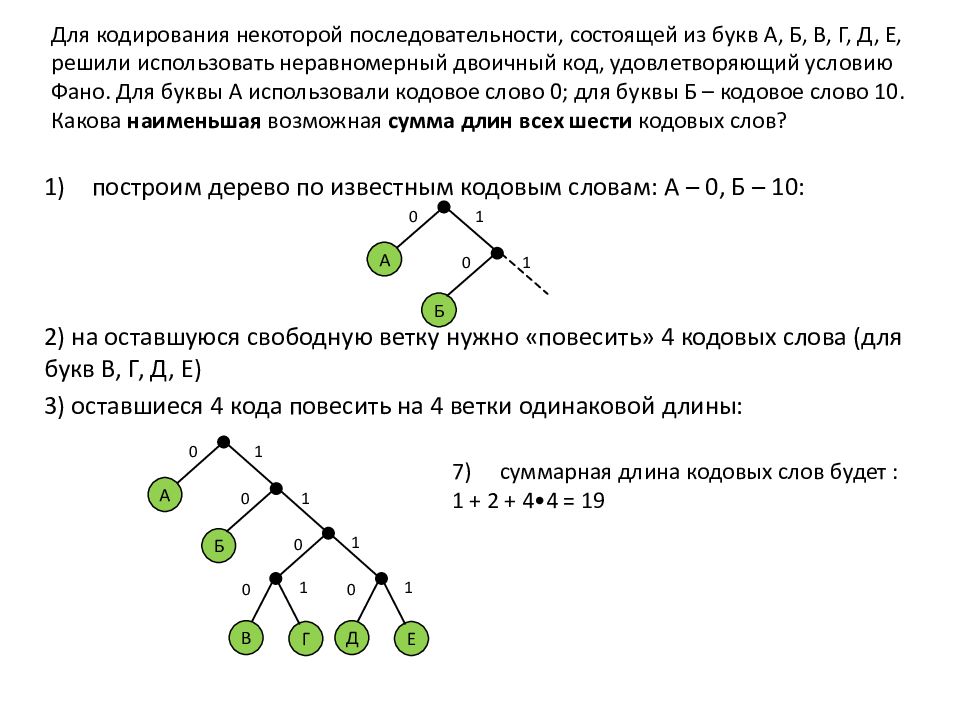
Слайд 10: Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0; для буквы Б – кодовое слово 10. Какова наименьшая возможная сумма длин всех шести кодовых слов?
построим дерево по известным кодовым словам: А – 0, Б – 10 : 2) на оставшуюся свободную ветку нужно «повесить» 4 кодовых слова (для букв В, Г, Д, Е) 3) оставшиеся 4 кода повесить на 4 ветки одинаковой длины: 7) суммарная длина кодовых слов будет : 1 + 2 + 4•4 = 19
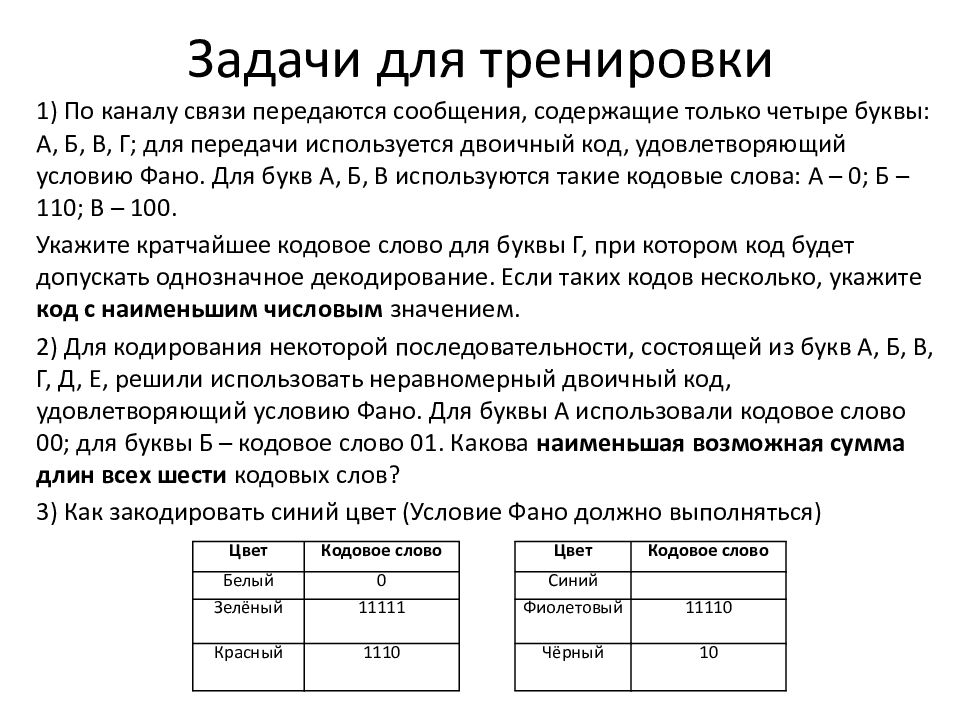
Слайд 11: Задачи для тренировки
1) По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В используются такие кодовые слова: А – 0; Б – 110; В – 100. Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. 2) Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 00; для буквы Б – кодовое слово 01. Какова наименьшая возможная сумма длин всех шести кодовых слов ? 3) Как закодировать синий цвет (Условие Фано должно выполняться) Цвет Кодовое слово Цвет Кодовое слово Белый 0 Синий Зелёный 11111 Фиолетовый 11110 Красный 1110 Чёрный 10
Последний слайд презентации: Занятие №4 Логика. Условие Фано: любое количество символов от нуля ? – ровно один символ
№4. Маски. В каталоге находятся файлы со следующими именами: primera.dat primera.doc merchant.doc k-mer.doc omerta.doc Tamerlan.docx Определите, по какой из масок будет выбрано ровно два файла: 1) * mer ?*.d* 2 ) * mer *?.doc * 3) ?* mer ?*.doc 4 ) *? mer *?.doc*