Слайд 2: Алгебра логики
Алгеброй логики называется аппарат, который позволяет выполнять действия над высказываниями. Действия, которые производятся над высказываниями, записываются в виде логических выражений. Логические выражения могут быть простыми и сложными. Простое логическое выражение состоит из одного высказывания и не содержит логические операции. В простом логическом выражении возможно только два результата — либо «истина», либо «ложь ». Пример высказывания: « Я сегодня получил пятерку по математике». Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания. Пример высказывания: «Я сегодня получил пятерку по математике И физике»
Слайд 3
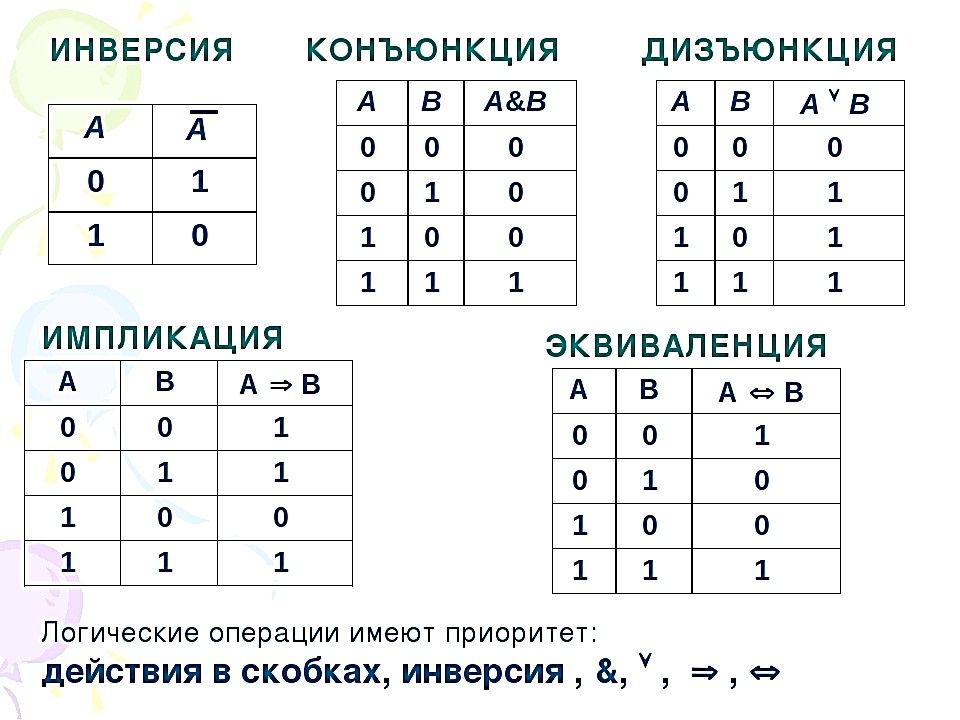
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении, например: таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции; в таблице истинности двуместной логической операции — четыре строки: 4 различных сочетания значений аргументов — 00, 01, 10 и 11 и 4 соответствующих им значения функции; Количество строк таблицы истины рассчитывается по формуле: M = где N – количество переменных ( высказываний), M – количество строк
Слайд 6: Пример №1
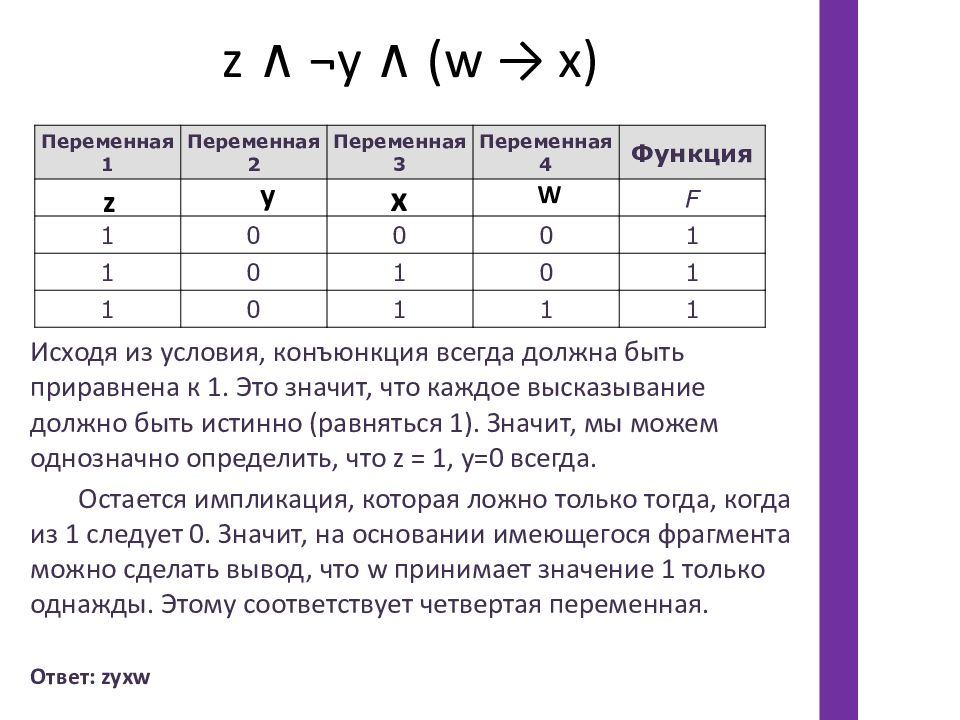
Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x ) На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция ??? ??? ??? ??? F 1 0 0 0 1 1 0 1 0 1 1 0 1 1 1 В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Слайд 7: z ∧ ¬y ∧ (w → x)
Исходя из условия, конъюнкция всегда должна быть приравнена к 1. Это значит, что каждое высказывание должно быть истинно (равняться 1). Значит, мы можем однозначно определить, что z = 1, y=0 всегда. Остается импликация, которая ложно только тогда, когда из 1 следует 0. Значит, на основании имеющегося фрагмента можно сделать вывод, что w принимает значение 1 только однажды. Этому соответствует четвертая переменная. Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция F 1 0 0 0 1 1 0 1 0 1 1 0 1 1 1 z y W x Ответ: zyxw
Слайд 8: Ответ: yxwz
Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция ??? ??? ??? ??? F 1 0 0 0 1 1 0 1 0 1 1 0 1 1 1 Логическая функция F задаётся выражением ¬ x ∧ y ∧ ( z → w ). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
Слайд 9: Пример №2
Перем. 1 Перем. 2 Перем. 3 Функция ??? ??? ??? F 0 1 0 1 1 1 0 1 1 1 1 1 Логическая функция F задаётся выражением (x ∧ y ∧¬z) ∨ (x ∧ y ∧ z) ∨ (x ∧¬y ∧¬z) Решение. Оно равно единице в трех случаях: ( x ∧ y ∧¬z)= 1, (x ∧ y ∧ z) = 1 или (x ∧¬y ∧¬z) = 1. Каждое из этих равенств выполняется только при одном наборе переменных. Первое : x = 1, y = 1, z = 0. Второе: x = 1, y = 1, z = 1. Третье : x = 1, y = 0, z = 0. Так, из второго значения функции видим, что переменная 3 — z. А из первого, что переменная 2 — x, тогда переменная 1 — y. Ответ: yxz.
Слайд 10: Пример №2
Перем. 1 Перем. 2 Перем. 3 Функция ??? ??? ??? F 0 1 0 1 1 1 0 1 1 1 1 1 Логическая функция F задаётся выражением (x ∧ y ∧¬z) ∨ (x ∧ y ∧ z) ∨ (x ∧¬y ∧¬z) Решение 2 способ. 1) Рассмотрим строчку 1, когда две переменные равны 0, а одна = 1. Если х = 0, то каждое выражение будет равно нулю, что противоречит условию. Отсюда делаем вывод, что х всегда равен 1. х=1. Это переменная 2. 2) Выяснив, что х=1 всегда, согласно законам логики преобразуем выражение: (x ∧ y ∧¬z) ∨ (x ∧ y ∧ z) ∨ (x ∧¬y ∧¬z ) = ( 1 ∧ y ∧¬z) ∨ ( 1 ∧ y ∧ z) ∨ ( 1 ∧¬y ∧¬z ) = (y ∧¬z) ∨ (y ∧ z) ∨ (¬y ∧¬z ) =1. Исходя из этого выражения можно судить, о том, что: У=1 z=1 Y=1 z=0 Y=0 z=0. Переменная z принимает значение 0 дважды, что соответствует переменной 3. Ответ : yxz.
Слайд 11
Перем. 1 Перем. 2 Перем. 3 Функция ??? ??? ??? F 0 0 0 1 1 0 0 1 1 0 1 1 Логическая функция F задаётся выражением: (¬ x ∧ y ∧ z ) ∨ (¬ x ∧ y ∧ ¬ z ) ∨ (¬ x ∧ ¬ y ∧ ¬ z ) Рассмотрим данное выражение. Оно равно единице в трех случаях: (¬ x ∧ y ∧ z ) = 1, (¬ x ∧ y ∧ ¬ z ) = 1 или (¬ x ∧ ¬ y ∧ ¬ z ) = 1. Каждое из этих равенств выполняется только при одном наборе переменных. Первое : x = 0, y = 1, z = 1. Второе : x = 0, y = 1, z = 0. Третье : x = y = z = 0. Так, из второго значения функции видим, что переменная 1 — y. А из третьего, что переменная 2 — x, тогда переменная 3 — z. Ответ: yxz.
Слайд 12
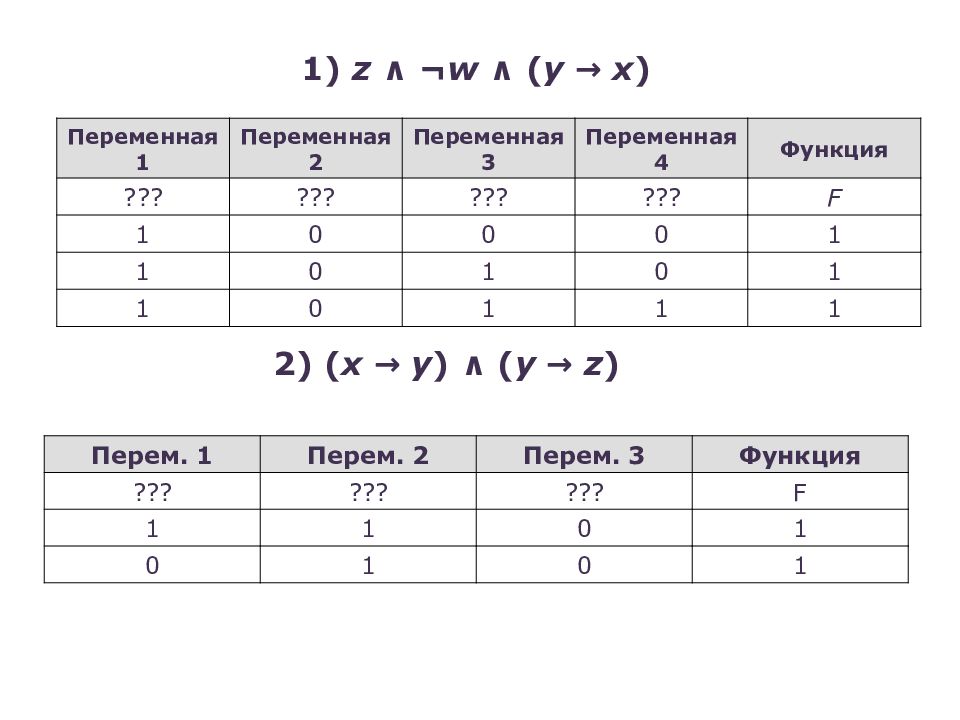
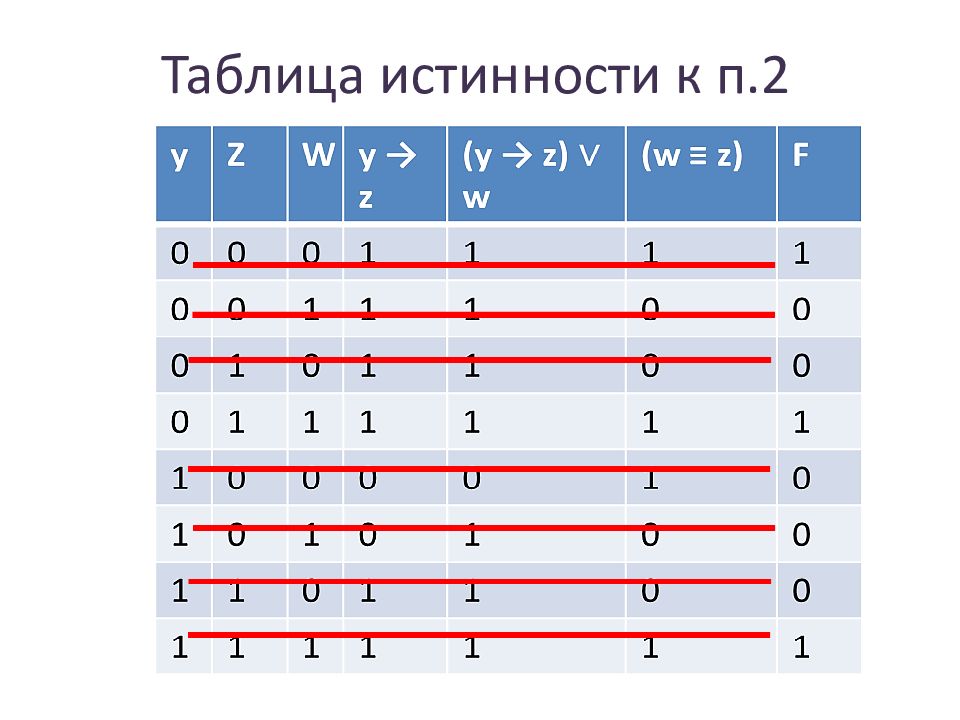
Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция ??? ??? ??? ??? F 1 0 0 0 1 1 0 1 0 1 1 0 1 1 1 1) z ∧ ¬ w ∧ ( y → x ) Перем. 1 Перем. 2 Перем. 3 Функция ??? ??? ??? F 1 1 0 1 0 1 0 1 2) ( x → y ) ∧ ( y → z )
Слайд 13: Логическая функция F задаётся выражением (( y → z) ∨ (¬x ∧ w)) ≡ (w ≡ z )
Перем. 1 Перем. 2 Перем. 3 Перем. 4 Функция F 1 0 0 1 0 0 0 1 1 0 1 1 1) Рассмотрим вторую строку таблицы. Только 1 переменная равна 1, когда остальные равны нулю. Проверим поочередно каждую из них. (приравняем к 1) При х=1 функция истинна, значит можем точно определит перем.4 – х. Х Y Z W 2) Рассмотрим первую строку. Известно, что х=0, тогда можно упростить выражение: ((y → z) ∨ w) ≡ (w ≡ z). Построим таблицу истинности для этого выражения. Из нее получим, что y=0, z=1, w=1. Из этого делаем вывод, что переменная 3 – Y. 3) Оставшиеся переменные w и z соответствуют 1 и 2 столбикам, то есть они разные согласно строке 3. Таким образом вторая часть выражения будет равняться 0, а значит первая тоже должна быть равна 0: (y → z) ∨ (¬x ∧ w). Отсюда следует: y=1, z=0, w=1, x=1.
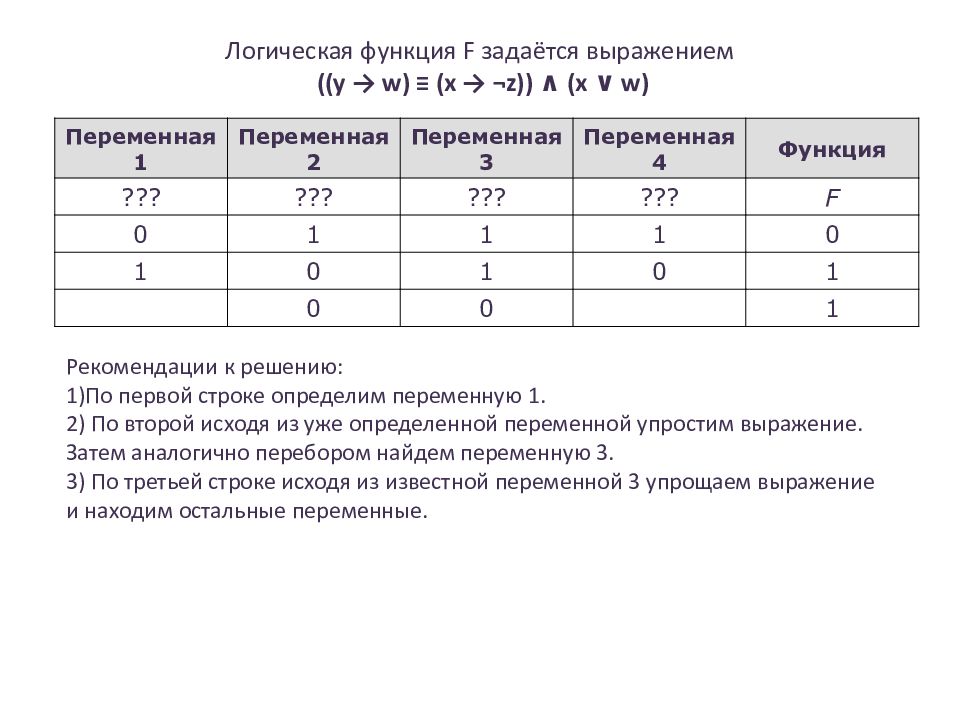
Слайд 15: Логическая функция F задаётся выражением (( y → w) ≡ (x → ¬z)) ∧ (x ∨ w )
Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция ??? ??? ??? ??? F 0 1 1 1 0 1 0 1 0 1 0 0 1 Рекомендации к решению: 1)По первой строке определим переменную 1. 2) По второй исходя из уже определенной переменной упростим выражение. Затем аналогично перебором найдем переменную 3. 3) По третьей строке исходя из известной переменной 3 упрощаем выражение и находим остальные переменные.
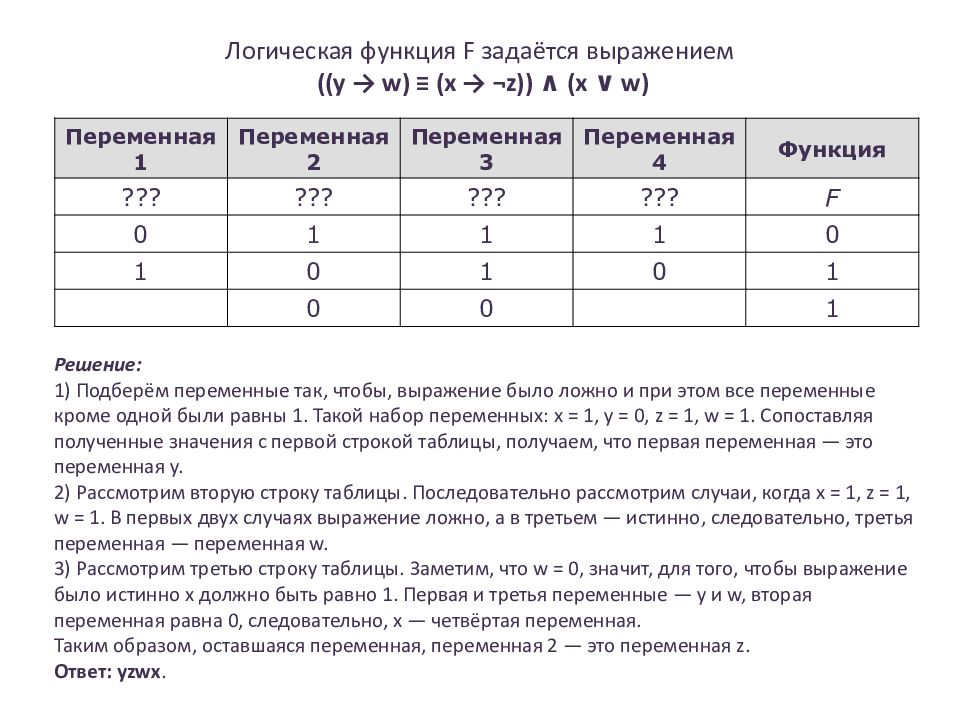
Слайд 16: Логическая функция F задаётся выражением (( y → w) ≡ (x → ¬z)) ∧ (x ∨ w )
Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция ??? ??? ??? ??? F 0 1 1 1 0 1 0 1 0 1 0 0 1 Решение : 1) Подберём переменные так, чтобы, выражение было ложно и при этом все переменные кроме одной были равны 1. Такой набор переменных: x = 1, y = 0, z = 1, w = 1. Сопоставляя полученные значения с первой строкой таблицы, получаем, что первая переменная — это переменная y. 2) Рассмотрим вторую строку таблицы. Последовательно рассмотрим случаи, когда x = 1, z = 1, w = 1. В первых двух случаях выражение ложно, а в третьем — истинно, следовательно, третья переменная — переменная w. 3) Рассмотрим третью строку таблицы. Заметим, что w = 0, значит, для того, чтобы выражение было истинно x должно быть равно 1. Первая и третья переменные — y и w, вторая переменная равна 0, следовательно, x — четвёртая переменная. Таким образом, оставшаяся переменная, переменная 2 — это переменная z. Ответ: yzwx.
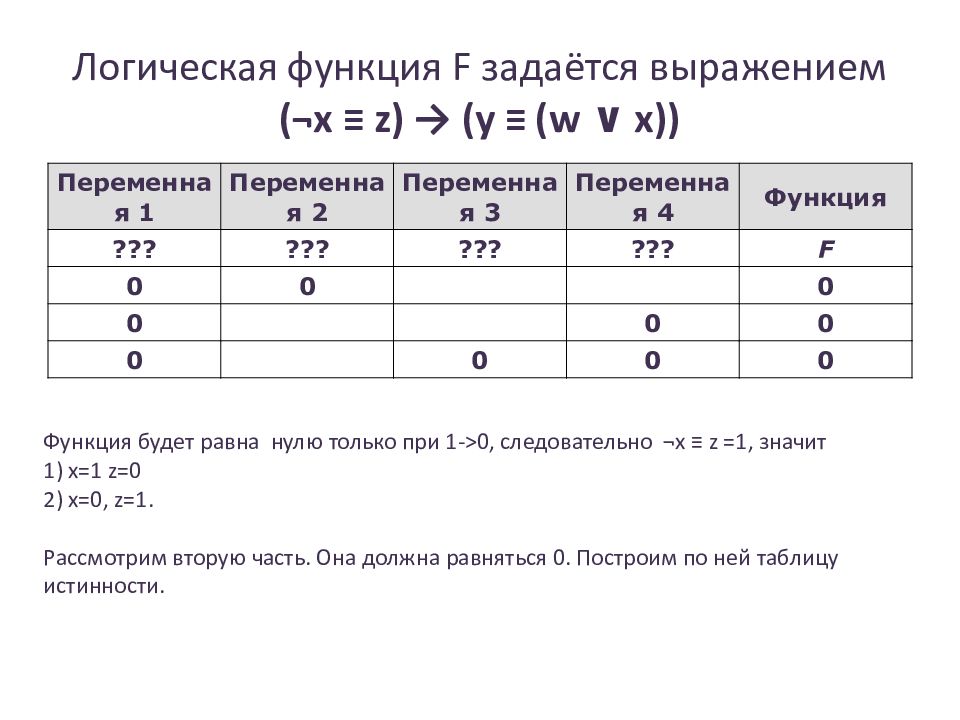
Слайд 17: Логическая функция F задаётся выражением (¬x ≡ z) → (y ≡ (w ∨ x ))
Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция ??? ??? ??? ??? F 0 0 0 0 0 0 0 0 0 0 Функция будет равна нулю только при 1- > 0, следовательно ¬ x ≡ z =1, значит 1) х=1 z=0 2) x=0, z=1. Рассмотрим вторую часть. Она должна равняться 0. Построим по ней таблицу истинности.
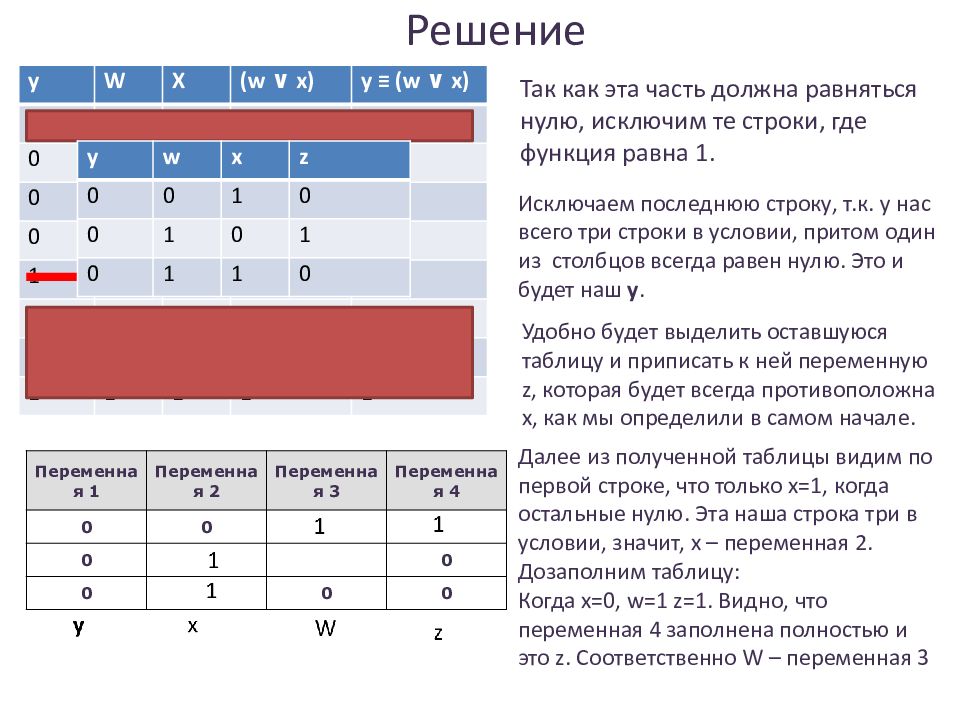
Слайд 18: Решение
Исключаем последнюю строку, т.к. у нас всего три строки в условии, притом один из столбцов всегда равен нулю. Это и будет наш y. Переменная 1 Переменная 2 Переменная 3 Переменная 4 0 0 0 0 0 0 0 y W X (w ∨ x) y ≡ (w ∨ x) 0 0 0 0 1 0 0 1 1 0 0 1 0 1 0 0 1 1 1 0 1 0 0 0 0 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 Так как эта часть должна равняться нулю, исключим те строки, где функция равна 1. Удобно будет выделить оставшуюся таблицу и приписать к ней переменную z, которая будет всегда противоположна х, как мы определили в самом начале. y w x z 0 0 1 0 0 1 0 1 0 1 1 0 Далее из полученной таблицы видим по первой строке, что только х=1, когда остальные нулю. Эта наша строка три в условии, значит, х – переменная 2. Дозаполним таблицу: Когда х=0, w=1 z=1. Видно, что переменная 4 заполнена полностью и это z. Соответственно W – переменная 3
Слайд 19
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом : 1. Строится двоичная запись числа N. 2. К этой записи дописываются справа ещё два разряда по следующему правилу : а ) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001 ; б ) над этой записью производятся те же действия — справа дописывается остаток от деления суммы её цифр на 2. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, которое превышает число 55 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления. 1) Переведем число 55 в двоичную систему: 55 2 = 32+16+4+2+1 = 110111 2 2)По условию наш ответ должен быть больше 55, значит прибавляем единичку справа. 110111+1=111000. Согласно алгоритму последние два разряда – результат его работы. Проверим: 1+1+1 = 3, остаток от деления на 2 будет равен 1, которую было необходимо добавить на предпоследнюю справа позицию, но у нас там 0. Значит это число не подходит. Ближайшим будет число, которое оканчивается на 10. Это число 111010. В 10СС это 32+16+8+2=58. Ответ: 58
Слайд 20: Задача №5
Р-13 (демо-2021). На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1. Строится двоичная запись числа N. 2. К этой записи дописываются справа ещё два разряда по следующему правилу: а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001; б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления.
Слайд 21
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2 ) К этой записи дописываются справа ещё два разряда по следующему правилу: а) находится остаток от деления на 2 суммы двоичных разрядов N, полученный результат дописывается в конец двоичной последовательности N. б ) пункт а повторяется для вновь полученной последовательности. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, которое превышает 123 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе. Рассмотрим числа, большие 123, и найдем минимальное число, которое является результатом работы алгоритма. 124 10 = 1111100 2 — не может являться результатом работы алгоритма. 125 10 = 1111101 2 — не может являться результатом работы алгоритма. 126 10 = 11111 10 2 — является результатом работы алгоритма. Ответ: 126.
Слайд 22
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом. 1. Строится двоичная запись числа N. 2. К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы. Например, двоичная запись 1001 числа 9 будет преобразована в 100111. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма. Укажите минимальное число N, для которого результат работы алгоритма будет больше 115. В ответе это число запишите в десятичной системе счисления. 115 переведем в двоичную систему. 115 = 64+32+16+2+1 = 1110011. Берем следующее число, т.к. по условию оно должно быть больше 115. 116 = 11101 00. Проверим. 00 дописывается, если число N – четное. 11101 – оканчивается на 1, значит оно нечетное. Берем следующее число. 117 = 11101 01 118 = 11101 10 119 = 11101 11 – алгоритм выполнился, значит определяем N = 16+8+4+1=29 Ответ: 29 N
Слайд 23
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1. Строится двоичная запись числа N. 2. К этой записи дописываются справа ещё два разряда по следующему правилу : а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001 ; б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите такое наименьшее число N, для которого результат работы алгоритма больше 97. В ответе это число запишите в десятичной системе счисления. Посмотрим на чётные числа, превосходящие 97. 98 = 11000 10 — на конце 10, но сумма остальных разрядов чётна, не подходит. 100 = 11001 00 — на конце 00, но сумма остальных разрядов нечётна, не подходит. 102 = 11001 10 — на конце 10, а сумма остальных разрядов нечётна. Число подходит значит, число, из которого оно было получено, равно 11001 = 16+8+1=25. Ответ: 25