Первый слайд презентации: Разбор 5 задания ЕГЭ по информатике
Слайд 2: Содержание
1.Условие Фано. 2.Пример №1 3.Пример №2 4.Пример №3 5.Пример №4
Условие Фано : для того, чтобы сообщение, записанное с помощью неравномерного по длине кода, однозначно раскодировалось, достаточно, чтобы никакой код не был началом другого (более длинного) кода. Обратное условие Фано также является достаточным условием однозначного декодирования неравномерного кода. В нём требуется, чтобы никакой код не был окончанием другого (более длинного) кода. Для возможности однозначного декодирования досточно выполнения одного из условий — или прямого, или обратного. Заметим, что существуют варианты неравномерного кодирования, для которых оба условия нарушены, и тем не менее они однозначно раскодируемые.
А Б 1 0 1 0 В 1 Г 0 1 0 Д Е 1 0 А Б 1 0 1 0 3) оставшиеся 4 кода повесить на 4 ветки одинаковой длины: 4) суммарная длина кодовых слов будет в этом случае меньше, чем в предыдущем случае: 1 + 2 + 4·4 = 19 Ответ: 19. это задание удобнее решать с помощью дерева; условие Фано выполняется тогда, когда все выбранные кодовые слова заканчиваются в листьях дерева построим дерево по известным кодовым словам: А – 0, Б – 10:
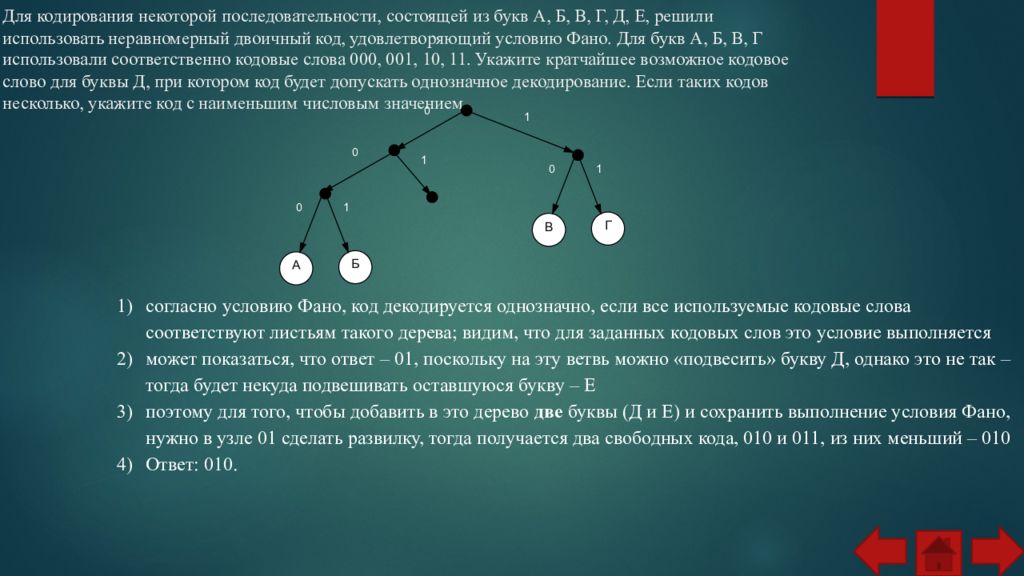
Слайд 5: Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением
А Б 0 0 0 1 1 1 В Г 0 1 согласно условию Фано, код декодируется однозначно, если все используемые кодовые слова соответствуют листьям такого дерева; видим, что для заданных кодовых слов это условие выполняется может показаться, что ответ – 01, поскольку на эту ветвь можно «подвесить» букву Д, однако это не так – тогда будет некуда подвешивать оставшуюся букву – Е поэтому для того, чтобы добавить в это дерево две буквы (Д и Е) и сохранить выполнение условия Фано, нужно в узле 01 сделать развилку, тогда получается два свободных кода, 010 и 011, из них меньший – 010 Ответ: 010.
Слайд 6: По каналу связи с помощью равномерного двоичного кода передаются сообщения, содержащие только 4 буквы: X, Y, Z, W ; для кодировки букв используются кодовые слова длины 5. При этом для набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях. Это свойство важно для расшифровки сообщений при наличии помех. Для кодирования букв X, Y, Z используются 5-битовые кодовые слова: X : 01111, Y : 00001, Z : 11000. Определите 5-битовое кодовое слово для буквы W, если известно, что оно начинается с 1 и заканчивается 0
По условию кодовое слово для буквы W соответствует маске 1***0, где вместо звёздочек можно поставить 0 или 1. Найдем расстояния Хэмминга – количество позиций, в которых отличается это кодовое слово от известных кодовых слов букв X, Y и Z : X: 01111 Y: 00001 Z: 11000 W: 1***0 W: 1***0 W: 1***0 2+? 2+? 0+? Знаки вопроса обозначают неизвестные неотрицательные числа – количество различающихся позиций в тех битах, которые в кодовом слове для буквы W неизвестны. 3) Как видим, наиболее критичная ситуация сложилась для пары Z - W. Для того, чтобы эти кодовые слова различались в трёх позициях, все неизвестные биты кодового слова буквы W должны иметь значения, обратные соответствующим битам кодового слова для буквы Z, то есть, W = 10110 4) Проверяем полученное кодовое слово: находим расстояние Хэмминга в парах X - W и Y - W : X: 01111 Y: 00001 Z: 11000 W: 10110 W: 10110 W: 10110 3 4 3 5) Как видим, для все пар расстояние не меньше трёх, что соответствует условию задачи. 6) Ответ: 10110.
Слайд 7: Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0, для буквы Б – кодовое слово 110. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов? 1) 7 2) 8 3) 9 4) 10
А Б 1 0 1 0 0 В Г условие Фано означает, что ни одно кодовое слово не совпадает с началом другого кодового слова; при этом в дереве кода все кодовые слова должны располагаться в листьях дерева, то есть в узлах, которые не имеют потомков; построим дерево для заданных кодовых слов А – 0 и Б – 110: штриховыми линиями отмечены две «пустые» ветви, на которые можно «прикрепить» листья для кодовых слов букв В (10) и Г (111) таким образом, выбрав кодовые слова А – 0, Б – 110, В – 10, Г – 111, получаем суммарную длину кодовых слов 9 символов Ответ: 3.
Слайд 8: Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 0; Б – 100; В – 1010; Г – 111; Д – 110. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать? 1) для буквы В – 101 2) это невозможно 3) для буквы В – 010 4) для буквы Б – 10
код однозначно декодируется, если выполняется условие Фано или обратное условие Фано ; в данном случае «прямое» условие Фано выполняется: с кода буквы А (0) не начинается ни один другой код, оставшиеся короткие коды (Б, Г и Д) не совпадают с началом длинного кода буквы В; таким образом, при сокращении нужно сохранить выполнение условия Фано вариант 3 не подходит, потому что новый код буквы В начинается с 0 (кода А), поэтому условие Фано нарушено вариант 4 не подходит, потому что код буквы В начинается с 10 (нового кода б), поэтому условие Фано нарушено вариант 1 подходит, условие Фано сохраняется (все трёхбитные коды различны, ни один не начинается с 0) Ответ: 3.