1 Учебные вопросы: Определение объема выборки Точечные и интервальные оценки вариационного ряда Характеристики вариационного ряда Измерение вариации признака Статистические критерии согласия Статистические методы обработки экспериментальных данных
2 Лекция 3: Числовые характеристики статистического распределения. Приложения математической статистики для решения правовых задач Учебный вопрос 1: Определение объема выборки
3 1. Определение объема выборки На практике часто возникает вопрос «Какой объем должна иметь выборка, чтобы получить результаты нужной точности?» Конечно, чем большее количество первичного материала имеет исследователь, тем не хуже. Однако из практики социально-правовых исследований известно, что чем больше первичного материала, тем больше необходимо провести вычислений, и, соответственно увеличиваются затраты на получение и обработку этого материала Поэтому целесообразно ориентироваться на тот минимальный объем, который экономичен и дает возможность получить удовлетворительные результаты
4 1. Определение объема выборки Объем выборки в существенной мере зависит от способа организации выборки. Различают следующие способы отбора выборочных данных: - собственно случайный отбор; - механический отбор ; - типический отбор; - серийный (гнездовой) отбор ; - комбинированный отбор Наиболее доступным и распространенным является собственно случайный отбор
5 1. Определение объема выборки. Собственно случайный отбор Этот способ означает выборку конкретных единиц из генеральной совокупности без дробления генеральной совокупности на группы. При этом существуют два варианта отбора: - повторный (отобранная единица вновь участвует в последующей процедуре отбора); - бесповторный (отобранная единица не участвует в последующей процедуре отбора)
6 Собственно случайный отбор: примеры бесповторной и повторной выборок В архиве суда тома уголовных дел отбираются и откладываются в сторону – это бесповторная выборка В архиве суда тома уголовных дел отбираются по их номеру несколькими независимыми экспертами – это повторная выборка
7 Собственно случайный отбор Целями выборочного исследования могут быть: а) изучение некоторых средних характеристик: - средний срок осуждения; - количество судимостей; - средний возраст освобождающихся из мест лишения свободы и др.; б) изучение долей определенных категорий в генеральной совокупности: - доля рецидивистов среди содержащихся в исправительно-трудовой колонии строгого режима; - доля осужденных за кражи; - доля ложных сигналов в дежурную часть органа внутренних дел и др.
8 Соотношения для определения объема выборки В зависимости от цели социально-правового исследования различаются и формальные соотношения для объема проектируемой выборки Способ отбора Повторный Бесповторный Изучение средних величин Изучение долей
9 Собственно случайный отбор В таблице приняты следующие обозначения: σ – среднее квадратическое отклонение; δ – доля определенных элементов в генеральной совокупности; N – объем генеральной совокупности; Δ – требуемая точность оценки характеристик генеральной совокупности; t - параметр, связанный с вероятностью, надежностью получения оценки
10 Собственно случайный отбор В связи с тем, что величины σ и δ априори неизвестны, рекомендуется брать их приближенные оценки, полученные в других исследованиях или наблюдениях В частности, если даже приблизительно неизвестна доля изучаемых элементов в генеральной совокупности, то следует вместо произведения δ(1- δ) подставить в формулы для объемов выборки его максимальное значение, равное 0,25
В этом случае соотношения во второй строке таблицы примут вид: - для повторной выборки; - для бесповторной выборки
12 Собственно случайный отбор При очень больших (более 1000 единиц) объемах генеральной совокупности формулы для повторной и бесповторной выборок практически совпадают При вероятности (надежности) 0,95 обеспечения заданной точности выборочных оценок t = 2, а при вероятности 0,99 - t = 3 В социально-правовых исследованиях, как правило, надежность в 95% является вполне приемлемой
13 Пример 1 проектирования выборочного наблюдения Пусть необходимо определить средний срок расследования преступлений в N -ом управлении внутренних дел Требуемая точность Δ – одна неделя Общее число уголовных дел в последний год – 15000 Требуемая надежность – 95% (то есть t = 2) Произведенные пробные выборки дали приближенную оценку для дисперсии σ2 = 49
14 Пример 1 проектирования выборочного наблюдения По формуле для бесповторной выборки применительно к средним величинам получаем объем выборочной совокупности для указанных условий n = 194 (проверить самостоятельно) Поскольку объем генеральной совокупности достаточно велик, то можно воспользоваться более простой формулой для повторной выборки В этом случае n = 196 (проверить самостоятельно)
15 Пример 2 проектирования выборочного наблюдения Пусть необходимо провести выборочное наблюдение для оценки доли осужденных за кражи, содержащихся в колонии общего режима с фактической наполняемостью в 1200 человек Если никаких предварительных данных о размере этой доли не имеется то произведение δ(1- δ) в формуле таблицы заменяем на 0,25 Требуемая точность определения доли – 5% с надежностью 0,95 Воспользовавшись выражением для бесповторной выборки, оцениваем ее объем n = 303
16 Собственно случайный отбор Основной принцип организации собственно-случайной выборки – это обеспечение равной возможности быть отобранным каждому элементу генеральной совокупности Для этого используются таблицы случайных чисел или датчики случайных чисел для ЭВМ
17 Механический отбор При механическом отборе генеральная совокупность «механически» делится на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект Примеры: - если нужно отобрать для анализа личности правонарушителя 20% уголовных дел, связанных с совершением тяжких телесных повреждений, то отбирают каждое пятое дело; - если требуется отобрать 5% уголовных дел, то отбирают каждое двадцатое
18 Механический отбор Можно пронумеровать элементы генеральной совокупности, а затем в зависимости от объема выборки, установив шаг отбора, произвести их отбор Иногда механический отбор может не обеспечить репрезентативность выборки
19 Типический отбор При типическом отборе генеральная совокупность по тому или иному признаку делится на типические группы таким образом, чтобы максимально уменьшить в каждой типической группе колеблемость признака Количество единиц из каждой типической группы выбирается пропорционально среднему квадратическому отклонению признака в этой группе При типическом отборе получаются более точные результаты, чем при механическом отборе
20 Серийный (гнездовой) отбор При серийном отборе генеральную совокупность делят на ряд групп (серий), а затем случайным образом производят выборку из них. Серии, попавшие в выборку, обследуются сплошным образом Серийная выборка применяется в том случае, когда сложно организовать выборочное наблюдение путем собственно случайного отбора, механического отбора или типического отбора в силу ограниченности ресурсов (людских, материальных и др.) участников выборочного наблюдения Пользуются серийным отбором тогда, когда обследуемый признак колеблется в различных сериях незначительно
21 Комбинированный отбор При комбинированном отборе отбор проводится следующим образом: - на первом этапе проводится выборочный отбор серий одинакового объема; - на втором этапе простым случайным отбором выбирают несколько серий; - на третьем этапе из каждой серии простым случайным отбором извлекают отдельные объекты, то есть выборочный отбор единиц из этих серий
22 Лекция 3: Числовые характеристики статистического распределения. Приложения математической статистики для решения правовых задач Учебный вопрос 2: Точечные и интервальные оценки вариационного ряда
23 2. Точечные и интервальные оценки вариационного ряда Оценки вариационного ряда могут быть: - точечными; - интервальными Точечной называют оценку, определяемую одним числом При выборке малого объема точечная оценка может существенно отличаться от оцениваемого параметра, и, как следствие, приводит к грубым ошибкам По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками
24 2. Точечные и интервальные оценки вариационного ряда Интервальной называют оценку, определяемую двумя числами – концами интервала Интервальная оценка, в отличие от точечной, позволяют установить: - точность оценок; - надежность (доверительную вероятность) оценок
25 Точность оценки вариационного ряда Точностью оценки называют некоторое положительное число δ, с помощью которого можно определить абсолютную величину разности между действительным значением неизвестного параметра R и найденной по данным выборки статистической характеристикой ( R * ), служащей оценкой этого неизвестного параметра R То есть если δ > 0 и | R – R * | < δ, то, чем меньше δ, тем оценка точнее
26 Точность оценки вариационного ряда Однако статистические методы не позволяют категорически утверждать, что оценка R * удовлетворяет неравенству | R – R * | < δ Можно говорить лишь о некоторой вероятности γ, с которой это неравенство выполняется Поэтому при интервальной оценке вводят понятие надежности (доверительной вероятности) оценки
27 Надежность оценки вариационного ряда Надежностью (доверительной вероятностью) оценки R по R * называют вероятность γ, с которой осуществляется неравенство | R – R * | < δ. Обычно надежность оценки задается наперед, причем в качестве γ берут значение, близкое к 1 (обычно это: 0,95; 0,99; 0,999)
28 Надежность оценки вариационного ряда Пусть вероятность того, что | R – R * | < δ, равна γ : P [ | R – R * | < δ] = γ Если в этом соотношении заменить неравенство | R – R * | < δ равносильным ему двойным неравенством: - δ< R – R * < δ, или R * - δ < R < R * + δ, то получаем: P[R * - δ < R < R * + δ ]= γ
29 Понятие доверительного интервала Полученное соотношение следует понимать так: - вероятность того, что интервал ( R * - δ, R * + δ ) заключает в себе (покрывает) неизвестный параметр R, равна γ Интервал ( R * - δ, R * + δ ), покрывающий неизвестный параметр с заданной надежностью γ называют доверительным интервалом
30 Понятие доверительного интервала Интервал ( R * - δ, R * + δ ) имеет случайные концы (их называют доверительными границами). В разных выборках получаются различные значения R *, следовательно от выборки к выборке будут изменяться и концы доверительного интервала, то есть доверительные границы сами являются случайными величинами – функциями от x 1, x 2,…, x n А так как случайной величиной является не оцениваемый параметр R, а доверительный интервал, то правильнее будет говорить не о вероятности попадания R в доверительный интервал, а о вероятности того, что доверительный интервал покроет R
31 Пример построения вариационного ряда при дискретной и непрерывной вариации Основные черты социальных и социально-правовых систем - это случай и время, то есть они развиваются во времени отчасти при непредсказуемом поведении их элементов Как мы уже знаем, изучение уголовно-правовых массовых явлений начинается со сбора статистических данных, то есть со статистического наблюдения Также нам известно, что полученный в результате наблюдения первичный материал подвергается в дальнейшем группировке, то есть равносоставную массу элементов разделяют по тому или иному признаку на однородные группы
32 Пример построения вариационного ряда при дискретной и непрерывной вариации Пусть в качестве изучаемого признака ( X ) совокупности лиц, осужденных за тяжкие телесные повреждения, взят возраст Анализ возрастных способностей названной группы применительно к 55 осужденным дал следующие результаты: 16, 22, 20, 19, 18, 24, 21, 17, 23, 18, 19, 16, 22, 18, 23, 20, 19, 22, 20, 19, 20, 18, 21, 18, 19, 24, 17, 16, 23, 19, 25, 21, 20, 18, 19, 22, 20, 18, 17, 21, 19, 20, 23, 25, 22, 20, 17, 24, 19, 17, 21, 18, 19, 21, 26
33 Пример построения вариационного ряда при дискретной и непрерывной вариации На основе полученного статистического наблюдения может быть составлен следующий вариационный ряд Объем выборки n = 55 Возраст в годах, x i 16 17 18 19 20 21 22 23 24 25 26 Число осужден- ных, n i 3 5 8 10 8 6 5 4 3 2 1
34 Дискретная и непрерывная вариации Изменение (вариация) признака может быть: - дискретной; - непрерывной При дискретной вариации значения признака отличаются друг от друга на некоторое (обычно целое) число, например: - число судимостей; - число сообщений о происшествиях, поступивших в дежурную часть; - число эпизодов в уголовном деле и др.
35 Дискретная и непрерывная вариации При непрерывной вариации значения признака могут отличаться на сколь угодно малую величину, например: - время достижения патрульной группой места происшествия; процент выполнения нормы выработки на предприятиях исправительно-трудовых учреждений (ИТУ) и др. При непрерывной (а часто и при дискретной) вариации разделение признака называется интервальным, то есть частоты относятся не к отдельному значению признака, а к некоторому интервалу
36 Пример, вариационного ряда распределения работающих в ИТУ по норме выработки Объем выборки n = 696 Выполнение норм выработки в ИТУ (интервалы), % 65-70 70-75 75-80 80-85 85-90 90-95 95-100 100-105 105-110 110-115 Число работающих, n i 68 81 95 120 88 77 64 45 33 25
37 Дискретная и непрерывная вариации От выбора интервала во многом зависят результата последующего анализа: - при чрезмерно зауженном интервале начинает значительно сказываться случайность наблюдений, различные «шумовые» эффекты; - при неоправданном расширении интервала нивелируются важные особенности наблюдаемого социально-правового явления
38 Дискретная и непрерывная вариации От этих неприятных последствий уходят путем выбора интервала по формуле: где: x max - x min – размах вариации, характеризующий разность между наибольшей и наименьшей вариантами; n – объем выборки
39 Дискретная и непрерывная вариации Для данных таблицы 1 получаем величину интервала k = 1,3; а для данных таблицы 2 k = 3,8 Полученные значения близки к выбранным, то есть к интервалам 1 и 5 соответственно
40 Лекция 3: Числовые характеристики статистического распределения. Приложения математической статистики для решения правовых задач Учебный вопрос 3: Характеристики вариационного ряда
41 3. Характеристики вариационного ряда Характеристиками вариационного ряда являются: - среднее арифметическое; - среднее геометрическое; - средняя квадратичная; - средняя логарифмическая и др. сред-ние; - медиана; - мода
42 Среднее арифметическое Среднее арифметическое вычисляется с использованием формулы: В частности, для данных таблицы 1 средний возраст осужденных за тяжкие телесные повреждения (среднее арифметическое) равно: (1/55)*(16*3+17*5+18*8+19*10+20*8+21*6+22*5+23*4+24*3+25*2+26*1)=20,05 (года), для данных таблицы 2 средняя норма выработки (среднее арифметическое) равна 85,9%
43 Среднее геометрическое Среднее геометрическое вычисляется с использованием формулы: Среднее геометрическое применяется главным образом для изучения динамики социально-правовых явлений В случае, когда вариационный ряд является интервальным, для расчета показателей средних арифметического и геометрического применяются значения вариант, относящиеся к середине соответствующих интервалов
44 Медиана Медиана ( Ме ) – это такое значение варианты, которое приходится на середину вариационного ряда В случае, если число членов ряда нечетное, Ме = а +1, где а – целая часть от деления пополам количества вариант вариационного ряда Таким образом для ряда в таблице 1 Ме = а + 1 = 11/2 + 1 = 5 +1 = 6, то есть Ме = 21 (см. таблицу 1)
45 Медиана В случае, если вычисляется медиана интервального вариационного ряда, используется следующая приближенная формула: Ме = Х 1 н +К 1 м ( n /2 – T i -1 )/ n i, (4) где: Х 1 н – значение начала медианного варианта; К 1 м – длина медианного интервала; n /2 – полуобъем выборки в процентах; T i -1 – сумма частот интервалов, предшествующих медианному (определяется по первой накопленной частоте, превышающей половину всего объема вариационного ряда, то есть более 50%); n i – частота медианного интервала
46 Медиана Для вариационного ряда, представленного в таблице 2, значение медианы в соответствии с этой формулой, будет: Ме = 80+5(50 – 35,1)/17,2 = 84,3 Медиана обладает замечательным свойством – сумма абсолютных величин отклонений вариантов от нее меньше, в том числе и от средней арифметической На практике это свойство может быть применено, например, при: - проектировании маршрутов патрульных групп; - выборе места для пункта управления подразделениями ГИБДД на протяженных участках дороги и др.
47 Мода Мода ( Мо ) – значение варианты, имеющей максимальную частоту в вариационном ряду В таблице 1 максимальная частота (максимальное количество осужденных за тяжкие телесные повреждения) – 19 (лет)
48 Мода Модальное значение интервального ряда вычисляется с использованием формулы: Мо = Х 1 н +( К 1 м / ( 1 + ((n i - n i+1 ) / (n i - n i-1 ))), (5) где: Х 1 н – значение начала медианного варианта; К 1 м – длина модального интервала; n i – частота модального интервала; n i -1 и n i +1 – соответственно частоты предшествующего и последующего интервалов по отношению к модальному
49 Мода Для вариационного ряда, характеризующего распределение работающих в ИТУ по норме выработки (таблица 2) это следующие значения: Х 1 н = 80; К 1 м = 5; n i = 120; n i -1 = 95; n i +1 = 88
50 Мода Мода интервального ряда, представленного в таблице 2, равна 82,2. Это и есть оценка значения нормы выработки, которую выполняет наибольшая группа осужденных Сравнивая значения средней арифметической, моды и медианы, можно определить, каким является вариационный ряд: - симметричным или асимметричным (скошенным)
51 Симметричный и асимметричный ряды Если ряд умеренно отличается от симметричного, то должно выполняться соотношение: (6) Так, для вариационного ряда, характеризующего распределение работающих в ИТУ по норме выработки (таблица 2), получается значение, равное 2,3. Это приводит к выводу о незначительном отличии ряда от симметричного Характерно, что для таких рядов медиана расположена между модой и средней арифметической
52 Лекция 3: Числовые характеристики статистического распределения. Приложения математической статистики для решения правовых задач Учебный вопрос 4: Измерение вариации признака
53 4. Измерение вариации признака Рассмотренные числовые характеристики вариационного ряда, и, в частности, параметры, характеризующие средние величины и максимум ряда, не учитывают вариации признака различных социально-правовых процессов Для измерения вариации признака применяют такие показатели, как: - вариационный размах; - дисперсии; - среднее квадратическое отклонение; - относительный коэффициент вариации
54 Вариационный размах Вариационный размах ( R ) (широта распределения) – это показатель, характеризующий разность между крайними значениями вариационного ряда: R = x max – x min, (7) где x max и x min – варианты вариационного ряда Например, вариационный размах для ряда, характеризующего число осужденных за тяжкие телесные повреждения (таблица 1) составляет R = 26 -16 = 10 лет
55 Вариационный размах Но, несмотря на простоту рассматриваемого критерия вариации признака ( R ), при практическом использовании он чрезвычайно зависит от случайностей, весьма неустойчив и поэтому может служить лишь для грубой оценки колеблемости вариационного ряда Более надежным и наиболее часто применяемым на практике, хотя и более сложным для вычисления, являются показатели дисперсии и среднего квадратического отклонения
56 Дисперсия Дисперсия вычисляется по формуле: (8) Например, дисперсия показателя возраста осужденных за тяжкие телесные повреждения (вариационный ряд в таблице 1) равна 6,02
57 Среднее квадратическое отклонение Среднее квадратическое отклонение ( σ ) является производным от дисперсии Рассчитывается среднее квадратическое отклонение по формуле: Для рассматриваемого примера σ = 2,45 Очевидно, что чем больше показатели вариации признака, в частности, дисперсия, тем менее однородна исследуемая совокупность социально-правовых явлений
58 Среднее квадратическое отклонение С учетом того, что среднее квадратическое отклонение представляет собой абсолютную величину и зависит от единицы измерения, для сопоставимости различных исследований нужно использовать относительный коэффициент вариации
59 Относительный коэффициент вариации Относительный коэффициент вариации ( V ) – это коэффициент, представляющий собой отношение среднего квадратического отклонения от средней арифметической, выраженное в процентах: (10) Значение относительного коэффициента вариации применительно к возрастному распределению осужденных за тяжкие телесные повреждения (таблица1) равно 12,2%
60 4. Измерение вариации признака В практике социально-правовых исследований довольно часто встречаются случаи, когда при анализе вариационного ряда числовое значение того или иного признака резко выделяется, вызывая большие сомнения с точки зрения включения его в дальнейшую обработку Причинами такого положения могут быть следующие: - в первичном материале произошла грубая ошибка (ошибку необходимо исправить); - значительное отличие варианты от других, когда ее значение выходит за пределы случайной вариации (варианту следует исключить из рассмотрения как ошибочную
61 4. Измерение вариации признака Но нередко бывает и такая ситуация, когда вызвавший сомнение объект, характеризующийся маловероятным значением признака, на самом деле является уникальным и должен быть повергнут индивидуальному социально-правовому анализу Таким образом, исключение вариантов не должно быть автоматическим, его следует производить с большой осторожностью
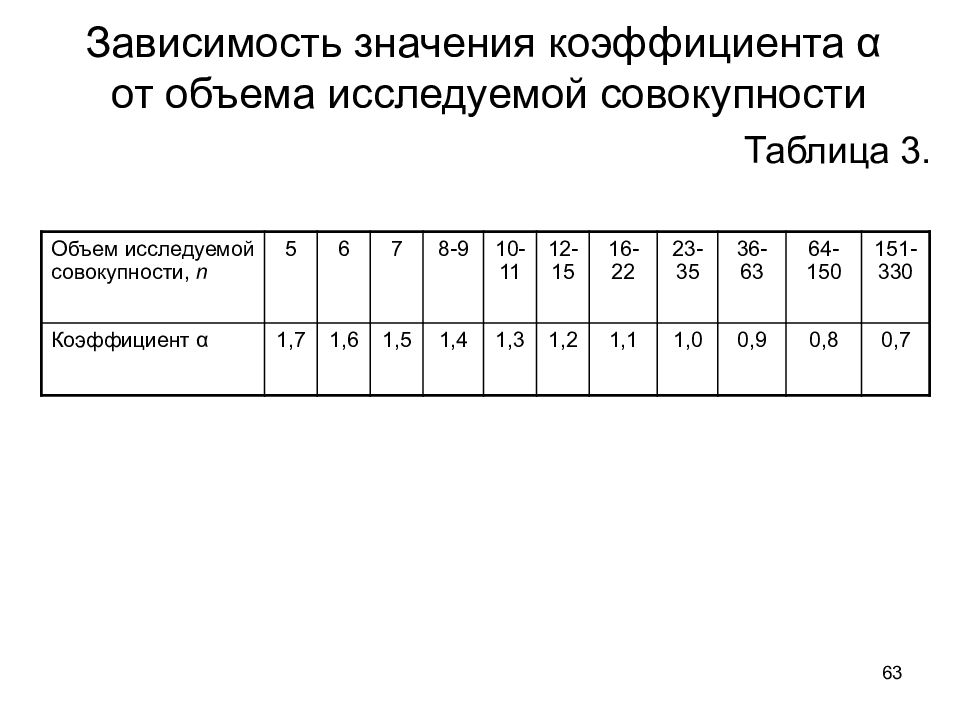
62 4. Измерение вариации признака При исключении испытуемого варианта из вариационного ряда следует следовать следующему алгоритму: Шаг 1. Вычислить среднюю арифметическую без включения в нее признаков испытуемого варианта x R. Шаг 2. Вычислить вариационный размах R без включения признаков испытуемого варианта. Шаг 3. Определить, заключается ли величина испытуемого варианта ( S ) в следующих пределах: , (11) где коэффициент α находится из таблицы 3:
63 Зависимость значения коэффициента α от объема исследуемой совокупности Таблица 3. Объем исследуемой совокупности, n 5 6 7 8-9 10-11 12-15 16-22 23-35 36-63 64-150 151-330 Коэффициент α 1,7 1,6 1,5 1,4 1,3 1,2 1,1 1,0 0,9 0,8 0,7
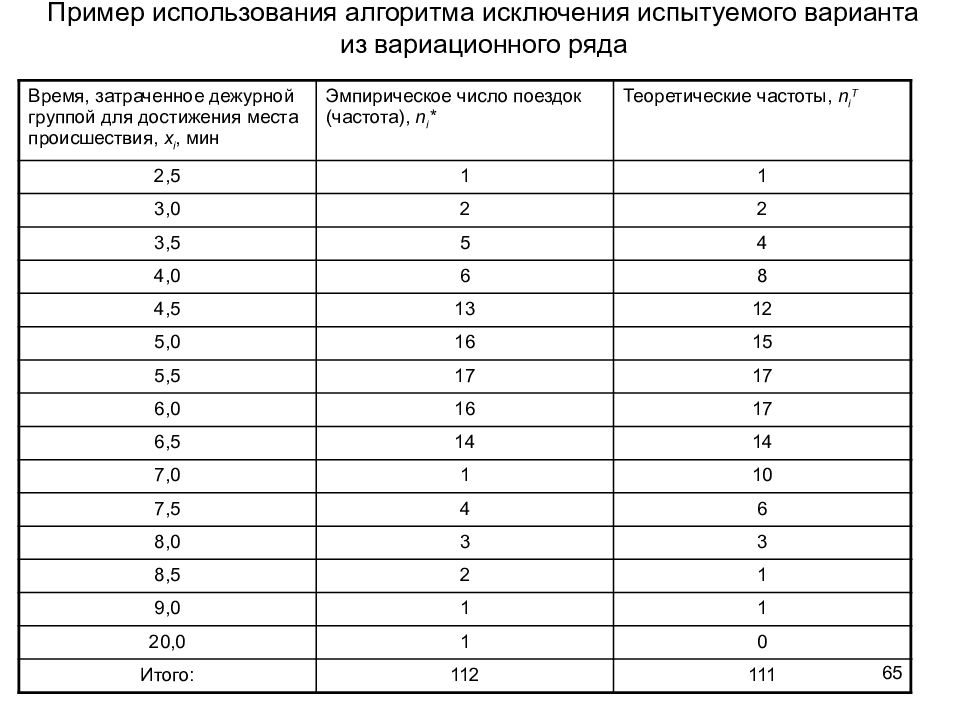
64 Пример использования алгоритма исключения испытуемого варианта из вариационного ряда Постановка задачи: Пусть имеется вариационный ряд: распределение времени, затраченного дежурной группой для достижения места происшествия (таблица 4):
65 Пример использования алгоритма исключения испытуемого варианта из вариационного ряда Время, затраченное дежурной группой для достижения места происшествия, x i, мин Эмпирическое число поездок (частота), n i * Теоретические частоты, n i T 2,5 1 1 3,0 2 2 3,5 5 4 4,0 6 8 4,5 13 12 5,0 16 15 5,5 17 17 6,0 16 17 6,5 14 14 7,0 1 10 7,5 4 6 8,0 3 3 8,5 2 1 9,0 1 1 20,0 1 0 Итого: 112 111
66 Пример использования алгоритма исключения испытуемого варианта из вариационного ряда Сомнение вызывает варианта 20,0 Средняя арифметическая равна 5,59Вариационный размах R = 6,5 при n = 112 и α = 0,8Таким образом, допустимые границы вариации определяются соотношением: 0,39 < S < 10,79 Так как варианта 20,0 почти в два раза превосходит максимально допустимую границу случайного колебания, то при дальнейшей обработке вариационного ряда ее надо исключить
67 4. Измерение вариации признака Графическое представление вариационного ряда в виде полигона принято называть также эмпирической кривой распределения Для обеспечения анализа, предсказания различных свойств исследуемой совокупности стремятся описать эмпирический ряд с помощью некоторой математической модели – закона распределения Самым известным законом распределения в природе и обществе, в частности, проявляющимся в действии социально-правовых процессов, выступает закон нормального распределения
68 4. Измерение вариации признака Кривая функции плотности нормального распределения описывается с помощью следующего соотношения: (12) Нормальное распределений той или иной случайной величины возникает в силу влияния на нее большого числа случайных причин, не имеющих значительного преимущества в этом влиянии друг перед другом. Такими случайными величинами могут выступать: - возраст преступников; - количество сигналов о происшествиях за единицу времени; - время раскрытия преступления и др.
69 4. Измерение вариации признака Покажем, что эмпирический вариационный ряд, отражающий время, затрачиваемое дежурной группой для достижения места преступления (таблица 4), подчиняется закону нормального распределения Средняя арифметическая этого ряда (математическое ожидание – m ) равна 5,64 Среднее квадратическое отклонение σ = 1,26 Подставляя известные значения в формулу для функции плотности нормального распределения (формула 12), получим формулу конкретного эмпирического нормального распределения времени: f ( x )* = 0,316* exp (- 0,313 * ( x – 5,64) 2 ) (13)
70 4. Измерение вариации признака Для получения теоретических частот нормального распределения ( n i T ), то есть вычисленных с помощью математической модели частоты нормального распределения, необходимо значение функции f ( x )* умножить на k * n, то есть: n i T = f ( x )* k * n (14) Этим самым учитывается величина выборочной совокупности и интервал наблюдения эмпирических данных
71 4. Измерение вариации признака Применительно к рассматриваемому примеру (исходные данные в таблице 4), получим формулу конкретного теоретического нормального распределения времени: f ( x ) = 17,5* exp (- 0,313 * ( x – 5,64) 2 ) (15) Результаты расчетов приведены в правом столбце таблицы 4, где в нижней строке представлены значения теоретических частот, вычисленных по формуле (15)
72 4. Измерение вариации признака В том, что эмпирическая и теоретическая функции плотности распределения выездов дежурных групп примерно совпадают (то есть теоретическое нормальное распределение достаточно верно отражает эмпирическое распределение исследуемой совокупности), можно убедиться, построив график распределения выездов дежурных групп по времени достижения места происшествия (график строится самостоятельно) На графике по оси абсцисс откладывается время (от 0 до 10 мин.), а по оси ординат – количество выездов (от 0 до 20)
73 4. Измерение вариации признака На графике можно увидеть, что кривая нормального распределения располагается симметрично относительно средней арифметической, поэтому величину средней называют центром распределения Влияние величины среднего квадратического отклонения ( σ ) сказывается следующим образом: - чем σ меньше, тем более вытянута кривая вдоль оси ординат; - чем σ больше, тем более плоской становится кривая, растягиваясь вдоль оси абсцисс
74 4. Измерение вариации признака Для практических приложений в социально-правовых исследованиях используется правило «трех сигм»: - случайная величина с нормальным распределением практически не принимает значений, которые отличаются от средней арифметической на величину больше, чем 3 σ Если указать точнее, то: - в интервал (+-) σ попадает 68% всех наблюдений; - в интервал (+-)2 σ попадает 96% всех наблюдений ; - в интервал (+-)3 σ попадает 99,7% всех наблюдений
75 4. Измерение вариации признака Если проанализировать самостоятельно построенный график для рассматриваемого примера, то можно убедиться, что в интервал (+-)2 σ попало 93,8% всех выездов дежурных групп Таким образом и интервала (+-)2 σ достаточно, чтобы оценить основное число вариант в исследуемых совокупностях, характеризующих те или иные социально-правовые процессы Важно знать, что при нормальном распределении величины средней арифметической, моды и медианы совпадают
76 Лекция 3: Числовые характеристики статистического распределения. Приложения математической статистики для решения правовых задач Учебный вопрос 5: Статистические критерии согласия
77 5. Статистические критерии согласия Визуальное сравнение эмпирического и теоретического распределений является первым этапом проверки соответствия статистических моделей реальным социально-правовым процессам Для более точного анализа разработан целый ряд статистических критериев согласия
78 5. Статистические критерии согласия В практике правовых исследований наибольшее распространение получили два таких критерия: - критерий (разработан английским статистиком Пирсоном); - критерий Колмогорова
79 Критерий Критерий Пирсона выражается следующей формулой: Вычисление значения критерия для сравнения эмпирического и теоретического распределений времени, затраченного дежурной группой для достижения места происшествия (таблица 4), дает результат: = 2,73 Много это, или мало? Ответ на это дает специальная таблица значения функции распределения F ( ), имеющаяся в справочниках по вероятностным расчетам
80 Критерий Для рассматриваемого примера по таблице находим, что для 13 степеней свободы (число вариант ряда минус единица) и критерия = 3 (даже превышающего вычисленный) вероятность соответствия эмпирического распределения теоретическому равна 0,998
81 Критерий Колмогорова Критерий русского математика Колмогорова выражается следующей формулой: где n – объем исследуемой совокупности В числителе этой формулы представляется максимальная разница накопленных частот
82 Критерий Колмогорова Для примера, представленного в таблице 4, По специальной таблице (из справочника) можно найти, что для полученного значения критерия с вероятностью, близкой к 1, теоретическая и эмпирическая частоты совпадают
