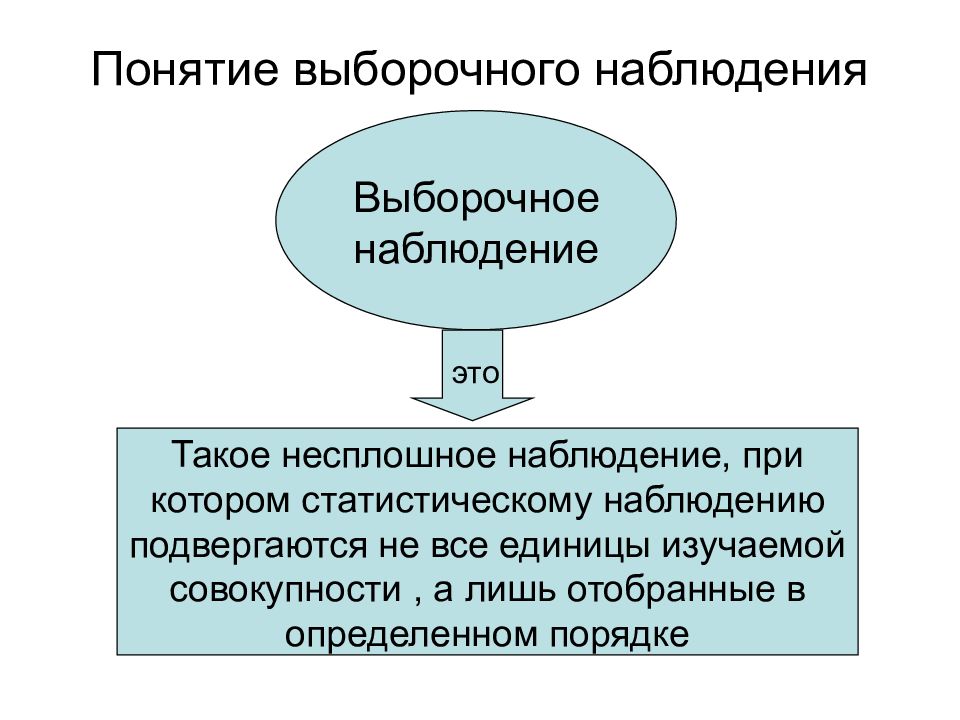
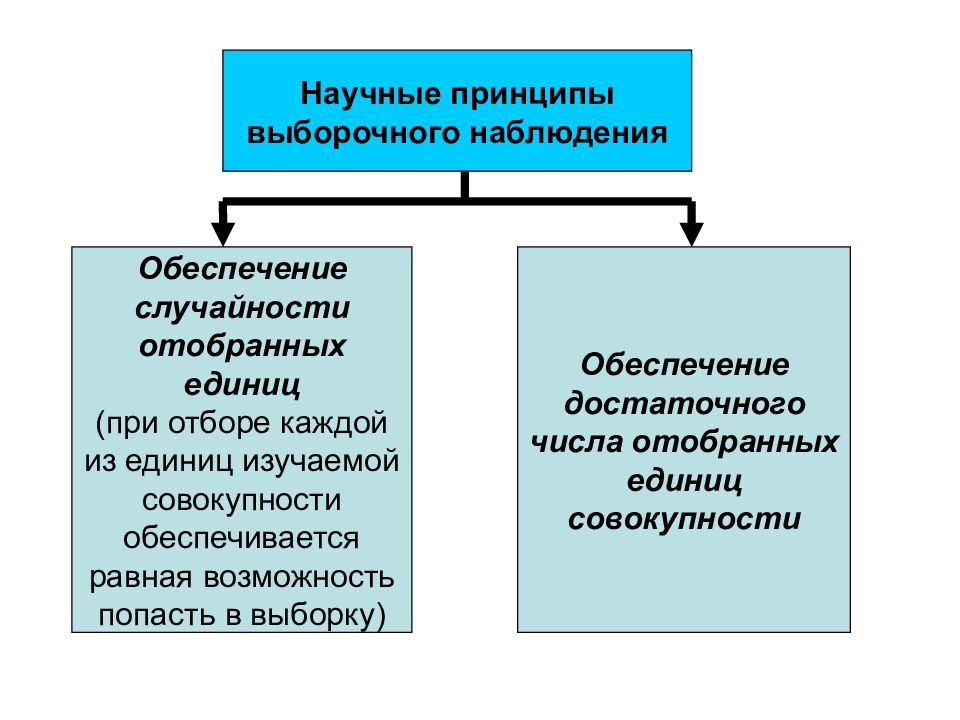
Слайд 2: Понятие выборочного наблюдения
Выборочное наблюдение Такое несплошное наблюдение, при котором статистическому наблюдению подвергаются не все единицы изучаемой совокупности, а лишь отобранные в определенном порядке это
Слайд 3
Статистическое наблюдение можно организовать как сплошное и несплошное. Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности явлений, несплошное – лишь его части. Цель выборочного наблюдения состоит в том, чтобы по характеристикам отобранной части единиц судить о характеристиках всей совокупности.
Слайд 4
Преимущества выборочного наблюдения Достижение большей точности результатов обследования благодаря сокращению ошибок регистрации Экономия трудовых и денежных средств и времени в результате сокращения объема работы Возможность детального обследования каждой единицы наблюдения за счет расширения программы наблюдения Сведение к минимуму уничтожения и приведения в негодность обследуемых единиц совокупности Уточнение результатов сплошного наблюдения
Слайд 5
Научные принципы выборочного наблюдения Обеспечение случайности отобранных единиц (при отборе каждой из единиц изучаемой совокупности обеспечивается равная возможность попасть в выборку) Обеспечение достаточного числа отобранных единиц совокупности
Генеральная совокупность ( N) – это совокупность, из которой производится отбор единиц совокупности. Выборочная совокупность ( n ) – совокупность отобранных в определенном порядке единиц, по которым собирается информация.
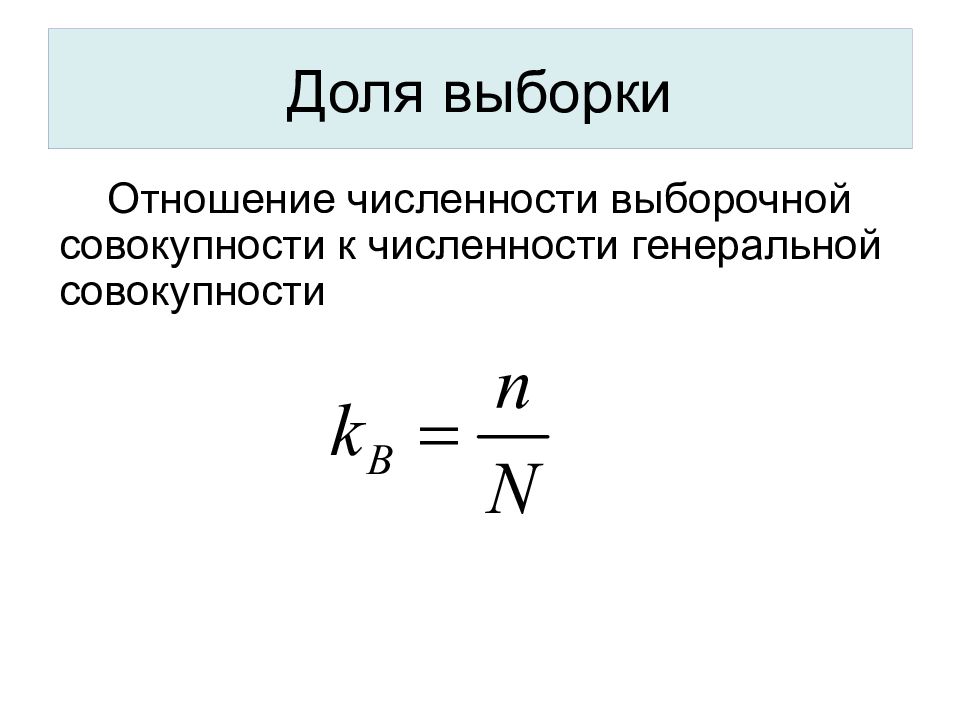
Слайд 7: Доля выборки
Отношение численности выборочной совокупности к численности генеральной совокупности
Слайд 9: Выборочная средняя
Среднее значение признака у единиц, которые подверглись выборочному наблюдению
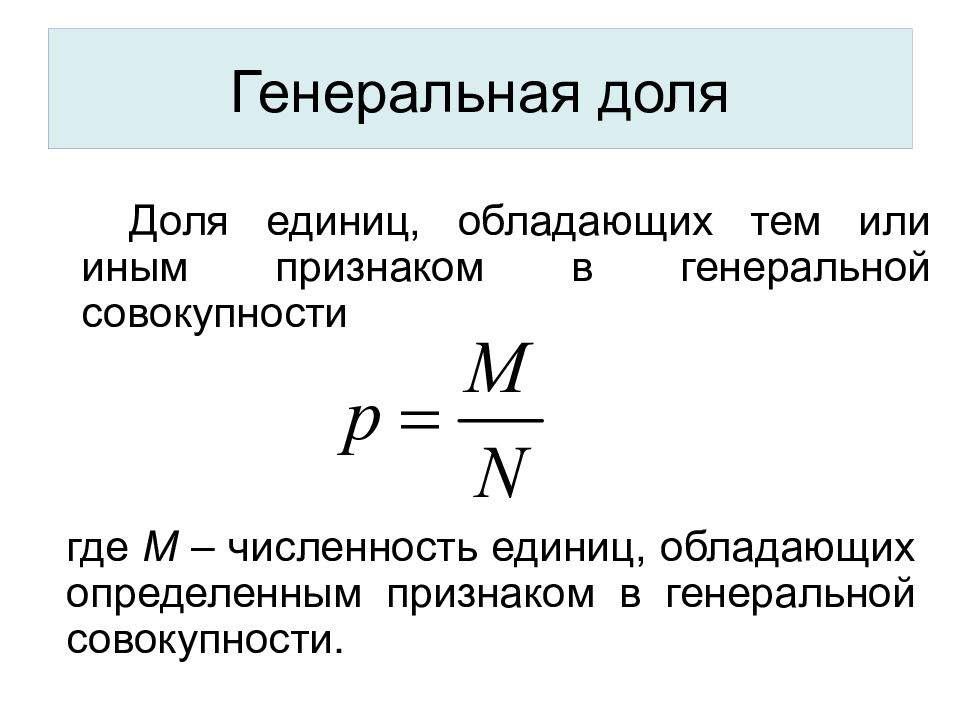
Слайд 10: Генеральная доля
где М – численность единиц, обладающих определенным признаком в генеральной совокупности. Доля единиц, обладающих тем или иным признаком в генеральной совокупности
Слайд 11: Выборочная доля или частность
где т – численность единиц, обладающих определенным признаком в выборочной совокупности. Доля единиц, обладающих тем или иным признаком в выборочной совокупности
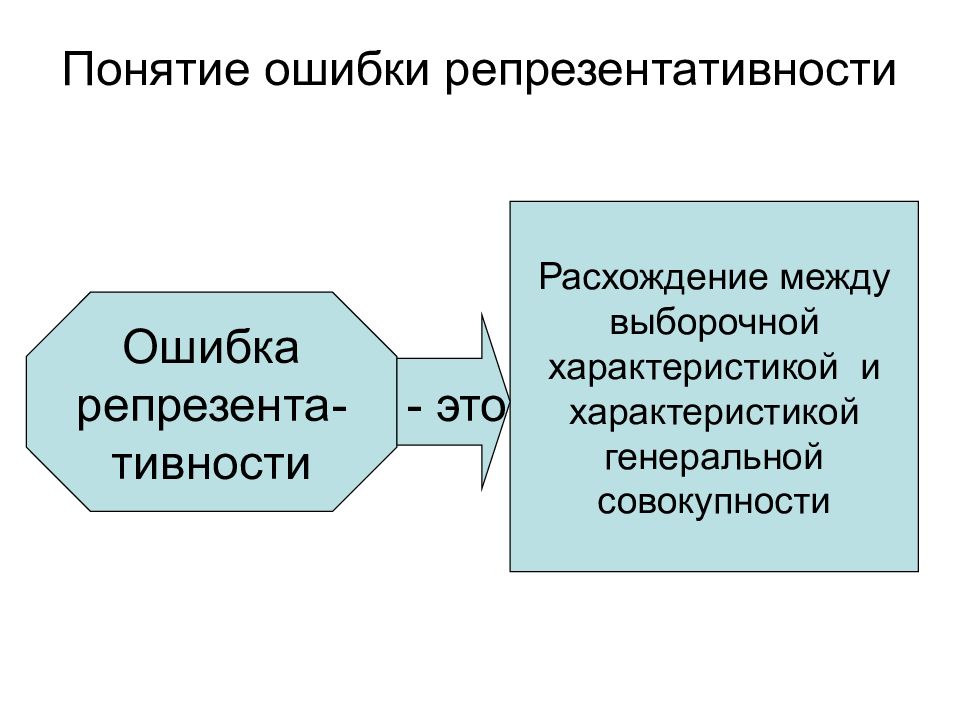
Слайд 16: Понятие ошибки репрезентативности
Расхождение между выборочной характеристикой и характеристикой генеральной совокупности Ошибка репрезента-тивности - это
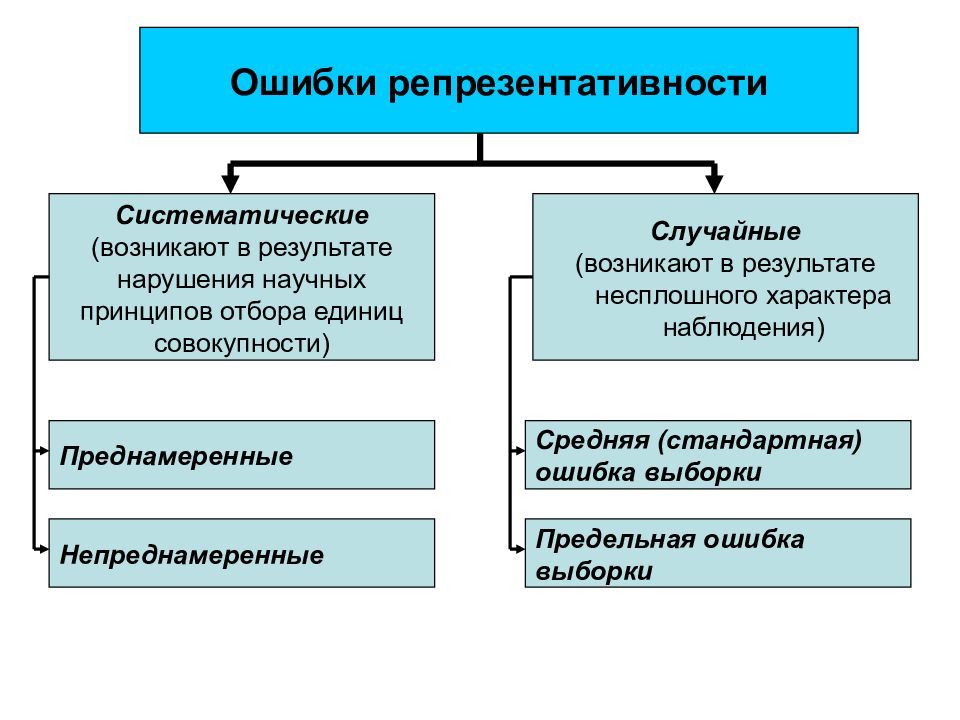
Слайд 17
Ошибки репрезентативности Случайные (возникают в результате несплошного характера наблюдения) Систематические (возникают в результате нарушения научных принципов отбора единиц совокупности) Преднамеренные Непреднамеренные Средняя (стандартная) ошибка выборки Предельная ошибка выборки
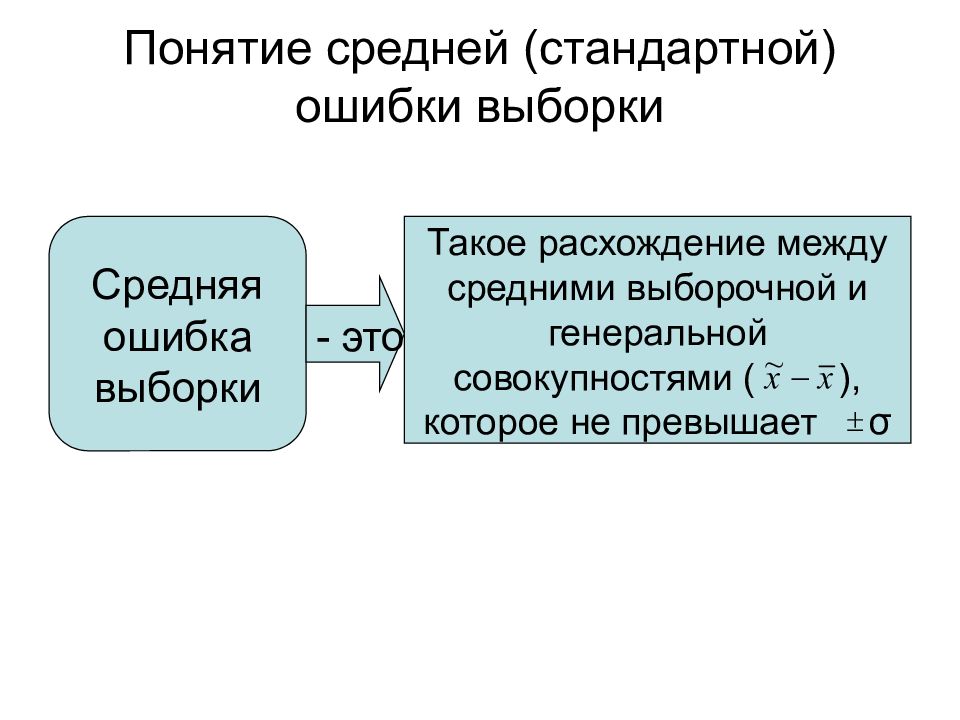
Слайд 18: Понятие средней (стандартной) ошибки выборки
Такое расхождение между средними выборочной и генеральной совокупностями ( ), которое не превышает σ Средняя ошибка выборки - это
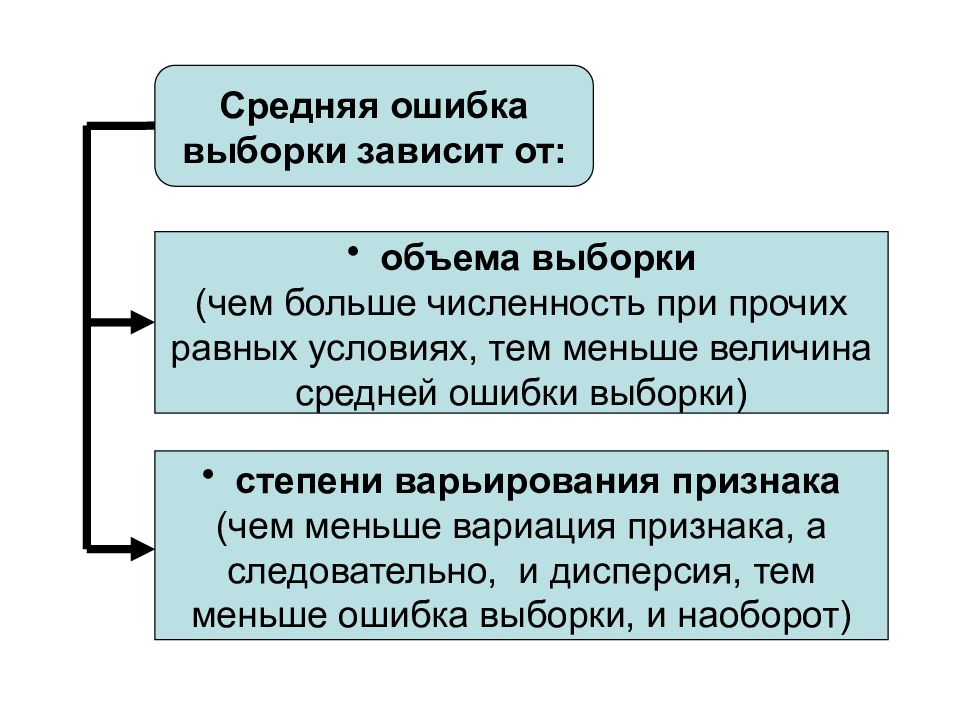
Слайд 19
Средняя ошибка выборки зависит от: объема выборки (чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки) степени варьирования признака (чем меньше вариация признака, а следовательно, и дисперсия, тем меньше ошибка выборки, и наоборот)
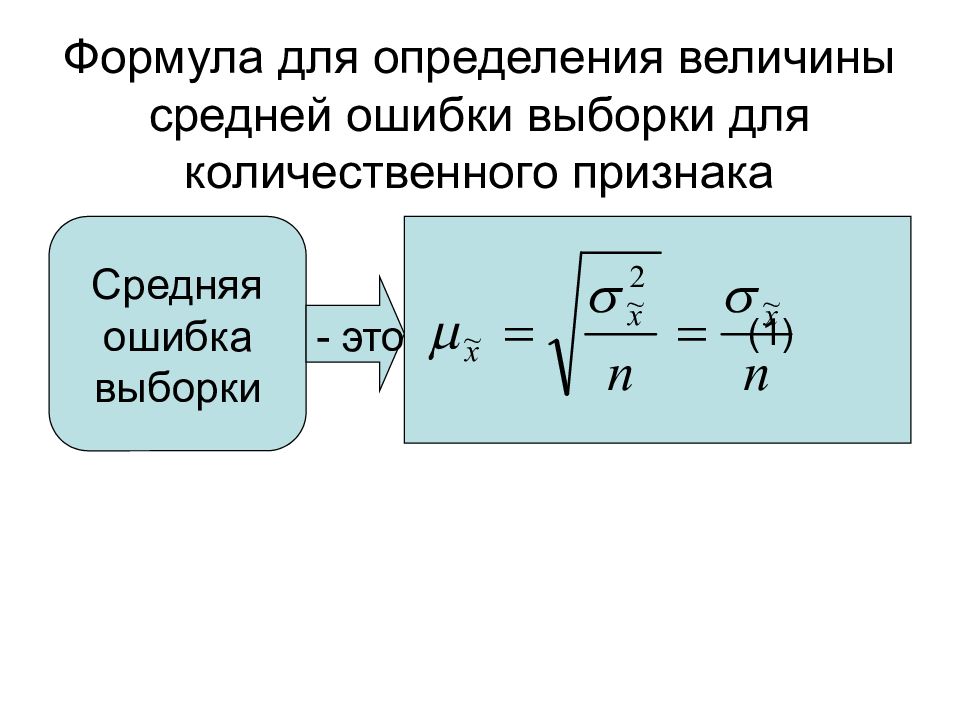
Слайд 20: Формула для определения величины средней ошибки выборки для количественного признака
(1) Средняя ошибка выборки - это
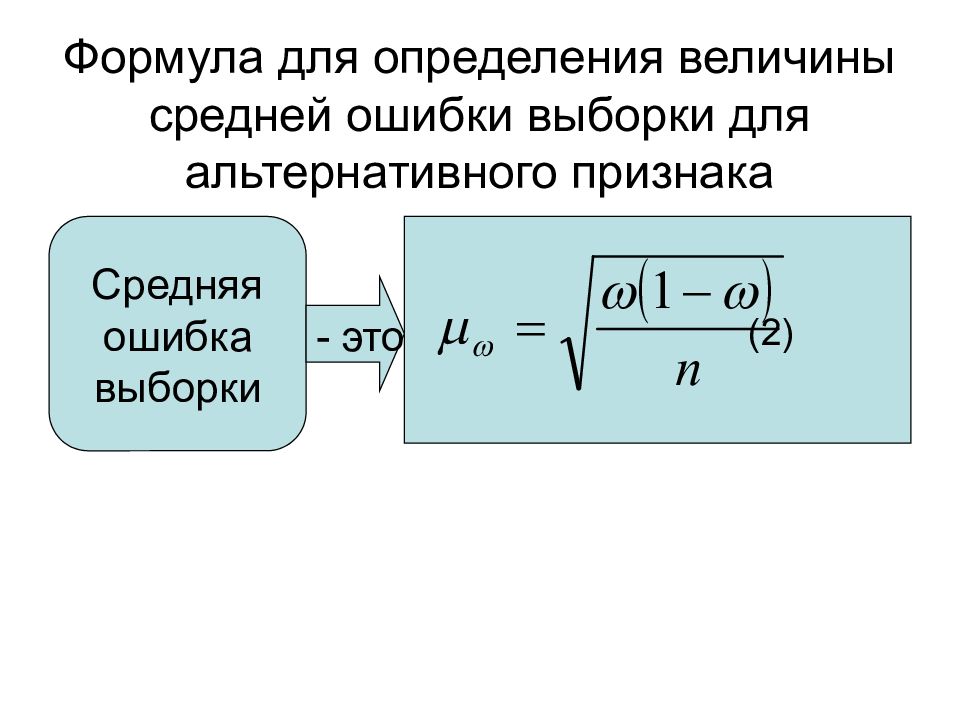
Слайд 21: Формула для определения величины средней ошибки выборки для альтернативного признака
(2) Средняя ошибка выборки - это
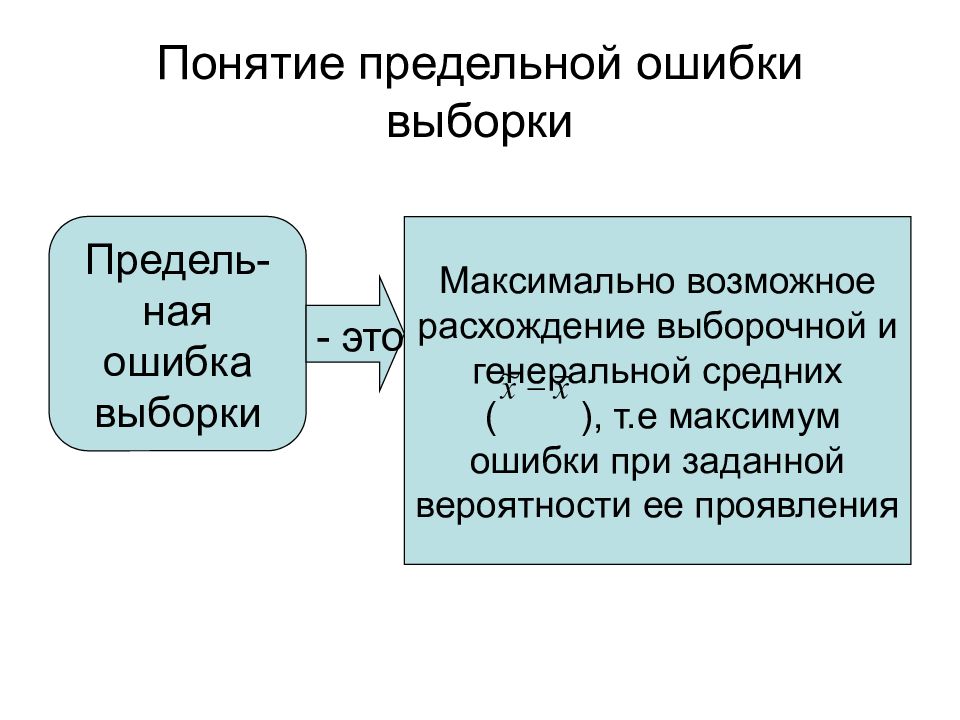
Слайд 22: Понятие предельной ошибки выборки
Максимально возможное расхождение выборочной и генеральной средних ( ), т.е максимум ошибки при заданной вероятности ее проявления Предель-ная ошибка выборки - это
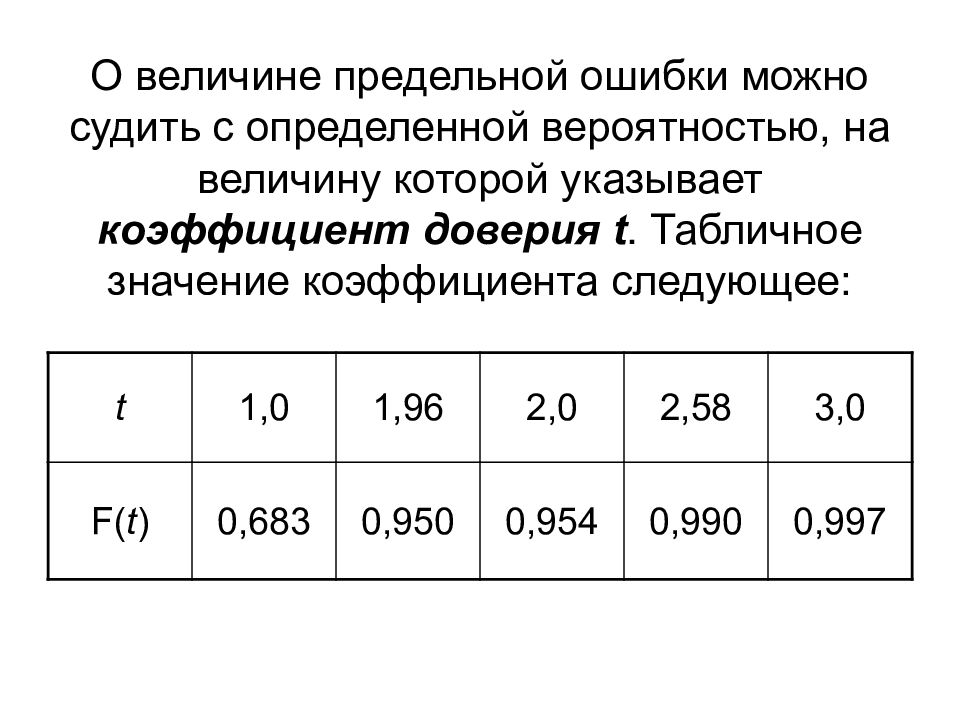
Слайд 23: О величине предельной ошибки можно судить с определенной вероятностью, на величину которой указывает коэффициент доверия t. Табличное значение коэффициента следующее:
t 1,0 1,96 2,0 2,58 3,0 F( t ) 0,683 0,950 0,954 0,990 0,997
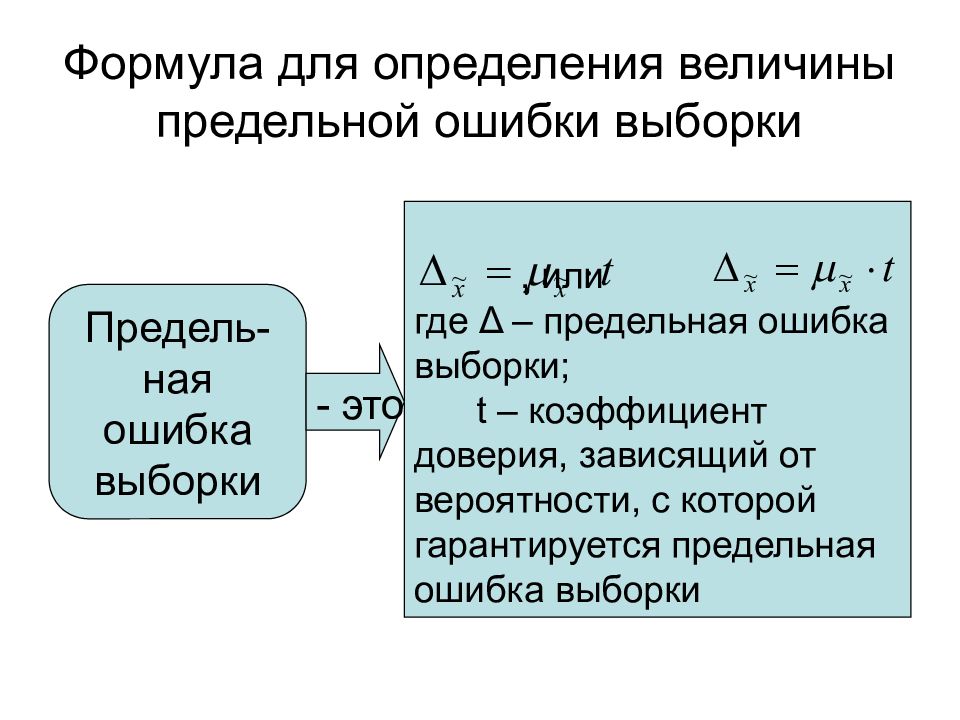
Слайд 24: Формула для определения величины предельной ошибки выборки
, или где Δ – предельная ошибка выборки; t – коэффициент доверия, зависящий от вероятности, с которой гарантируется предельная ошибка выборки Предель-ная ошибка выборки - это
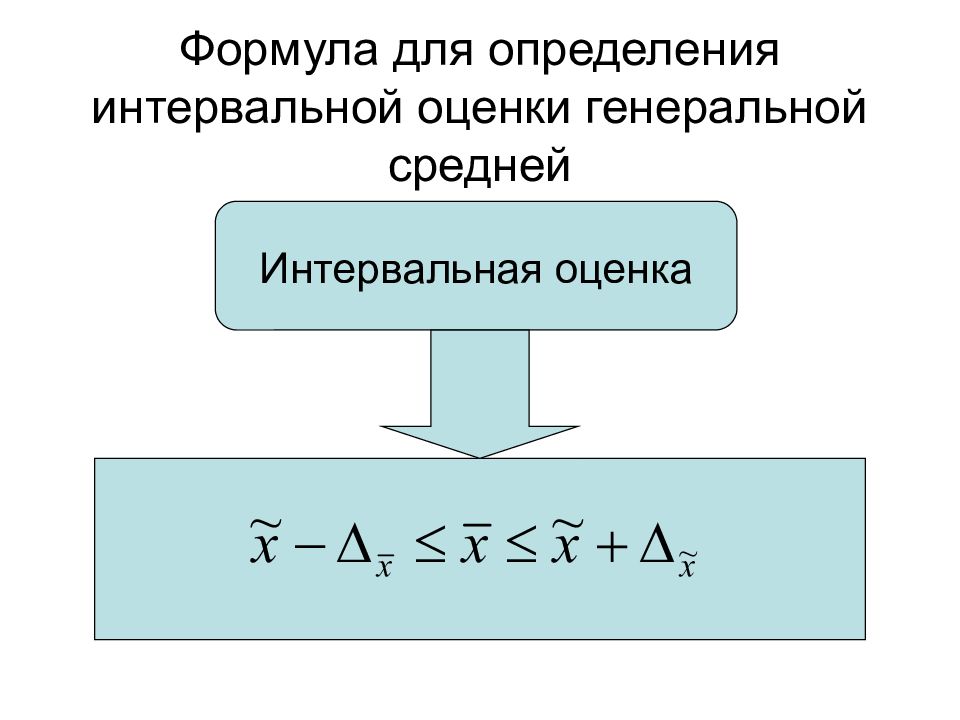
Слайд 25: Формула для определения интервальной оценки генеральной средней
Интервальная оценка
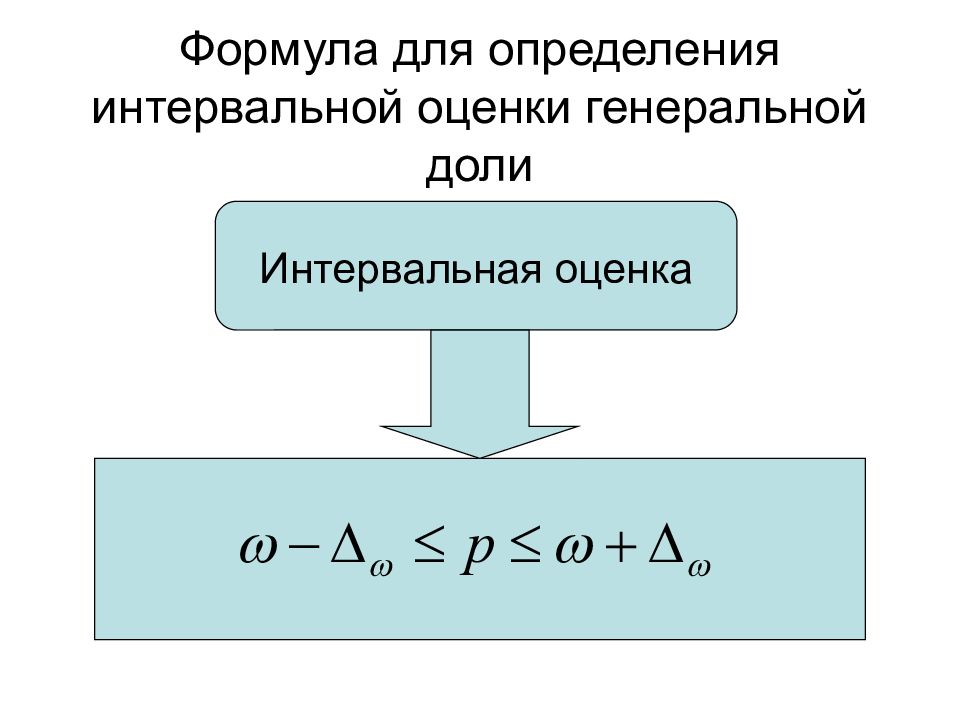
Слайд 26: Формула для определения интервальной оценки генеральной доли
Интервальная оценка
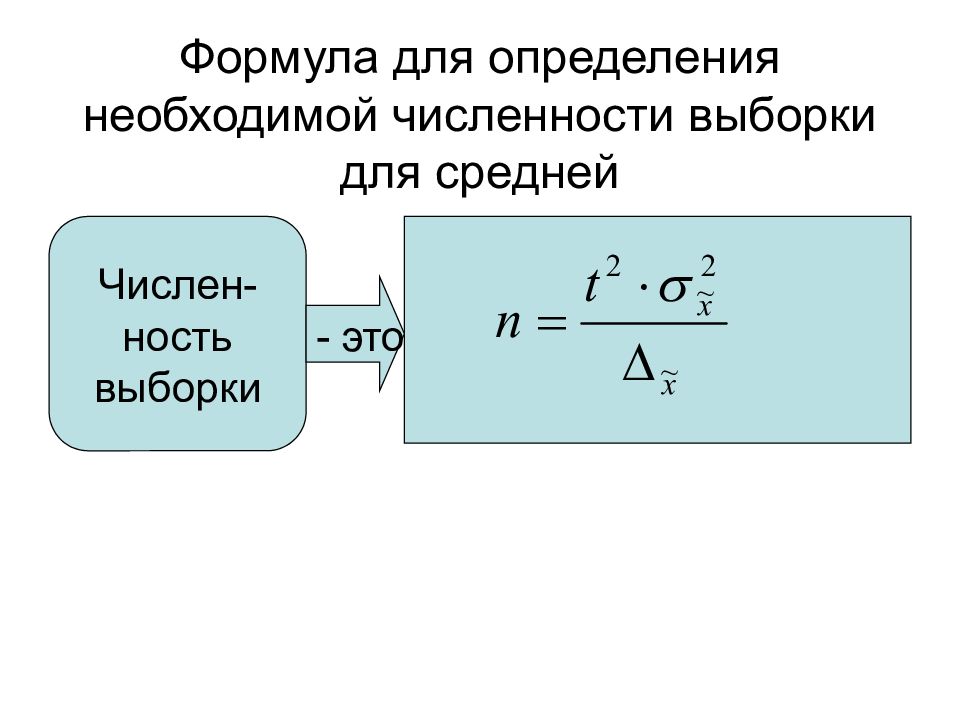
Слайд 27: Формула для определения необходимой численности выборки для средней
Числен-ность выборки - это
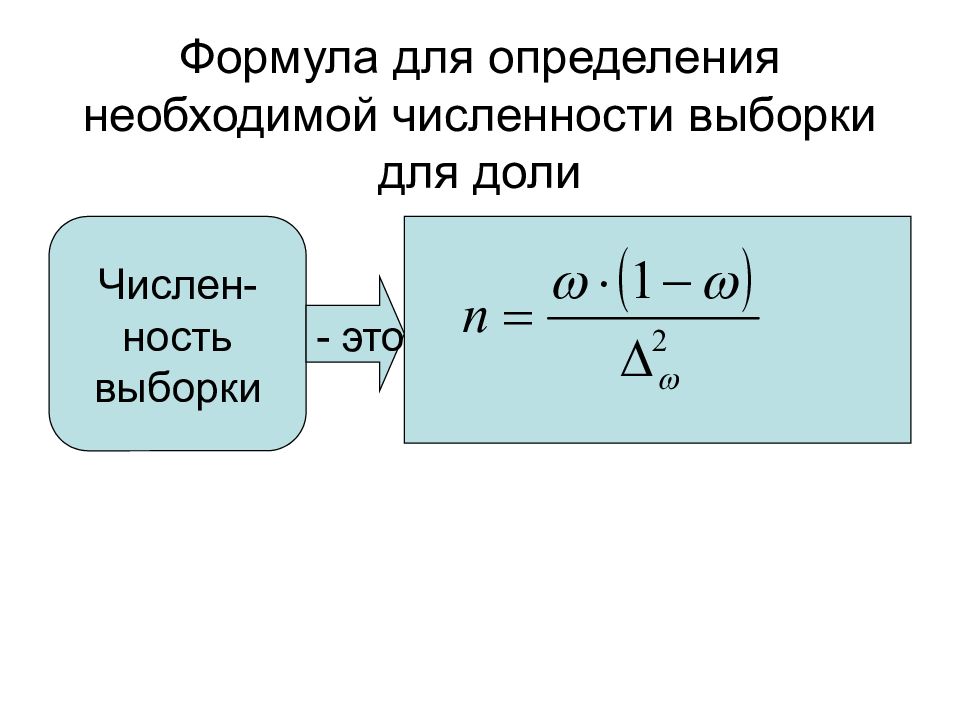
Слайд 28: Формула для определения необходимой численности выборки для доли
Числен-ность выборки - это
Слайд 30: Повторный отбор
Каждая единица, отобранная в случайном порядке, после обследования возвращается в генеральную совокупность и в последующем отборе может снова попасть в выборку. При таком отборе вероятность попасть в выборку для каждой единицы генеральной совокупности не меняется не зависимо от числа отобранных единиц
Слайд 31: Бесповторный отбор
Каждая единица, отобранная в случайном порядке, после обследования в генеральную совокупность не возвращается. Вероятность попасть в выборку для каждой единицы генеральной совокупности увеличивается по мере производства отбора
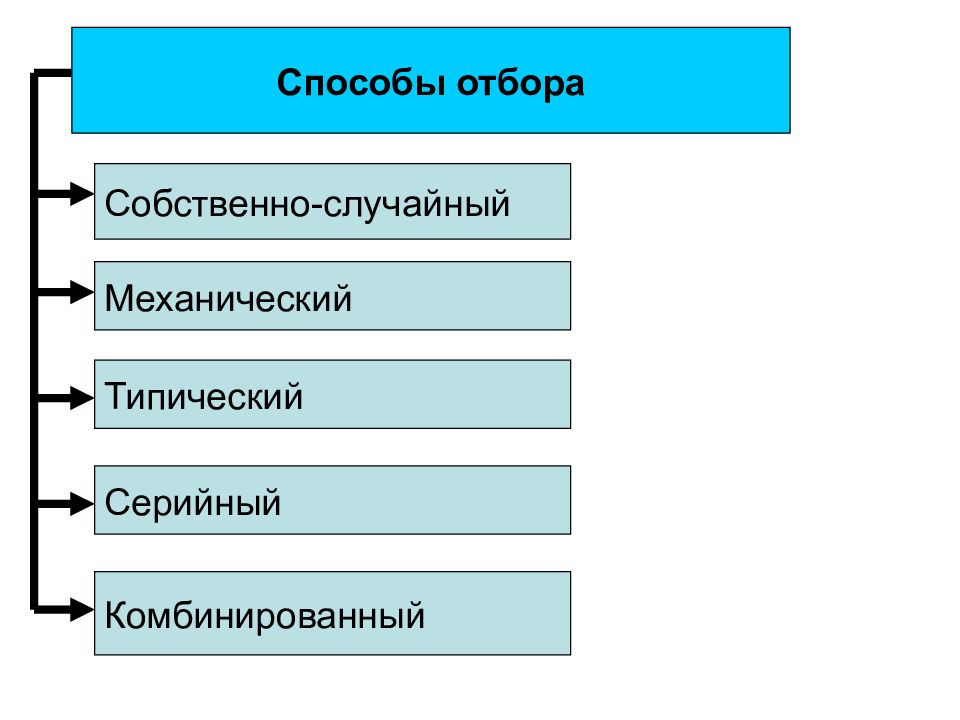
Слайд 33
Способы отбора Собственно-случайный Механический Типический Серийный Комбинированный
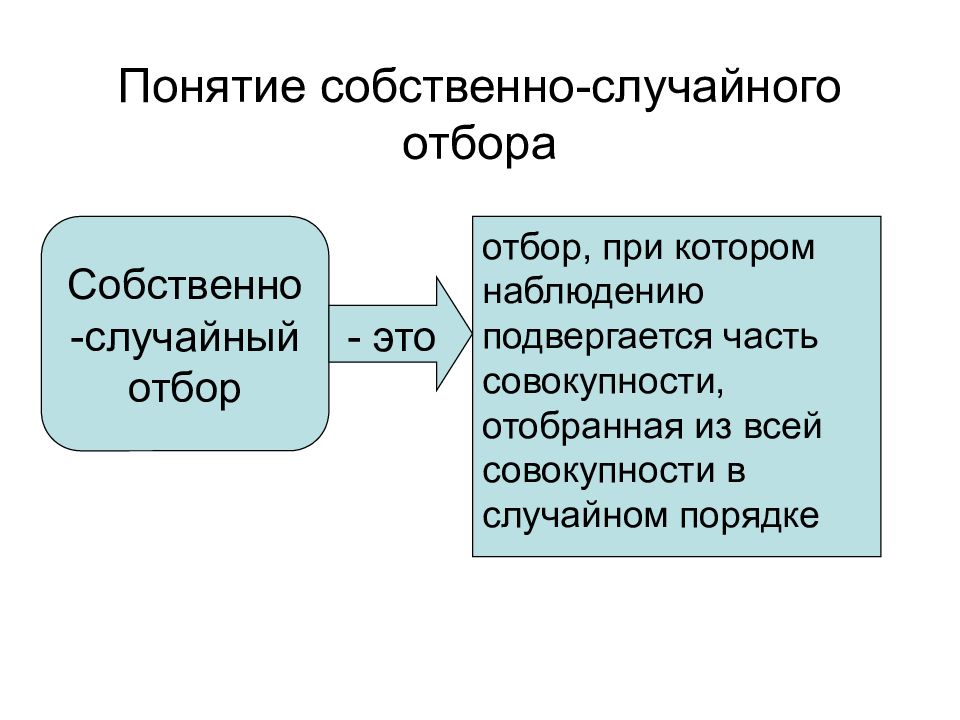
Слайд 34: Понятие собственно-случайного отбора
отбор, при котором наблюдению подвергается часть совокупности, отобранная из всей совокупности в случайном порядке Собственно-случайный отбор - это
Слайд 35: Основные формулы, используемые при собственно-случайном отборе
Повторная выборка Бесповторная выборка Средняя ошибка выборки для средней
Слайд 36: Основные формулы, используемые при собственно-случайном отборе
Повторная выборка Бесповторная выборка Средняя ошибка выборки для доли
Слайд 37: Основные формулы, используемые при собственно-случайном отборе
Повторная выборка Бесповторная выборка Численность выборки при определении среднего размера признака
Слайд 38: Основные формулы, используемые при собственно-случайном отборе
Повторная выборка Бесповторная выборка Численность выборки при определении доли признака
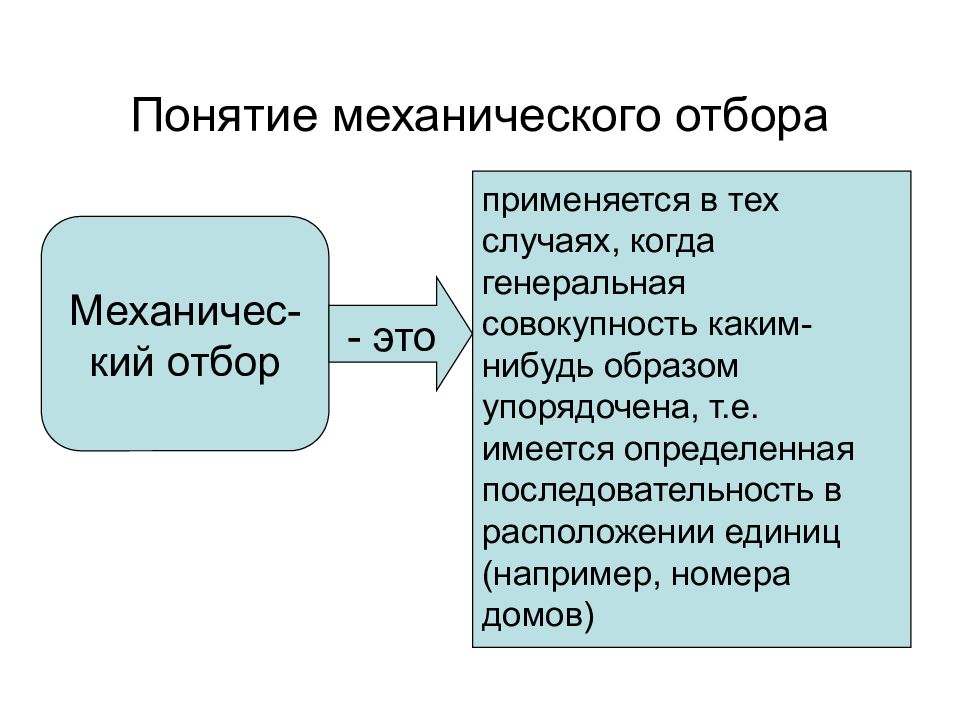
Слайд 39: Понятие механического отбора
применяется в тех случаях, когда генеральная совокупность каким-нибудь образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (например, номера домов) Механичес-кий отбор - это
Слайд 40
При механическом отборе устанавливается шаг отсчета, т.е. расстояние между отбираемыми единицами ( N/n – величина, обратная доле выборки) и начала отсчета – номер единиц, которая должна быть обследована первой. Механический отбор всегда бывает бесповторным. При этом отборе применяются те же формул, что и при собственно-случайном бесповторном отборе. Механический отбор имеет преимущество перед случайным отбором, его не только легче организовать, но при нем единицы выборочной совокупности равномернее распределяются в генеральной совокупности.
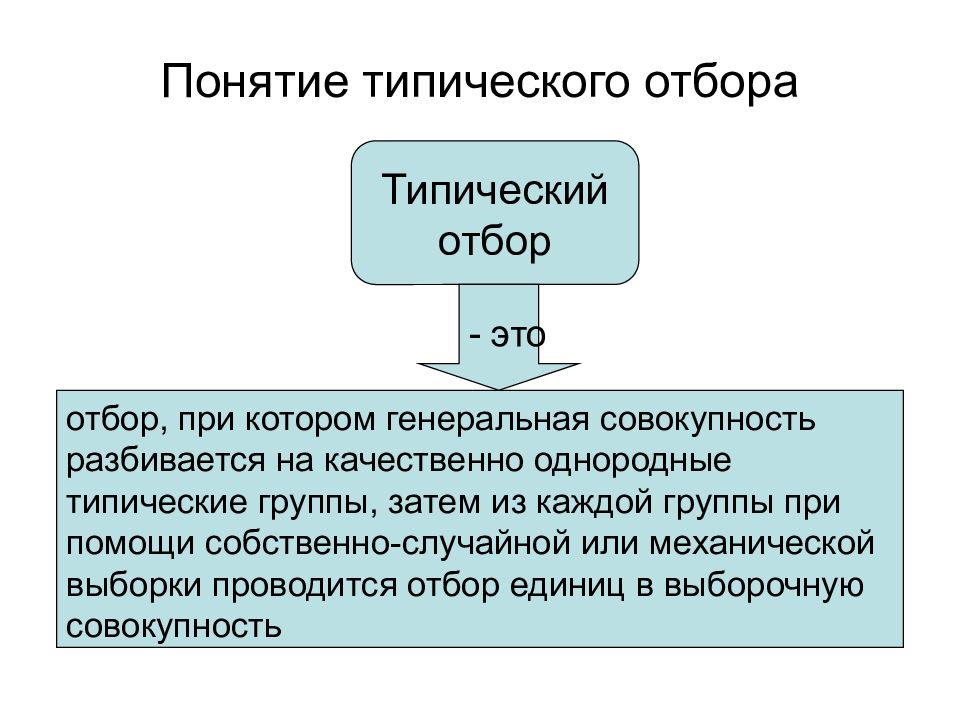
Слайд 41: Понятие типического отбора
отбор, при котором генеральная совокупность разбивается на качественно однородные типические группы, затем из каждой группы при помощи собственно-случайной или механической выборки проводится отбор единиц в выборочную совокупность Типический отбор - это
Слайд 43
где n i – объем выборки из i -й типической группы; N i – объем i -й типической группы в генеральной совокупности Объем выборки из типической группы при отборе пропорциональном численности единиц типических групп определяется по формуле
Слайд 44
Разбивка на типические группы дает возможность избежать влияния межгрупповой вариации на точность выборки. Так как в типическую выборку должны попасть представители всех групп, средняя ошибка типической выборки зависит только от средней из внутригрупповых дисперсий, или, а не от общей дисперсии, или.
Слайд 45: Основные формулы, используемые при типическом отборе
Повторная выборка Бесповторная выборка Средняя ошибка выборки для средней
Слайд 46: Основные формулы, используемые при типическом отборе
Повторная выборка Бесповторная выборка Средняя ошибка выборки для доли
Слайд 47: Основные формулы, используемые при типическом отборе
Повторная выборка Бесповторная выборка Численность выборки при определении среднего размера признака
Слайд 48: Основные формулы, используемые при типическом отборе
Повторная выборка Бесповторная выборка Численность выборки при определении доли признака
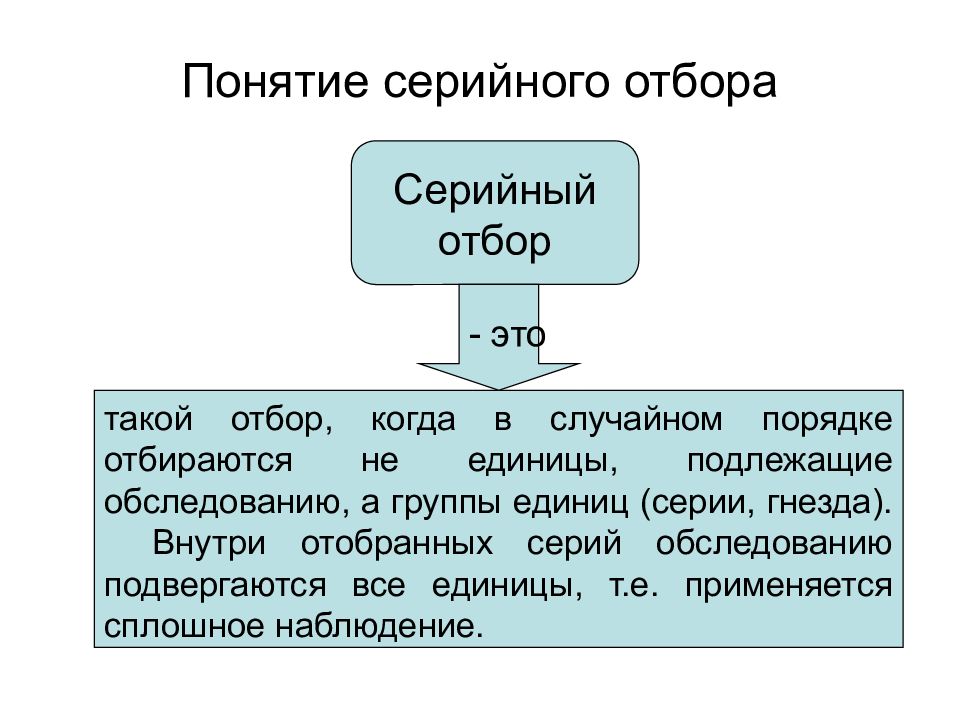
Слайд 49: Понятие серийного отбора
такой отбор, когда в случайном порядке отбираются не единицы, подлежащие обследованию, а группы единиц (серии, гнезда). Внутри отобранных серий обследованию подвергаются все единицы, т.е. применяется сплошное наблюдение. Серийный отбор - это
Слайд 50: Обозначения
- средняя i – ой серии; - средняя по всей выборочной совокупности; - межгрупповая дисперсия доли, определяемая по формуле Обозначения R – общее число серий; r – число отобранных серий; - межгрупповая дисперсия средних, определяемая по формуле - доля признака i – ой серии; - общая доля по всей выборочной совокупности.
Слайд 51: Основные формулы, используемые при серийном отборе
Повторная выборка Бесповторная выборка Средняя ошибка выборки для средней
Слайд 52: Основные формулы, используемые при серийном отборе
Повторная выборка Бесповторная выборка Средняя ошибка выборки для доли
Слайд 53: Основные формулы, используемые при серийном отборе
Повторная выборка Бесповторная выборка Численность выборки при определении среднего размера признака
Слайд 54: Основные формулы, используемые при типическом отборе
Повторная выборка Бесповторная выборка Численность выборки при определении доли признака
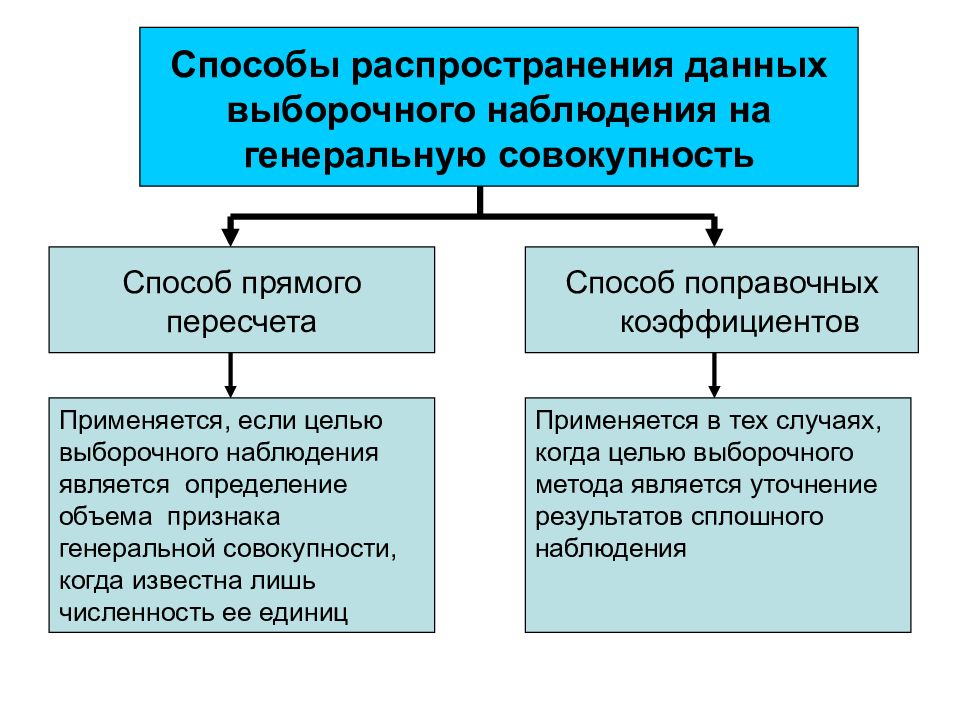
Слайд 55
Способы распространения данных выборочного наблюдения на генеральную совокупность Способ поправочных коэффициентов Способ прямого пересчета Применяется, если целью выборочного наблюдения является определение объема признака генеральной совокупности, когда известна лишь численность ее единиц Применяется в тех случаях, когда целью выборочного метода является уточнение результатов сплошного наблюдения
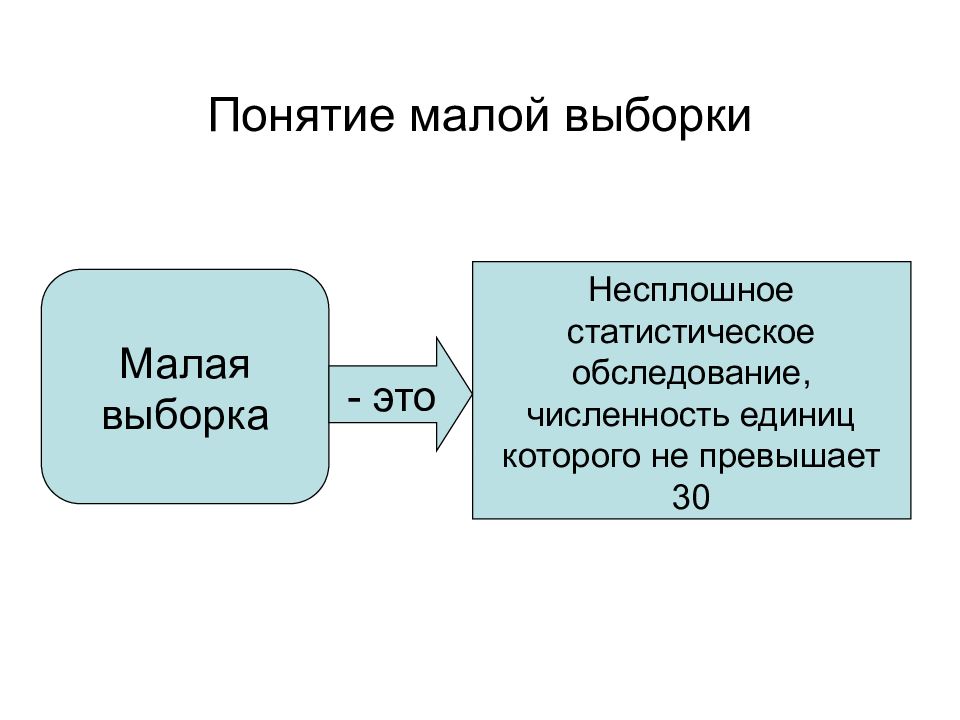
Слайд 56: Понятие малой выборки
Несплошное статистическое обследование, численность единиц которого не превышает 30 Малая выборка - это
Слайд 57
Для определенного способа отбора единиц величина стандартной ошибки зависит от объема выборки и степени колеблемости изучаемого признака в генеральной совокупности. Чем меньше объем выборки, тем большую величину стандартной ошибки следует ожидать, а это снижает точность оценки параметров генеральной совокупности.
Слайд 58
где - величина среднего квадрати-ческого отклонения малой выборки: Для оценки возможных пределов ошибки малой выборки применяется отношение Стьюдента:
Последний слайд презентации: Выборочное наблюдение
Таким образом, для теоретического распределения отношения Стьюдента t имеются величины, определяемые непосредственно по данным выборки. Для определенных значений t и n доверительную вероятность малой выборки находят по специальным таблицам Стьюдента. Величина σ вычисляется на основе данных выборочного наблюдения: Предельная ошибка малой выборки: