Первый слайд презентации: Лекция 4 Основные понятия теории вероятностей
1 Лекция 4 Основные понятия теории вероятностей Понятие случайного события и случайной величины Вероятность события и способы ее вычисления. Логические действия над событиями. Функция распределения и плотность вероятности случайной величины.
Слайд 3: B = f(A)
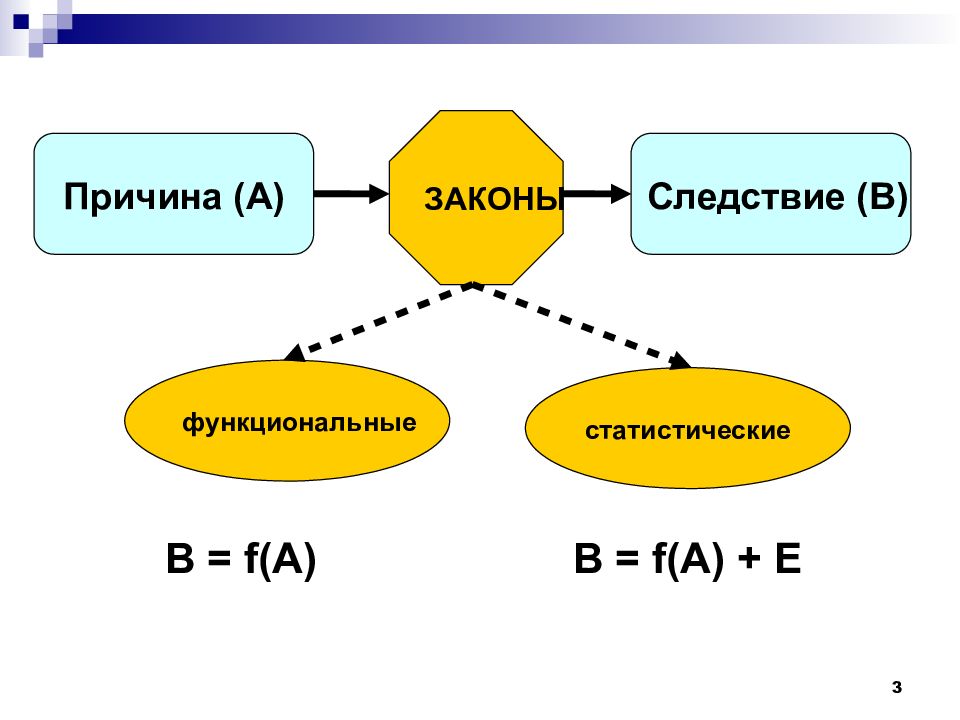
3 Причина (А) Следствие (В) ЗАКОНЫ функциональные статистические B = f(A) B = f(A) + E
Слайд 4
4 Разнообразные случайные факторы, которые трудно поддаются учету, но существенно влияющие на происходящий процесс, называются стохастическими. Закономерности, обусловленные влиянием стохастических факторов, называются статистическими.
Слайд 5
5 Испытание — это наблюдение какого-либо явления в рамках определенного числа контролируемых факторов Случайным называется событие, которое при осуществлении совокупности условий может произойти либо не произойти
Слайд 7
7 Величина, которая в результате испытания может принимать некоторое заранее неизвестное значение, называется случайной Дискретные случайные величины принимают при измерениях одно из дискретного множества значений. Непрерывные случайные величины принимают разные возможные значения из непрерывного промежутка.
Слайд 8
8 Вероя́тность (вероятностная мера) — численная мера возможности наступления некоторого события. Тео́рия вероя́тностей — это наука, изучающая закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
Слайд 9
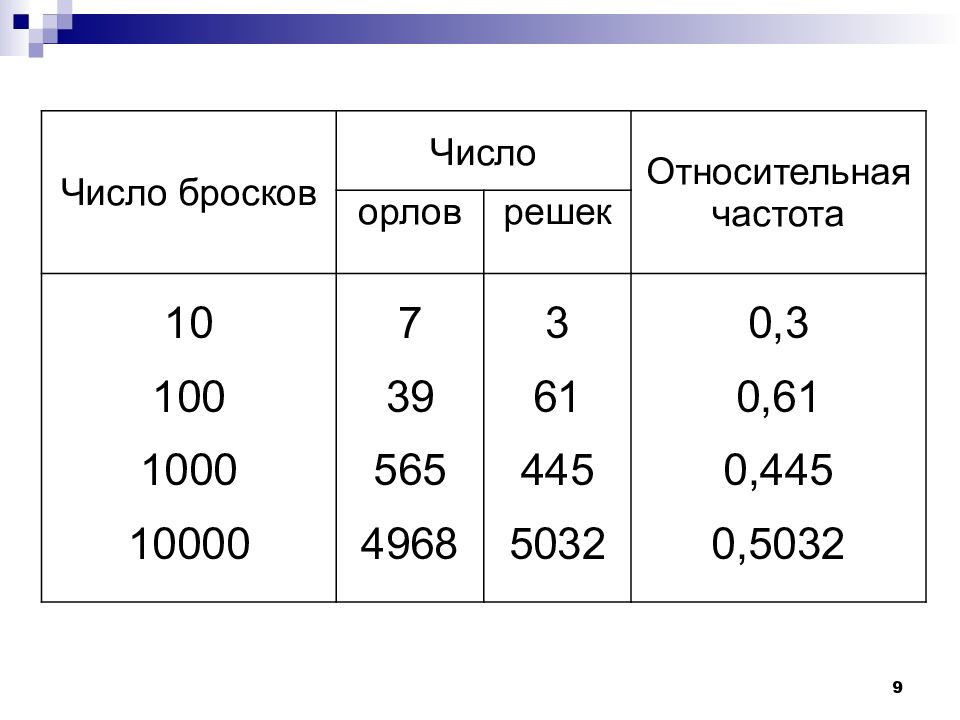
9 Число бросков Число Относительная частота орлов решек 10 100 1000 10000 7 39 565 4968 3 61 445 5032 0,3 0,61 0,445 0,5032
Слайд 10
10 Классическое определение вероятности сводится к модели Лапласа. В модели Лапласа вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу: где: т – число элементарных исходов, благоприятствующих наступлению события А; п – число всех возможных элементарных исходов испытания.
Слайд 11: Свойства вероятности
11 Свойства вероятности Вероятность достоверного события равна единице Вероятность невозможного события равна нулю Вероятность случайного события есть положительное число, заключенное между нулем и единицей
Слайд 12
12 Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний где т - число появлений события А, n - общее число испытаний.
Слайд 13
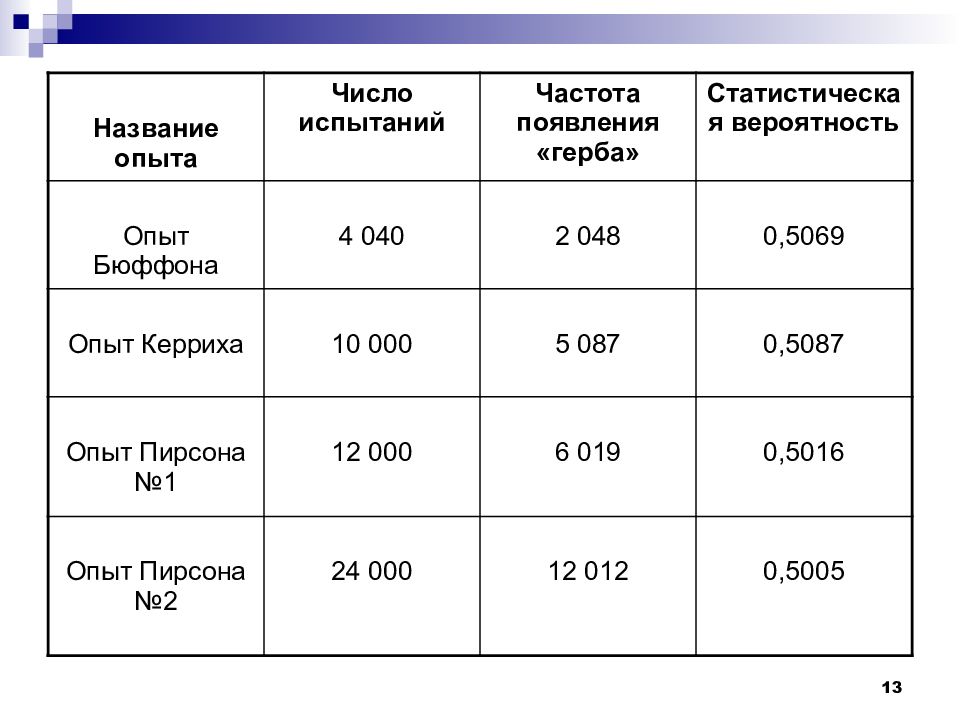
13 Название опыта Число испытаний Частота появления «герба» Статистическая вероятность Опыт Бюффона 4 040 2 048 0,5069 Опыт Керриха 10 000 5 087 0,5087 Опыт Пирсона №1 12 000 6 019 0,5016 Опыт Пирсона №2 24 000 12 012 0,5005
Слайд 14
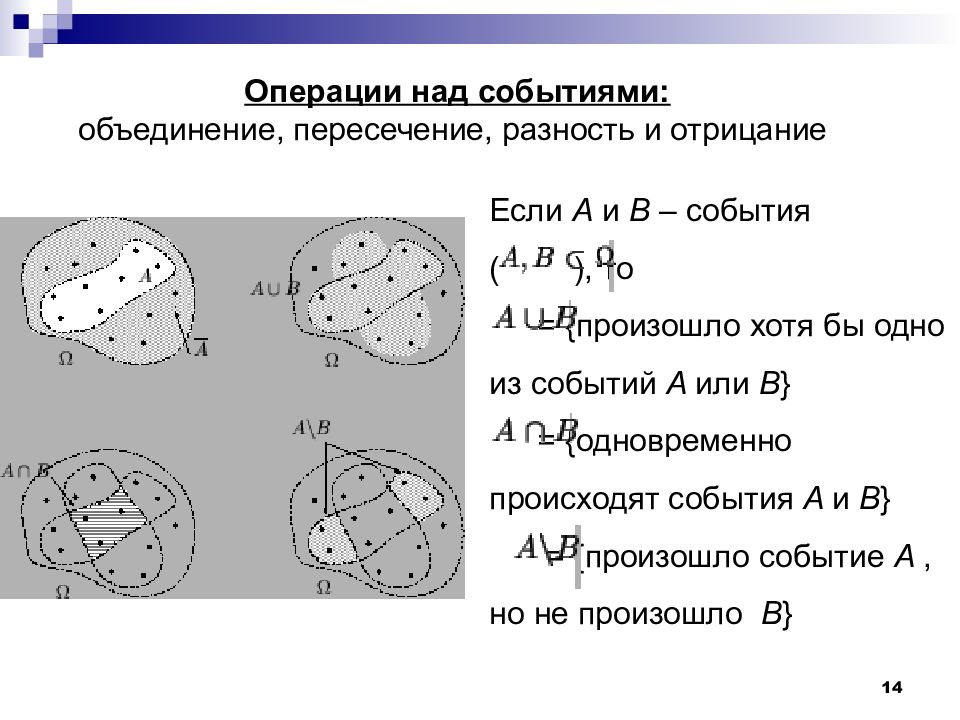
14 Операции над событиями: объединение, пересечение, разность и отрицание Если A и B – события ( ), то = { произошло хотя бы одно из событий A или B } = { одновременно происходят события A и B } = { произошло событие A, но не произошло B }
Слайд 15
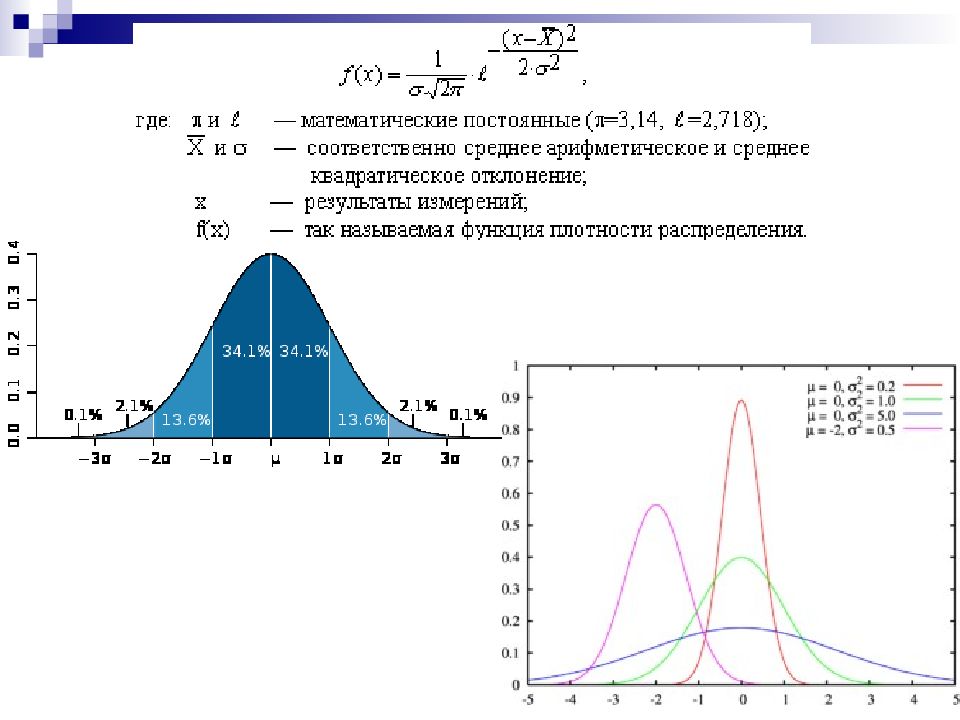
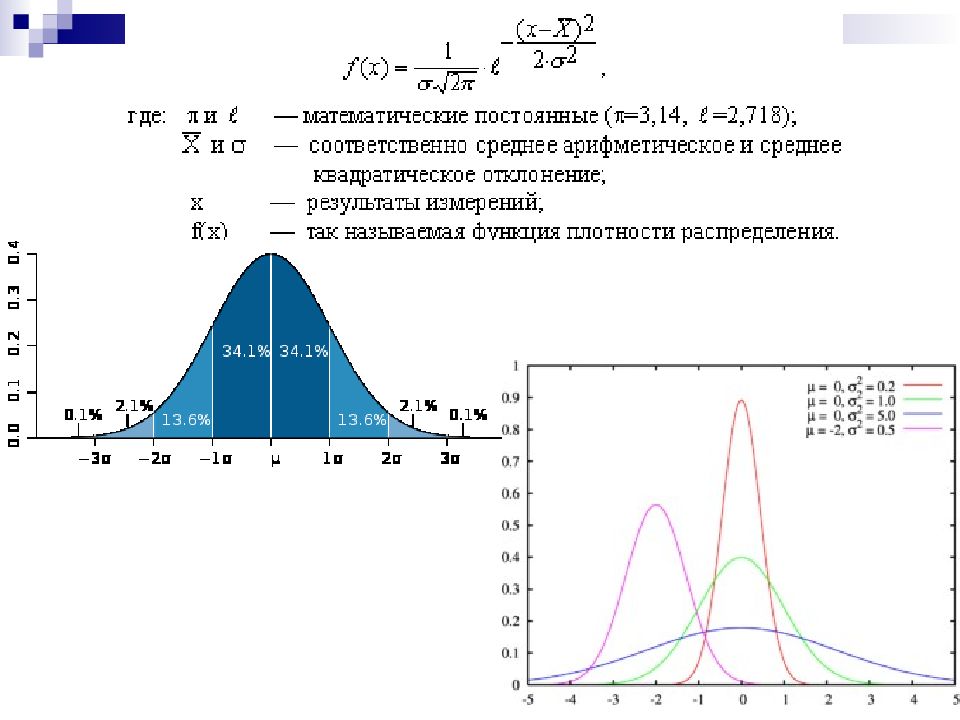
15 Функцией распределения случайной величины Х называется функция F(X), выражающая вероятность того, что Х принимает значение, меньшее или равное заданному числу х F(X)=P(X≤x i ) Величина, равная производной от функции распределения, называется плотностью вероятности случайной величины
Слайд 16
16 ~ Равномерное распределение ~ Экспоненциальное (показательное) распределение ~ Распределение хи-квадрат (c 2 - распределение) ~ F-распределение Фишера ~ Распределение Парето ~ Логистическое распределение ~ Логнормальное распределение ~ Вета-распределение ~ Распределение Вейбулла ~ Распределение Коши ~ Гамма-распределение ~ Распределение Лапласа ~ Нормальное распределение Наиболее распространенные распределения непрерывных случайных величин:
Слайд 18
18 Разные методы определения вероятности как численной меры степени объективной возможности события Формула полной вероятности Формула Бернулли , где q = 1- p
Слайд 19
19 Статистические данные – это все собранные сведения, которые в дальнейшем подвергаются статистической обработке. Статистический признак – это общее свойство, присущее нескольким статистическим данным. Статистической совокупностью называют несколько статистических данных, объединенных в группу хотя бы одним статистическим признаком.
Слайд 20
20 Число данных в статистической совокупности называют ее объемом и обозначают n. Различают следующие совокупности: бесконечные — n →∞ конечные — n – конечное число; генеральные — содержащие все данные, обусловленные постановкой задачи; выборочные — репрезентативные части генеральных совокупностей. большие — n > 30; малые — n ≤ 30;
Слайд 21
21 Виды представления статистических данных: текстовый вид; табличный вид; вариационный ряд; графический вид. x i ~ 2, 3, 3, 5, 5, 6, 6, 6, 6, 7 (неубывающая совокупность) x i ~ 7, 6, 6, 6, 5, 5, 3, 3, 3, 2 (невозрастающая совокупность). Ранжирование – это операция расположения чисел в порядке/ возрастания / убывания. Место каждой варианты в ранжированном ряду называется рангом.
Слайд 22
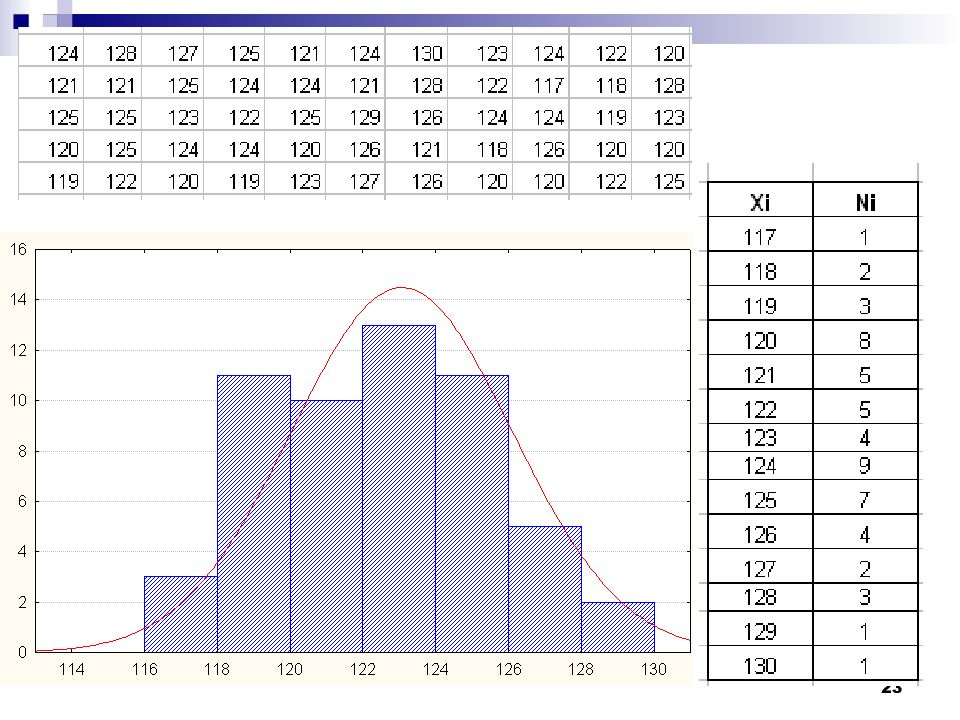
22 1,25 1,25 1,25 1,30 1,30 1,30 1,30 1,30 1,32 1,32 1,32 1,32 1,32 1,32 1,36 1,36 1,36 1,36 1,36 1,36 1,36 1,36 1,36 1,38 1,38 1,38 1,38 1,38 1,38 1,38 1,38 1,40 1,40 1,40 1,40 1,40 1,42 1,42 1,42 1,42 1,45 1,45 1,45 x i 1,25 n i 3 1,30 5 1,32 6 1,36 9 1,38 8 1,40 5 1,42 4 1,45 3 Вариационный ряд — это двойной столбец ранжированных чисел, где слева стоит собственно показатель — вариант, а справа — его количество — частота. n = 43
Слайд 26: Классификация данных по количеству переменных :
26 Классификация данных по количеству переменных :
Слайд 27: Группы числовых характеристик вариационного ряда
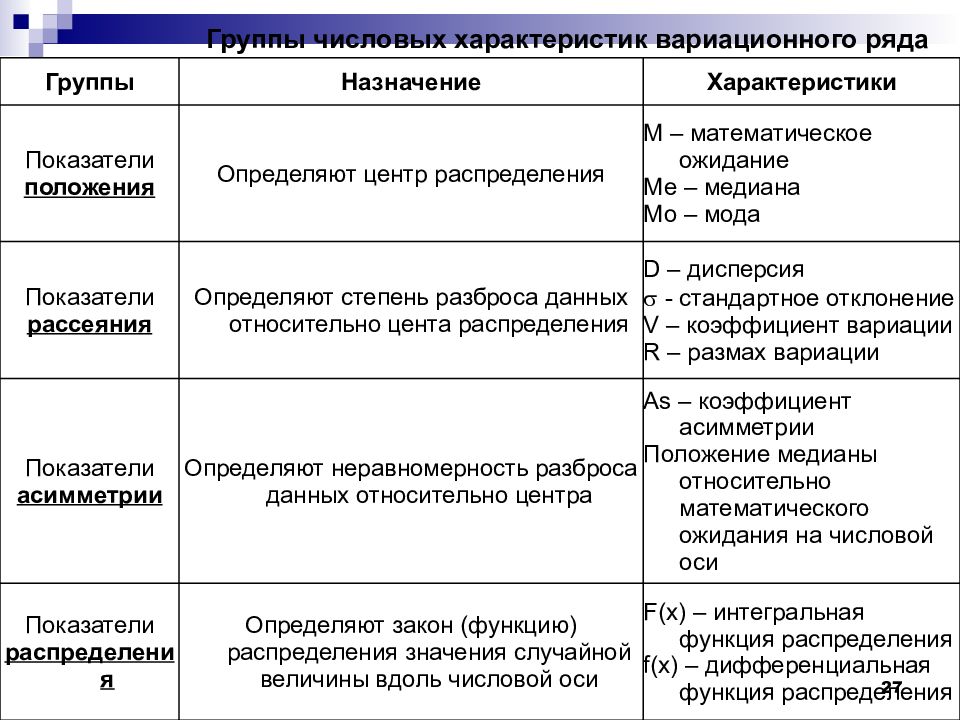
27 Группы числовых характеристик вариационного ряда Группы Назначение Характеристики Показатели положения Определяют центр распределения М – математическое ожидание Ме – медиана Мо – мода Показатели рассеяния Определяют степень разброса данных относительно цента распределения D – дисперсия - стандартное отклонение V – коэффициент вариации R – размах вариации Показатели асимметрии Определяют неравномерность разброса данных относительно центра As – коэффициент асимметрии Положение медианы относительно математического ожидания на числовой оси Показатели распределения Определяют закон (функцию) распределения значения случайной величины вдоль числовой оси F ( x ) – интегральная функция распределения f ( x ) – дифференциальная функция распределения
Слайд 29
29 Медиана ( Ме ) - это такое значение признака Х, когда одна половина значений экспериментальных данных меньше ее, а другая половина - больше (среднее значение вариационного ряда). Порядковый номер медианы в вариационном ряду (ранг) определяется как: Если выборка содержит парное число членов, то медианой принято считать среднее арифметическое средних членов выборки. Мода ( Мо ) - это значение признака, который встречается в выборке чаще всего.
Слайд 30
30 Средним арифметическим называется частное от деления суммы всех значений вариант рассматриваемой совокупности на их число: где Σ – знак суммирования x i – варианты или значения признака n – объем выборки
Слайд 31
31 2. Дисперсия и стандартное отклонение (среднее к вадратическое отклонение) – указывают на варьирование, т.е. рассеивание исходных данных относительно средней арифметической величины 2. Среднее квадратическое (или стандартное) отклонение.
Слайд 32
32 3. Стандартная ошибка или ошибка репрезентативности: 4. Коэффициент вариации: Если, от 0 до 10 - группа однородная; от 10-15 - средняя степень однородности; > 15 - группа неоднородная.
Слайд 33: ПОНЯТИЕ О СТАТИСТИЧЕСКОЙ ДОСТОВЕРНОСТИ
33 ПОНЯТИЕ О СТАТИСТИЧЕСКОЙ ДОСТОВЕРНОСТИ Статистически достоверным различием выборок называется такое, при котором они различаются значимо и принципиально, т. е. принадлежат к разным генеральным совокупностям.
Слайд 34
34 Определение критерия Стьюдента 1. Находим критерий Стьюдента t по следующей формуле: 2. Практика в ФКС показала, что для спортивной работы достаточно принять надежность счета Р= 0,95. Для надежности счета: Р = 0,95 (α = 0,05), при числе степеней свободы k = n 1 + n 2 - 2 по таблице находим величину граничного значения критерия ( t гр ). 3. На основании свойств нормального закона распределения в критерии Стьюдента осуществляется сравнение t и t гр. 4. Делаем выводы: - если t t гр, то различие между сравниваемыми выборками статистически достоверно; - если t < t гр, то различие статистически недостоверно.
Слайд 35
35 Определение критерия Фишера 1. Находим к ритерий Фишера F по формуле: , при D 1 > D 2 2. Задаем надежность счета: Р = 0,95 — и определяем числа степеней свободы для обеих выборок: k 1 = n 1 – 1; k 2 = n 2 - 1. 3. По таблице находим граничное значение критерия F гр. 4. Сравнение критериев F и F гр позволяет сформулировать выводы: - если F F гр, то различие между выборками статистически достоверно; - если F < F гр, то различие между выборками статистически недостоверно
Слайд 36: 4. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ - ОЦЕНКА ВЗАИМОСВЯЗИ МЕЖДУ ИЗУЧАЕМЫМИ ПРИЗНАКАМИ
36 4. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ - ОЦЕНКА ВЗАИМОСВЯЗИ МЕЖДУ ИЗУЧАЕМЫМИ ПРИЗНАКАМИ. Цель заключается в определении формы, направленности, а также тесноты существующей взаимосвязи между варьирующими признаками. Под корреляционной зависимостью понимается зависимость между переменными случайными величинами, при которой каждому значению одной из них соответствует определенная групповая средняя из множества значений другой.
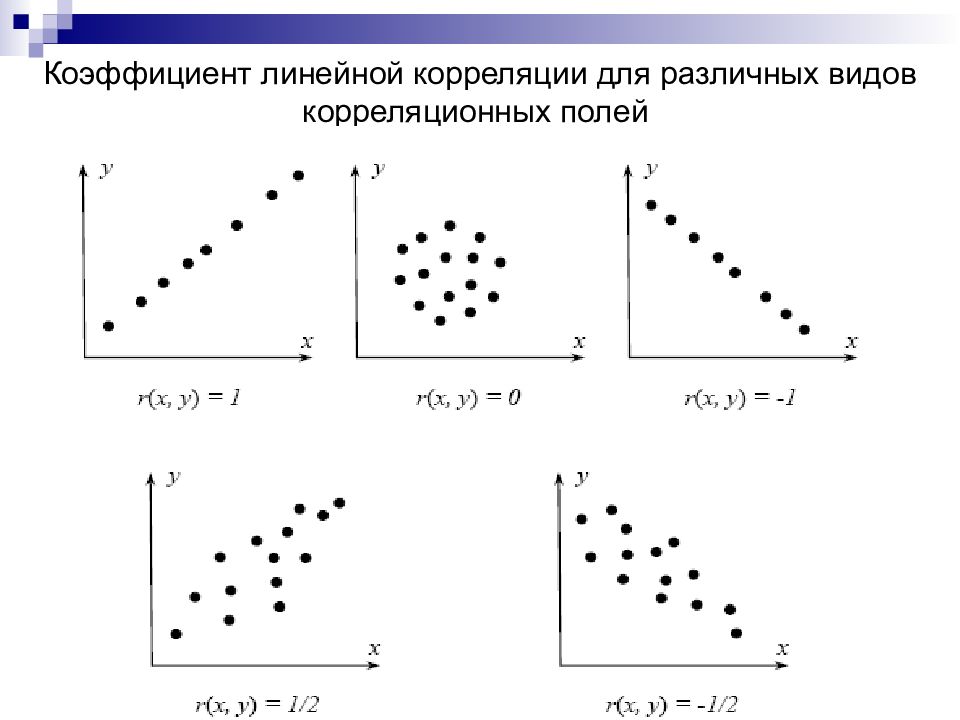
Слайд 37: Коэффициент линейной корреляции для различных видов корреляционных полей
37 Коэффициент линейной корреляции для различных видов корреляционных полей
Слайд 38
38 Коэффициент корреляции Пирсона Свойства коэффициента корреляции Коэффициент корреляции находится в пределах – 1 ≤ r xy ≤ 1. 1. Если r xy = 0, то связь между признаками отсутствующий. 2. Если r xy = ±1, то связь между признаками очень тесна. 3. Принято считать, что r xy = 0,20-0,49 представляет слабую связь, r xy = 0,50-0,69 представляет среднюю связь, r xy = 0,70-0,99 представляет тесную связь. 4. Знак коэффициента корреляции отображает направление связи - положительное или отрицательное.
Слайд 39: Коэффициент ранговой корреляции Спирмена
39 Коэффициент ранговой корреляции Спирмена Это непараметрический критерий, который определяет степень связи между признаками по парному сравнению показателей их рангов. Данный метод может быть использован не только для количественно выраженных данных, но также и в случаях, когда регистрируемые значения признаков являются номинальными
Слайд 40: Эмпирическое значение коэффициента Спирмена
40 Эмпирическое значение коэффициента Спирмена где n – число парных наблюдений d i = d xi - d yi представляет собой разность рангов сравниваем ы х пар i =1,2,…, n
Последний слайд презентации: Лекция 4 Основные понятия теории вероятностей: Алгоритм определения коэффициента ранговой корреляции Спирмена
41 Алгоритм определения коэффициента ранговой корреляции Спирмена Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию). Определить разности рангов каждой пары сопоставляемых значений. Возвести в квадрат каждую разность и суммировать полученные результаты. Вычислить коэффициент корреляции рангов по приведенной формуле. оценить по таблице степень связи между признаками