Лекция 2 Статистическая обработка данных Ростов-на-Дону 2012
Содержание лекции №2 Генеральная совокупность и выборка. Статистическое распределение. Гистограмма. Характеристики положения и рассеяния. Оценка параметров генеральной совокупности по выборке. Доверительный интервал и доверительная вероятность. Сравнение средних.
Математическая статистика (МС) – это наука, изучающая методы обработки результатов наблюдений массовых случайных явлений, обладающих статистической устойчивостью, закономерностью с целью выявления этой закономерности по исследованию части этого массива данных. Возможности МС Выявляет закономерности массовых явлений (т.е. царица в области больших чисел ). 2. Предсказывает наличие внешних влияний.
Два основных направления МС: Оценка неизвестных параметров. 2. Проверка статистических гипотез. генеральная совокупность выборка Основные понятия МС: Задачи математической статистики или
Генеральная совокупность и выборка Генеральная совокупность – это множество всех мыслимых значений наблюдений, однородных относительно некоторого признака, которые могли быть сделаны. Объем генеральной совокупности N Пример : число единиц товара, произведенных фирмой за год. Рост студентов I курса всей Ростовской области
Выборка – совокупность случайно отобранных наблюдений. Выборка характеризуется : - варианта - частота встречаемости Выборка – это множество случаев, с помощью определенной процедуры выбранных из генеральной совокупности для участия в исследовании. Зачем используют выборку? ВОПРОС: Объект исследования очень большой. Существует необходимость сбора первичной информации
Объем выборки. Репрезентативность Объем выборки – это количественная характеристика выборки. Это количество вариант в выборке. Это число случаев, включенных в выборочную совокупность. n А есть качественная характеристика выборки? ВОПРОС: Да. Кого или Что именно выбирают. Какие способы построения выборки для этого используют.
Выборка должна быть репрезентативной, то есть свойства выборки должны отражать свойства генеральной совокупности. Репрезентативность ( фр. r epresentation – представление) – это соответствие характеристик выборки характеристикам генеральной совокупности. Репрезентативность – это свойство выборки представлять параметры генеральной совокупности.
Статистическое распределение (вариационный ряд) Пример : Рост 175 см встретился 5 раз; рост 168 см – 7 раз; 180 см – 8 раз. Вариационный ряд - это та же самая выборка, но расположенная в порядке возрастания элементов. Пример : 168 см – 7 раз; 175 см – 5 раз; 180 см – 8 раз. Статистическое распределение – это совокупность вариант и соответствующих им частот. - варианта - частота встречаемости
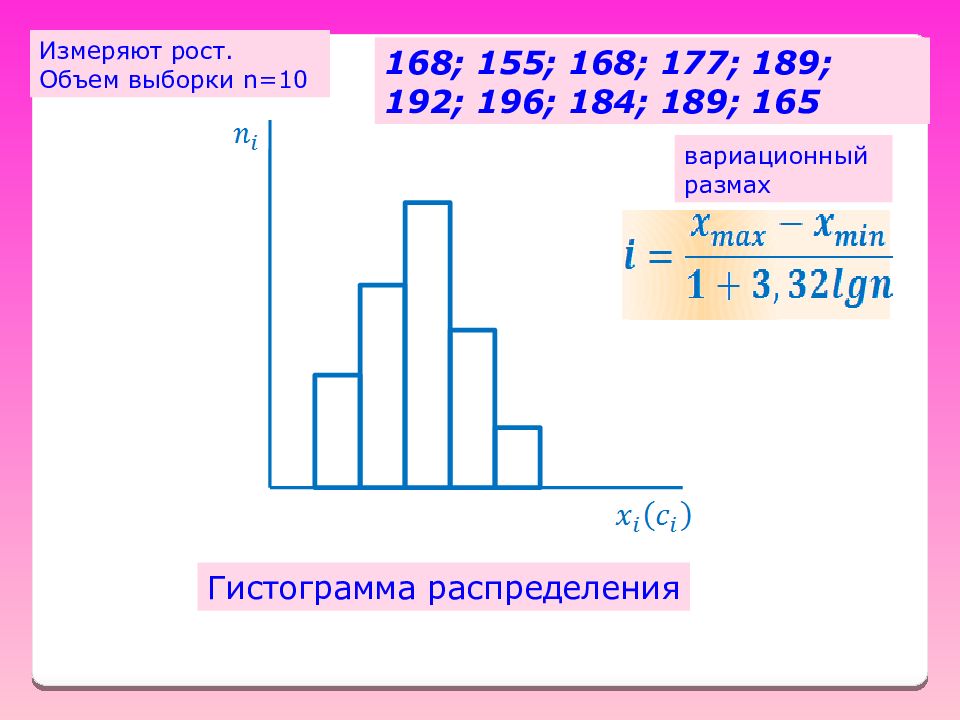
Гистограмма – это ступенчатая фигура, состоящая из смежных прямоугольников, построенных на одной прямой, основания которых одинаковы и равны ширине класса, а высоты равны относительной частоте. Ширина класса вариационный размах Формула Стерджеса Гистограмма
Гистограмма распределения 168; 155; 168; 177; 189; 192; 196; 184; 189; 165 вариационный размах Измеряют рост. Объем выборки n= 10
Характеристики положения (мода, медиана, выборочное среднее) и рассеяния (выборочная дисперсия и выборочное среднее квадратическое отклонение). Мода (Мо) – наиболее часто встречающаяся варианта в данной совокупности. Пример : 1 4 7 25 3 2 19 6 7 Характеристики положения:
Мода – это такое значение варианты, что предшествующие и следующие за ней значения имеют меньшие частоты встречаемости. 172, 168, 172, 175, 187, 172, 164 4 8 10 17 20 5 3 1 2 9 6 10
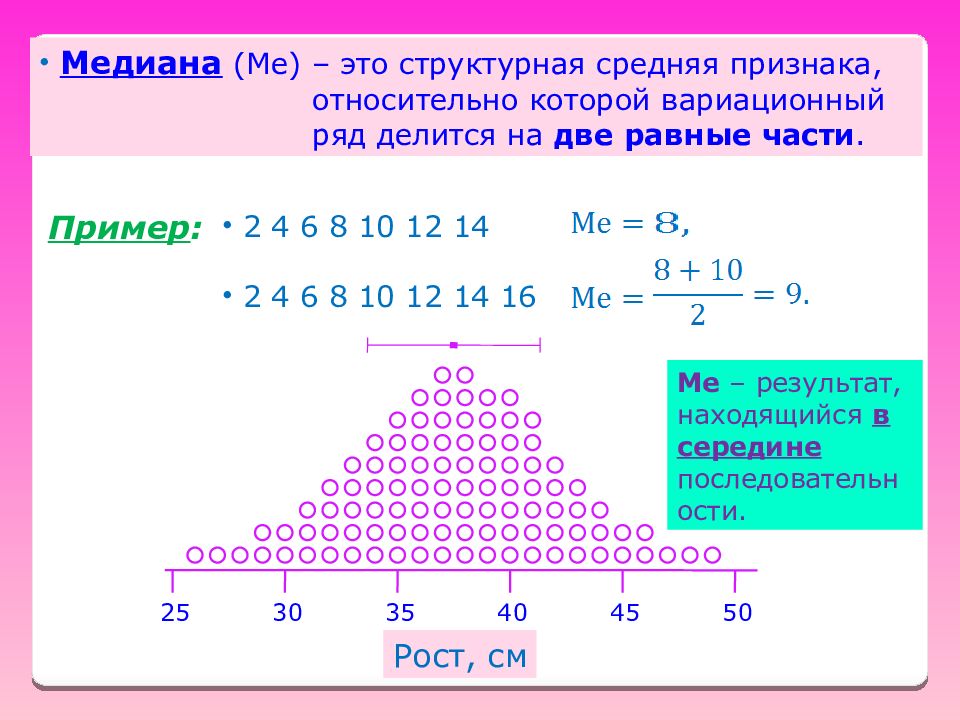
Медиана ( Ме ) – это структурная средняя признака, относительно которой вариационный ряд делится на две равные части. Пример : 2 4 6 8 10 12 14 2 4 6 8 10 12 14 16 25 30 35 40 45 50 Рост, см Ме – результат, находящийся в середине последовательности.
Выборочная средняя – это среднее арифметическое значение вариант статистического ряда. Пример: Гемоглобин ( He ) в крови одной группы мужчин ( n 1 =30) равен 70%, а для другой группы мужчин того же возраста ( n 2 = 20) – 50%. Найти среднюю арифметическую этих двух средних. n - объем выборки - частота встречаемости -варианта
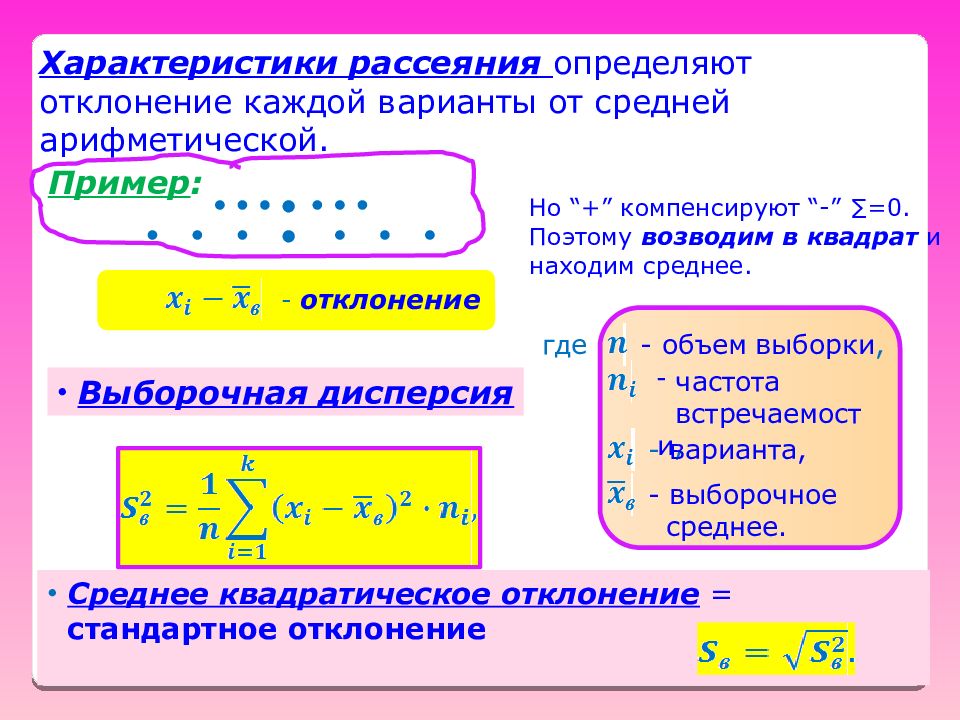
- отклонение Но “ + ” компенсируют “ - ” ∑=0. Поэтому возводим в квадрат и находим среднее. Выборочная дисперсия Пример : Среднее квадратическое отклонение = стандартное отклонение где - объем выборки, частота встречаемости, - варианта, - выборочное среднее. Характеристики рассеяния определяют отклонение каждой варианты от средней арифметической.
Пример : Дана выборка 1 2 3 4 20 15 1 0 5
Пример. Дана выборка 3, 4, 5
Оценка параметров генеральной! совокупности по характеристикам ее выборки! (точечная и интервальная) Требования Оценка параметра – это любая функция от значений выборки. несмещенная состоятельная эффективная Генеральная совокупность –это гипотетическое множество элементов, объединенных общей характеристикой. Выборка - множество испытуемых из генеральной совокупности.
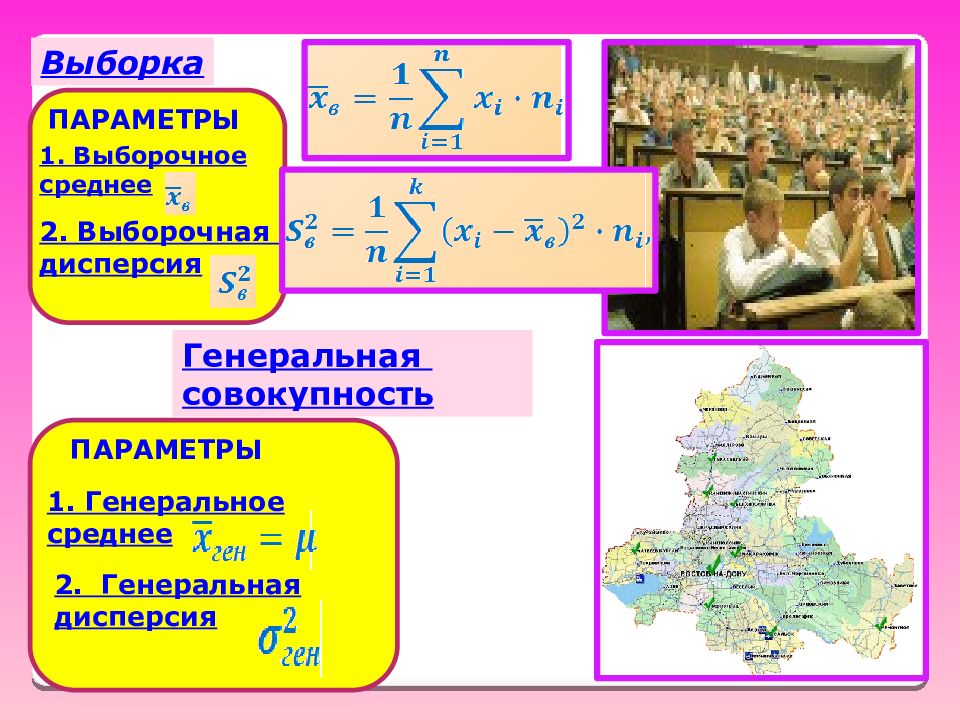
ПАРАМЕТРЫ 1. Выборочное среднее 2. Выборочная дисперсия Выборка Генеральная совокупность ПАРАМЕТРЫ 1. Генеральное среднее 2. Генеральная дисперсия
Точечная оценка – это выборочная характеристика, используемая в качестве приближенного значения неизвестной генеральной характеристики. Определяется одним числом (точкой на числовой оси). Выборка должна быть большого объема. Дает лишь некоторое приближенное значение параметра. I. Точечная оценка
- это несмещенная оценка математического ожидания - это смещенная оценка дисперсии Генеральное среднее Генеральная дисперсия Генеральное среднее равно математическому ожиданию выборочной средней Генеральная дисперсия не равна математическому ожиданию выборочной дисперсии
Исправленная дисперсия (более точная ) Генеральная дисперсия равна математическому ожиданию исправленной дисперсии. - средняя ошибка выборочной средней, - исправленное среднее квадратическое отклонение, - объем выборки, - коэффициент вариации. Характеризует изменчивость признака в единых единицах %
II. Интервальная оценка – это числовой интервал, содержащий неизвестный параметр генеральной совокупности с заданной вероятностью. Определяется двумя числами –границами интервала. Более точная, надежная и информативная, так как дает информацию о степени близости к соответствующему теоретическому параметру. Используется, если выборка малого объема.
Доверительный интервал и доверительная вероятность Доверительный интервал – это интервал, в котором с той или иной заранее ! заданной вероятностью ! находится генеральный параметр. - выборочное среднее, - средняя ошибка выборочной средней. (Р≥0,95) - нормированный показатель распределения Стьюдента, с ( n-1 ) степенями свободы
- нормированный показатель распределения Стьюдента, с ( n-1 ) степенями свободы, который определяется вероятностью попадания генерального параметра в этот интервал. Стьюдент (Уильям Д. Госсет ) 1876-1937гг. 1899г. Дублин, Ирландия, Пивоваренный завод Гиннеса f/ α 0.1 0.05 1. 6,314 12,706 2. 2,920 4,303 3. 2,353 3,182 4. 2,132 2,776 5. 2,015 2,571 6. 1,943 2,447 7. 1,895 2,365 8. 1,860 2,306 9. 1,833 2,262 10. 1,812 2,228 11. 1,796 2,201 12. 1,782 2,179 13. 1,771 2,160 14. 1,761 2,145 15. 1,753 2,131
Доверительная вероятность Р – это такая вероятность, что событие 1-Р – можно считать невозможным. Признана достаточной для уверенного суждения о генеральных параметрах на основании известных выборочных показателей. Обычно в качестве доверительных используют вероятности, близкие к 1. Тогда событие, что генеральный параметр попадет в этот интервал будет практически достоверным. Уровень значимости = уровень ошибки,
В жизни : Гипотеза ( hypothesis ) H – предположение, описывающее возможную взаимосвязь между событиями. В науке : Гипотеза – предположение, вызывающее сомнение ! В математической статистике: Гипотеза – предположение, которое в ызывает сомнение, и которое мы собираемся проверять! Статистическая гипотеза – это всякое в ысказывание о генеральной ! ( всегда !) совокупности, проверяемое по выборке ! Статистическая проверка гипотез.
Например : Статистическая гипотеза – это п редположение о виде неизвестного распределения или о параметрах известного распределения. Тест: Какая гипотеза, из нижеприведенных, я вляется статистической? 1. Генеральная совокупность распределена по нормальному закону. 2. Зимой на экзамене я, может быть, получу “ 4 ”. 3. Генеральные дисперсии равны 4. Летом, может быть, я поеду на море. Ответ: 1, 3.
Общая постановка задачи проверки гипотез Проверка гипотезы – это процедура сопоставления высказанной гипотезы о генеральной совокупности с выборочными данными. Этапы проверки гипотезы (общая схема) 1 Выдвигают нулевую гипотезу H 0. Это основная гипотеза. Сущность H 0 : разница между сравниваемыми генеральными параметрами = 0, и различия, наблюдаемые между выборочными данными носят случайный! характер. 2 Формулируют альтернативную гипотезу H 1, к онкурирующую с H 0. Это логическое отрицание H 0.
3 Задаются уровнем значимости критерия α. Уровень значимости критерия α – это вероятность ошибки отвергнуть H 0, если на самом деле она верна. Откуда ошибка? Решение о справедливости H 0 принимается по выборочным данным, т.е. по ограниченному ряду наблюдений. оно может быть ошибочным. α задается заранее! малым числом. Почему малым? Потому что это вероятность ошибочного заключения. Каким малым числом? Обычно это стандартное значение Но можно выбрать более ограничивающее ВОПРОС: ВОПРОС: ВОПРОС:
( из выборочных данных ). Для проверки H 0 вычисляют величину критерия К, отвечающего H 0. Статистический критерий – это правило, позволяющее основываясь т олько на выборке принять или отвергнуть H 0. Критерий – это случайная величина, которая служит для проверки H 0. Эти функции распределения табулированы и приводятся в специальных таблицах для различных степеней свободы f (или объема выборки n ) и разных α. 4 5 или ( из таблиц). По таблице известного распределения вероятности определяют критическое значение, превышение которого при справедливости H 0 маловероятно.
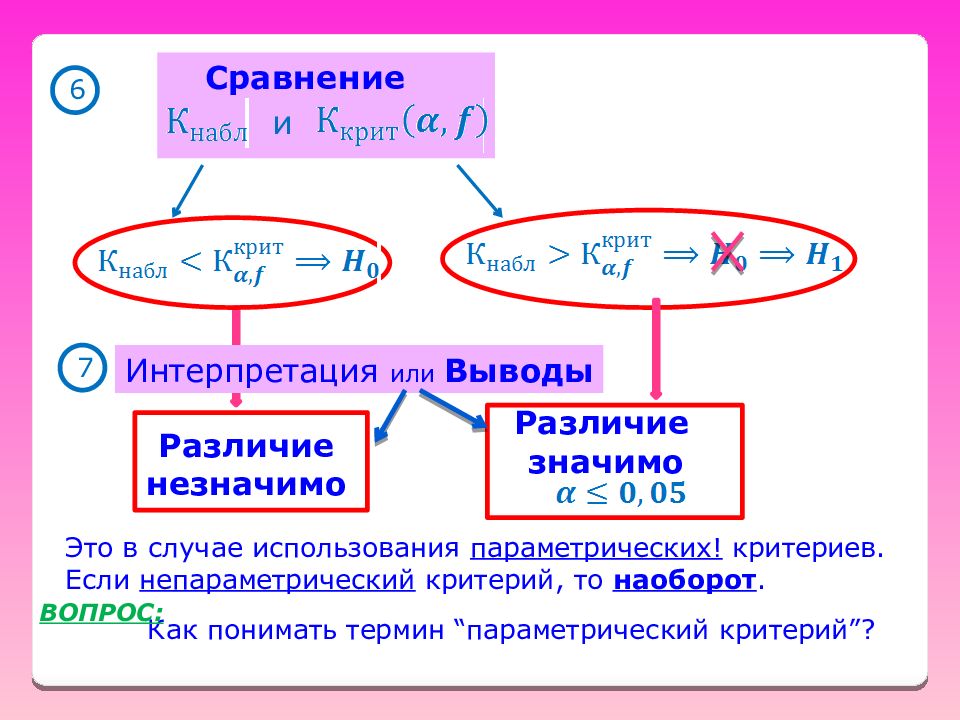
6 Сравнение и 7 Интерпретация или Выводы Различие незначимо Различие значимо Это в случае использования параметрических! критериев. Если непараметрический критерий, то наоборот. Как понимать термин “ параметрический критерий ” ? ВОПРОС:
Проверка гипотез относительно средних Одна серия экспериментов Другая серия, например, контроль Средний результат отличается это расхождение случайно или оно вызвано некоторыми закономерностями ? Возникает вопрос:
1 или 2 3 4 Для проверки можно использовать параметрический критерий Стьюдента, если выполняются следующие Требования к критерию Стьюдента ( t -критерий ) 2 1 НЗР По выборочным данным рассчитываем, отвечающее. Общая схема проверки гипотезы : 1 Выдвигаем 2 3 Задаем 4 Рассчитываем ( по выборке ) 5 Находим ( из таблиц) 6 7 Сравниваем и Выводы Выдвигаем
Это отношение имеет t -распределение Стьюдента с степенями свободы. 5 По таблице известного распределения находим 1908г. 6 Сравниваем Различие недостоверно. Если Если Различие достоверно Различие значимо Выводы:
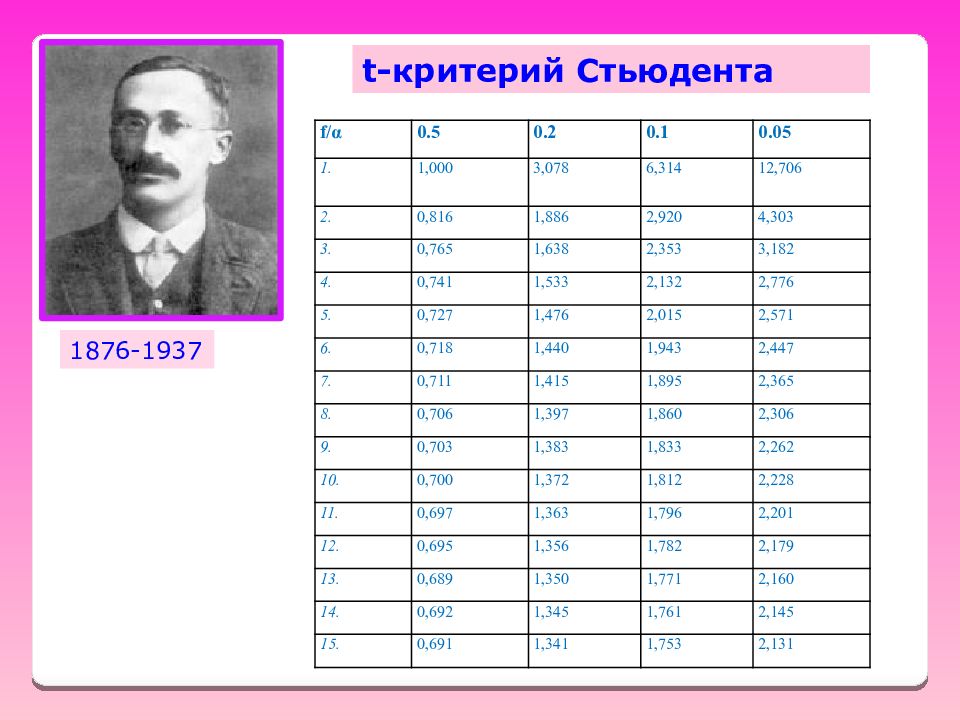
t- критерий Стьюдента 1876-1937 f/ α 0.5 0.2 0.1 0.05 1. 1,000 3,078 6,314 12,706 2. 0,816 1,886 2,920 4,303 3. 0,765 1,638 2,353 3,182 4. 0,741 1,533 2,132 2,776 5. 0,727 1,476 2,015 2,571 6. 0,718 1,440 1,943 2,447 7. 0,711 1,415 1,895 2,365 8. 0,706 1,397 1,860 2,306 9. 0,703 1,383 1,833 2,262 10. 0,700 1,372 1,812 2,228 11. 0,697 1,363 1,796 2,201 12. 0,695 1,356 1,782 2,179 13. 0,689 1,350 1,771 2,160 14. 0,692 1,345 1,761 2,145 15. 0,691 1,341 1,753 2,131
