2022 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ. НЕПРЕРВНОСТЬ В ТОЧКЕ МАТЕМАТИЧЕСКИЙ АНАЛИЗ И ЛИНЕЙНАЯ АЛГЕБРА БФУ имени И. Канта
2 2022 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Постоянная функция ( константа ) ; ; функция четная: ; график: прямая.
3 2022 СТЕПЕННЫЕ ФУНКЦИИ Степенные функции Линейные функции ; ; функция нечетная: график: прямая.
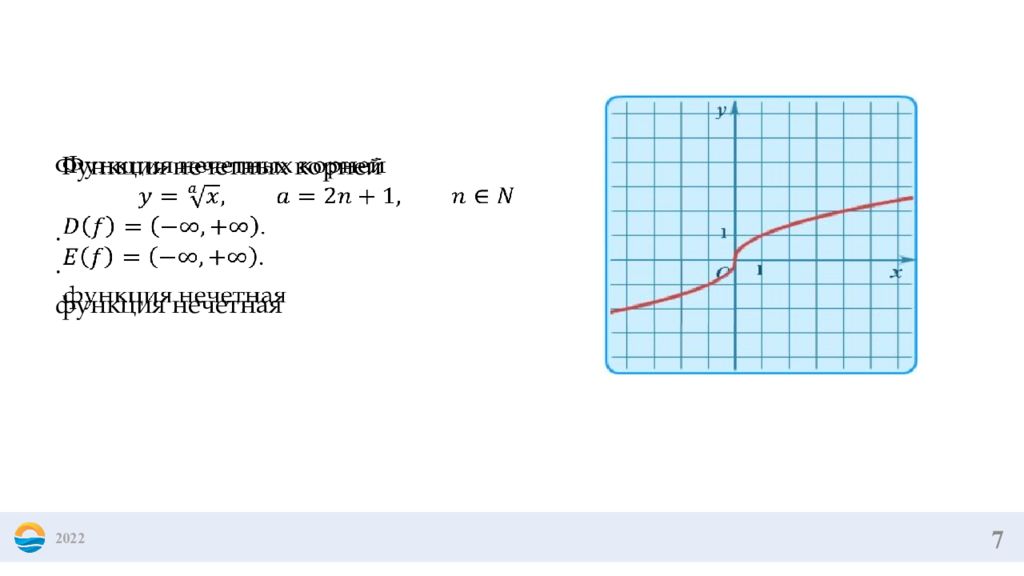
4 2022 Функции с четной степенью ; ; функция четная : график: парабола. Функции с нечетной степенью ; ; функция нечетная: график: кубическая парабола
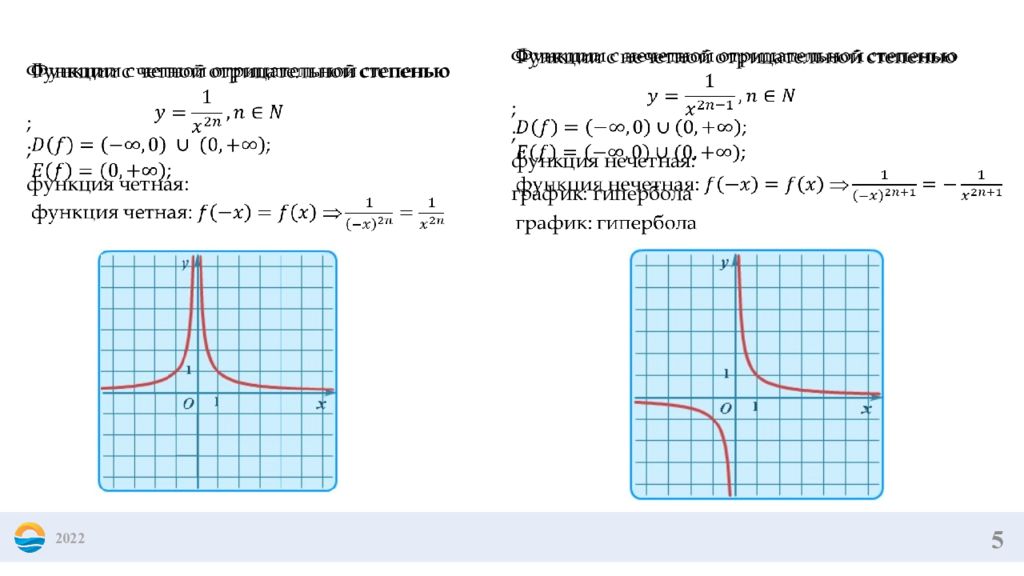
5 2022 Функции с четной отрицательной степенью ; ; функция четная: Функции с нечетной отрицательной степенью ; ; функция нечетная: график: гипербола
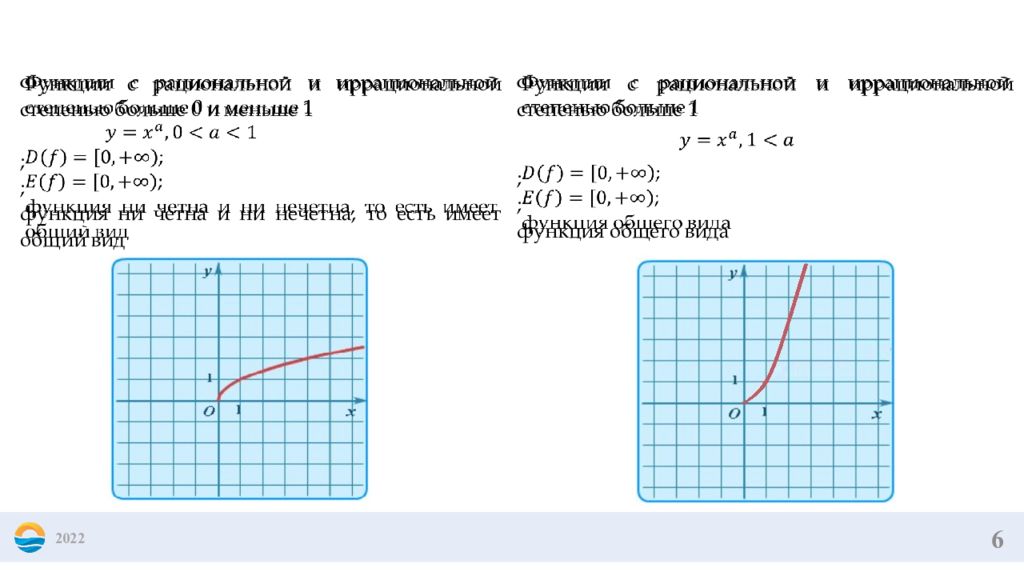
6 2022 Функции с рациональной и иррациональной степенью больше 0 и меньше 1 ; ; функция ни четна и ни нечетна, то есть имеет общий вид Функции с рациональной и иррациональной степенью больше 1 ; ; функция общего вида
7 2022 Функция нечетных корней . . функция нечетная
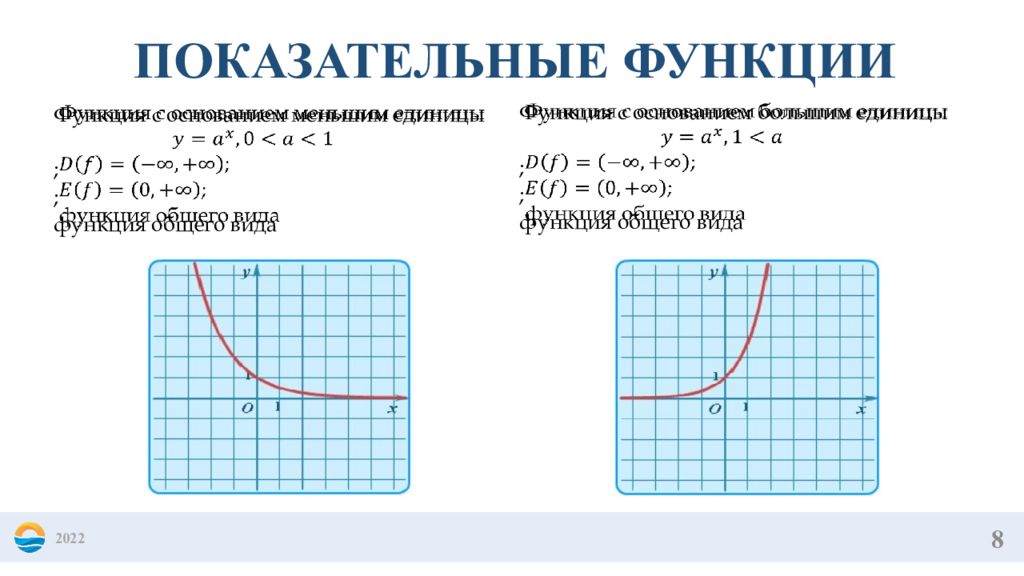
8 2022 ПОКАЗАТЕЛЬНЫЕ ФУНКЦИИ Функция с основанием меньшим единицы ; ; функция общего вида Функция с основанием большим единицы ; ; функция общего вида
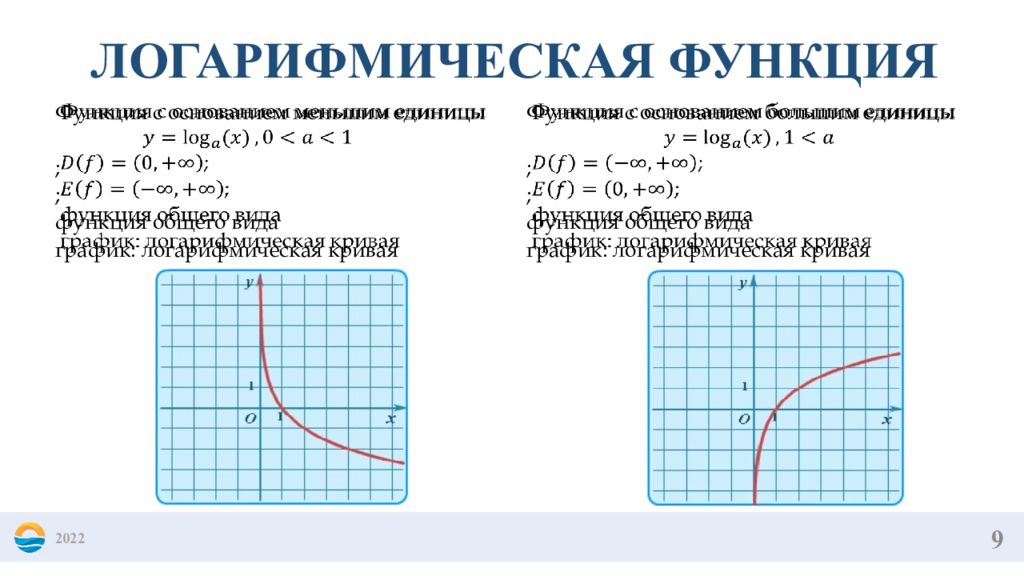
9 2022 ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ Функция с основанием меньшим единицы ; ; функция общего вида график: логарифмическая кривая Функция с основанием большим единицы ; ; функция общего вида график: логарифмическая кривая
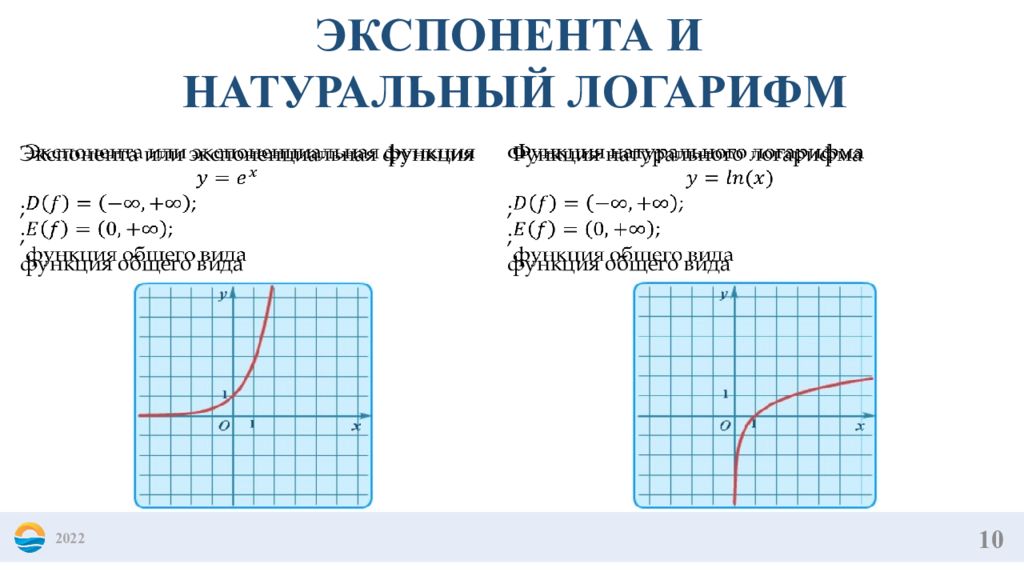
10 2022 ЭКСПОНЕНТА И НАТУРАЛЬНЫЙ ЛОГАРИФМ Функция натурального логарифма ; ; функция общего вида Экспонента или экспоненциальная функция ; ; функция общего вида
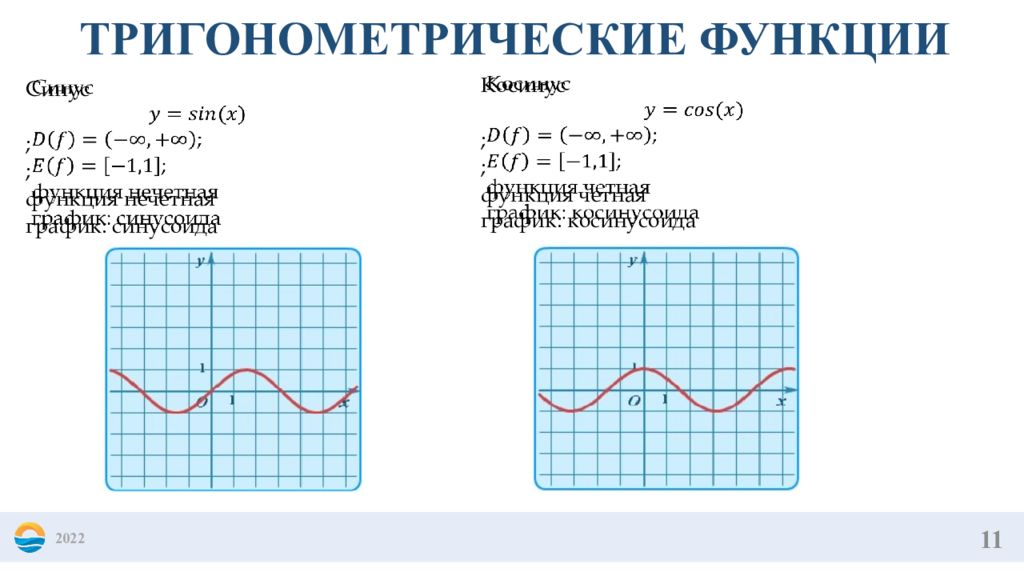
11 2022 ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Синус ; ; функция нечетная график: синусоида Косинус ; ; функция четная график : косинусоида
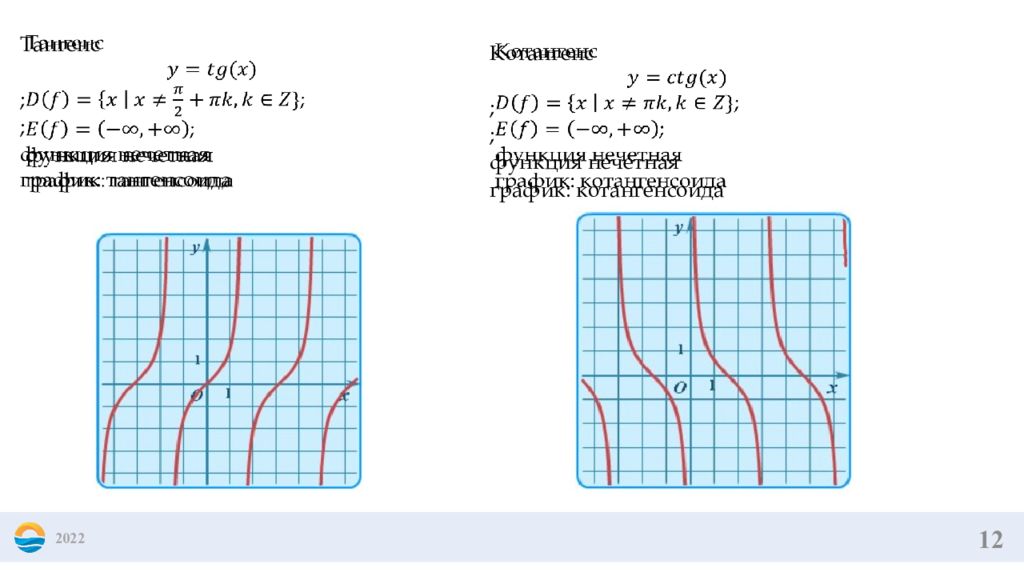
12 2022 Тангенс ; ; функция нечетная график: тангенсоида Котангенс ; ; функция не четная график : котангенсоида
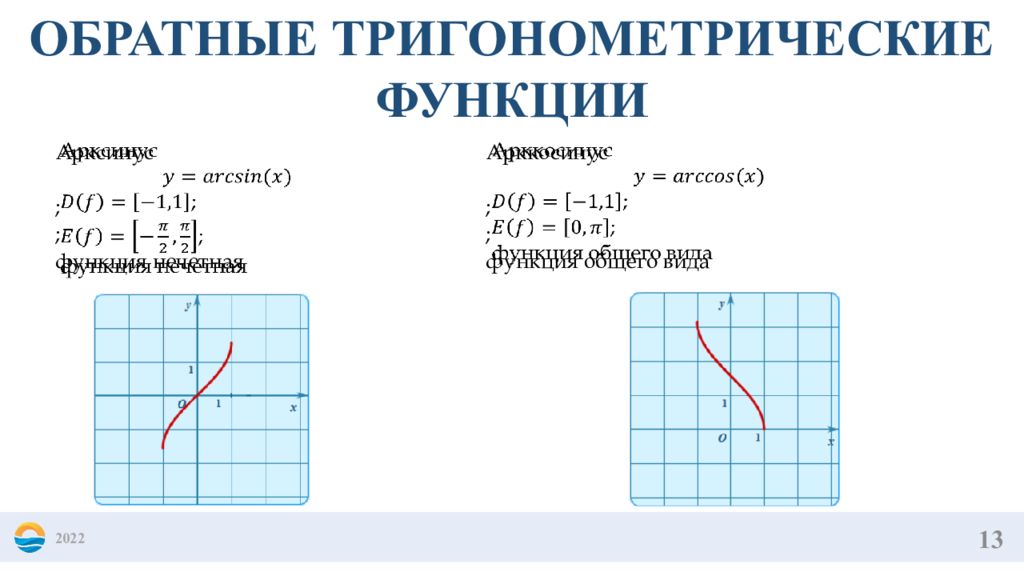
13 2022 ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Арксинус ; ; функция нечетная Арккосинус ; ; функция общего вида
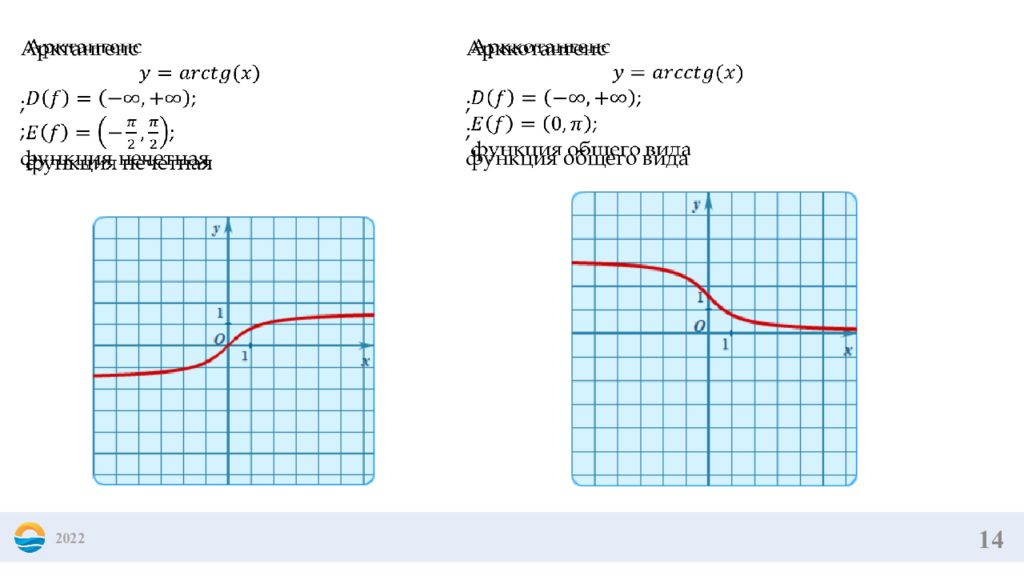
14 2022 Арктангенс ; ; функция не четная Арккотангенс ; ; функция общего вида
15 2022 ПРЕОБРАЗОВАНИЕ ФУНКЦИИ — сдвигом вдоль оси на единиц (вверх, если, и вниз, если ) ; — сдвигом вдоль оси на единиц (вправо, если, и влево, если ) ; — растяжением вдоль оси в раз; — сжатием по оси в раз; — симметричным отражением относительно оси ; — симметричным отражением относительно оси ; , следующим образом: часть графика, расположенная не ниже оси, остается без изменений, а «нижняя» часть графика симметрично отражается относительно оси ; , следующим образом: правая часть графика (при ) остается без изменений, а вместо «левой» строится симметричное отражение «правой» относительно оси.
16 2022 НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ Функция называется непрерывной в точке, если: 1) эта функция определена в некоторой окрестности точки ; 2) существует предел ; 3) этот предел равен значению функции в точке, т.е.
17 2022 Последнее условие равносильно условию где — приращение аргумента, — приращение функции, соответствующее приращению аргумента, т.е. функция непрерывна в точке тогда и только тогда, когда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
18 2022 ОДНОСТОРОННЯЯ НЕПРЕРЫВНОСТЬ Функция называется непрерывной слева в точке, если она определена на некотором полуинтервале и Аналогичное условие и с непрерывностью справа. Функция непрерывна в точке тогда и только тогда, когда она непрерывна и слева и справа в этой точке. При этом
19 2022 НЕПРЕРЫВНОСТЬ ФУНКЦИИ НА МНОЖЕСТВЕ Функция называется непрерывной на множестве, если она является непрерывной в каждой точке этого множества. При этом если функция определена в конце некоторого промежутка числовой оси, то под непрерывностью в этой точке понимается непрерывность справа или слева. Функция называется непрерывной на отрезке, если: непрерывна в каждой точке интервала ; непрерывна справа в точке ; непрерывна слева в точке ;
20 2022 ТОЧКИ РАЗРЫВА ФУНКЦИИ Точка, принадлежащая области определения функции или являющаяся граничной точкой этой области, называется точкой разрыва данной функции, если не является непрерывной в этой точке.
21 2022 Точки разрыва бывают первого и второго рода: I. Если существует конечные пределы и, причем не все три числа, то называется точкой разрыва I рода. Примечание: 1 ) Если левый и правый пределы функции равны между собой, но не равны значению этой точке, то называется точкой устранимого разрыва, то есть можно видоизменить функцию, чтобы доопределить функцию по непрерывности. 2 ) называется скачком функции в точке. 3 ) Скачок функции в точке устранимого разрыва равен 0.
22 2022 II. Точки разрыва, не являющиеся точками разрыва первого рода, называются точками разрыва II рода. Точка разрыва II рода является точка, в которой не существует или бесконечен хотя бы один из односторонних пределов и.
23 2022 СВОЙСТВА Если функции и непрерывны в точке, то функции также непрерывны в точке. Если функция непрерывна в точке, а функция непрерывна в точке, то и сложная функция непрерывна в точке. Все основные элементарные функции непрерывны в каждой точке своих областей определения. Примечание: Из свойств 1–3 следует, что все элементарные функции (функции, полученные из основных элементарных функций с помощью конечного числа арифметических операций и операции композиции) также непрерывны в каждой точке своих областей определения.
24 2022 СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ Теорема о промежуточных значениях. Пусть функция определена и непрерывна на отрезке. Тогда для любого числа, заключенного между числами и найдется хотя бы одна точка, такая что. Теорема Больцано —Коши. Пусть функция определена и непрерывна на отрезке и принимает на его концах значения различных знаков. Тогда найдется хотя бы одна точка, такая что.
25 2022 1-я теорема Вейерштрасса. Пусть функция определена и непрерывна на отрезке. Тогда эта функция ограничена на этом отрезке. 2-я теорема Вейерштрасса. Пусть функция определена и непрерывна на отрезке. Тогда эта функция достигает на отрезке своего наибольшего и наименьшего значений, т.е. существуют такие точки, что для любой точки справедливы неравенства.
26 2022 РАВНОМЕРНАЯ НЕПРЕРЫВНОСТЬ ФУНКЦИИ Функция называется равномерно непрерывной на множестве, если выполняется следующие условие: Теорема Кантора. Непрерывная на отрезке функция равномерно непрерывна на этом отрезке.
2022 Спасибо за внимание! МАТЕМАТИЧЕСКИЙ АНАЛИЗ И ЛИНЕЙНАЯ АЛГЕБРА БФУ имени И. Канта
