Лекция № 7
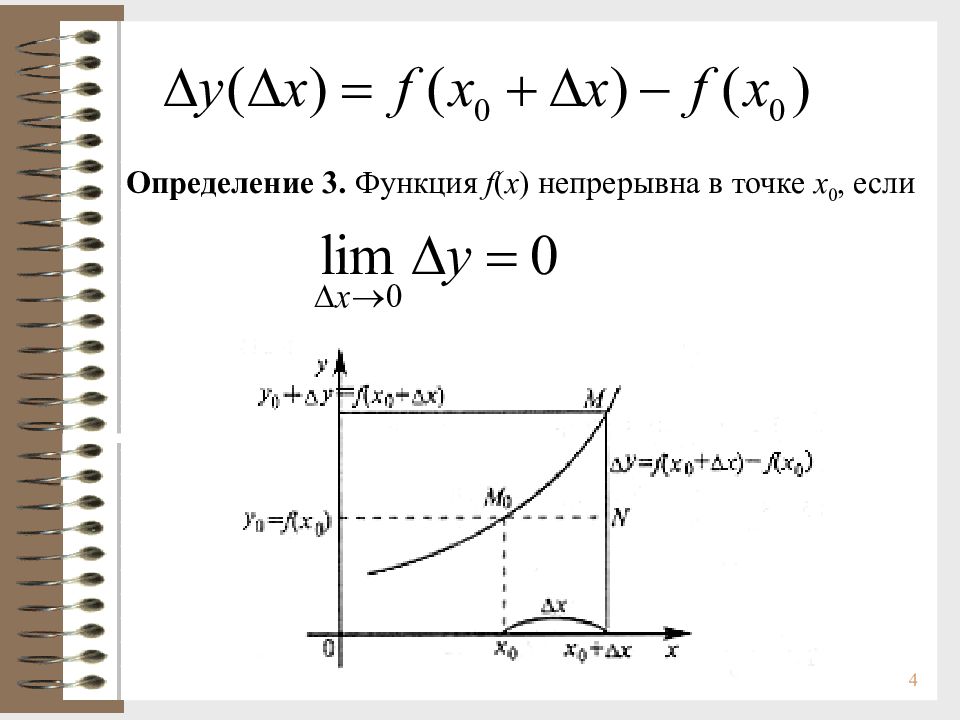
2 Непрерывность функции Определение 1. Функция f ( x ) называется непрерывной в точке x 0, если предел этой функции и ее значение в этой точке равны, т.е. 1.1. Через односторонние пределы: 1.2. На языке e – d
3 Определение 2 (на языке последовательностей). Функция f ( x ) называется непрерывной в точке х 0, если для любой последовательности значений аргумента { x n }, сходящейся к х 0, последовательность соответствующих значений функций { f ( x n )} сходится к f ( x 0 ). Если то функцию f ( x ) называют непрерывной в точке х 0 справа (слева). Если функция f ( x ) непрерывна в точке х 0 и справа и слева, то она непрерывна в этой точке.
4 Определение 3. Функция f ( x ) непрерывна в точке х 0, если
5 Арифметические действия над непрерывными функциями Теорема. Пусть функции f ( x ) и g ( x ) непрерывны в точке х 0. Тогда функции f ( x ) g ( x ), f ( x ) g ( x ) и f ( x ) / g ( x ) также непрерывны в этой точке (последняя при g ( x ) 0). Доказательство. Теорема следует из определения непрерывности функций.
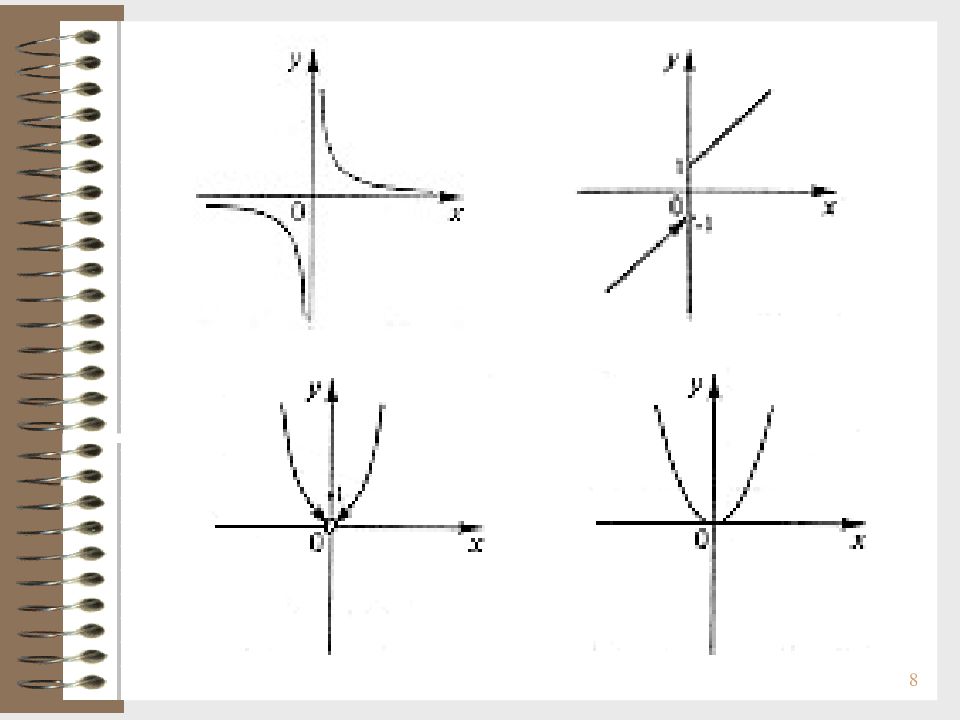
6 Классификация точек разрыва функций Определение. Точка х 0 называется точкой разрыва функции f ( x ), если f ( x ) в точке х 0 не является непрерывной. Точка х 0 называется точкой разрыва 1- го рода функции f ( x ), если в этой точке функция имеет конечные, но не равные друг к другу правый и левый пределы : Если существует, но функция в точке x 0 не определена, то разрыв функции в точке называется устранимым. Пример.
7 Определение. Точка х 0 называется точкой разрыва 2-го рода функции f ( x ), если в этой точке функция не имеет по крайней мере одного из односторонних пределов или хотя бы один из них из односторонних пределов бесконечен. Определение. Функция называется кусочно-непрерывной на отрезке [ a, b ], если она непрерывна во всех внутренних точках [ a, b ], за исключением, быть может, конечного числа точек, в которых имеет разрыв 1-го рода и, кроме того, имеет односторонние пределы в точках а и b. Определение. Функция называется кусочно-непрерывной на числовой прямой, если она кусочно-непрерывна на любом отрезке.
8
9 Основные свойства непрерывных функций Теорема (об устойчивости знака непрерывной функции) Пусть функция f ( x ) непрерывна в точке х 0 и f ( x 0 ) 0. Тогда существует d > 0 такое, что для всех х ( х 0 – , х 0 + ) функция f ( x ) имеет тот же знак, что f ( x 0 ).
10 Доказательство : Пусть f ( x 0 ) > 0. Тогда в силу определения 2 непрерывности функции для >0 >0 такое, что неравенство | f ( x ) – f ( x 0 )|< выполняется для всех х, удовлетворяющих неравенству | x – x 0 | < . Или f ( x 0 ) – < f ( x ) < f ( x 0 ) + для всех х ( х 0 – , х 0 + ). Возьмем = f ( x 0 ). Тогда f ( x ) > 0 для всех х ( х 0 – , х 0 + ). Ч.т.д.
11 Теорема (1-ая теорема Больцано-Коши) Пусть функция f ( x ) непрерывна на отрезке [ a, b ] и на концах отрезка имеет значения разных знаков. Тогда существует точка с ( a, b ), в которой f ( с ) = 0.
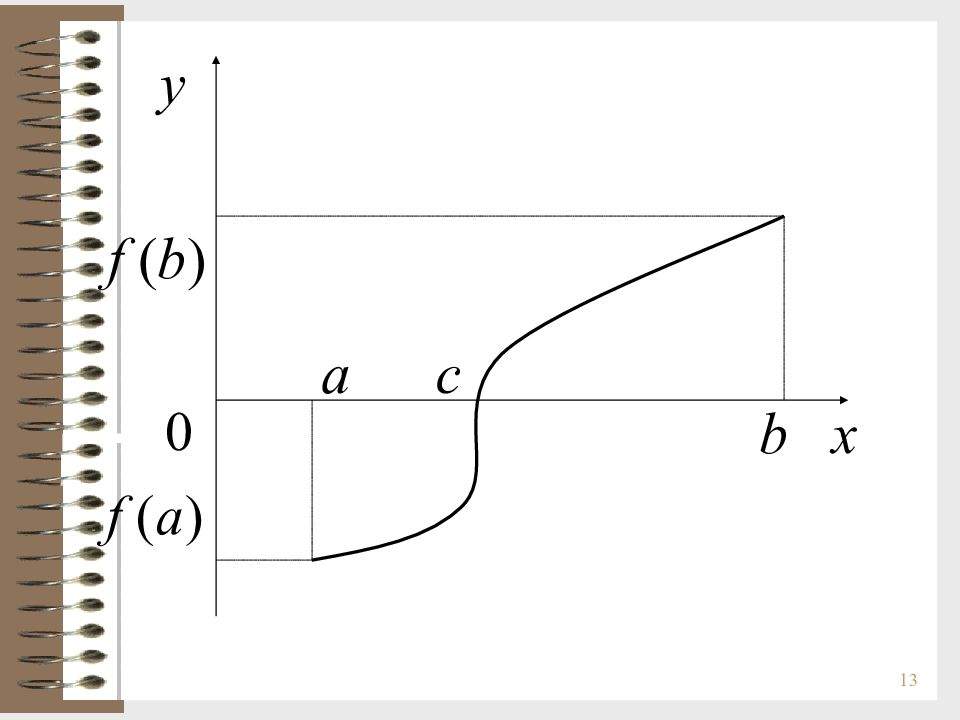
12 Доказательство : Пусть для определенности f ( a )<0 и f ( b )>0. Разделим [ a, b ] пополам. Если значение функции в середине [ a, b ] равно нулю, то теорема доказана. В противном случае выберем тот из двух полученных отрезков, на концах которого f ( x ) имеет значения разных знаков, обозначим его [ a 1, b 1 ]. Разделим его пополам. Если значение функции в середине отрезка [ a 1, b 1 ] равно нулю, то теорема доказана. В противном случае выберем тот из двух полученных отрезков, на концах которого f ( x ) имеет значения разных знаков. Обозначим его [ a 2, b 2 ]. И т.д. Получим последовательность [ a, b ] [ a 1, b 1 ] [ a 2, b 2 ] … [ a n, b n ] … вложенных отрезков. По теореме о вложенных отрезках с, принадлежащая всем отрезкам, причем f ( с )=0. Ч.т.д. Теорема имеет простой геометрический.смысл.
13
14 Пусть функция f ( x ) непрерывна на отрезке [ a, b ], причем f ( a ) = A, f ( b ) = B. Пусть С – любое число, заключенное между А и В. Тогда на отрезке [ a, b ] найдется точка с такая, что f ( с ) = С. Другими словами, непрерывная функция при переходе от одного значения к другому принимает и все промежуточные значения. Теорема (вторая теорема Больцано-Коши)
15 Теорема (первая теорема Вейерштрасса) Если функция f ( х ) определена и непрерывна на отрезке [ a, b ], то она ограничена на этом отрезке. Замечание. Теорема неверна, если отрезок [ a, b ] заменить интервалом ( а, b ).
16
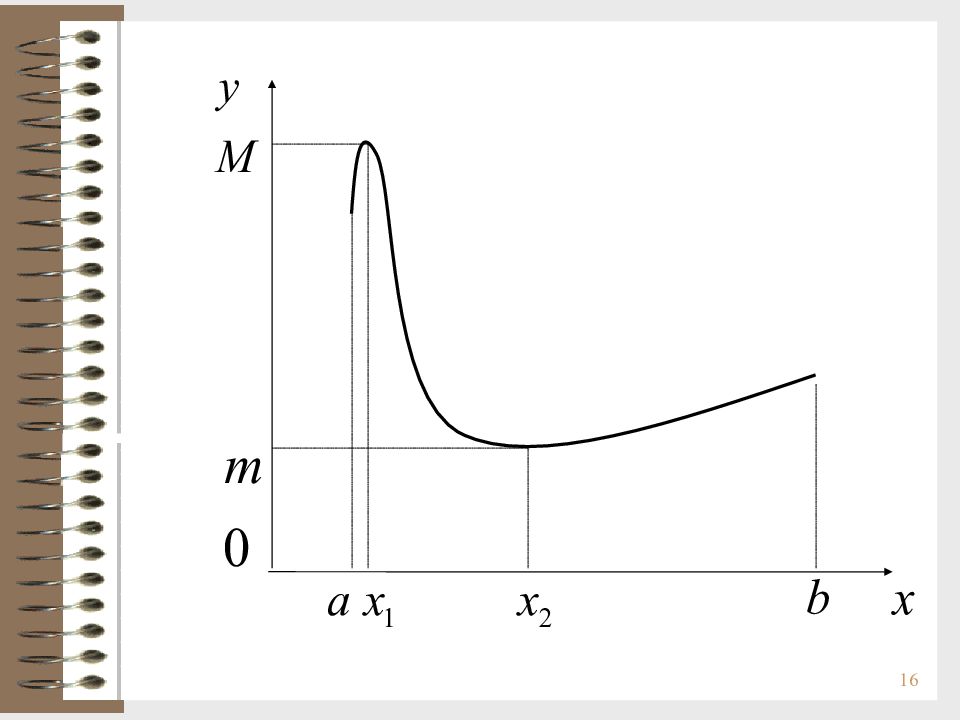
17 Теорема (вторая теорема Вейерштрасса) Если функция f ( x ) непрерывна на отрезке [ a, b ], то она имеет на этом отрезке наибольшее и наименьшее значения. Замечание Разность между наибольшим и наименьшим значениями непрерывной функции f ( x ) на отрезке [ a, b ] называется колебанием непрерывной функции.
18 Понятие равномерной непрерывности функции Определение. Функция f ( х ) называется равномерно- непрерывной на промежутке Х, если для любого > 0 существует > 0 такое, что для любых двух точек х 1, х 2 Х, удовлетворяющих неравенству | x 2 – x 1 | < , выполняется неравенство | f ( х 2 ) – f ( x 1 )| < . Символика : Теорема Кантора (о равномерной непрерывности) Если функция f ( x ) непрерывна на отрезке [ a, b ], то она и равномерно непрерывна на нем.
