Непрерывность функции в точке Точки разрыва функции Основные теоремы о непрерывных функциях Непрерывность функции на интервале и на отрезке Свойства функций, непрерывных на отрезке Примеры решения задач 1
Пусть функция y = f(x) определена в некоторой окрестности точки x 0, и в самой точке x 0. Функция y = f(x) называется непрерывной в точке x 0, если существует предел функции в этой точке и он равен значению функции в этой точке: ( 1 ) Равенство ( 1 ) означает выполнение трех условий: 1 Функция y = f(x) определена в точке x 0 и в ее окрестности. 2 Функция y = f(x) имеет предел при 3 Предел функции в точке x 0 равен значению функции в этой точке. 2
Так как то равенство ( 1 ) можно записать в виде: Это значит, что при нахождении предела непрерывной функции можно перейти к пределу под знаком функции: Равенство справедливо в силу непрерывности функции y = e x 3
Пусть функция y = f(x) определена в некоторой интервале ( a; b). Возьмем произвольную точку Разность x – x 0 называется приращением аргумента х в точке х 0 и обозначается: y 0 х х 0 y 0 = f(x 0 ) х y = f(x ) Разность соответствующих значений функций f(x) – f(x 0 ) называется приращением функции f(x) в точке х 0 и обозначается: Приращения и могут быть положительными и отрицательными. 4
х y y 0 х х 0 y 0 Преобразуем равенство (1) : Полученное равенство является еще одним определением непрерывности функции в точке: Функция y = f(x) называется непрерывной в точке x 0, если она определена в точке x 0 и ее окрестности и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. 5
Точки, в которых нарушается непрерывность функции, называется точками разрыва функции. Если x = x 0 – точка разрыва функции, то в ней не выполняется по крайней мере одно из условий первого определения непрерывности, а именно: y 0 х 2 Функция f(x) определена в окрестности точки х 0, но не определена в самой точке х 0 : 1 не определена в точке х = 2, но определена в любой окрестности этой точки, поэтому х = 2 - точка разрыва. Функция 6
y 0 х 2 Функция f(x) определена в точке х 0 и в ее окрестности, но не существует предела f(x) при 2 определена в точке х = 2, но но не имеет предела при Функция не существует, значит х = 2 - точка разрыва 7
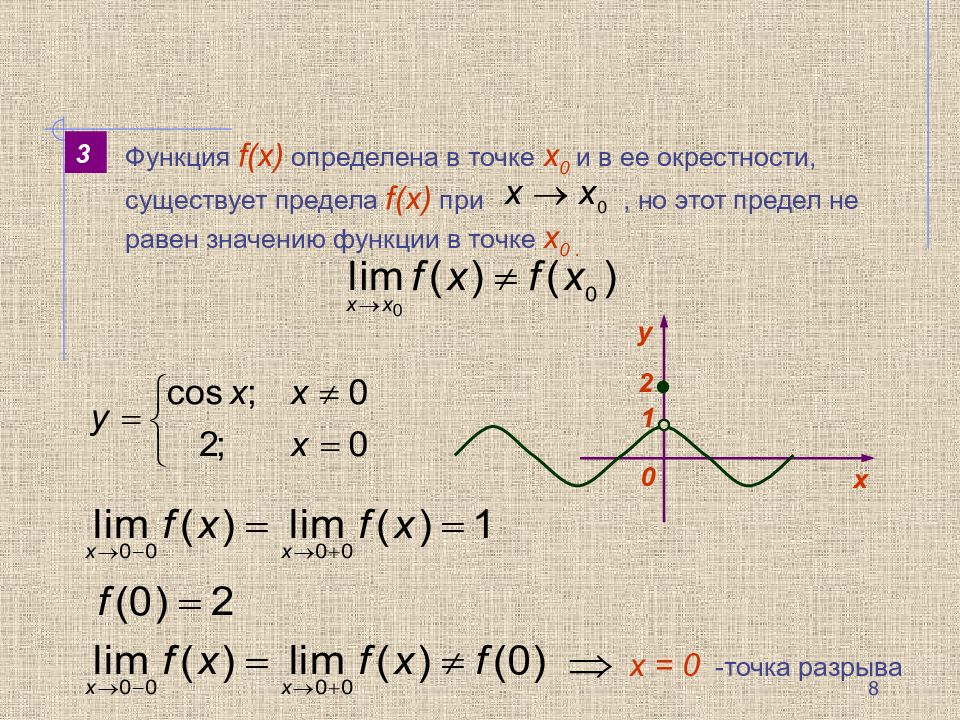
y 0 х 2 3 х = 0 -точка разрыва Функция f(x) определена в точке х 0 и в ее окрестности, существует предела f(x) при, но этот предел не равен значению функции в точке х 0. 1 8
Точка разрыва х 0 называется точкой разрыва 1 рода функции f(x), если в этой точке существуют конечные пределы слева и справа: При этом: а) если, то х 0 - точка устранимого разрыва (в примере 3: х = 0 – точка устранимого разрыва 1 рода) б) если, то х 0 - точка конечного разрыва Величину называют скачком функции в точке разрыва 1 рода. ( в примере 2: х = 2 – точка разрыва 1 рода, скачек функции равен: ) 9
Точка разрыва х 0 называется точкой разрыва 2 рода функции f(x), если по крайней мере один из односторонних пределов не существует или равен бесконечности. В примере 1: х = 2 – точка разрыва 2 рода. 10
Сумма, произведение и частное непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, где знаменатель равен нулю) Теорема 1 Теорема 2 Пусть функция u = g(x) непрерывна в точке x 0, а функция y = f(u) непрерывна в точке u 0 = g(x 0 ). Тогда сложная функция y = f(g ( x ) ) непрерывна в точке x 0. Можно доказать, что все основные элементарные функции непрерывны при всех значениях х, при которых эти функции определены. Поэтому из приведенных выше теорем вытекает: всякая элементарная функция непрерывна в каждой точке, в которой она определена. 11
Функция y = f( х ) называется непрерывной на интервале ( a; b ), если она непрерывна в каждой точке этого интервала. Функция y = f( х ) называется непрерывной на отрезке [ a; b ], если она непрерывна на интервале ( a; b ), и в точке x = a непрерывна справа: а в точке x = b непрерывна слева: 12
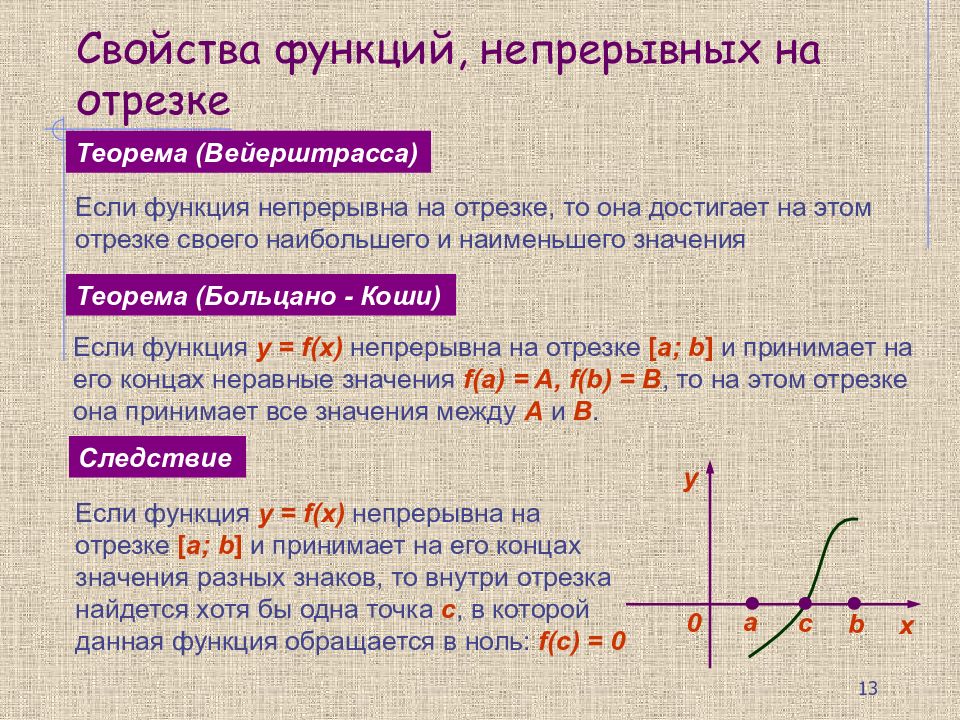
Теорема (Вейерштрасса) Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значения Если функция y = f( х ) непрерывна на отрезке [ a; b ] и принимает на его концах неравные значения f(a) = A, f(b) = B, то на этом отрезке она принимает все значения между A и B. Теорема (Больцано - Коши) Следствие Если функция y = f( х ) непрерывна на отрезке [ a; b ] и принимает на его концах значения разных знаков, то внутри отрезка найдется хотя бы одна точка с, в которой данная функция обращается в ноль: f( с) = 0 y 0 х a b c 13
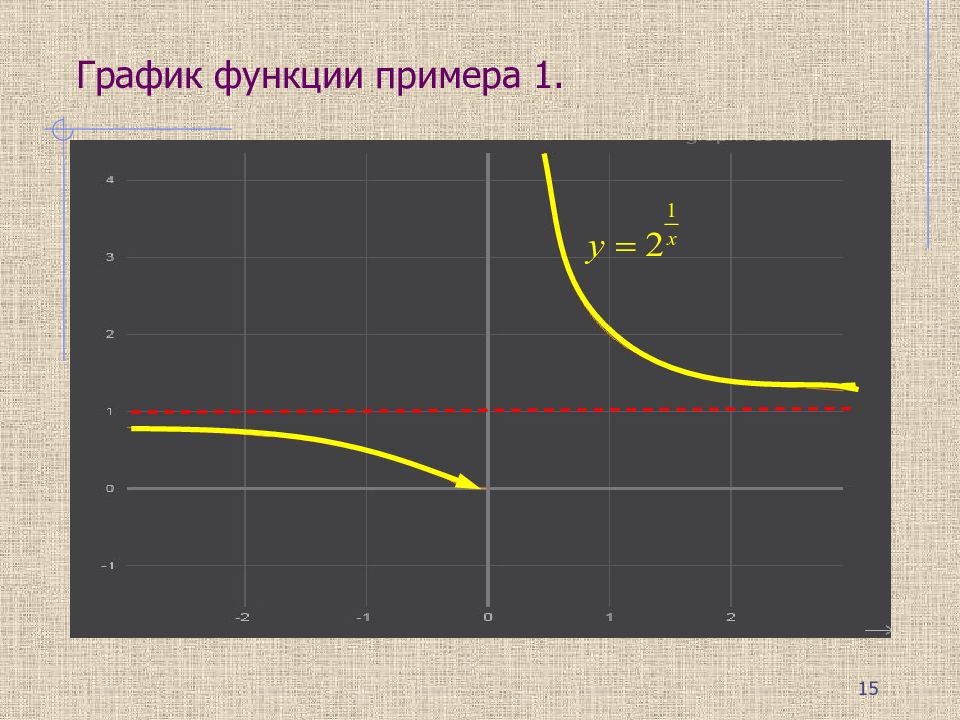
Пример 1. При x=0 функция f(x) неопределена. Левосторонний предел: Правосторонний предел: Так как один из односторонних пределов бесконечен, то x=0 – точка разрыва второго рода. Исследовать на непрерывность 14
15
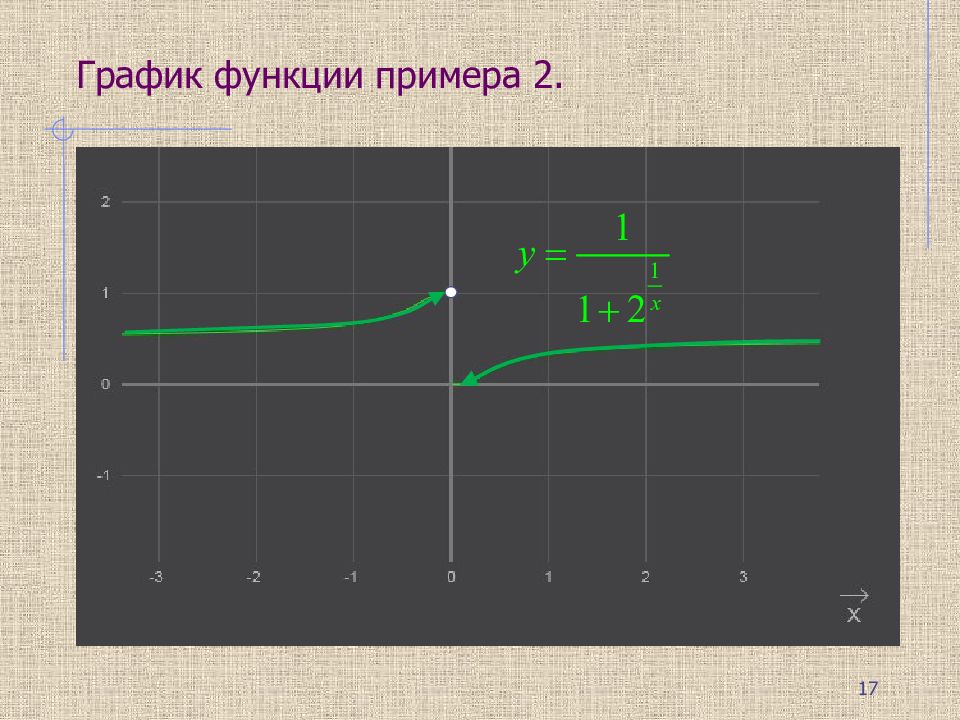
Пример 2. При x=0 функция f(x) неопределена. Левосторонний предел: Правосторонний предел: Так как пределы функции слева и справа от точки x=0 – конечны, то x=0 - точка разрыва первого рода. 16
17
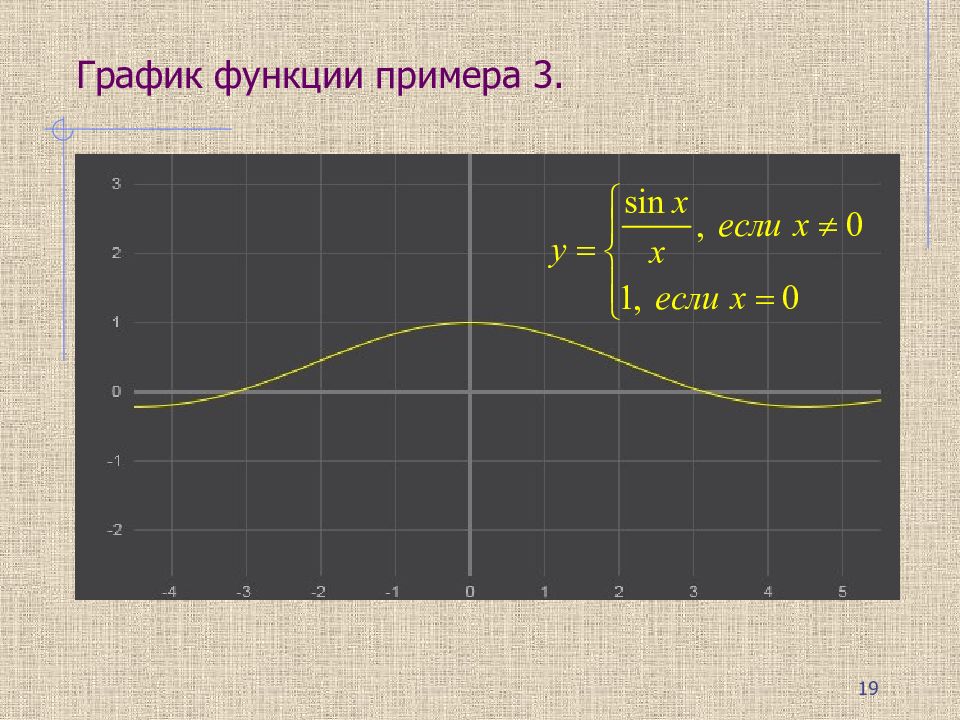
Пример 3. При x=0 функция f(x) =1. Левосторонний предел: Правосторонний предел: Так как пределы функции слева и справа от точки x=0 – конечны и равны значению функции в точке x =0, то функция непрерывна. 18
19
