Первый слайд презентации: АЛГЕБРА (3-й семестр)
2010-11 учебный год Доцент Мартынова Т. А.
Слайд 3: 2. Многочлены над полем действительных чисел
Основными задачами этого раздела являются рассмотрение вопросов: Сопряжённые корни многочленов. Неприводимые над R многочлены. Отделение действительных корней многочлена и метод Штурма.
Слайд 4: 2. Отделение действительных корней
Уравнения степени выше 4 неразрешимы в радикалах. Поэтому большую роль играют приближенные методы решения алгебраических уравнений. Обычно при этом выделяют 3 этапа: 1. Нахождение границ действительных корней многочлена. 2. Отделение корней, т.е. нахождение таких интервалов ( a i, b i ), в каждом из которых лежит только один действительный корень. 3. Приближенное вычисление самих корней, т.е. построение последовательности, сходящейся к тому или иному корню.
Слайд 5: 2. Отделение действительных корней
Из леммы о модуле старшего члена следует, что все действительные корни многочлена f ( x ) из R (x) находятся в промежутке (–M,M), где Таким образом мы указали один из способов для нахождения границ действительных корней многочлена с действительными коэффициентами.
Слайд 6: 2. Отделение действительных корней
Для решения задачи об отделении действительных корней многочлена с действительными коэффициентами наиболее безупречным в теоретическом отношении является метод Штурма, имеющий чисто алгебраический характер.
Слайд 7: 2. Отделение действительных корней
Применим к многочлену f ( x ) и его производной f ’ ( x ) алгоритм Евклида, но при этом остатки будем брать с противоположными знаками:
Слайд 8: 2. Отделение действительных корней
Система многочленов называется системой функций Штурма для многочлена f ( x ). В дальнейшем будем рассматривать только многочлены, не имеющие кратных корней. Известно, что такие многочлены взаимно просты со своей производной и поэтому f m ( x ) =c (const). Обозначим через w ( a ) число перемен знаков в системе чисел: ( 6 )
Слайд 9: 2. Отделение действительных корней
Покажем на примере, как, используя теорему Штурма, можно определить корни многочлена. Замечание. Многочлены ряда Штурма можно находить с точностью до положительных множителей, т.е., при вычислениях можно умножать и делить многочлены на числа, но только на положительные, так как знак многочленов играет в этом методе существенную роль. Теорема Штурма. Если a < b, то w ( a ) w ( b ) и число действительных корней многочлена f ( x ) в промежутке [ a, b ] равно w ( a ) – w ( b ).
Слайд 10: 2. Отделение действительных корней
Пример 4. Отделить действительные корни многочлена f ( x )= x 3 – 10 x + 2. ◘ M = A / | a n | + 1 = 10/1 + 1 = 11. Т.образом, корни находятся в промежутке (-11,11). Далее находим производную f’ ( x )=3 x 2 – 10. Затем применяя алгоритм Евклида, находим систему многочленов Штурма: Таким образом, ряд функций Штурма: x 3 – 10 x + 2, 3 x 2 – 10, 10 x – 3, 1.
Слайд 11: 2. Отделение действительных корней
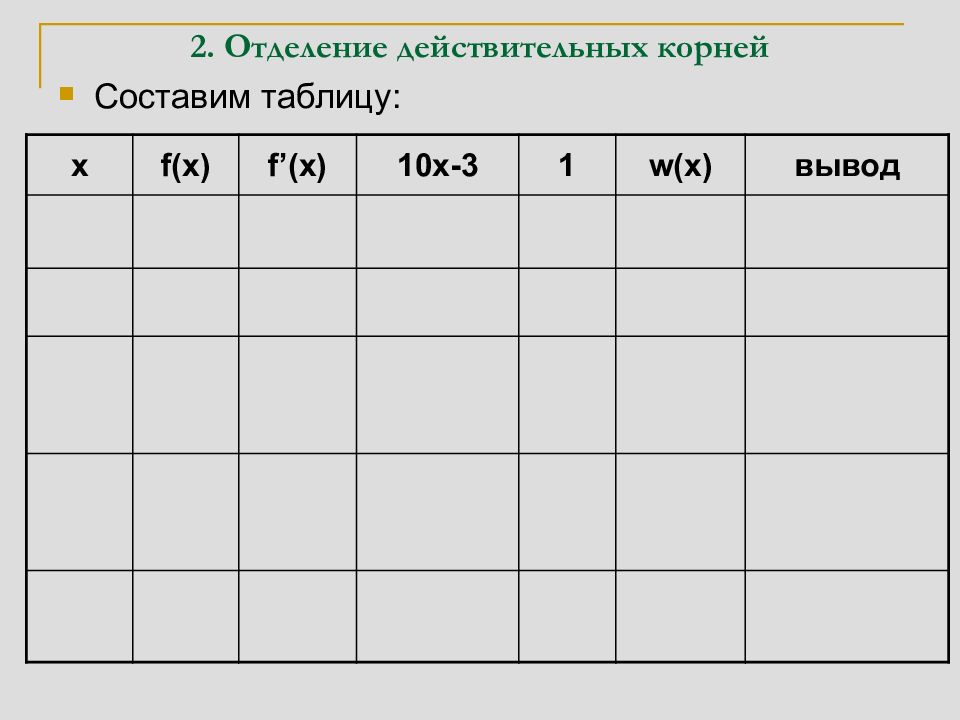
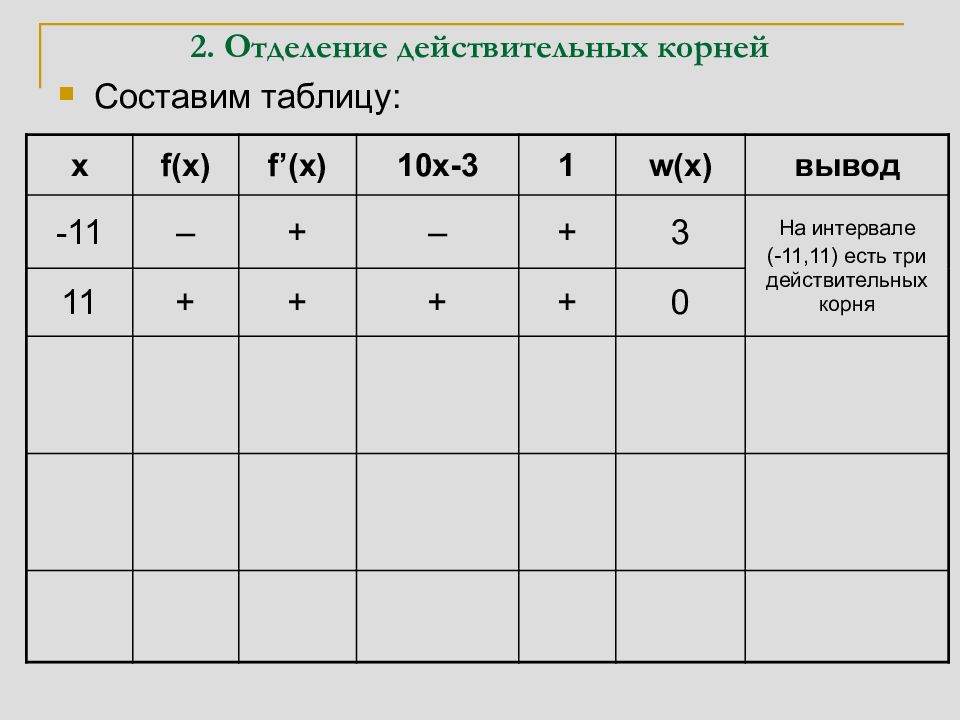
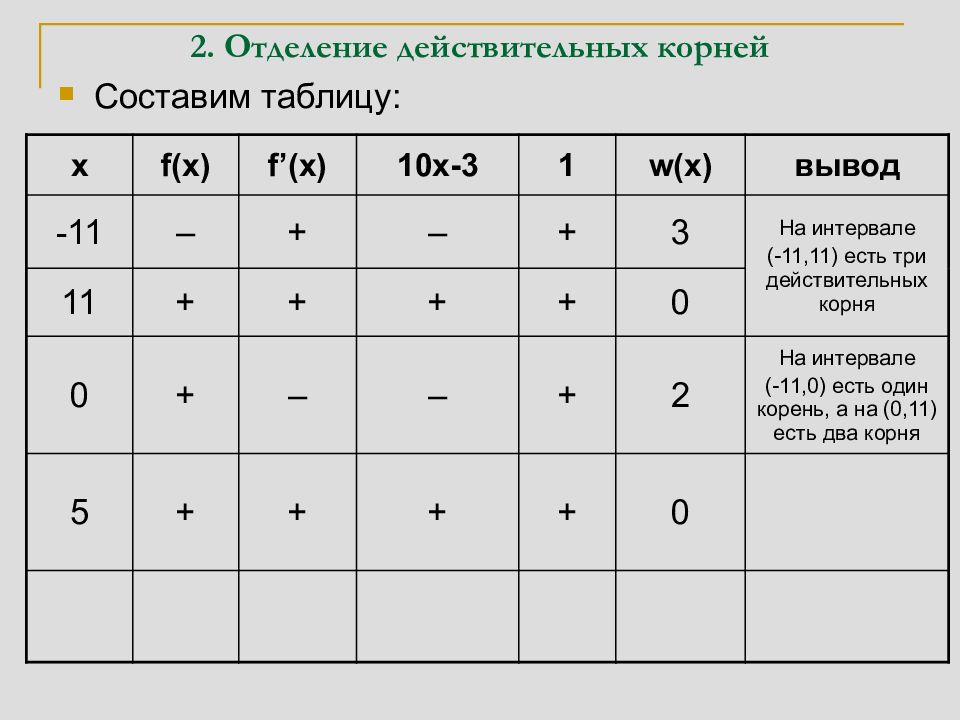
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три 11 + + + + 0 действительных корня 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 12: 2. Отделение действительных корней
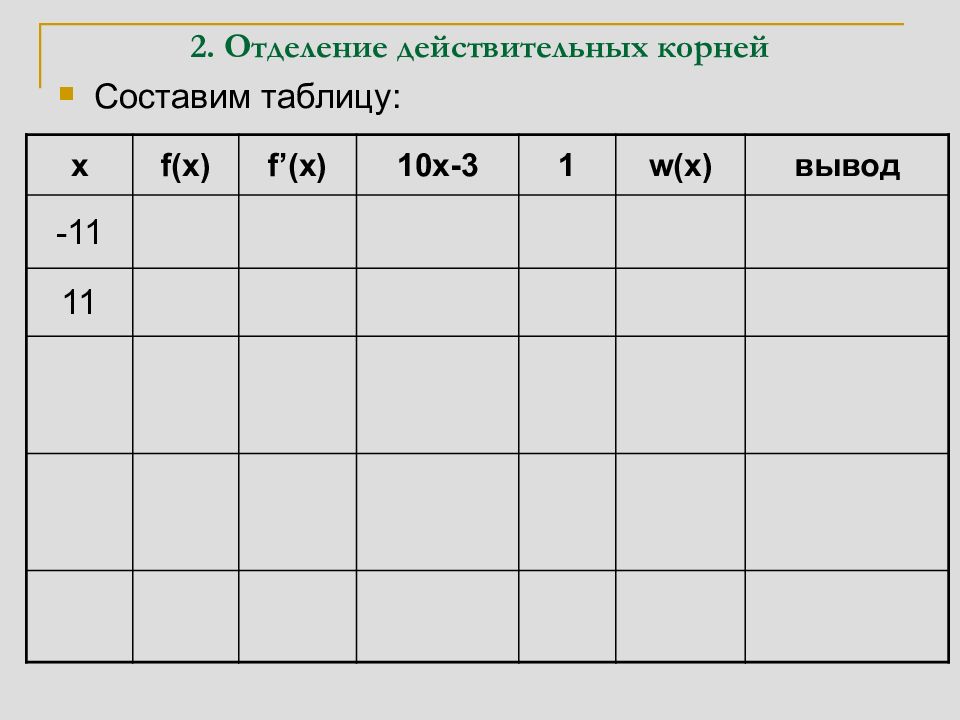
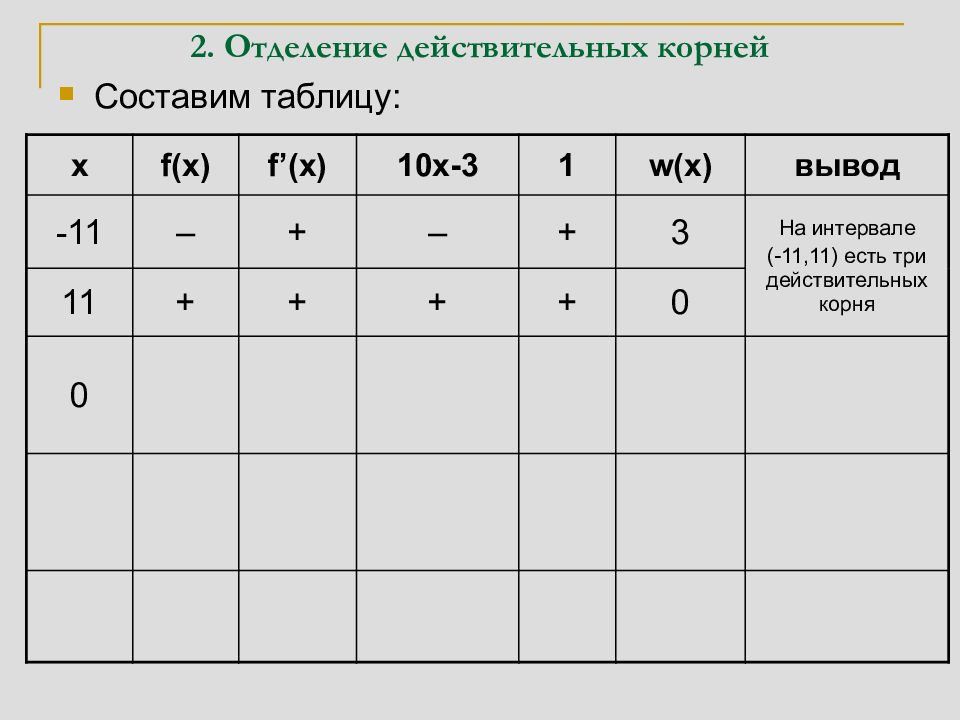
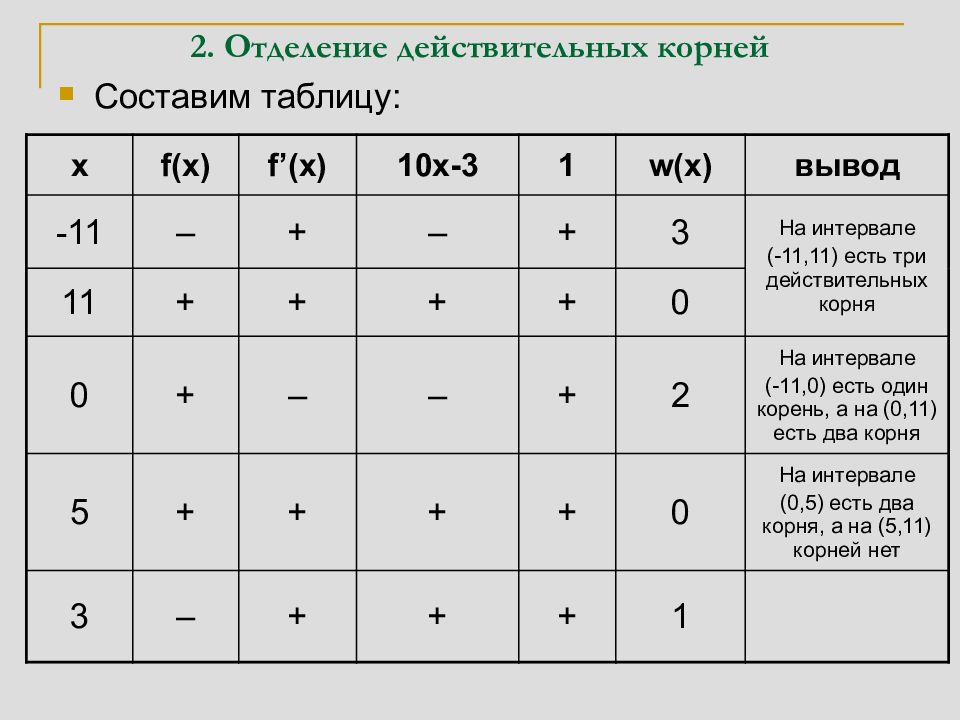
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три 11 + + + + 0 действительных корня 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 13: 2. Отделение действительных корней
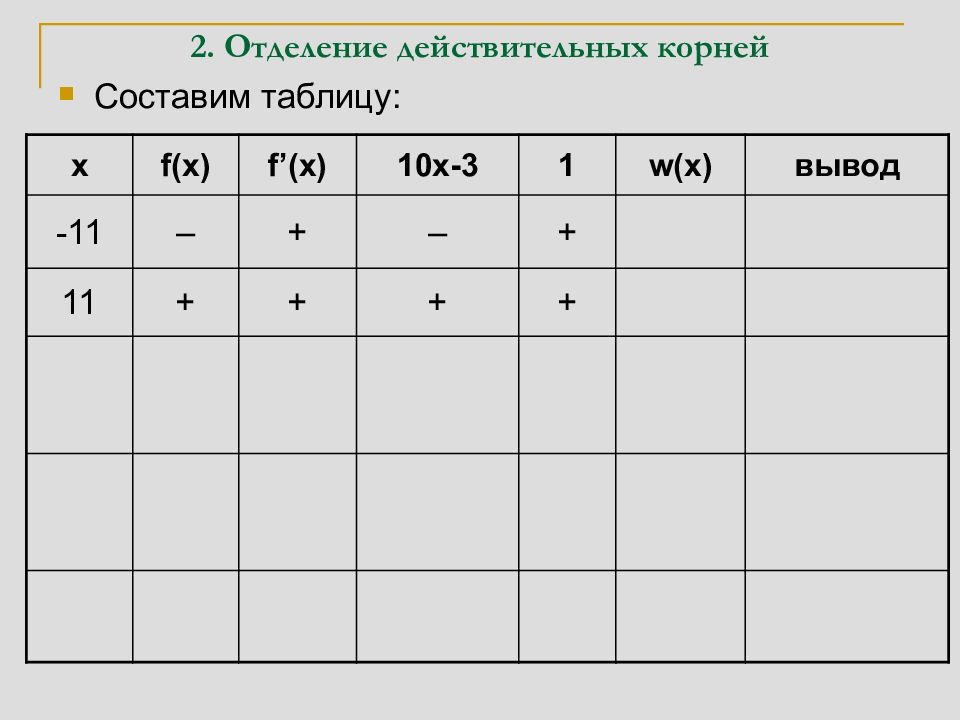
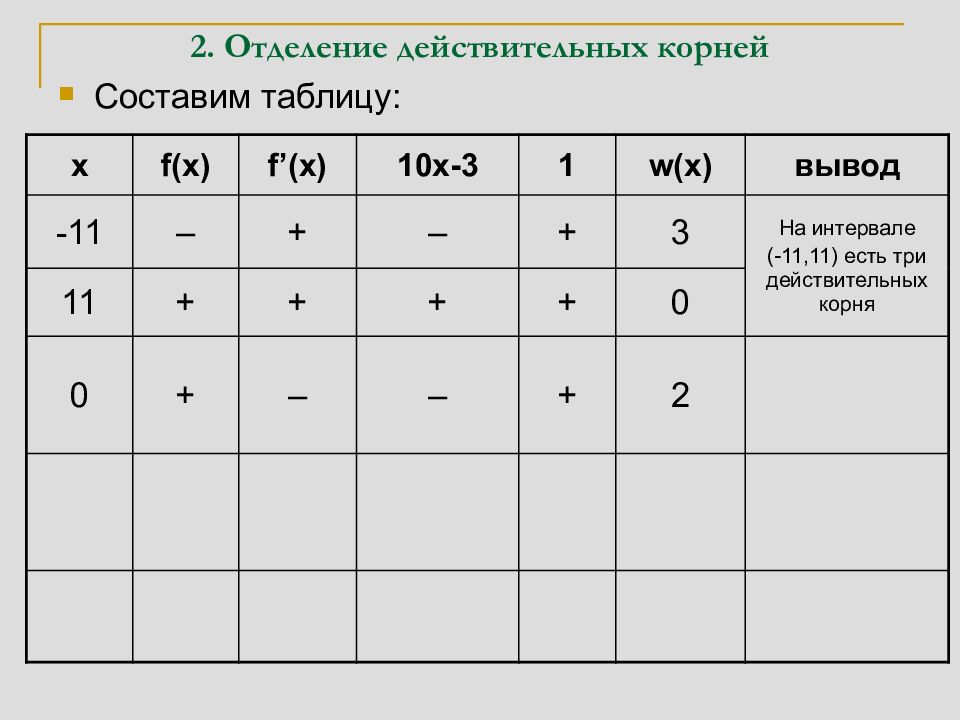
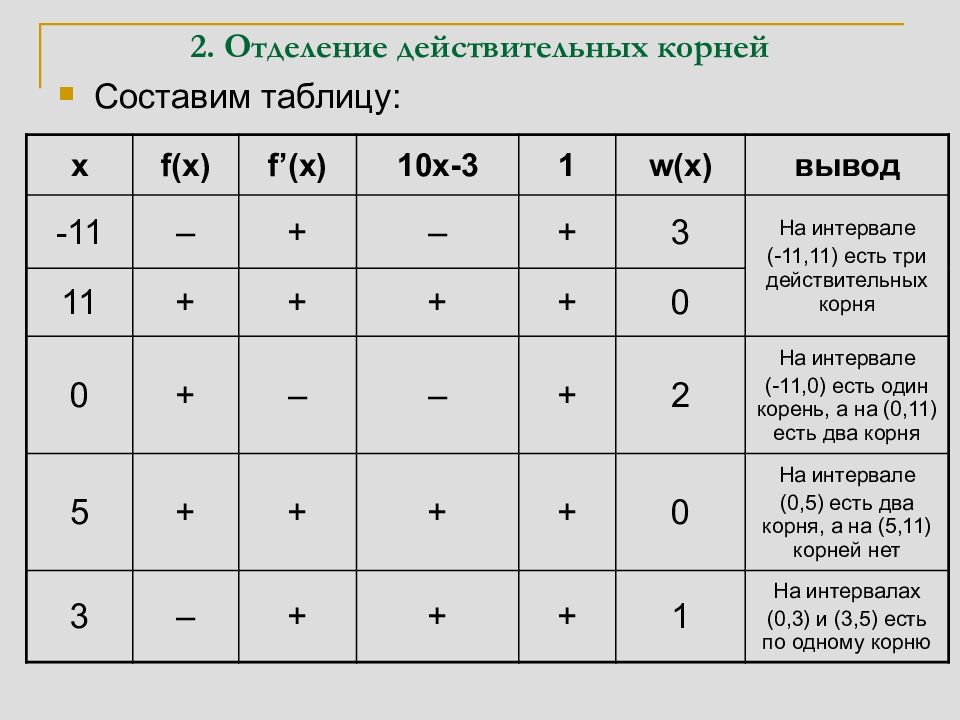
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три 11 + + + + 0 действительных корня 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 14: 2. Отделение действительных корней
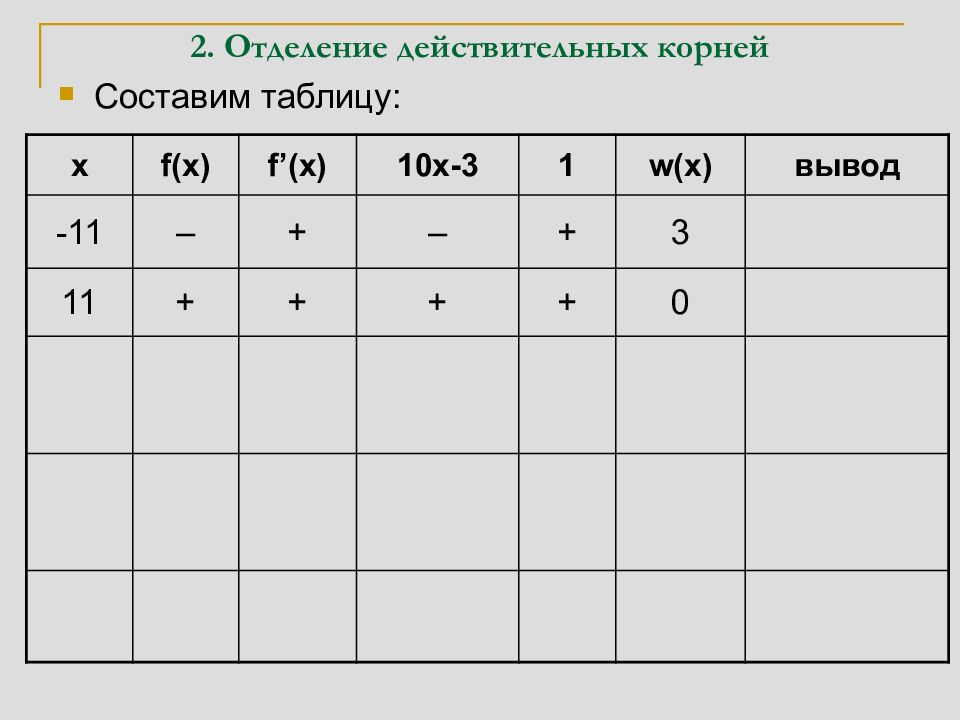
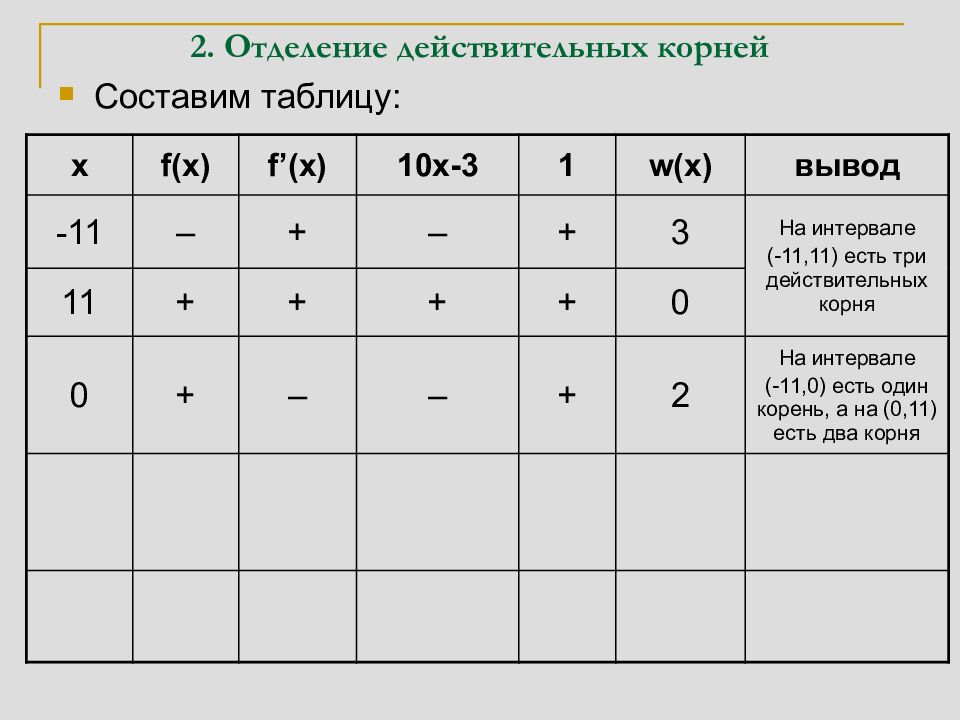
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три 11 + + + + 0 действительных корня 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 15: 2. Отделение действительных корней
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три действительных корня 11 + + + + 0 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 16: 2. Отделение действительных корней
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три действительных корня 11 + + + + 0 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 17: 2. Отделение действительных корней
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три действительных корня 11 + + + + 0 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 18: 2. Отделение действительных корней
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три действительных корня 11 + + + + 0 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 19: 2. Отделение действительных корней
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три действительных корня 11 + + + + 0 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 20: 2. Отделение действительных корней
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три действительных корня 11 + + + + 0 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 21: 2. Отделение действительных корней
Составим таблицу: x f(x) f’(x) 10x-3 1 w(x) вывод -11 – + – + 3 На интервале (-11,11) есть три действительных корня 11 + + + + 0 0 + – – + 2 На интервале (-11,0) есть один корень, а на (0,11) есть два корня 5 + + + + 0 На интервале (0,5) есть два корня, а на (5,11) корней нет 3 – + + + 1 На интервалах (0,3) и (3,5) есть по одному корню
Слайд 22: 2. Отделение действительных корней
Таким образом, корни находятся на промежутках (–11,0), (0,3), (3,5). Для приближенного вычисления корней можно сузить эти промежутки, учитывая, что на концах промежутка, имеющего корни, f ( x ) принимает значения с противоположными знаками. 1. Сузим промежуток (-11, 0) f (–5)= –125+50+2<0, f (0)>0 – корень принадлежит (–5,0); f (–3)= –27+30+2>0 – корень принадлежит (–5,–3); f (–4)=–64+40+2<0 – корень принадлежит (–4,–3). ◙
Слайд 23: 2. Отделение действительных корней
2. Сузим промежуток (0, 3). f (2) = 8 – 20 + 2 < 0, f (0)>0 – корень принадлежит (0, 2); f (1) = 1 – 10 + 2 < 0, f (0)>0 – корень принадлежит (0, 1) ; 3. Сузим промежуток (3, 5). f (4) = 64 – 40 +2 > 0, f (3) = 27 – 30 + 2 < 0 – корень принадлежит (3, 4). Ответ. f ( x )= x 3 – 10 x + 2 имеет три действительных корня находящихся в промежутках (–4,–3), (0, 1) и (3, 4).
Основными задачами этого параграфа являются рассмотрение вопросов: Целые и рациональные корни многочленов из Q[x]. Примитивные многочлены и связь между приводимостью многочленов над полем Q и над кольцом Z. Признаки приводимости и неприводимости в кольце Q [ x ] (критерий Эйзенштейна и метод Кронекера).
Слайд 25: 1. Целые и рациональные корни многочленов из Q [ x ]
Пусть - некоторый многочлен из Q [ x ]. Умножив его на общий знаменатель q всех его коэффициентов, мы получим новый многочлен с целыми коэффициентами, который имеет те же корни, что и f ( x ). Таким образом, достаточно рассмотреть вопрос о целых и рациональных корнях многочленов с целыми коэффициентами. Поэтому в дальнейшем считаем что многочлен f ( x ) имеет целые коэффициенты.
Слайд 26: 1. Целые и рациональные корни многочленов из Q [ x ]
Теорема 1. Если несократимая дробь l / m ( m >0) является корнем многочлена f ( x ) с целыми коэффициентами, то a 0 l и a n m. ◘ Так как l/m – корень f ( x ), то Умножая обе части этого равенства на m n, имеем: Отсюда: Так как НОД( l, m ) = 1, то из равенства (1) и (2) заключаем, что a n m и a 0 l. ◙ ( 1 ) ( 2 ) 1. Целые и рациональные корни многочленов из Q [ x ]
Слайд 27: 1. Целые и рациональные корни многочленов из Q [ x ]
Следствие 1. Целый корень многочлена f ( x ) с целыми коэффициентами является делителем свободного члена. ◙ Следствие 2. Если старший коэффициент a n многочлена f ( x ) с целыми коэффициентами равен 1, то все рациональные корни этого многочлена целые. ◙ 1. Целые и рациональные корни многочленов из Q [ x ] Теорема 1. Если несократимая дробь l / m ( m >0) является корнем многочлена f ( x ) с целыми коэффициентами, то a 0 ÷l и a n ÷m.
Слайд 28: 1. Целые и рациональные корни многочленов из Q [ x ]
Так как число делителей целых чисел a 0 и a n конечно, то и число несократимых дробей вида l/m, где a 0 l и a n m, тоже конечно. Следовательно, все дроби l/m можно выписать и путём конечного числа испытаний проверить, какие из этих дробей будут корнями, а какие нет. Тем самым мы найдем все рациональные корни многочлена f ( x ), или убедимся, что их нет. Следствия 1 и 2 в некоторых случаях упрощают эту задачу. 1. Целые и рациональные корни многочленов из Q [ x ]
Слайд 29: 1. Целые и рациональные корни многочленов из Q [ x ]
Пример 1. Найти рациональные корни многочлена f(x) =3 x 4 +5 x 3 + x 2 +5 x -2. ◘ l = 1, 2 – делители свободного члена; m = 1,3 – положительные делители старшего коэффициента; l/m= ±1, ± 2, ±1/3, ± 2/3 – кандидаты в корни. Непосредственной проверкой (используя схему Горнера) убеждаемся, что рациональные корни данного многочлена исчерпываются числами –2 и 1/3. ◙ 1. Целые и рациональные корни многочленов из Q [ x ]
Слайд 30: 1. Целые и рациональные корни многочленов из Q [ x ]
Однако число испытаний может оказаться большим и задача громоздкой. Чтобы уменьшить число испытаний и отсеять лишних кандидатов, мы укажем еще одно необходимое (но недостаточное) условие того, что несократимая дробь l/m является корнем многочлена (1). Теорема 2. Если несократимая дробь l/m ( m >0 ) является корнем многочлена f ( x ) с целыми коэффициентами, то для любого целого числа k, такого, что l - km 0, f ( k ) делится на l – km. 1. Целые и рациональные корни многочленов из Q [ x ]
Слайд 31: 1. Целые и рациональные корни многочленов из Q [ x ]
◘ Умножим многочлен f ( x ) на m n и запишем в виде: Положим mx = y. Тогда причём число x 0 является корнем многочлена f ( x ) тогда и только тогда, когда число y 0 =mx 0 является корнем φ (y). Значит, если x 0 = l/m – корень f ( x ), то число y 0 = m ∙(l/m) = l – целый корень многочлена φ (y), и, следовательно, φ (y) =( y-l)q(y). Заметим, что q ( y ) имеет целые коэффициенты, так как они могут быть получены делением φ (y) на y-l с помощью схемы Горнера, а φ (y) и y-l из Z [x]. 1. Целые и рациональные корни многочленов из Q [ x ]
Слайд 32: 1. Целые и рациональные корни многочленов из Q [ x ]
Так как φ (y) =( y-l)q(y) и q(y) Z [ x ], значит, целым будет и число Докажем, что НОД( m, l – km )=1. Если бы это было не так, то дробь была бы сократимой, т.е., m 1 < m. Отсюда: 1. Целые и рациональные корни многочленов из Q [ x ] ( 3 )
Слайд 33: 1. Целые и рациональные корни многочленов из Q [ x ]
Таким образом, вопреки условию теоремы, дробь l/m оказалась сократимой (ведь m 1 < m ). Полученное противоречие доказывает, что НОД( m, l – km )=1. Из равенства (3) заключаем теперь, что что и требовалось доказать. ◙ 1. Целые и рациональные корни многочленов из Q [ x ] ( 3 )
Слайд 34: 1. Целые и рациональные корни многочленов из Q [ x ]
Замечание. Обычно теорему 2 используют при k=±1. При этом дроби и называют контрольными. Согласно теореме 2, в случае когда несократимая дробь l/m ( m >0 ) является корнем многочлена f ( x ) с целыми коэффициентами и l ± m 0, обе контрольные дроби обязаны быть целыми числами. Это позволяет отсеивать значительное число кандидатов в корни, которые определяются на основании теоремы 1. 1. Целые и рациональные корни многочленов из Q [ x ]
Слайд 35: 1. Целые и рациональные корни многочленов из Q [ x ]
Пример 2. Найти рациональные корни многочлена f ( x )=2 x 4 - x 3 +3 x 2 - x -12. ◘ Имеем:
Слайд 36: 1. Целые и рациональные корни многочленов из Q [ x ]
Составим таблицу: l/m 2 -2 3 -3 4 -4 6 -6 12 -12 1/2 -1/2 3/2 -3/ 2 -9/( l-m ) Ц Ц Д Д Ц Д Д Д Д Д Ц Ц Ц Д -5/( l+m ) Д Ц - - Ц - - - - - Д Ц Ц -
Слайд 37: 1. Целые и рациональные корни многочленов из Q [ x ]
Составим таблицу: l/m 2 -2 3 -3 4 -4 6 -6 12 -12 1/2 -1/2 3/2 -3/ 2 -9/( l-m ) Ц Ц Д Д Ц Д Д Д Д Д Ц Ц Ц Д -5/( l+m ) Д Ц - - Ц - - - - - Д Ц Ц -
Слайд 38: 1. Целые и рациональные корни многочленов из Q [ x ]
Составим таблицу: l/m 2 -2 3 -3 4 -4 6 -6 12 -12 1/2 -1/2 3/2 -3/ 2 -9/( l-m ) Ц Ц Д Д Ц Д Д Д Д Д Ц Ц Ц Д -5/( l+m ) Д Ц - - Ц - - - - - Д Ц Ц -
Слайд 39: 1. Целые и рациональные корни многочленов из Q [ x ]
Составим таблицу: l/m 2 -2 3 -3 4 -4 6 -6 12 -12 1/2 -1/2 3/2 -3/ 2 -9/( l-m ) Ц Ц Д Д Ц Д Д Д Д Д Ц Ц Ц Д -5/( l+m ) Д Ц - - Д - - - - - Д Ц Ц -
Слайд 40: 1. Целые и рациональные корни многочленов из Q [ x ]
Данные таблицы показывают, что рациональные корни многочлена f ( x ) находятся среди чисел –2, – 1/2 и 3/2. С помощью схемы Горнера вычисляем значения f ( –2 ), f( – 1/2) и f(3/2) и убеждаемся что число 3/2 является единственным рациональным корнем данного многочлена. ◙
Слайд 41: 2. Примитивные многочлены и связь между приводимостью многочленов над полем Q и над кольцом Z
Определение 1. Содержанием многочлена f ( x ) Z [ x ] называется НОД его коэффициентов. Если коэффициенты многочлена f ( x ) взаимно простые, то он называется примитивным многочленом. Пример 3. Содержанием многочлена f ( x )=3 x 3 -18 x +6 является число 3. Многочлен g ( x )= x 3 -6 x +2 является примитивным.
Слайд 42: 2. Примитивные многочлены и связь между приводимостью многочленов над полем Q и над кольцом Z
Теорема 3. Если f ( x ) Z [ x ], то он единственным образом представим в виде: где d – содержание f ( x ), а f 1 ( x ) - примитивный. ◘ Вынеся НОД коэффициентов многочлена f ( x ) за скобки, мы и получим разложение (4). Единственность вытекает из единственности НОД. ◙ ( 4 )
Слайд 43: 2. Примитивные многочлены и связь между приводимостью многочленов над полем Q и над кольцом Z
Теорема 4 (лемма Гаусса). Произведение примитивных многочленов - тоже примитивный многочлен. ◘ Пусть – примитивные многочлены из кольца Z [ x ] и Если h ( x ) не является примитивным, то его содержание d имеет в своем разложении по крайней мере один простой делитель p Z.
Слайд 44: 2. Примитивные многочлены и связь между приводимостью многочленов над полем Q и над кольцом Z
Так как f и g примитивны, не все их коэффициенты делятся на p. Пусть a i и b j – первые коэффициенты в f и g, которые не делятся на p. Поскольку где a k = 0 при k > n и b k = 0 при k > m Учитывая, что и все слагаемые как слева так и справа от a i b j тоже делятся на p, мы приходим к выводу, что a i b j p. Но это невозможно, так как a i и b j не делятся на p, а p – простое число. Таким образом, h ( x ) – примитивный многочлен, что и требовалось доказать. ◙













![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/082d84e045d74e95777dc44982e54c3b/f45245ed-bb40-492d-8f16-6ed6060a7a8f.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/fbcc88114457f4d51826b336f9ecdd7a/79cbc28c-9946-4951-9539-979768529078.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/f31a545a2d967aa94feb4d29193b0b93/17662e25-519a-4d7c-af9c-17521acf8edc.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/fb1cbdd55caf9ee5f947a77875fd39ea/415aceee-49db-4741-8c4e-5917b6a2c174.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/d27949058f8ad52a230c6b794eb0ecbe/25dfda80-85b7-4b16-be51-ed48d10d2b14.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/50fe16447105311f46b30b0a50cf8f24/1c1fc9cf-69eb-4767-8b29-827450524e4f.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/155482432242be21a13bd78294b917ae/a4483437-0505-4e21-b3dd-29af6b244aae.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/786a5896cceced8130b4d40bfd0aa463/20f3d229-b458-4017-bad5-67578f58aa15.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/0ce7ebfa435bc80a3b3fc111cebf1ac7/9983ec72-87a6-4bc3-8462-56937d529e74.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/a0249824ecf7f56d7602e94ffb0e6d15/4c1e38a2-8c06-4ceb-ba2c-d70e7d944d40.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/3b385e2bdea8f93414a5b16928b141ec/f7333d59-e13a-46eb-9bde-60d98217b569.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/badd45ad7931381c70c1e94067b19c26/61c6570d-fc8f-4932-8e58-5ffa9e903bf9.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/ed27a558a7148485e23ab4f45e78b423/0105628e-6352-4558-9e91-4362bfd08795.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/3ea98acc06532fd73b4199c97ed08677/c2093007-0370-4159-972d-8c3cf77b3780.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/fb2812830d3378e7dccb8cb235599253/94f9efae-9132-4f7b-9da0-cf5d87de3d03.jpeg)
![АЛГЕБРА (3-й семестр) 1. Целые и рациональные корни многочленов из Q [ x ]](https://s1.showslide.ru/s_slide/9feeebf0a285e207d71782cface61ee2/dcc67b8f-794d-4adf-b027-876f8ce056cd.jpeg)










