2 Линейные дифференциальные уравнения n- го порядка Определение. Линейными дифференциальными уравнениями n- го порядка называют уравнения вида a 0 ( x ) y ( n ) + a 1 ( x ) y ( n- 1) + …+ a n- 1 ( x ) y ' + a n ( x ) y = b ( x ), (1) где a 0 ( x ), a 1 ( x ), …, a n ( x ) и свободный член b ( x ) – заданные функции аргумента x и a 0 ( x ) 0. Если a i ( x ) = const, i = 1,…, n, то уравнение называется линейным ДУ n - го порядка с постоянными коэффициентами. Если b ( x ) 0, то уравнение называется линейным однородным. Если b ( x ) 0, то уравнение называется линейным неоднородным (или уравнением с правой частью ). .
Слайд 3
Так как a 0 ( x ) ≢ 0 , то уравнение ( 1 ) можно записать в виде: y ( n ) + p 1 ( x ) y ( n – 1) + … + p n – 1 ( x ) y + p n ( x ) y = f ( x ) . ( 2 ) Уравнение ( 2 ) называют приведенным. Уравнение (2) -линейное неоднородное уравнение. В дальнейшем будем работать только с приведенным уравнением. Кроме того, будем предполагать, что p i ( x ) ( i = 1, 2, …, n ) и f ( x ) непрерывны на некотором отрезке [ a ; b ]. Тогда для уравнения ( 2 ) будут выполняться условия теоремы существования и единственности решения. Следовательно, x 0 [ a ; b ] и y 0 , y 0 i ℝ существует един - ственное решение уравнения ( 2 ), удовлетворяющее условию y ( x 0 ) = y 0 , y ( x 0 ) = y 01 , y ( x 0 ) = y 02 , … , y ( n –1) ( x 0 ) = y 0 n –1 . 3
Слайд 4: Линейные ДУ высшего порядка
4 Линейные ДУ высшего порядка Если f ( x ) 0, то уравнение ( 1 ) принимает вид: y ( n ) + p 1 ( x ) y ( n- 1) + …+ p n- 1 ( x ) y ' + p n ( x ) y = 0 -ЛОДУ ( 3 ) Свойства решений ЛОДУ в п. 1. Если y 1 ( x ) – решение ЛОДУ в п y ( n ) + p 1 ( x ) y ( n- 1) + …+ p n- 1 ( x ) y ' + p n ( x ) y = 0, ( 3 ) то функция y = C y 1 ( x ), где С = const, тоже является решением этого ДУ. 2. Если y 1, y 2 – решения ЛОДУ в п (2), то функция ( y 1 + y 2 ) – тоже является решением этого ДУ. 3. Если y 1, y 2, …, y k – решения ЛОДУ в п (2), то функция ( С 1 y 1 + С 2 y 2 + С k y k ) – тоже является решением этого ДУ для любых постоянных С 1, С 2, …, С k.
Слайд 5: Линейно зависимые и линейно независимые функции
5 Линейно зависимые и линейно независимые функции Пусть система из n функций y 1, y 2,…, y n – определена и непрерывна на интервале ( a, b ). Определение. Функции y 1, y 2,…, y n называются линейно зависимыми на ( a, b ) если существует числа 1, 2,…, n R такие, что на этом интервале выполняется тождество 1 y 1 + 2 y 2 +…+ n y n 0, ( 4 ) причем хотя бы одно i 0. Если тождество (4) справедливо лишь при 1 = 2 =…= n = 0, то функции y 1, y 2,…, y n называются линейно независимыми на ( a, b ).
Слайд 6: ОПРЕДЕЛИТЕЛЬ ВРОНСКОГО
6 ОПРЕДЕЛИТЕЛЬ ВРОНСКОГО Определение. Определитель Вронского (вронскиан) функций y 1, y 2,…, y n, определенных и ( n -1) раз дифференцируемых на интервале ( a, b ) – это определитель порядка n следующего вида: .
Слайд 7
7 Теорема 1. ( необходимые условия линейной зависимости функций ) Если функции y 1, y 2,…, y n линейно зависимые и имеют производные до ( n -1)-го порядка, то их определитель Вронского тождественно равен нулю. Теорема 2. Если n решений y 1, y 2,…, y n ЛОДУ высшего порядка (3) линейно независимы на ( a, b ), то их определитель Вронского не может обращаться в ноль ни в одной точке интервала ( a, b ). Следствие. Определитель Вронского системы функций y 1, y 2,…, y n, являющихся решениями ЛОДУ в. п. (3), либо тождественно равен нулю, если система решений линейно зависима, либо не обращаться в ноль ни в одной точке, если система решений линейно независима.
Слайд 8: Структура общего решения ЛОДУ
8 Структура общего решения ЛОДУ Определение. Система n линейно независимых решений ЛОДУ n – го порядка называется его фундаментальной системой. (Ф.С.Р.) Теорема 3. ( О с труктуре общего решения ЛОДУ ) Если функции y 1 ( x ), y 2 ( x ),…, y n ( x ), x ( a, b ) – образуют фундаментальную систему решений ЛОДУ (3) на интервале ( a, b ), то, y ( x ) = c 1 y 1 ( x ) + c 2 y 2 ( x ) +…+ c n y n ( x ) ( 5 ) где c i – const, является общим решением этого уравнения.
Слайд 9: ЛОДУ с постоянными коэффициентами
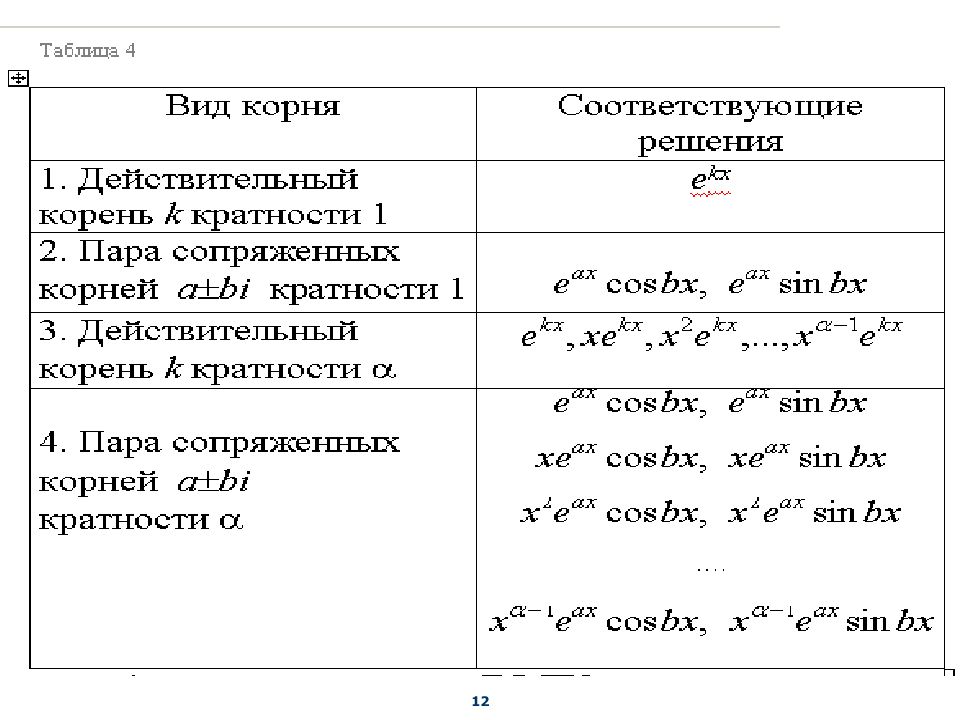
9 ЛОДУ с постоянными коэффициентами Определение. Линейными однородными дифференциальными уравнениями с постоянными коэффициентами называют уравнения вида y ( n ) + p 1 y ( n- 1) + …+ p n- 1 y ' + p n y = 0, (6) где коэффициенты p 1, p 2, …, p n- 1, p n – const. Частные решения будем искать в виде: y = e kx (7) Определение. Уравнение k n + p 1 k n- 1 + …+ p n- 1 k + p n = 0 (8) называется характеристическим уравнением ЛОДУ с постоянными коэффициентами, а многочлен k n + p 1 k n- 1 + …+ p n- 1 k + p n – характеристическим многочленом.
Слайд 10
y ( n ) + p 1 y ( n- 1) + …+ p n- 1 y ' + p n y = 0, (6) Решения уравнения ( 6 ) будем искать в виде y = e k x , где k – некоторая постоянная. Имеем: y = k e k x , y = k 2 e k x , y = k 3 e k x , …, y ( n ) = k n e k x . Подставляем y , y , y , … , y ( n ) в уравнение ( 6 ) и получаем: k n e k x + p 1 k n – 1 e k x + … + p n – 1 k e k x + p n e k x = 0 k n + p 1 k n – 1 + … + p n – 1 k + p n = 0- ( 8 ) характеристическое уравнение ЛОДУ с постоянными коэффициентами. 10
Слайд 11
11 Алгоритм решения ЛОДУ n -го постоянными коэффициентами 1. Составить характеристическое уравнение k n + p 1 k n – 1 + … + p n – 1 k + p n = 0 2. Найти его корни k 1, k 2, … k n. 3. По характеру корней найти частные линейно независимые решения y 1 ( x ), y 2 ( x ),…, y n ( x ) (Ф.С.Р.) согласно таблице 4. 4. Записать общее решение y ( x ) = C 1 y 1 ( x ) + C 2 y 2 ( x ) +…+ C n y n ( x ).
Слайд 18: ЛНДУ с произвольными коэффициентами
18 ЛНДУ с произвольными коэффициентами Пусть ЛНДУ имеет вид y ( n ) + p 1 ( x ) y ( n- 1) + …+ p n- 1 ( x ) y ' + p n ( x ) y = f ( x ), (2) где p 1 ( x ), p 2 ( x ), …, p n ( x ), f ( x ) – заданные функции аргумента x, причем f ( x ) 0. Теорема 4. ( О с труктуре общего решения ЛНДУ ) Общее решение ЛНДУ есть сумма его частного решения и общего решения соответствующего однородного уравнения. При n = 2, ЛНДУ 2-го порядка y '' + p 1 ( x ) y ' + p 2 ( x ) y = f ( x ).
Слайд 19: ЛНДУ с произвольными коэффициентами
19 ЛНДУ с произвольными коэффициентами Теорема 5. ( Принцип суперпозиции решений ) Если функции y i ( x ) – являются решениями ЛНДУ y ( n ) + p 1 ( x ) y ( n- 1) + …+ p n- 1 ( x ) y ' + p n ( x ) y = f i ( x ), ( 9 ) то функция y = 1 y 1 + 2 y 2 +…+ k y k является решением уравнения y ( n ) + p 1 ( x ) y ( n- 1) + …+ p n ( x ) y = 1 f 1 ( x ) + 2 f 2 ( x ) +…+ k f k ( x ). ( 1 0 ) При n = 2, ЛНДУ 2-го порядка y'' + p 1 ( x ) y' + p 2 ( x ) y = 1 f 1 ( x ) + 2 f 2 ( x ).
Слайд 20: ЛНДУс постоянными коэффициентами
20 ЛНДУс постоянными коэффициентами Рассмотрим ЛНДУ с постоянными коэффициентами y ( n ) + p 1 y ( n- 1) + …+ p n- 1 y ' + p n y = f ( x ), (11) где коэффициенты p 1, p 2, …, p n- 1, p n – const. Метод неопределенных коэффициентов можно применить, если правая часть имеет вид f ( x ) = e px [ P m ( x ) cos q x + Q l ( x ) sin q x ], где P m ( x ) и Q l ( x ) – многочлены степени m и l соответственно, p и q – некоторые числа.
Слайд 22: ЛНДУ n - го порядка
22 ЛНДУ n - го порядка Замечание 1. Степени многочленов P m ( x ) и Q l ( x ) в случаях 3,4 таблицы 5 можно считать одинаковой ( max { m, l }). В этом случае коэффициенты при недостающих степенях одного из многочленов можно считать равными нулю. Замечание 2. Правая часть уравнения может содержать несколько слагаемых; в этом случае частное решение также составляется из нескольких слагаемых в соответствии с теоремой 5.
Слайд 23: ПРИМЕР
Найти общее решение линейного неоднородного дифференциального уравнения: 23
Рассмотрим линейное неоднородное уравнение y ( n ) + p 1 ( x ) y ( n- 1) + …+ p n- 1 ( x ) y ' + p n ( x ) y = b ( x ), (2) Если известно общее решение соответствующего ЛОДУ y ( n ) + p 1 ( x ) y ( n- 1) + …+ p n- 1 ( x ) y ' + p n ( x ) y = 0, ( 3 ), то можно найти и общее решение ЛНДУ ( 2 ). Действительно, пусть y 1 , y 2 , … , y n – ф.с.р. уравнения ( 3 ). Тогда его общее решение будет иметь вид y = C 1 y 1 + C 2 y 2 + … + C n y n , ( 12) где C 1 , C 2 , … , C n – произвольные постоянные. Полагаем, что РЕШЕНИЕ ЛНДУ ПО СТРУКТУРЕ совпадает с решением соответствующего ЛОДУ, т.е. имеет вид y = C 1 ( x ) y 1 + C 2 ( x ) y 2 + … + C n ( x ) y n , ( 1 3 ) где C 1 ( x ) , C 2 ( x ) , … , C n ( x ) – некоторые функции. 24
Слайд 25
Функции C 1 ( x ) , C 2 ( x ) , … , C n ( x ) должны удовлетворять системе ( 1 4 ) ( 14 ) – система n линейных уравнений с n неизвестными. Ее определитель – определитель Вронского W [ y 1 , y 2 , … , y n ] . 25
Слайд 26
Так как y 1 , y 2 , … , y n образуют ф.с.р. однородного уравнения, то по теореме2 W [ y 1 , y 2 , … , y n ] 0 , x [ a ; b ]. система ( 14 ) совместна и имеет единственное решение: Откуда получаем где C̃ i – произвольные постоянные. Общее решение неоднородного уравнения тогда имеет вид y = C 1 ( x ) y 1 + C 2 ( x ) y 2 + … + C n ( x ) y n , (1 3 ) Изложенный выше метод нахождения решения линейного неоднородного уравнения n -го порядка получил название метода вариации произвольных постоянных. 26
Слайд 27
27 Алгоритм решения ЛНДУ n -го порядка методом вариации произвольных постоянных 1. Найти ФСР ЛОДУ соответствующего ЛНДУ и записать его общее решение: y ( x ) = C 1 y 1 ( x ) + C 2 y 2 ( x ) +…+ C n y n ( x ). 2. Записать решение ЛНДУ в форме общего решения ЛОДУ, считая C i = C i ( x ), i = 1, 2, …, n : y ( x ) = C 1 ( x ) y 1 ( x ) + C 2 ( x ) y 2 ( x ) +…+ C n ( x ) y n ( x ). 3. Построить систему для определения C i ' ( x ) и решить ее согласно ( 14). 4. Найти C i ( x ) и подставить их в общее решение ЛНДУ ( 13).
Слайд 35: 4.1.2. Метод Эйлера самостоятельно!!!! См., например, д.т.письменный «конспект лекций по высшей математике» :полный курс
Глава 10, параграф 52. Системы дифференциальных уравнений. 35
Слайд 42: Равенство двух комплексных чисел ОПРЕДЕЛЕНИЕ
Пусть z 1 = x 1 + i y 1 , z 2 = x 2 + i y 2 . z 1 = z 2 если 42
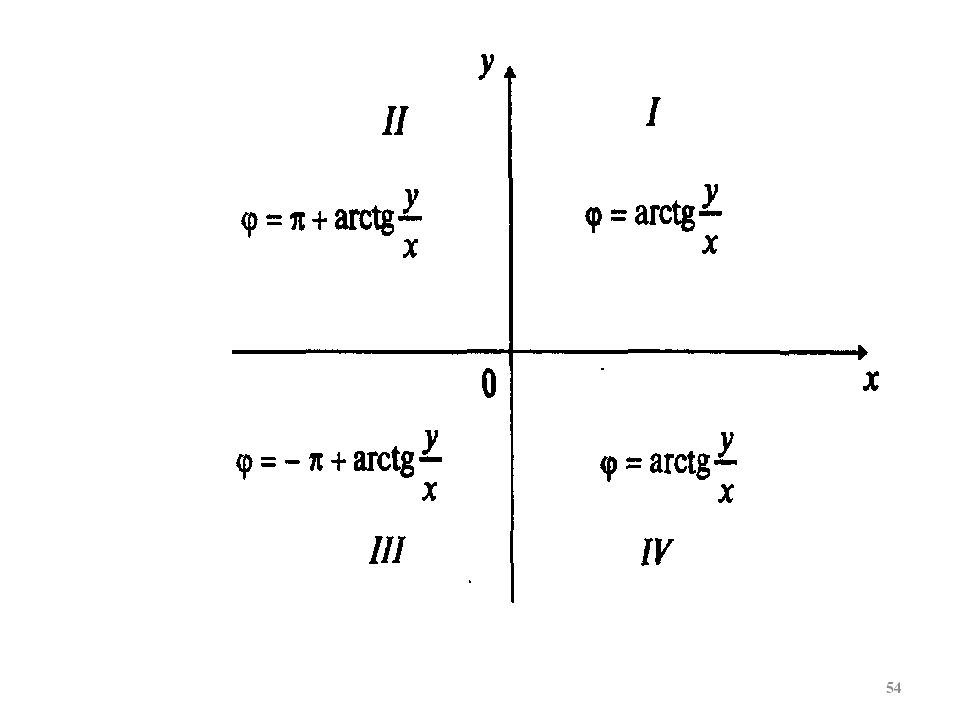
Слайд 57: Переход от алгебраической формы записи комплексного числа к тригонометрической
Z = x + i y, Пример. Представить в тригонометрической форме комплексное число: Z= 1+i. x=1, y=1. 57
Слайд 58: П ример
Представить в тригонометрической форме комплексное число: Z= 1+i - алгебраическая форма к.ч. Решение. -тригонометрическая форма комплексного числа. 58
Слайд 79: ЗАМЕЧАНИЕ
Основные понятия теории функций – предел функции, непрерывность функции и соответствующие им теоремы переносятся на функции комплексной переменной. Отличия начинаются в понятии производной. 79
Слайд 80: ЗАМЕЧАНИЕ
Смотри подробнее самостоятельно в книге: Письменный Конспект лекций по Высшей математике. Пункт 74.2. Предел и непрерывность функции комплексного переменного. ( стр. 526-527). 80
Слайд 94: ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ И ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Arcsin z , Arccos z , Arctg z , Arcctg z , Arcsh z , Arcch z , Arcth z , Arccth z (САМОСТОЯТЕЛЬНО!!!)
Слайд 95
w = f ( z ) Доказательство w = u + iv w = z n w = e z w = Lnz заполнить w = z p, p C заполнить w=sinz w=cosz заполнить w=tgz w=ctgz w=shz w=chz заполнить w=Arcsinz w=Arccosz заполнить w=Arctgz w=Arcctgz Основные элементарные функции w = | z | n ( cos n j + i sin n j ) w = e x e iy = e x ( cos y + i sin y ) ln | z |+ i ( argz +2 p k ) 95
Слайд 96: 4. Дифференцирование функции комплексной переменной
Опр. Пусть однозначная функция w = f ( z ) определена в точке z и некоторой ее окрестности. Тогда предел е сли он существует, наз. производной функции f ( z ) в точке, а функция f ( z ) наз. дифференцируемой в точке z. 96
Слайд 97
Дифференцирование функции комплексной переменной Пусть однозначная функция w = f ( z ) определена в точке z и некоторой ее окрестности. Этот предел называется производной функции w = f ( z ) в точке z и обозначается 97
Слайд 98
Теорема. (Достаточные условия дифференцируемости) Если действительная u ( x, y ) и мнимая v ( x, y ) части функции w = f ( z ) в точке z имеют полные дифференциалы и удовлетворяют условиям Коши – Римана, то функция f ( z ) = u ( x, y ) + i v ( x, y ) дифференцируема в точке z. Теорема. Условия Коши-Римана. (Необходимые условия дифференцируемости ) Если функция w = f ( z ) дифференцируема в точке z, то её действительная и мнимая части обладают частными производными первого порядка, которые удовлетворяют условиям Коши – Римана: и (4.2) Доказать ОПР. Функция f ( z ) называется дифференцируемой в области D, если она дифференцируема в каждой точке этой области. Все правила и формулы дифференцирования функций действительного переменного остаются в силе и для функций комплексного переменного. 98
Слайд 101
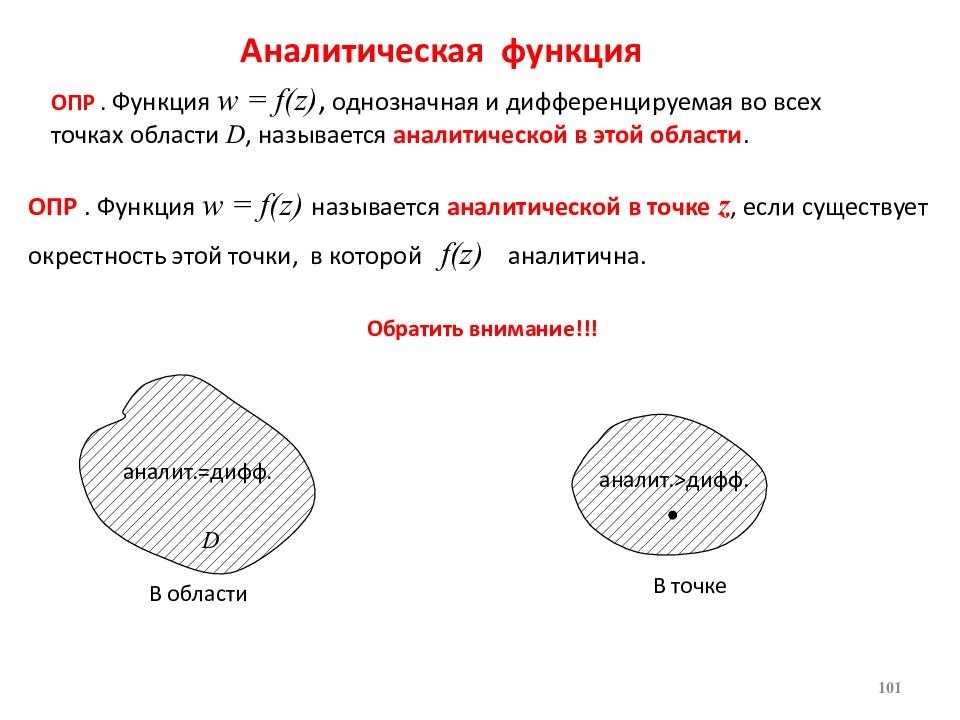
Аналитическая функция ОПР. Функция w = f ( z ) называется аналитической в точке z, если существует окрестность этой точки, в которой f ( z ) аналитична. ОПР. Функция w = f ( z ), однозначная и дифференцируемая во всех точках области D, называется аналитической в этой области. Обратить внимание!!! D В области аналит.=дифф. В точке аналит. > дифф. 101
Слайд 102
Теорема. Действительная и мнимая части аналитической функции в области D являются гармоническими в этой области. ДОКАЗАТЬ САМОСТОЯТЕЛЬНО Гармонические функции ОПР. Уравнение вида называется уравнением Лапласа. ОПР. Действительная функция двух действительных переменных j ( x, y ), непрерывная в области D, имеющая непрерывные частные производные второго порядка, являющаяся решением уравнения Лапласа, называется гармонической в области D. 102
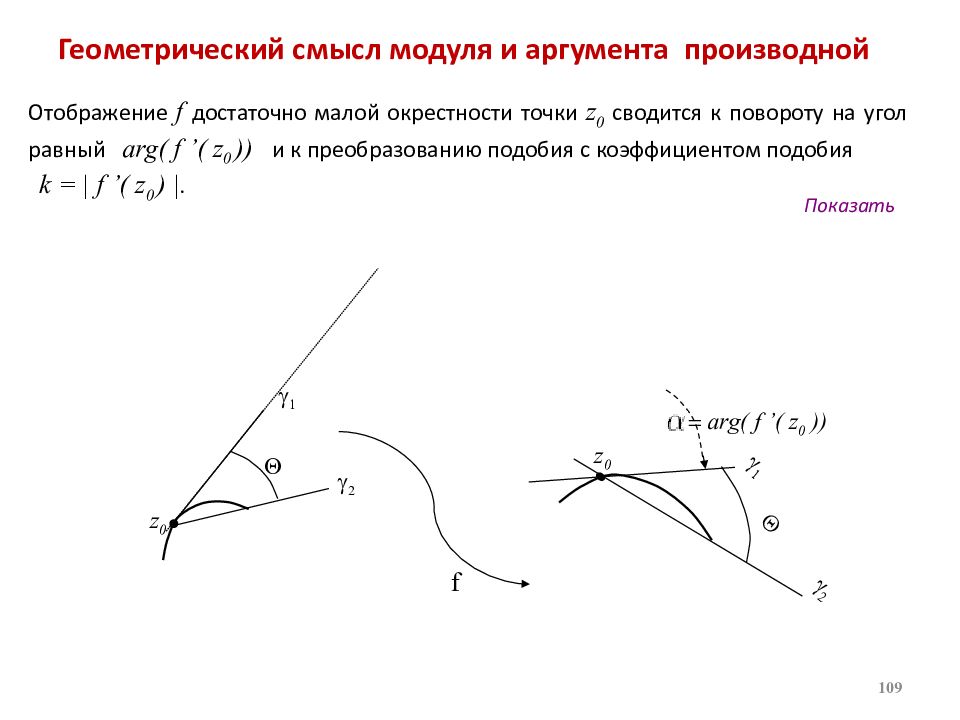
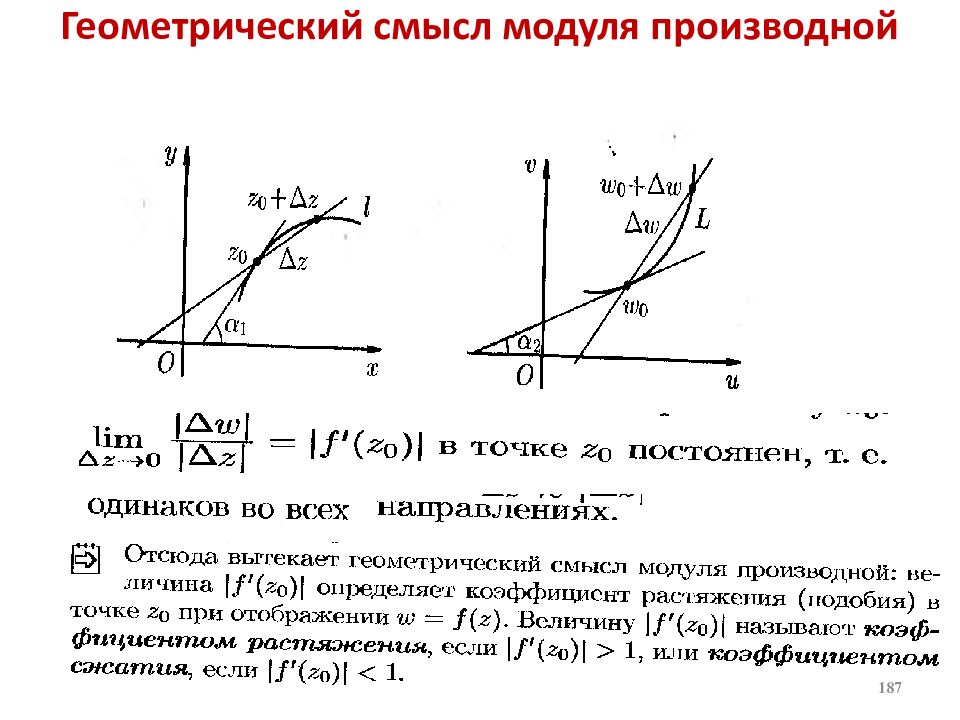
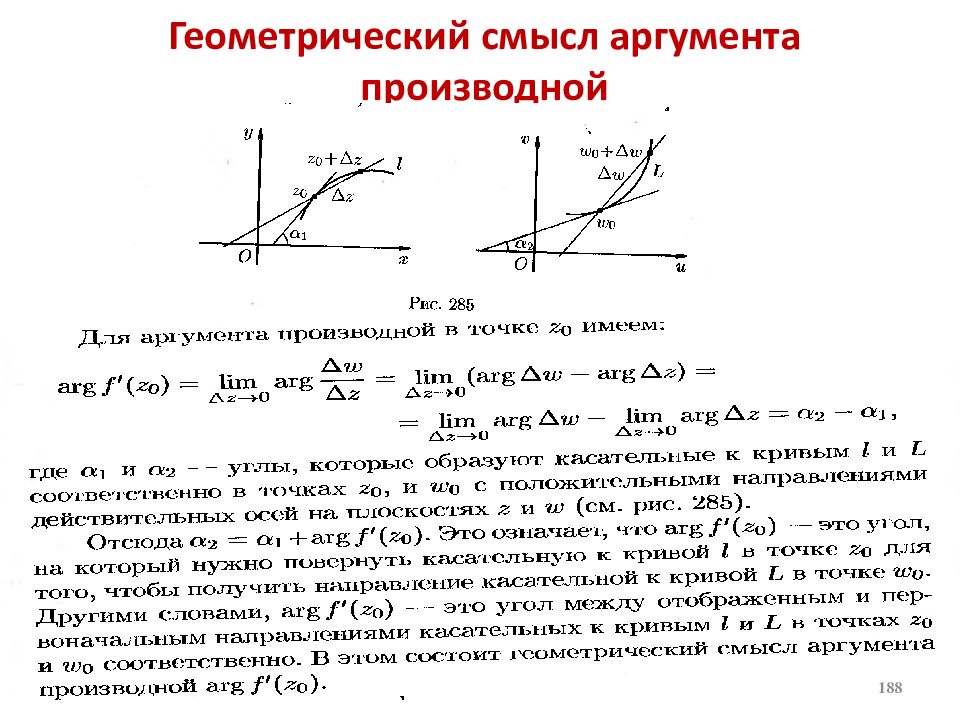
Слайд 108: Геометрический смысл модуля и аргумента производной
Теорема. Если в точке z 0 производная аналитической функции не равна нулю, то все бесконечно малые дуги, выходящие из точки z 0, при отображении поворачиваются на один и тот же угол, равный аргументу производной, и получают одно и то же растяжение, равное модулю производной. 108
Слайд 109
Отображение f достаточно малой окрестности точки z 0 сводится к повороту на угол равный arg ( f ’( z 0 )) и к преобразованию подобия с коэффициентом подобия k = | f ’( z 0 ) |. Геометрический смысл модуля и аргумента производной Показать f g 1 g 2 Q z 0 g 1 g 2 Q z 0 j = arg ( f ’( z 0 )) 109
Слайд 164
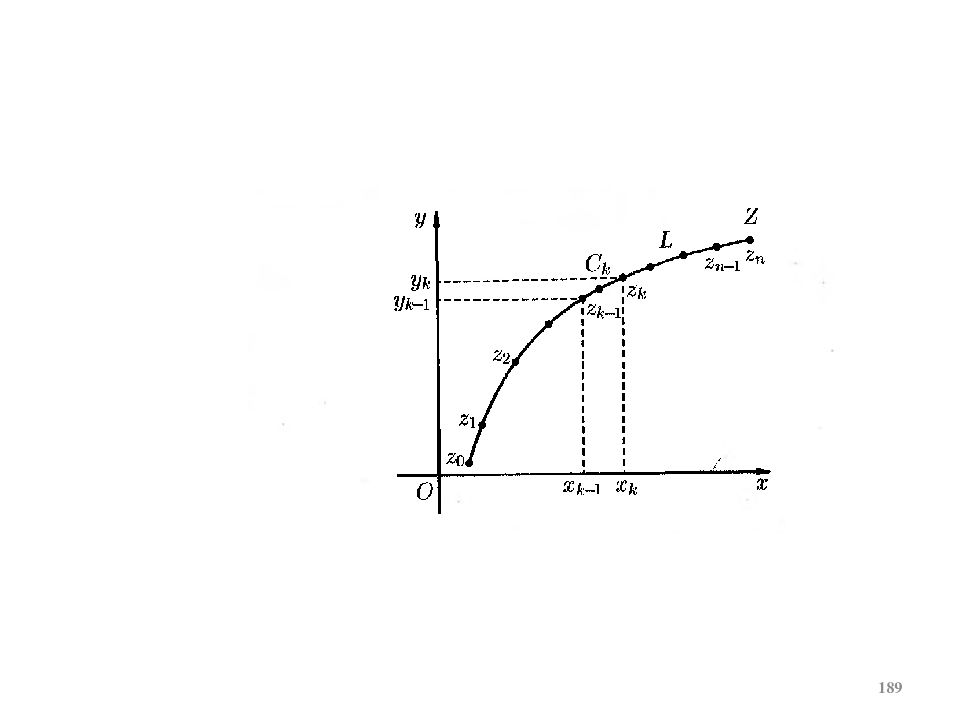
а) Г: { А = z 0, z 1, z 2, …, z n = В }, б) z k ∊ ( z k, z k +1 ) в) г) d = max | z k, z k +1 | Предел комплексной интегральной суммы при d → 0 называется интегралом от функции f ( z ) вдоль кривой Г и обозначается § 5. И нтегрирование функции комплексной переменной z 1 z 2 z k z k+1 z n-1 z n А = z 0 В = z n z 1 z 2 z k z n-1 ОПР. Пусть в области D задана однозначная и непрерывная ф. к. п. w = f ( z ) и пусть Г ( АВ ) – произвольная кусочно-гладкая ориентированная кривая ( Г ∊ D ). D (5.1 ) 164
Слайд 175: ЛОДУ 2-го порядка, с произвольными коэффициентами
Р ассмотрим уравнение y + a 1 ( x ) y + a 2 ( x ) y = 0 . Пусть y 1 ( x ) любое ненулевое решение этого уравнения Тогда его общее решение имеет вид ПРИМЕР. Найти общее решение уравнения если известно, что его решением является функция ( С амостоятельно). 175
Слайд 176
Уравнение ( 8 ) называется характеристическим уравнением (для) уравнения ( 6 ). М ногочлен в левой части ( 8 ) называется характеристичес - ким многочленом, К орни уравнения ( 8 ) называются характеристическими корнями уравнения ( 6 ). Замечани я. 1) Формально характеристическое уравнение ( 8 ) получается из ( 6 ) заменой производных искомой функции на соответ - ствующие степени k, а самой функции – на k 0 = 1 . 2) Уравнение ( 8 ) – алгебраическое уравнение n -й степени. оно имеет n корней, но 1) каждый корень считается столько раз, какова его кратность; 2) корни могут быть комплексными (причем, комплексные корни попарно сопряжены). Следовательно, функции вида e x в общем случае не дадут всю ф.с.р. уравнения ( 6 ). 176
Слайд 177: ОБЩЕЕ РЕШЕНИЕ ЛОДУ 2-го ПОРЯДКА
Для линейного однородного дифференциального уравнения 2-го порядка ф ундаментальная система решений (Ф.С.Р.) с остоит из двух линейно независимых решений Его общее решение находится по формуле: 177
Слайд 184: ДУ в.п., допускающие понижение порядка
184 ДУ в.п., допускающие понижение порядка № Вид ДУ Замена Решение 1. F ( x, y ( n ) ) = 0 а) – Последовательное понижение порядка ДУ ( n - кратное интегрирование) б) ДУ нельзя разрешить относительно y ( n ) 2. (1 k n ) ( нет y, y ', …, y ( k -1) ) Понижение порядка ДУ на ( n - k ) Если решение ДУ, то ( k -кратное интегрирование ) 3. (нет x ) Понижение порядка ДУ на 1 ,, …
Слайд 185: П ример
Пример. Представить в тригонометрической форме комплексное число: Z= 1+i. 185
Слайд 186: Переход от алгебраической формы записи комплексного числа к тригонометрической
Z = x + i y, 186