Слайд 2
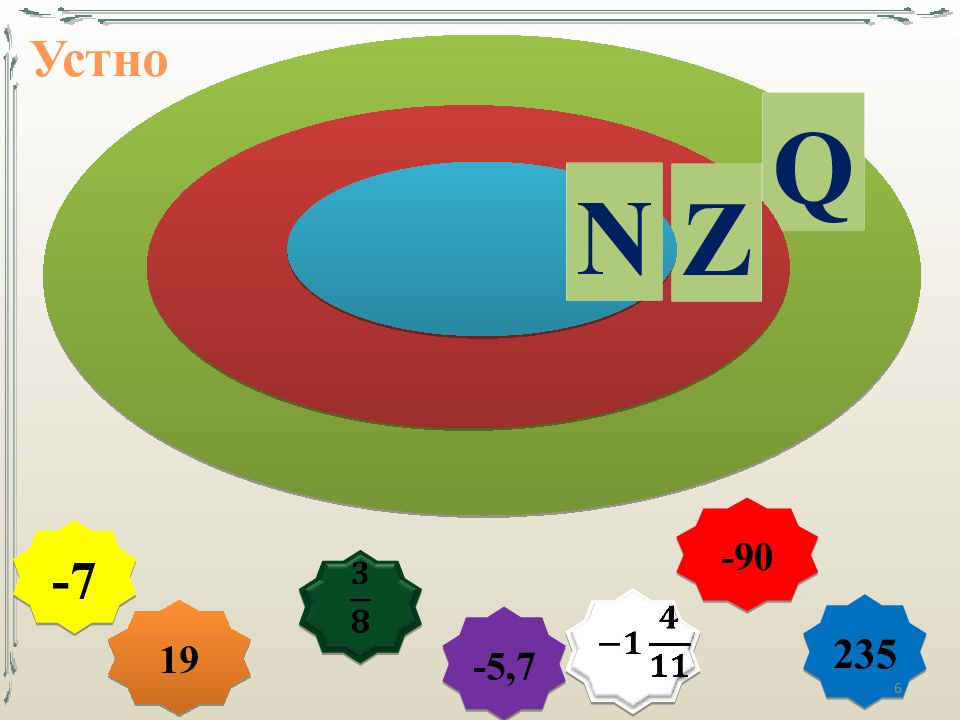
Числа 1, 2, 3 … - натуральные числа Натуральные числа – числа, возникающие естественным образом при счёте. Существуют два подхода к определению натуральных чисел — числа, используемые при: перечислении ( нумеровании ) предметов ( первый, второй, третий, …); обозначении количества предметов ( нет предметов, один предмет, два предмета, …). 1-й танк 2-й танк 3-й танк N 2
Слайд 3
Множество целых чисел = натуральные числа + противоположные им числа и нуль -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 Z 3
Слайд 7
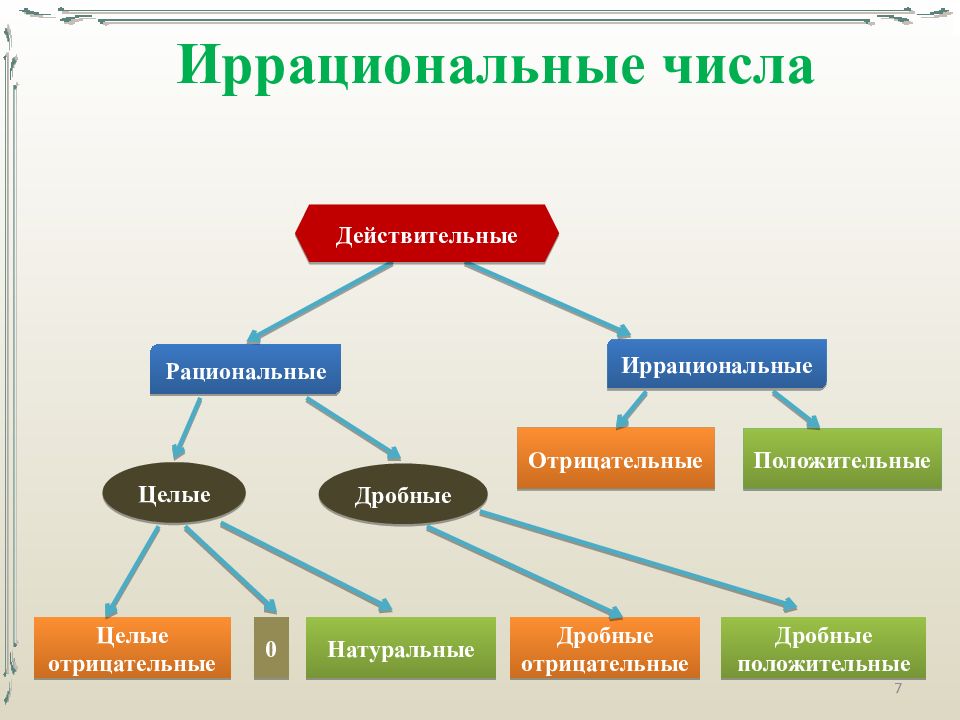
7 Иррациональные числа Целые отрицательные 0 Натуральные Дробные отрицательные Дробные положительные Целые Дробные Рациональные Иррациональные Отрицательные Положительные Действительные
Слайд 8
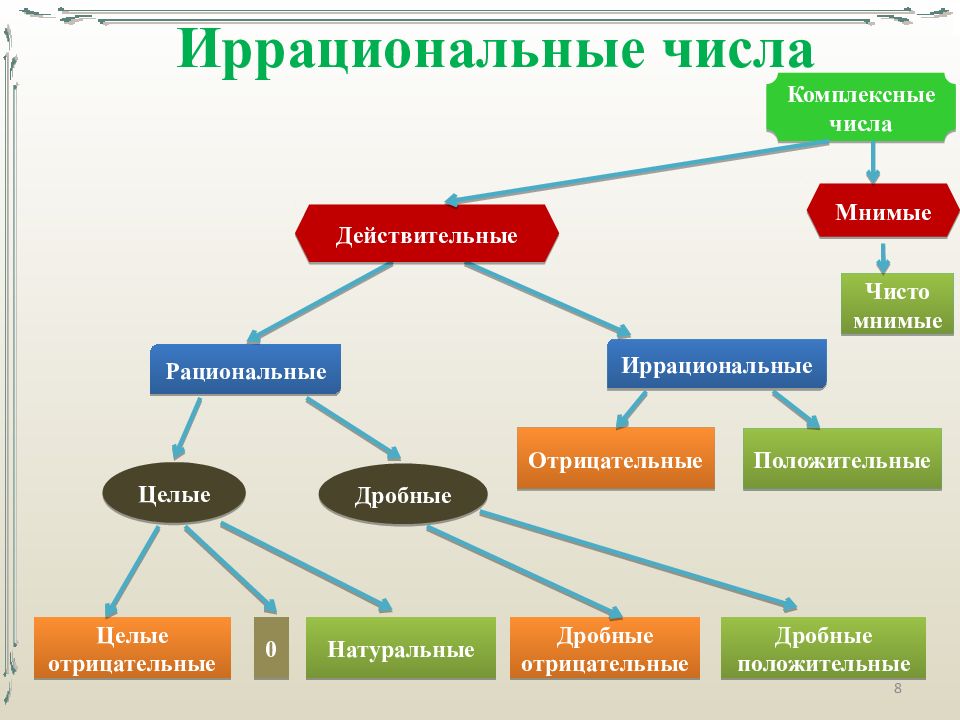
8 Иррациональные числа Целые отрицательные 0 Натуральные Дробные отрицательные Дробные положительные Целые Дробные Рациональные Иррациональные Отрицательные Положительные Действительные Комплексные числа Мнимые Чисто мнимые
Слайд 10
Число Иррациональным является число, выражающее отношение длины окружности к диаметру: = 3,1415926… 10
Слайд 11
11 Рациональным называется число, которое может быть представлено в виде десятичной, бесконечной, периодической дроби. Например: 7 =7,(0); -13, 1= - 13,1(0); = 0,(3); 0 = 0,(0) Иррациональным называется число, которое может быть представлено в виде десятичной, бесконечной, непериодической дроби. Например: =3,14… ; =1,41…
Слайд 12
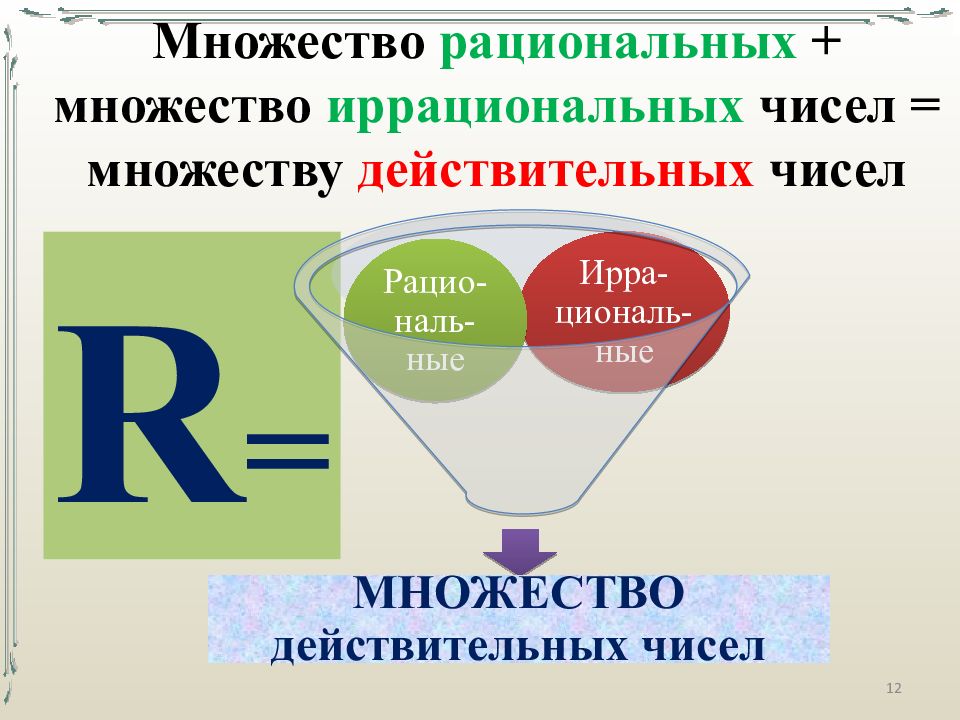
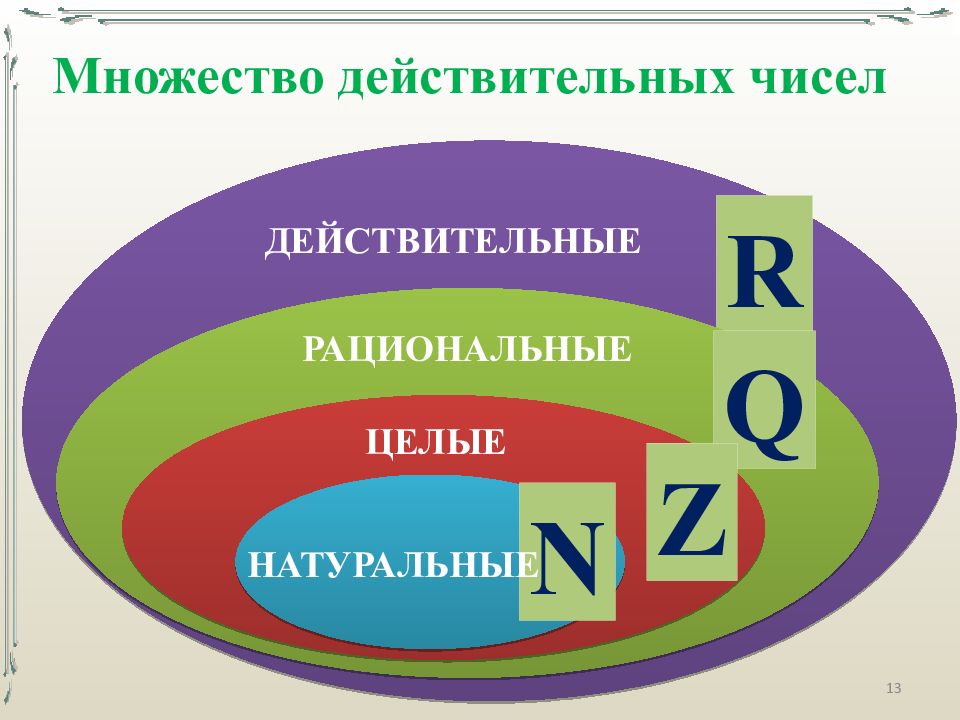
Множество рациональных + множество иррациональных чисел = множеству действительных чисел R = 12
Слайд 13
R 13 Q Z N НАТУРАЛЬНЫЕ ЦЕЛЫЕ РАЦИОНАЛЬНЫЕ ДЕЙСТВИТЕЛЬНЫЕ Множество действительных чисел
Слайд 14
Множество рациональных чисел + множество иррациональных чисел называют множеством действительных чисел. …, 3,010010001…, … 0 …, – 5,020022000222...,… 14
Слайд 15
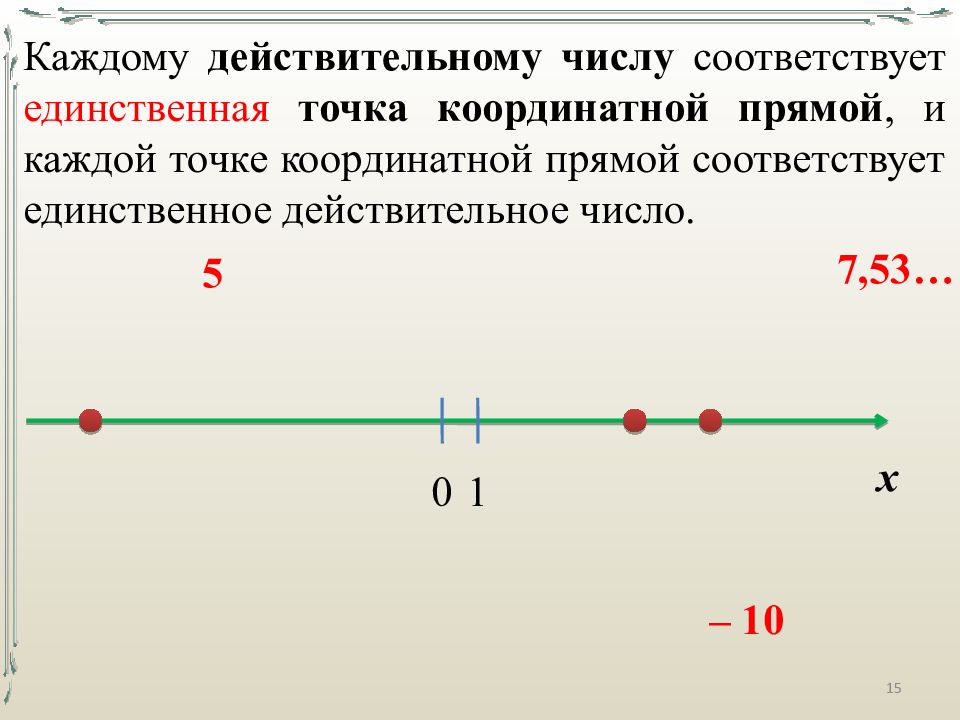
Каждому действительному числу соответствует единственная точка координатной прямой, и каждой точке координатной прямой соответствует единственное действительное число. х 5 0 1 – 10 7,53… 15
Слайд 16
Между множеством действительных чисел и множеством точек координатной прямой существует взаимно однозначное соответствие. 16
Слайд 17
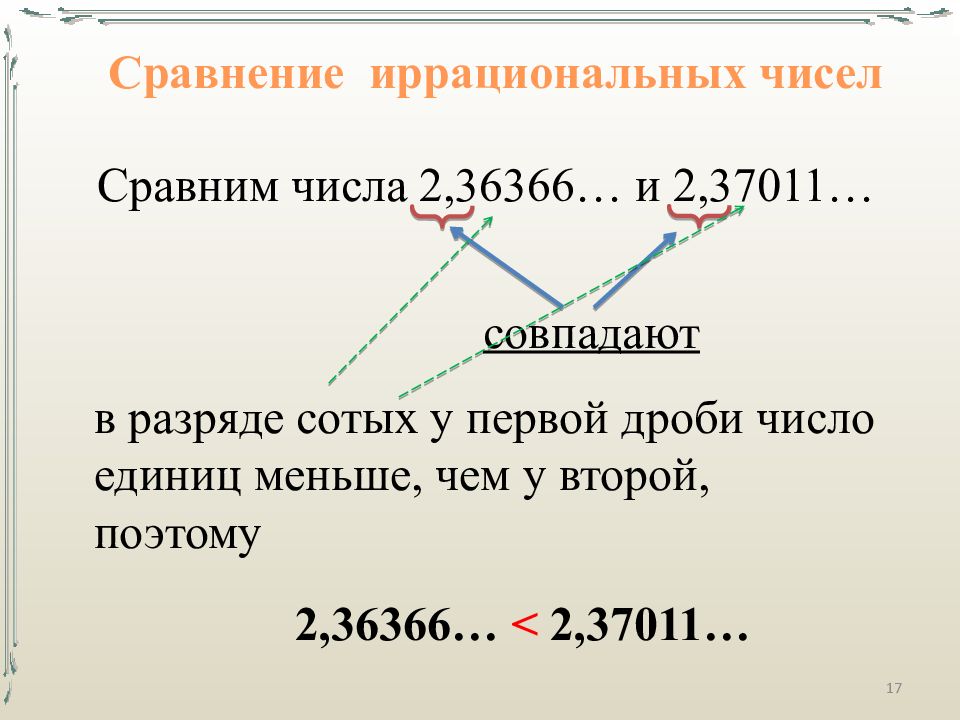
Сравнение иррациональных чисел Сравним числа 2,36366… и 2,37011… совпадают в разряде сотых у первой дроби число единиц меньше, чем у второй, поэтому 2,36366… < 2,37011… 17
Слайд 19
Кластер Иррациональные числа Натуральные числа Целые числа Рациональные числа 9 0 7 –6(3) 7,020020002… 345 π 1,24(53) 19
Слайд 21: Вычислите
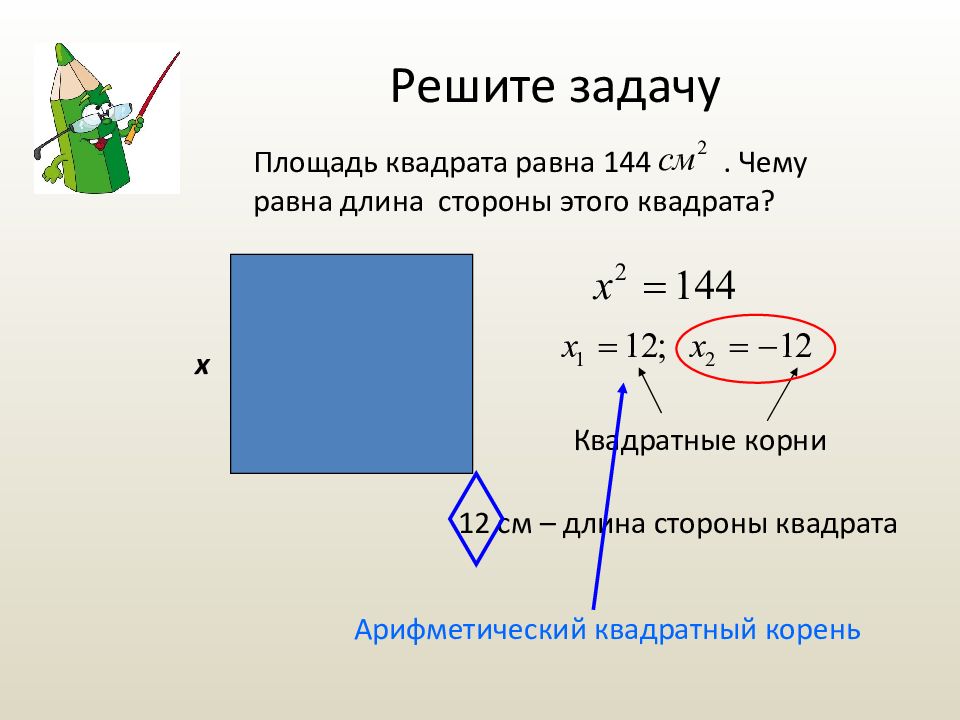
Слайд 22: Решите задачу
Площадь квадрата равна 144. Чему равна длина стороны этого квадрата? x Квадратные корни 12 см – длина стороны квадрата Арифметический квадратный корень
Слайд 23
Арифметический квадратный корень числа 144 = 12 Арифметическим квадратным корнем из числа a называется неотрицательное число b, квадрат которого равен a. При a 0 выражение не имеет смысла - не имеет смысла
Слайд 28
Ответы запишите на карточках: а) 5 и-5 нет такого числа Ø нет такого числа Ø д) 0
Слайд 29
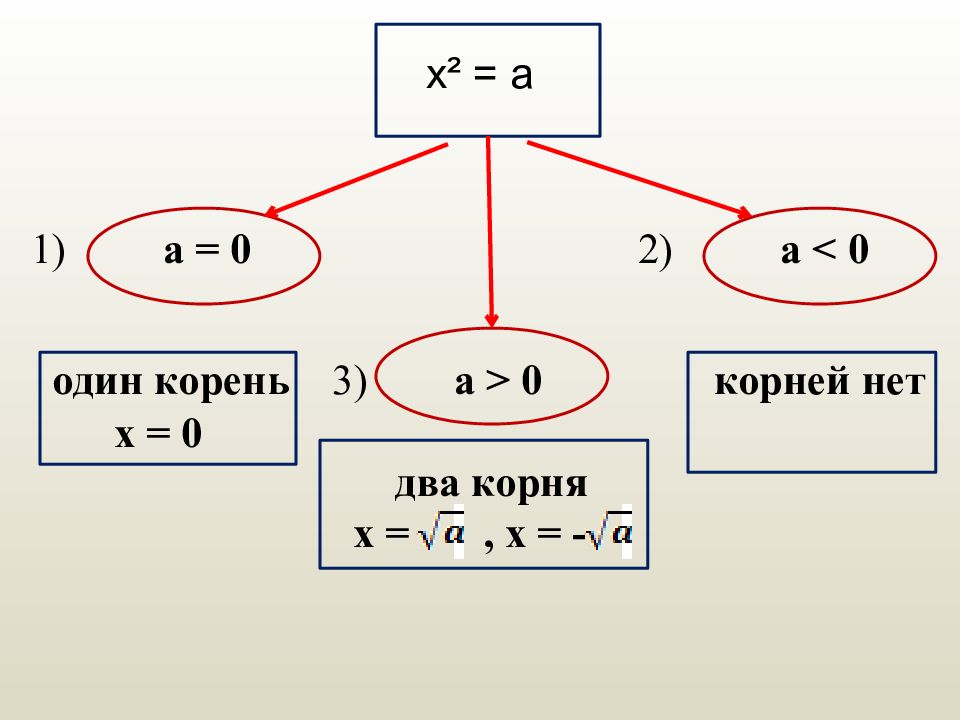
два корня x =, x = - x ² = a 1) а = 0 2) а < 0 один корень 3) а > 0 корней нет х = 0
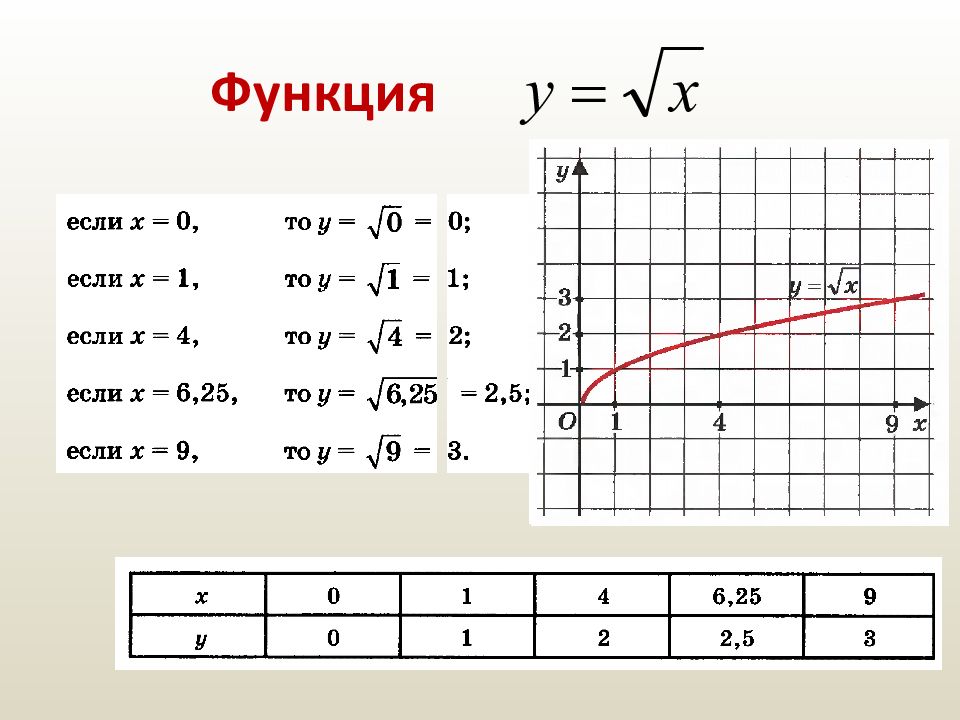
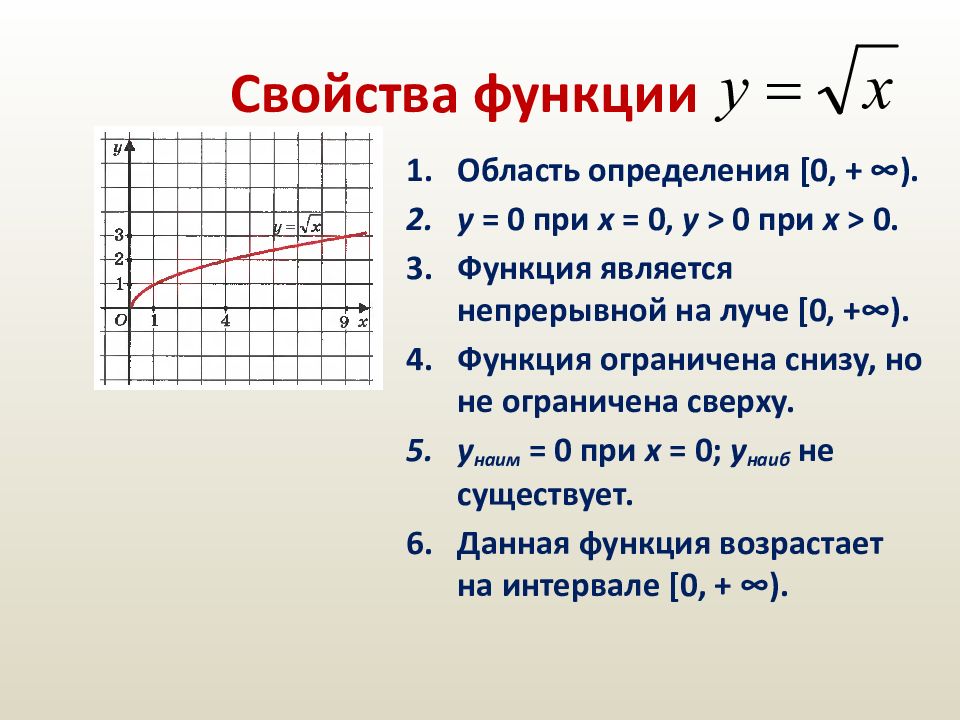
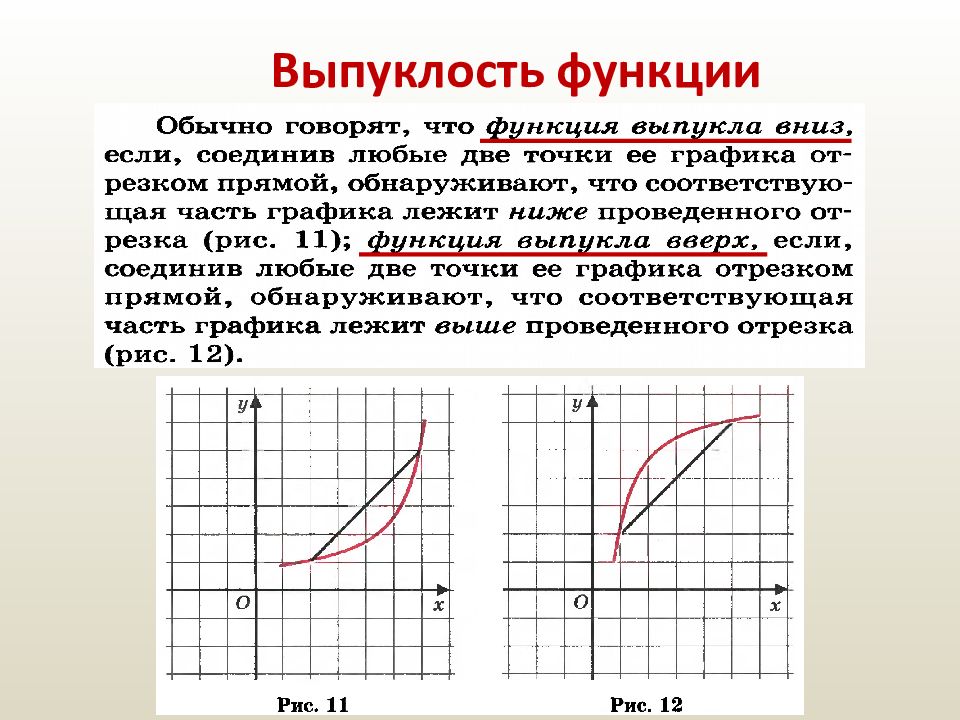
Слайд 33: Свойства функции
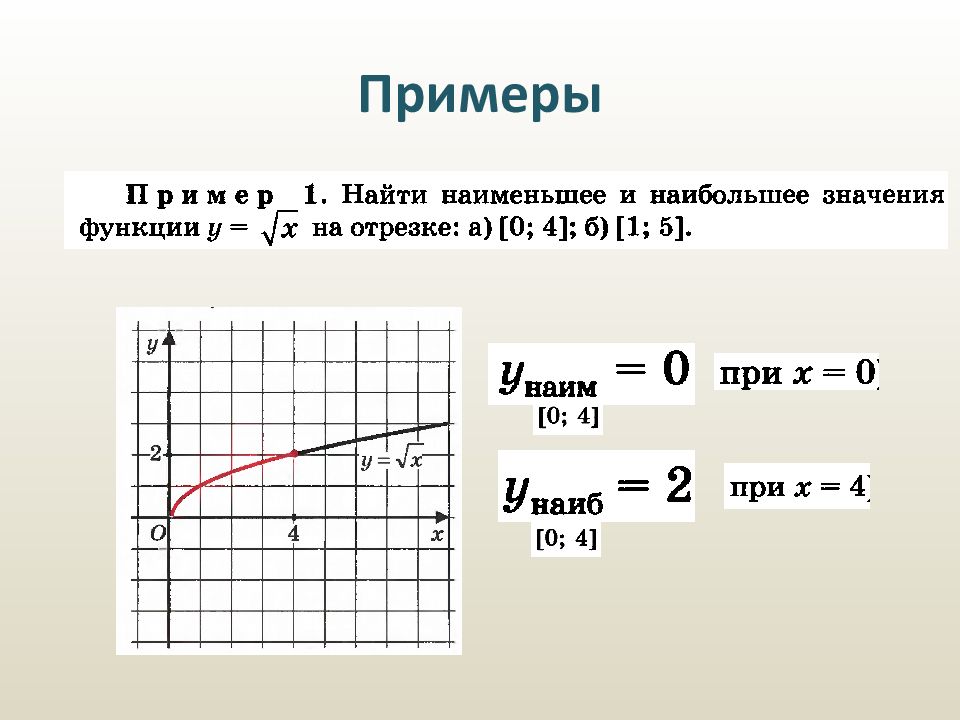
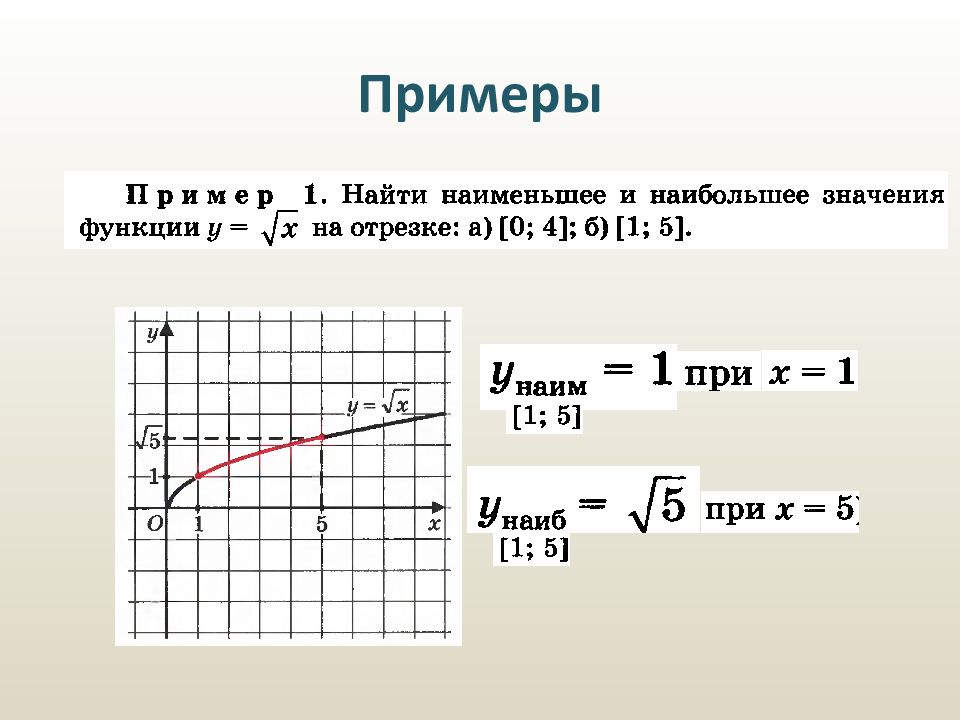
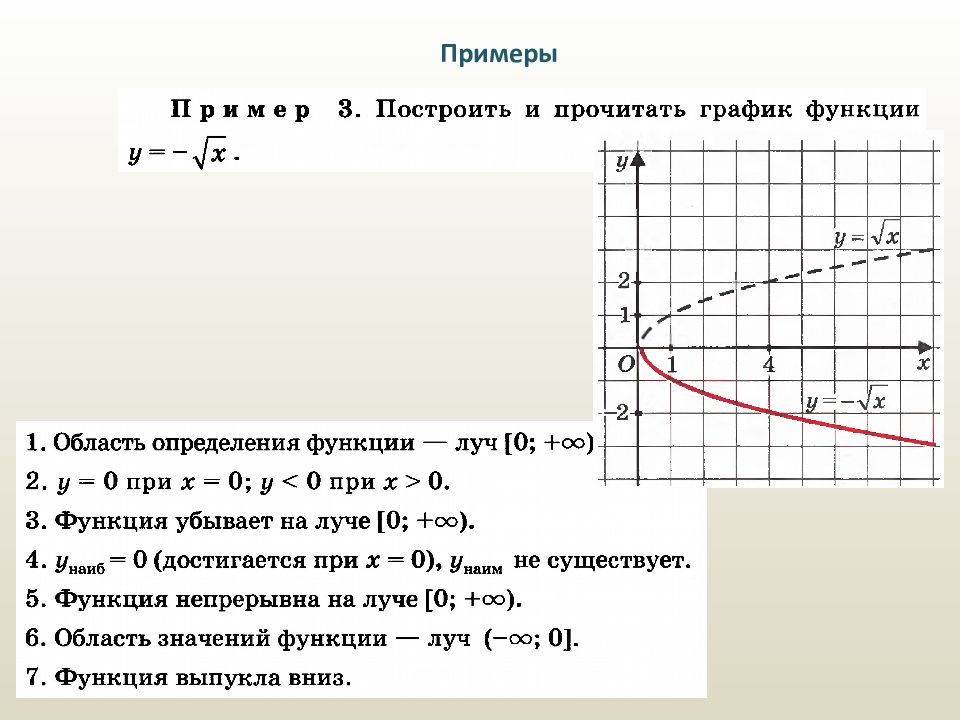
Область определения [0, + ∞). y = 0 при x = 0, y > 0 при x > 0. Функция является непрерывной на луче [0, +∞). Функция ограничена снизу, но не ограничена сверху. y наим = 0 при x = 0; y наиб не существует. Данная функция возрастает на интервале [0, + ∞).
Слайд 35: Свойства функции
Область определения [0, + ∞). y = 0 при x = 0, y > 0 при x > 0. Функция является непрерывной на луче [0, +∞). Функция ограничена снизу, но не ограничена сверху. y наим = 0 при x = 0; y наиб не существует. Данная функция возрастает на интервале [0, + ∞). Данная функция выпукла вверх. Область значений данной функции: луч [0, + ∞).