Цели обучения Lesson objective 10.2.1.6 – находить корни многочлена методом разложения его на множители 10.2.1.7 - выполнять деление «уголком» многочлена на многочлен
Критерии оценивания - умеет раскладывать многочлен на множители - умеет производить деление многочлена на многочлен
Что вы понимаете под выражением «корень многочлена»? 2. В чем на ваш взгляд состоит важность нахождения корня многочлена? 3. Сколько действительных корней может иметь многочлен четной (нечетной степени)?
Является ли число 4 корнем многочлена Найдите корни многочлена
Р (x) = a n x n + a n-1 x n-1 +…+ a 3 x 3 + a 2 x 2 + a 1 x + a o - канонический вид многочлена Р(х) a n x n – старший член многочлена Р(х) a n – коэффициент при старшем члене Если a n = 1, то многочлен Р(х) называется приведенным Если a n ≠ 1, то многочлен Р(х) называется неприведенным a о – свободный член многочлена р ( х ) n – степень многочлена
Р (x) = a n x n + a n-1 x n-1 +…+ a 3 x 3 + a 2 x 2 + a 1 x + a o Число а называют корнем многочлена Р(х), если Р(а) = 0 (т.е. если а – корень уравнения, то Р(а) =0). Если многочлен Р(х) делится на х – а, то а – корень этого многочлена. В самом деле, Р(х) = ( х – а) Q ( x ), и поэтому Р(а) = (а – а) Q (а )= 0.
P(x) = S(x) Q(x) Говорят, что многочлен Р(х) делится на многочлен S(x), если существует такой многочлен Q(x), что выполняется тождество P(x) – делимое (или кратное) S(x) – делитель Q(x) – частное
частное делитель Деление многочленов уголком х 2 + 5 х 3 + 5х − − 3х 2 − 15 х − 3х 2 − 15 0 т. к. х 3 − 3х 2 + 5х − 15 = (х 2 + 5)( х − 3), то многочлен х 3 − 3х 2 + 5х − 15 делится на многочлены х 2 + 5 и х − 3. Пример 1 − 3 − делимое х 3 − 3х 2 + 5х − 15
частное делитель Деление многочленов х 3 − х 2 + 2х − 1 х 5 − х 4 + 2х 3 − х 2 − − х 3 + х 2 − 2х +1 х 2 − х 3 + х 2 − 2х + 1 0 Необходимо разделить многочлен х 5 − х 4 + х 3 − 2х +1 на многочлен х 3 − х 2 + 2х − 1 Пример 2 − 1 − делимое х 5 − х 4 + х 3 − 2х +1
р (x) = s(x) q(x) + r ( х ) Для любых двух многочленов ненулевой степени P (х) и S(x) существует пара многочленов Q(x) и R(x) такая, что степень многочлена R(x) меньше степени многочлена ( делителя ) S(x) и выполняется тождество: P(x) – делимое (или кратное) S(x) – делитель Q(x) – неполное частное R(x) – остаток P(x) = S(x) Q(x) + R (х)
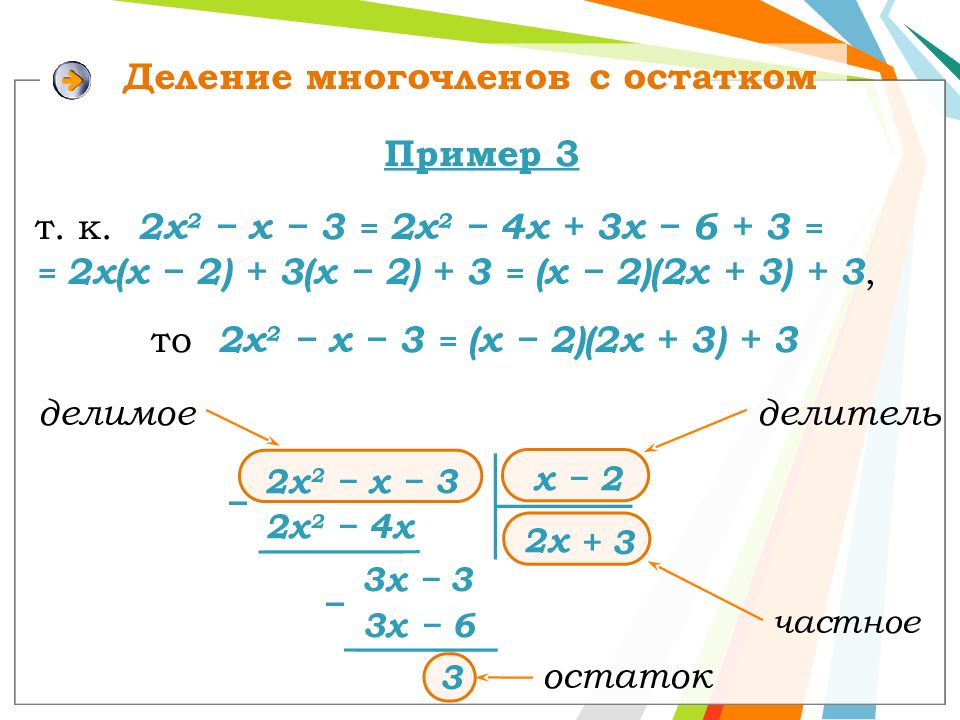
остаток частное делитель делимое 2х 2 − х − 3 х − 2 2х 2 − 4х − 3х − 6 2х 3х − 3 3 т. к. 2х 2 − х − 3 = 2х 2 − 4х + 3х − 6 + 3 = = 2х( х − 2) + 3( х − 2) + 3 = ( х − 2)(2х + 3) + 3, Пример 3 + 3 Деление многочленов с остатком то 2х 2 − х − 3 = ( х − 2)(2х + 3) + 3 −
ФРОНТАЛЬНАЯ РАБОТА P(x) = S(x) Q(x) + R (х)
