Тема 16
Вычислительный процесс называется разветвляющимся, если направление его продолжения на некотором этапе в зависимости от исходных данных или результатов промежуточных вычислений осуществляется по одному из возможных вариантов Варианты вычислений называются ветвями Разветвляющиеся алгоритмы реализуются через алгоритмические структуры « ветвление » и « выбор » Разветвляющиеся алгоритмы
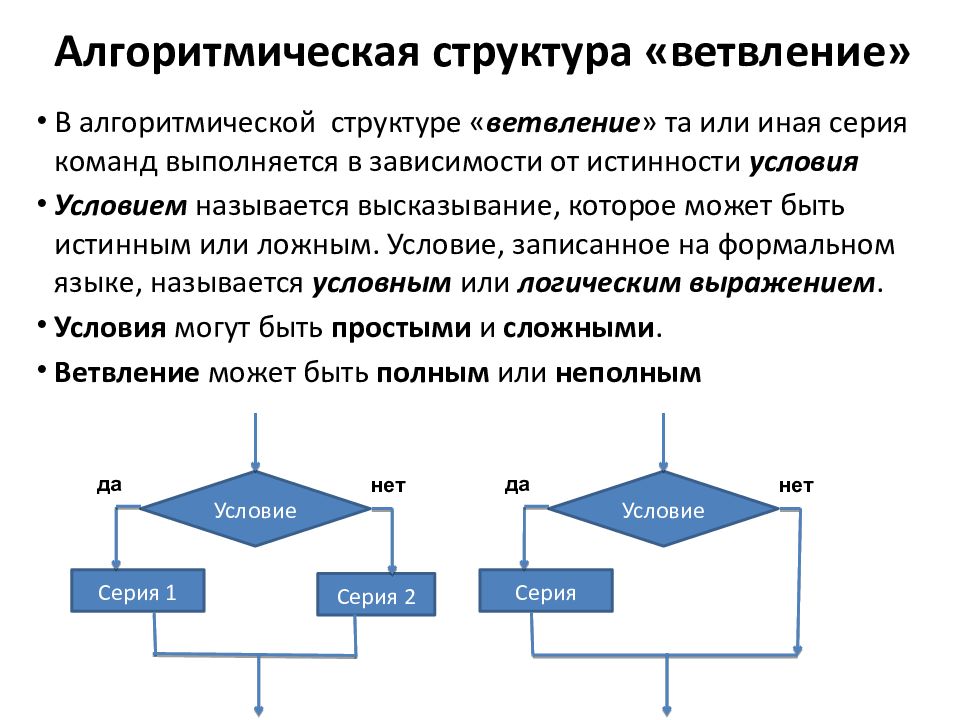
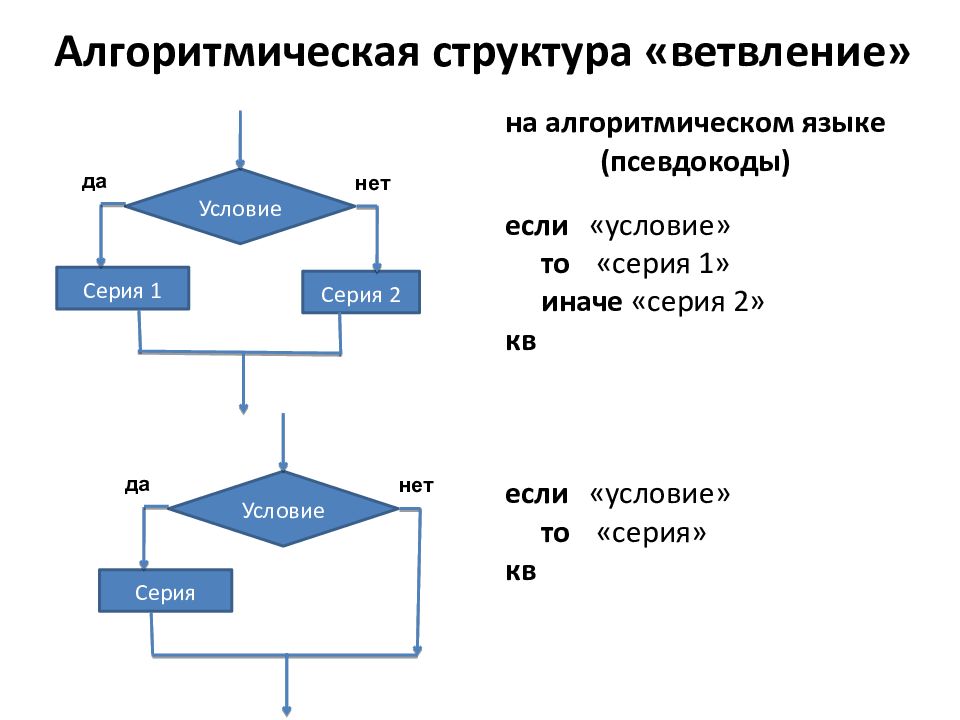
В алгоритмической структуре « ветвление » та или иная серия команд выполняется в зависимости от истинности условия Условием называется высказывание, которое может быть истинным или ложным. Условие, записанное на формальном языке, называется условным или логическим выражением. Условия могут быть простыми и сложными. Ветвление может быть полным или неполным Серия 1 Условие Серия 2 нет да Серия Условие нет да
на алгоритмическом языке (псевдокоды) если «условие» то «серия 1» иначе «серия 2» кв если «условие» то «серия» кв Серия 1 Условие Серия 2 нет да Серия Условие нет да
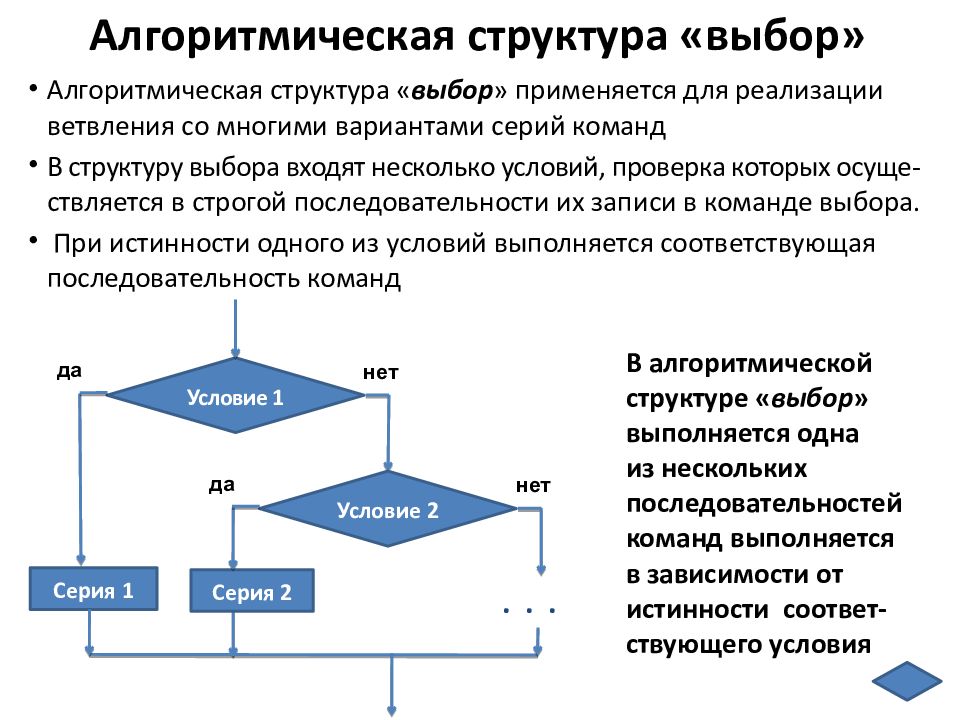
В алгоритмической структуре « выбор » выполняется одна из нескольких последовательностей команд выполняется в зависимости от истинности соответ-ствующего условия Алгоритмическая структура « выбор » применяется для реализации ветвления со многими вариантами серий команд В структуру выбора входят несколько условий, проверка которых осуще -ствляется в строгой последовательности их записи в команде выбора. При истинности одного из условий выполняется соответствующая последовательность команд Серия 1 Условие 1 нет да Серия 2 Условие 2 ... 2 нет да
Выбор (минимума или максимума) из 2 величин из n величин Упорядочение (по возрастанию или по убыванию) 2 величин n величин
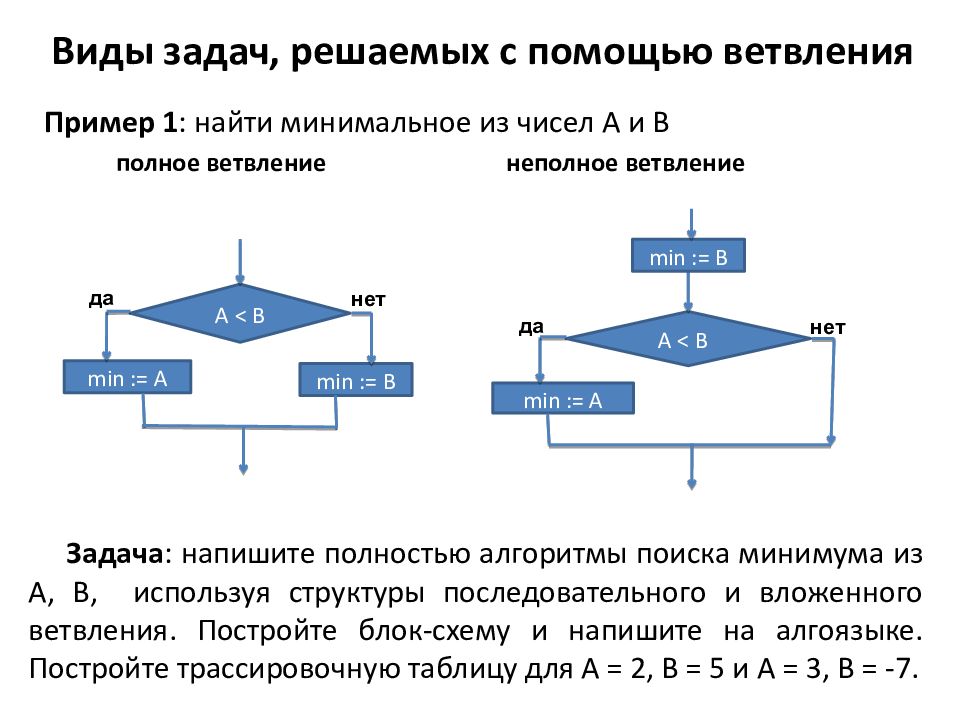
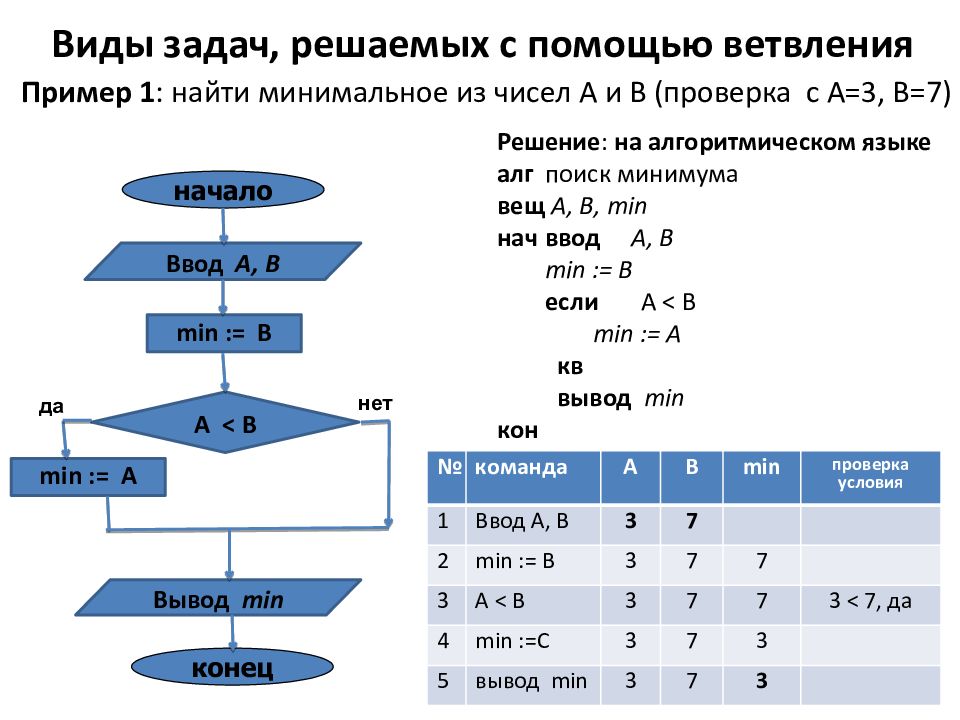
Пример 1 : найти минимальное из чисел А и В полное ветвление неполное ветвление min := A А < B min := B нет да min := A А < B нет да min := B Задача : напишите полностью алгоритмы поиска минимума из А, В, используя структуры последовательного и вложенного ветвления. Постройте блок-схему и напишите на алгоязыке. Постройте трассировочную таблицу для А = 2, В = 5 и А = 3, В = -7.
Решение : на алгоритмическом языке алг поиск минимума вещ А, В, min нач ввод А, В min := B если A < B min := A кв вывод min кон Пример 1 : найти минимальное из чисел А и В ( проверка с A=3, B=7) конец Ввод А, В Вывод min min := A А < B нет да начало min := B № команда А В min проверка условия 1 Ввод А, В 3 7 2 min := B 3 7 7 3 А < В 3 7 7 3 < 7, да 4 min :=С 3 7 3 5 вывод min 3 7 3
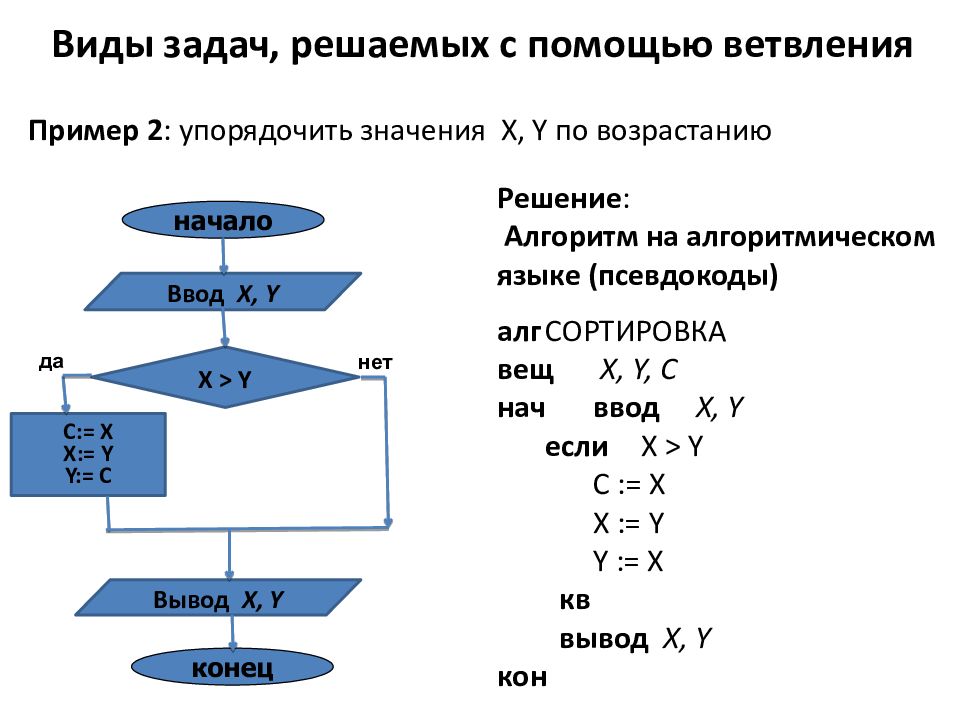
конец Ввод X, Y Вывод X, Y C:= X X:= Y Y:= C X > Y нет да начало Решение : Алгоритм на алгоритмическом языке (псевдокоды) алг СОРТИРОВКА вещ X, Y, C нач ввод X, Y если X > Y C := X X := Y Y := X кв вывод X, Y кон Пример 2 : упорядочить значения X, Y по возрастанию
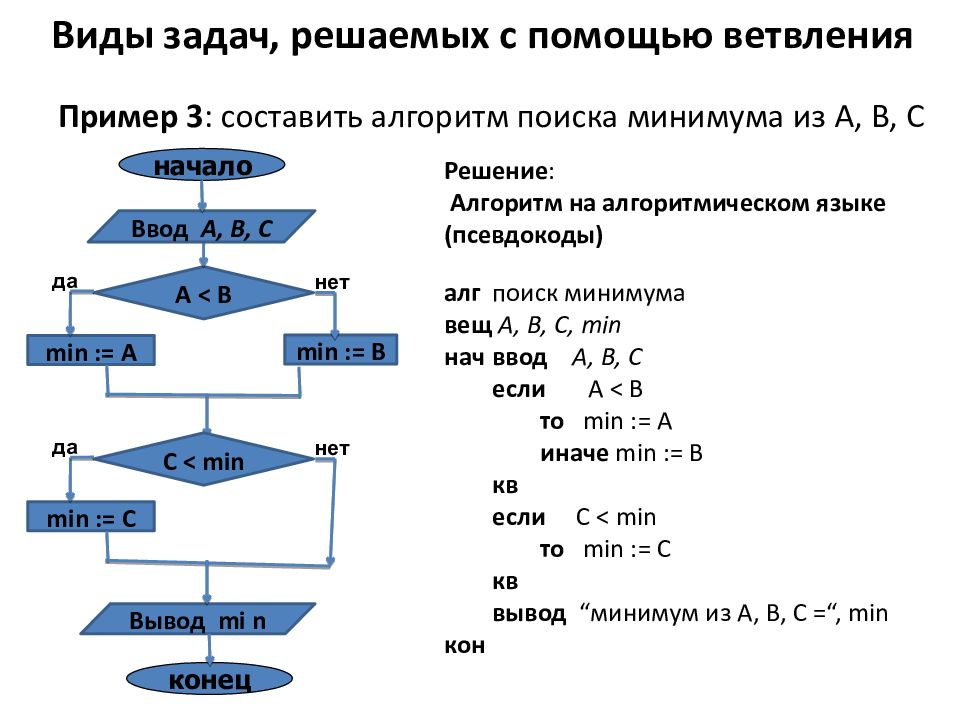
Пример 3 : составить алгоритм поиска минимума из А, В, С Решение : Алгоритм на алгоритмическом языке (псевдокоды) алг поиск минимума вещ А, В, С, min нач ввод А, В, С если А < B то min := A иначе min := B кв если C < min то min := C кв вывод “ минимум из А, В, С = “, min кон min := A А < B min := B нет да конец Ввод А, В, С Вывод mi n min := C С < min нет да начало
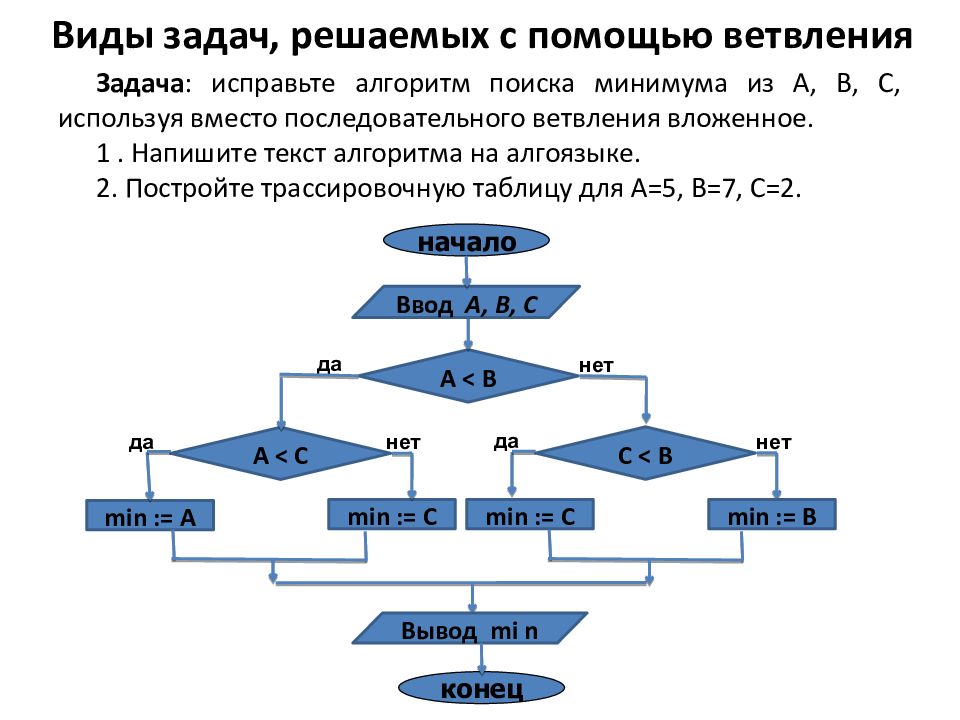
Задача : исправьте алгоритм поиска минимума из А, В, С, используя вместо последовательного ветвления вложенное. 1. Напишите текст алгоритма на алгоязыке. 2. Постройте трассировочную таблицу для А=5, В=7, С=2. min := A А < B нет да конец Ввод А, В, С Вывод mi n min := C начало А < C нет да C < B нет да min := C min := B
Любой алгоритм должен приводить к определенному результату и завершать работу, какими бы ни были исходные и промежуточные данные. Задача 1: исправьте блок-схему алгоритма деления двух дробей, учитывая, что на 0 делить нельзя. Задача 2: постройте блок-схему решения квадратного уравнения ax 2 + bx + c = 0, учитывая случаи возможного ввода исходных a = 0, b = 0, c = 0, и случай d < 0.
Задача 1: составить алгоритм поиска минимума из А, В, С, D Задача 2: постройте блок-схему для проверки существо-вания треугольника с углами α и β, а в случае удачи также проверьте, будет ли он прямоугольным. Задача 3: постройте блок-схему для проверки, какая из точек A(x 1, y 1 ) или В (x 2, y 2 ) лежит ближе к началу координат. Задача 4: постройте блок-схему для вычисления значения функции Y = |X|. Задача 5: постройте блок-схему для проверки, попадает ли точка A(x, y) в определенную область на координатной плоскости (например, а) в первый квадрант, б) в окружность определенного радиуса с центром в начале координат)
Домашняя работа на разветвляющиеся алгоритмы Построить блок-схемы разветвляющихся алгоритмов Задача 1: «Геометрическая задача» - по вариантам (по карточкам). Задача 2 : «Математическая задача» - по вариантам (по карточкам).
Тема 17
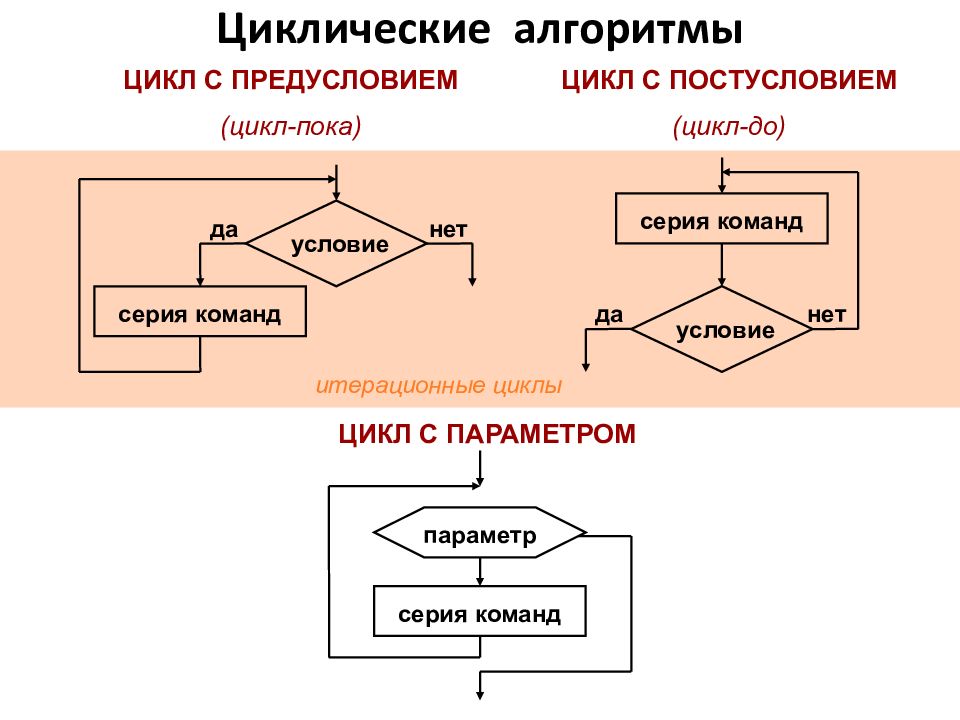
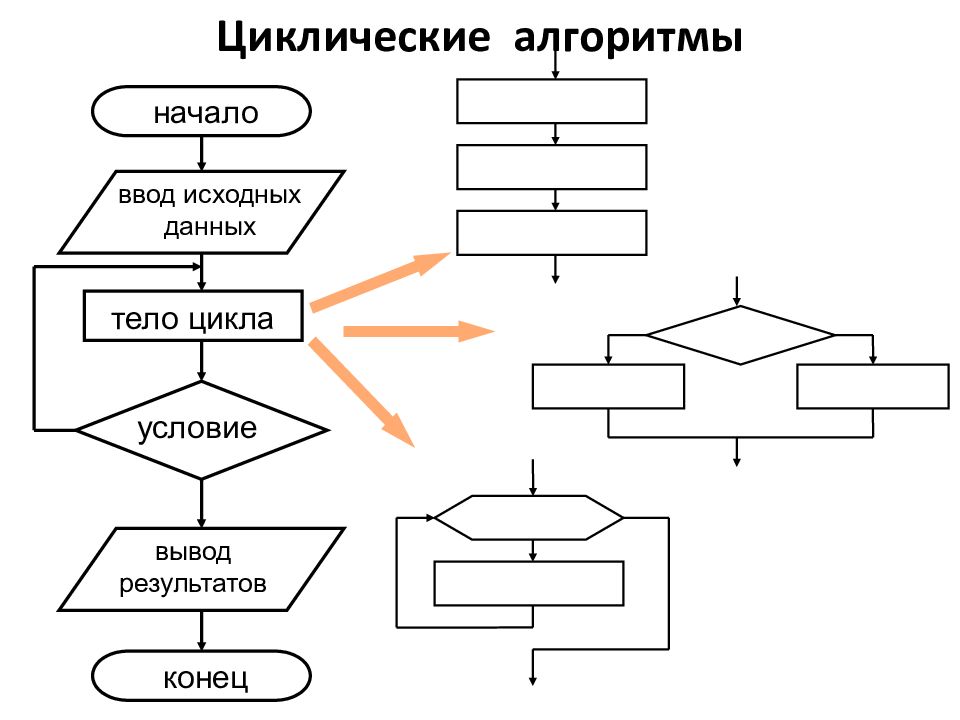
Циклическим называется такой алгоритм, в котором одна и та же последовательность действий выполняется несколько раз, до тех пор пока выполняется (или пока не выполняется) некоторое условие Повторяющаяся последовательность действий называ-ется телом цикла Циклы С условием С параметром (итерационные) (со счетчиком) С предусловием С постусловием Циклические алгоритмы
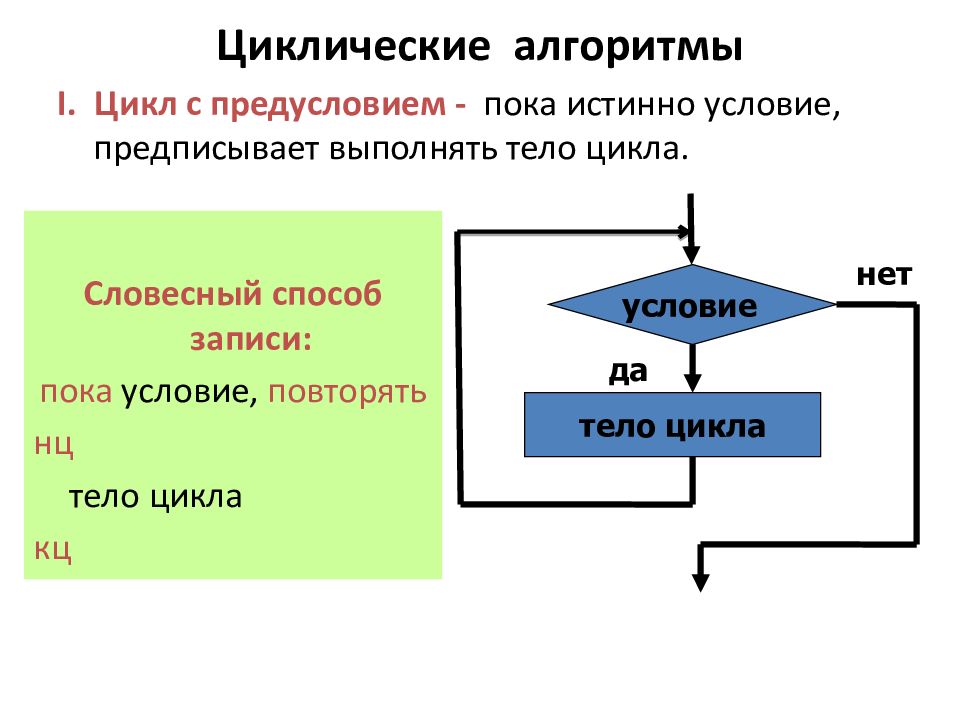
Словесный способ записи: пока условие, повторять нц тело цикла кц нет Циклические алгоритмы I. Цикл с предусловием - пока истинно условие, предписывает выполнять тело цикла. условие тело цикла да
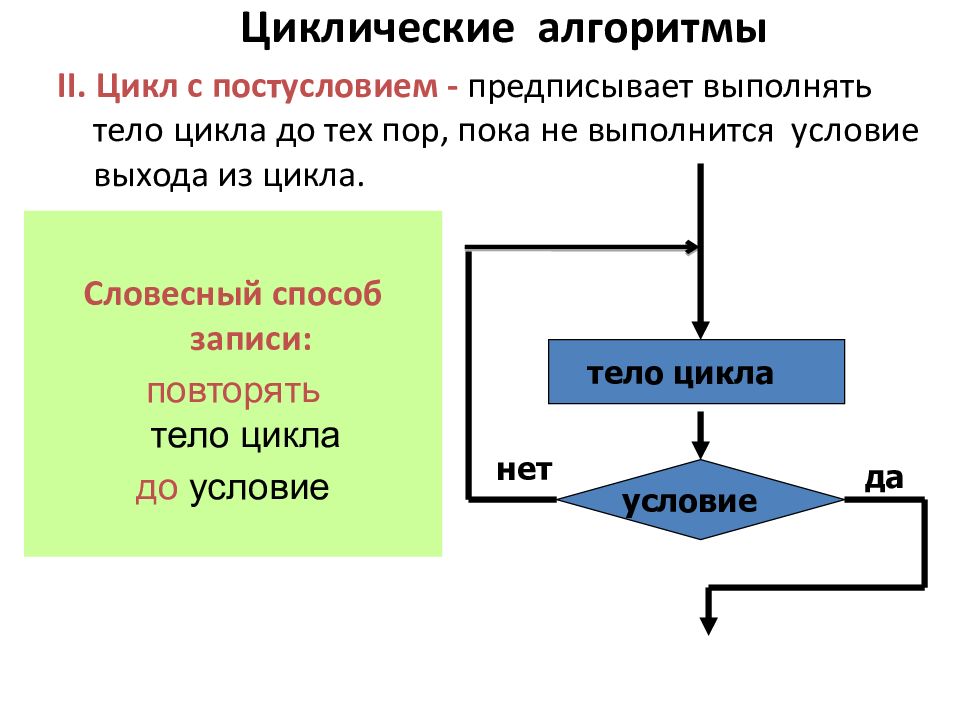
Словесный способ записи: повторять тело цикла до условие Циклические алгоритмы II. Цикл с постусловием - предписывает выполнять тело цикла до тех пор, пока не выполнится условие выхода из цикла. да условие тело цикла нет
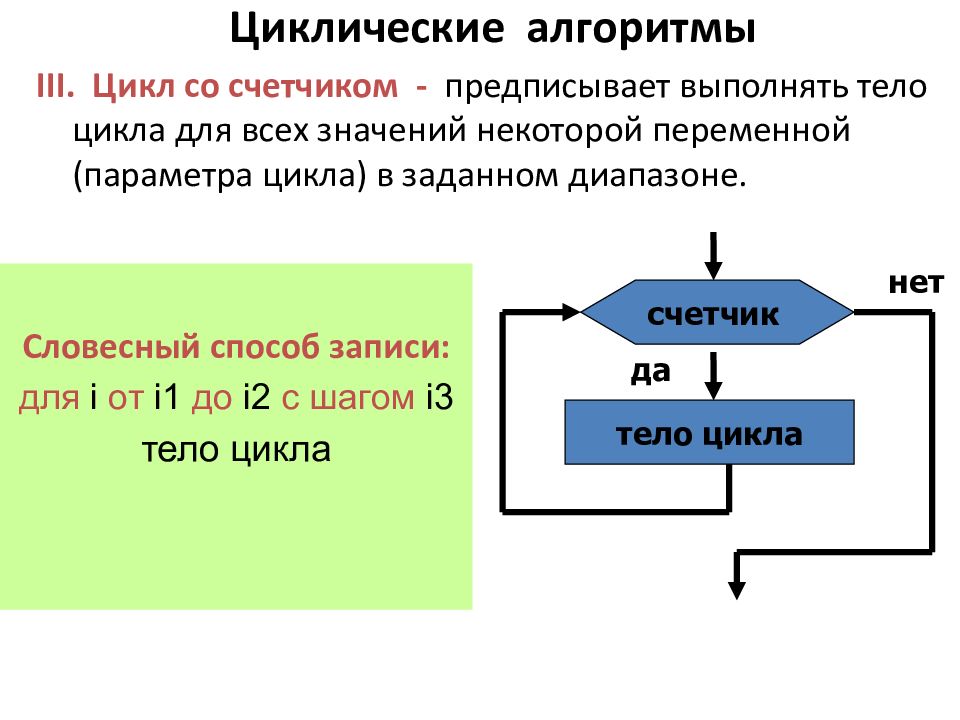
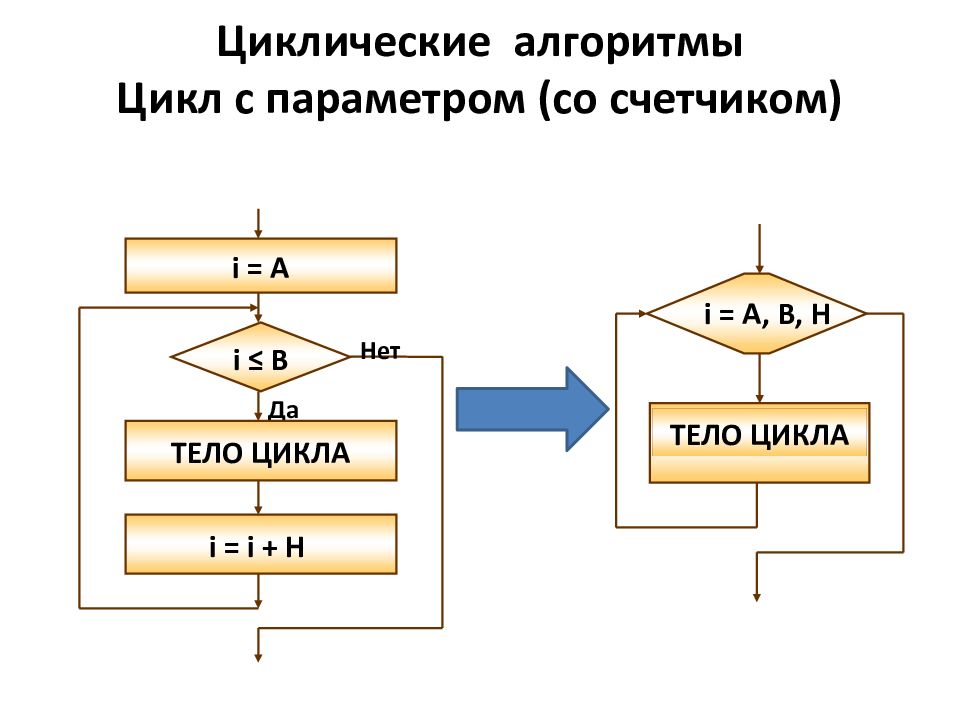
Словесный способ записи: для i от i1 до i2 с шагом i3 тело цикла Циклические алгоритмы III. Цикл со счетчиком - предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне. счетчик тело цикла да нет
условие серия команд да нет да нет условие серия команд ЦИКЛ С ПРЕДУСЛОВИЕМ (цикл-пока) ЦИКЛ С ПОСТУСЛОВИЕМ (цикл-до) ЦИКЛ С ПАРАМЕТРОМ серия команд параметр итерационные циклы Циклические алгоритмы
тело цикла условие начало ввод исходных данных вывод результатов конец Циклические алгоритмы
Да i = A i ≤ B ТЕЛО ЦИКЛА i = i + H Нет Циклические алгоритмы Цикл с параметром (со счетчиком) i = A, B, H ТЕЛО ЦИКЛА
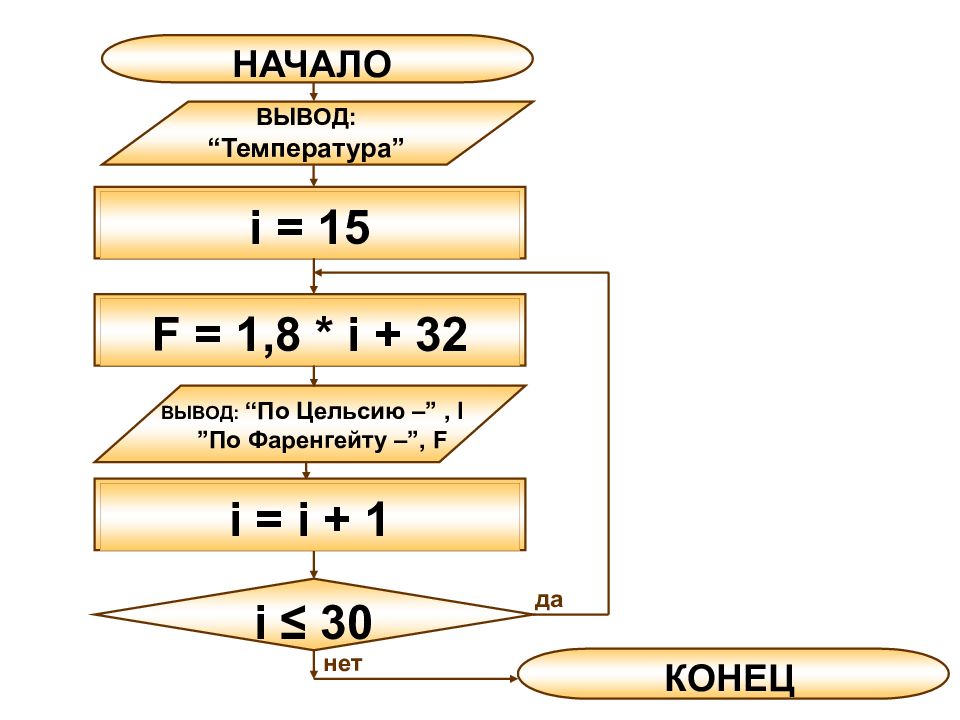
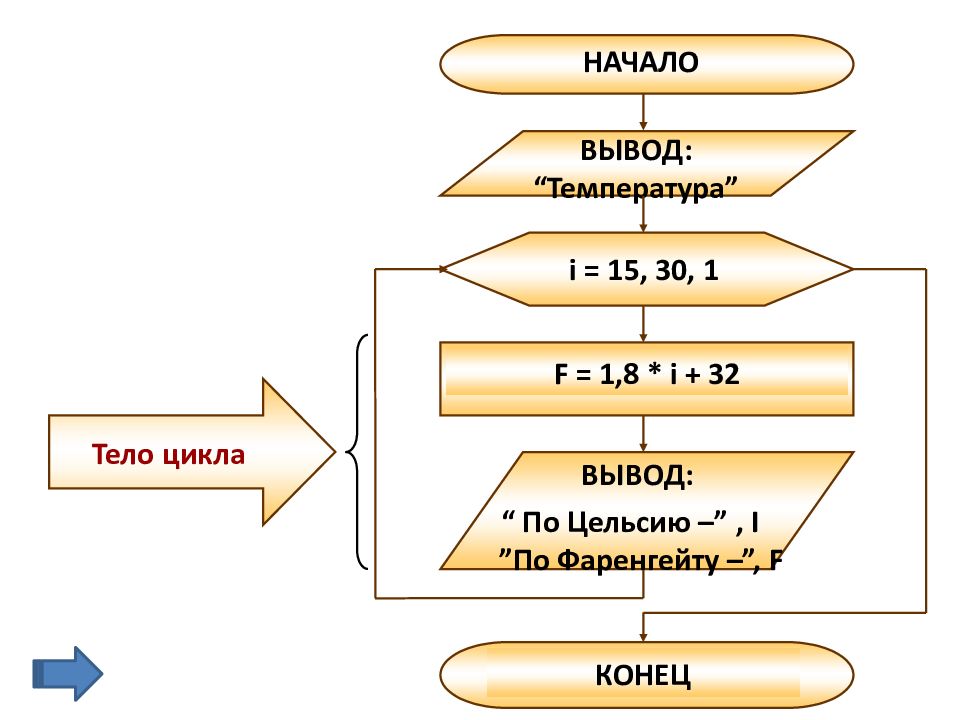
Циклические алгоритмы Цикл с параметром (со счетчиком) Пример: Составить блок-схему алгоритма перевода из градусов по шкале Цельсия (С) в градусы по шкале Фаренгейта (F) для значений от 15 ° С до 30 ° С с шагом 1 °. Перевод осуществлять по формуле F = 1,8 C + 32
нет КОНЕЦ НАЧАЛО ВЫВОД: “ Температура ” F = 1,8 * i + 32 ВЫВОД: “ По Цельсию – ”, I ” По Фаренгейту – ”, F i = 15 i = i + 1 i ≤ 3 0 да
НАЧАЛО ВЫВОД: “ Температура ” i = 15, 30, 1 F = 1,8 * i + 32 КОНЕЦ ВЫВОД: “ По Цельсию – ”, I ” По Фаренгейту – ”, F Тело цикла
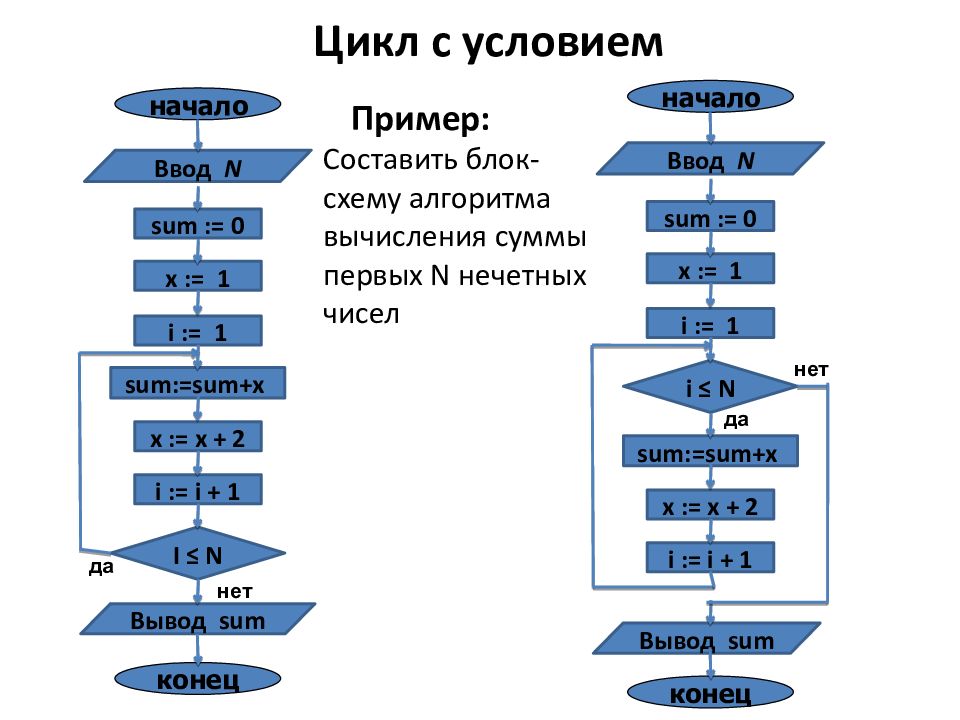
Цикл с условием конец Ввод N Вывод sum sum:= sum+x I ≤ N нет да начало sum := 0 i := 1 i := i + 1 x := x + 2 x := 1 конец Ввод N Вывод sum sum:= sum+x i ≤ N нет да начало sum := 0 i := 1 i := i + 1 x := x + 2 x := 1 Пример: Составить блок-схему алгоритма вычисления суммы первых N нечетных чисел
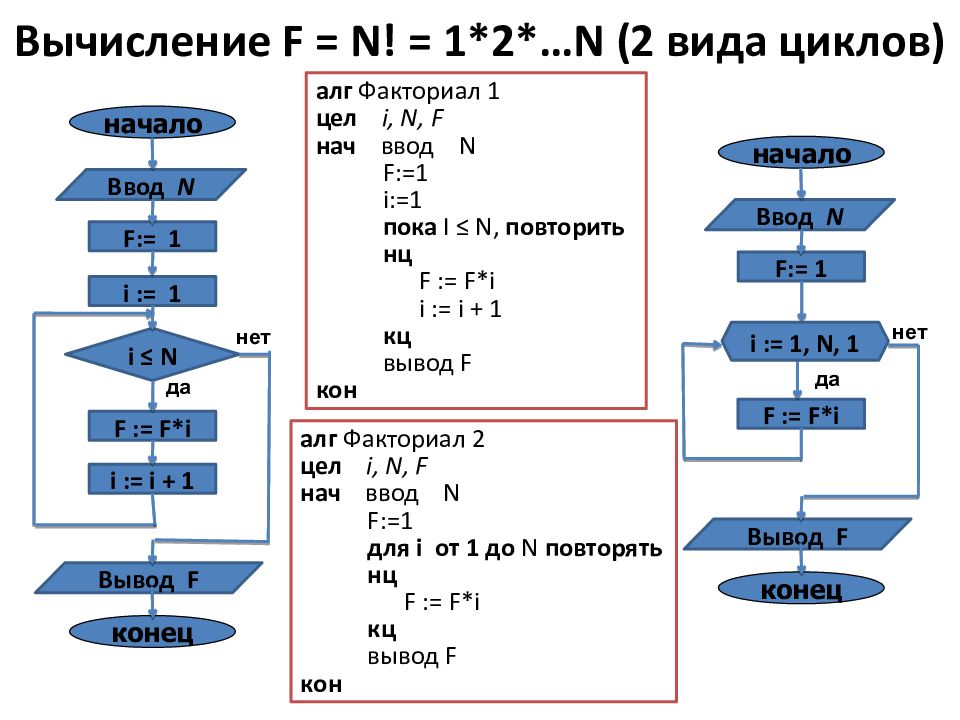
Вычисление F = N! = 1*2*…N (2 вида циклов) конец Ввод N Вывод F i ≤ N нет да начало i := 1 i := i + 1 F := F* i F:= 1 алг Факториал 1 цел i, N, F нач ввод N F:=1 i :=1 пока I ≤ N, повторить нц F := F* i i := i + 1 кц вывод F кон конец Ввод N Вывод F нет да начало F := F* i F:= 1 i := 1, N, 1 алг Факториал 2 цел i, N, F нач ввод N F:=1 для i от 1 до N повторять нц F := F* i кц вывод F кон
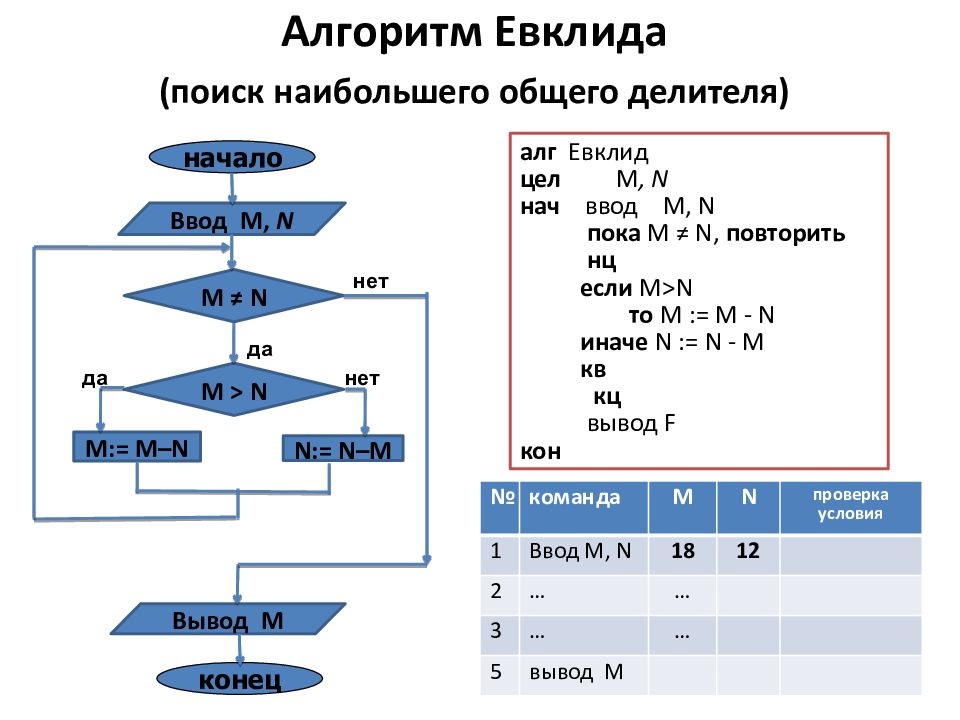
Алгоритм Евклида (поиск наибольшего общего делителя) алг Евклид цел M, N нач ввод M, N пока M ≠ N, повторить нц если M>N то M := M - N иначе N := N - M кв кц вывод F кон M := M–N М > N N:= N–M нет да конец Ввод M, N Вывод M M ≠ N нет да начало № команда M N проверка условия 1 Ввод M, N 18 12 2 … … 3 … … 5 вывод M
Виды задач, решаемых с помощью циклов Задача 1: в кошельке есть S монет, один пирожок стоит Р монет, сколько пирожков можно купить и съесть? Задача 2: начав тренировку, спортсмен в первый день пробежал Х км. В каждый следующий день он увеличивал дневную норму на 10% от предыдущего дня. Через сколько дней его суммарный пробег составит Y км? В какой день он пробежит Z км? Успеет ли он пробежать S км за К дней? Задача 3: В первый день мальчик прочитал Х страниц, а в каждый последующий – на 2 больше. Сколько дней ему потребуется, чтобы прочитать всю книгу из Z страниц ?. Задача 4: Последовательно вводятся N целых чисел. Найти количество ( сумму) отрицательных среди них. Задача 5: Последовательно вводятся N целых чисел. Найти максимальное (минимальное) из них (только положительных, только четных, …) значений.
Домашняя работа на циклические алгоритмы Построить блок-схемы циклических алгоритмов Задача 1: Последовательно вводятся N целых чисел. Определить, каких среди них чисел больше : положительных или отрицательных. Задача 2 : Гусеница ползет от земли вверх по столбу, высота которого Х метров. За день она поднимается на Y метров, а за ночь опускается на Z метров. Через сколько дней она доползет до верхушки ? (Подсказка: ввести переменную H – высота гусеницы над землей к концу текущего дня. Если H ≥ X, то все, доползла).
