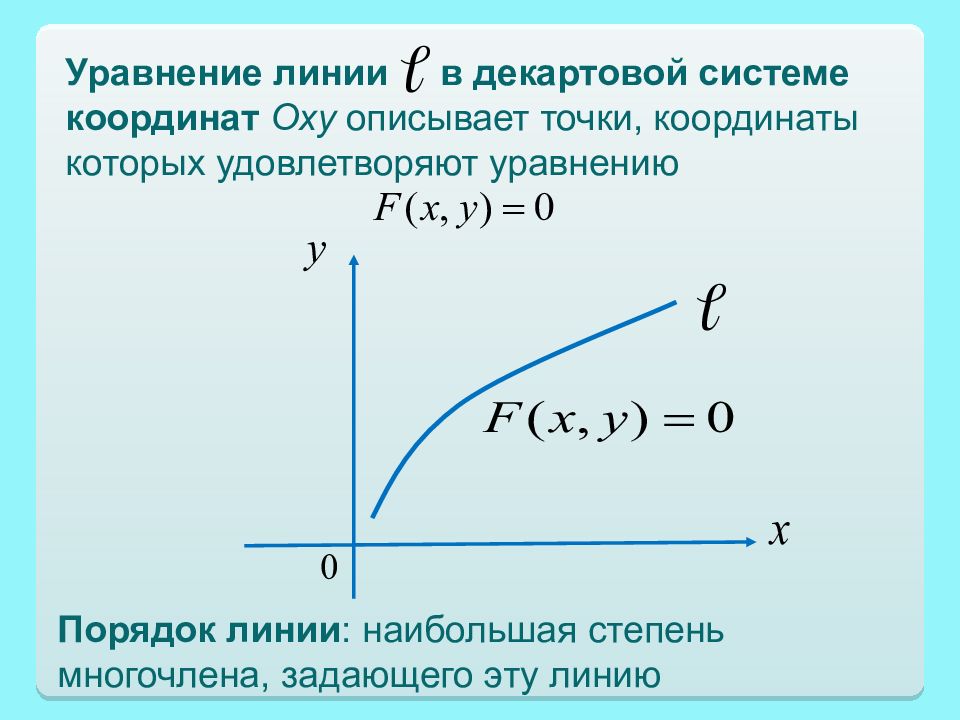
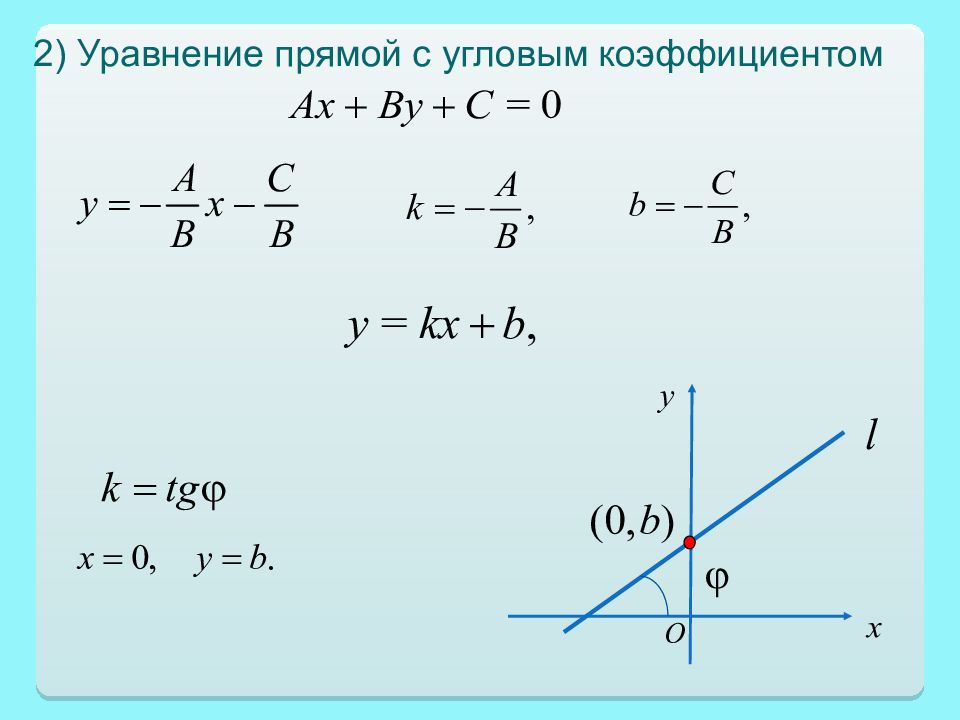
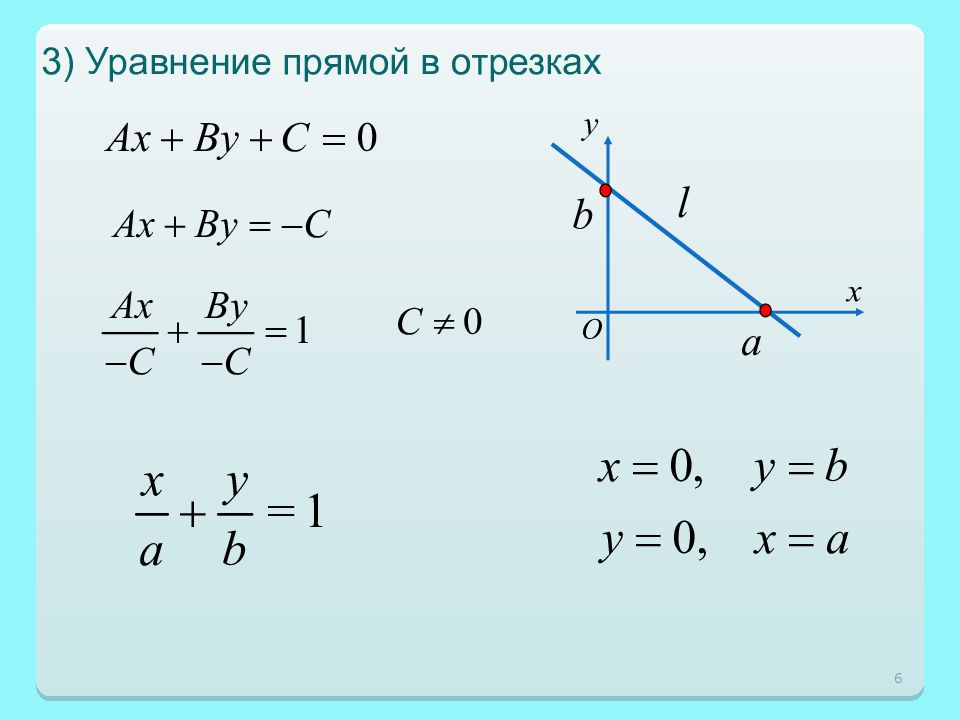
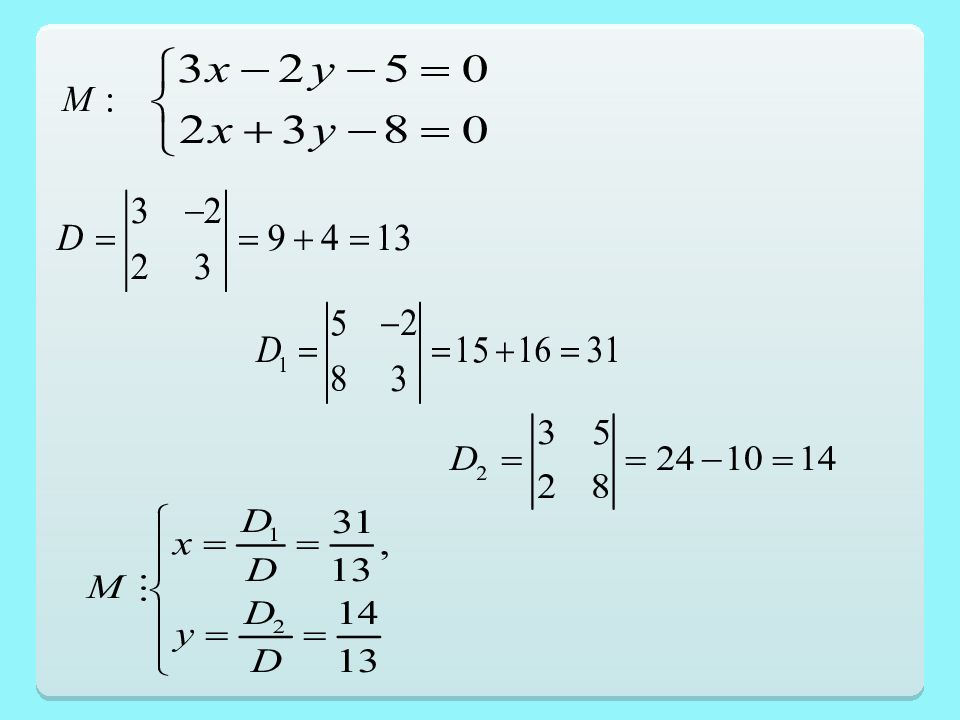Порядок линии : наибольшая степень многочлена, задающего эту линию
Слайд 3
-множество точек, удаленных на расстояние R от точки -биссектриса первого и третьего координатных углов 3 Примеры. - уравнение оси Ох -точка с координатами (3,2)
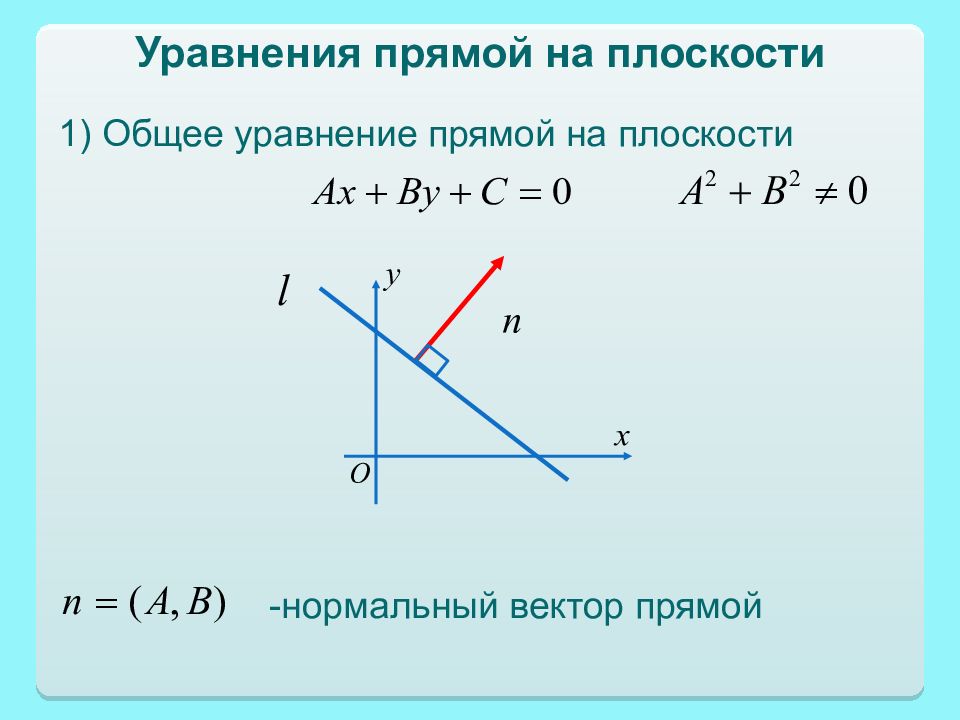
Слайд 4: Уравнения п рямой на плоскости
1) Общее уравнение прямой на плоскости -нормальный вектор прямой
Слайд 7
4) Уравнение прямой, проходящей через данную точку и перпендикулярно данному вектору
Слайд 8
5 ) Параметрические и канонические уравнения прямой, проходящей через точку параллельно вектору
Слайд 10
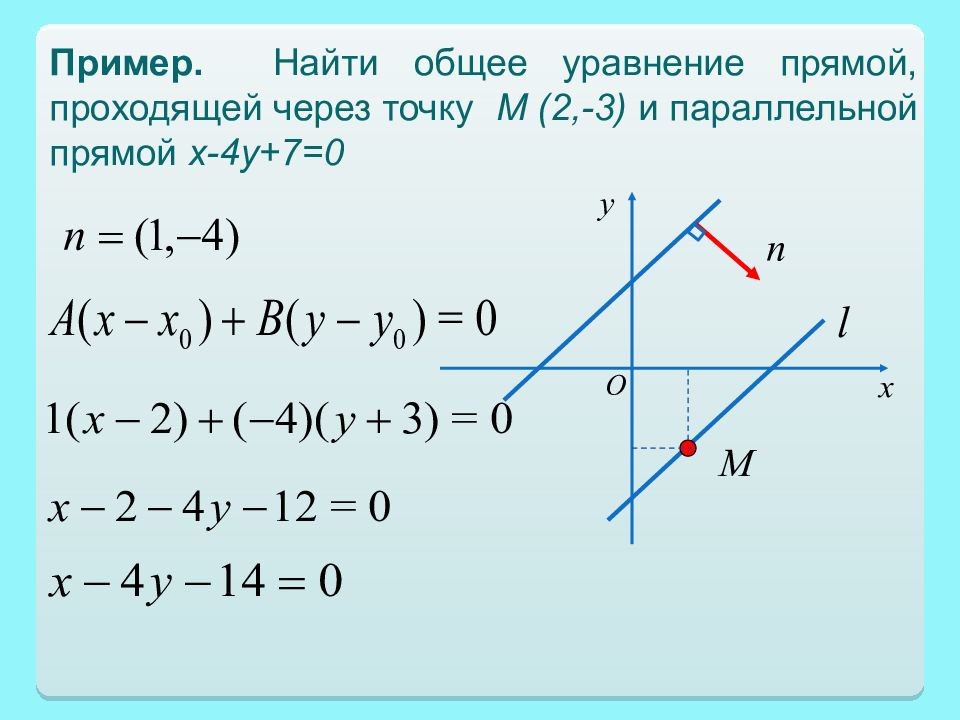
Пример. Найти общее уравнение прямой, проходящей через точку М (2,-3) и параллельной прямой x -4 y +7=0
Слайд 11
Пример. Найти общее уравнение прямой, проходящей через точку М (-1,3) и перпендикулярной прямой 3 x -4 y +1=0
Слайд 12
Пример. Составить уравнение прямой, проходящую через точку М(2,5) и отсекающую на оси ОУ отрезок равный 7
Слайд 13
Пример. Определить расстояние от точки М(2,-1) до прямой, отсекающей на оси Ох отрезок, равный 4, а на Оу – равный 3.
Слайд 15
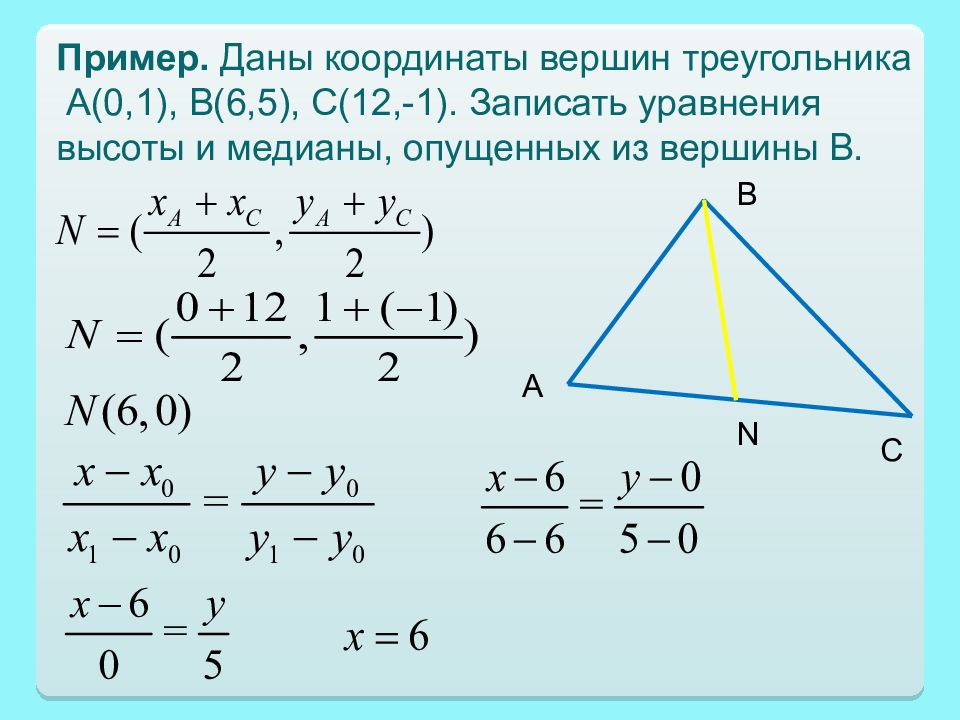
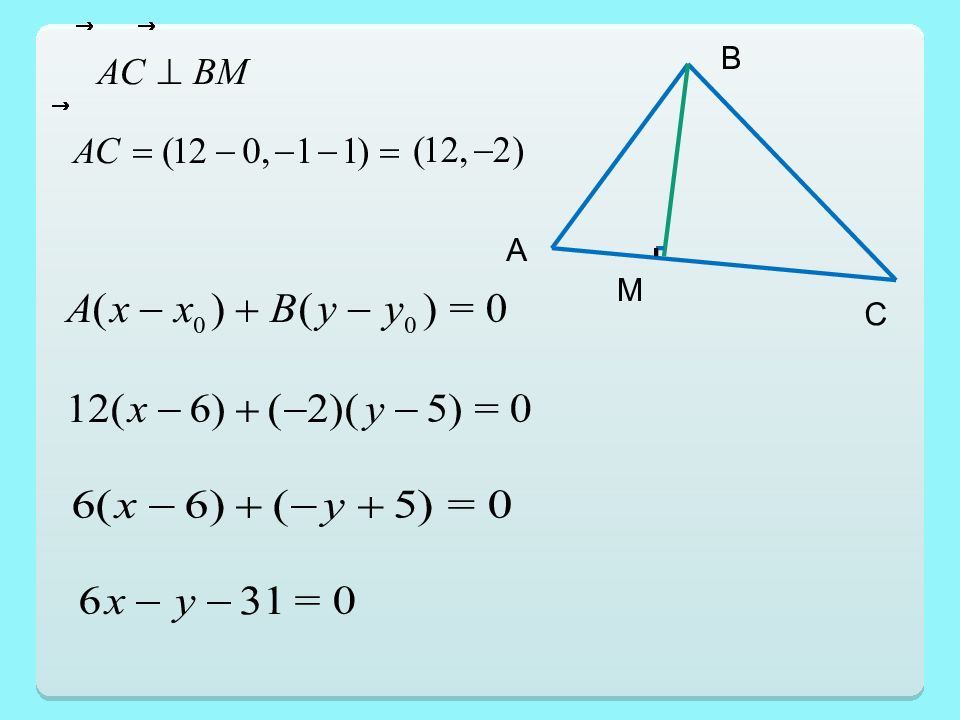
Пример. Даны координаты вершин треугольника А(0,1), В(6,5), С(12,-1). Записать уравнения высоты и медианы, опущенных из вершины В. В А С N
Слайд 17
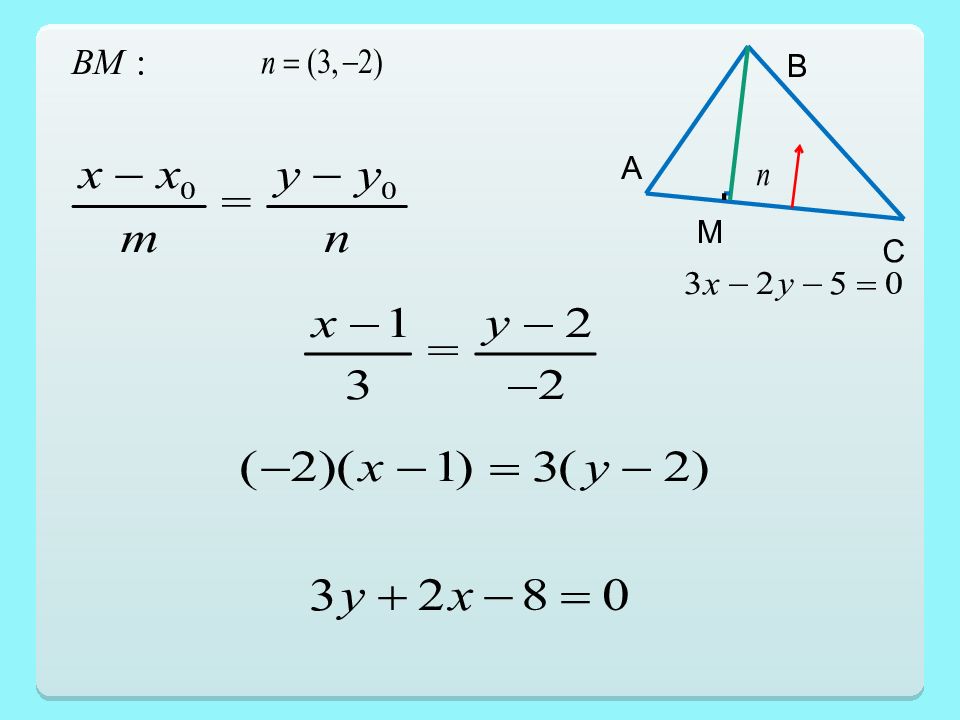
Пример. Даны уравнения сторон треугольника АВС. AB: AC: BC: Написать уравнение высоты, опущенной из вершины В и найти проекцию этой вершины на основание АС. В А С М
Слайд 20
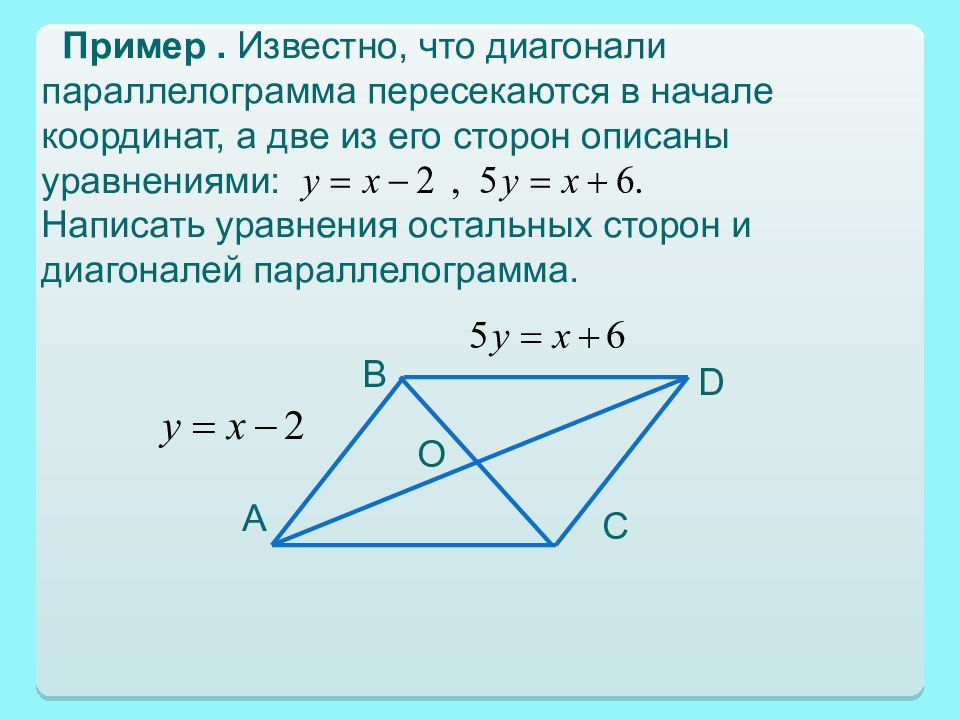
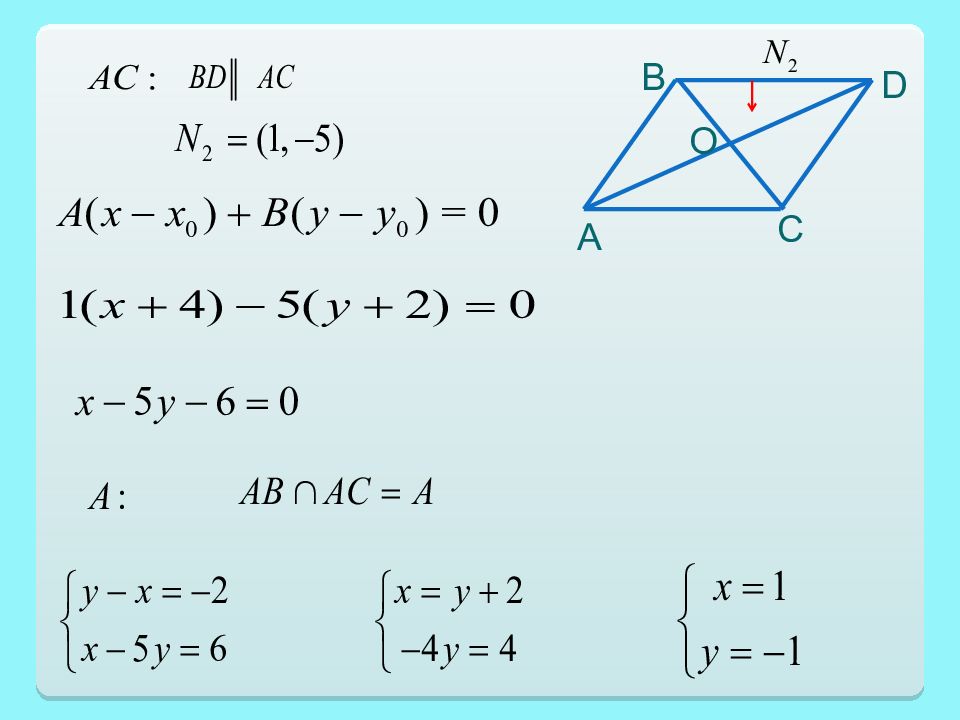
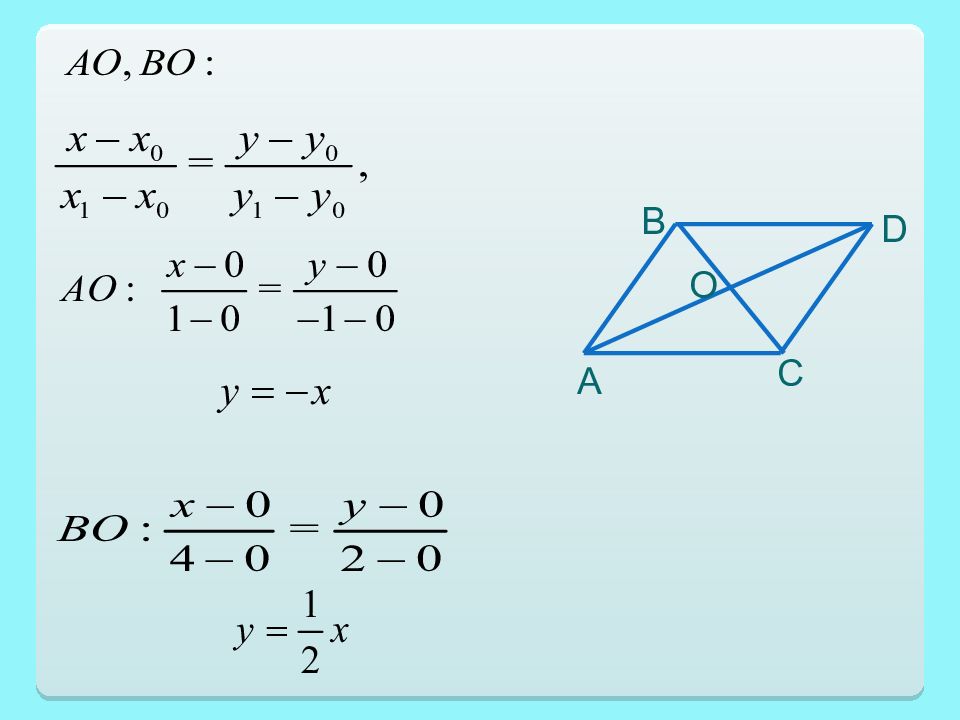
Пример. Известно, что диагонали параллелограмма пересекаются в начале координат, а две из его сторон описаны уравнениями : Написать уравнения остальных сторон и диагоналей параллелограмма. О В А С D
Слайд 21
Точка С симметрична точке В относительно начала координат О, поэтому С(-4, -2). О В С D А
Слайд 24
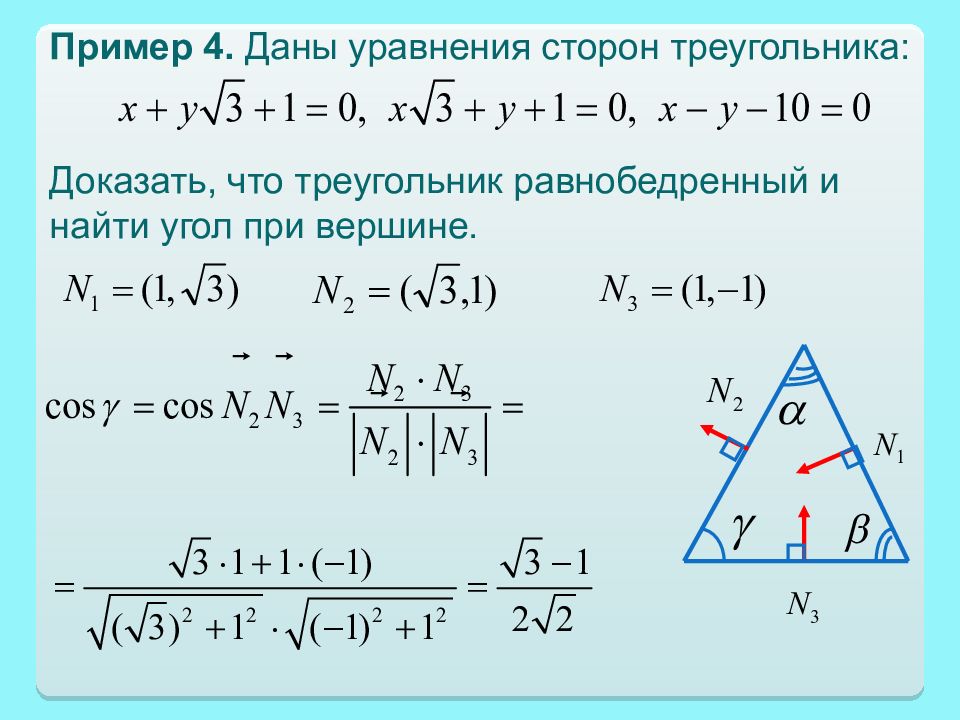
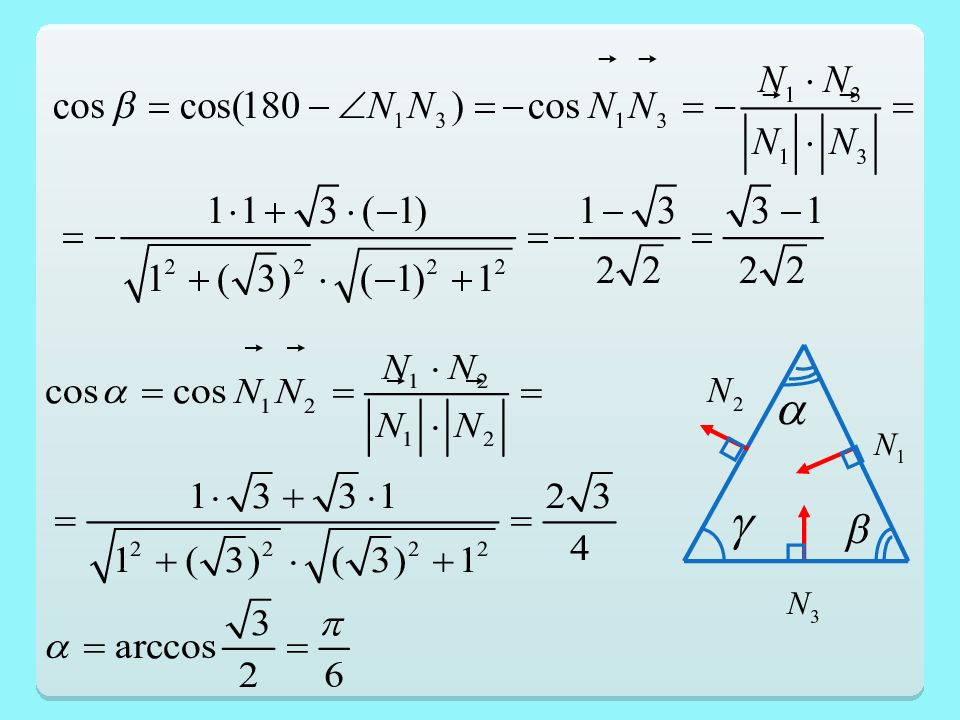
Пример 4. Даны уравнения сторон треугольника : Доказать, что треугольник равнобедренный и найти угол при вершине.