Первый слайд презентации: АНАЛИЗ ДАННЫХ
Лекция 1 к.т.н. Кирпичёва Елена Юрьевна kirphel@mail.ru
Слайд 2: ВВЕДЕНИЕ В «АНАЛИЗ ДАННЫХ»
Данные – это воспринимаемые человеком факты, события, сообщения, измеряемые характеристики, регистрируемые сигналы.
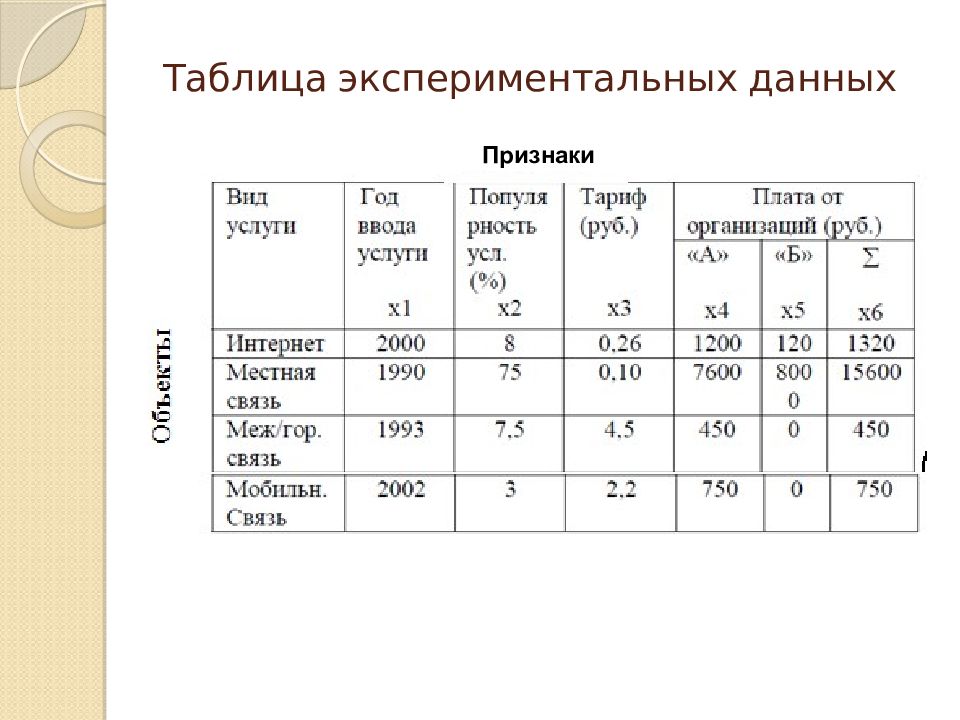
Слайд 3: Шкалы измерений
Измерение - присвоение символов образцам в соответствии с некоторым правилом. Эти символы могут быть буквенными или числовыми. Числовые символы также могут представлять категории или быть числовыми. 6 типов шкал измерений : Шкала наименований - используется только для классификации. Каждому классу данных присваивается свое обозначение так, чтобы обозначения различных классов не совпадали ( номера телефонов, автомашин, паспортов, студенческих билетов, ИНН-индивидуальный номер налогоплательщика, пол людей, раса, национальность, цвет глаз, волос. Порядковая шкала - позволяет не только разбивать данные на классы, но и упорядочить сами классы. Каждому классу присваивается различные обозначения так, чтобы порядок обозначений соответствовал порядку классов (номера домов, экспертные оценки, оценки успеваемости в средней школе - 2, 3, 4, 5 ; оценки успеваемости в высшей школе - неудовлетворительно, удовлетворительно, хорошо, отлично). В порядковой шкале допустимыми являются все строго возрастающие преобразования. Все шкалы измерения делят на две группы - шкалы качественных признаков и шкалы количественных признаков.
Слайд 4: Шкалы измерений
Интервальная шкала- позволяет не только классифицировать и упорядочивать данные, но и количественно оценивать различие между классами. Для проведения таких сравнений необходимо ввести единицу измерения и произвольное начало отсчета (нуль- пункт). (Температурная шкала) Шкала отношений. наиболее распространенная из количественных шкал в науке и практике. Эта шкала отличается от интервальной шкалы лишь тем, что в ней задано абсолютное начало отсчета. Т.е. в данной шкале можно определить, во сколько раз одно измерение превосходит другое. Например: рост человека в дюймах принадлежит шкале отношений, в которой в которой 0 дюймов есть фиксированное начало отсчета, а 1 дюйм – единица измерения. Шкала разностей. В шкале разностей есть естественная единица измерения, но нет естественного начала отсчета. Время измеряется по шкале разностей, если год (или сутки - от полудня до полудня) принимаем естественной единицей измерения, и по шкале интервалов в общем случае. На современном уровне знаний естественного начала отсчета указать нельзя. Дату сотворения мира различные авторы рассчитывают по-разному, равно как и момент рождества Христова. Абсолютная шкала. Только для абсолютной шкалы результаты измерений - числа в обычном смысле слова. Примером является число людей в комнате. Для абсолютной шкалы допустимым является только тождественное преобразование.
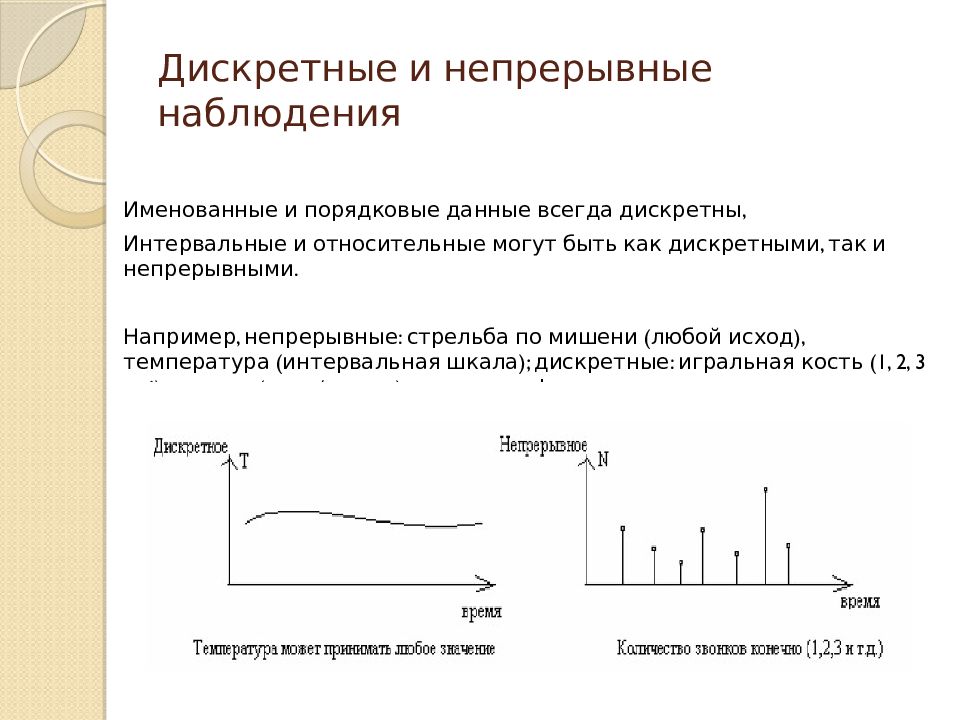
Слайд 5: Дискретные и непрерывные наблюдения
Именованные и порядковые данные всегда дискретны, Интервальные и относительные могут быть как дискретными, так и непрерывными. Например, непрерывные: стрельба по мишени (любой исход), температура (интервальная шкала); дискретные: игральная кость (1, 2, 3 …6), монета (орел/решка), число телефонных вызовов за один час (шкала отношений)
Слайд 11
Вероятность Вероятность - математическая, числовая характеристика степени возможности появления какого-либо события в тех или иных определенных, могущих повторяться неограниченное число раз условиях. Способы вычисления вероятности : использование теории : наблюдения :
Слайд 13
Случайная величина х может быть дискретной или непрерывной. Как непрерывная, так и дискретная случайная величина имеют плотность распределения вероятностей, которая часто называется плотностью вероятности и обозначается как f(x) (для непрерывной случайной величины) или р(х) (для дискретной случайной величины). Распределения вероятностей
Слайд 14
Самой важной вероятностной характеристикой случайной величины является функция распределения, определяемая следующим образом: Распределения вероятностей
Слайд 15
Дискретная случайная величина принимает значения с различными вероятностями. Соответствие между значениями и их вероятностями называют законом распределения вероятностей дискретной случайной величины. Дискретная случайная величина Значения X x 1 x 2 … x n Вероятности p 1 p 2 … p n p1 + p2 +... + pn = 1. Значения 1 2 3 4 5 6 Вероятности 1/6 1/6 1/6 1/6 1/6 1/6
Слайд 16
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И МОМЕНТЫ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Пусть х — случайная величина, h(x) — некоторая функция от х. Математическим ожиданием случайной функции h(x), которое обозначается как M{h(x)}, называется средняя величина, взвешенная по отношению к плотности вероятности случайной величины х. При заданной плотности вероятности р(х) или f(x) (для дискретной и непрерывной случайных величин соответственно) величина M{h(x) } вычисляется следующим образом:
Слайд 17
В течение первой недели каждого месяца человек рассылает письма. С этой целью он обычно покупает 20 почтовых марок. Число используемых марок является случайной величиной, принимающей значения от 10 до 24 с равными вероятностями. Чему равно среднее число оставшихся марок? Пусть х — количество используемых марок, тогда плотность вероятности х такова: Количество оставшихся марок определяется соотношением Вероятность того, что вообще не останется марок, равна
Слайд 19
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Бросание игральной кости
Слайд 20
Структурные средние параметры дискретной величины: мода и медиана. Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. Медиана – это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части. Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле: Ме = (n(число признаков в совокупности) + 1)/2, в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).
Слайд 21
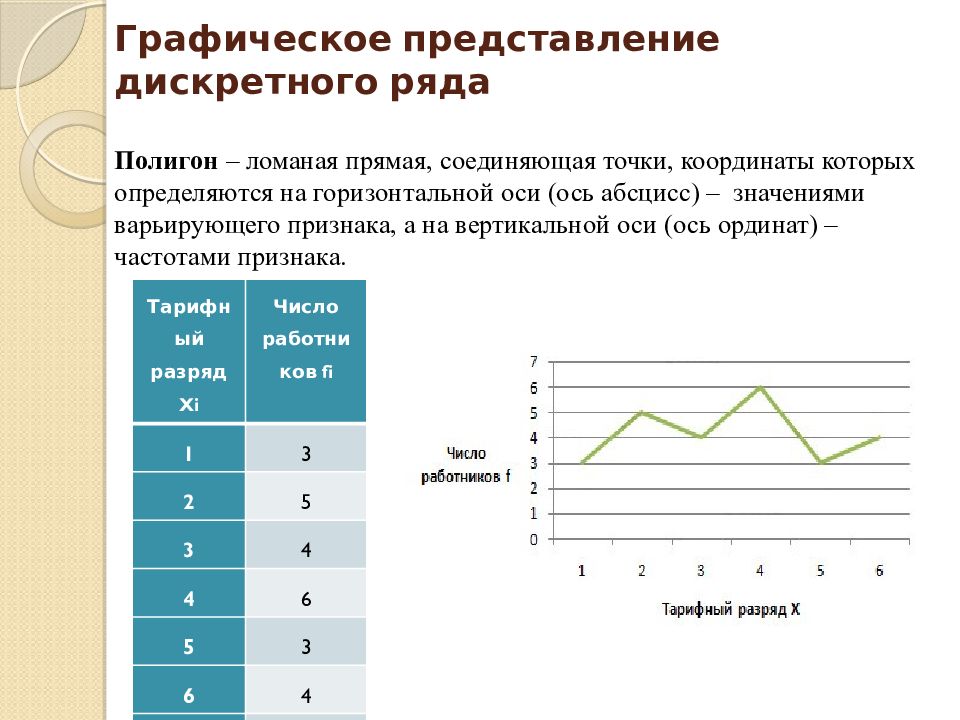
Графическое представление дискретного ряда Полигон – ломаная прямая, соединяющая точки, координаты которых определяются на горизонтальной оси (ось абсцисс) – значениями варьирующего признака, а на вертикальной оси (ось ординат) – частотами признака. Тарифный разряд Xi Число работников fi 1 3 2 5 3 4 4 6 5 3 6 4 Итого: 25
Слайд 22
Графическое представление дискретного ряда Гистограмма – столбчатая фигура, основанием каждого столбца которой по оси абсцисс выступают значения границ интервалов случайной величины, а высота прямоугольников пропорциональна частотам. Размер заработной платы руб. в месяц Численность работников чел. до 5000 4 5000 — 7000 12 7000 — 10000 8 10000 — 15000 6 Итого: 30
Слайд 26
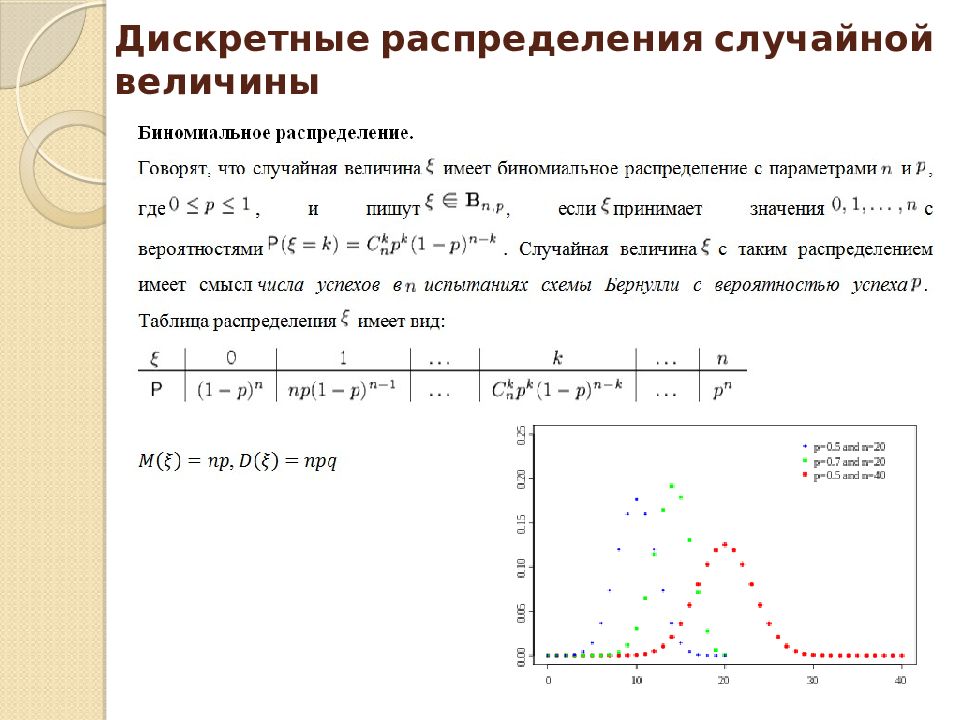
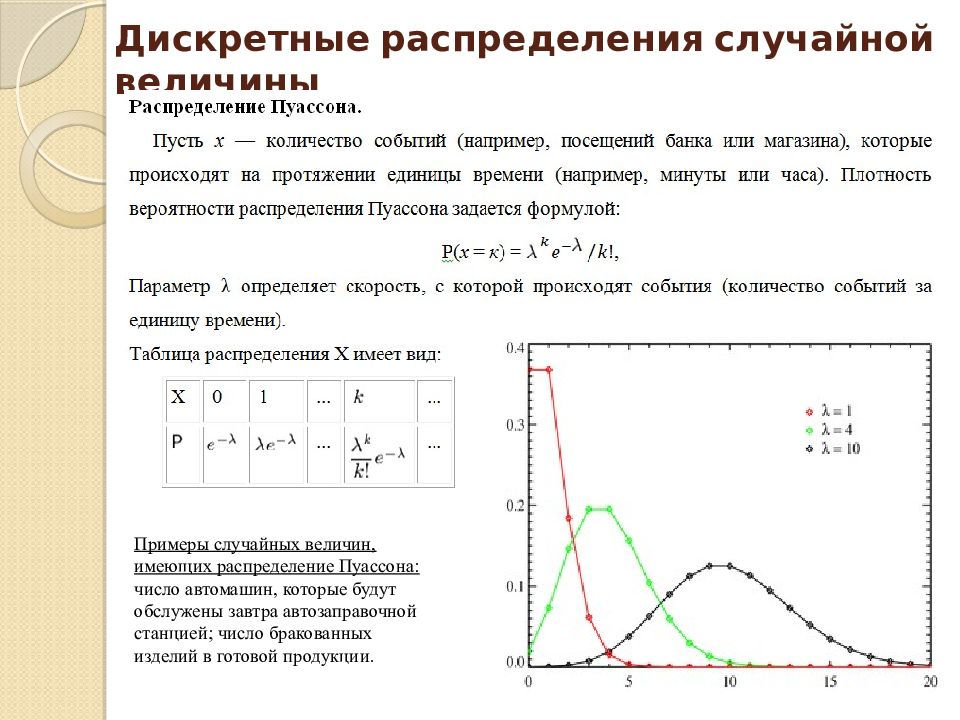
Дискретные распределения случайной величины Примеры случайных величин, имеющих распределение Пуассона: число автомашин, которые будут обслужены завтра автозаправочной станцией; число бракованных изделий в готовой продукции.
Слайд 27
Дискретные распределения случайной величины Пример на распределение Пуассона
Слайд 30
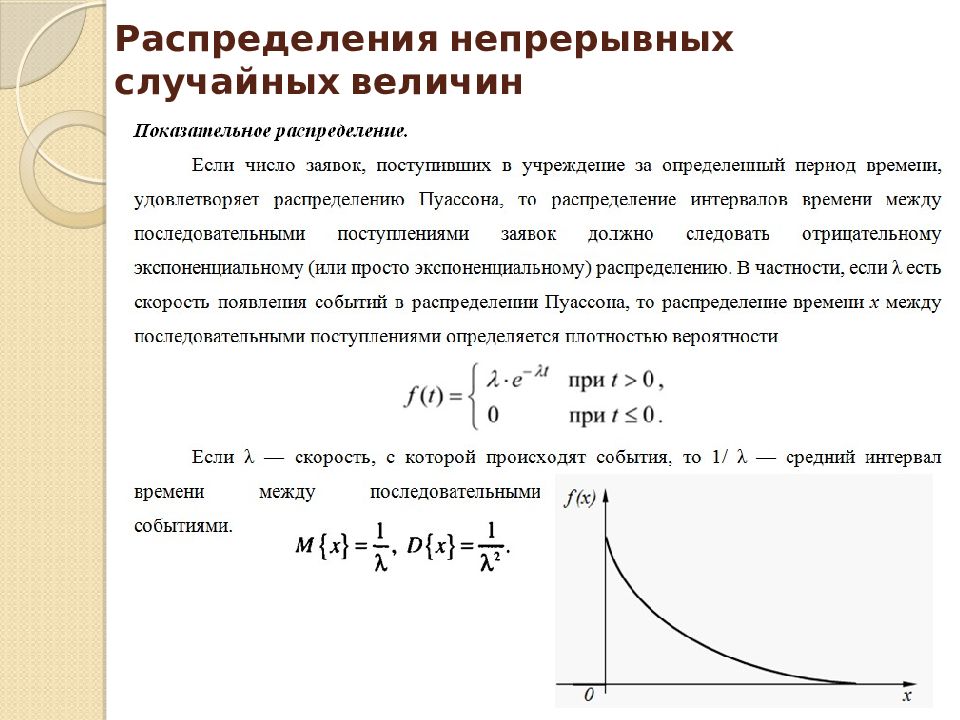
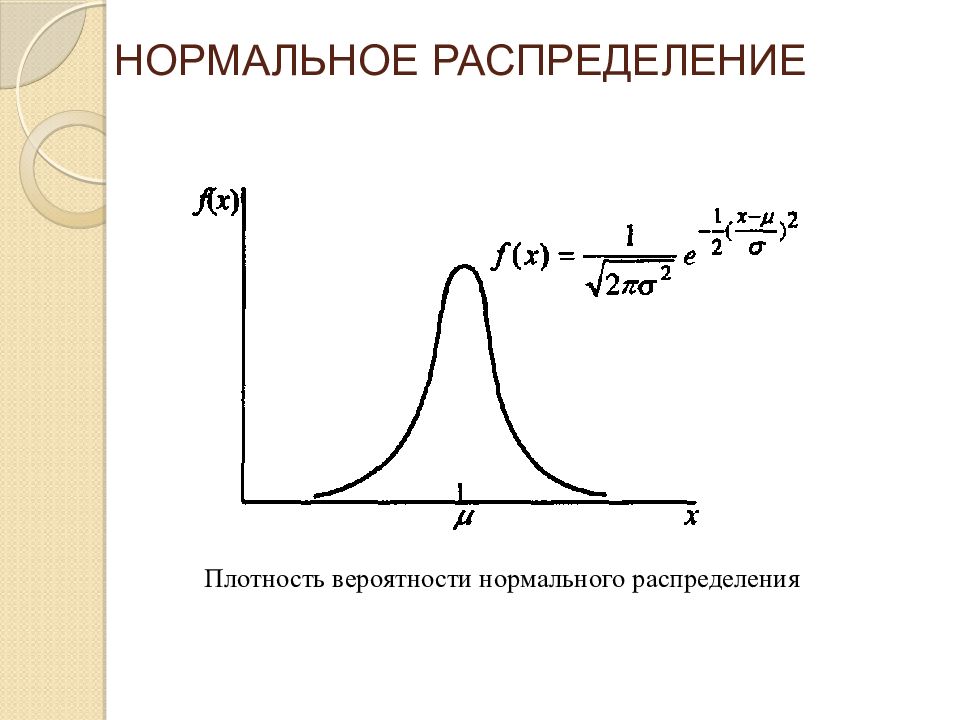
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Нормальное распределение описывает многие случайные явления, которые происходят в каждодневной жизни, включая анализ счетов, распределение веса и роста людей и многое другое. Плотность вероятности нормального распределения : Нормальное распределение с математическим ожиданием μ и стандартным отклонением σ обозначается как N( μ, σ ).
Слайд 31
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Плотность вероятности нормального распределения