Лекция 1 Введение; Основы теории вероятностей
Содержание лекции №1 Введение Основы теории вероятностей Случайные события Случайные величины Нормальный и экспоненциальный законы распределения
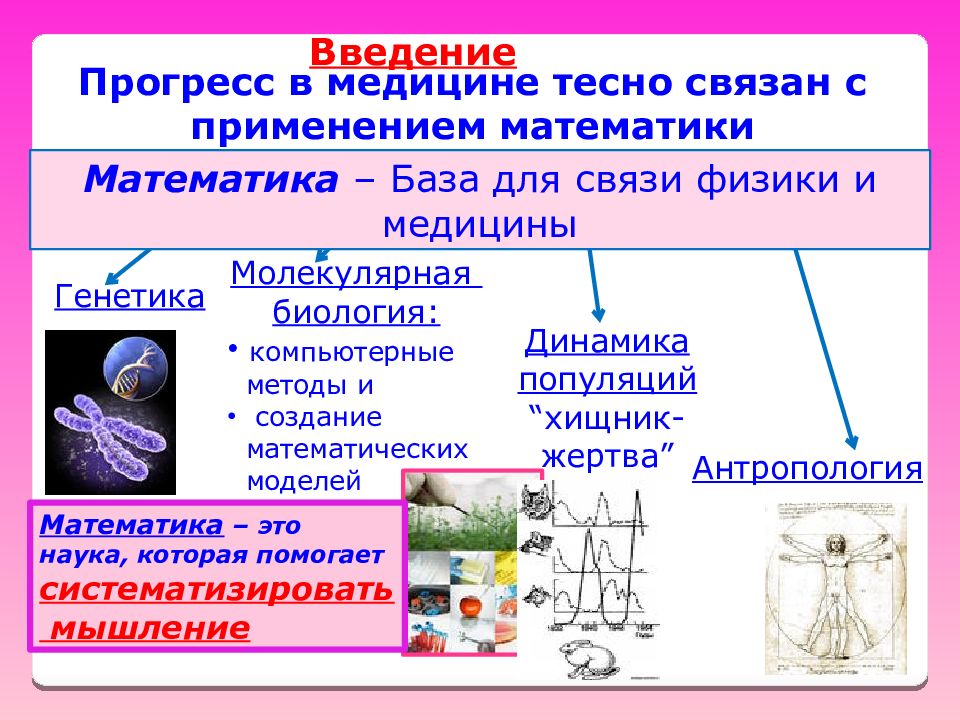
Прогресс в медицине тесно связан с применением математики Генетика Молекулярная биология: компьютерные методы и создание математических моделей Антропология Динамика популяций “ хищник-жертва ” Математика – это наука, которая помогает систематизировать мышление Математика – База для связи физики и медицины Введение
Леонардо да Винчи 1452-1519 гг. “ Никакое человеческое исследование не может почитаться истинной наукой, если оно не изложено математическими ! способами выражения ” “ Книга о живописи ”
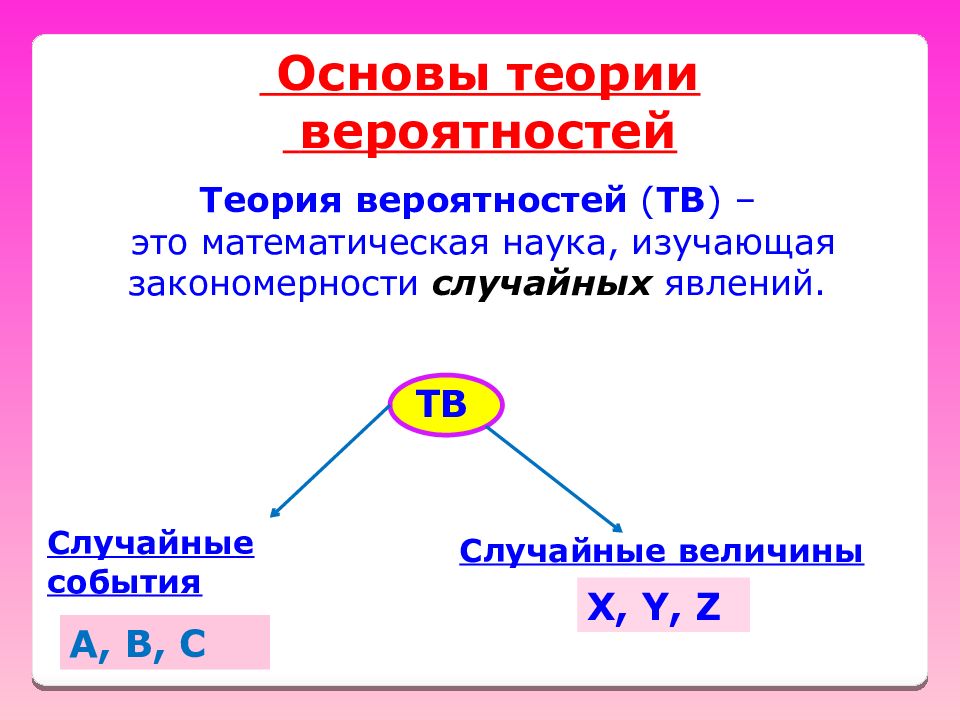
Основы теории вероятностей Теория вероятностей ( ТВ ) – это математическая наука, изучающая з акономерности случайных явлений. ТВ Случайные события A, B, C Случайные величины X, Y, Z
Случайное событие Событие – это факт, который в результате и спытания может произойти или не произойти. Это испытание Это событие
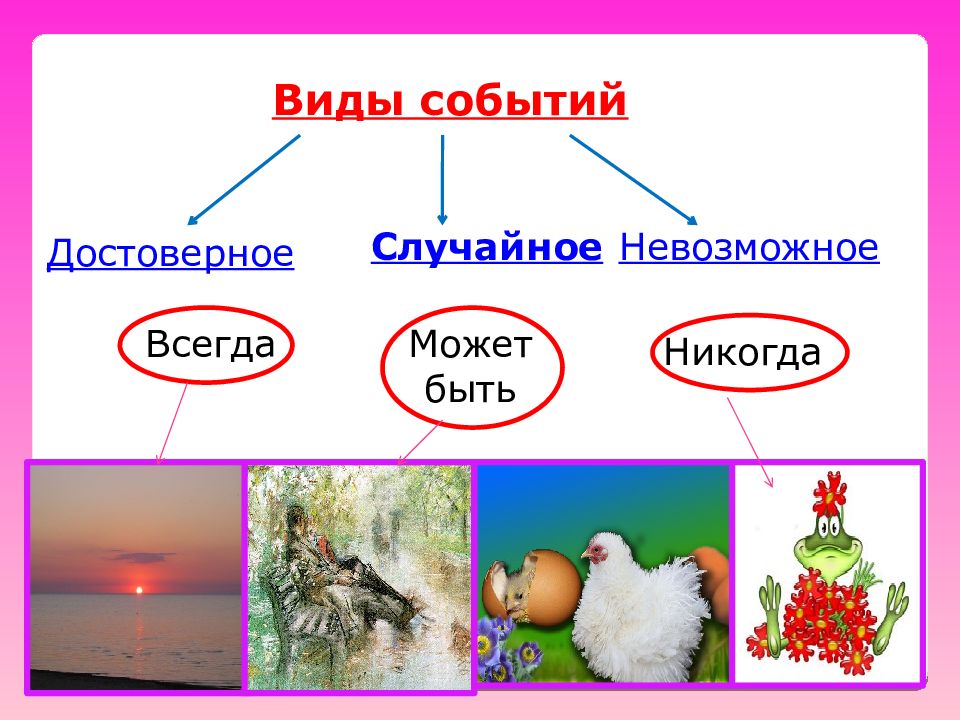
Виды событий Достоверное Случайное Н евозможное Всегда Может быть Никогда
Какие события относятся к случайным? А. Появление орла при подбрасывании монеты Б. Равномерное движение материальной точки В. Восход солнца Г. Рождение мальчика Ответ: А, Г.
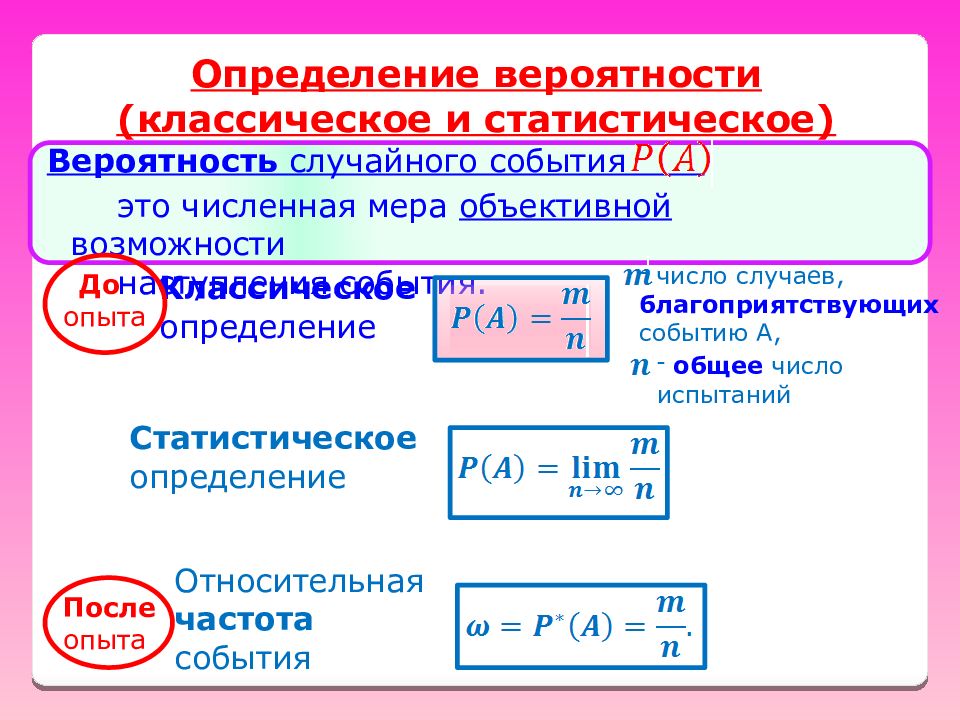
Вероятность случайного события это численная мера объективной возможности н аступления события. Классическое определение Статистическое определение До опыта Относительная частота события После опыта число случаев, благоприятствующих событию А, общее число испытаний Определение вероятности (классическое и статистическое)
Английский математик Карл Пирсон бросал монету 24000 раз. Герб выпал 12012 раз. Какова частота выпадения герба?
Свойства вероятности Р дост. (А)=1 Р невозм. (А)=0 0≤Р(А) ≤1
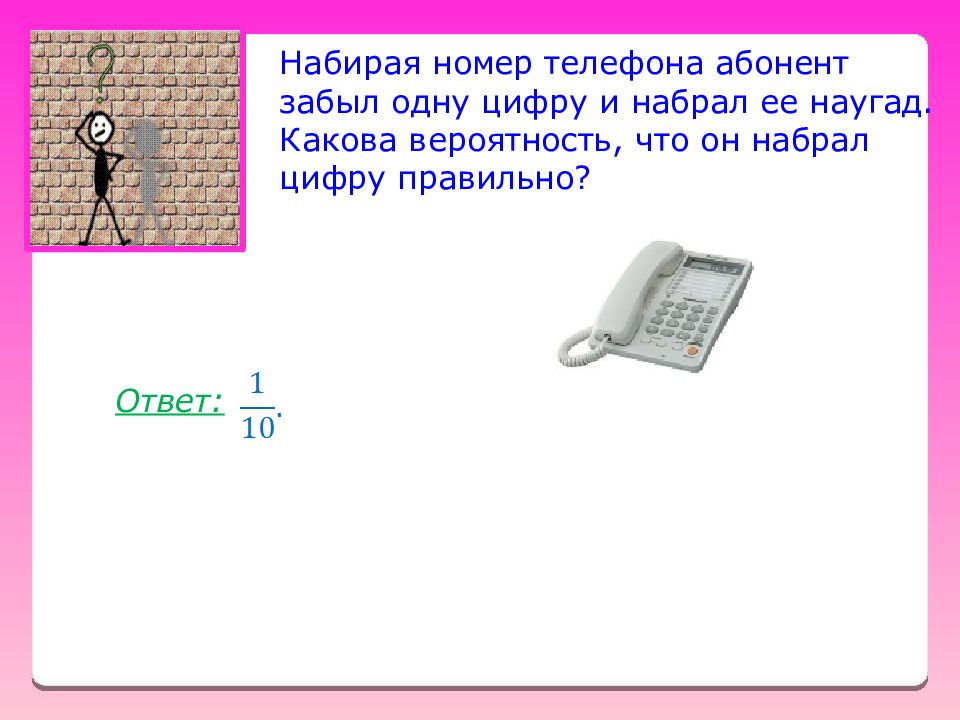
Набирая номер телефона абонент забыл одну цифру и набрал ее наугад. Какова вероятность, что он набрал цифру правильно? Ответ:
Понятие о несовместных и совместных событиях События А и В несовместны, если появление одного события исключает появления другого события. ПРИМЕРЫ События А и В совместны, если появление одного из них не исключает появления другого в одном и том же испытании. ПРИМЕРЫ
Понятие о независимых и зависимых событиях Два события называются независимыми, если вероятность одного из них не зависит от появления или непоявления другого ПРИМЕРЫ Два события называются зависимыми, если вероятность одного из них зависит от появления другого.
Условия нормировки Полная сумма вероятностей дискретных событий системы равна 1.
Условная вероятность 1 й 2 й Это вероятность осуществления события при условии, что событие уже произошло. Какова вероятность вытащить подряд 2 белых шара? А может ли быть ответ 4 / 9?
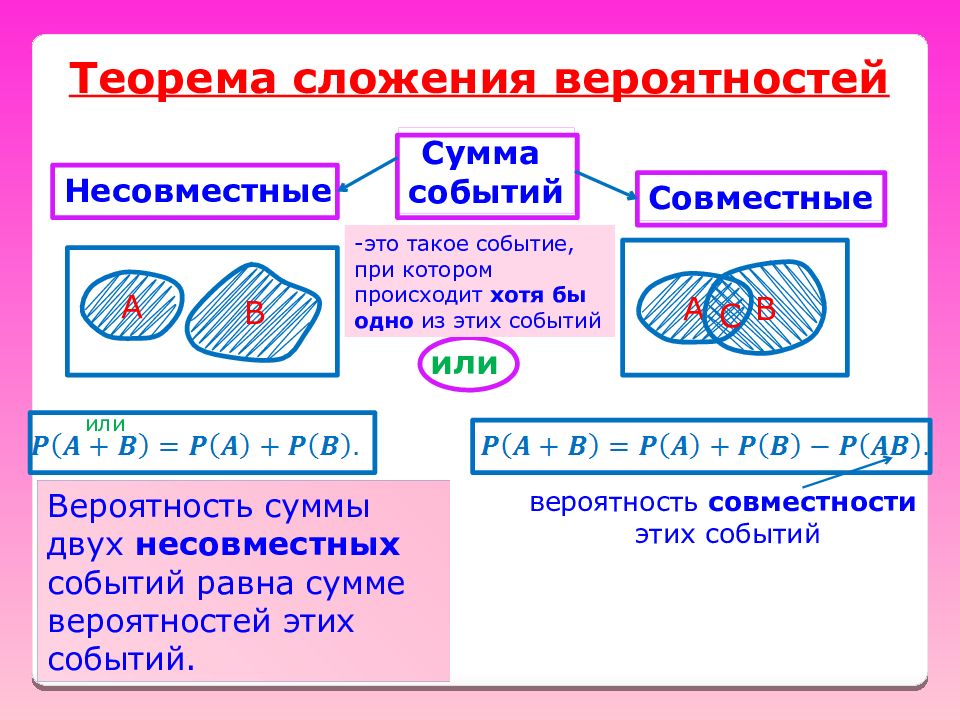
Теорема сложения вероятностей Сумма событий Несовместные Совместные или А B вероятность совместности этих событий А B C или -это такое событие, при котором происходит хотя бы одно из этих событий Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
В корзине 30 цветных рубашек: 10 красных, 5 синих, 15 белых. Какова вероятность вытащить цветную рубашку? Ответ: или
Два стрелка. Вероятность попадания в цель 1 го стрелка – 0,8, а 2 го – 0,7. Какова вероятность, что при одновременном выстреле цель будет поражена. Цель считается пораженной при попадании в нее хотя бы одной из 2 х пуль. Решение:
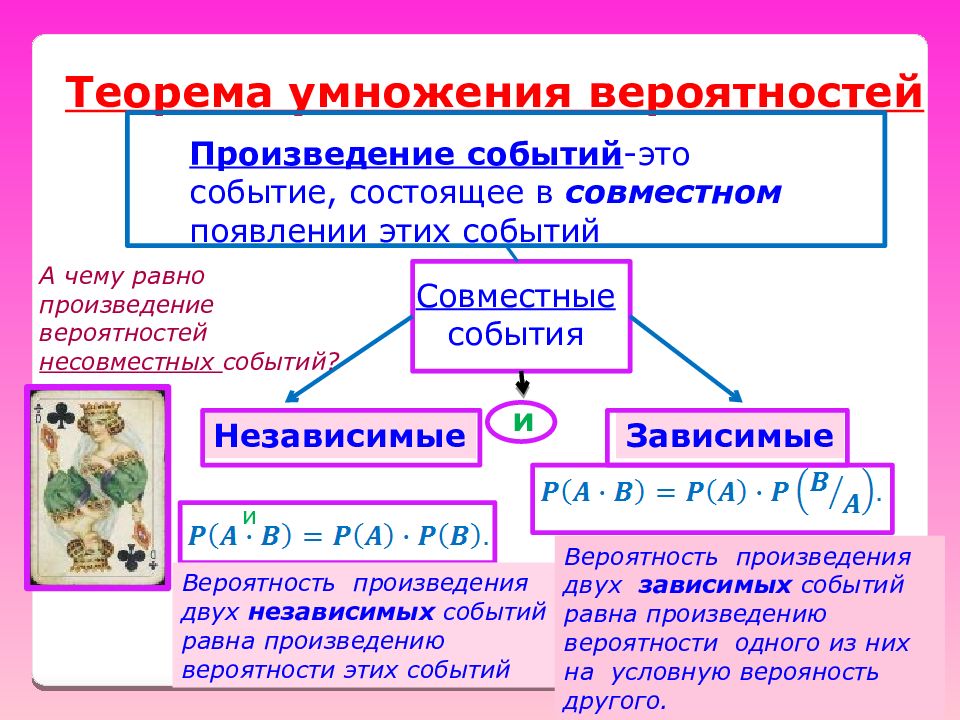
Теорема умножения вероятностей Произведение событий -это событие, состоящее в совместном появлении этих событий Совместные события и Независимые Зависимые и А чему равно произведение вероятностей несовместных событий? Вероятность произведения двух независимых событий равна произведению вероятности этих событий Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную верояность другого.
Брошены 2 монеты. Какова вероятность, что “ появился герб ” и появилась «решка»? Ответ: Брошены монеты и игральная кость. Найти вероятность совмещения событий “ появился герб ”, “ появилось 6 очков ”. Ответ :
Известно, что в 3 х случаях из 250 на свет появляются близнецы. Причем лишь в одном из 3 х – это истинные близнецы (монозиготные). Какова априорная вероятность того, что у определенной беременной женщины родятся близнецы мальчик и девочка, т.е. дизиготные ? Решение:
Понятие о доказательной медицине Доказательная медицина ( англ. Evidence-based medicine ) – это медицина, основанная на доказательствах. Термин предложен группой канадских ученых в 1990 г. Это подход к медицинской практике, при котором решения о применении профилактических, диагностических и лечебных мероприятий принимаются исходя из имеющихся доказательств их эффективности и безопасности. Такие доказательства подвергаются поиску, сравнению, обобщению и широкому распространению для использования в интересах больных.
Случайные величины Дискретные Непрерывные Счет Измерения Случайная величина - это величина, которая в результате испытания примет одно и только одно возможное значение заранее неизвестное
Что в этом тесте дискретного, а что непрерывного? Иванов – 170 см Петров – 182 см Сидоров – 167 см 170
Распределение дискретных и непрерывных случайных величин и их характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение Распределение = закон распределения – это совокупность значений случайной величины и вероятностей их появления.
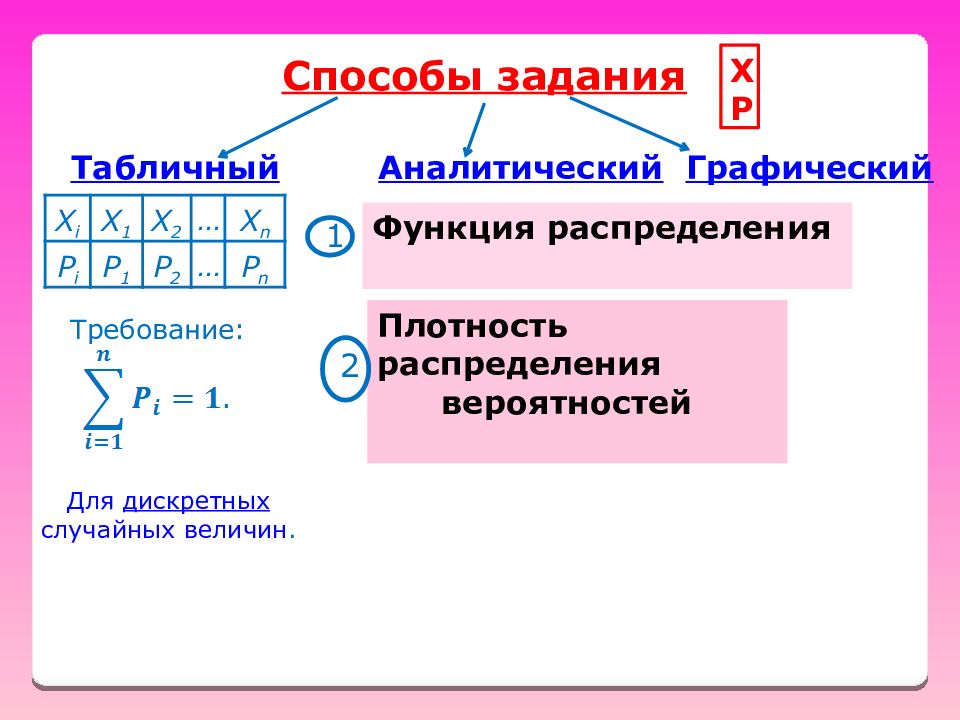
Способы задания X P Табличный Аналитический Графический Требование: Для дискретных случайных величин. X i X 1 X 2 … X n P i P 1 P 2 … P n Функция распределения Плотность распределения вероятностей 1 2
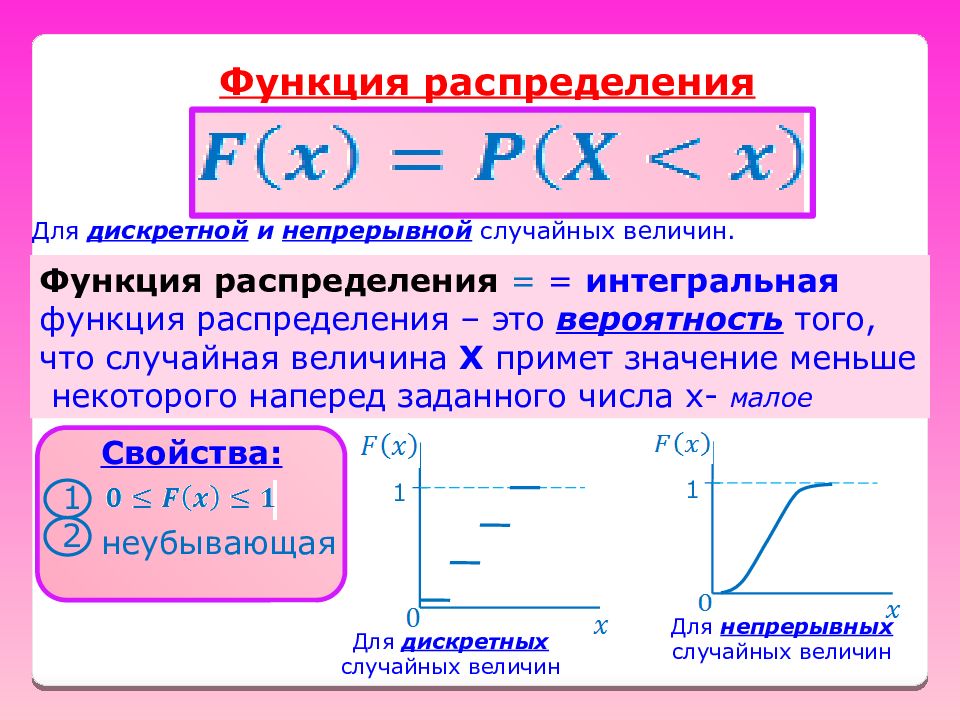
Функция распределения Функция распределения = = интегральная функция распределения – это вероятность того, что случайная величина Х примет значение меньше некоторого наперед заданного числа х - малое Свойства: 1 2 неубывающая 1 Для дискретных случайных величин 1 Для непрерывных случайных величин Для дискретной и непрерывной случайных величин.
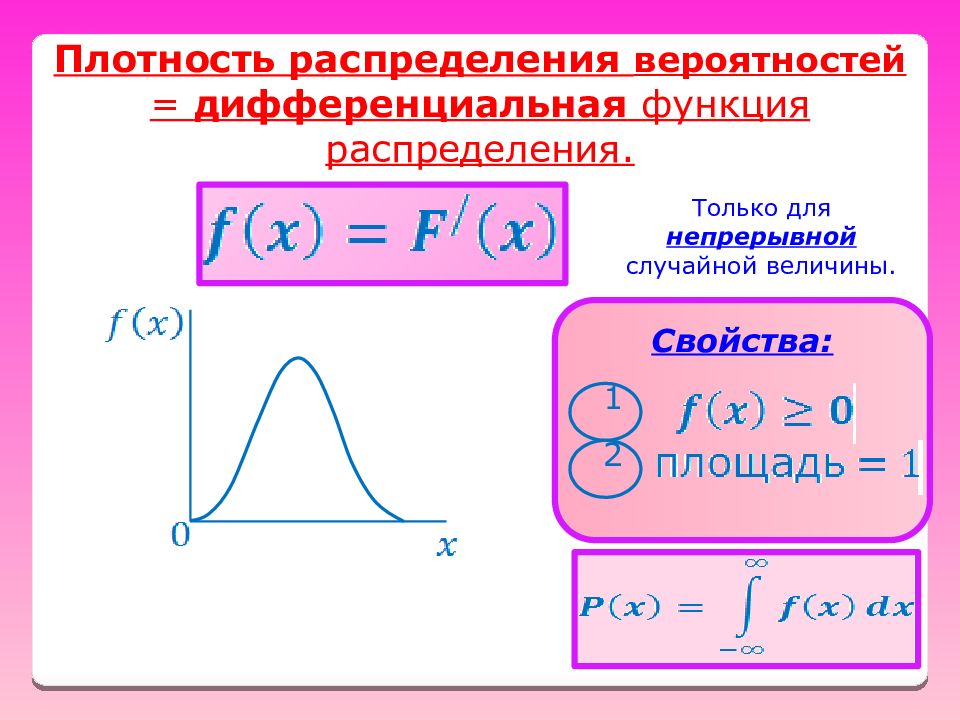
Плотность распределения вероятностей = дифференциальная функция распределения. Только для непрерывной случайной величины. Свойства: 1 2
Характеристики случайных величин 1 Математическое ожидание Для дискретных случайных величин Для непрерывных случайных величин Математическое ожидание – это сумма произведений случайных величин на вероятность их появления.
2 Дисперсия – рассеяние вокруг математического ожидания Для дискретных случайных величин Для непрерывных случайных величин Дисперсия – это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. отклонение
3 Среднее квадратичное отклонение Среднее квадратичное отклонение – это корень квадратный из дисперсии. Стандартное отклонение Стандарт
Пример. X 1 2 5 P 0,3 0,5 0,2 - постоянное число
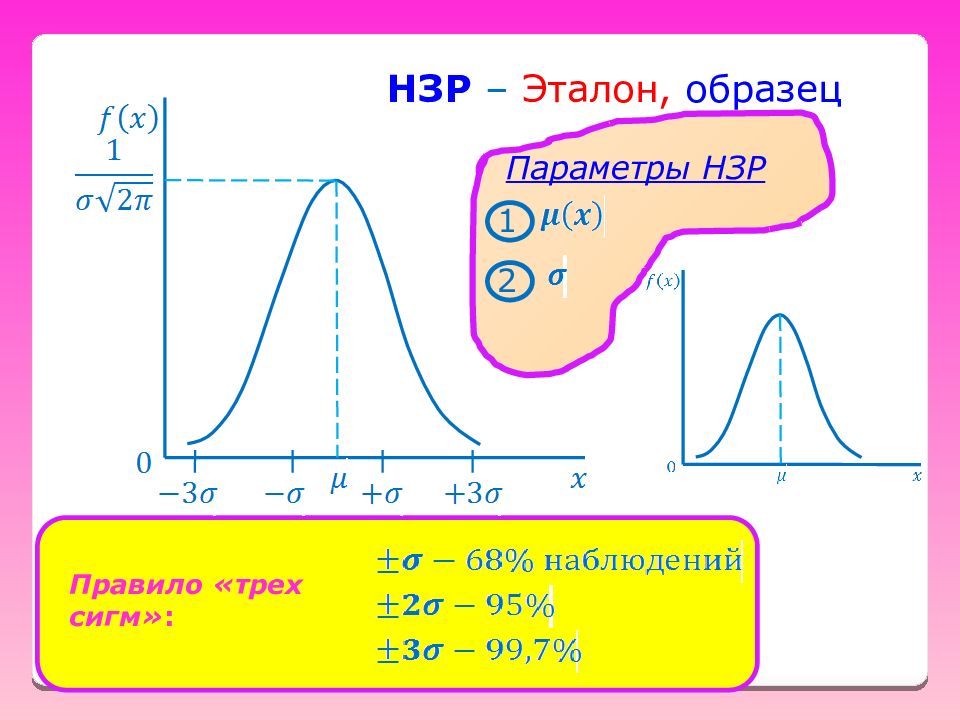
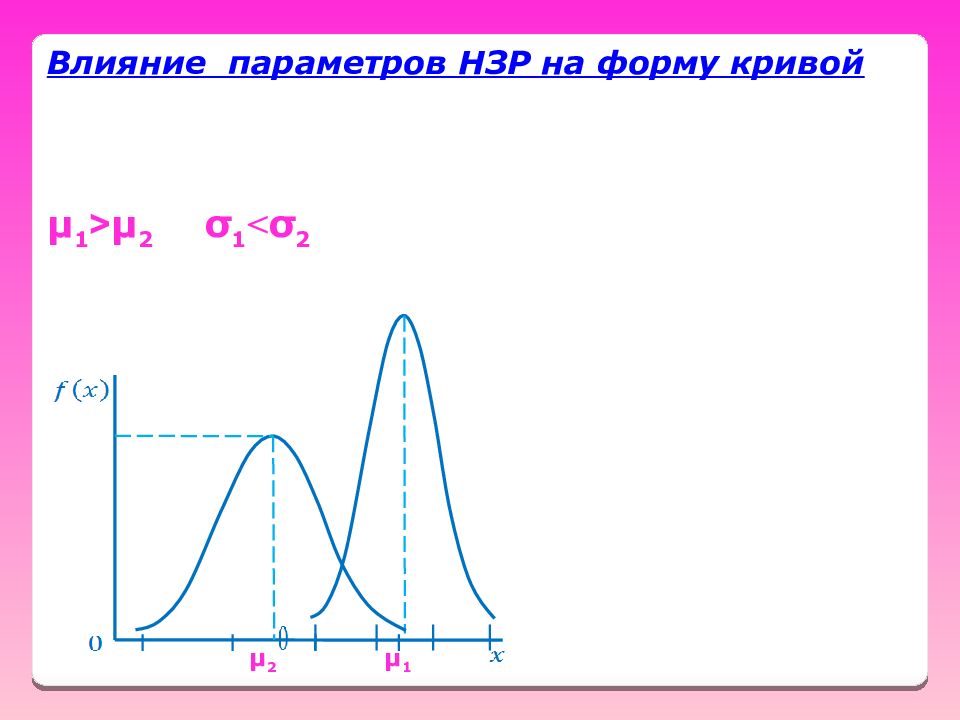
Нормальный закон распределения ( НЗР ) = закон Гаусса НЗР – это распределение вероятностей непрерывной! случайной величины, которое описывается дифференциальной функцией Карл Фридрих Гаусс 1777-1855 гг. Звездный час Гаусса в 8 лет ! или 1 2 . . 99 100 1,2,3,.,18,..,99,100
НЗР – Эталон, образец Параметры НЗР 2 1 Правило «трех сигм» :
μ 1 ˃ μ 2 σ 1 ˂ σ 2 μ 1 μ 2 Влияние параметров НЗР на форму кривой
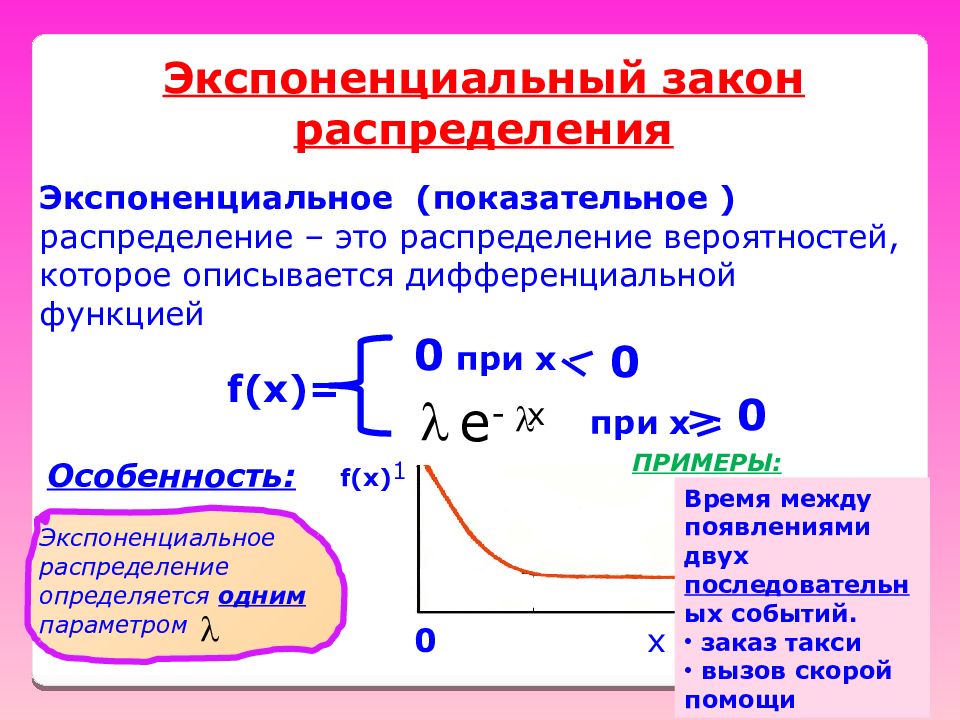
Экспоненциальный закон распределения Экспоненциальное (показательное ) распределение – это распределение вероятностей, которое описывается дифференциальной функцией f(x)= 0 при х 0 e - x при х 0 Экспоненциальное распределение определяется одним параметром Особенность: х f(x) 0 1 ПРИМЕРЫ: Время между появлениями двух последовательн ых событий. заказ такси вызов скорой помощи
