Слайд 2: Схема Бернулли
Рассмотрим последовательность n независимых однородных испытаний (экспериментов). Испытания считаем независимыми, если результат испытания не зависит от номера испытания и от того, что произошло до этого испытания. Однородными испытаниями считаем такие, которые проводятся в одинаковых условиях. Пусть в каждом испытании событие А может произойти с вероятностью р
Слайд 3: Формула Бернулли
Вероятность того, что при n испытаниях событие А наступит к -раз:
Слайд 4: Схема Бернулли
Пример. Вероятность того, что образец бетона при испытании выдержит нормативную нагрузку, равна 0,9. Найти вероятность того, что из 7 образцов 5 выдержат испытания. Решение. По формуле Бернулли
Слайд 5: Схема Бернулли
Асимптотические формулы. 1. Формула Пуассона. Пусть число испытаний n - велико ( n →∞ ) Вероятность р события А – мала ( р →0 ) Причем Тогда при любом фиксированном к Закон редких событий
Слайд 6: Схема Бернулли
Пример 1. Известно, что при транспортировке 2,5% декоративной плитки повреждается. Определить вероятность того, что в партии из 200 плиток оказалось поврежденными: а) ровно 4 плитки; б) не более 6 плиток. Решение. Вероятность того, что плитка окажется поврежденной, р=0.025 – мала, число испытаний n =200 – велик о, причем np=5 <10. По формуле Пуассона: а) б)
Слайд 7: Схема Бернулли
2. Локальная теорема Муавра-Лапласа. Пусть число испытаний n – велико ( n →∞ ) Вероятность р события А – не очень мала ( 0 << р << 1 ) ( р не близко к 0 и к 1 ) Тогда при любом фиксированном к
Слайд 8: Схема Бернулли
3. Интегральная теорема Муавра-Лапласа. Пусть число испытаний n – велико ( n→∞ ) Вероятность р события А – не очень мала ( 0 << р << 1 ) ( р не близко к 0 и к 1 ) Тогда вероятность того, что событие А наступит не менее к-раз и не более m -раз, приближенно равна
Слайд 9: Схема Бернулли
Пример 2. Завод изготавливает 80% высоконапорных железобетонных труб первого сорта. Определить вероятность того, что из 100 труб 75 будет первого сорта. Решение. n =100 – велико, р=0,8 –не близко к 0 и к 1. По локальной теореме Муавра –Лапласа:
Слайд 10: Схема Бернулли
Пример 3. Вероятность поражения цели при одном выстреле равна 0,8. Производится 100 выстрелов. Норматив считается выполненным, если цель будет поражена не менее 75 раз. Определить вероятность выполнения норматива. Решение. По интегральной теореме Муавра-Лапласа:
Слайд 11: Случайная величина
Определение. Случайной величиной называется числовая величина (числовая функция), значение которой может меняться в зависимости от результата стохастического эксперимента. Обозначения: Пример 1. 1. Число вызовов, поступивших от абонентов на телефонную станцию в течение определенного промежутка времени, является случайным и принимает те или иные значения в зависимости от случайных обстоятельств.
Слайд 12: Случайная величина
Пример 2. Рассмотрим схему Бернулли: последовательность n независимых однородных испытаний, событие А – случайное событие, которое может наступить при каждом испытании. , если при i- ом испытании событие А наступило, и , если оно не наступило. Случайная величина - число наступлений события А в схеме Бернулли.
Слайд 14: Случайная величина
Дискретная случайная величина – такая случайная величина, которая может принимать конечное или счетное множество значений. Значения непрерывной случайной величины –принадлежат интервалу (конечному или бесконечному).
Слайд 15: Случайная величина
Пример 3. Рассмотрим схему Бернулли: последовательность n независимых однородных испытаний, А – случайное событие, которое может наступить при каждом испытании. Пусть Х – число наступлений события А. Х= { 0, 1,2,…,п } – дискретная случайная величина. Пример 4. Проводятся независимые однородные испытания до первого появления события А. Пусть ξ – функция, равная числу испытаний, проведенных до первого появления события А. ξ ={0, 1,2,3,… } – дискретная случайная величина. Обзор
Слайд 16: Случайная величина
Пример 5. Случайным образом бросают точку на отрезок [ а,в ]. Х – координата точки попадания. Х є [ а,в ] – непрерывная случайная величина. Пример 6. Время работы прибора без поломки μ – непрерывная случайная величина. μ є ( 0, ∞ )
Слайд 17: Способы задания случайной величины
Функция распределения и ее свойства. Определение. Функция, равная вероятности того, что случайная величина примет значение меньше х, называется функцией распределения: Свойства. 1. Область определения F(x) : х є ( -∞, ∞). 2. Область значений : 0 ≤ F(x) ≤ 1. 3. Функция F(x) – неубывающая: 4. 5. Вероятность попадания в интервал (а,в):
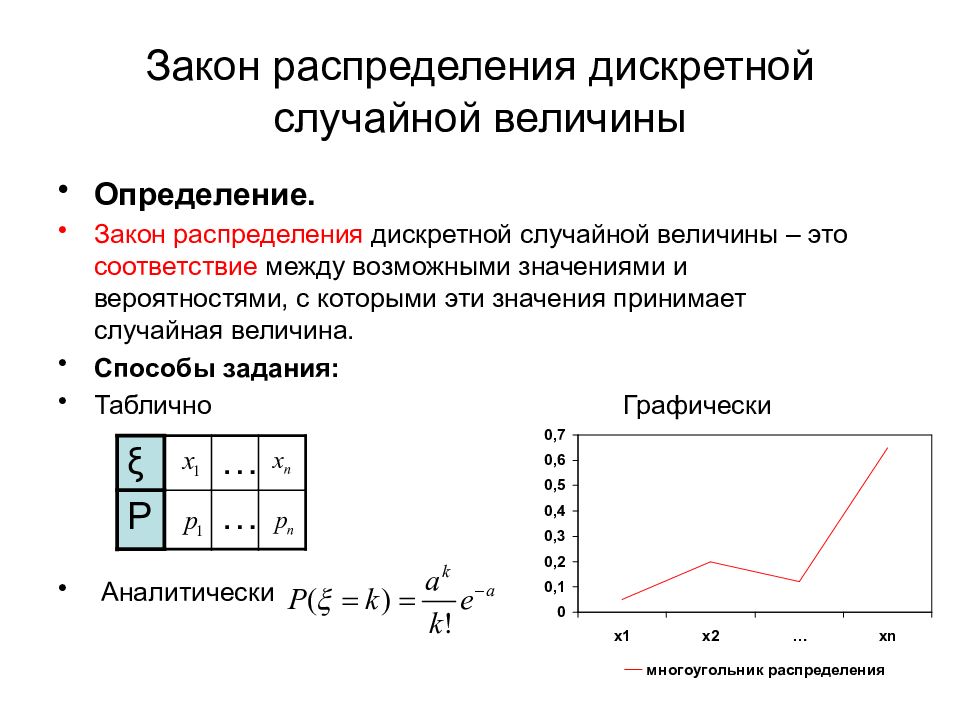
Слайд 18: Закон распределения дискретной случайной величины
Определение. Закон распределения дискретной случайной величины – это соответствие между возможными значениями и вероятностями, с которыми эти значения принимает случайная величина. Способы задания: Таблично Графически Аналитически ξ … Р …
Слайд 19: Закон распределения дискретной случайной величины
Примеры. 1. Биномиальный закон ( в схеме Бернулли ): 2. Равномерное распределение ( в классической схеме ): 3. Распределение Пуассона:
Слайд 20: Дискретная случайная величина
Основное свойство закона распределения: Функция распределения – кусочно- непрерывная функция. График функции распределения – ступенчатая фигура. х 1
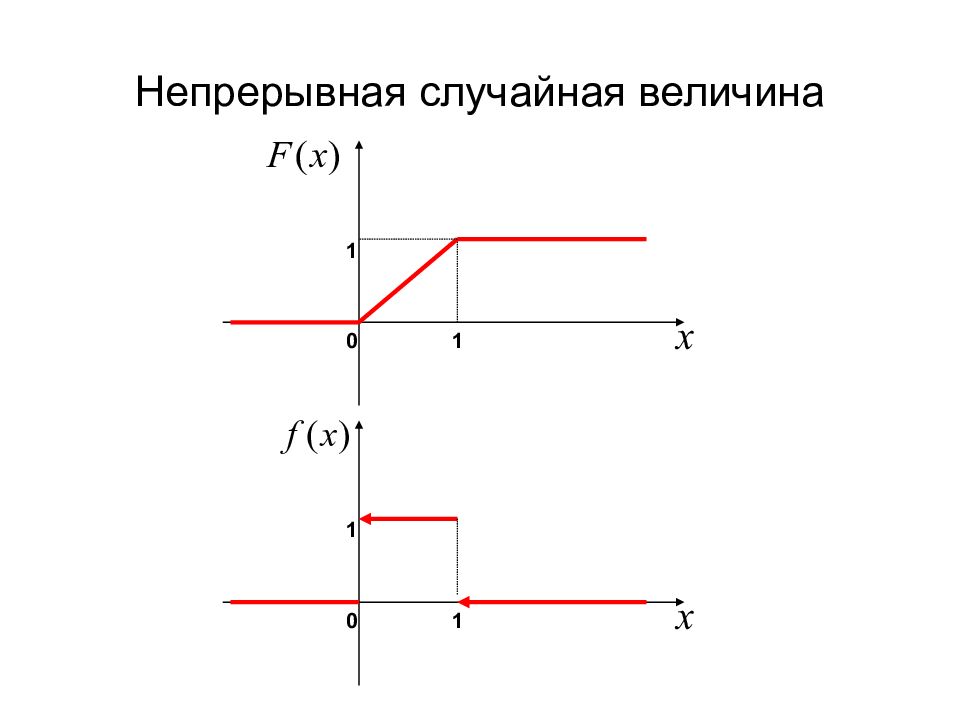
Слайд 21: Непрерывная случайная величина
Определение. Случайная величина ξ называется непрерывной, если ее функция распределения F(x) - непрерывная при всех х и имеет почти всюду производную F ' (x)=f(x). В этом случае функция f(x) называется плотностью распределения вероятности. Замечания. В некоторых учебниках такие случайные величины называют абсолютно непрерывными. Если F(x) - непрерывная и не дифференцируемая функция, то в этом случае случайную величину называют сингулярной.
Слайд 23: Непрерывная случайная величина
Пример. Случайным образом бросают точку на отрезок [ 0,1 ]. ξ – координата точки попадания. Найти функцию распределения F(x) и плотность f(x). Решение. Из определения: Обзор
Слайд 25: Числовые характеристики случайных величин
Математическое ожидание. Определение. Математическим ожиданием дискретной случайной величины ξ называется число, равное
Слайд 26: Числовые характеристики случайных величин
Математическим ожиданием непрерывной случайной величины ξ называется число, равное
Слайд 27: Числовые характеристики случайных величин
Свойства математического ожидания. 1. 2. 3. 4.
Слайд 28: Числовые характеристики случайных величин
Пример 1. Случайным образом бросают точку на отрезок [ 0,1 ]. ξ – координата точки попадания. Найти математическое ожидание Решение. Из определения:
Слайд 29: Числовые характеристики случайных величин
Дисперсия случайной величины. Определение. Дисперсией случайной величины ξ называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания :
Слайд 30: Числовые характеристики случайных величин
Свойства дисперсии. 1. 2. 3. 4. Следствие.
Слайд 32: Числовые характеристики случайных величин
Среднеквадратическое отклонение случайной величины. Определение. Среднеквадратическим отклонением случайной величины ξ называется число Свойства. 1. 2.
Слайд 33: Числовые характеристики случайных величин
Пример 2. Случайным образом бросают точку на отрезок [ 0,1 ]. ξ – координата точки попадания. Найти дисперсию и среднеквадратическое отклонение. Решение. Из формулы:
Слайд 36: Биномиальное распределение
ξ =(число «успехов» при n испытаниях в схеме Бернулли). Закон распределения: Пример
Слайд 38: Геометрическое распределение
ξ =(0,1,2,…, n,… ) Закон распределения: Пример
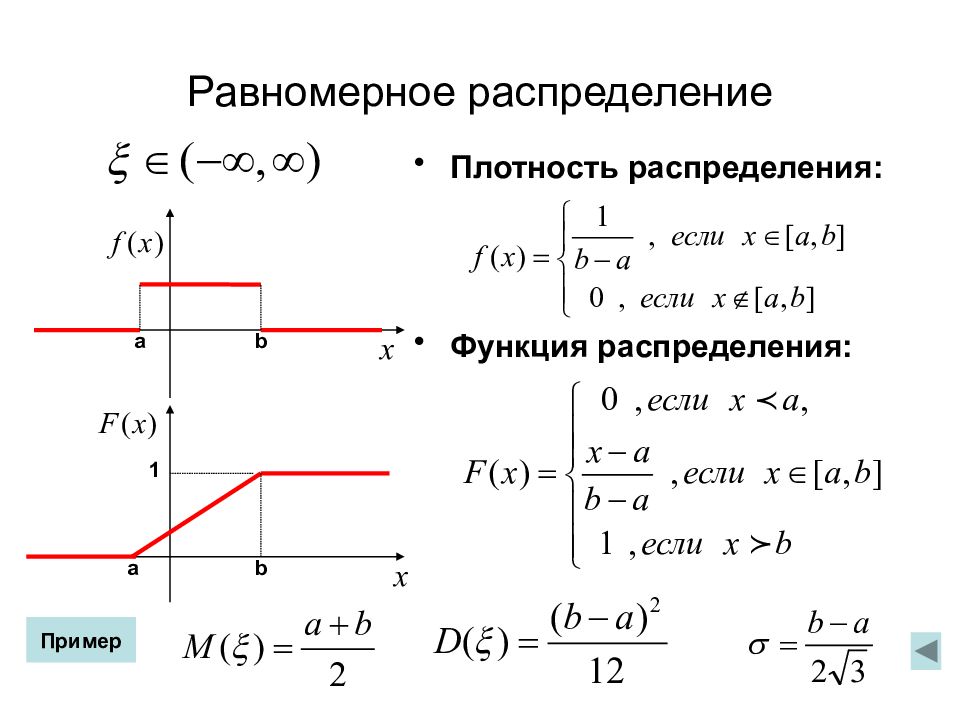
Слайд 39: Равномерное распределение
Плотность распределения: Функция распределения: 1 b b a a Пример
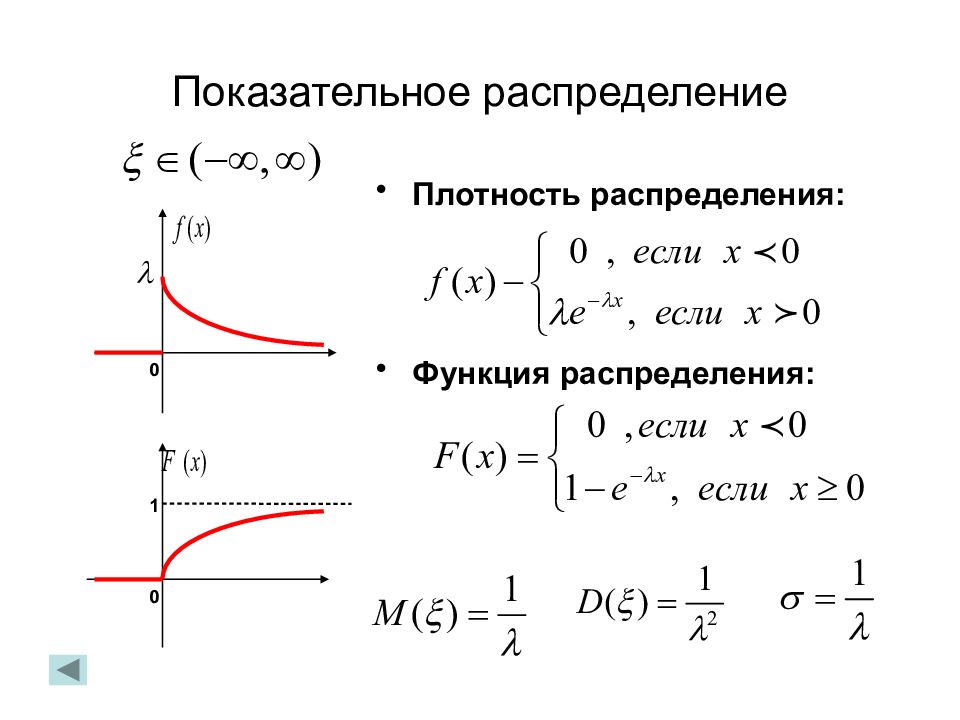
Слайд 40: Показательное распределение
Плотность распределения: Функция распределения: 0 1 0
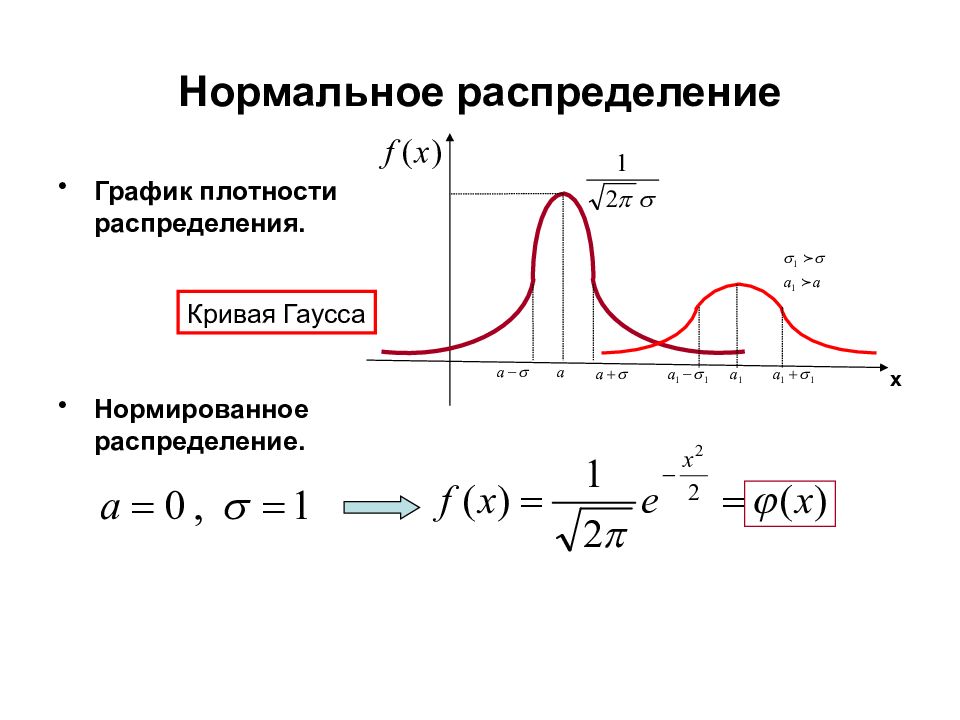
Слайд 41: Нормальное распределение
Определение. Непрерывная случайная величина ξ имеет нормальное распределение с параметрами a и σ, если плотность распределения Вероятностный смысл параметров:
Слайд 42: Нормальное распределение
График плотности распределения. Нормированное распределение. Кривая Гаусса х
Слайд 44: Нормальное распределение
Вероятность попадания в интервал. Следствие: (вероятность отклонения ξ от а не более чем на ε )
Последний слайд презентации: Теория вероятностей: Нормальное распределение
Пример. Отклонение длины изготавливаемой детали от стандарта - случайная величина, распределенная по нормальному закону. Если стандартная длина – 40 см, а среднеквадратическое отклонение – 0,4 см, то какое отклонение длины изделия от стандарта можно ожидать с вероятностью 0,8 ? Решение.