Слайд 2
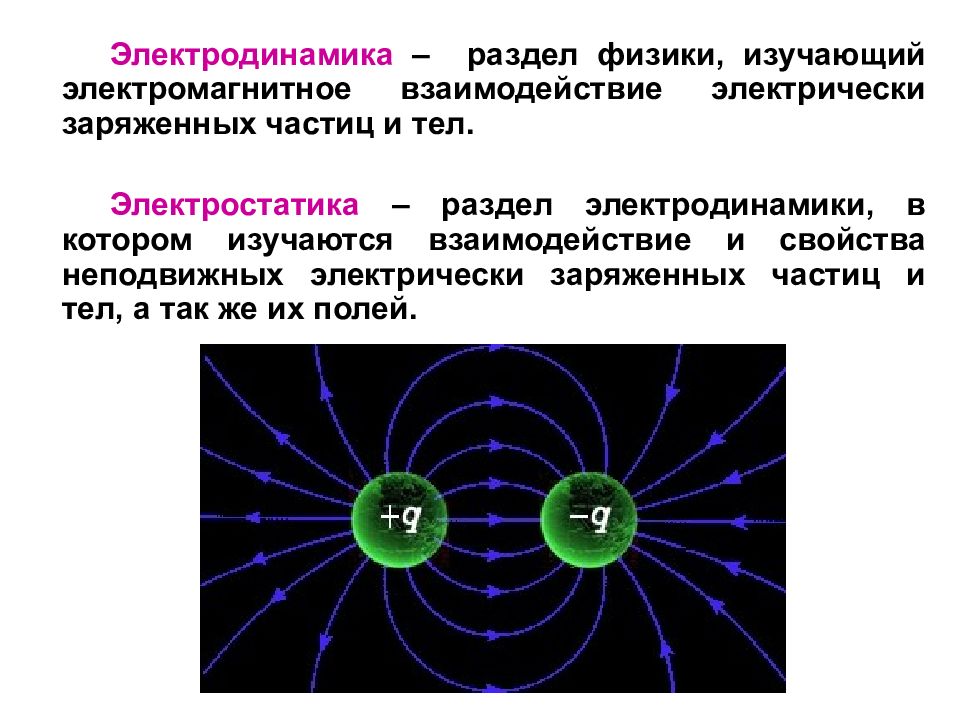
Электродинамика – раздел физики, изучающий электромагнитное взаимодействие электрически заряженных частиц и тел. Электростатика – раздел электродинамики, в котором изучаются взаимодействие и свойства неподвижных электрически заряженных частиц и тел, а так же их полей.
Слайд 3
Электромагнитные силы – силы притяжения и отталкивания, возникающие между электрически заряженными частицами и телами. Электрический заряд Q, q – скалярная физическая величина, характеризующая свойство некоторых частиц или тел вступать при определенных условиях в электромагнитное взаимодействие и определяющая значения силы и энергий этих взаимодействий. Единица измерения – 1 Кл (кулон) = 1 А. с.
Существуют два вида электрических зарядов ( положительные и отрицательные ). Одноименные заряды отталкиваются, разноименные – притягиваются. Электрический заряд инвариантен – его величина не зависит от системы отсчета, т.е. не зависит от того, движется он или покоится. Электрический заряд дискретен - заряд любого тела составляет целое число, кратное элементарному заряду е = 1,6. 10 -19 Кл. Электрический заряд аддитивен заряд любой системы тел (частиц) равен сумме зарядов тел ( частиц), входящих в систему.
Слайд 5
Электрон – носитель элементарного отрицательного заряда: Q = - e = - 1,6. 10 -19 Кл; m = 9,1. 10 -31 кг. Протон – носитель элементарного положительного заряда : Q = + e = + 1,6. 10 -19 Кл; m = 1,67. 10 -27 кг. Закон сохранения заряда Алгебраическая сумма электрических зарядов любой замкнутой системы остается неизменной, какие бы процессы не происходили внутри данной системы. Под замкнутой системой в данном случае понимают систему, которая не обменивается зарядами с внешними телами.
Сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, прямо пропорциональна произведению величин зарядов Q 1 и Q 2, обратно пропорциональна квадрату расстояния r 2 между ними и направлена вдоль линии, соединяющей заряды : Закон Кулона
Слайд 9
Закон Кулона для точечных зарядов, находящихся в диэлектрической среде (веществе) где ε - диэлектрическая проницаемость среды – безразмерная величина, показывающая во сколько раз сила взаимодействия зарядов в среде F меньше, чем в вакууме F 0.: ε = F 0 / F. , ,
Слайд 10
Электрическое (электромагнитное) поле – особый вид материи, посредством которого электрические заряды взаимодействую друг с другом. Электростатическое поле – электрическое поле, созданное неподвижными электрическими зарядами и не изменяющееся со временем. Электростатическое поле описывается двумя величинами : напряженностью (силовая векторная характеристика поля) и потенциалом ( энергетическая скалярная характеристика поля). Пробный заряд Q 0 – небольшой по величине, точечный положительный заряд, который не искажает исследуемое электрическое поле.
Слайд 11
Напряженность электрического поля E – векторная физическая величина, численно равная силе, с которой поле действует на пробный единичный положительный заряд, помещенный в данную точку поля. Направление вектора напряженности E совпадает с направлением вектора силы F, с которой поле действует на положительный заряд. Единица измерения – 1 Н / Кл = 1 В / м
Слайд 12: Напряженность поля точечного заряда Q
- в скалярной форме; - в векторной форме ; - радиус – вектор, направленный от заряда Q в точку поля А; - единичный вектор.
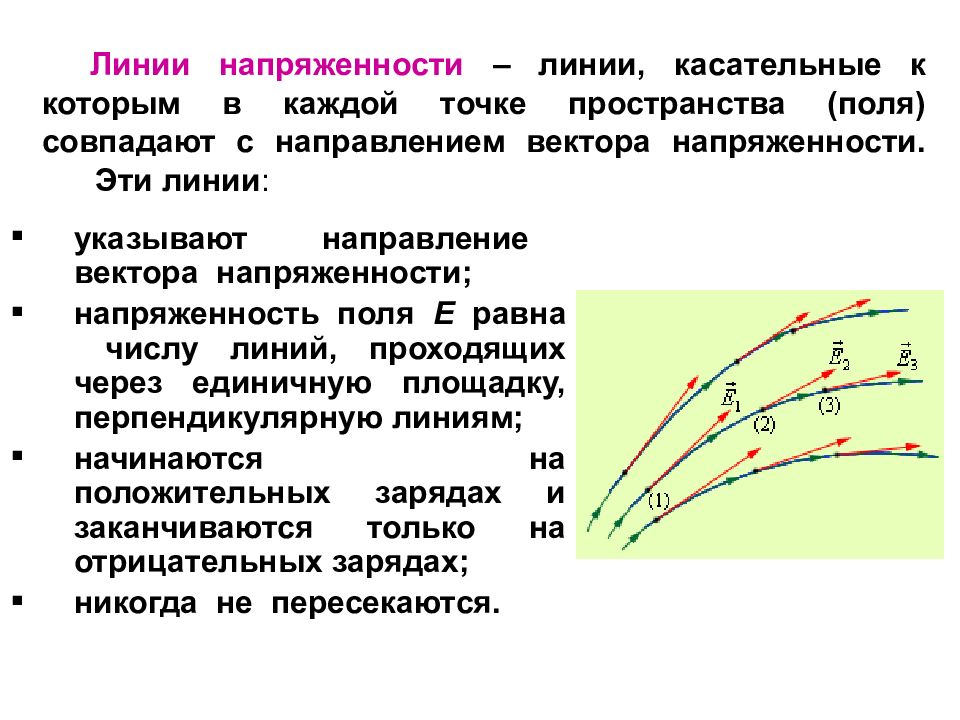
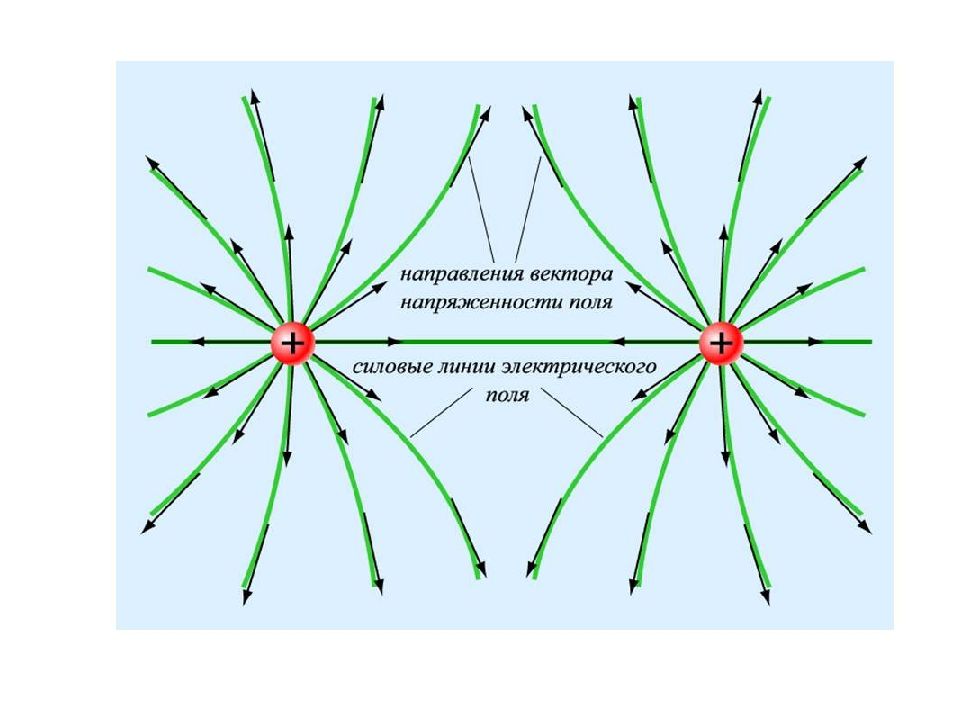
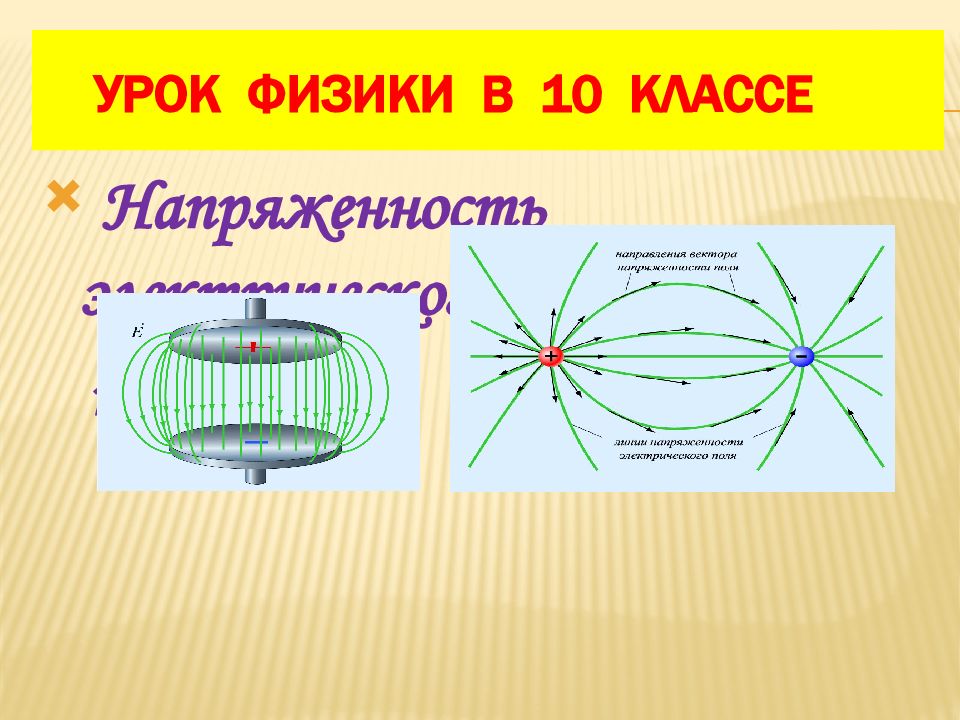
Слайд 13: Линии напряженности – линии, касательные к которым в каждой точке пространства (поля) совпадают с направлением вектора напряженности. Эти линии :
указывают направление вектора напряженности; напряженно c ть поля E равна числу линий, проходящих через единичную площадку, перпендикулярную линиям; начинаются на положительных зарядах и заканчиваются только на отрицательных зарядах; никогда не пересекаются.
Напряженность результирующего поля E, создаваемого системой зарядов Q i, равна векторной сумме напряженностей полей E i, создаваемых в данной точке каждым из зарядов в отдельности.
Слайд 16
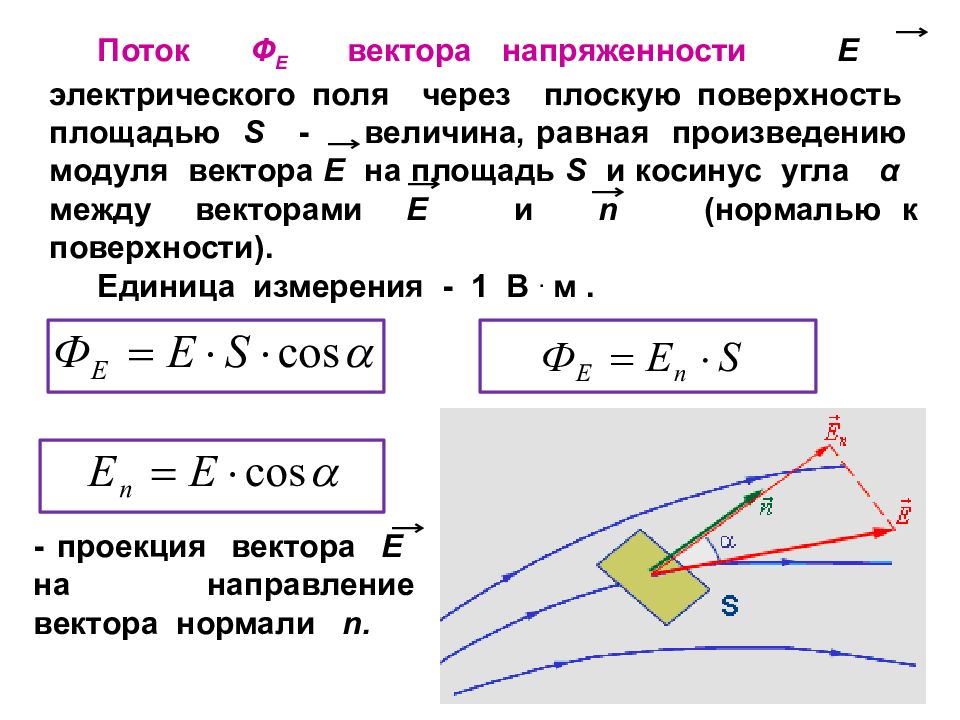
Поток Ф Е вектора напряженности E электрического поля через плоскую поверхность площадью S - величина, равная произведению модуля вектора E на площадь S и косинус угла α между векторами E и n (нормалью к поверхности). Единица измерения - 1 В. м. - проекция вектора E на направление вектора нормали n.
Слайд 17
- другая формула потока; - вектор площадки. Поток Ф Е численно равен количеству линий напряженности, пронизывающих поверхность S, является алгебраической величиной. Поток вектора напряженности величина скалярная. Знак потока определяется направлением положительной нормали к поверхности. За положительное направление принимается направление внешней нормали к поверхности.
Слайд 18
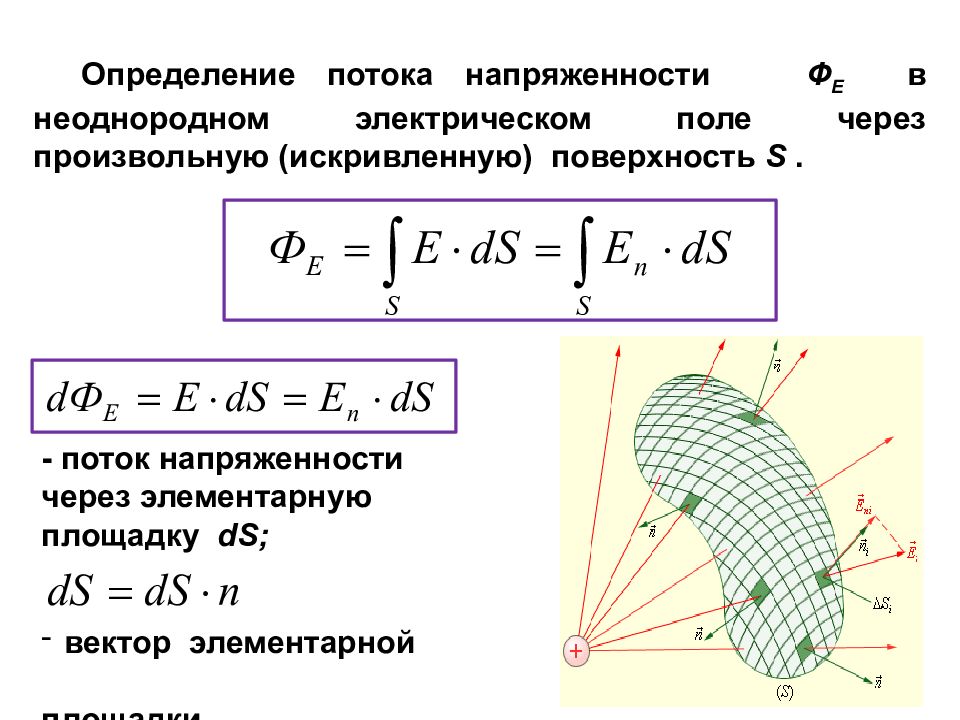
Определение потока напряженности Ф Е в неоднородном электрическом поле через произвольную (искривленную) поверхность S. - поток напряженности через элементарную площадку dS ; вектор элементарной площадки.
Слайд 19
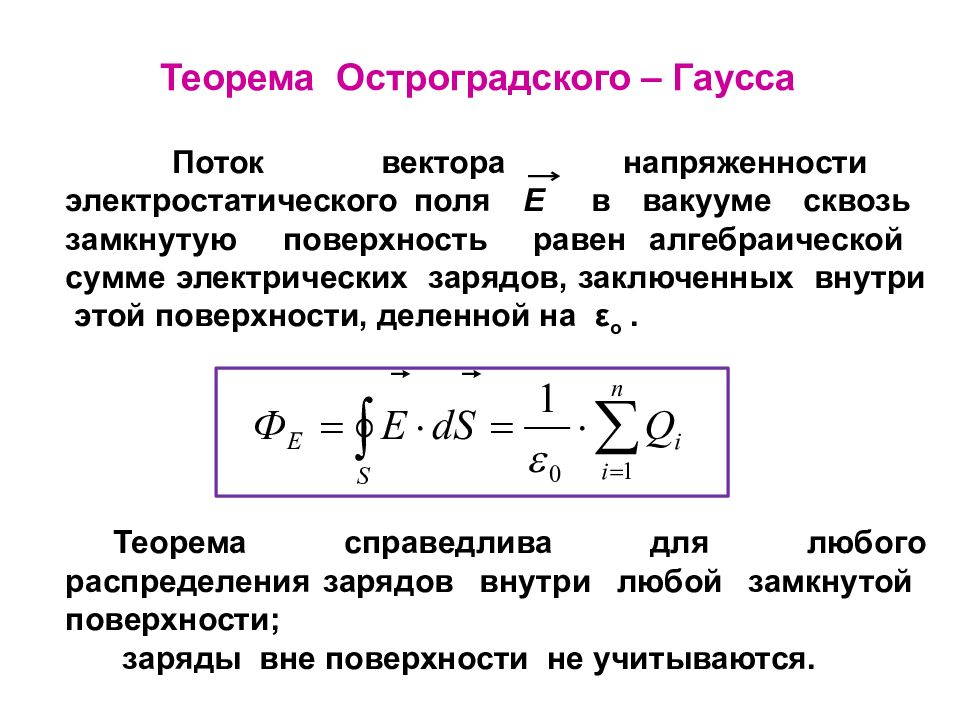
Теорема Остроградского – Гаусса Поток вектора напряженности электростатического поля E в вакууме сквозь замкнутую поверхность равен алгебраической сумме электрических зарядов, заключенных внутри этой поверхности, деленной на ε о. Теорема справедлива для любого распределения зарядов внутри любой замкнутой поверхности; заряды вне поверхности не учитываются.
Слайд 20
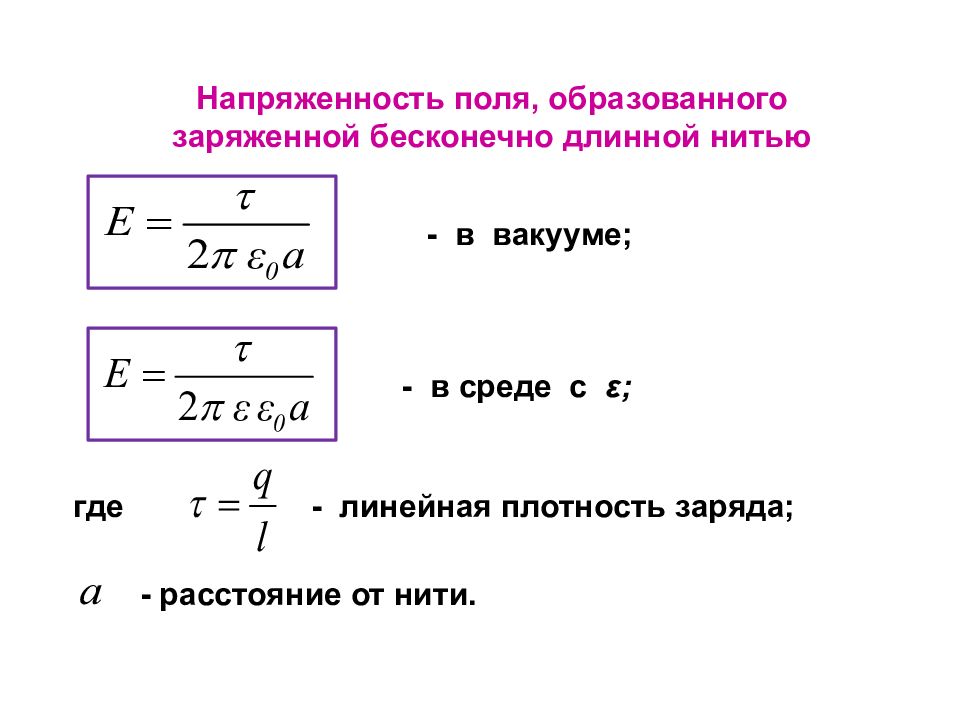
Напряженность поля, образованного заряженной бесконечно длинной нитью - в вакууме; - в среде с ε ; где - линейная плотность заряда; - расстояние от нити.
Слайд 21
Электрическое поле равномерно заряженной бесконечной плоскости - в вакууме; - в среде с ε, где - поверхностная плотность заряда. Поле двух бесконечных параллельных плоскостей, заряженных разноимённо ( поле плоского конденсатора)
Слайд 22
Поле равномерно заряженной сферической поверхности 1) Область пространства на поверхности сферы и вне её : Если r ≥ R, то. Поле заряженной сферы совпадает с полем точечного заряда, равного заряду сферы и находящегося в центре сферы. 2) Область внутри сферы. Если r < R, то Е = 0.
Слайд 23
Потенциал. Работа электростатического поля. Электростатическое поле является потенциальным. Работа сил электростатического поля по перемещению электрического заряда не зависит от вида (формы) траектории, а определяется только начальным и конечным положениями заряда в поле. При перемещении в электростатическом поле заряда по замкнутой траектории работа сил поля равна нулю. Потенциальность электростатического поля имеет математическое определение с помощью понятия циркуляция вектора напряженности.
Слайд 24
- работа на элементарном перемещении - работа по перемещению единичного заряда - циркуляция вектора напряжённости электростатического поля по замкнутому контуру (кривой) L Эта величина представляет собой полную работу А электрических сил по перемещению единичного положительного заряда Q 0 = + 1 Кл по замкнутому пути ( вдоль кривой L ).
Слайд 25
Циркуляция вектора напряженности электростатического поля по замкнутому контура равна нулю. Работа электростатических сил по перемещению заряда Q из одного положения (точки 1) в другое положение (точку 2) равна убыли потенциальной энергии заряда и не зависит от пути перемещения заряда. A 12 = - ( U 2 - U 1 ) = U 1 - U 2
Слайд 26
Потенциал электростатического поля φ - скалярная физическая величина, численно равная потенциальной энергии единичного положительного заряда, помещенного в данную точку поля. Единица измерения : 1 В = 1 Дж/Кл. Работа сил электростатического поля А 12 равна произведению величины перемещаемого заряда Q на разность потенциалов в начальном (1) и конечном (2) положениях заряда.
Слайд 27
Разность потенциалов между двумя точками 1 и 2 электростатического поля равна работе, совершаемой силами поля при перемещении единичного положительного заряда из одной точки поля (начальной) в другую точку поля (конечную). Второе определении потенциала. Потенциал поля в данной точке пространства – физическая величина, определяемая работой по перемещению единичного положительного заряда из данной точки поля в бесконечность.
Слайд 28: Потенциал электростатического поля точечного заряда Q в вакууме ( на расстоянии r от него )
Единица потенциала и разности потенциалов - вольт : 1 В = 1Дж / Кл.
Слайд 29
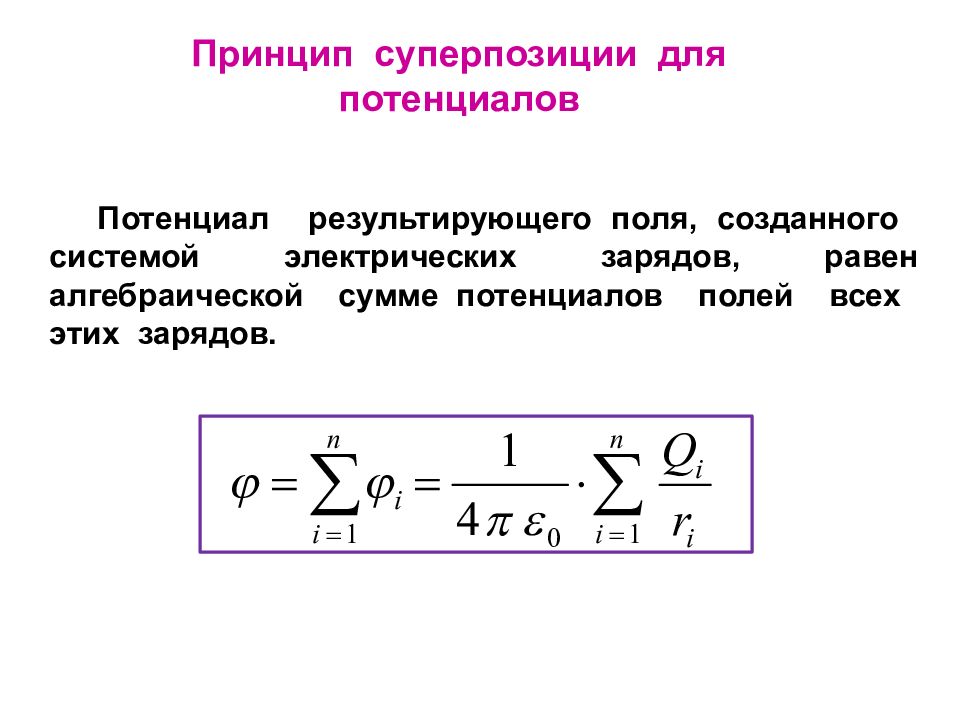
Потенциал результирующего поля, созданного системой электрических зарядов, равен алгебраической сумме потенциалов полей всех этих зарядов. Принцип суперпозиции для потенциалов
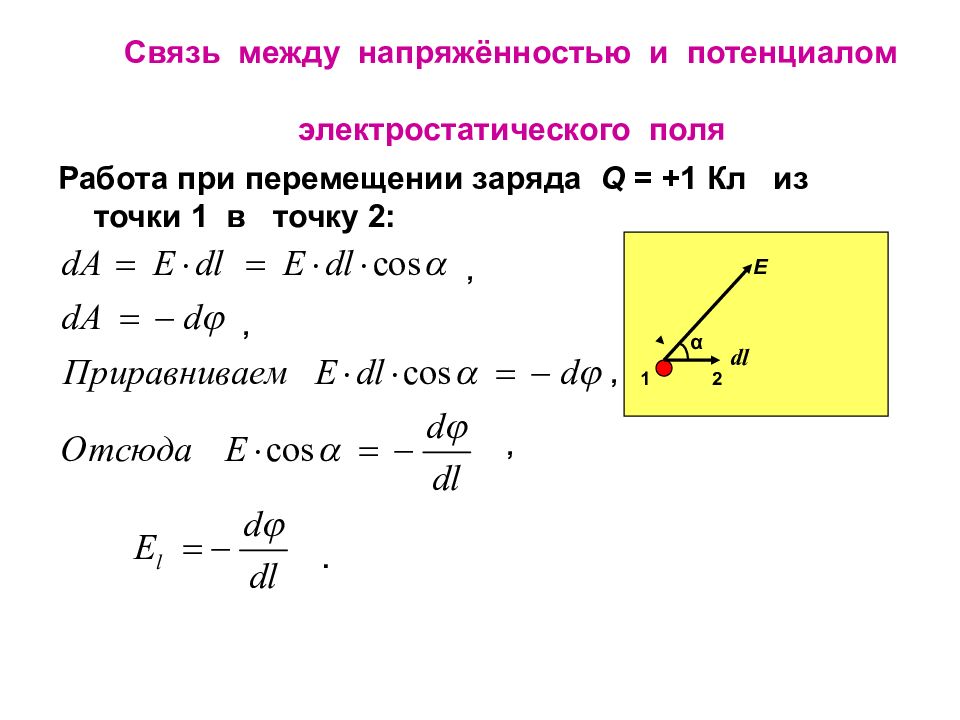
Слайд 30: Связь между напряжённостью и потенциалом электростатического поля
Работа при перемещении заряда Q = +1 Кл из точки 1 в точку 2: E dl α 1 2 . , , , ,
Слайд 31
В окрестности какой - либо точки электростатического поля потенциал поля φ наиболее быстро изменяется в направлении линии напряженности. где d φ - изменение потенциала, вызванное перемещением единичного заряда на dl вдоль линии напряжённости. , - это величина (модуль) градиента потенциала grad φ электростатического поля, характеризующего быстроту изменения потенциала φ в пространстве.
Слайд 32
В векторном виде связь между напряженностью E и потенциалом φ имеет вид : Физический смысл: Напряжённость поля в данной точке электростатического поля измеряется уменьшением потенциала поля, приходящимся на единицу длины линии напряжённости.
Слайд 33: В случае однородного электростатического поля
φ 1 и φ 2 - потенциалы в точках 1 и 2 ; Δ l - расстояние между точками 1 и 2 вдоль линии напряжённости поля ( расстояние между эквипотенциальными поверхностями ). , ,
Слайд 34
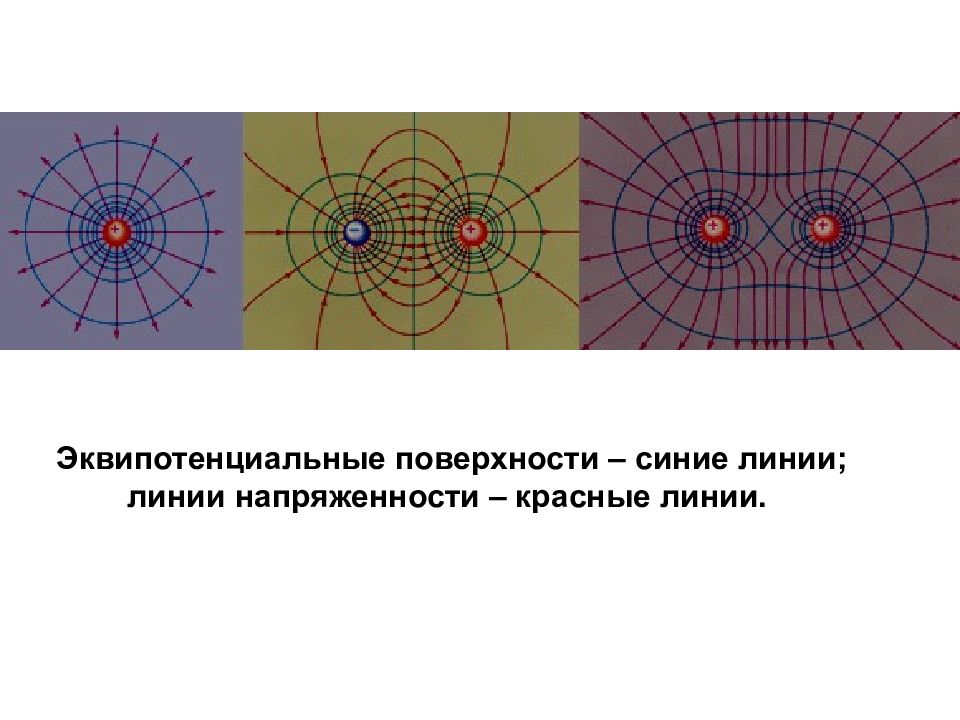
Эквипотенциальная поверхность - это поверхность, во всех точках которой потенциал φ имеет одинаковое значение. Работа, совершаемая при перемещении заряда по одной и той же эквипотенциальной поверхности, равна нулю. Линии напряжённости всегда перпендикулярны к ним. Эти поверхности проводят с определённой густотой, так, чтобы разность потенциалов между любыми двумя соседними поверхностями была одинакова ( через 1 В ).