Первый слайд презентации
Физические Процессы в Мембранах. Биопотенциалы. Потенциал покоя. Потенциал действия. Функции мембран их физические свойства. Перенос молекул (атомов) через мембраны, уравнение Фика. Перенос заряженных частиц, электродиффузионное уравнение Нернста-Планка. Виды транспорта через мембраны: пассивный и активный. Биоэлектрические Потенциалы. Потенциаал покоя. Потенциал действия. Распространение нервного импульса вдоль возбудимого волокна. Многие патологические процессы в клетке связаны с нарушением функций мембран. Общая площадь мембран десятки тысяч м.кв., обеспечивающих жизнеспособность человека.
Слайд 2
Функции мембран Механическое разделение. (тонкая регуляция; внутриклеточные мембраны; диэлектрическая граница). Транспортная функция. Селективный барьер (защита от проникновения нежелательных частиц и веществ). Рецепция. Через мембрану происходит распознавание других клеток, веществ. Распространение нервного импульса (генерация электрического потенциала). Матрица. Мембрана является матрицей (основой) для удержания белков, ферментов. Если функции мембраны нарушаются, то происходит изменение нормального функционирования клеток и, как следствие, заболевание организма.
Слайд 4: C труктура биологических мембран
Слайд 5
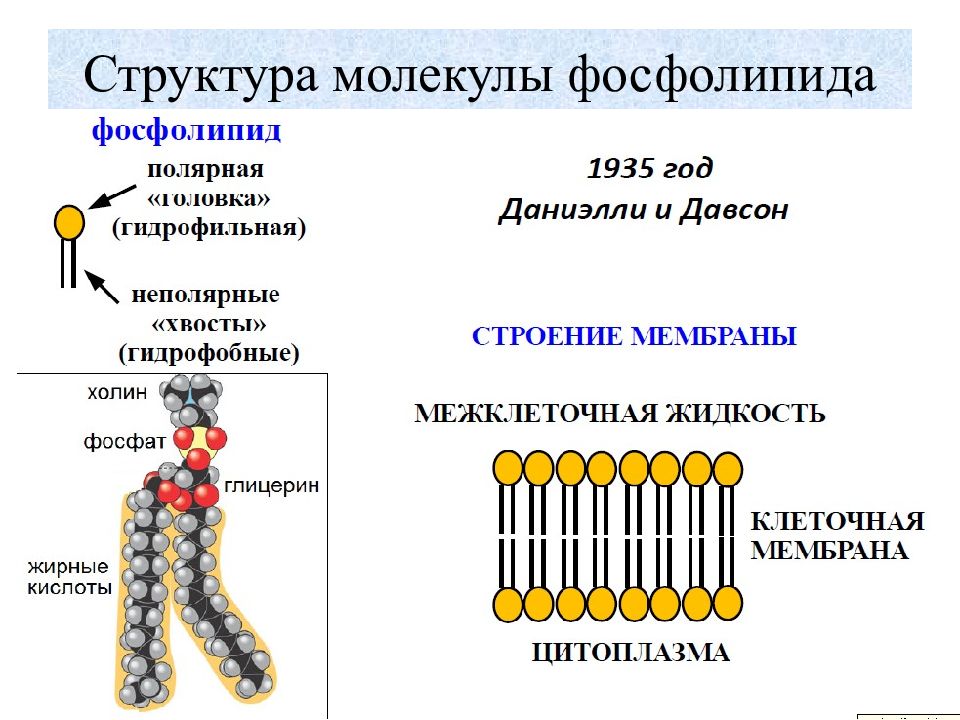
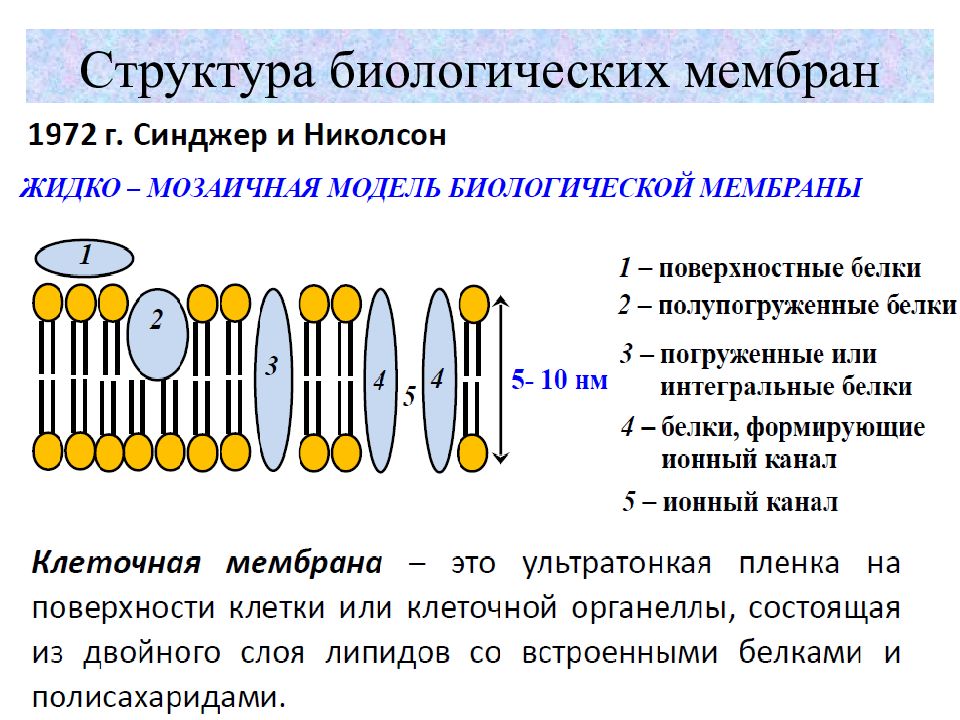
Рис.1. Строение мембраны: L — толщина мембраны (8-10 нм.); пб — поверхностные белки; иб — интегральные белки; к - белки, формирующие ионный канал (пору) В мембране молекулы фосфолипидов ориентированы так, что их гидрофильные головки выходят наружу и образуют внешнюю и внутреннюю поверхности мембраны, а гидрофобные «хвосты» обращены к середине бимолекулярного слоя, то есть внутрь мембраны.
Слайд 6: БМ
Функциональные структуры клетки, которые ограничивают цитоплазму и большинство внутриклеточных структур, образуют единую систему канальцев, складок и замкнутых полостей Толщина 10нм масса 1/2 массы сухой клетки Состав: липиды, белки, углеводы
Слайд 7
Белковые молекулы ( пб ) удерживаясь преимущественно электростатическими силами покрывают 75-80 % поверхности мембраны с обеих сторон и придают ей эластичность и устойчивость к механическим повреждениям. Таким образом, образуется рыхлый поверхностный слой, выполняющий роль носителя электростатического заряда. Интегральные белки ( иб ) - главный компонент, ответственным за избирательную проницаемость клеточной мембраны, пронизывающий двойной слой липидов насквозь. Некоторые из них (к) образуют систему селективных каналов (пор), функционируют как ионные насосы и регулируют электрохимическую систему возбуждения клетки. Диаметр каналов составляет 0,35-0,8 нм., а вся площадь каналов составляет 0,06% от площади поверхности.
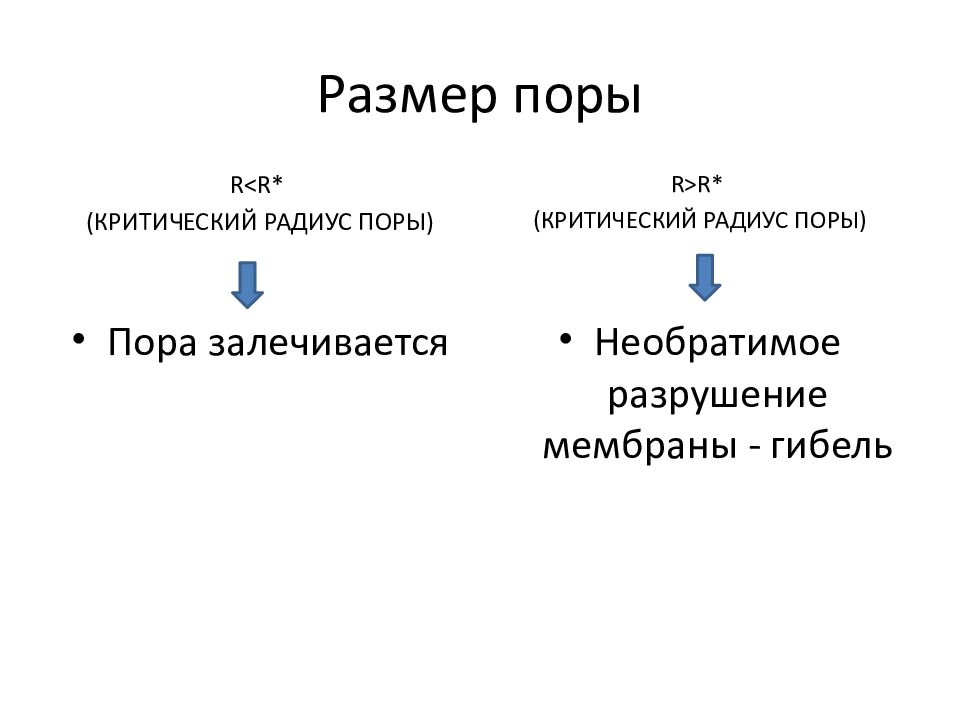
Слайд 9: Размер поры
r<r* (критический радиус поры) r>r* (критический радиус поры) Пора залечивается Необратимое разрушение мембраны - гибель
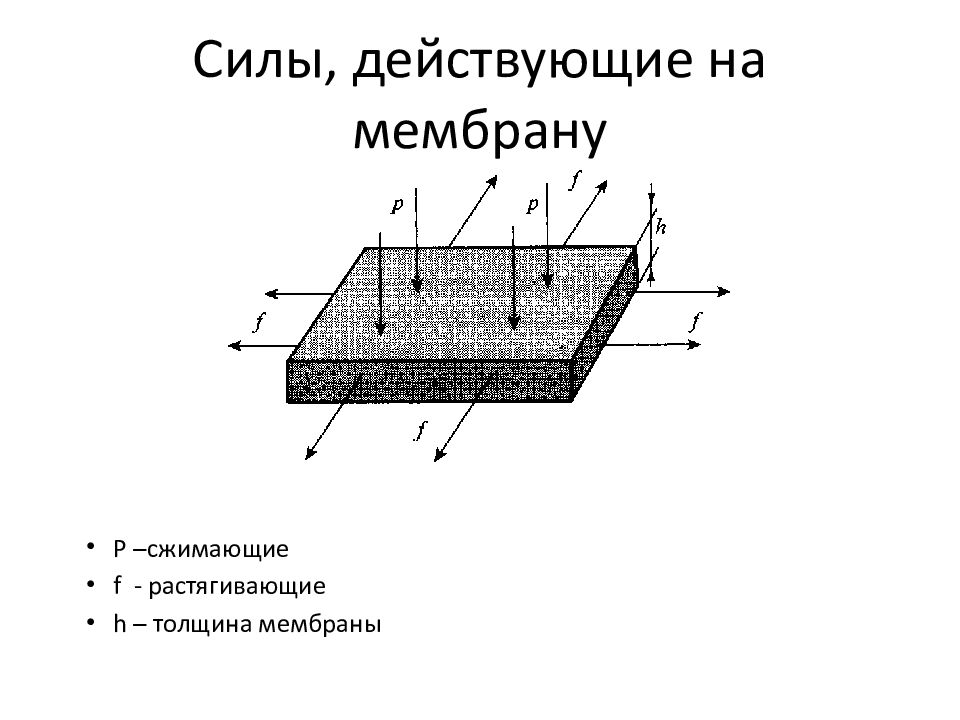
Слайд 10: Силы, действующие на мембрану
Р –сжимающие f - растягивающие h – толщина мембраны
Слайд 11: Разрушение БМ
Слияние клеток Лизис (разрушение) Гемолиз (разрушение эритроцитов с выделением гемоглобина) Липидные мембраны – метастабильные системы Значительные отклонения параметров БМ от равновесных, приводят к возникновению и накоплению дефектов в структуре
Слайд 12
Физические свойства мембран Плотность липидного бислоя составляет 800 кг/м 3, что меньше, чем у воды. Размеры. По данным электронной микроскопии, толщина мембраны ( L ) меняется от 4 до 13 нм. Прочность низка. Чтобы довести мембрану до разрыва, достаточно внутреннего давления 100 Па. Живая клетка может осуществлять осморегуляцию только за счет изменения своей формы, но не за счет растяжения мембраны. Деформируемость. Клеточная мембрана легко подвергается деформации сдвига. Например, в потоке эритроцитов с градиентом скорости происходит вращение мембраны вокруг содержимого клетки. Это явление получило название «феномен гусеницы танка».
Слайд 13
Вязкость мембраны η= 30-100 мПа • с (что соответствует вязкости растительного масла). Поверхностное натяжение (0,03-3 мН • м -1 ) ниже на 2-3 порядка, чем у воды. Коэффициент проницаемости мембранного вещества для воды - 25-33 • 10 -4 см/с. Мембрана — конденсатор. Двойной фосфолипидный слой уподобляет мембрану плоскому конденсатору, обкладки которого образованы поверхностными белками, а роль диэлектрика выполняет липидный бислой. Электроемкость 1 см 2 мембраны составляет 0,5-1,3 мкФ.
Слайд 14
Напряженность электрического поля в мембране составляет приблизительно 20•10 6 В/м ( U / d = 0,2 В / 10 нм =20•10 6 В/м). Диэлектрическая проницаемость мембраны составляет: для фосфолипидной области ε = 2,0-2,2 ; для гидрофильной области ε = 10-20. Электросопротивление 1 см 2 поверхности мембраны составляет 10 2 -10 5 Ом (что в десятки миллионов раз больше сопротивления внеклеточной жидкости или цитоплазмы). Электроизоляционные свойства мембраны значительно превосходят свойства технических изоляторов.
Слайд 15
Для мембраны характерно жидкокристаллическое состояние, при котором вещество обладает текучестью, но сохраняет упорядоченность в расположении молекул и анизотропию свойств. При изменении температуры в мембране можно наблюдать фазовые переходы: плавление липидов при нагревании и кристаллизацию при охлаждении — липиды превращаются в гель. При фазовых переходах меняется толщина двойного слоя, а также могут образовываться каналы, по которым через мембрану способны проходить различные ионы и низкомолекулярные соединения. Показатель преломления вещества мембраны равен 1,55 (показатель преломления глицерина -1,47).
Слайд 16
Живые системы - открытые системы на всех уровнях организации Необходимое условие существования клетки – транспорт веществ через БМ, который обеспечивает: -метаболизм клетки -биоэнергетические процессы создания потенциалов и генерации нервного импульса Нарушение транспортной функции БМ – развитие патологии
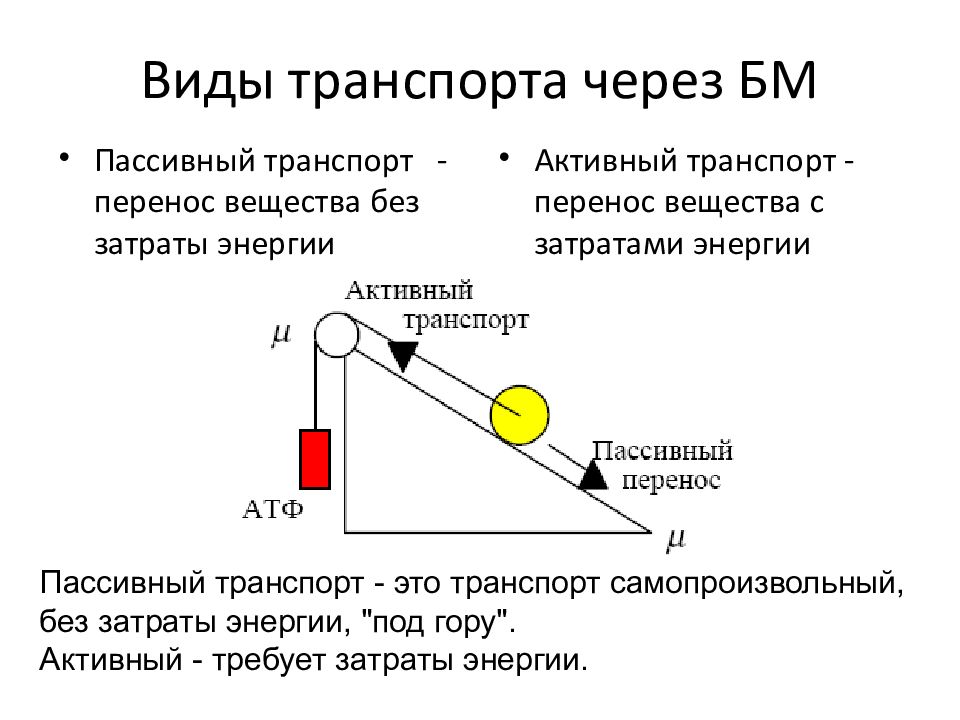
Слайд 17: Виды транспорта через БМ
Пассивный транспорт - перенос вещества без затраты энергии Активный транспорт - перенос вещества с затратами энергии Пассивный транспорт - это транспорт самопроизвольный, без затраты энергии, "под гору". Активный - требует затраты энергии.
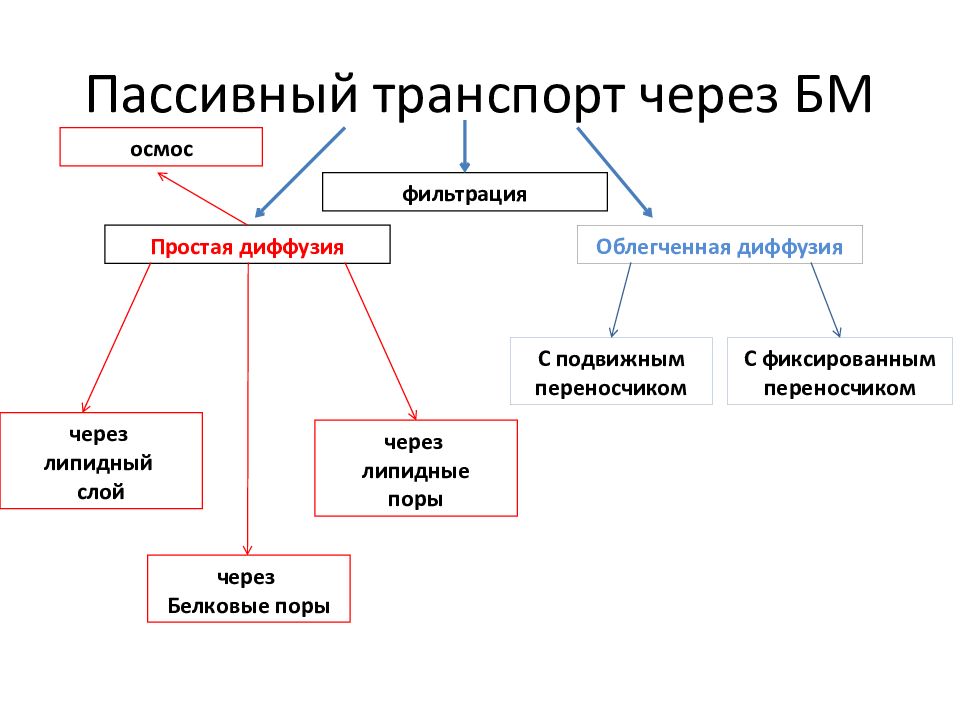
Слайд 18: Пассивный транспорт через БМ
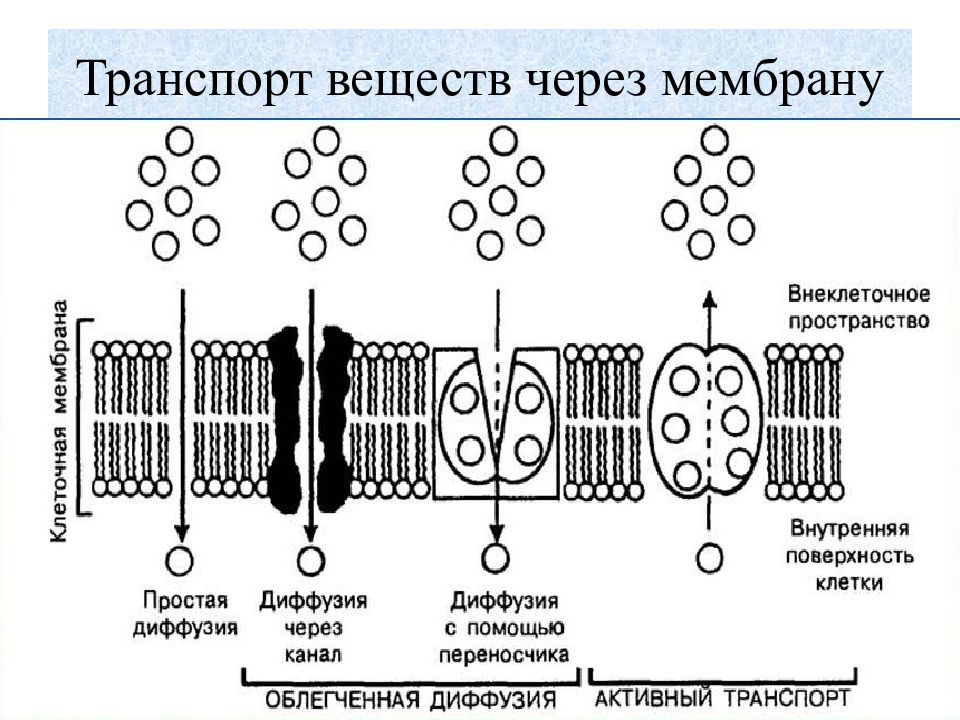
Простая диффузия Облегченная диффузия фильтрация осмос через липидный слой через липидные поры через Белковые поры С подвижным переносчиком С фиксированным переносчиком
Слайд 19
Перенос молекул (атомов) через мембраны. диффузия (перенос массы); вязкость (перенос импульса из слоя в слой); теплопроводность (перенос энергии); электропроводность (перенос электрического заряда). Как синоним переноса частиц в биофизике используется термин транспорт частиц (веществ). Диффузия — явление самопроизвольного переноса массы вещества из области с большей концентрацией в область с меньшей. Диффузия приводит к равномерному распределению вещества по всему объему. Количественно диффузия описывается специальными параметрами.
Слайд 20: Транспорт веществ через мембраны
Количественными характеристиками транспорта веществ являются: поток вещества (Ф) – количество вещества, которое переносится за единицу времени: Ф = dm/dt ; [ Ф ] = моль/с. Плотность потока вещества ( J ): J = Ф /S = dm/(dt ∙ S) ; [J] = моль/(с ∙ м 2 ). Плотность потока - количество вещества, которое переносится за единицу времени, через единицу площади.
Слайд 21
1.Потоком вещества (Ф) через элемент поверхности, который перпендикулярен направлению диффузии, называется количество этого вещества, переносимого через данный элемент за единицу времени. Количество переносимого вещества можно измерять в килограммах ( m ) или молях ( ν ). В зависимости от этого поток определяется формулами: Ф = m / t [ кг/с ] или Ф = ν / t [ моль/с ]. (1) Поток пропорционален площади S выделенного элемента и градиенту концентрации ( dc / dx ) диффундирующего вещества. Поэтому для расчета потока используют уравнение Фика : Ф = - D ( dc / dx ) S. (2) Коэффициент пропорциональности D – коэффициент диффузии. Знак «—» означает, что поток направлен в сторону убывания концентрации (плотности) вещества. Размерность коэффициента диффузии: [ D ] — м 2 /с.
Слайд 22: Коэффициент диффузии D k
Зависит от размера и формы молекул Для малых молекул Для сферических молекул
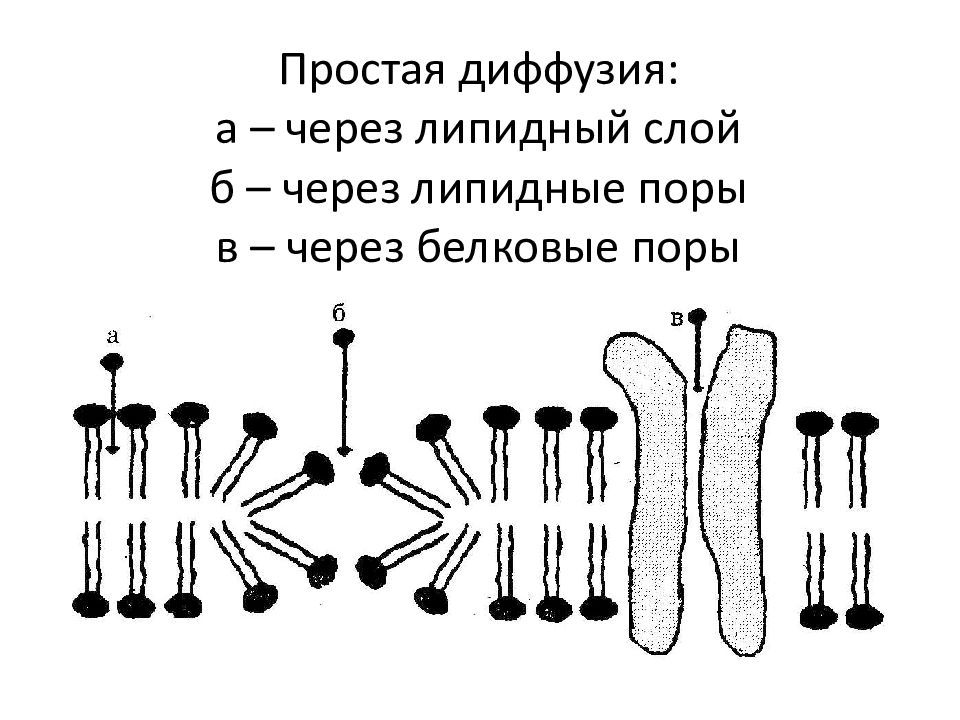
Слайд 23: Простая диффузия: а – через липидный слой б – через липидные поры в – через белковые поры
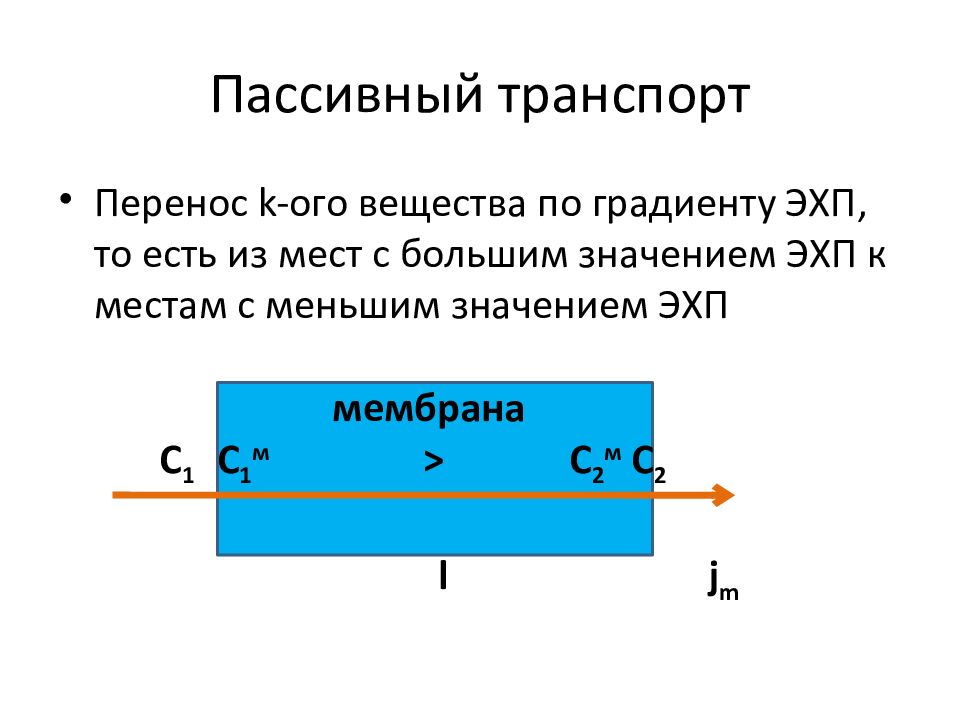
Слайд 25: Пассивный транспорт
Перенос k -ого вещества по градиенту ЭХП, то есть из мест с большим значением ЭХП к местам с меньшим значением ЭХП мембрана С 1 С 1 м > С 2 м С 2 l j m
Слайд 27
Поскольку в диффузии участвуют не только нейтральные вещества, но и ионы разной полярности, Нернст и Планк предложили формулу: Ф = uRT (dc/dx) cuz F (d /dx) где: u = D/RT (называется подвижностью молекул) R универсальная газовая постоянная; T абсолютная температура; с активная концентрация вещества; z валентность; F постоянная Фарадея; (dc/dx), (d /dx) градиент концентрации и градиент потенциала (то же, что электрическая напряжённость).
Слайд 28
Коэффициент D зависит от свойств жидкости, свойств диффундирующих частиц, температуры. Его численное значение выражается формулой D = (σ 2 /3τ), где σ — среднее перемещение молекул ( среднее расстояние между молекулами ), τ — среднее время «оседлой жизни» молекулы. 2. Плотность потока вещества Плотностью потока вещества ( J ) называется отношение потока вещества (Ф) через элемент поверхности к площади этого элемента ( S ): J = Ф/ S. Единица плотности потока — [ кг/(м 2 • с) ] или [ моль/(м 2 • с) ]. В соответствии с определением и формулой (2) плотность потока выражается уравнением диффузии (уравнение Фика): J = - D ( dc / dx ) (3)
Слайд 29
3. Уравнение Фика для мембраны. Уравнение Фика описывает диффузию в однородной среде. Модифицируем его для случая диффузии через мембрану. Введем понятие проницаемости мембраны(м/с) как коэффициент: Р= D / L, который зависит от коэффициента диффузии - D, а также от толщины биомембраны - L. Под проницаемостью понимают способность мембраны пропускать сквозь себя определенные вещества. Окончательно имеем уравнение Фика для диффузии в мембранах: j = P (с i - c o ). (4) Это уравнение Фика определяет плотность потока вещества при диффузии через мембрану, то есть описывает пассивный транспорт в мембранах.
Слайд 30
При отсутствии градиента концентрации главная движущая сила при переносе ионов - это электрическое поле. На отдельный ион в электрическом поле действует сила F о = qE, где Е — напряженность электрического поля, в котором находится ион, a q = Ze — заряд иона. Напряженность поля выражается через градиент электрического потенциала: Е = - grad = - d / dx. Поэтому можно записать: F о = - Ze ( d / dx ). (5) В общем случае перенос частиц определяется как градиентом их концентрации, так и воздействием электрического поля.
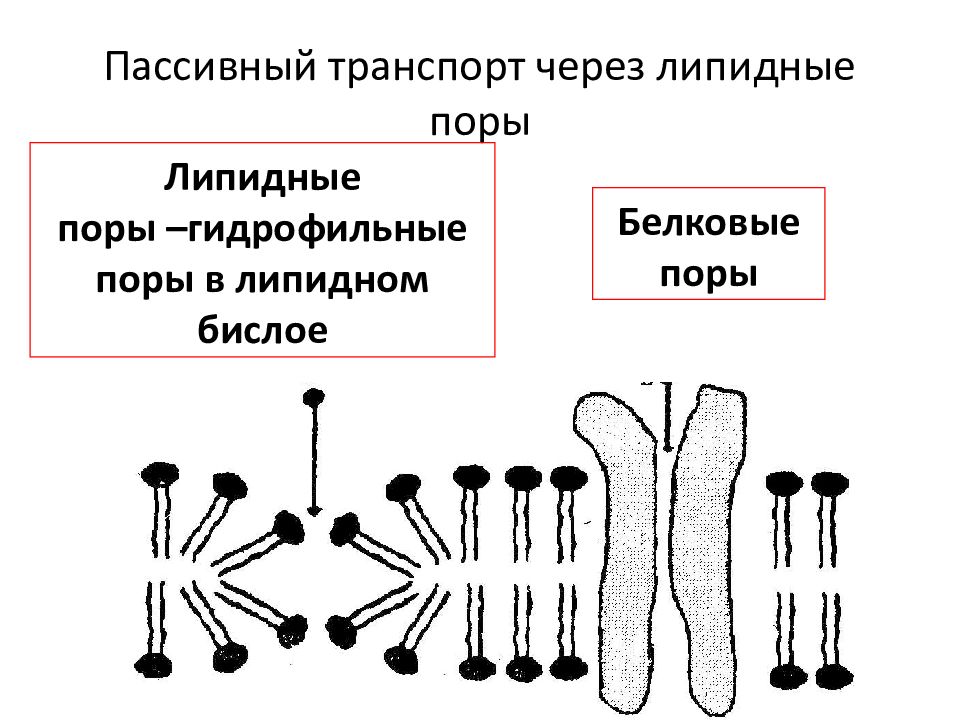
Слайд 31: Пассивный транспорт через липидные поры
Липидные поры –гидрофильные поры в липидном бислое Белковые поры
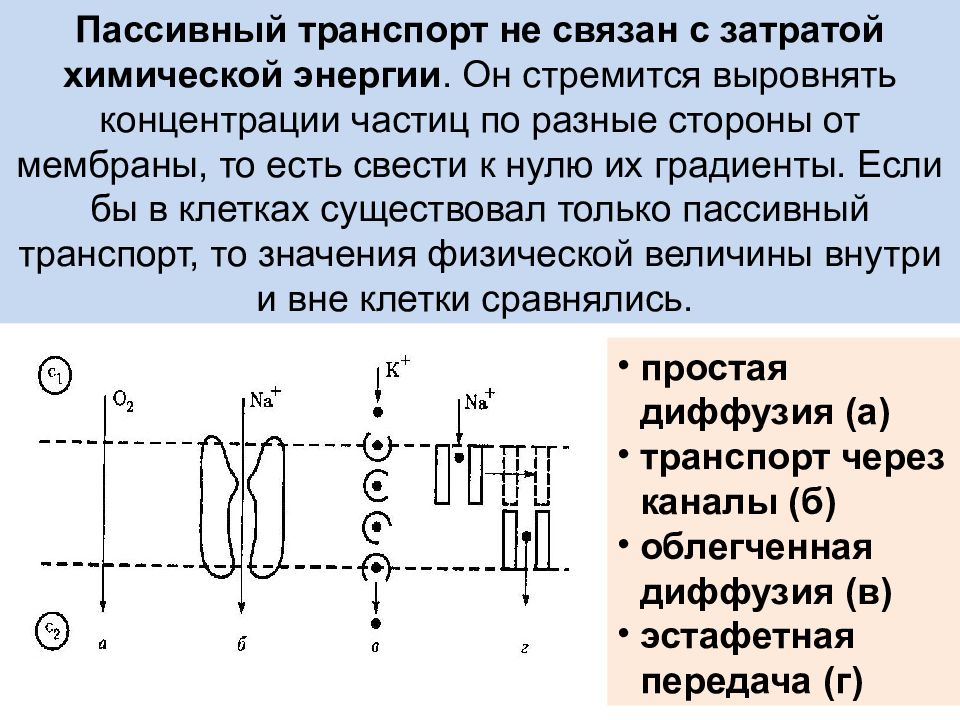
Слайд 32
Пассивный транспорт не связан с затратой химической энергии. Он стремится выровнять концентрации частиц по разные стороны от мембраны, то есть свести к нулю их градиенты. Если бы в клетках существовал только пассивный транспорт, то значения физической величины внутри и вне клетки сравнялись. простая диффузия (а) транспорт через каналы (б) облегченная диффузия (в) эстафетная передача (г)
Слайд 33: Пассивный и активный транспорт
Чтобы определить вид транспорта нужно знать, где и каких веществ больше. 1. Концентрация К + внутри клетки в 20-40 раз больше чем снаружи; 2. Концентрация Na + снаружи клетки в 10-20 раз больше, чем внутри; 3. Концентрация Cl - снаружи клетки в 10-20 раз больше, чем внутри. Пассивный и активный транспорт
Слайд 34: Функции АТ
Создание градиента концентрации вещества Создание градиента электрического потенциала Создание градиента давления АТ УДЕРЖИВАЕТ ОРГАНИЗМ В НЕРАВНОВЕСНОМ СОСТОЯНИИ Функции АТ
Слайд 35
Активный транспорт — перенос молекул и ионов, который происходит при затрате химической энергии в направлении от меньших значений величин к большим. При этом нейтральные молекулы переносятся в область большей концентрации, а ионы переносятся против сил, действующих на них со стороны электрического поля. Экспериментально установлено, что энергии распада одной молекулы АТФ достаточно для выведения наружу трех ионов натрия и введения внутрь клетки двух ионов калия.
Слайд 36
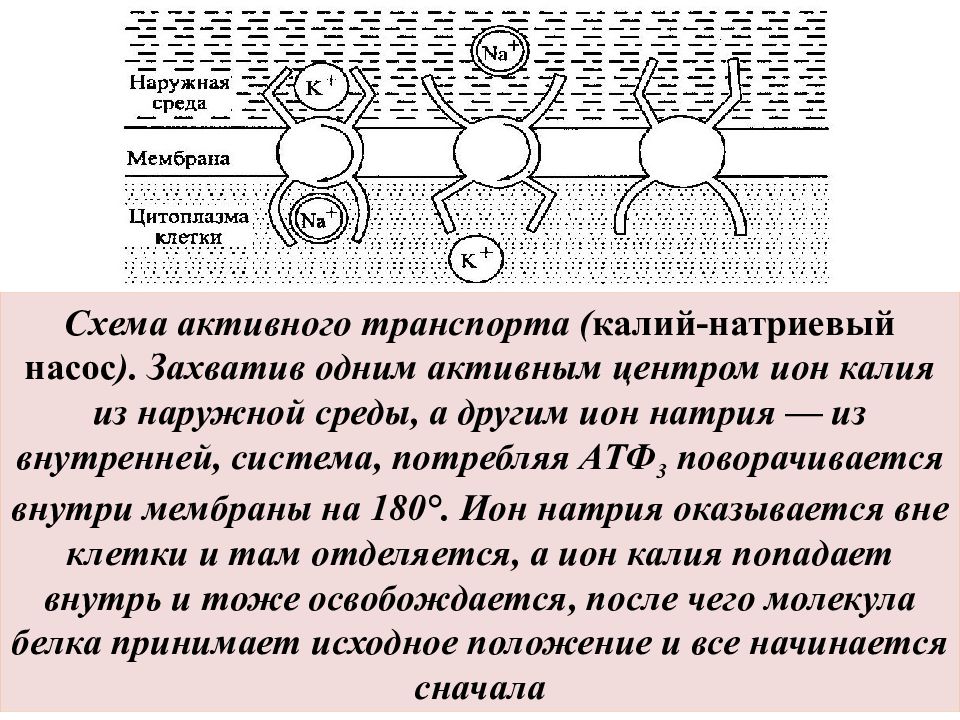
Схема активного транспорта ( калий-натриевый насос ). Захватив одним активным центром ион калия из наружной среды, а другим ион натрия — из внутренней, система, потребляя АТФ 3 поворачивается внутри мембраны на 180°. Ион натрия оказывается вне клетки и там отделяется, а ион калия попадает внутрь и тоже освобождается, после чего молекула белка принимает исходное положение и все начинается сначала
Слайд 37
Одна из важнейших функций биологической мембраны - генерация и передача биопотенциалов. Это явление лежит в основе возбудимости клеток, регуляции внутриклеточных процессов, работы нервной системы, регуляции мышечного сокращения, рецепции. Диагностические методы : электрокардиография, электроэнцефалография, электромиография и другие. Практикуется и лечебное воздействие на ткани и органы внешними электрическими импульсами при электростимуляции.
Слайд 38: ВИДЫ БИОПОТЕНЦИАЛОВ (Б.П.)
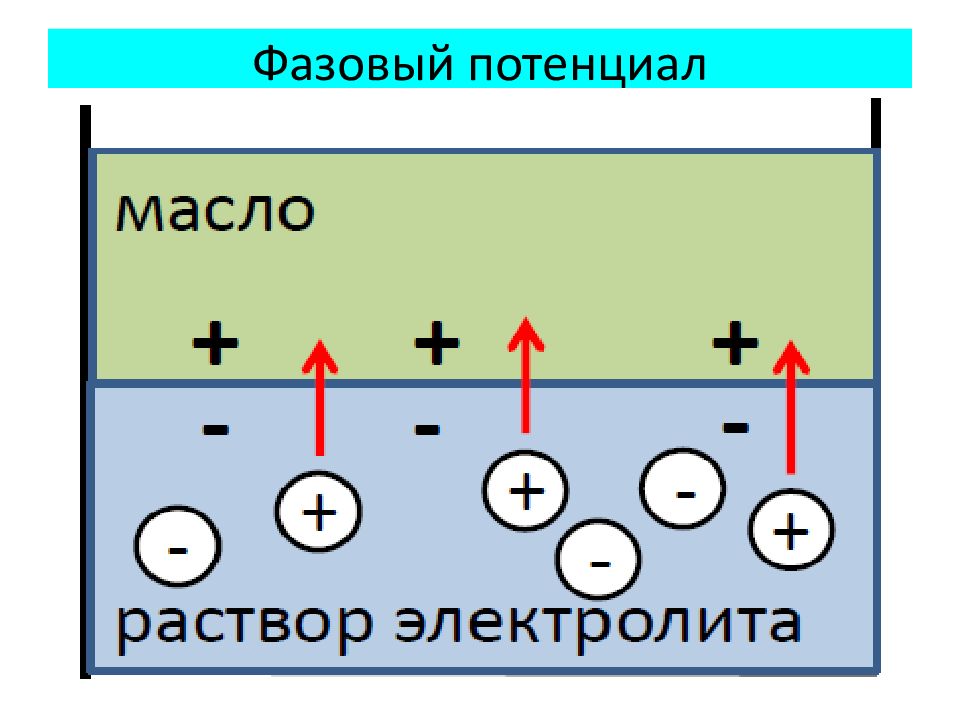
По своей природе Б.П. подразделяют на дифузионные, фазовые и мембранные. Диффузионные – потенциалы, возникающие на границе раздела двух жидких сред в результате наличия градиента концентраций веществ и различной подвижности ионов (катионов и анионов).
Слайд 40
Мембранные - вследствие градиента концентрации ионов и переноса ионов через мембрану. Биопотенциалы, регистрируемые в организме, — это в основном мембранные потенциалы ( потенциалы покоя и потенциалы действия ). Мембранным потенциалом называется разность потенциалов между внутренней (цитоплазматической) и наружной поверхностями мембраны : ∆φ м =φ вн -φ нар
Слайд 41
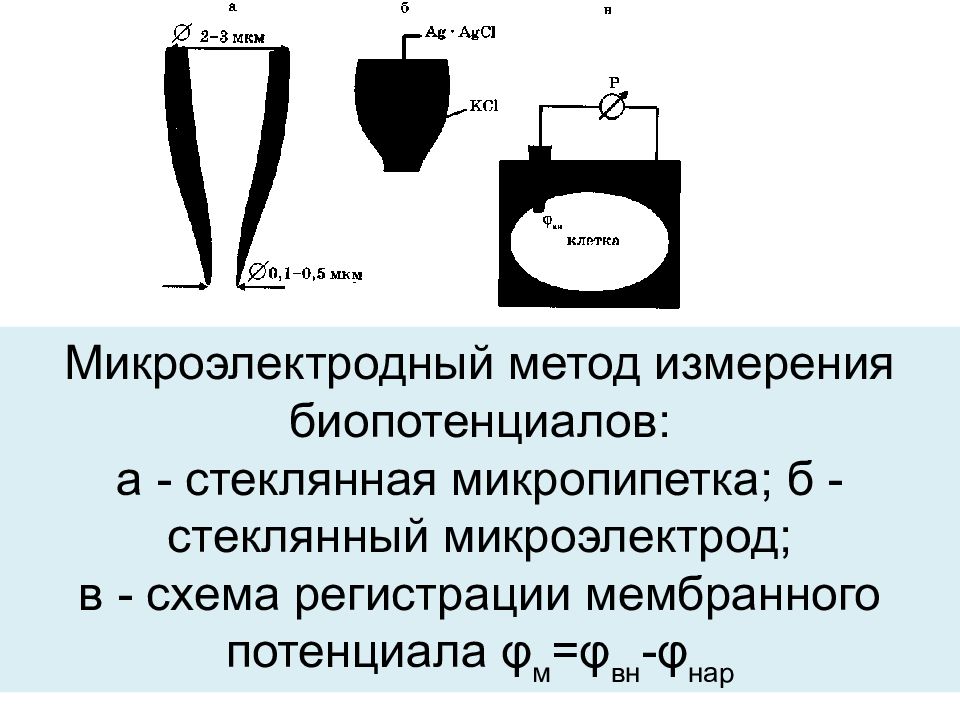
Микроэлектродный метод измерения биопотенциалов: а - стеклянная микропипетка; б - стеклянный микроэлектрод ; в - схема регистрации мембранного потенциала φ м = φ вн -φ нар
Слайд 42
Потенциал покоя - стационарная разность электрических потенциалов, регистрируемая между внутренней и наружной поверхностями мембраны в невозбужденном состоянии. Потенциал покоя определяется разной концентрацией ионов по разные стороны мембраны и диффузией ионов через мембрану. Формула Нернста-Планка для равновесного мембранного потенциала
Слайд 43
Одновременная диффузия через мембрану ионов К +, Na + и С l - учитывается уравнением Гольдмана. В состоянии покоя проницаемость мембраны для ионов К + значительно больше, чем для Na +, и больше, чем для С1 - : Р к >>Р Na, P K > P Cl Для аксона кальмара, например, P K : P Na : P Cl = 1 : 0,04 : 0,4
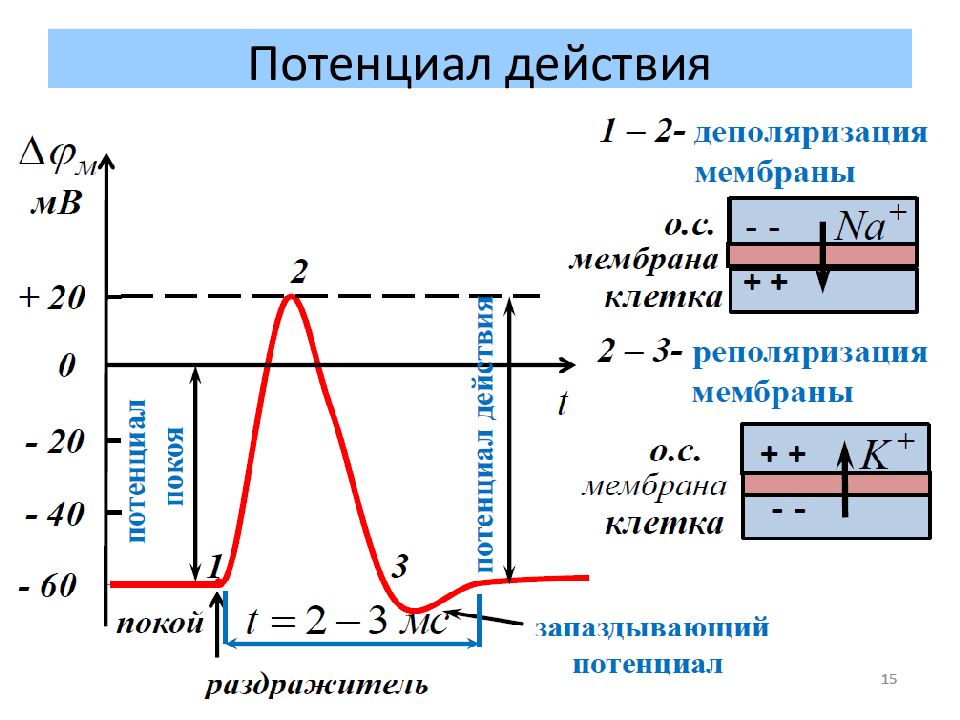
Слайд 44: Потенциал действия
Электрический импульс, обусловленный изменением ионной проницаемости мембраны и связанный с распространением по нервам и мышцам волны возбуждения Методы: Микроэлектродов с использованием высокоомных измерителей напряжения Меченных атомов
Слайд 48: Потенциал действия
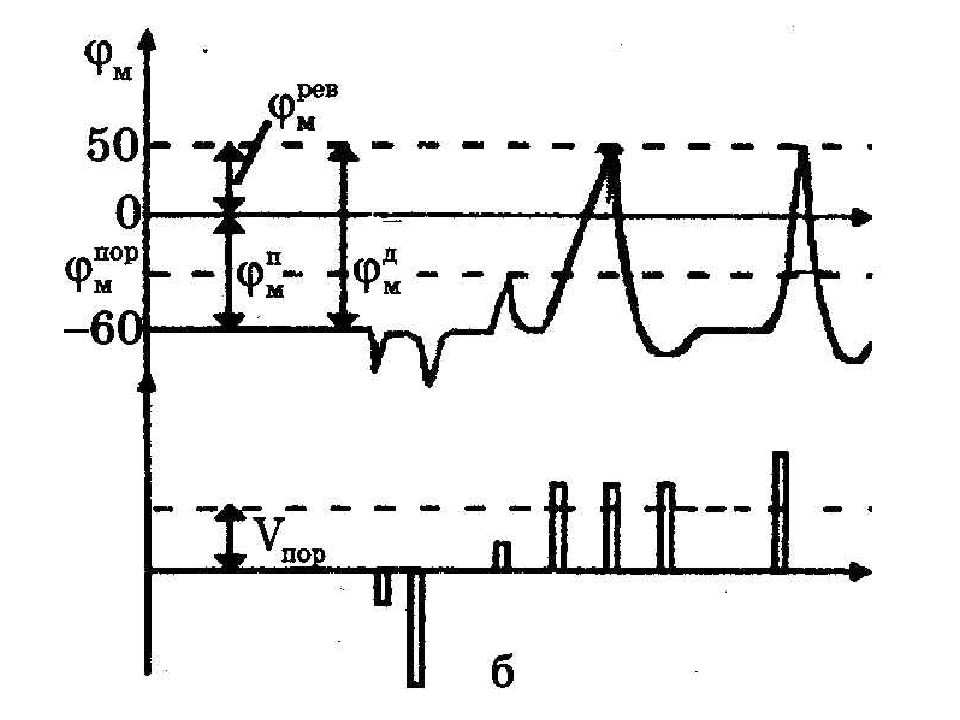
Потенциалом действия называют кратковременное изменение мембранного потенциала под действием пороговых и сверхпороговых раздражителей
Слайд 49
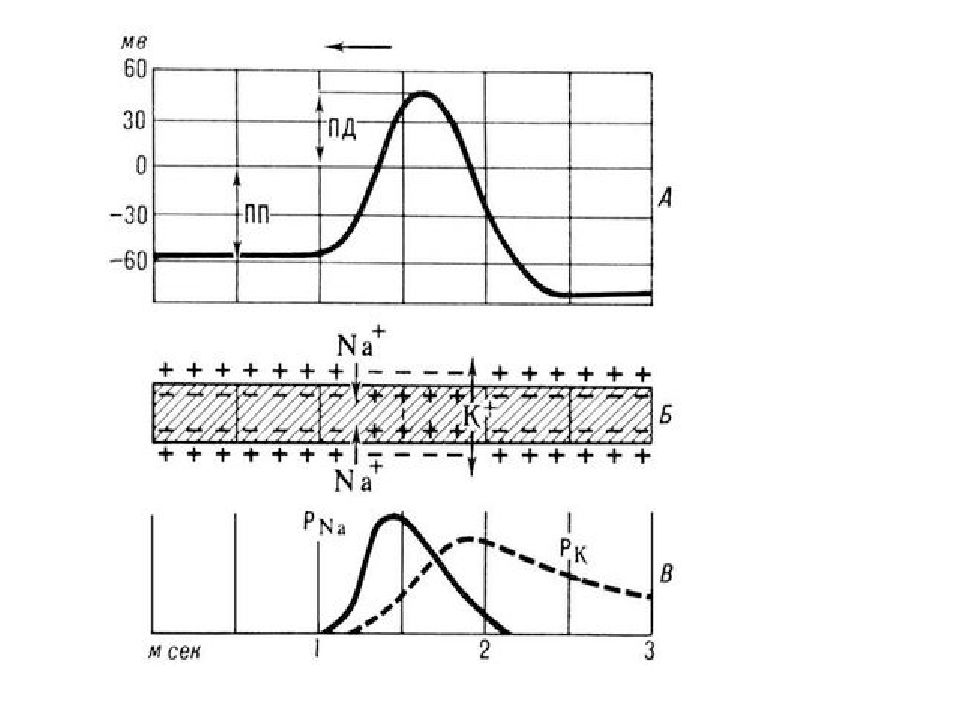
Если в состоянии покоя соотношение коэффициентов проницаемости мембраны аксона кальмара для разных ионов: P K : P Na : P Cl = 1 : 0,04 : 0,45 то в состоянии возбуждения: P K : P Na : P Cl = 1 : 20 : 0,45 то есть, по сравнению с невозбужденным состоянием, при возбуждении коэффициент проницаемости для натрия возрастает в 500 раз.
Слайд 51
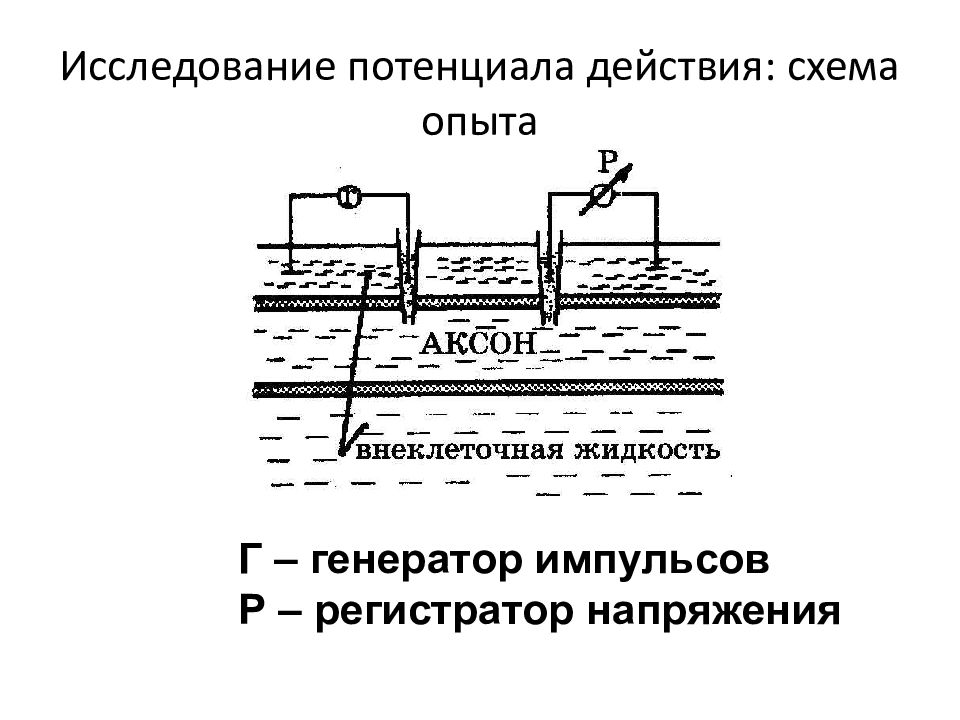
Посредством электрических нервных импульсов (потенциалов действия) в живом организме передается информация от рецепторов к нейронам мозга и от нейронов мозга к мышцам. Живой организм является полностью электрифицированной системой. Без электричества нет жизни. То, что нервный импульс представляет собой импульс электрического тока, было доказано лишь к середине 20-го века, в основном в работах английского физиолога А. Ходжкина и его сотрудников. В1963 году Ходжкину, Хаксли и Иклсу была присуждена Нобелевская премия по медицине "за оперирование нервных клеток" Потенциал действия был открыт раньше потенциала покоя ( 1791 г.) Гальвани.
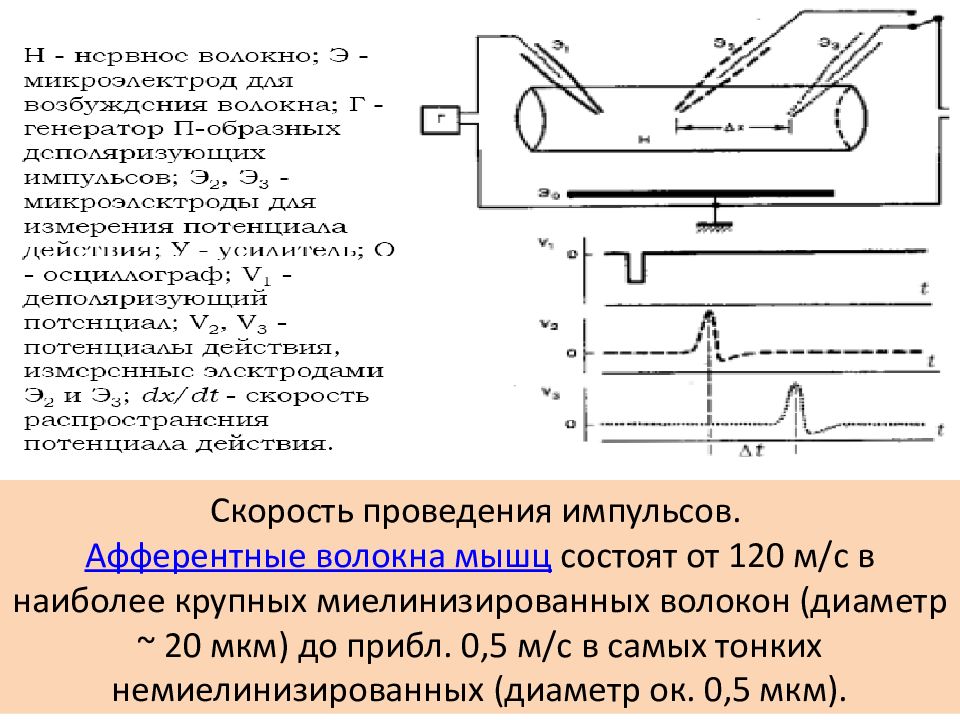
Г – генератор импульсов Р – регистратор напряжения
Слайд 53: Потенциал действия
Общее изменение разности потенциалов между клеткой и средой, происходящее при пороговом и сверхпороговом возбуждении клеток Обеспечивает проведение возбуждения по нервным волокнам Индуцирует процессы мышечного сокращения Индуцирует секрецию железистых клеток
Слайд 54: Свойства ПД
Наличие порогового значения деполяризующего потенциала Закон «все или ничего» Период рефрактерности Резкое снижение сопротивления БМ в момент возбуждения (покой: 0,1 Ом*м 2, возбуждение: 0,0025 Ом*м 2 )
Слайд 55: Распространение «П.Д.» по нервным волокнам
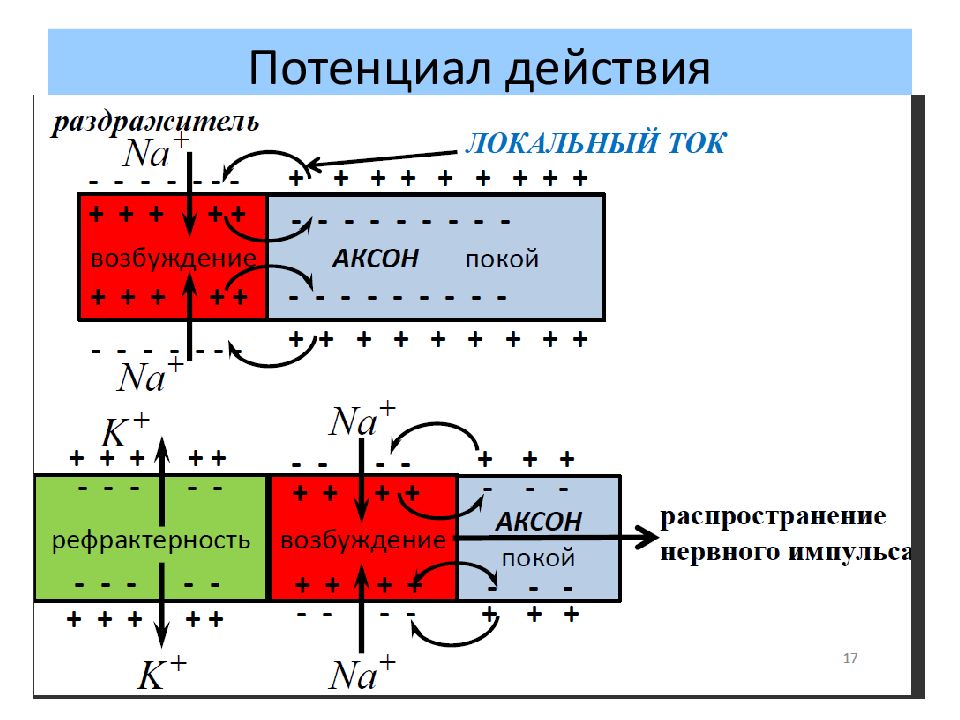
Распространение «П.Д.» зависит от вида нервных волокон. В случае, когда волокна не имеют миэлиновой оболочки (безмякотные), распространение «П.Д.» происходит вдоль всей поверхности нервного волокна за счет локальных токов, возникающих между возбужденными и невозбужденными участками. Этот процесс происходит с затуханием.
Слайд 56: Распространение «П.Д.» по безмякотным волокнам
U = U 0 e - x/ Распространение происходит с затуханием!
Слайд 57
Константа длины нервного волокна где r m - удельное электрическое сопротивление оболочки волокна, δ - толщина оболочки, а - радиус нервного волокна, r i - удельное электрическое сопротивление цитоплазмы. Чем больше константа длины мембраны, тем больше скорость распространения нервного импульса.
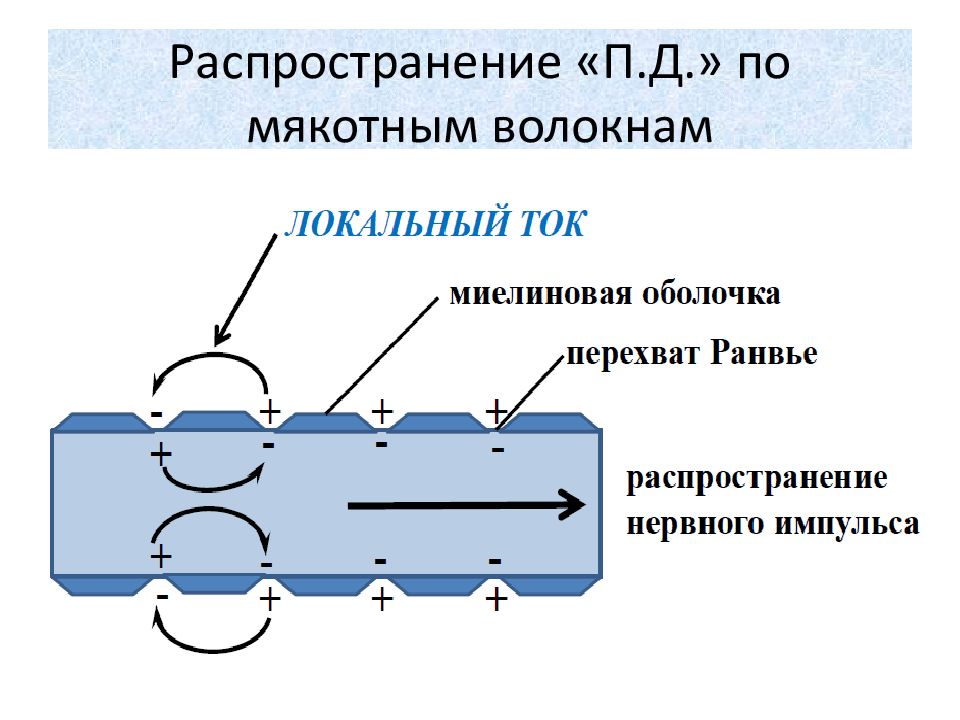
Слайд 58: Распространение «П.Д.» по мякотным волокнам
Распространение «П.Д.» по мякотным волокнам происходит без затухания, сальтаторно (скачкообразно) от одного перехвата Ранвье к другому.
Слайд 60
Скорость проведения импульсов. Афферентные волокна мышц состоят от 120 м/с в наиболее крупных миелинизированных волокон (диаметр ~ 20 мкм) до прибл. 0,5 м/с в самых тонких немиелинизированных (диаметр ок. 0,5 мкм).
Слайд 61: Примеры задач на уравнение Нернста:
Изменится ли величина потенциала покоя, если при прочих равных условиях температура повысится от 360 С до 400 С? 2 /1 =Т2 / Т1 = (273 + 40) / (273 + 36) = 1,01
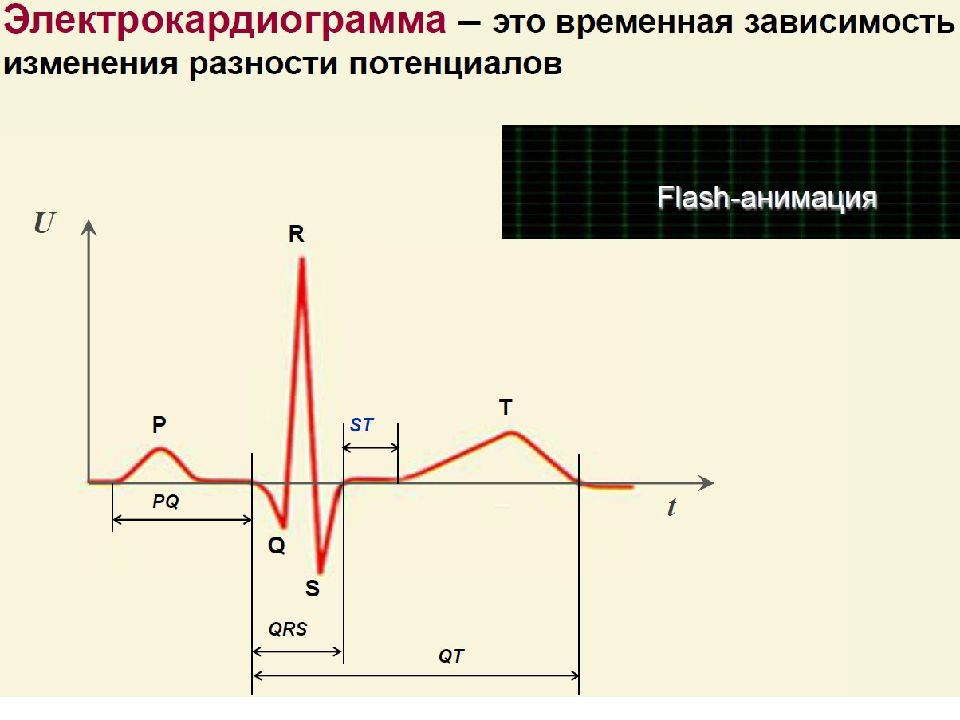
При функционировании органов и тканей, как и отдельных клеток, сопровождающемся электрической активностью, в организме создается электрическое поле. Так как организм является проводником, то два электрода, приложенные к разным участкам тела, регистрируют разность потенциалов. Зависимость от времени разности потенциалов, возникающей при функционировании какого-либо органа или ткани, называется электрограммой.
Слайд 66: Основные задачи изучения электрограмм:
Можно сформулировать две основные задачи изучения электрограмм: первая (прямая) заключается в выяснении механизма возникновения электрограмм, или расчет потенциала в области измерения по заданным характеристикам электрической модели органа; вторая (обратная, или диагностическая) - в выявлении состояния организма по характеру его электрограмм.
Слайд 68: Эквивалентный электрический генератор
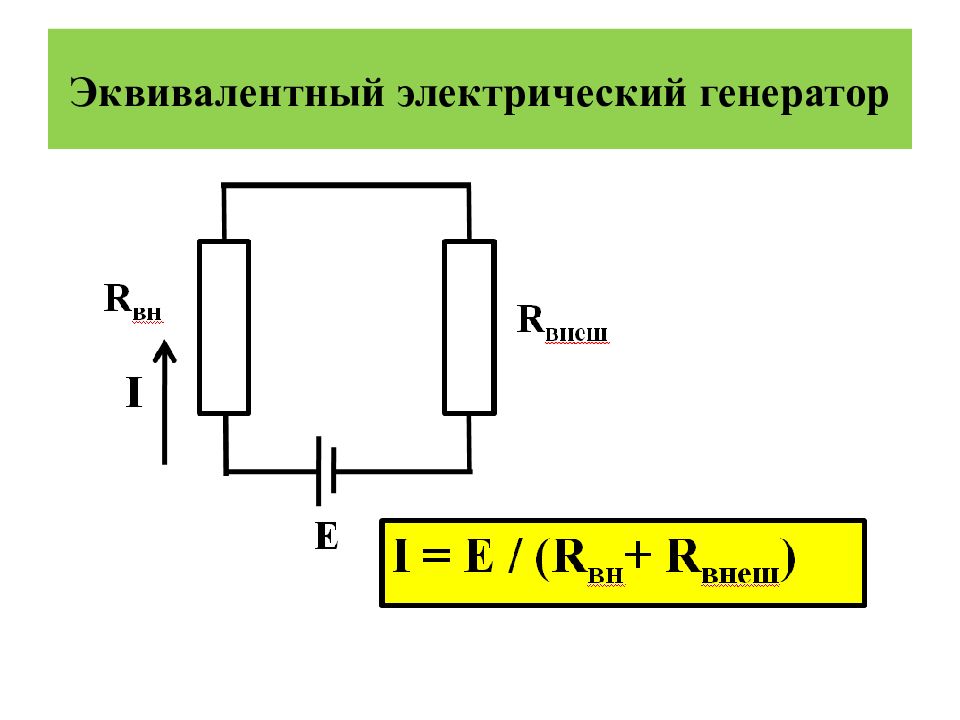
При изучении механизма возникновения электрограмм ткани и органы как источники электрического поля представляют в виде эквивалентного электрического генератора, который можно охарактеризовать электродвижущей силой Е и внутренним сопротивлением R вн. Так как организм является проводящей средой, то это вызывает появление электрического тока, величину которого можно найти из закона Ома для полной цепи.
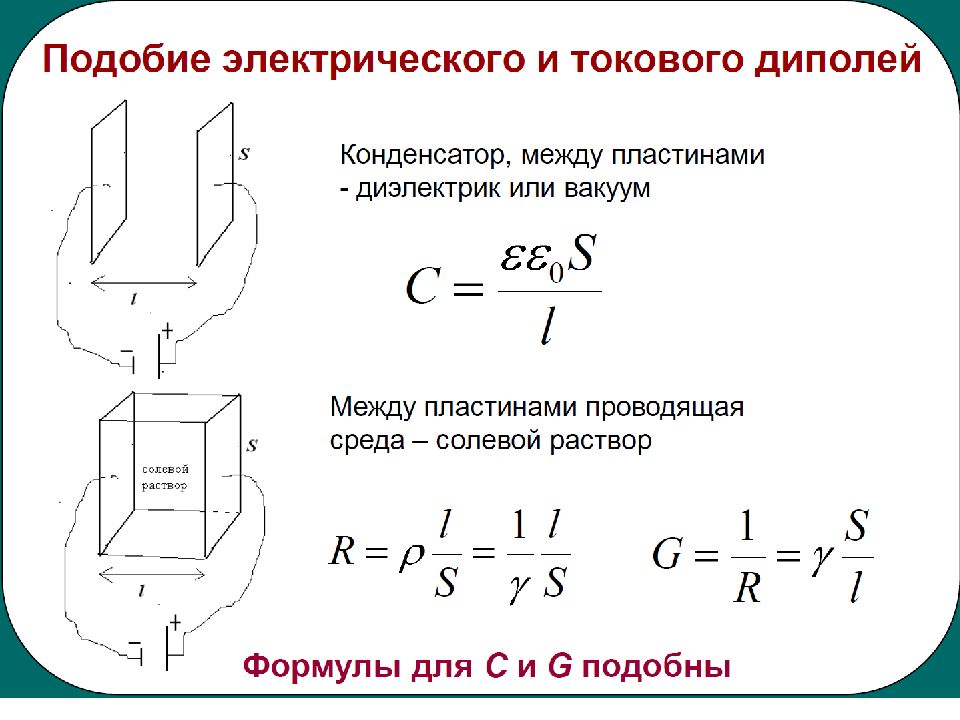
Слайд 70: Понятие о токовом диполе
Особенностью эквивалентного генератора является то, что его внутреннее сопротивление во много раз больше сопротивления, окружающей среды : R вн R Поэтому органы и ткани, электрическую активность которых изучают можно представить в виде токового диполя : D = I •L
Слайд 73: Токовый диполь
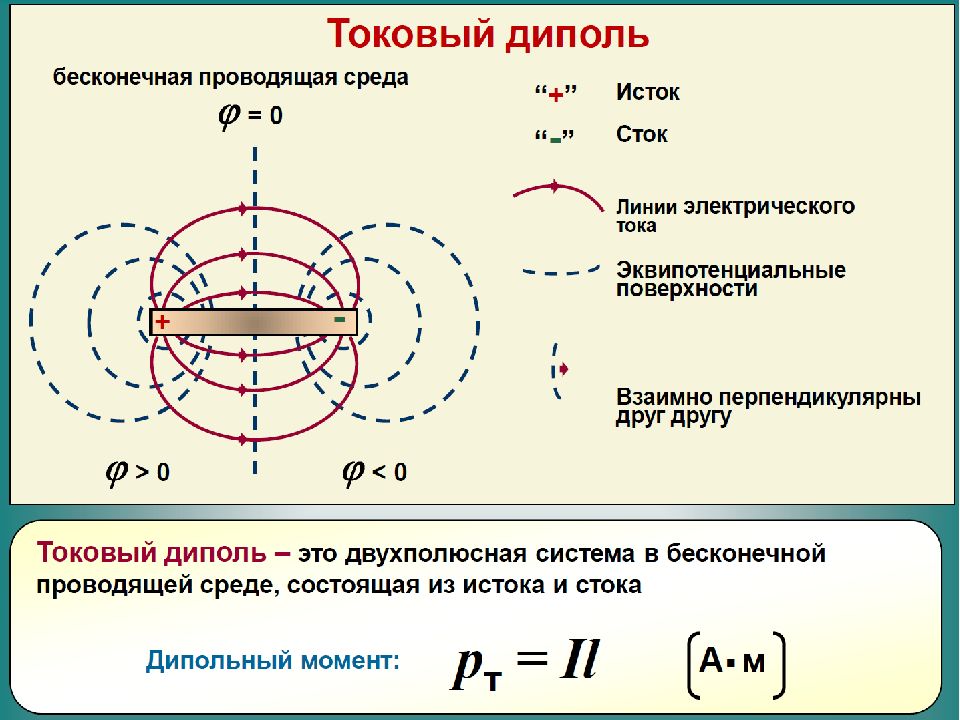
Направление вектора токового дипольного момента принимается от отрицательного полюса к положительному. Диполи в зависимости от их размера подразделяют на точечные и конечные. Точечным называют диполь, который занимает бесконечно малый объем пространства.
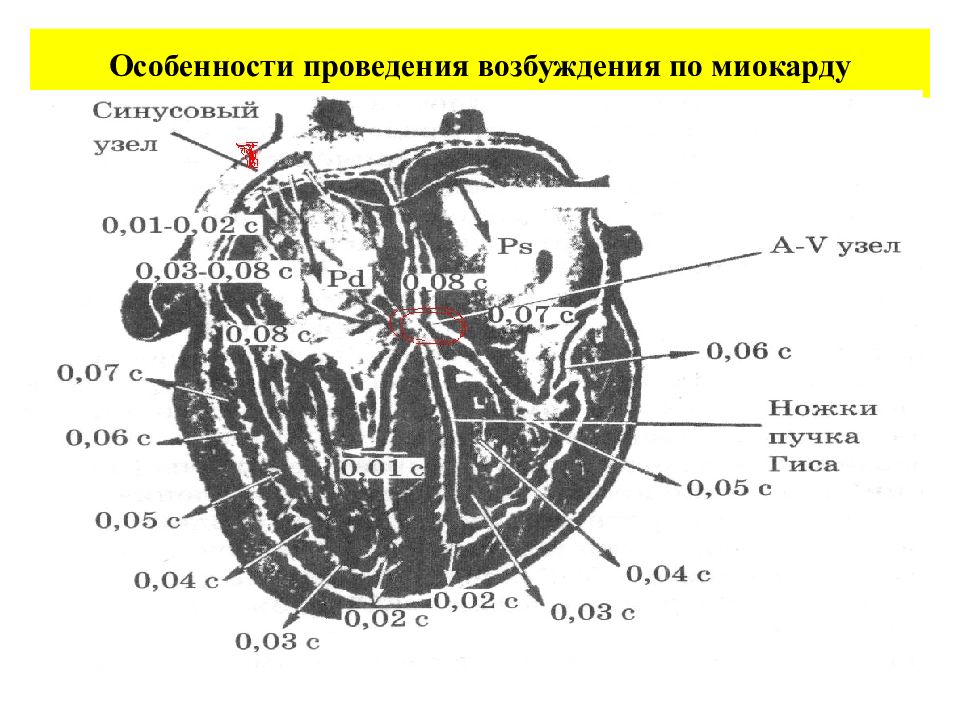
Слайд 80: Особенности проведения возбуждения по миокарду
Периодическая деятельность сердца осуществляется благодаря наличию проводящей системы. Проводящая система сердца начинается синусовым узлом, расположенным в верхней части правого предсердия. В узле находятся два вида клеток: Р- клетки, генерирующие электрические импульсы для возбуждения сердца и Т- клетки, преимущественно осуществляющие проведение импульсов от синусового узла к предсердиям.
Слайд 81: Синусовый узел
Основной функцией синусового узла является генерация электрических импульсов нормальной периодичности, составляющей 60 - 80 импульсов в минуту. Синусовый узел обладает наибольшим автоматизмом и его называют водителем ритма первого порядка.
Слайд 82: Генез электрокардиограммы
Возбуждение синусового узла не отражается на обычной ЭКГ. После латентного периода, продолжающегося несколько сотых долей секунды, импульс из синусового узла достигает миокарда предсердий. Возбуждение охватывает сразу всю толщу миокарда предсердий. На ЭКГ возбуждению предсердий соответствует возникновение Р зубца. Скорость проведения возбуждения по ним составляет 1 м/с.
Слайд 83: Генез электрокардиограммы
Из предсердий импульс попадает в атриовентрикулярный узел, расположенный в нижней части правого предсердия справа от межпредсердной перегородки рядом с устьем коронарного синуса. На уровне атриовентрикулярного узла волна возбуждения значительно задерживается до 5 - 20 см/с, что обусловлено его анатомическими особенностями. Генез электрокардиограммы
Слайд 84: Генез электрокардиограммы
Это создает возможность для окончания возбуждения и сокращения предсердий до того, как начнется возбуждение желудочков. Атриовентрикулярный узел называют автоматическим водителем ритма второго порядка. Водитель ритма второго порядка может вырабатывать 40 - 60 импульсов в минуту. Генез электрокардиограммы
Слайд 85: Генез электрокардиограммы
От атриовентрикулярного узла отходит пучок Гиса, разделяющийся на правую и левую ножки, которые направляются к мышцам правого и левого желудочков, к которым они передают возбуждение по волокнам Пуркинье. Моменту возбуждения желудочков на ЭКГ соответствует комплекс QRS. Фазе реполяризации желудочков соответствует на ЭКГ возникновение Т – зубца. Ножки пучка Гиса и волокна Пуркинье являются автоматическим водителем ритма третьего порядка, вырабатывают 15 - 30 импульсов в минуту. Генез электрокардиограммы
Слайд 86: Генез электрокардиограммы
В норме существует только один водитель ритма, дающий импульсы для возбуждения всего сердца - синусовый узел. Автоматические центры второго и третьего порядка проявляют свою автоматическую функцию только в патологических условиях - при понижении автоматизма синусового узла или при повышении их автоматизма. Генез электрокардиограммы
Слайд 87: Генез электрокардиограммы
Автоматические центры третьего порядка становятся водителями ритма только при одновременном поражении автоматических центров первого и второго порядка или значительном повышении автоматизма центра третьего порядка. Генез электрокардиограммы
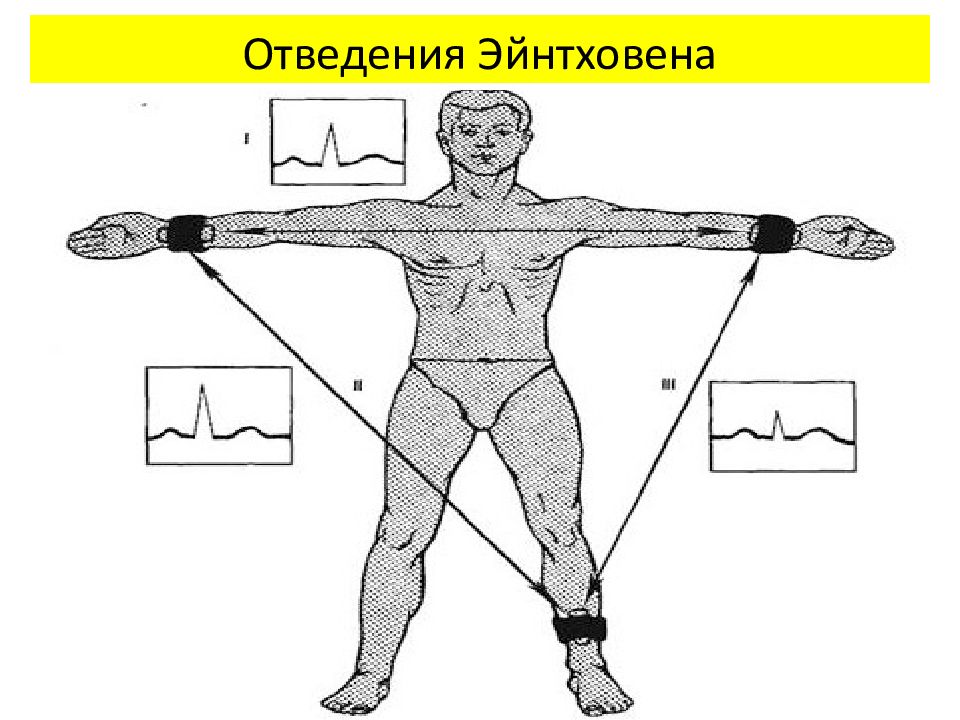
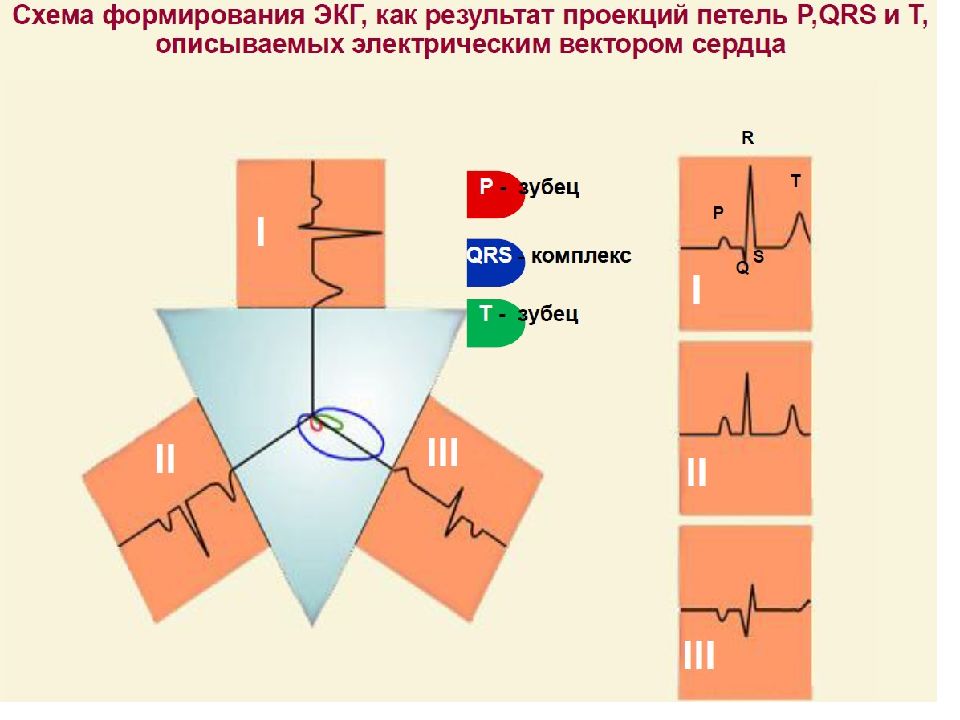
Слайд 88: Теория отведений Эйнтховена
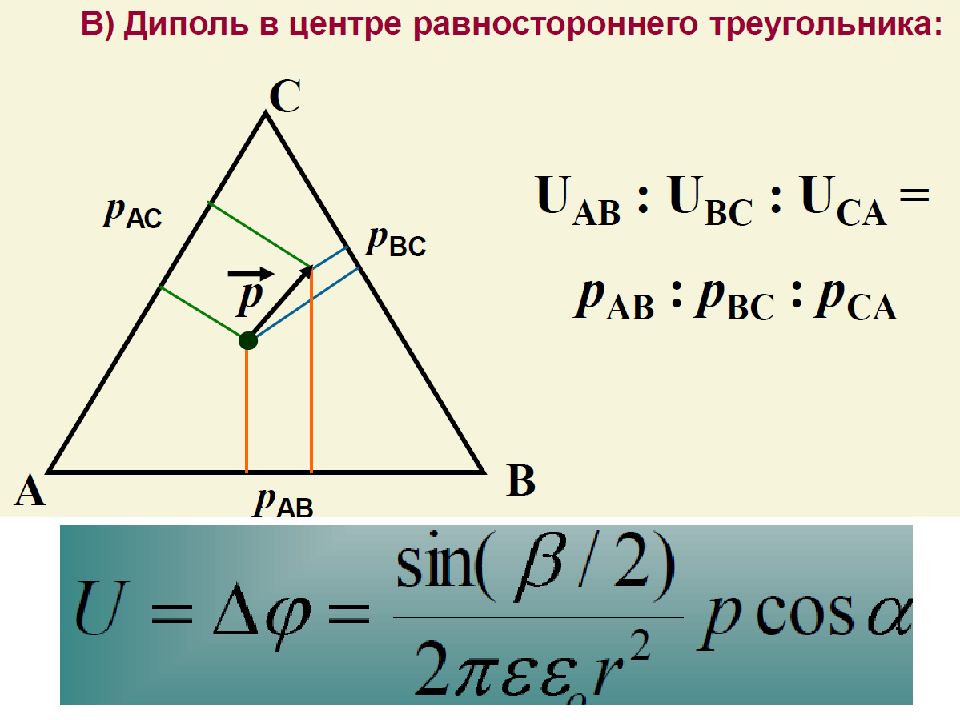
Исследуя изменения разности потенциалов на поверхности человеческого тела, можно судить о проекциях дипольного момента сердца, следовательно, о биопотенциалах сердца. Эта идея положена в основу теории отведений Эйнтховена, голландского ученого, создателя электрокардиографии, нобелевского лауреата 1924 г. Основные постулаты этой модели:
Слайд 89: Основные постулаты Эйнтховена
Эйнтховен сформулировал три постулаты, которые и легли в основу созданной им системы отведений: Рассматривать генератор сердечной ЭДС как точечный диполь. Рассматривать человеческое тело по отношению к этому диполю как однородную проводящую среду. Считать, что точечный диполь расположен в центре равностороннего треугольника, образованного двумя руками и левой ногой. Основные постулаты Эйнтховена
Слайд 93: Векторэлектрокардиограмма
Электрический вектор сердца за один сердечный цикл описывает сложную пространственную кривую. Метод электрокардиографии состоит в регистрации электрического вектора сердца на протяжении кардиоцикла. Траектория перемещения конца электрического вектора сердца в трехмерном пространстве в течение кардиоцикла называется векторэлектрокардиограммой.