Первый слайд презентации: ГЕОДЕЗИЧЕСКИЕ РАБОТЫ ПРИ СТРОИТЕЛЬСТВЕ И ЭКСПЛУАТАЦИИ МОСТОВ
Кафедра Инженерные изыскания и информационные технологии в строительстве 2011 – 12 уч. год Доц. А.Т.Глухов,
Слайд 2: Литература
Основная Интернет- ресурс : Михелев Д.Ш. Инженерная геодезия: учебник /Е.Б. Клюшин [и др.]; под ред. Д.Ш.Михелева, - 9-е изд. стер. – Электронные текстовые данные –М.: ИЦ «Академия», 2008. Инженерная геодезия: учебник для студ. высш. учеб. заведений / Е.Б. Клюшин, М.И. Киселев, Д.Ш. Михелев, В.Д. Фельдман; под ред. Д.Ш. Михелева. – 8-е изд., стер. – М.: Изд. Центр “Академия”, 2008. – 480 с. Федотов Г.А. Инженерная геодезия: учебник / Г.А. Федотов. – 4-е изд. стер. – М.: Высш. шк., 2007. – 463 с. Новиков В.И. Геодезические измерения в строительстве: учеб пособие / В.И.Новиков, А.Б.Рассада. Саратов: РИЦ, СГТУ, 2010, 187 с Новиков В.И. Геодезические съемки: учеб пособие / В.И.Новиков, А.Б.Рассада. Саратов: РИЦ, СГТУ, 2011, 136 с. Дополнительная Брайт П.И. Геодезические методы измерения деформаций оснований и сооружений. М.: Недра, 1965. - 298 с. Левчук. Г.П. Курс инженерной геодезии. Основные виды инженерно-геодезических работ. Геодезические работы при изысканиях и строительстве транспортных и промышленных сооружений. М. : Недра, 1970. - 408 с. Трунин А.Ф., Финаревский И.И., Чистяков С.В. Фототеодолитная съемка в крупных масштабах. Изд. 2, испр. и доп. М.: Недра, 1978. - 207 с. Федоров В.И. Инженерная геодезия: Учебник для вузов. М.: Недра, 19 90. - 357 с.
В период проектирования: сбор исходной картографической информации для принципиального решения вопроса размещения объекта строительства; съемочные работы в крупном масштабе для детального проектирования элементов объекта строительства. В период строительства: определение местоположения площадки строительства и пространственное размещение в плане и по высоте элементов запроектированного сооружения; геодезическое сопровождение строительства объекта для контроля правильности возведения конструкции в целом и взаимного расположения его элементов. В период эксплуатации: исполнительная съемка для контроля правильности завершенного строительства и выявления отступлений от проекта; геодезические работы по определению эксплуатационных сдвигов объекта в целом и смещений его элементов для контроля и прогноза устойчивости конструкции.
Требуемый масштаб составляемого плана
Слайд 5: Методы изысканий дорог и мостов
1. Геодезический метод Назначение морфоствора по карте ; Трассирование автомобильной дороги непосредственно в полевых условиях – определение положения ключевых точек ; Полный комплекс нивелировочных работ по трассе ; Тахеометрическая съемка сложных мест трассы (переходы через овраги, пересечения с иными объектами и др.) ; Привязка трассы к пунктам государственной сети ; Камеральная обработка материалов полевых работ. 2. Метод геоинформатки Съемка местности в крупном масштабе ; Составление электронной версии плана для полосы варьирования трассы ; Камеральное назначение и выбор трассы подходов и морфоствора из множества вариантов ; Камеральное определение координат ключевых точек трассы ; Вынос на местность ключевых точек трассы по координатам ; Трассирование и нивелировочные работы по трассе.
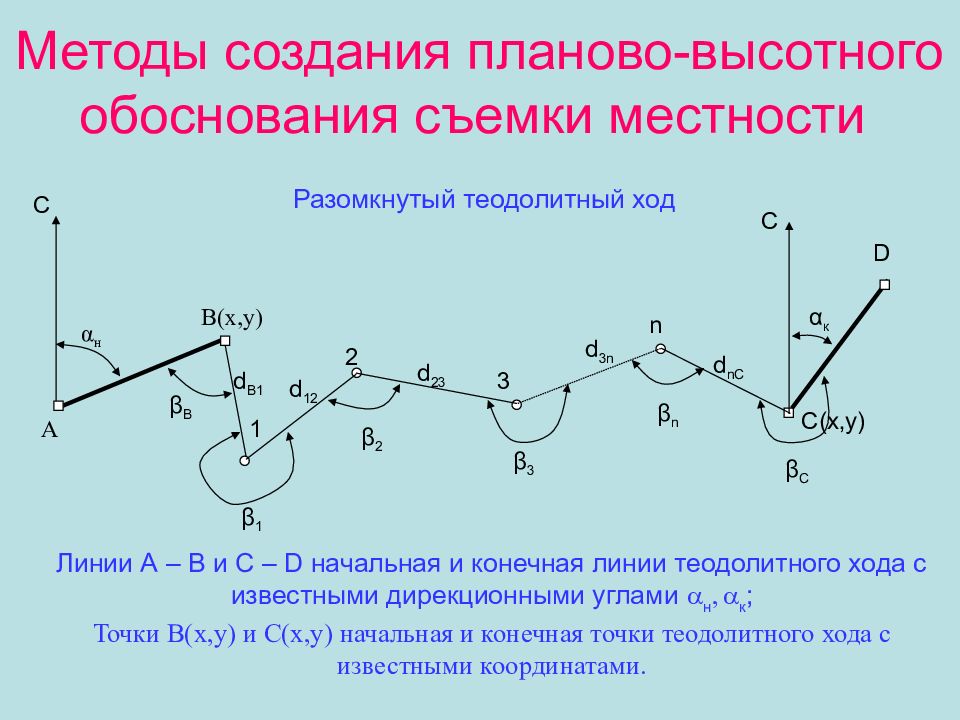
Слайд 6: Методы создания планово-высотного обоснования съемки местности
Разомкнутый теодолитный ход Линии А – В и С – D начальная и конечная линии теодолитного хода с известными дирекционными углами н, к ; Точки В ( x,y) и С (x,y) начальная и конечная точки теодолитного хода с известными координатами. А В (x,y) α н С С α к β В 1 2 3 n β 1 β 2 β 3 β n β C C(x,y) D d B1 d 12 d 23 d 3n d nC
Слайд 7: Вычисление разомкнутого теодолитного хода
Уравнивание углов : Фактическая угловая невязка Допустимая угловая невязка Поправки в измеренные углы Вычисление дирекционных углов линий
Слайд 8: Вычисление разомкнутого теодолитного хода
Уравнивание сторон : Линейные невязки по осям координат : Абсолютная погрешность Относительная погрешность Допустимая относительная погрешность
Слайд 9: Вычисление разомкнутого теодолитного хода
Вычисление координат Поправки в приращения координат Исправленные приращения координат Вычисление координат
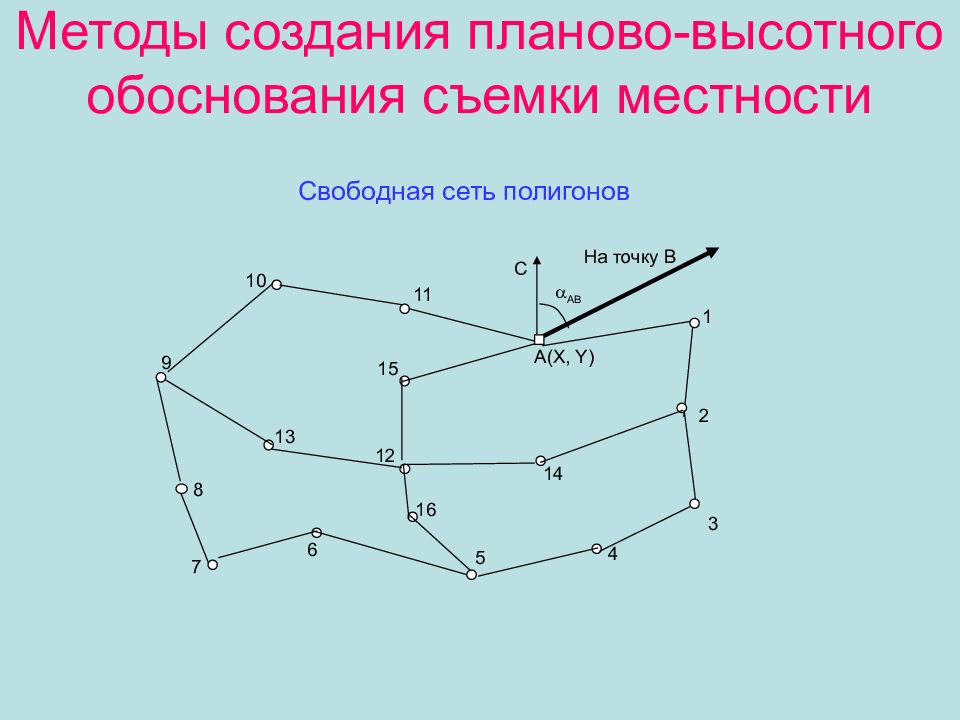
Слайд 10: Методы создания планово-высотного обоснования съемки местности
АВ 2 1 А( X, Y ) На точку В С 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Свободная сеть полигонов
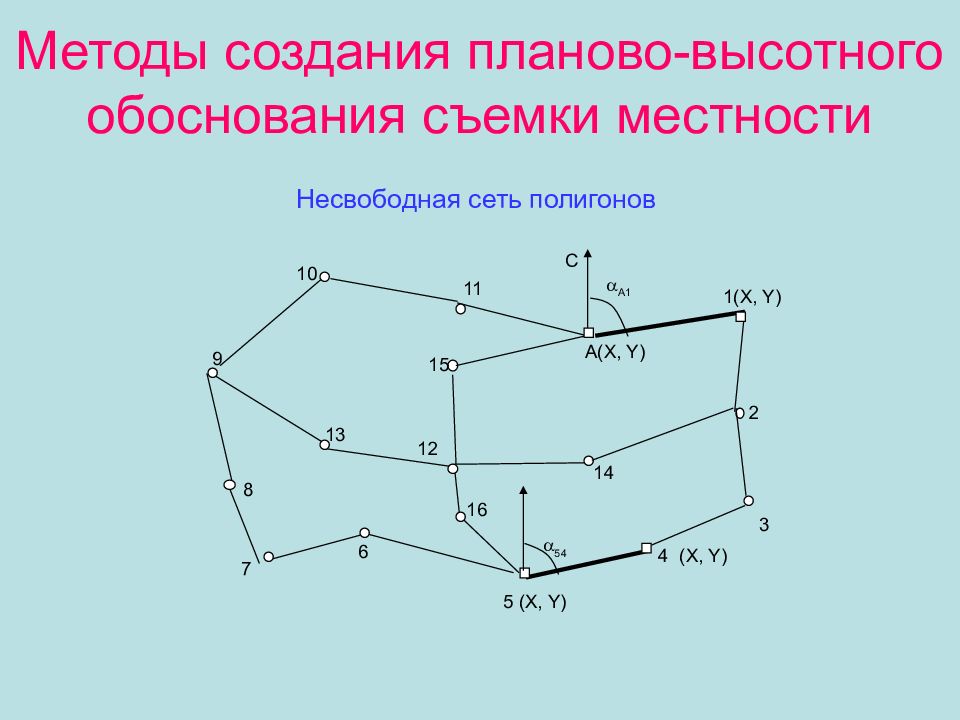
Слайд 11: Методы создания планово-высотного обоснования съемки местности
А1 2 1( X, Y) А( X, Y ) С 3 4 (X, Y) 5 (X, Y) 6 7 8 9 10 11 12 13 14 15 16 54 Несвободная сеть полигонов
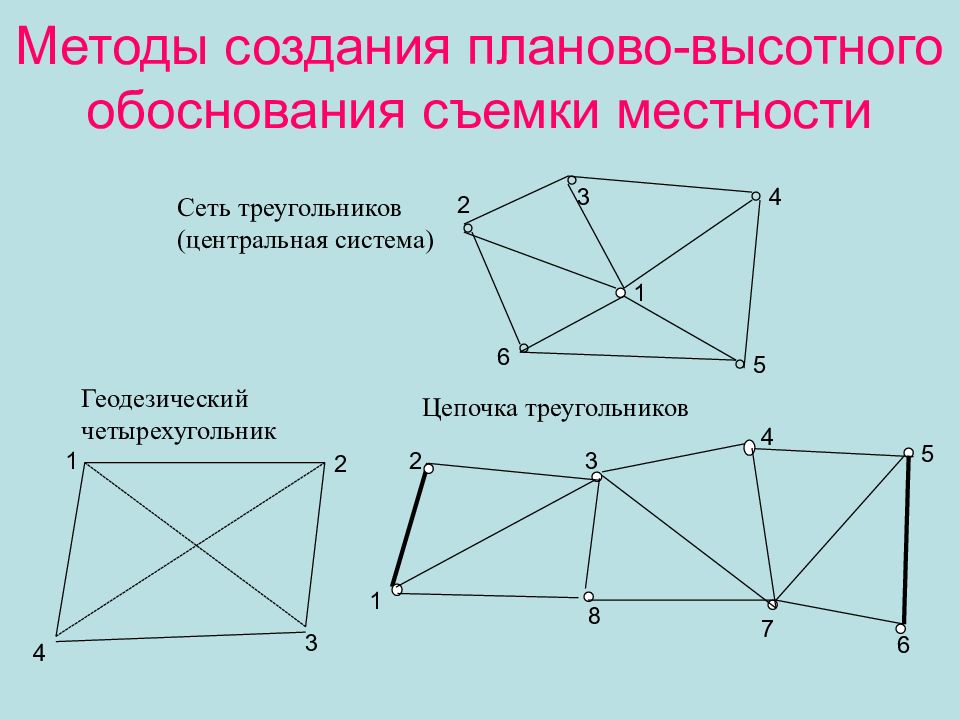
Слайд 12: Методы создания планово-высотного обоснования съемки местности
1 2 3 4 5 6 7 8 1 2 3 4 Сеть треугольников (центральная система) Ц епочка треугольников Геодезический четырехугольник 1 2 3 4 5 6
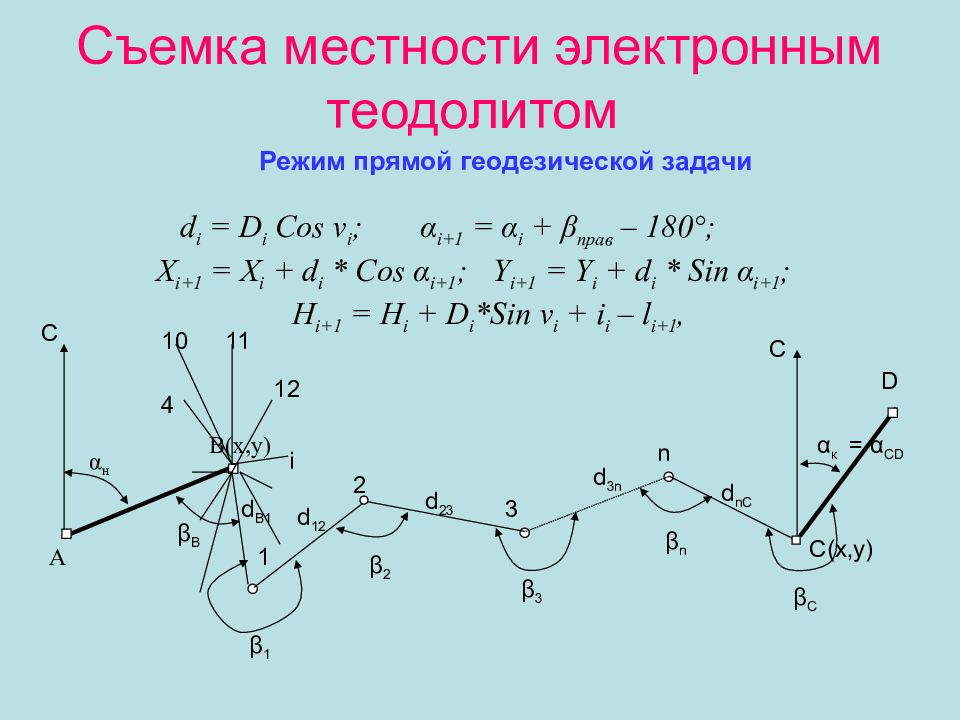
Слайд 13: Съемка местности электронным теодолитом
Режим прямой геодезической задачи d i = D i Cos ν i ; α i+1 = α i + β прав – 180°; X i+1 = X i + d i * Cos α i+1 ; Y i+1 = Y i + d i * Sin α i+1 ; H i+1 = H i + D i *Sin ν i + i i – l i+1, А В (x,y) α н С С α к β В 1 2 3 n β 1 β 2 β 3 β n β C C(x,y) D d B1 d 12 d 23 d 3n d nC 10 11 12 i 4 = α С D
Слайд 14: Съемка местности электронным теодолитом
1. Угловая невязка : : f β = α k - α CD, если, то “недопустимая угловая невязка ”; если,то β i = β i +(- f β / n ), α i +1 = α i + β i – 180°; 2. Линейная невязка : f x = X k - X С, f y = Y k - Y C, ; если f абс /∑ d ≥ 0.0005, то “недопустимая линейная невязка ” если f абс /∑ d ≤ 0.0005, то X i +1 = X i + d i * Cos α i + ; Y i +1 = X i + d i * Sin α i + 3. Высотная невязка : f H = H k - H C ; если f H ≥, то“недопустимая высотная невязка” если f H ≤, то H i +1 = H i + D i * Sin ν i + i i – l i +
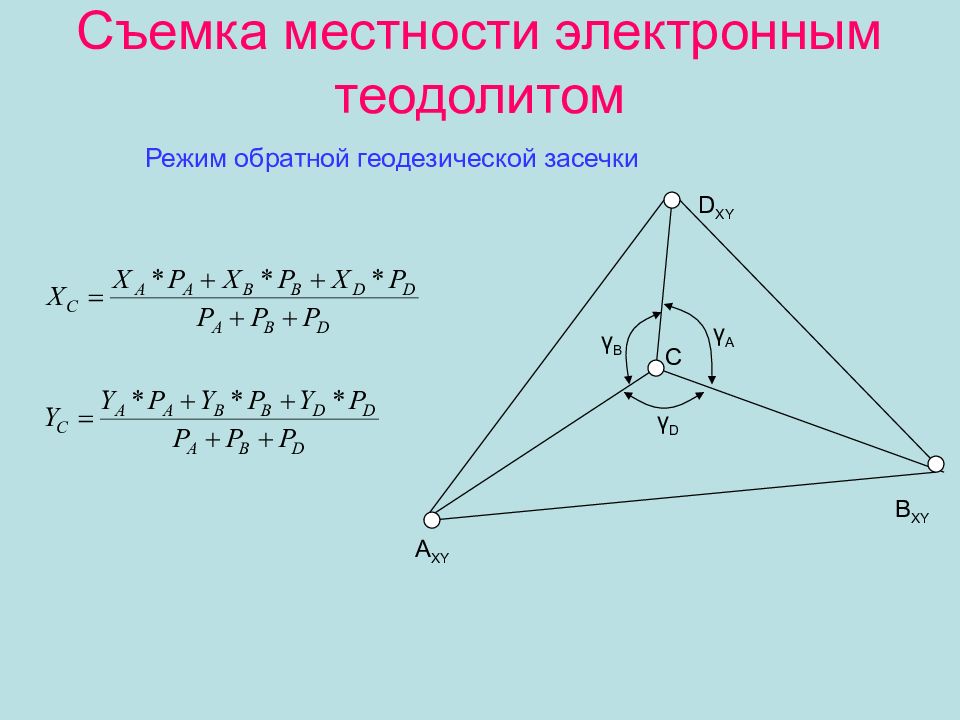
Слайд 15: Съемка местности электронным теодолитом
Режим обратной геодезической засечки А XY В XY D XY C γ D γ A γ B
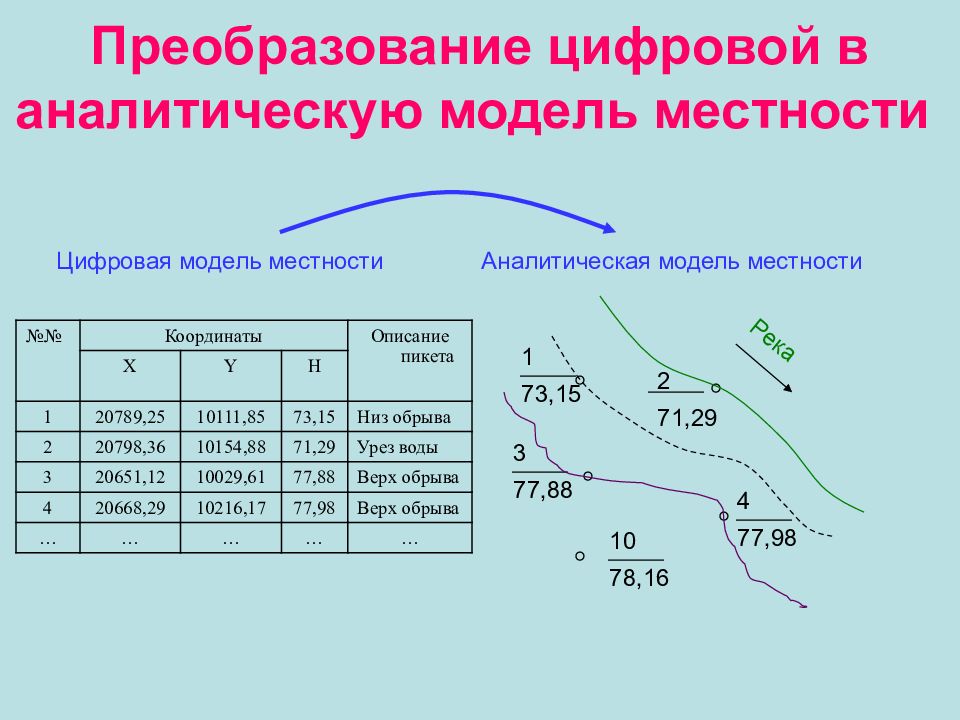
Слайд 16: Преобразование цифровой в аналитическую модель местности
№№ Координаты Описание пикета X Y H 1 20789,25 10111,85 73,15 Низ обрыва 2 20798,36 10154,88 71,29 Урез воды 3 20651,12 10029,61 77,88 Верх обрыва 4 20668,29 10216,17 77,98 Верх обрыва … … … … … 1 73,15 2 71,29 3 77,88 4 77,98 10 78,16 Река Цифровая модель местности Аналитическая модель местности
Слайд 17: Спутниковые методы геодезических измерений
ГЛОНАСС – ГЛОбальная НАвигационная Спутниковая Система ; NAVSTAR – GPS – NAVigation Sistem with Time And Rangiring – Global Positioning System ( Навигационная система определения расстояний и времени – глобальная позиционирования система). Состоят из трех сегментов : космического, контроля и управления, сегмент пользователя
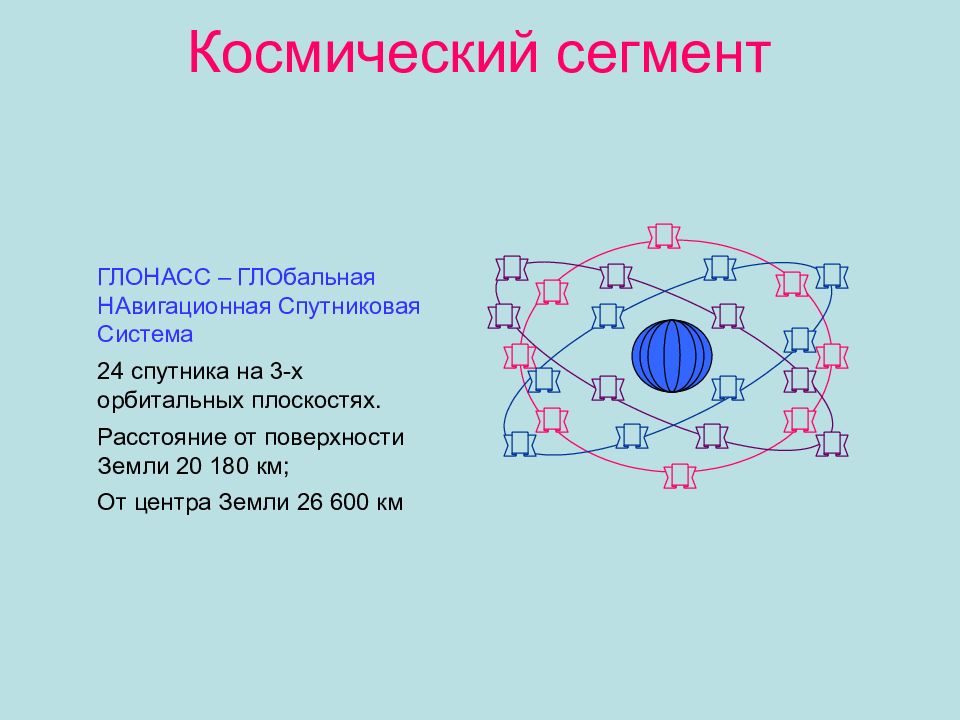
Слайд 18: Космический сегмент
ГЛОНАСС – ГЛОбальная НАвигационная Спутниковая Система 24 спутника на 3-х орбитальных плоскостях. Расстояние от поверхности Земли 20 180 км ; От центра Земли 26 600 км
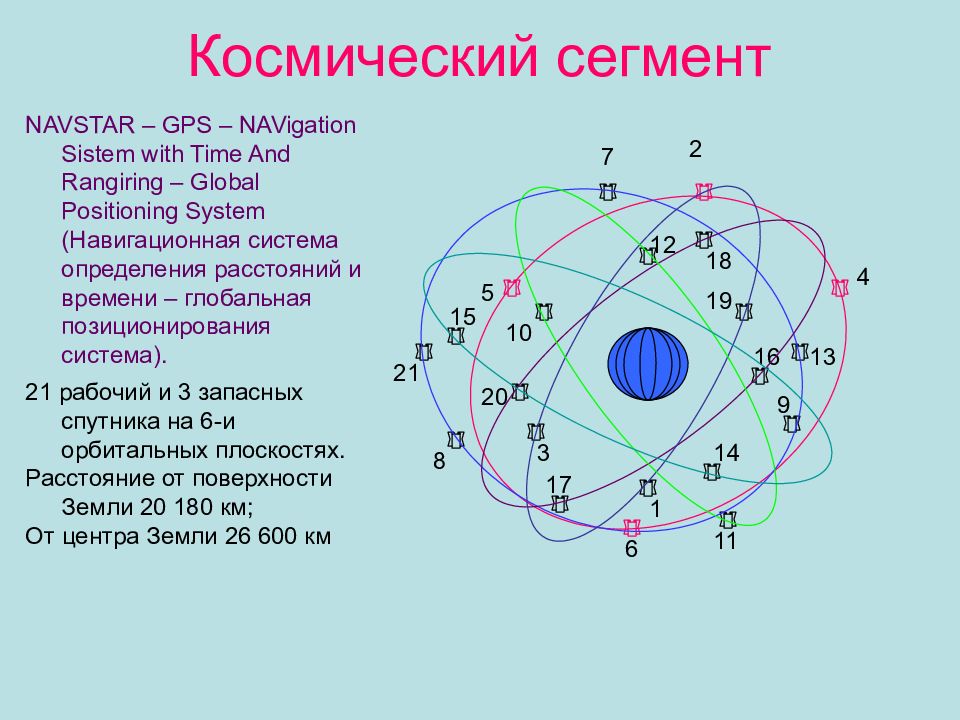
Слайд 19: Космический сегмент
NAVSTAR – GPS – NAVigation Sistem with Time And Rangiring – Global Positioning System ( Навигационная система определения расстояний и времени – глобальная позиционирования система). 21 рабочий и 3 запасных спутника на 6-и орбитальных плоскостях. Расстояние от поверхности Земли 20 180 км ; От центра Земли 26 600 км 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
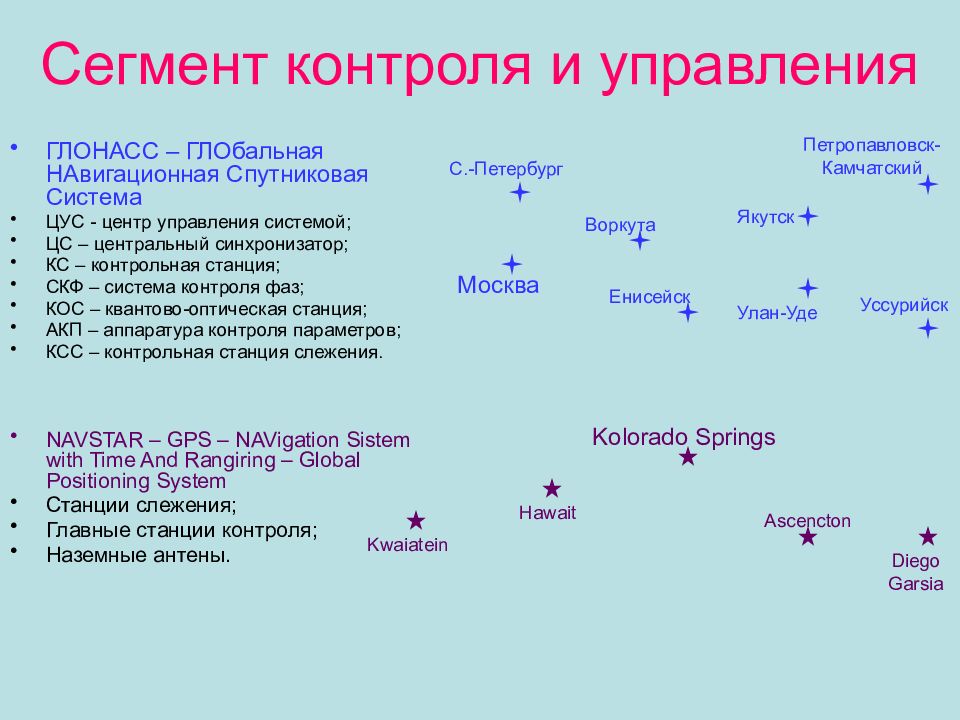
Слайд 20: Сегмент контроля и управления
ГЛОНАСС – ГЛОбальная НАвигационная Спутниковая Система ЦУС - центр управления системой ; ЦС – центральный синхронизатор ; КС – контрольная станция ; СКФ – система контроля фаз ; КОС – квантово-оптическая станция ; АКП – аппаратура контроля параметров ; КСС – контрольная станция слежения. NAVSTAR – GPS – NAVigation Sistem with Time And Rangiring – Global Positioning System Станции слежения ; Главные станции контроля ; Наземные антены. С.-Петербург Москва Воркута Якутск Петропавловск- Камчатский Енисейск Улан-Уде Уссурийск Kwaiatein Hawait Kolorado Springs Ascencton Diego Garsia
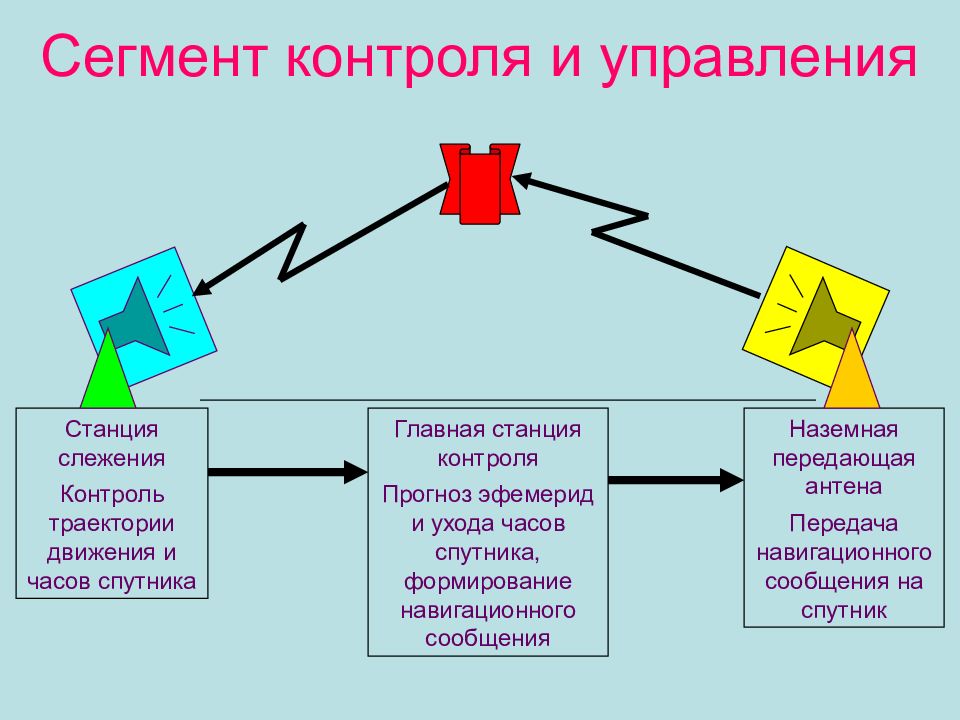
Слайд 21: Сегмент контроля и управления
Станция слежения Контроль траектории движения и часов спутника Главная станция контроля Прогноз эфемерид и ухода часов спутника, формирование навигационного сообщения Наземная передающая антена Передача навигационного сообщения на спутник
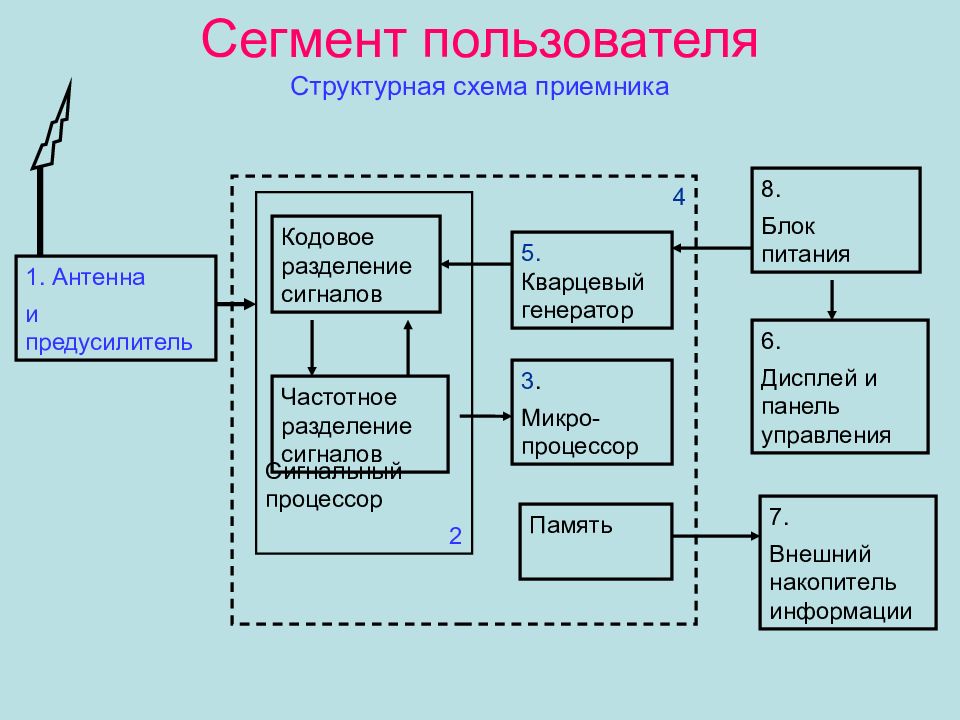
Слайд 22: Сегмент пользователя Структурная схема приемника
Частотное разделение сигналов Кодовое разделение сигналов 8. Блок питания 6. Дисплей и панель управления 7. Внешний накопитель информации 5. Кварцевый генератор 3. Микро-процессор Память Сигнальный процессор 2 1. Антенна и предусилитель 4
Слайд 23: Сегмент пользователя Структурная схема приемника
Антена с предусилителем ; Идентификатор сигралов и распределение частот по каналам ; Микропроцессор для управления работой приемника ; Расшифровка принятой информации, вычисление абсолютных координат и поправок в часы приемника, выполнение фазовых измерений ; Стабильный кварцевый генератор ; Дисплей и панель управления ; Блок памяти для записи и хранения информации ; Блок питания.
Слайд 24: Сегмент пользователя
Классификация приемников по кодировке сигнала : C/A код ; C/A код + фазовые измерения на частоте L 1 ; C/A код + фазовые измерения на частотах L 1 и L 2 ; C/A код + P- код + фазовые измерения на частотах L 1 и L 2 ; Определение расстояний и координат приемника Псевдодальность равна D ' = ( T П – Т С ) v ; Расстояние между спутником и приемником равно : D + δtv = ( T П – Т С ) v ; ИЛИ
Слайд 25: Сегмент пользователя
Режимы наблюдений : Статика ; Быстрая статика ; Кинематика ; Кинематика “ в полете ”; Кинематика в реальном времени. Преобразование координат : X R = X r (1+ μ ) – Z r ω y + Y r ω z + Δ X 0 ; Y R = Y r (1+ μ ) – Z r ω x + X r ω z + Δ Y 0 ; Z R = Z r (1+ μ ) – Y r ω x + X r ω y + Δ Z 0 ;
Слайд 26: Теоретические основы уравнивания геодезических измерений
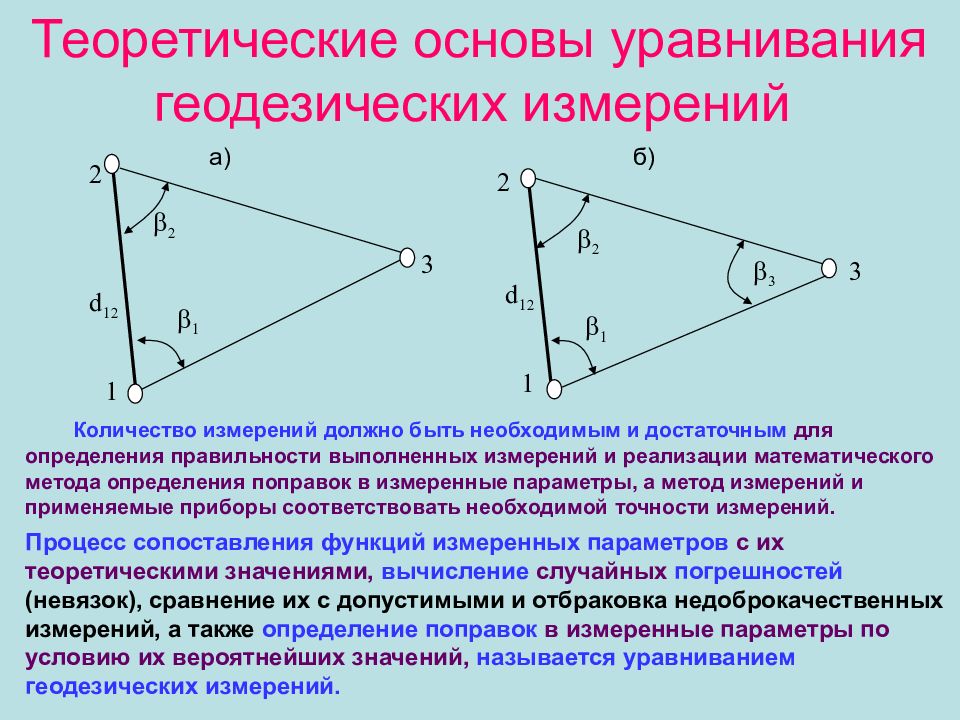
3 Количество измерений должно быть необходимым и достаточным для определения правильности выполненных измерений и реализации математического метода определения поправок в измеренные параметры, а метод измерений и применяемые приборы соответствовать необходимой точности измерений. Процесс сопоставления функций измеренных параметров с их теоретическими значениями, вычисление случайных погрешностей (невязок), сравнение их с допустимыми и отбраковка недоброкачественных измерений, а также определение поправок в измеренные параметры по условию их вероятнейших значений, называется уравниванием геодезических измерений. 1 d 12 2 1 1 2 3 d 12 2 1 2 3 а ) б)
Слайд 27: Теоретические основы уравнивания геодезических измерений Теория способа наименьших квадратов
Имеется серия измеренных параметров, функции которых определяются следующей последовательностью чисел: X 1, X 2, X 3, …, X n. Каждой функции в этой последовательности соответствуют погрешности: ∆ 1, ∆ 2, ∆ 3, …, ∆ n, По теореме умножения вероятностей : (1)
Слайд 28: Теория способа наименьших квадратов
Вероятности появления оптимальных значений совокупности распределения погрешностей в левой части уравнения ( 1 ) будет соответствовать условие : Или для поправок в измеренные параметры Весовой коэффициент равен (2) (3). Подставим (3) в (2), получим основное уравнение поправок → P i V i 2 min (4) Установим вероятнейшее значение величины X при неравноточных измерениях. Так как V i = X ср – X i, то используя (4), имеем f(x) = P i (X ср – X i ) 2 min. Отсюда X ср P i = P i X i, или
Слайд 29: Реализация способа наименьших квадратов Способ полигонов
Уравнивание углов ; Уравнивание приращений координат ; Уравнивание превышений. В основе уравнивания : способ наименьших квадратов ; основное уравнение поправок PV 2 min
Слайд 30: Способ полигонов Уравнивание углов
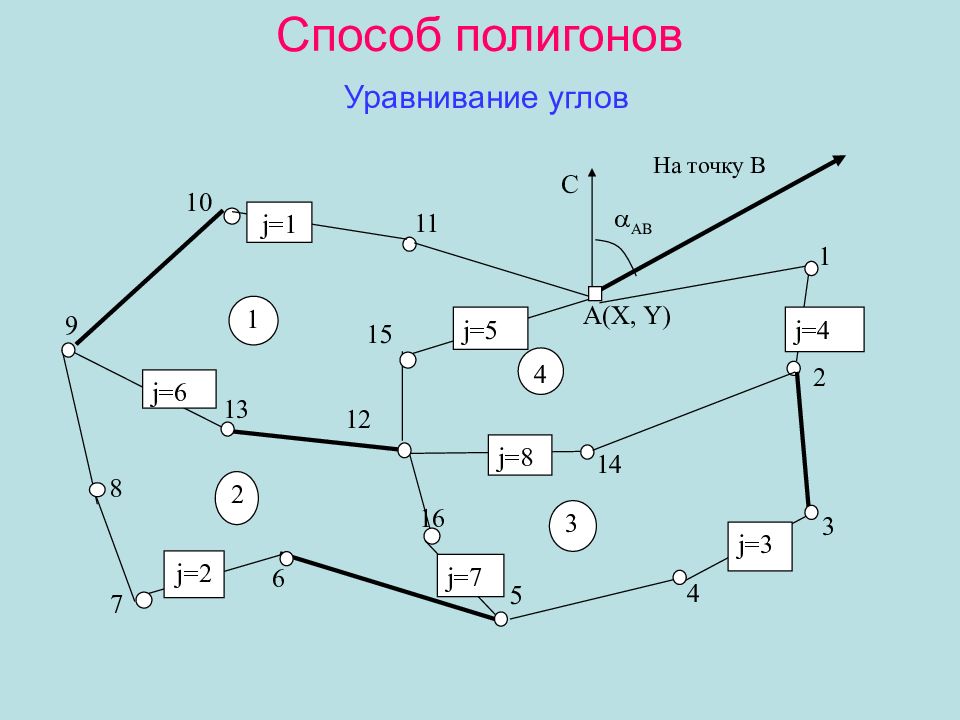
АВ 2 1 А( X, Y ) На точку В С 3 4 5 6 7 8 9 10 11 12 13 14 15 16 j=1 j=2 1 2 3 4 j= 3 j= 4 j= 5 j= 6 j= 7 j= 8
Слайд 31: Способ полигонов Уравнивание углов
Угловые невязки в полигонах Полигон 1, W 1 = – 180( n 1 – 2), n 1 = 7. Полигон 2, W 2 = – 180( n 2 – 2), n 2 = 8. Полигон 3, W 3 = – 180( n 3 – 2), n 3 = 7. Полигон 4, W 4 = – 180( n 4 – 2), n 4 = 6. W 1 + W 2 + W 3 + W 4 = W (1,2,3,4).
Слайд 32: Способ полигонов Уравнивание углов
Вычисление весовых коэффициентов и поправок в углы № звена ( J ) Зачения весовых коэффициентов в полигонах ( i ) Полигон 1 Полигон 2 Полигон 3 Полигон 4 1 3/8 = 0,38 2 4/9 = 0.45 3 3/9 = 0.34 4 3/9 = 0.34 5 3/8 = 0.37 3/9 = 0.33 6 2 /8 = 0.25 2/9 = 0.22 7 3/9 = 0.33 3/9 = 0.33 8 3/9 = 0.33 3/9 = 0.33 1.00 1.00 1.00 1.00 V j(i) = P j(i) W i.
Слайд 33: Способ полигонов Уравнивание приращений координат
Невязки в полигонах по координатам X, Y. Полигон 1, fx 1 = ΣΔ x (1) выч – ΣΔ x теор. fy 1 = ΣΔ y (1) выч – ΣΔ y теор. Полигон 2, fx 2 = ΣΔ x (2) выч – ΣΔ x теор. fy 2 = ΣΔ y (2) выч – ΣΔ y теор. Полигон 3, fx 3 = ΣΔ x (3) выч – ΣΔ x теор. fy 3 = ΣΔ y (3) выч – ΣΔ y теор. Полигон 4, fx 4 = ΣΔ x (4) выч – ΣΔ x теор. fy 4 = ΣΔ y (4) выч – ΣΔ y теор. fx 1 + fx 2 + fx 3 + fx 4 = fx (1,2,3,4). fy 1 + fy 2 + fy 3 + fy 4 = fy (1,2,3,4). ΣΔ x теор = 0 ΣΔ y теор = 0
Слайд 34: Способ полигонов Уравнивание приращений координат
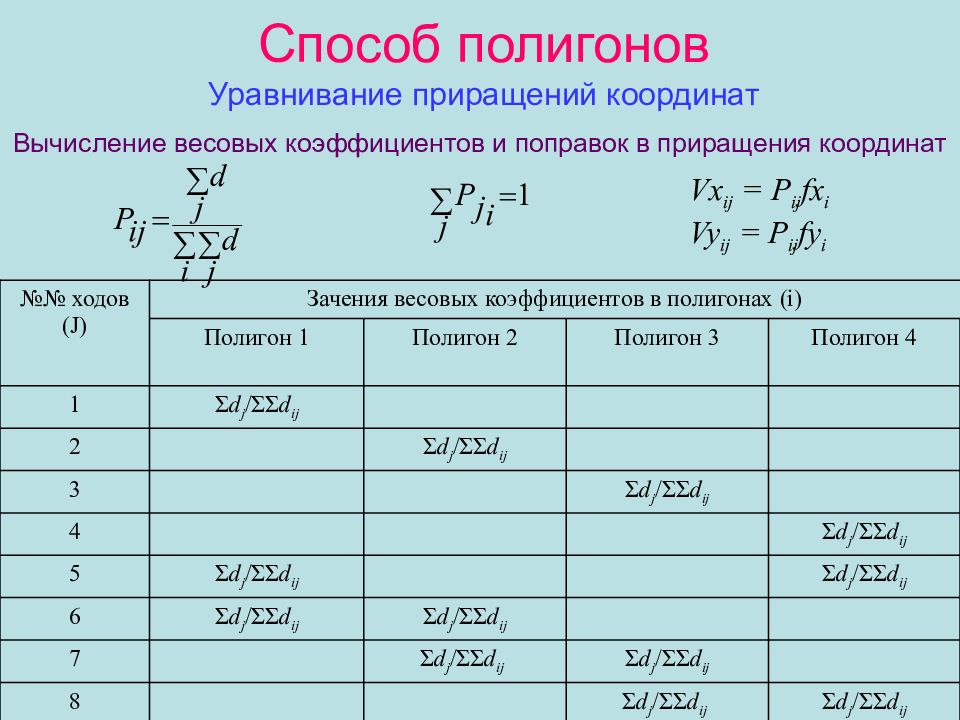
Вычисление весовых коэффициентов и поправок в приращения координат Vx ij = P ij fx i Vy ij = P ij fy i №№ ходов ( J ) Зачения весовых коэффициентов в полигонах ( i ) Полигон 1 Полигон 2 Полигон 3 Полигон 4 1 Σ d j / ΣΣ d ij 2 Σ d j / ΣΣ d ij 3 Σ d j / ΣΣ d ij 4 Σ d j / ΣΣ d ij 5 Σ d j / ΣΣ d ij Σ d j / ΣΣ d ij 6 Σ d j / ΣΣ d ij Σ d j / ΣΣ d ij 7 Σ d j / ΣΣ d ij Σ d j / ΣΣ d ij 8 Σ d j / ΣΣ d ij Σ d j / ΣΣ d ij 1.00 1.00 1.00 1.00
Слайд 35: Способ полигонов Уравнивание превышений, исходные данные
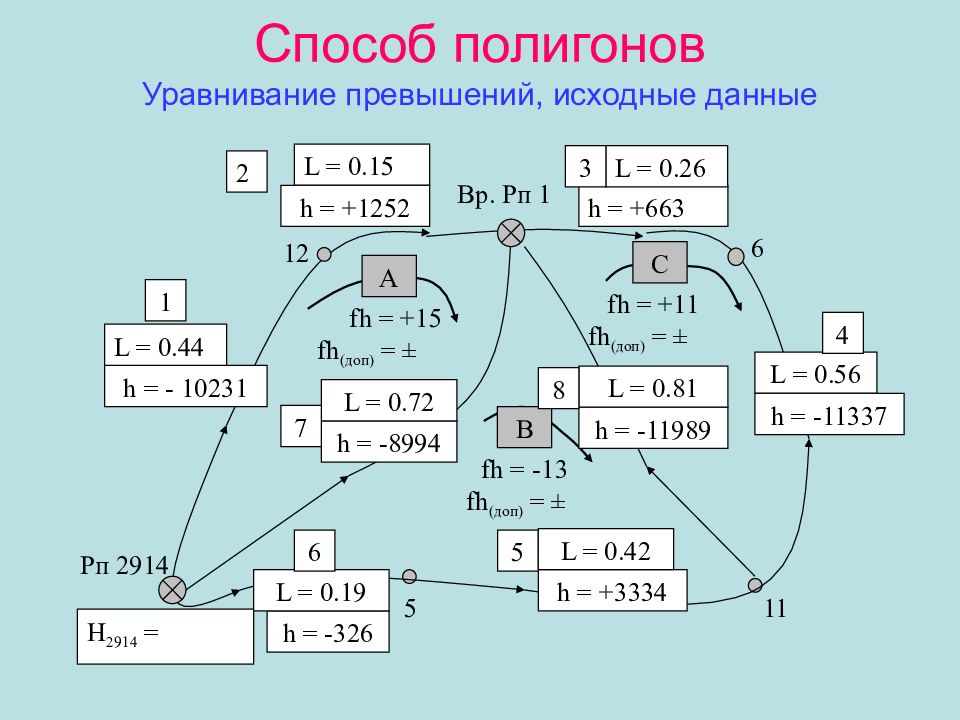
6 Рп 2914 Вр. Рп 1 h = - 10231 h = +1252 h = +663 h = -11337 h = -8994 h = -11989 h = -326 h = +3334 fh = +15 fh ( доп) = ± А В С fh = -13 fh ( доп) = ± fh = +11 fh ( доп) = ± H 2914 = L = 0.44 L = 0.15 L = 0.26 L = 0.56 L = 0.72 L = 0.42 L = 0.81 L = 0.19 1 2 3 4 5 6 7 8 12 11 5
Слайд 36: Способ полигонов Уравнивание превышений
Вычисление невязок в полигонах Полигон А, fh А = Σ h ( А ) выч – Σ h теор = = (-10231 +1252 +8994) - (0) = +15 мм. fh А(доп) = Полигон В, fh В = Σ h ( В ) выч – Σ h теор = = (-8994 +11989 -3334 +326) – (0) = -13 мм. fh А(доп) = Полигон С, fh С = Σ h ( С ) выч – Σ h теор = = (+663 + 11337 – 11989) – (0) = +11 мм. fh А(доп) = fh A + Fh B + fh C = +15 – 13 + 11 = +13 мм. fh (ABC) = - 10231 + 1252 +663 + 11337 – 3334 + 326 = +13 мм
Слайд 37: Способ полигонов Уравнивание превышений
Вычисление весовых коэффициентов и поправок в превышения №№ звена ( J ) Зачения весовых коэффициентов в полигонах ( i ) Полигон А Полигон В Полигон С 1 + 2 (0,44+0,15) / (0.44+0, 15+0, 72)= 0,45 3 + 4 (0, 26+0, 56)/ (0, 26+0, 56+0, 81)= 0.50 5 + 6 0, 42+0, 19)/ (0, 72+0, 81+0, 42+0, 19) = 0.28 7 0, 72/ (0, 44+0, 15+0, 72) = 0,55 0, 72/ (0, 72+0, 81+0, 42+0, 19) = 0.34 8 0, 81/ (0, 72+0, 81+0, 42+0, 19) = 0.38 0,81 / (0, 26+0, 56+0, 81)= 0.50 Σ P 1.00 1.00 1.00 Vh ij = P ij fh i
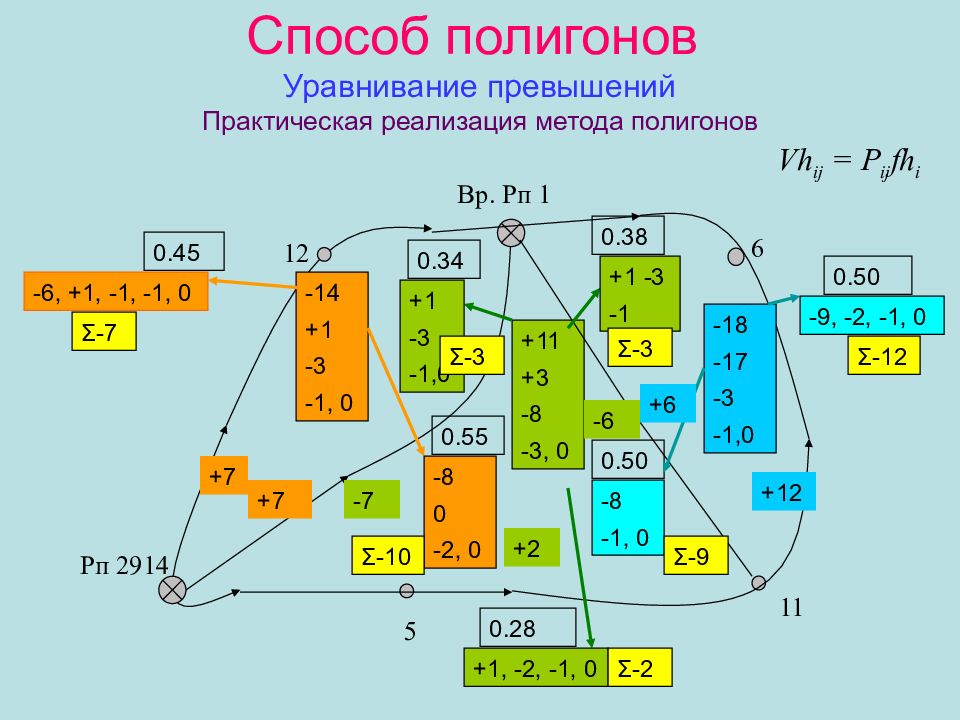
Слайд 38: Способ полигонов Уравнивание превышений Практическая реализация метода полигонов
6 Рп 2914 Вр. Рп 1 12 11 5 - 1 4 +1 -3 -1, 0 +11 +3 -8 -3, 0 - 1 8 -17 -3 -1, 0 Vh ij = P ij fh i 0.45 0.55 0.34 0.38 0.28 0.50 0.50 -6, +1, -1, -1, 0 -8 0 -2, 0 +1 -3 -1,0 +1 -3 -1 +1, -2, -1, 0 -9, -2, -1, 0 -8 -1, 0 Σ -7 Σ -3 Σ -10 Σ -2 Σ -12 Σ -9 Σ -3 +7 +7 -7 -6 +2 +6 +12
Слайд 39: Особенности геодезических работ Изыскания мостовых переходов
Урез воды в бытовом русле по оси мостового перехода; Изменение (превышение) горизонта воды в бытовом русле по оси мостового перехода при зарегулированном стоке за заданный период; Отметку горизонта высокой воды (ГВВ) по оси мостового перехода; Уклон водной поверхности бытового русла; Распределение направлений течения струй и их скорость в бытовом русле по поверхности водотока; Рельеф дна в пределах бытового русла реки.
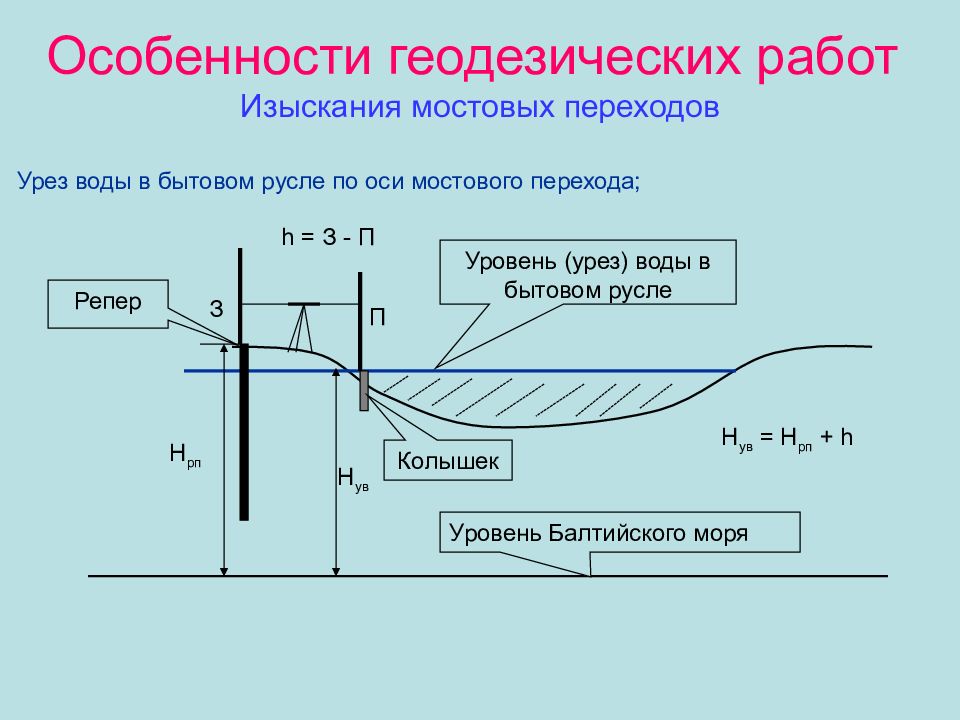
Слайд 40: Особенности геодезических работ Изыскания мостовых переходов
Урез воды в бытовом русле по оси мостового перехода; Репер Колышек Уровень (урез) воды в бытовом русле З П h = З - П H рп H ув H ув = H рп + h Уровень Балтийского моря
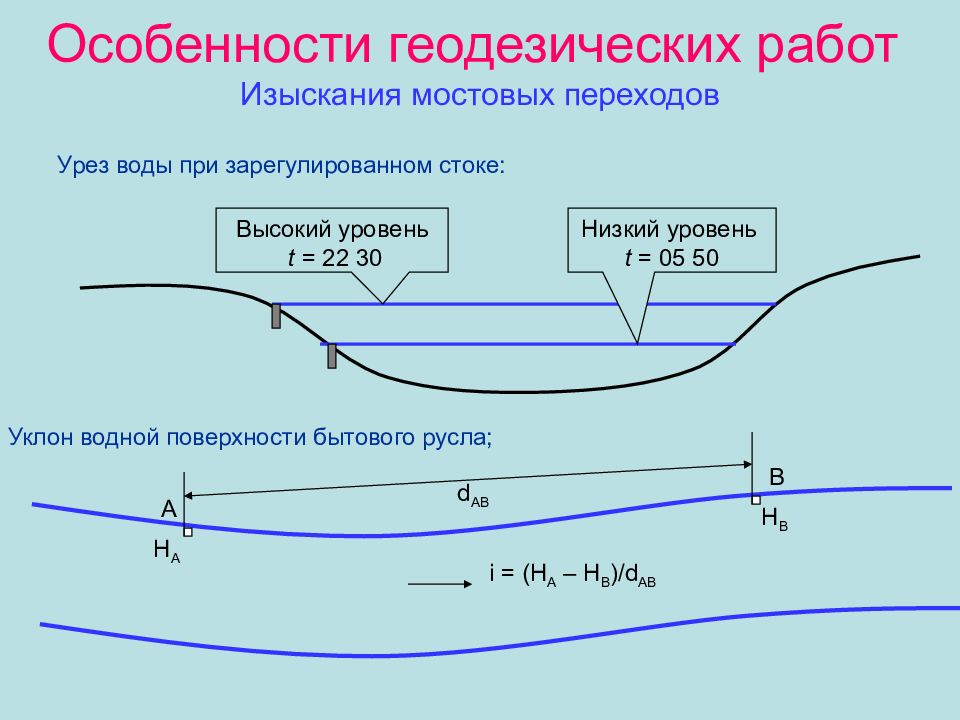
Слайд 41: Особенности геодезических работ Изыскания мостовых переходов
Урез воды при зарегулированном стоке : Низкий уровень t = 05 50 Высокий уровень t = 22 30 Уклон водной поверхности бытового русла; А В d АВ H А H В i = (H А – H В ) /d АВ
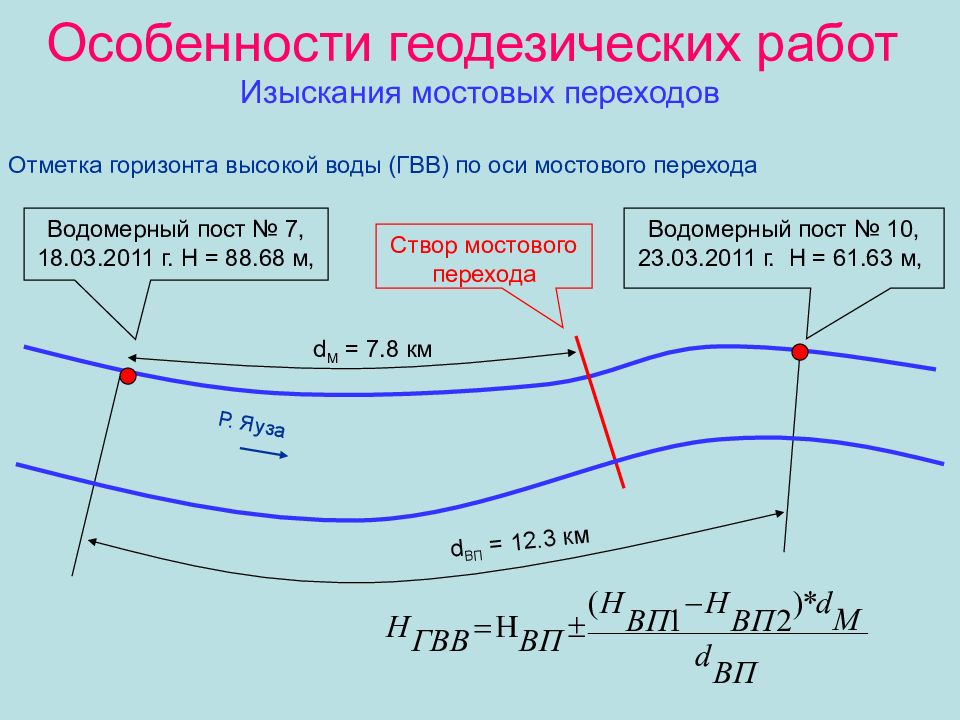
Слайд 42: Особенности геодезических работ Изыскания мостовых переходов
Отметка горизонта высокой воды (ГВВ) по оси мостового перехода Р. Яуза Водомерный пост № 7, 18.03.2011 г. H = 8 8.68 м, Водомерный пост № 10, 23.03.2011 г. H = 61. 63 м, d М = 7.8 км d ВП = 12. 3 км Створ мостового перехода
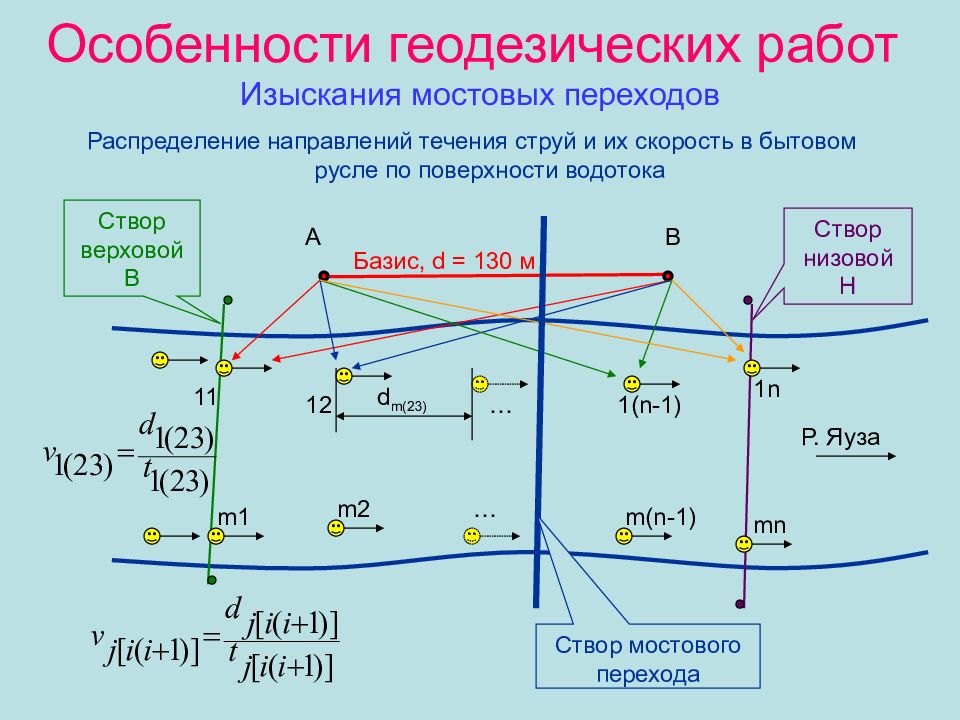
Слайд 43: Особенности геодезических работ Изыскания мостовых переходов
Распределение направлений течения струй и их скорость в бытовом русле по поверхности водотока 11 12 … 1(n-1) 1n m1 m2 … m(n-1) mn А В Базис, d = 130 м Створ верховой В Створ низовой Н Створ мостового перехода Р. Яуза d m(23)
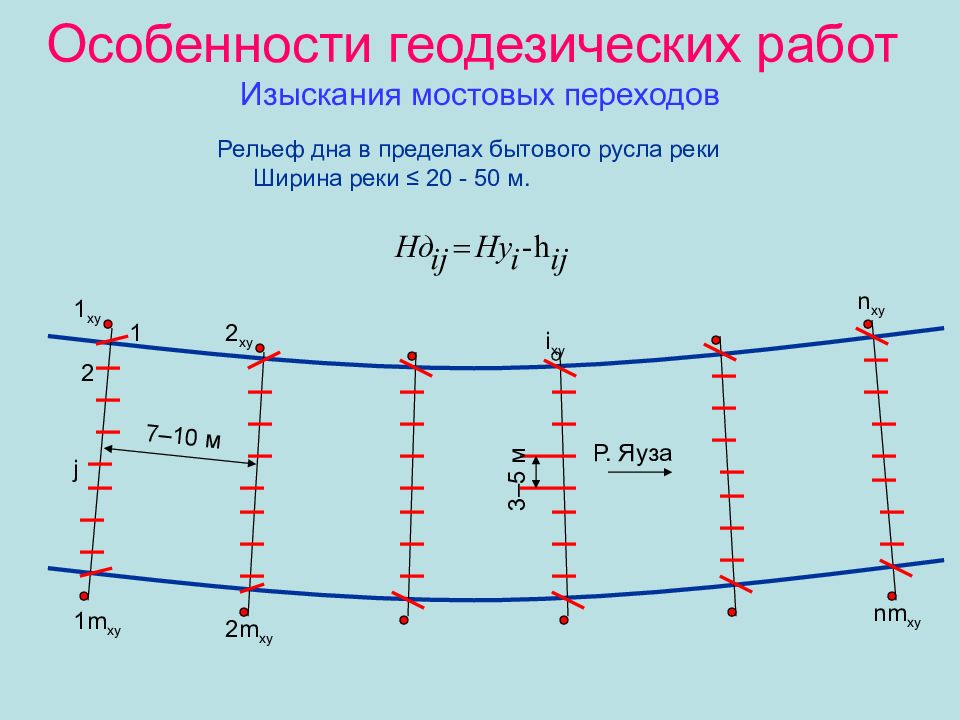
Слайд 44: Особенности геодезических работ Изыскания мостовых переходов
Рельеф дна в пределах бытового русла реки Ширина реки ≤ 20 - 50 м. 1 xy 2 xy i xy n xy 2 1m xy j 2m xy nm xy 7–10 м 3–5 м Р. Яуза 1
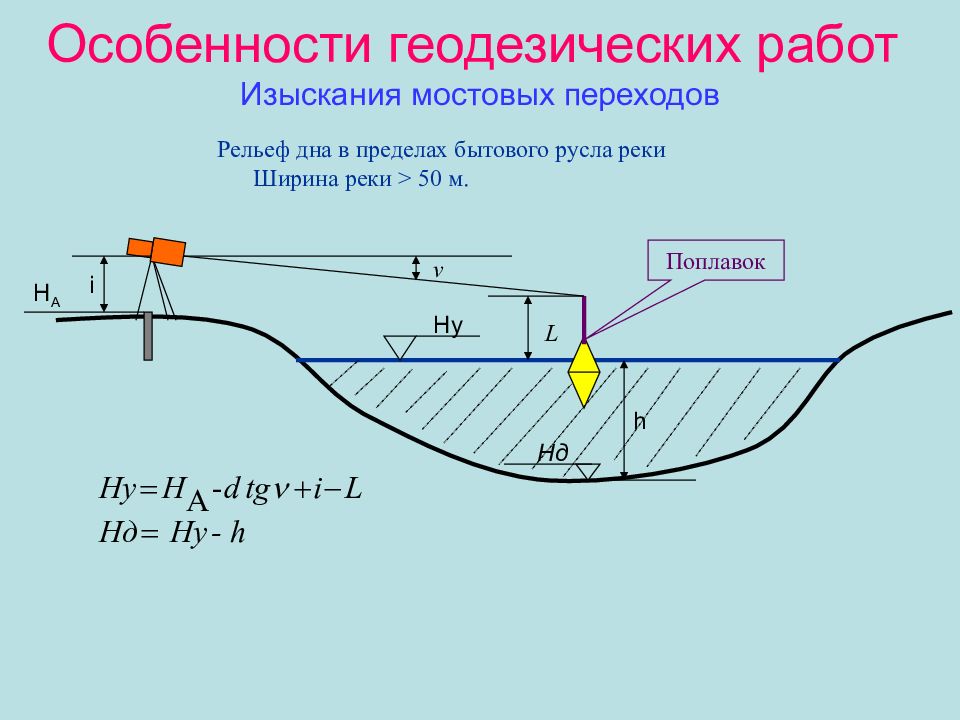
Слайд 45: Особенности геодезических работ Изыскания мостовых переходов
Рельеф дна в пределах бытового русла реки Ширина реки > 50 м. H А i L v h H д H у Поплавок
Слайд 46: Особенности геодезических работ Изыскания мостовых переходов
Рельеф дна в пределах бытового русла реки Ширина реки > 50 м.
Слайд 47: Особенности геодезических работ. Изыскания тоннелей. Условия использования способов съемки в горных условиях
Теодолитно-тахеометрическая съемка – не применяется в связи с трудоемкостью передвижений и переноской оборудования в условиях гор. применяется электронная техника для создания планово высотного обоснования. 2. Аэросъемка и аэрокосмическая съемка – не применяется : появляются недопустимые погрешности планового и высотного положения крутых горных склонов. 3. Спутниковые методы – не применяются в связи с трудоемкостью передвижений и переноской оборудования в условиях гор. применяется для создания планово высотного обоснования. 4. Наземная стереофотограмметрическая (фототеодолитная) съемка – применяется при готовом планово-высотном обосновании
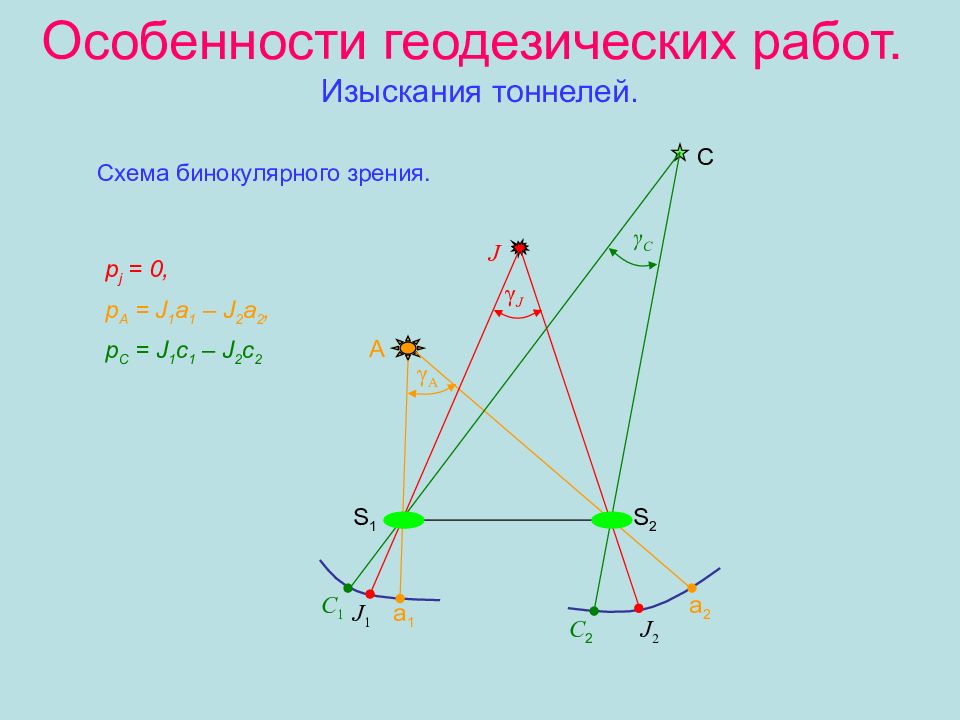
Слайд 48: Особенности геодезических работ. Изыскания тоннелей
J 1 р j = 0, р А = J 1 а 1 – J 2 а 2, р С = J 1 c 1 – J 2 c 2 S 1 S 2 J 2 А С J а 1 а 2 γ А γ J γ C C 1 C 2 Схема бинокулярного зрения.
Слайд 49: Особенности геодезических работ. Изыскания тоннелей
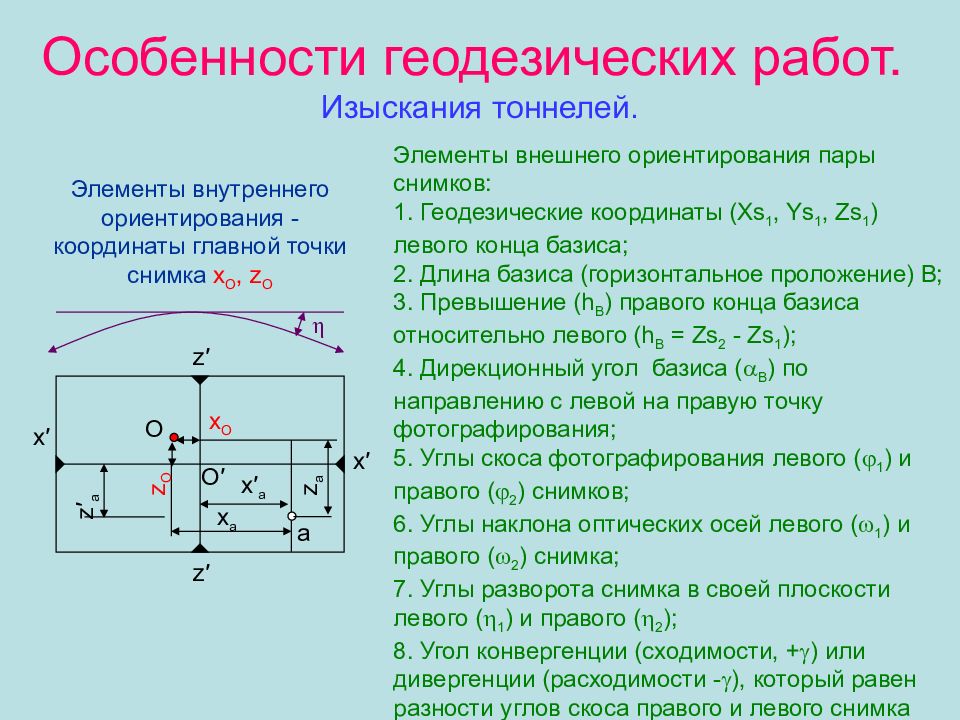
Элементы внутреннего ориентирования - координаты главной точки снимка x O, z O z ′ z′ x ′ x′ а О О ′ x O z O x ′ a z ′ a x a z a Элементы внешнего ориентирования пары снимков : 1. Геодезические координаты ( Xs 1, Ys 1, Zs 1 ) левого конца базиса; 2. Длина базиса (горизонтальное проложение) В; 3. Превышение ( h В ) правого конца базиса относительно левого ( h В = Zs 2 - Zs 1 ); 4. Дирекционный угол базиса ( В ) по направлению с левой на правую точку фотографирования; 5. Углы скоса фотографирования левого ( 1 ) и правого ( 2 ) снимков; 6. Углы наклона оптических осей левого ( 1 ) и правого ( 2 ) снимка; 7. Углы разворота снимка в своей плоскости левого ( 1 ) и правого ( 2 ); 8. Угол конвергенции (сходимости, + ) или дивергенции (расходимости - ), который равен разности углов скоса правого и левого снимка ( = 2 - 1 ). η
Слайд 50: Особенности геодезических работ. Изыскания тоннелей
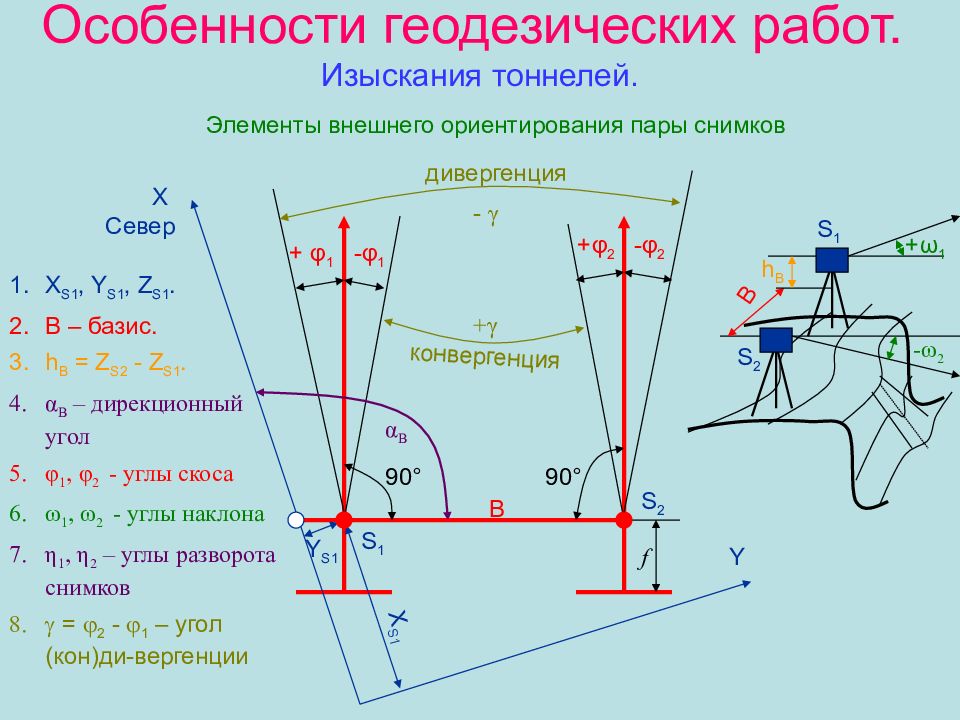
Элементы внешнего ориентирования пары снимков + φ 1 - φ 1 + φ 2 - φ 2 S 1 S 2 B + γ - γ конвергенция дивергенция 90 ° 90 ° X Север Y f α B X S1 Y S1 X S1, Y S1, Z S1. B – базис. h В = Z S 2 - Z S 1. α В – дирекционный угол φ 1, φ 2 - углы скоса ω 1, ω 2 - углы наклона η 1, η 2 – углы разворота снимков = 2 - 1 – угол (кон)ди-вергенции - ω 2 + ω 1 В S 1 S 2 h B
Слайд 51: Особенности геодезических работ. Изыскания тоннелей
Координаты снимка и координаты местности X = X S1 + NX 1 Y = Y S1 + NY 1 Z = Z S 1 + NZ 1 + Z где
Слайд 52: Особенности геодезических работ. Изыскания тоннелей
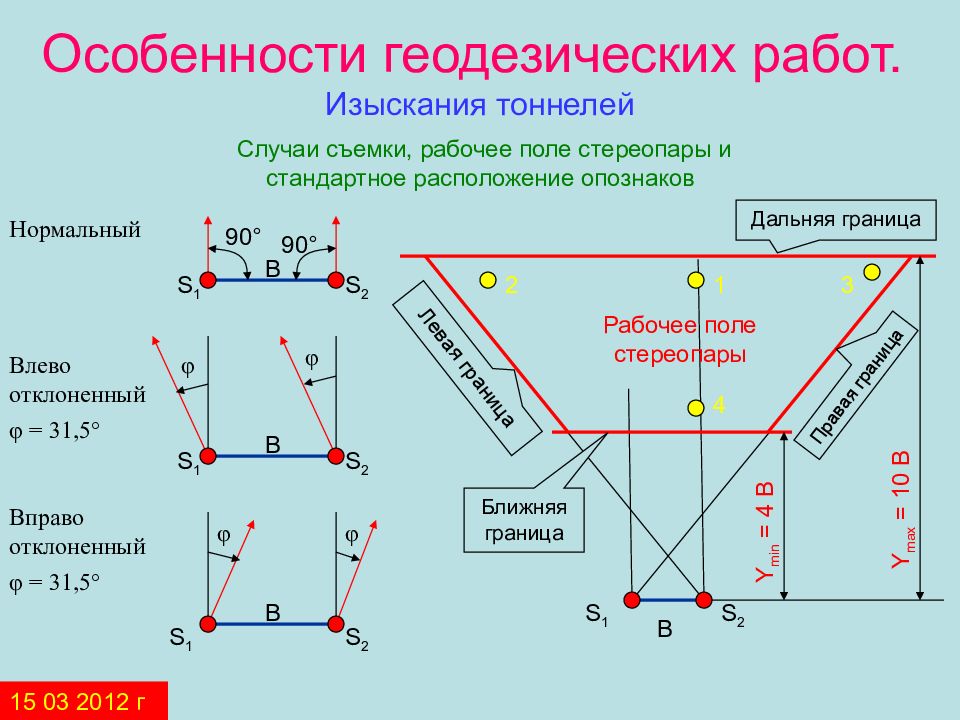
Случаи съемки, рабочее поле стереопары и стандартное расположение опознаков Нормальный Влево отклоненный φ = 31,5 ° Вправо отклоненный φ = 31,5 ° В В В φ φ φ φ 90 ° 90 ° S 1 S 2 S 1 S 2 S 1 S 2 В S 1 S 2 Ближняя граница Дальняя граница Y min = 4 В Y max = 10 B 1 2 3 4 Левая граница Правая граница Рабочее поле стереопары 15 03 2012 г
Слайд 53: Геодезическое сопровождение строительства Виды и нормы точности разбивочных работ
Разбивкой сооружения называют обозначение и закрепление на местности с необходимой точностью осей и ключевых точек объекта, которые определяют его местоположение и размеры. m П 2 = m P 2 + m Т 2, Геодезическое обоснование должно строиться в два раза точнее по отношению к требуемой точности разбивочных работ и в три раза точнее по отношению к точности приемки сооружения в эксплуатацию. если m Т = m П, то или
Слайд 54: Геодезическое сопровождение строительства Виды и нормы точности разбивочных работ
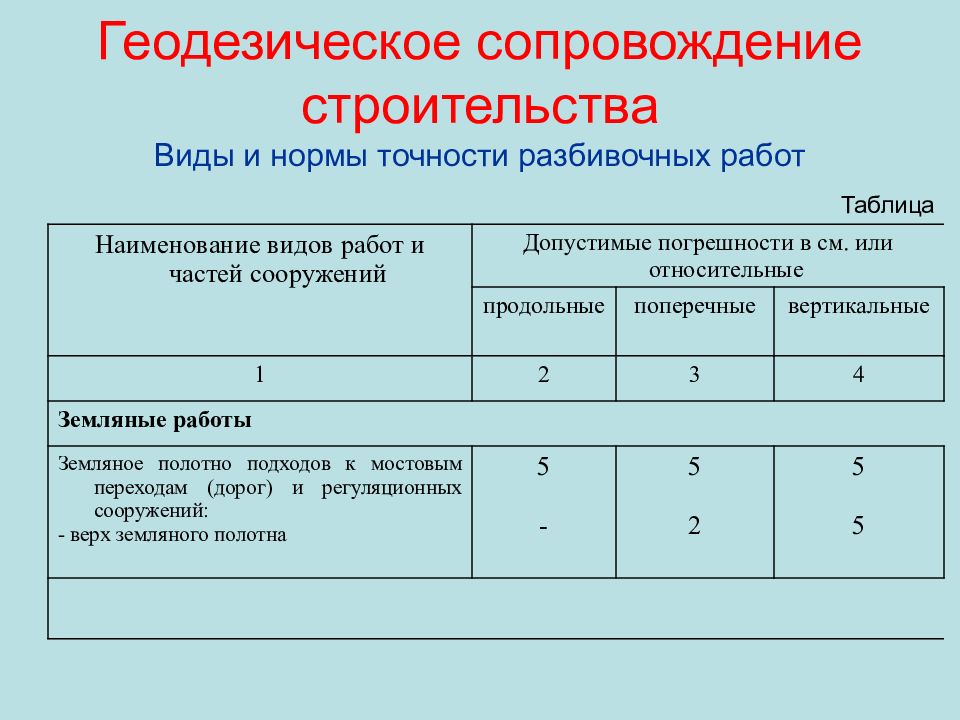
Наименование видов работ и частей сооружений Допустимые погрешности в см. или относительные продольные поперечные вертикальные 1 2 3 4 Земляные работы Земляное полотно подходов к мостовым переходам (дорог) и регуляционных сооружений: - верх земляного полотна 5 - 5 2 5 5 Таблица
Слайд 55: Геодезическое сопровождение строительства Виды и нормы точности разбивочных работ
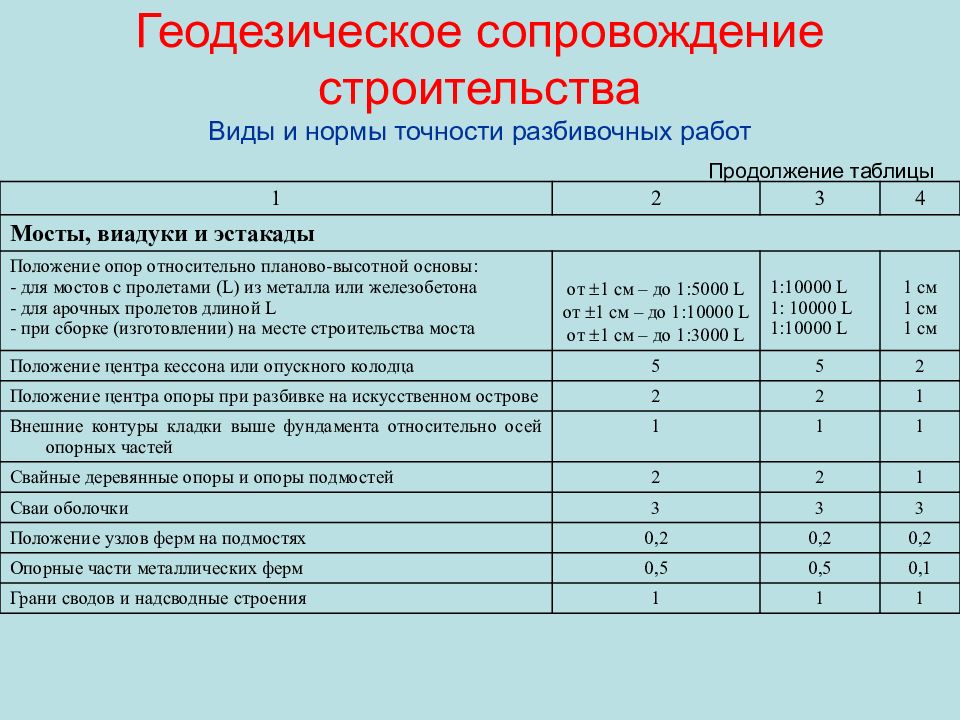
1 2 3 4 Мосты, виадуки и эстакады Положение опор относительно планово-высотной основы: - для мостов с пролетами ( L ) из металла или железобетона - для арочных пролетов длиной L - при сборке (изготовлении) на месте строительства моста от 1 см – до 1:5000 L от 1 см – до 1:10000 L от 1 см – до 1:3000 L 1:10000 L 1 : 10000 L 1:10000 L 1 см 1 см 1 см Положение центра кессона или опускного колодца 5 5 2 Положение центра опоры при разбивке на искусственном острове 2 2 1 Внешние контуры кладки выше фундамента относительно осей опорных частей 1 1 1 Свайные деревянные опоры и опоры подмостей 2 2 1 Сваи оболочки 3 3 3 Положение узлов ферм на подмостях 0,2 0,2 0,2 Опорные части металлических ферм 0,5 0,5 0,1 Грани сводов и надсводные строения 1 1 1 Продолжение таблицы
Слайд 56: Геодезическое сопровождение строительства Виды и нормы точности разбивочных работ
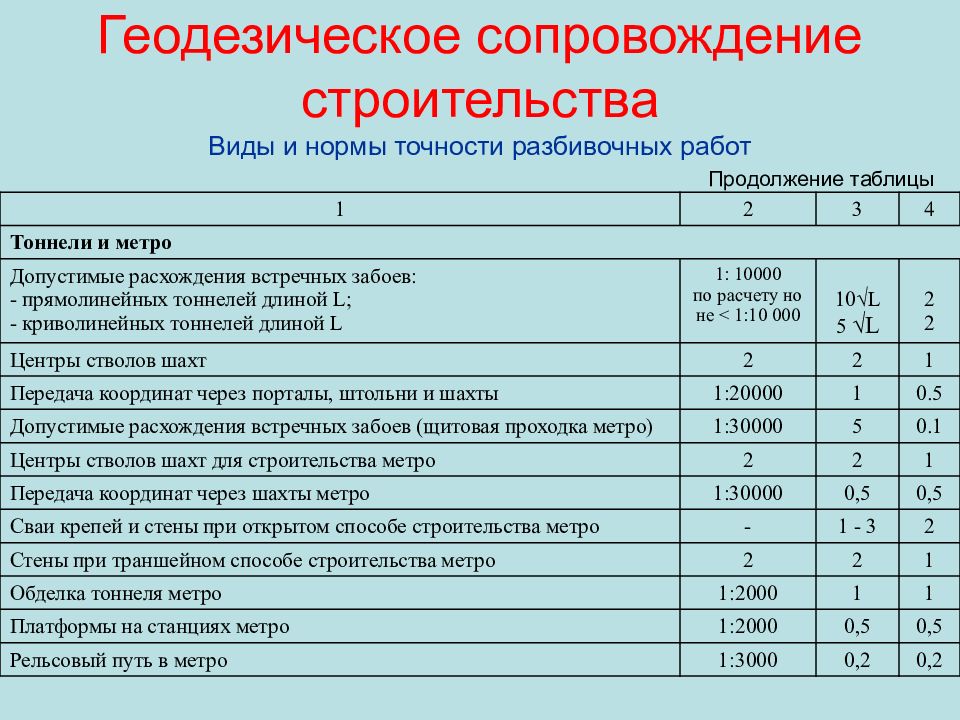
1 2 3 4 Тоннели и метро Допустимые расхождения встречных забоев: - прямолинейных тоннелей длиной L ; - криволинейных тоннелей длиной L 1: 10000 по расчету но не < 1:10 000 10√ L 5 √ L 2 2 Центры стволов шахт 2 2 1 Передача координат через порталы, штольни и шахты 1:20000 1 0.5 Допустимые расхождения встречных забоев ( щитовая проходка метро) 1:30000 5 0.1 Центры стволов шахт для строительства метро 2 2 1 Передача координат через шахты метро 1:30000 0,5 0,5 Сваи крепей и стены при открытом способе строительства метро - 1 - 3 2 Стены при траншейном способе строительства метро 2 2 1 Обделка тоннеля метро 1:2000 1 1 Платформы на станциях метро 1:2000 0,5 0,5 Рельсовый путь в метро 1:3000 0,2 0,2 Продолжение таблицы
Слайд 57: Геодезическое сопровождение строительства Опорная сеть для разбивки сооружений (проект)
Принципиальная схема с указанием альтернативных вариантов и методов разбивки ключевых точек мостового перехода или транспортного тоннеля; Геометрическая схема построения опорных точек разбивки сооружения (геодезический четырехугольник, цепочка треугольников, центральная система и др.) с указанием схемы привязки этих точек к государственной геодезической сети; Схема закрепления на местности точек опорной сети с указанием необходимого времени сохранности и способа обустройства закрепленных точек; Схема наблюдения углов и расстояний; Обоснование требуемой точности определения координат и отметок геодезического обоснования и предрасчет точности измерений; Перечень приборов и геодезического оборудования; Рекомендуемый метод уравнивания углов, расстояний и превышений.
Слайд 58: Геодезическое сопровождение строительства Методы разбивки сооружений
Метод координат: способ прямоугольных координат (способ перпендикуляров); способ полярных координат. Метод засечек: способ угловых засечек; способ микротриангуляции; способ обратной засечки; способ створных засечек; способ линейных засечек (геометрический).
Слайд 59: Геодезическое сопровождение строительства Методы разбивки сооружений (метод координат)
отложить в направлении оси координат OX расстояние d OA от начала координат О до точки А; центрировать на точке А теодолит и отложить угол ; отложить по направлению угла расстояние d A С от точки А до точки С; фиксировать положение точки С на местности. Y X А С С ′ О d OA X C Y C d AC β Δ Y Δ X M
Слайд 60: Геодезическое сопровождение строительства Методы разбивки сооружений (метод координат)
Погрешность метода координат
Слайд 61: Геодезическое сопровождение строительства Методы разбивки сооружений ( Метод засечек) Прямая угловая засечка
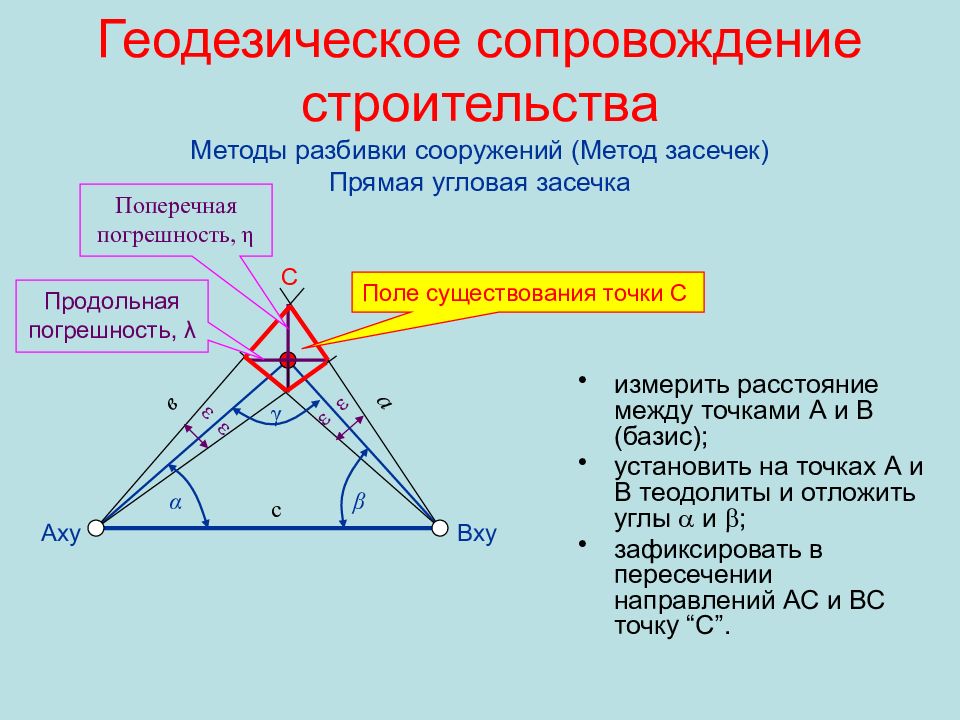
измерить расстояние между точками А и В (базис); установить на точках А и В теодолиты и отложить углы и ; зафиксировать в пересечении направлений АС и ВС точку “С”. А xy В xy С ε ε ε ε α β γ Поперечная погрешность, η Продольная погрешность, λ c a в Поле существования точки С
Слайд 62: Геодезическое сопровождение строительства Методы разбивки сооружений ( Метод засечек) Прямая угловая засечка
поперечном Влияние погрешности базиса в направлении : продольном Влияние погрешности отложения углов и в направлении : поперечном продольном Суммарная погрешность : поперечная продольная
Слайд 63: Геодезическое сопровождение строительства Методы разбивки сооружений ( Метод засечек) Способ микротриангуляции
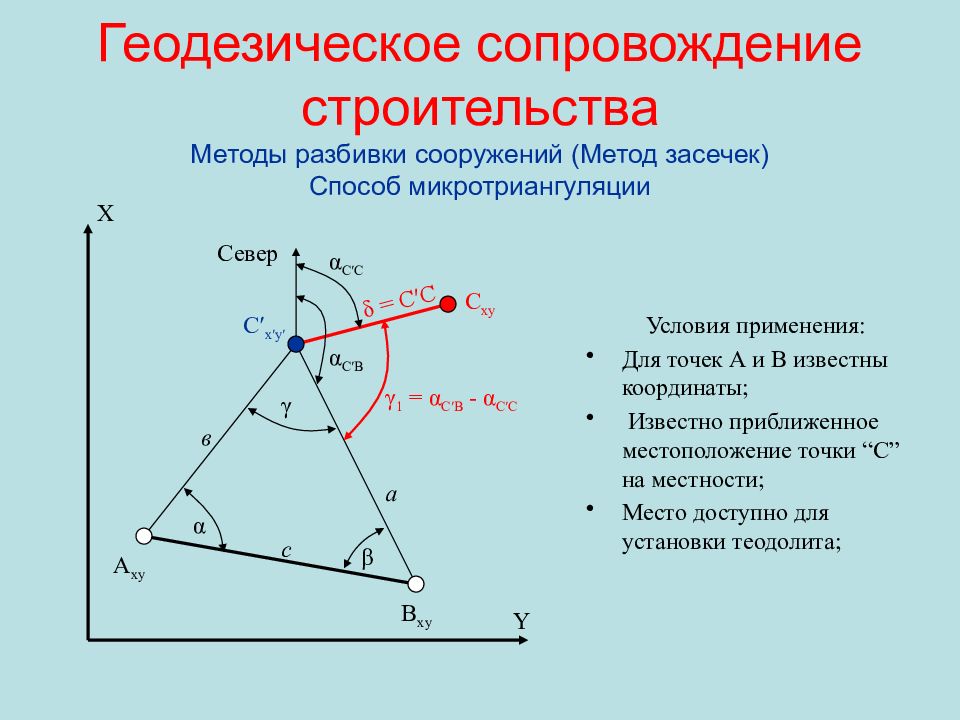
Условия применения : Для точек А и В известны координаты ; Известно приближенное местоположение точки “С” на местности ; Место доступно для установки теодолита ; А xy B xy C ′ x′y′ C xy Север α С′С α С′В γ 1 = α С′В - α С′С δ = С′С Y X а с в α β γ
Слайд 64: Геодезическое сопровождение строительства Методы разбивки сооружений ( Метод засечек) Способ микротриангуляции
Действия : В окрестностях точки “С” фиксируют точку “С ” и формируют треугольник АВС ′, в котором измеряют углы , и ; Уравнивают углы и вычисляют расстояния а и в ; Вычисляют координаты точки С ′ (x′, y′) и сопоставляют их с проектными координатами точки С ; Решением обратной геодезической задачи устанавливают расстояние δ = С С ′ и разбивочный угол γ 1 ; Откладывают угол γ 1 и по заданному направлению откладывают расстояние δ. Фиксируют точку С.
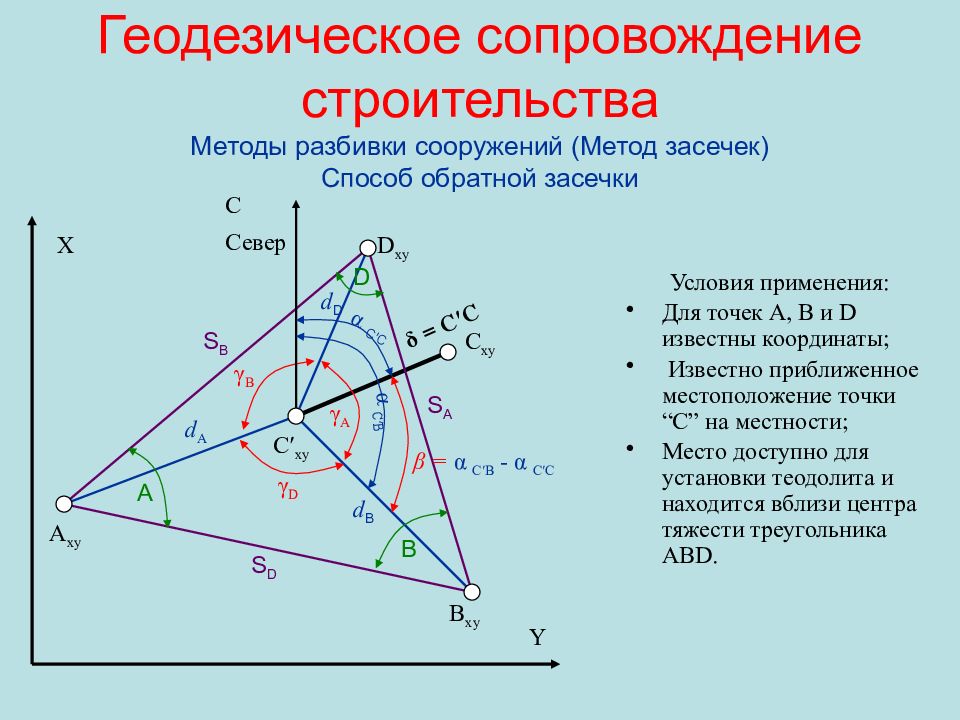
Слайд 65: Геодезическое сопровождение строительства Методы разбивки сооружений ( Метод засечек) Способ обратной засечки
Условия применения : Для точек А, В и D известны координаты ; Известно приближенное местоположение точки “С” на местности ; Место доступно для установки теодолита и находится вблизи центра тяжести треугольника ABD. Y X A xy B xy D xy C xy C ′ xy С Север γ D γ B γ A β = α C′B - α C′C δ = C′C α C′C α C′B A B D S A S D S B d A d B d D
Слайд 66: Геодезическое сопровождение строительства Методы разбивки сооружений ( Метод засечек) Способ обратной засечки
, где Погрешность положения точки С ′ , где
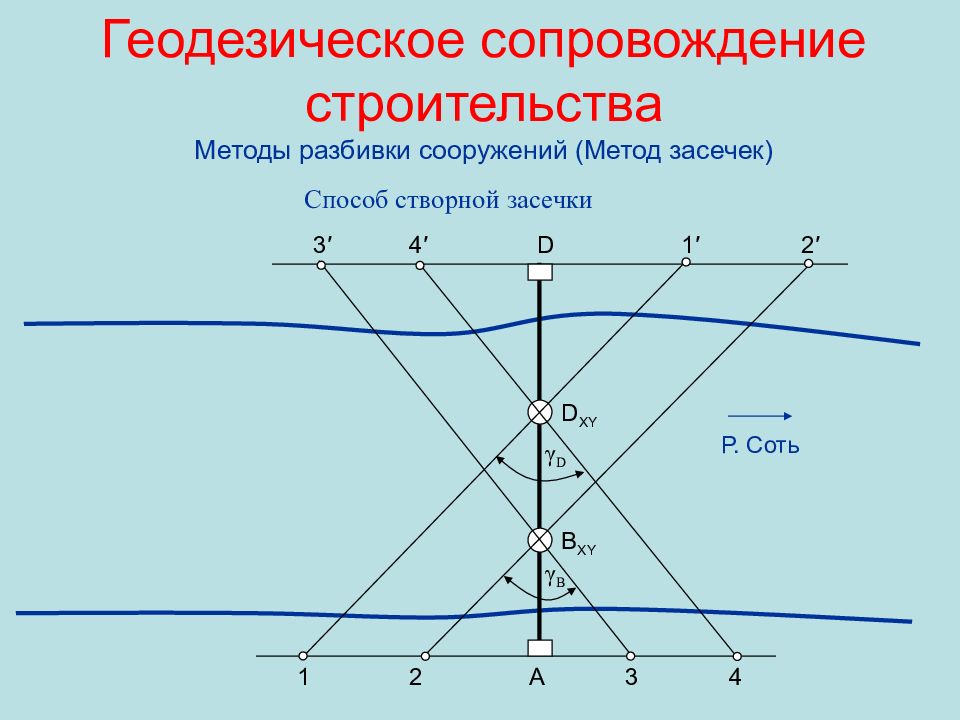
Слайд 67: Геодезическое сопровождение строительства Методы разбивки сооружений ( Метод засечек)
Способ створной засечки 1 2 А 3 4 1 ′ 2 ′ D 3 ′ 4 ′ B XY D XY γ B γ D Р. Соть
Слайд 68: Геодезическое сопровождение строительства Методы разбивки сооружений ( Метод засечек)
Способ линейной засечки B A b a λ η M C C ′ c τ τ
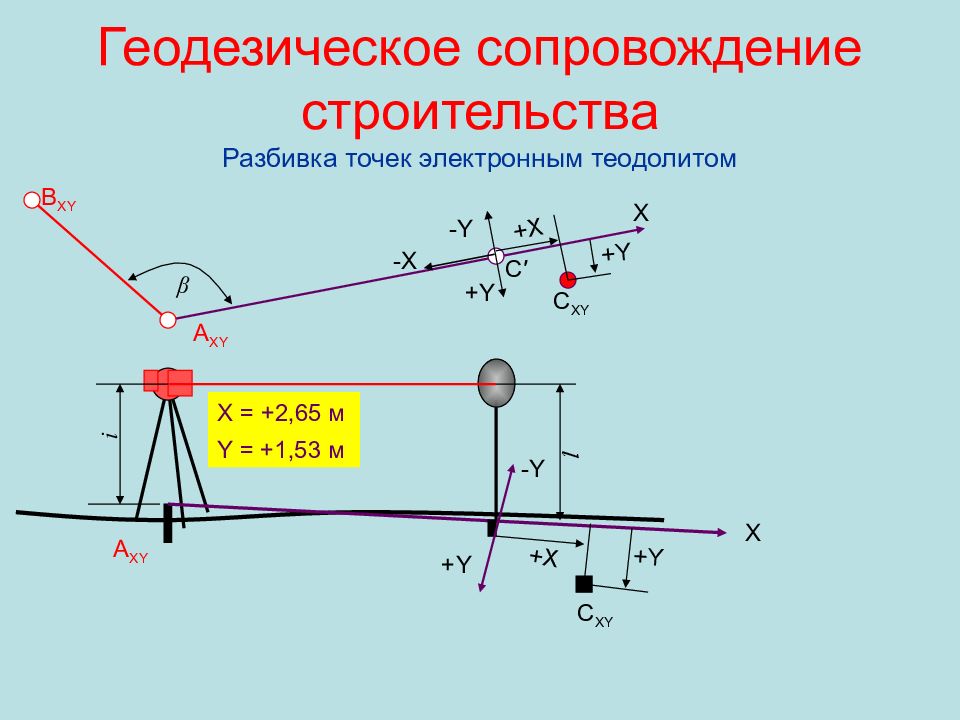
Слайд 69: Геодезическое сопровождение строительства Разбивка точек электронным теодолитом
C XY X = +2,65 м Y = +1,53 м +X +Y +X +Y A XY A XY B XY -Y β C XY X X +Y +Y -Y -X i l C ′
Слайд 70: Геодезическое сопровождение строительства Типичное размещение опорных точек для разбивки опор мостовых переходов
1. Оба берега реки крутые (не затопляемые) и их бровки находятся высоко над уровнем воды; 2. Один берег реки крутой (не затопляемый), а другой пологий с периодическим затоплением паводковой водой; 3. Оба берега реки крутые (не затопляемые) и их бровки находятся высоко над уровнем воды, при этом в средней части реки имеет место остров, который находится на некотором расстоянии от створа мостового перехода вверх или вниз по течению; 4. Один берег реки крутой (не затопляемый), а другой пологий с периодическим затоплением паводковой водой, но в середине реки имеет место остров, который находится в створе мостового перехода и имеет достаточную длину вдоль течения реки.
Слайд 71: Геодезическое сопровождение строительства Технологический островок под мостовой опорой
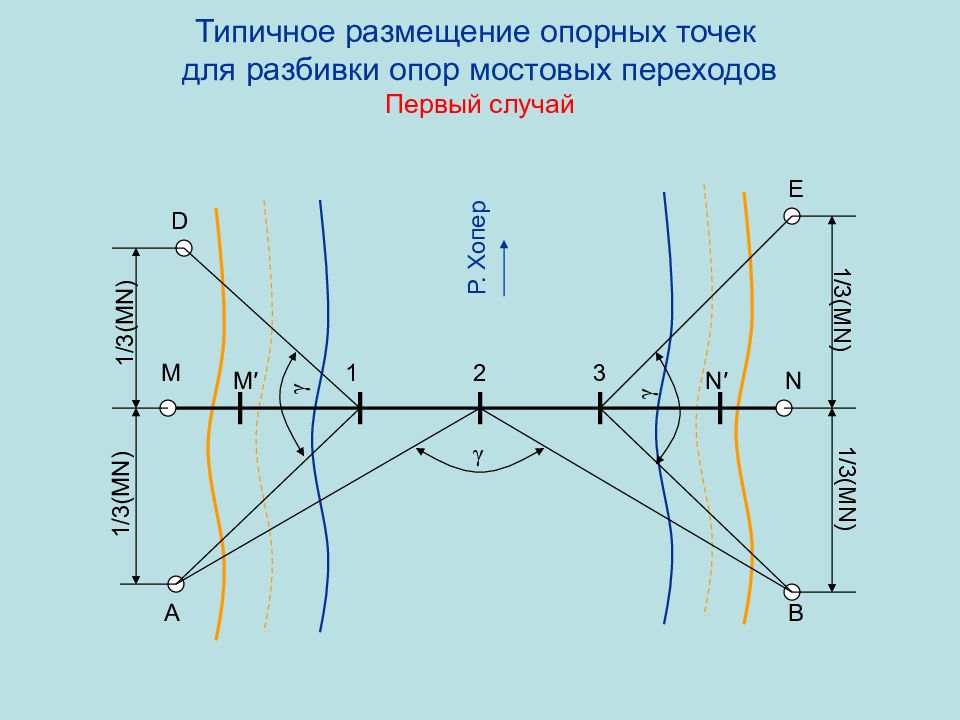
Слайд 72: Типичное размещение опорных точек для разбивки опор мостовых переходов Первый случай
1 /3(MN) 1 /3(MN) 1 /3(MN) 1 /3(MN) M N M ′ N ′ 1 2 3 A D B E Р. Хопер γ γ γ
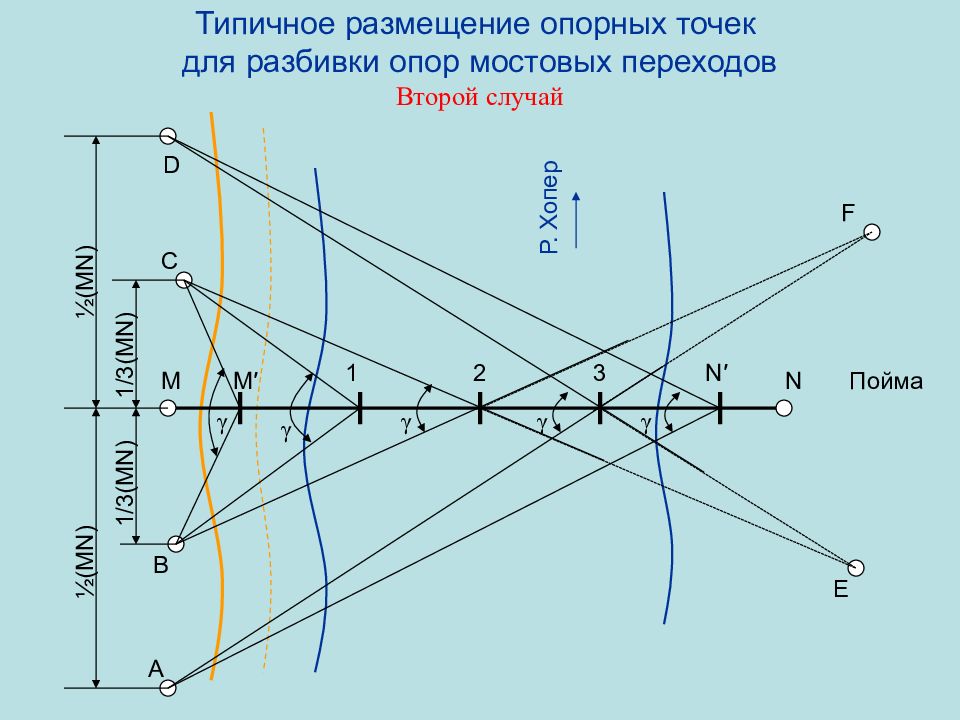
Слайд 73: Типичное размещение опорных точек для разбивки опор мостовых переходов Второй случай
1 /3(MN) 1 /3(MN) M N M ′ N ′ 1 2 3 A D Р. Хопер ½(MN) ½(MN) B C E F γ γ γ γ γ Пойма
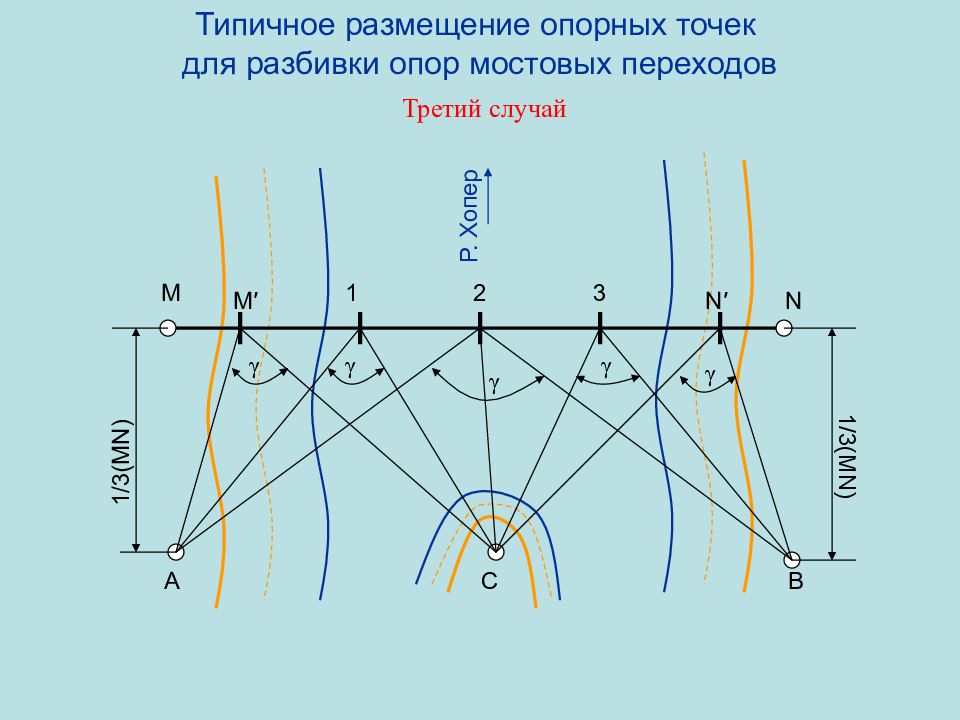
Слайд 74: Типичное размещение опорных точек для разбивки опор мостовых переходов Третий случай
1 /3(MN) 1 /3(MN) M N M ′ N ′ 1 2 3 A B Р. Хопер С γ γ γ γ γ
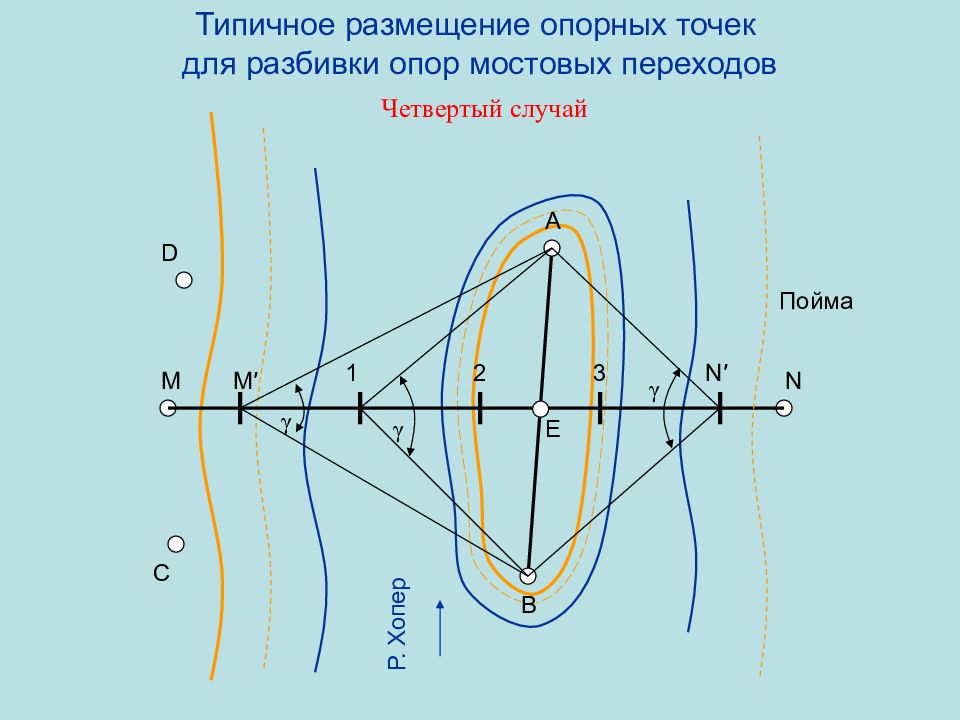
Слайд 75: Типичное размещение опорных точек для разбивки опор мостовых переходов Четвертый случай
M N M ′ N ′ 1 2 3 Р. Хопер B C γ А D Е γ γ Пойма
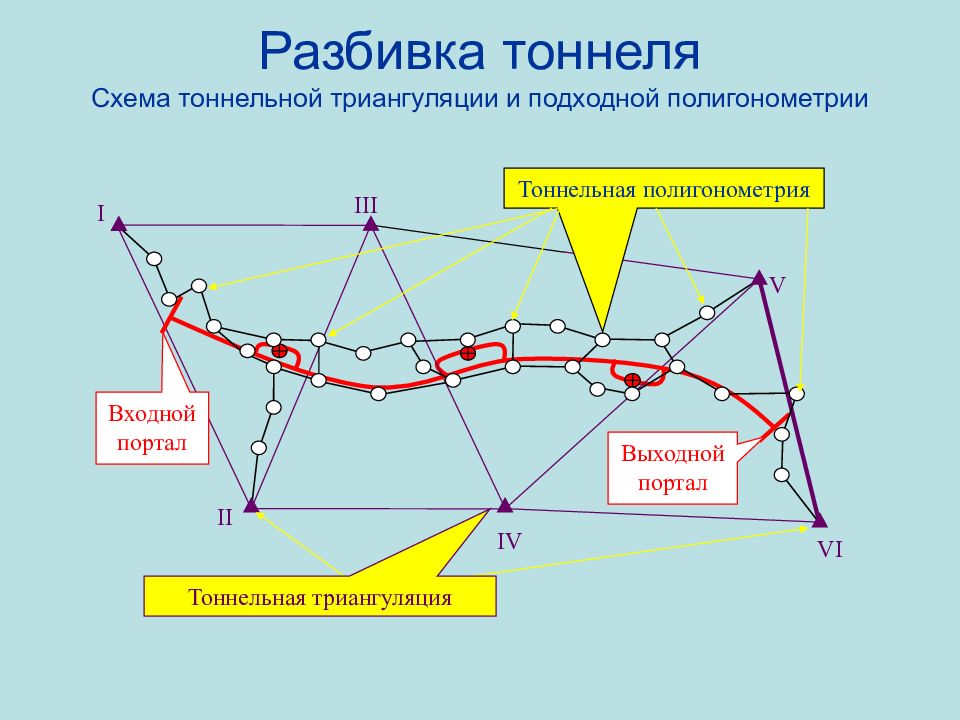
Слайд 76: Разбивка тоннеля Схема тоннельной триангуляции и подходной полигонометрии
I II III IV V VI Входной портал Выходной портал Тоннельная полигонометрия Тоннельная триангуляция
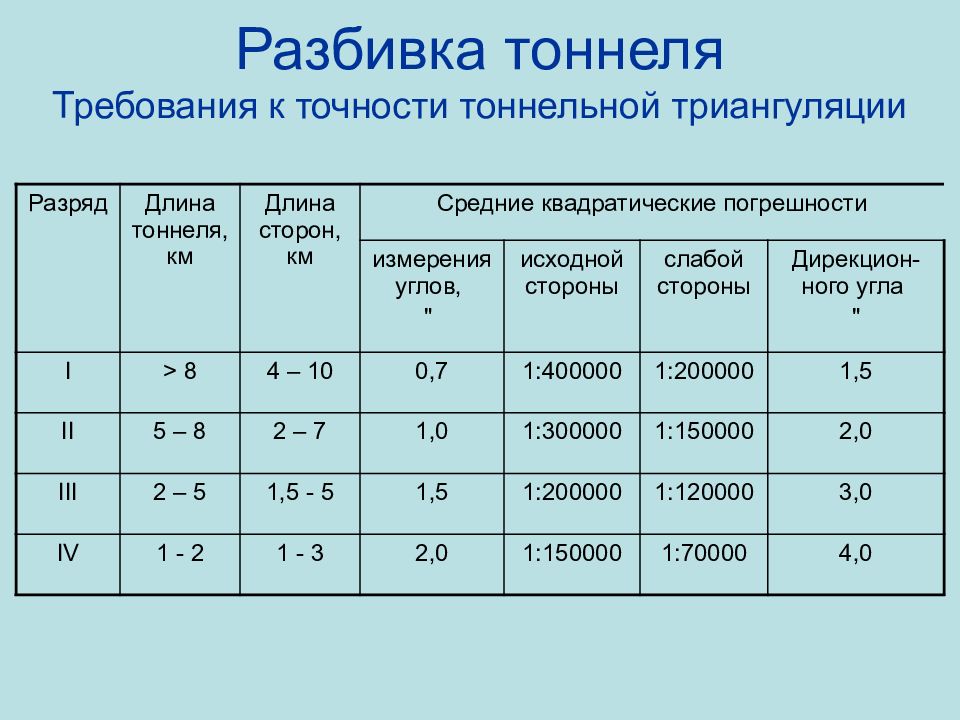
Слайд 77: Разбивка тоннеля Требования к точности тоннельной триангуляции
Разряд Длина тоннеля, км Длина сторон, км Средние квадратические погрешности измерения углов, " исходной стороны слабой стороны Дирекцион-ного угла " I > 8 4 – 10 0,7 1 :400000 1 :200000 1, 5 II 5 – 8 2 – 7 1,0 1 :300000 1 :150000 2,0 III 2 – 5 1,5 - 5 1,5 1 :200000 1 :120000 3, 0 IV 1 - 2 1 - 3 2,0 1 :150000 1 :70000 4,0
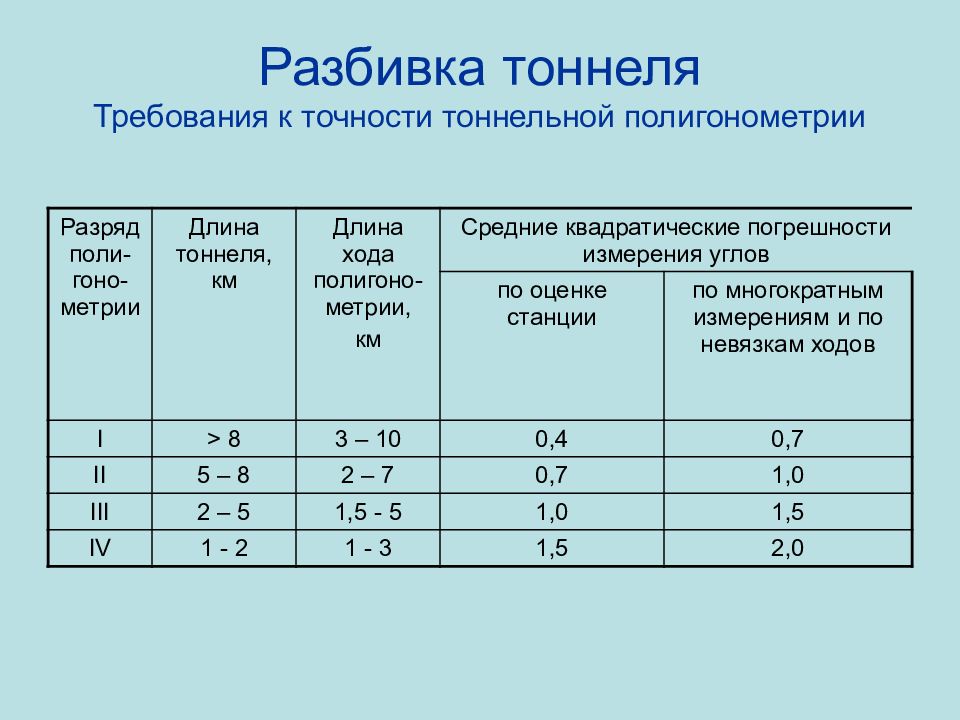
Слайд 78: Разбивка тоннеля Требования к точности тоннельной полигонометрии
Разряд поли-гоно-метрии Длина тоннеля, км Длина хода полигоно-метрии, км Средние квадратические погрешности измерения углов по оценке станции по многократным измерениям и по невязкам ходов I > 8 3 – 10 0,4 0,7 II 5 – 8 2 – 7 0,7 1,0 III 2 – 5 1,5 - 5 1,0 1,5 IV 1 - 2 1 - 3 1,5 2,0
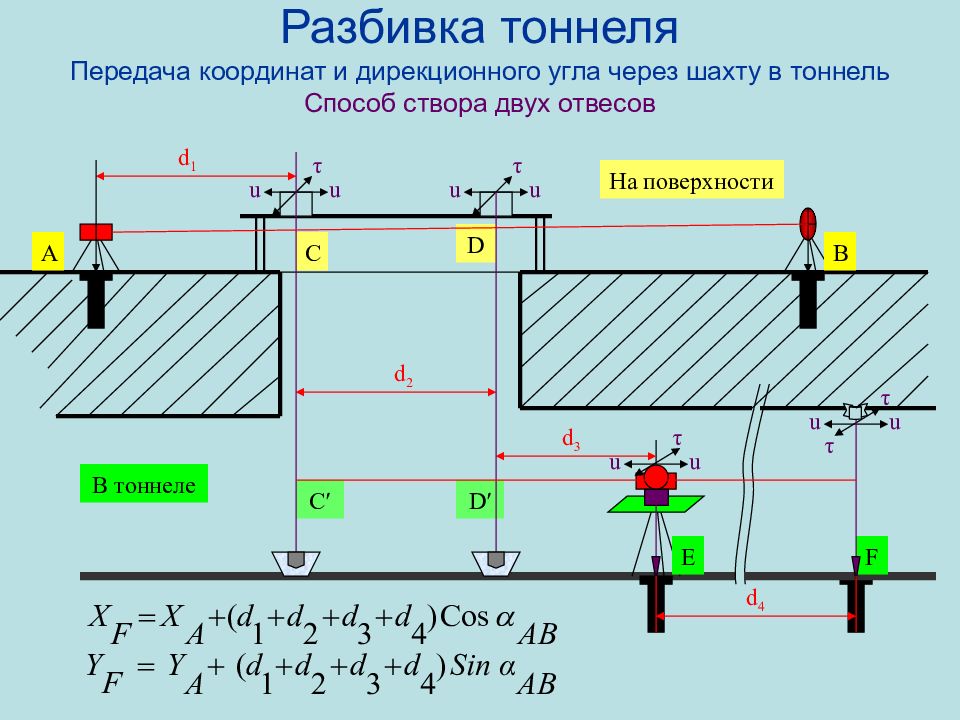
Слайд 79: Разбивка тоннеля Передача координат и дирекционного угла через шахту в тоннель Способ створа двух отвесов
А В С D C ′ D ′ E F d 1 d 2 d 3 d 4 u u τ u u τ На поверхности В тоннеле u u τ u u τ τ
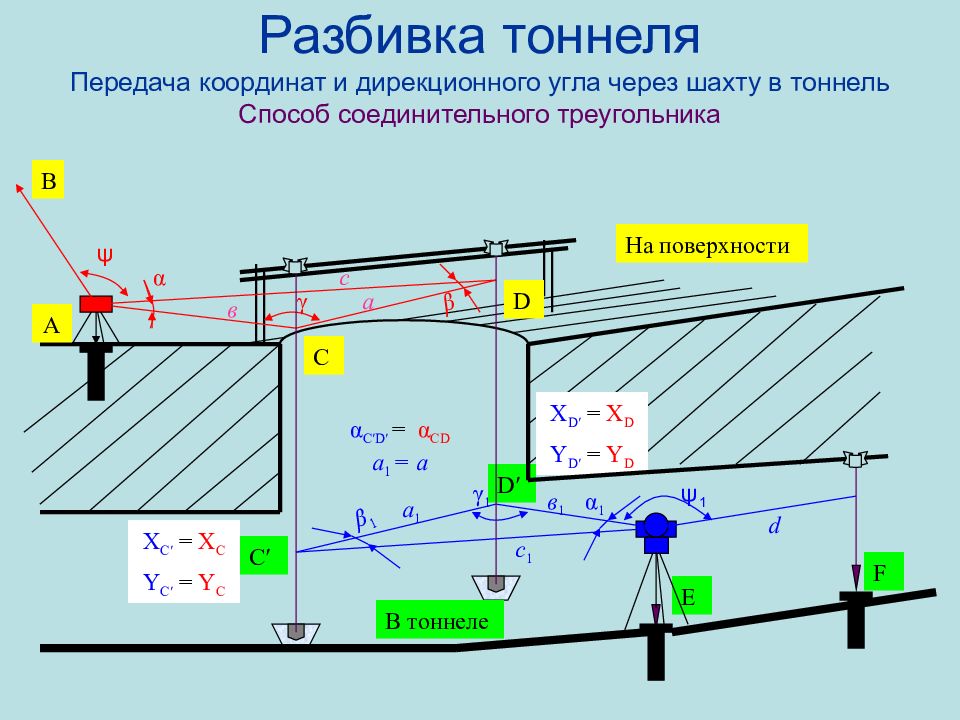
Слайд 80: Разбивка тоннеля Передача координат и дирекционного угла через шахту в тоннель Способ соединительного треугольника
F E D ′ Разбивка тоннеля Передача координат и дирекционного угла через шахту в тоннель Способ соединительного треугольника α β γ α 1 β 1 γ 1 ψ 1 A B D C ψ C ′ В тоннеле На поверхности в а с в 1 а 1 с 1 d α C′D′ = α CD а 1 = а X C ′ = X C Y C ′ = Y C X D ′ = X D Y D ′ = Y D
Слайд 81: Разбивка тоннеля Передача координат и дирекционного угла через шахту в тоннель Способ соединительного треугольника
Исходные данные : Координаты точки А : X A, Y A ; Дирекционный угол : α ВА. Измерения на поверхности : углы α, ψ, расстояния : а, в, с. Измерения в тоннеле : углы α 1, ψ 1, расстояния : а 1, в 1, с 1, d. Вычисление элементов треугольника на поверхности : Вычислить углы β, γ по формуле : Определить : Координаты : X Е, Y Е, X F, Y F ; Дирекционный угол : α EF. Вычислить дирекционные углы линий на поверхности : α AD = α BA + ψ − 180 α DC = α AD + (360- β ) − 180 α CA = α DC + (360- γ ) − 180 α AB = α CA + (360- α - ψ ) − 180 Вычислить координаты точек D, C на поверхности : X D = X A + c Cos α AD Y D = Y A + c Sin α AD X C = X D + a Cos α DC Y C = Y D + a Sin α DC X A = X C + в Cos α C А Y А = Y С + в Sin α C А
Слайд 82: Разбивка тоннеля Передача дирекционного угла через шахту в тоннель Способ соединительного треугольника
Вычислить углы β 1, γ 1 по формуле : Принять : α C′D′ = α CD ; X C′ = X C, Y C′ = Y C ; X D′ = X D, Y D′ = Y D. Вычислить дирекционные углы линий в тоннеле : α D ′ Е = α C ′ D ′ + 180 − γ 1 ; α C′ Е = α D′C′ + β 1 − 180; α Е F = α D′E + 180 − (360 - ψ 1 ); Контроль α Е F = α C′E + ( α 1 + ψ 1 ) − 180; Вычисление элементов треугольника в тоннеле : Вычислить координаты точек E, F в тоннеле : X E = X D ′ + в 1 Cos α D′ Е ; Y E = Y D′ + в 1 Cos α D′ Е X F = X E + d Cos α Е F ; Y F = Y E + d Sin α Е F Контроль X E = X С ′ + с 1 Cos α С ′ Е ; Y E = Y С ′ + с 1 Cos α С ′ Е X F = X E + d Cos α Е F ; Y F = Y E + d Sin α Е F
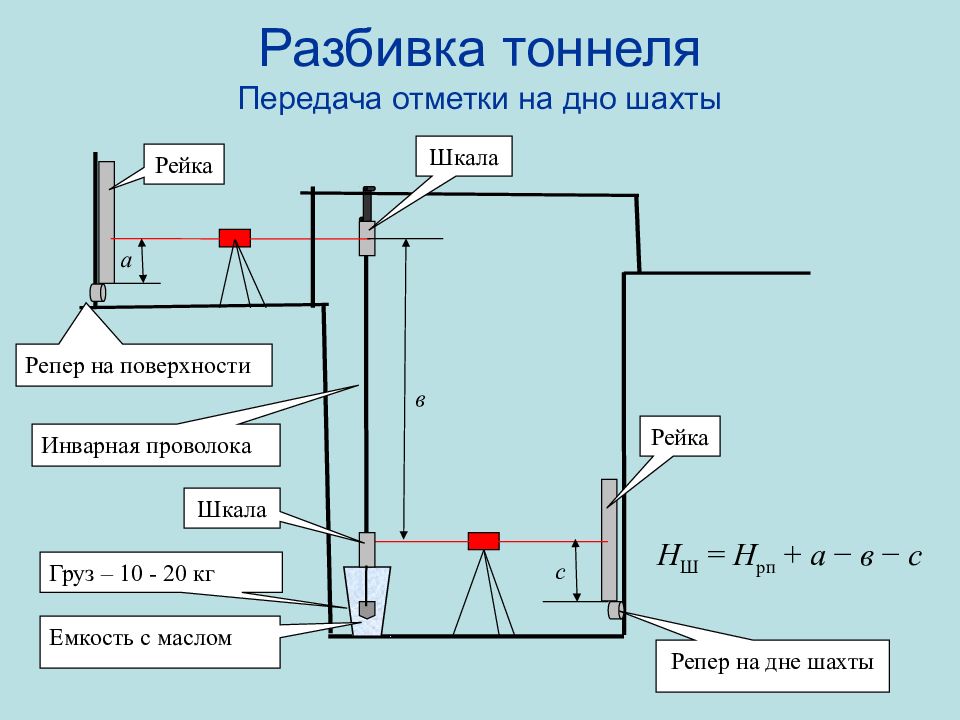
Слайд 83: Разбивка тоннеля Передача отметки на дно шахты
Емкость с маслом Груз – 10 - 20 кг Инварная проволока Н Ш = Н рп + а − в − с а в с Репер на дне шахты Репер на поверхности Шкала Рейка Рейка Шкала
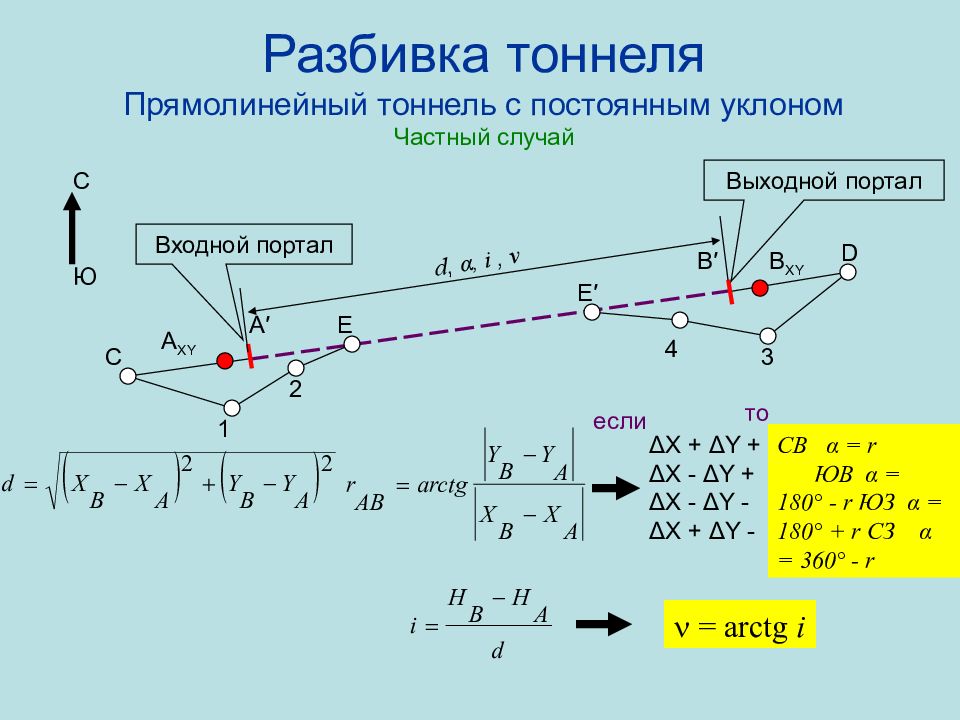
Слайд 84: Разбивка тоннеля Прямолинейный тоннель с постоянным уклоном Частный случай
А XY E E ′ В XY С D 1 2 4 3 А ′ В ′ d, α, i, v C Ю CB α = r ЮВ α = 180° - r ЮЗ α = 180° + r СЗ α = 360° - r = arctg i Входной портал Выходной портал Δ X + Δ Y + Δ X - Δ Y + Δ X - Δ Y - Δ X + Δ Y - если то
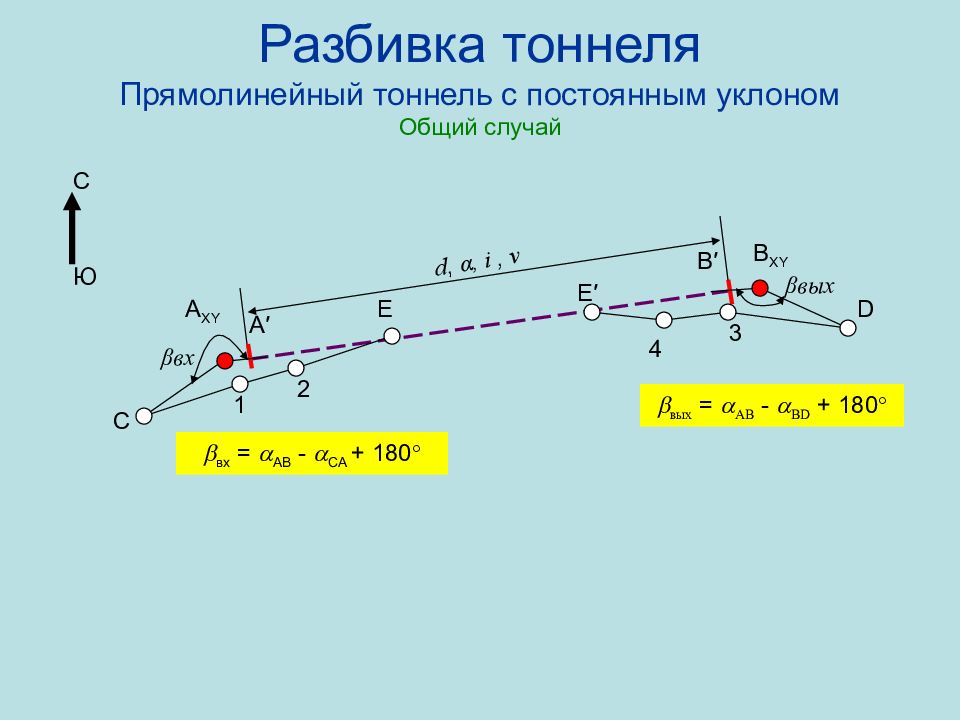
Слайд 85: Разбивка тоннеля Прямолинейный тоннель с постоянным уклоном Общий случай
А XY E E ′ В XY С D 1 2 4 А ′ В ′ d, α, i, v C Ю 3 β вх β вых вх = АВ - СА + 180 вых = АВ - BD + 180
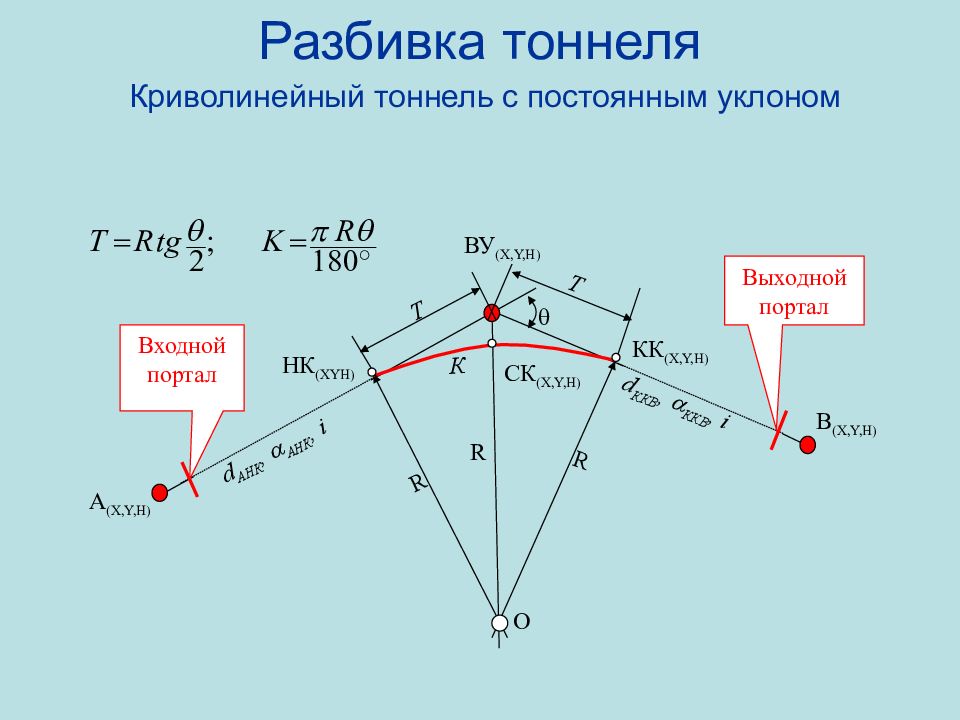
Слайд 86: Разбивка тоннеля Криволинейный тоннель с постоянным уклоном
НК ( XYH) A (X,Y,H) B (X,Y,H) КК (X,Y,H) ВУ (X,Y,H) СК (X,Y,H) R О R R Входной портал Выходной портал d A НК, A НК, i d ККВ, ККВ, i Т Т К
Слайд 87: Разбивка тоннеля Способы разбивки простых круговых кривых
Прямоугольных координат. Полярных координат (способ углов). Продолженных хорд. Трех точек. Описанного многоугольника. Вписанного многоугольника. Разбивка тоннеля с учетом переходных кривых
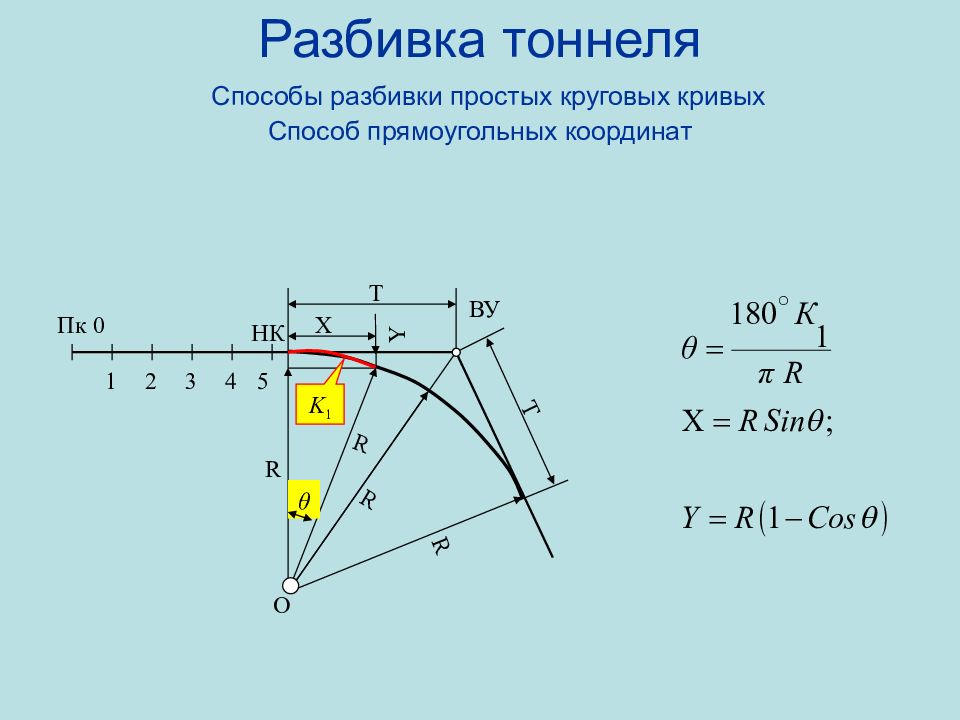
Слайд 88: Разбивка тоннеля Способы разбивки простых круговых кривых Способ прямоугольных координат
НК O Пк 0 1 5 4 3 2 Т Т ВУ X Y θ K 1 R R R R
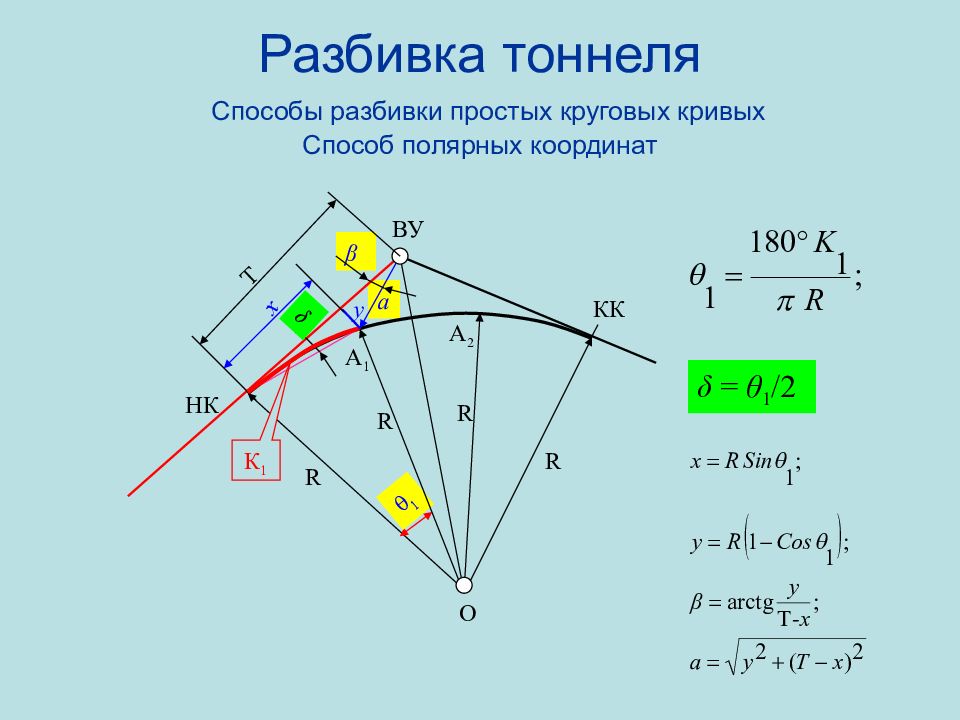
Слайд 89: Разбивка тоннеля Способы разбивки простых круговых кривых Способ полярных координат
β a Разбивка тоннеля Способы разбивки простых круговых кривых Способ полярных координат НК А 1 А 2 КК R R R R O ВУ θ 1 δ δ = θ 1 /2 Т x y К 1
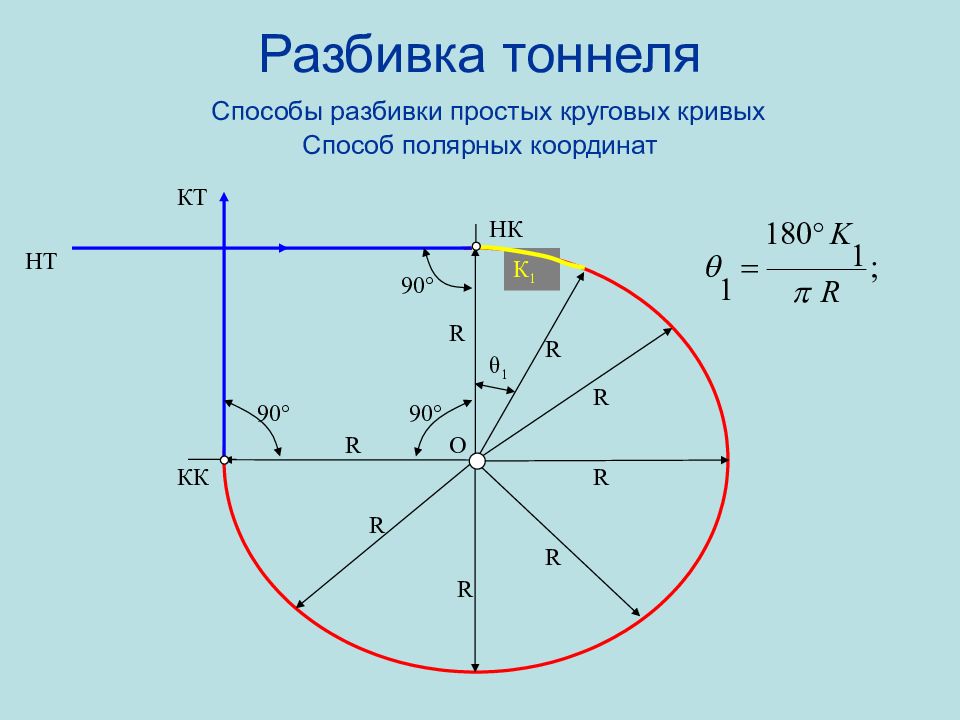
Слайд 90: Разбивка тоннеля Способы разбивки простых круговых кривых Способ полярных координат
НК КК R R R R R R R R НТ КТ O К 1 θ 1 90 ° 90 ° 90 °
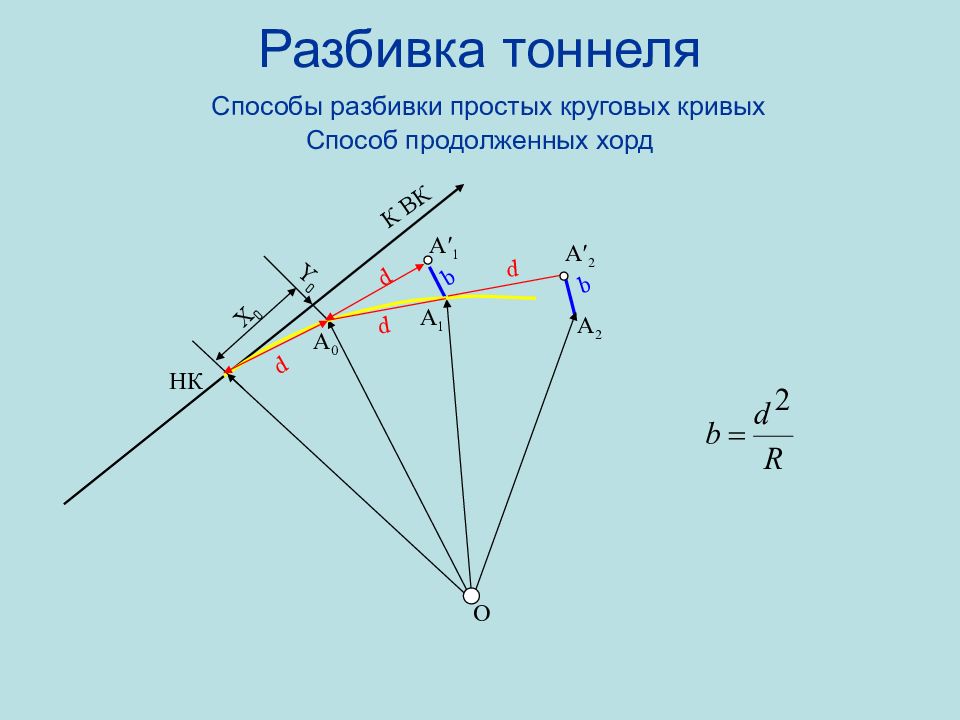
Слайд 91: Разбивка тоннеля Способы разбивки простых круговых кривых Способ продолженных хорд
X 0 Y 0 b d d НК А 0 А 1 b O d d A 2 К ВК А′ 1 А′ 2
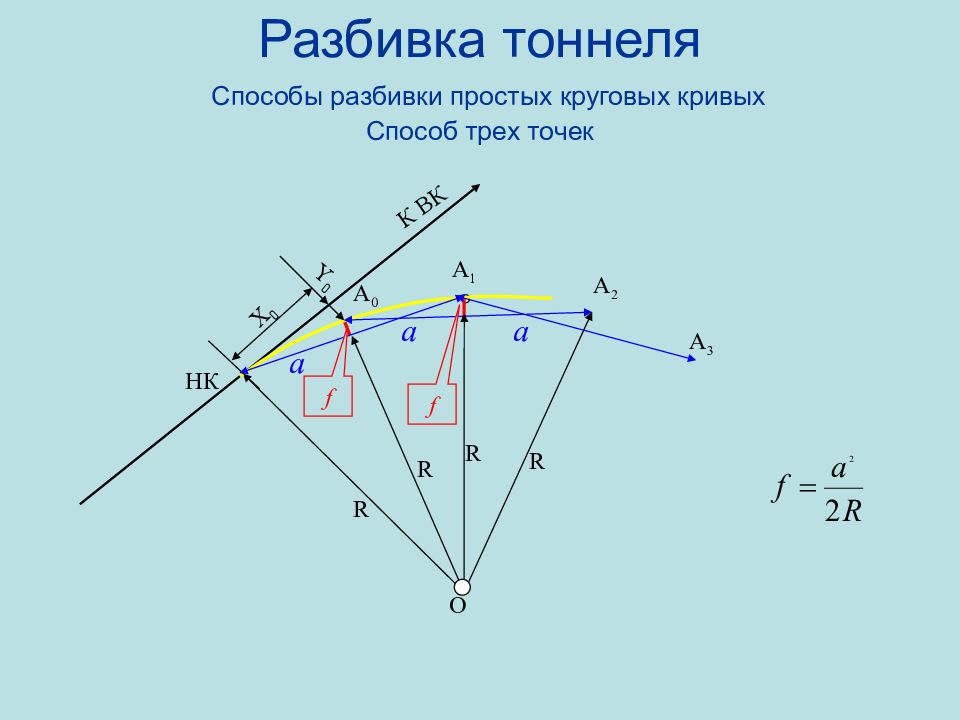
Слайд 92: Разбивка тоннеля Способы разбивки простых круговых кривых Способ трех точек
X 0 Y 0 a НК А 0 А 1 O A 2 К ВК f f A 3 a a R R R R
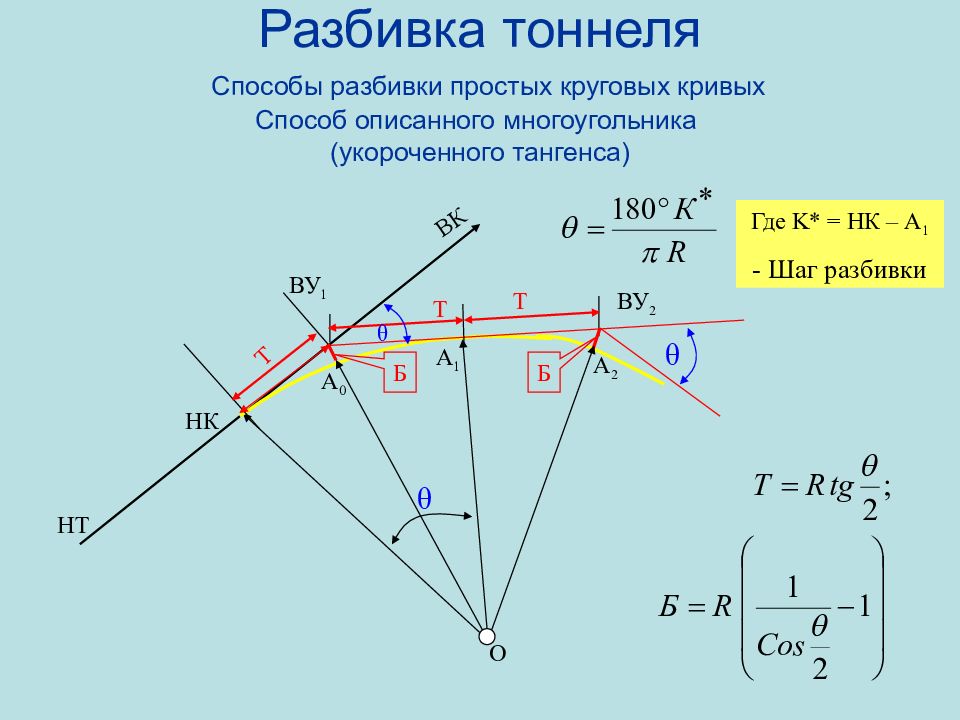
Слайд 93: Разбивка тоннеля Способы разбивки простых круговых кривых Способ описанного многоугольника (укороченного тангенса)
Т НК А 0 А 1 O A 2 ВК ВУ 1 ВУ 2 Т Т θ θ НТ θ Б Б Где K* = НК – А 1 - Шаг разбивки
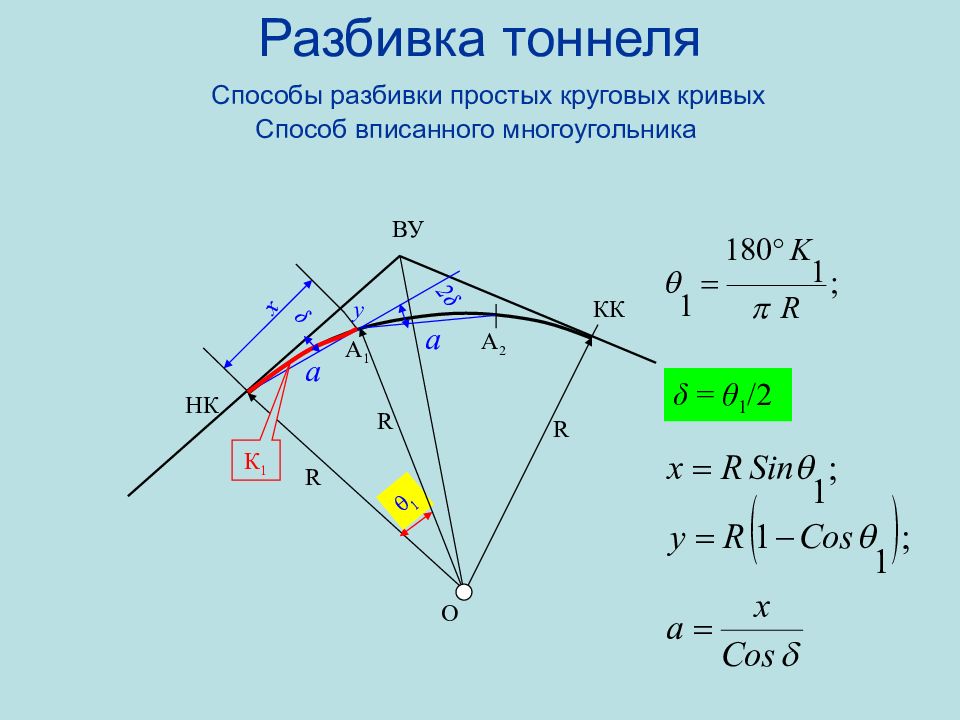
Слайд 94: Разбивка тоннеля Способы разбивки простых круговых кривых Способ вписанного многоугольника
НК А 1 КК R R ВУ θ 1 δ x y К 1 А 2 2 δ а а δ = θ 1 /2 R O
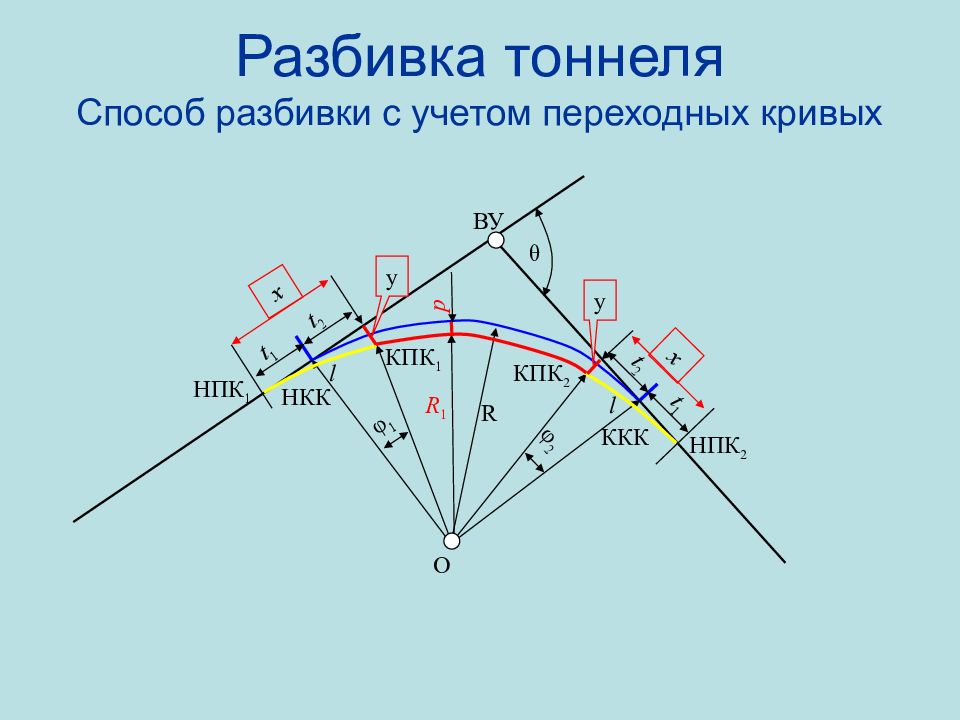
Слайд 95: Разбивка тоннеля Способ разбивки с учетом переходных кривых
θ p НПК 1 φ 1 φ 2 x t 1 t 2 НКК НПК 2 КПК 1 ККК x t 1 t 2 R КПК 2 R 1 O y y ВУ l l
Слайд 96: Разбивка тоннеля Способ разбивки с учетом переходных кривых
x = t 1 + t 2 Сдвижка круговой кривой : Расстояния от начала (конца) круговой кривой до начала ( t 1 ) и до конца ( t 2 ) переходной кривой R 1 = R - p Радиус сдвинутой круговой вставки Координаты конца переходной кривой в системе координат трассы тоннеля Контроль правильности вычисления координаты x Угол поворота переходной кривой
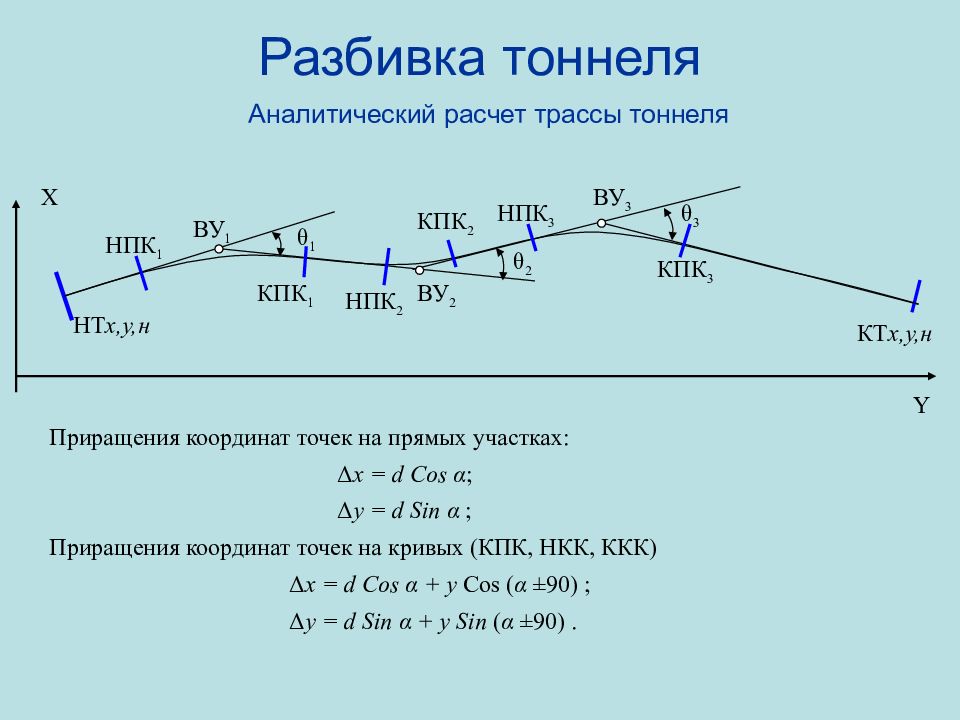
Слайд 97: Разбивка тоннеля Аналитический расчет трассы тоннеля
НТ x, y,н НПК 1 НПК 2 НПК 3 КПК 3 КПК 2 КПК 1 КТ x, y,н ВУ 1 ВУ 2 ВУ 3 X Y θ 1 θ 2 θ 3 Приращения координат точек на прямых участках : Δ x = d Cos α ; Δ y = d Sin α ; Приращения координат точек на кривых (КПК, НКК, ККК) Δ x = d Cos α + y Cos ( α ± 90) ; Δ y = d Sin α + y Sin ( α ± 90).
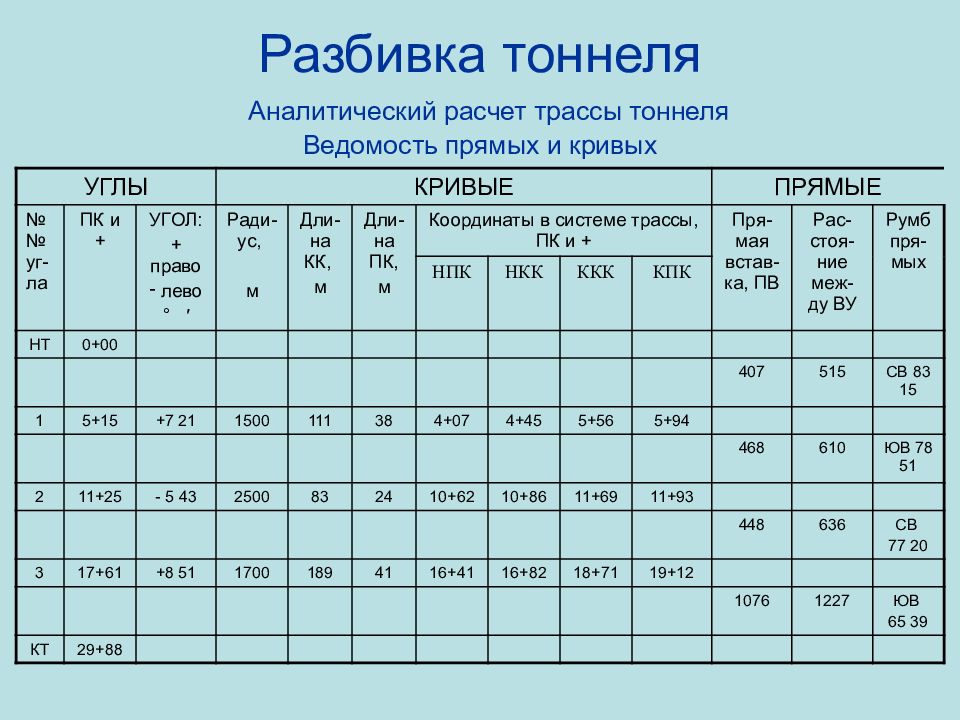
Слайд 98: Разбивка тоннеля Аналитический расчет трассы тоннеля Ведомость прямых и кривых
УГЛЫ КРИВЫЕ ПРЯМЫЕ №№ уг-ла ПК и + УГОЛ : + право лево ° ′ Ради-ус, м Дли-на КК, м Дли-на ПК, м Координаты в системе трассы, ПК и + Пря-мая встав-ка, ПВ Рас-стоя-ние меж-ду ВУ Румб пря-мых НПК НКК ККК КПК НТ 0+00 407 515 СВ 83 15 1 5+15 +7 21 1500 111 38 4+07 4+45 5+56 5+94 468 610 ЮВ 78 51 2 11+25 - 5 43 2500 83 24 10+62 10+86 11+69 11+93 448 636 СВ 77 20 3 17+61 +8 51 1700 189 41 16+41 16+82 18+71 19+12 1076 1227 ЮВ 65 39 КТ 29+88
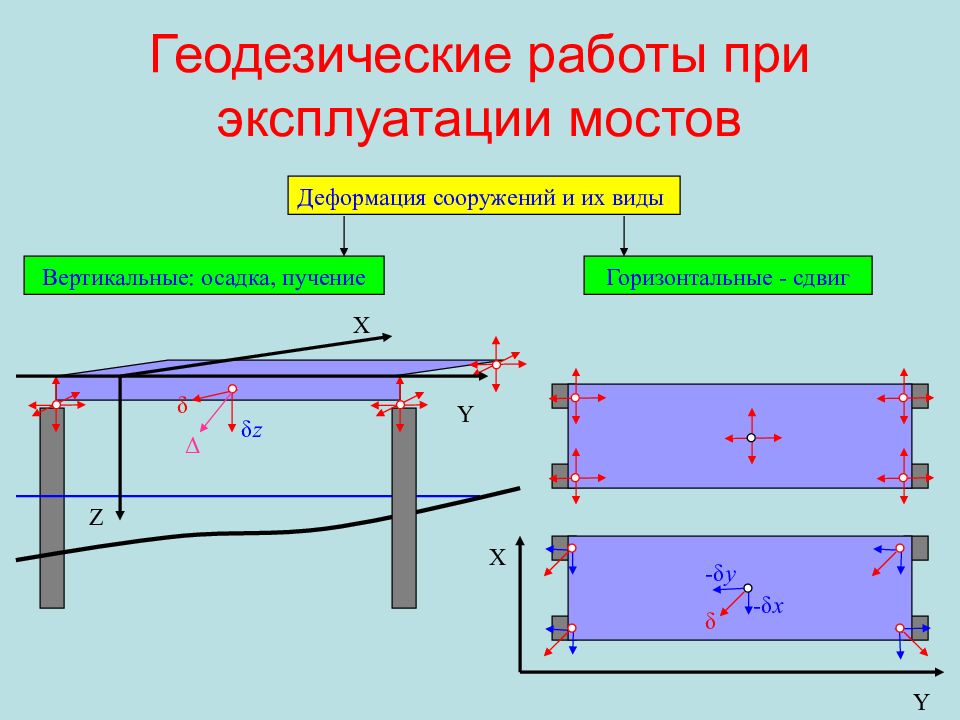
Слайд 99: Геодезические работы при эксплуатации мостов
Деформация сооружений и их виды Вертикальные : осадка, пучение Горизонтальные - сдвиг X Y - δ x - δ y δ δ δ z Δ Y Z X
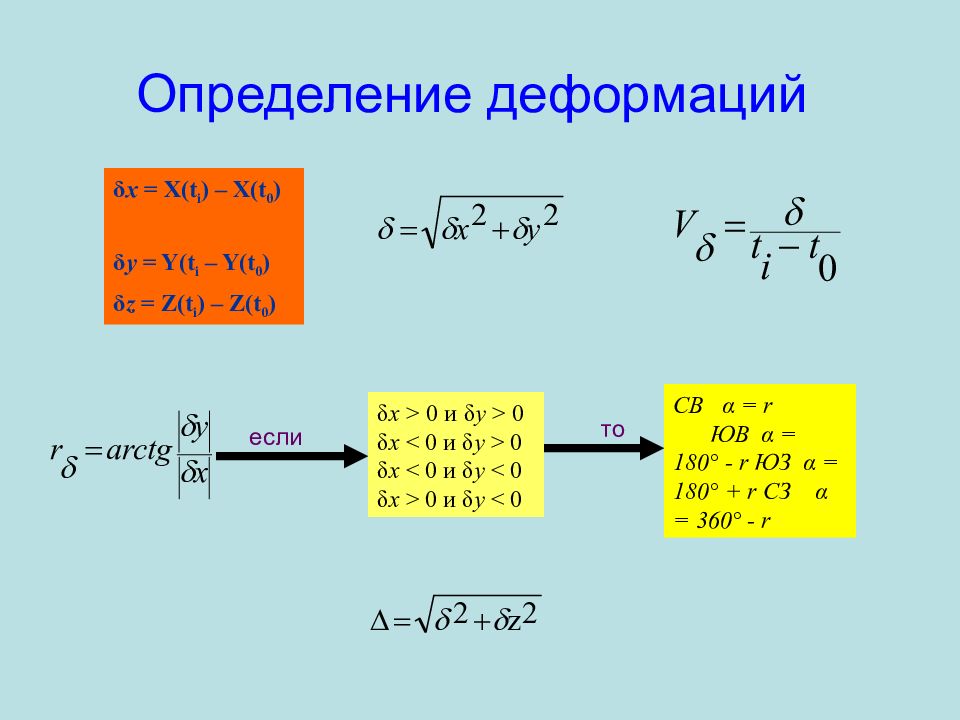
Слайд 100: Определение деформаций
CB α = r ЮВ α = 180° - r ЮЗ α = 180° + r СЗ α = 360° - r δ x > 0 и δ y > 0 δ x < 0 и δ y > 0 δ x < 0 и δ y < 0 δ x > 0 и δ y < 0 если то δ x = X(t i ) – X(t 0 ) δ y = Y(t i – Y(t 0 ) δ z = Z(t i ) – Z(t 0 )
Слайд 101: Геодезические методы определения деформаций
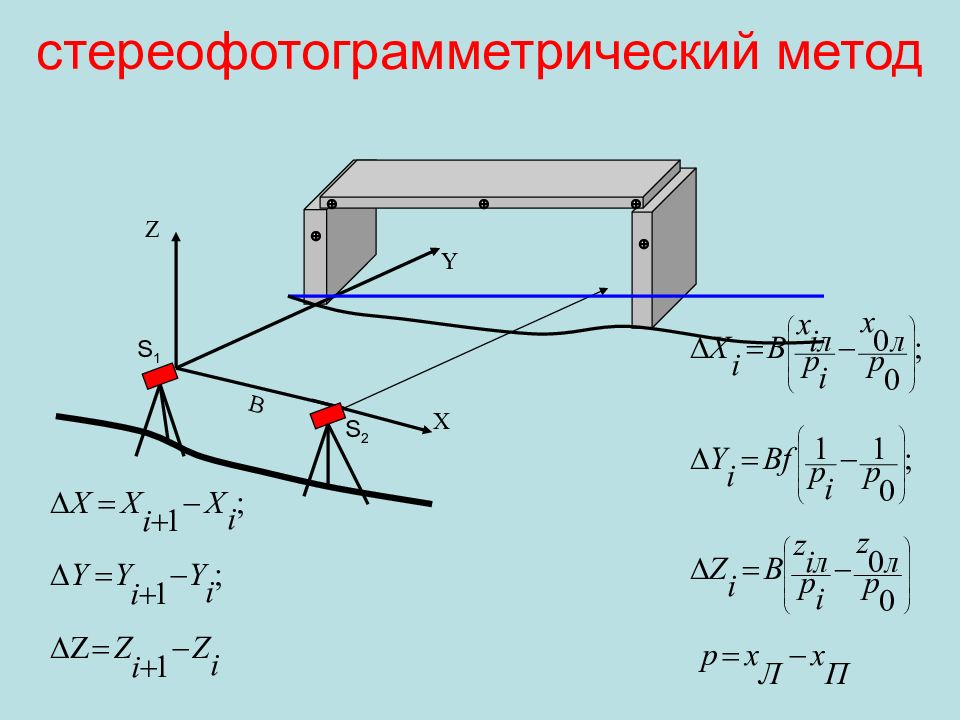
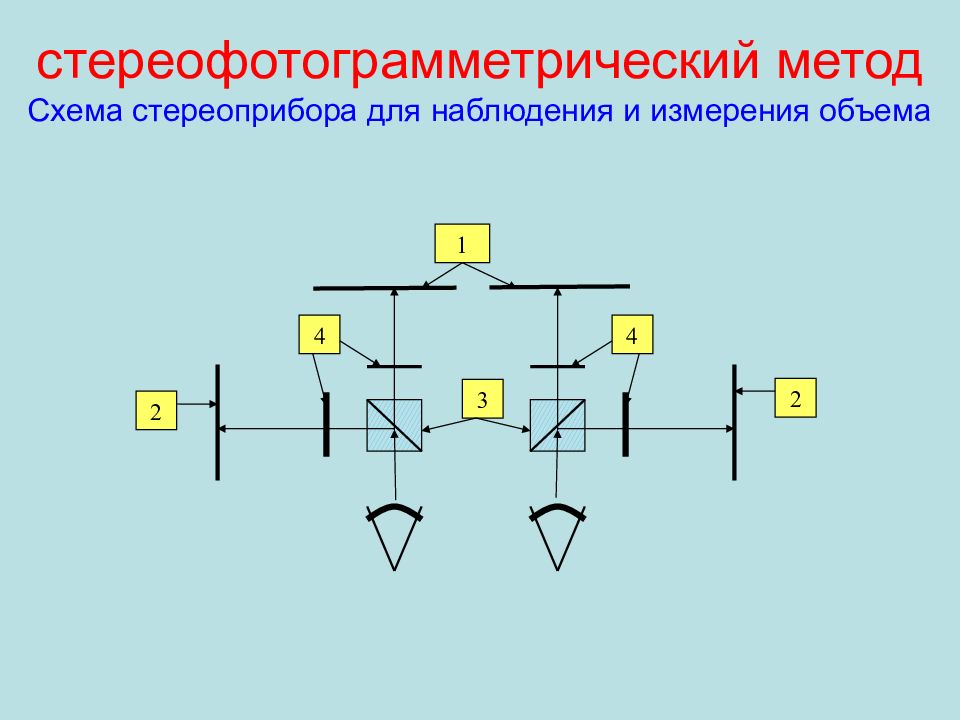
метод геометрического нивелирования I, II и III класса. Применяется для измерения осадок и пучения; метод гидронивелирования. Применяется для измерения относительных смещений деталей строительной конструкции, например, примыкающих друг к другу плит пролетных строений; метод угловых измерений. Применяется для определения горизонтальных смещений вертикальных (высотных) конструкций; метод координат. Применяется для определения горизонтальных смещений строительных конструкций, имеющих в верхнем строении площадки (верхние части опор, пролетные строения мостовых переходов или путепроводов; фотограмметрический метод. Применяется для определения горизонтальных и вертикальных смещений фасадов строительных конструкций сложной формы ; стереофотограмметрический метод. Применяется для определения горизонтальных и вертикальных смещений фасадов строительных конструкций сложной формы.
Слайд 102: метод геометрического нивелирования. Классы нивелирования и необходимая точность определения деформаций
I класс, fh ( доп ) = II класс, fh ( доп ) = III класс, fh ( доп ) = , применяется в научных целях, при выяснении подвижек Земной коры и при ожидаемой осадке < 1 мм. , применяется при ожидаемой осадке 1 – 5 мм. , применяется при ожидаемой осадке > 5 мм.
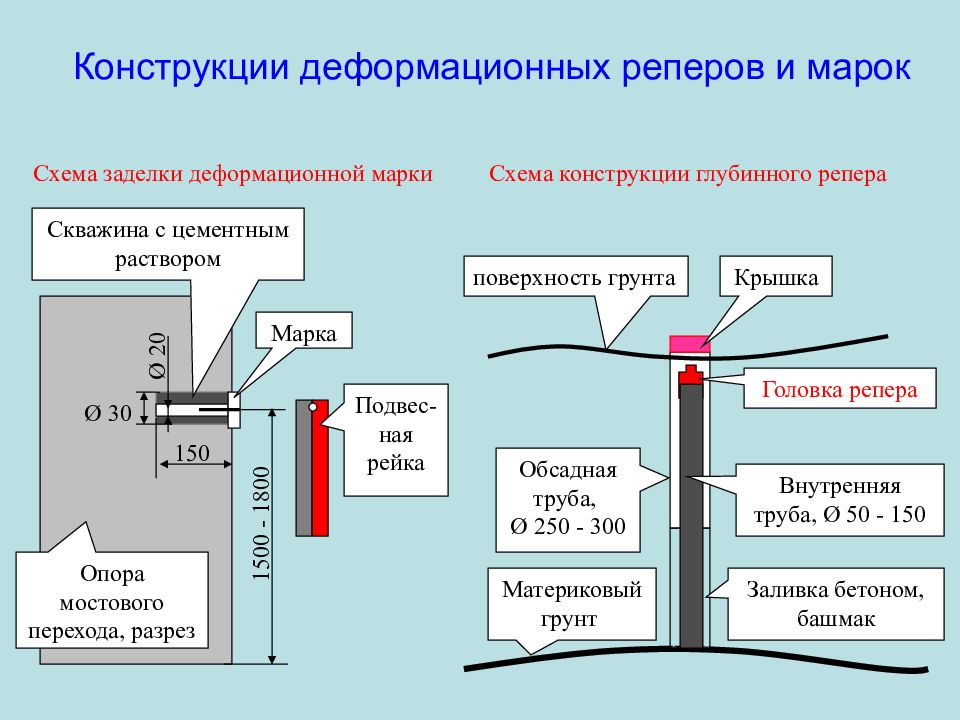
Слайд 103: Конструкции деформационных реперов и марок
Головка репера 75 50 150 10 20 30 Выступающая часть репера Несущая опора МП Рейка
Слайд 104: Конструкции деформационных реперов и марок
150 Ø 30 Скважина с цементным раствором Марка 1 5 00 - 1800 Ø 20 Опора мостового перехода, разрез поверхность грунта Материковый грунт Головка репера Обсадная труба, Ø 250 - 300 Внутренняя труба, Ø 50 - 150 Заливка бетоном, башмак Крышка Подвес-ная рейка Схема конструкции глубинного репера Схема заделки деформационной марки
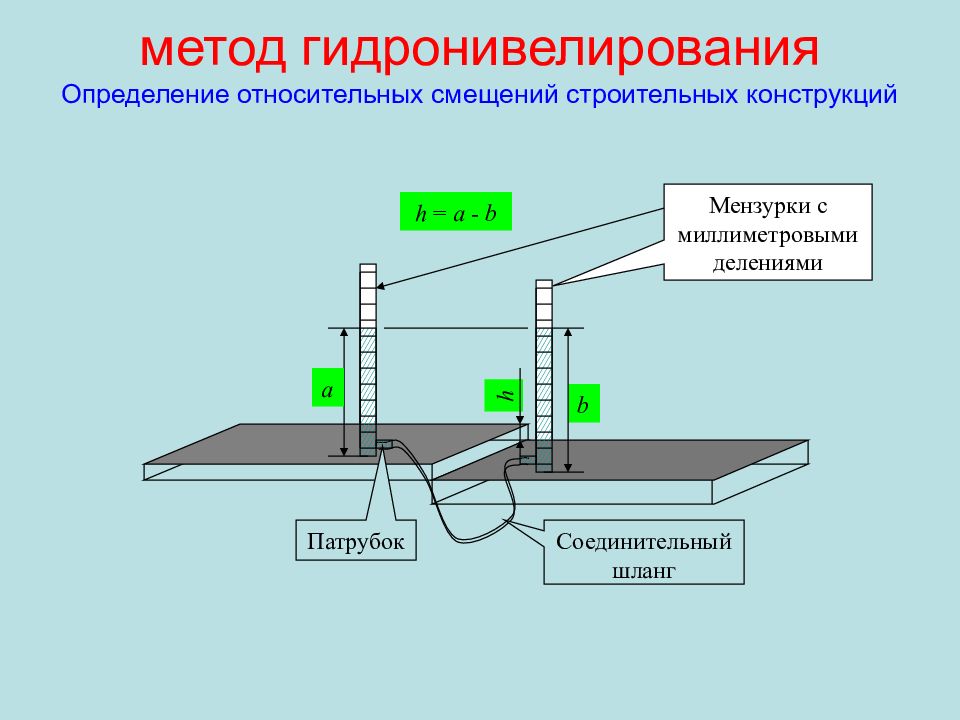
Слайд 105: метод гидронивелирования Определение относительных смещений строительных конструкций
а b h = a - b Мензурки с миллиметровыми делениями Соединительный шланг Патрубок h
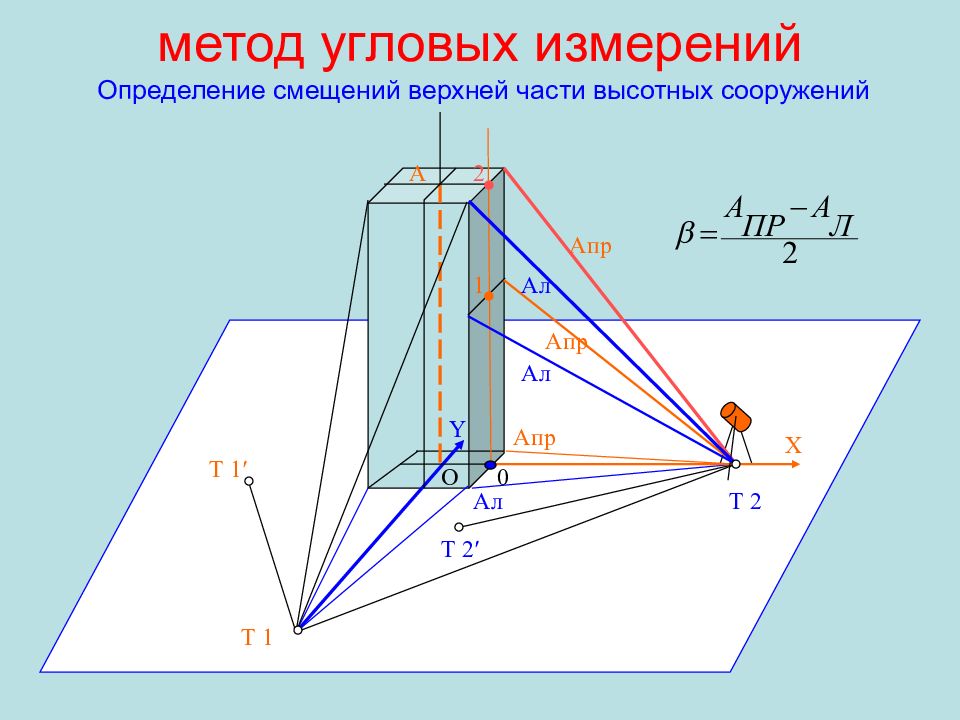
Слайд 106: метод угловых измерений Определение смещений верхней части высотных сооружений
A пр 0 2 1 O A Т 2 Т 1 X Y Т 2 ′ Т 1 ′ A пр A пр A л A л A л
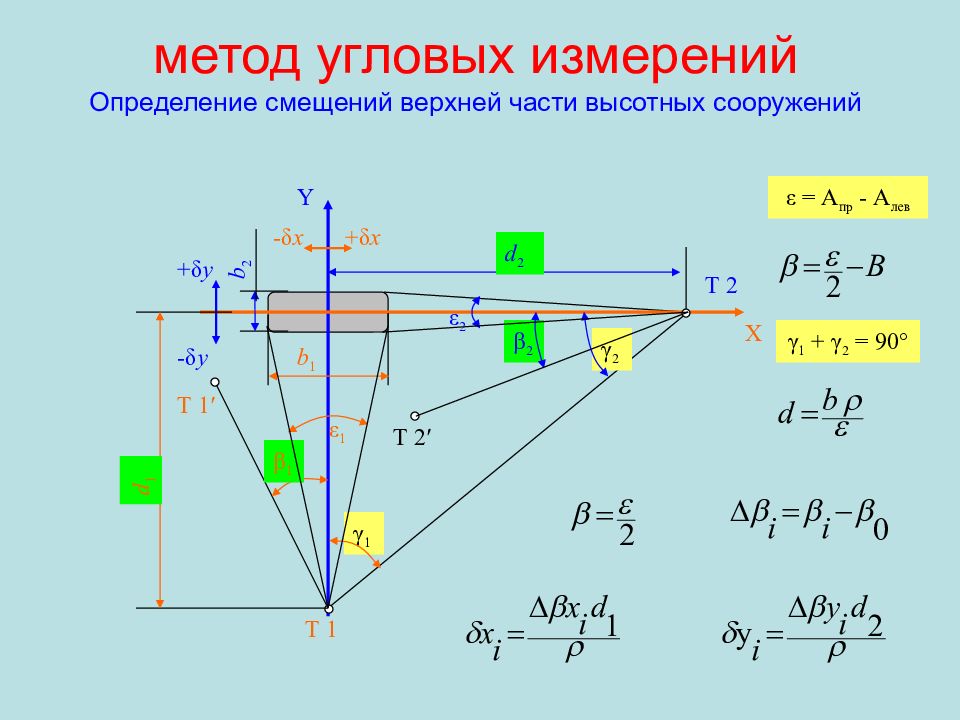
Слайд 107: метод угловых измерений Определение смещений верхней части высотных сооружений
Т 1 Т 2 Т 1 ′ Т 2 ′ Y X β 1 γ 1 γ 2 β 2 γ 1 + γ 2 = 90° + δ x - δ x + δ y - δ y d 1 d 2 ε 1 ε 2 b 1 b 2 ε = A пр - A лев
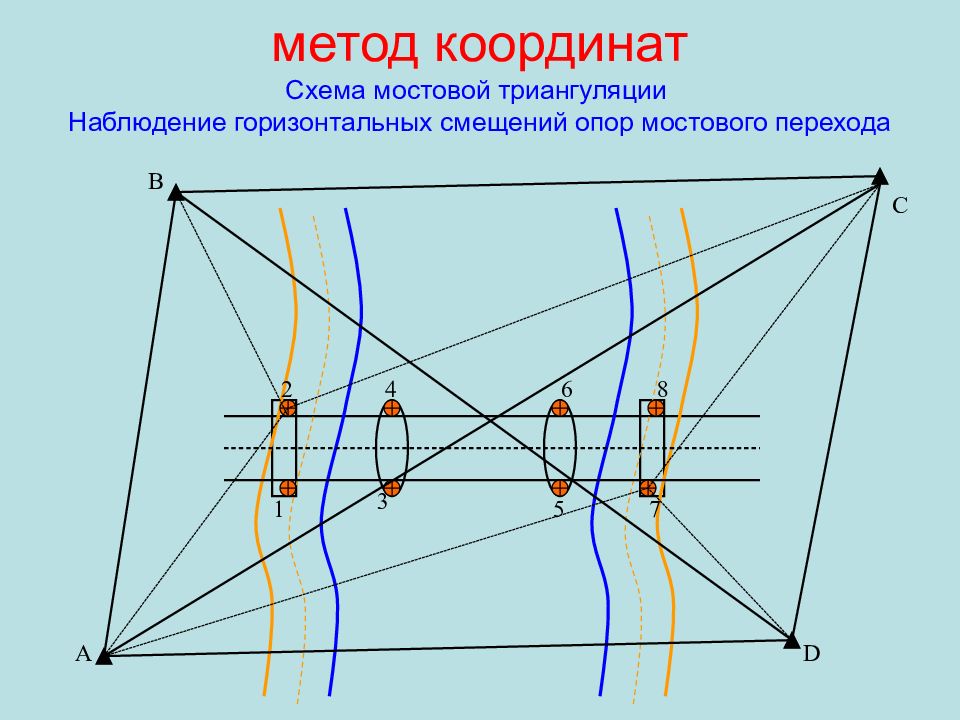
Слайд 108: метод координат Схема мостовой триангуляции Наблюдение горизонтальных смещений опор мостового перехода
5 6 4 3 2 1 C 8 7 D А B
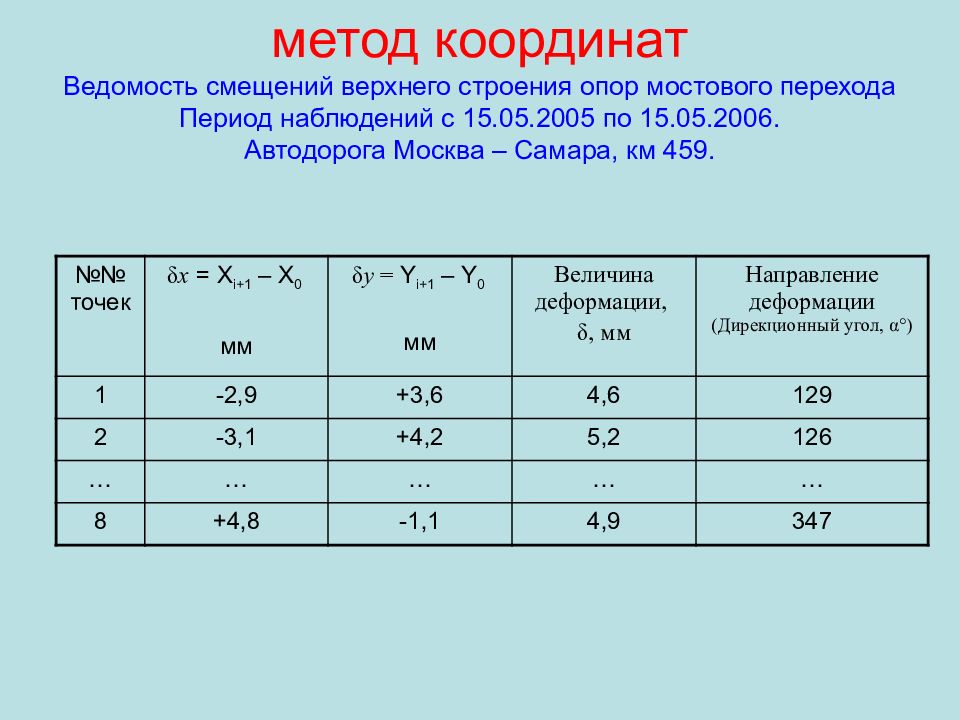
Слайд 109: метод координат Ведомость смещений верхнего строения опор мостового перехода Период наблюдений с 15.05.2005 по 15.05.2006. Автодорога Москва – Самара, км 459
№№ точек δ x = X i+1 – X 0 мм δ y = Y i+1 – Y 0 мм Величина деформации, δ, мм Направление деформации (Дирекционный угол, α ° ) 1 -2,9 +3,6 4,6 129 2 -3,1 +4,2 5,2 126 … … … … … 8 +4,8 -1,1 4,9 347
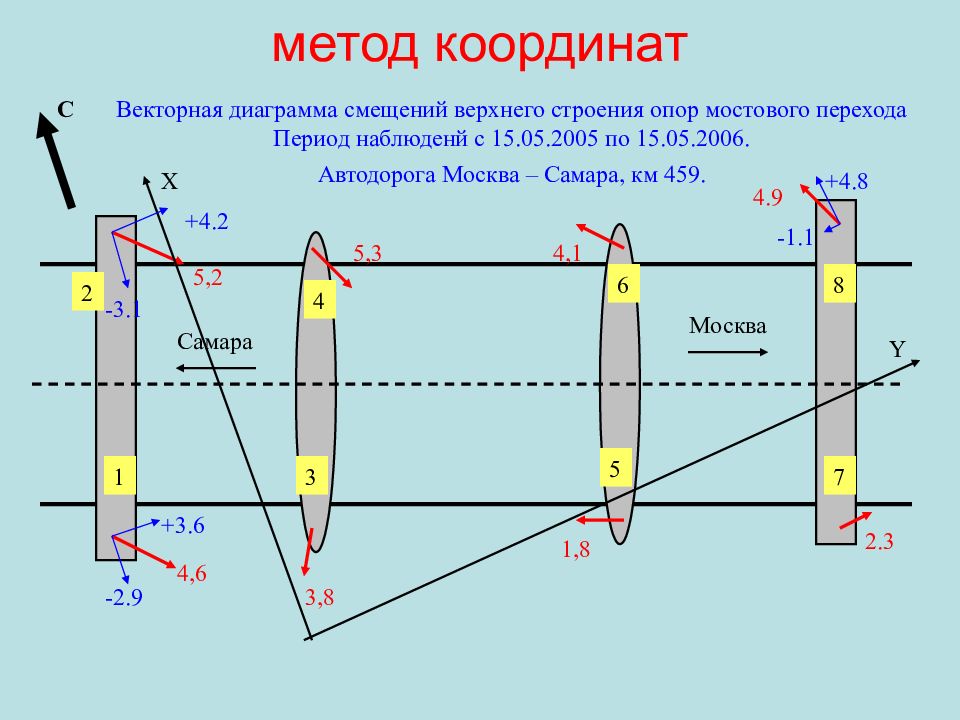
Слайд 110: метод координат
С 4,6 5,2 3,8 5,3 4,1 1,8 4.9 2.3 Векторная диаграмма смещений верхнего строения опор мостового перехода Период наблюденй с 15.05.2005 по 15.05.2006. Автодорога Москва – Самара, км 459. Москва Самара 5 6 4 3 2 1 8 7 X Y -2.9 +3.6 -3.1 +4.2 -1.1 +4.8
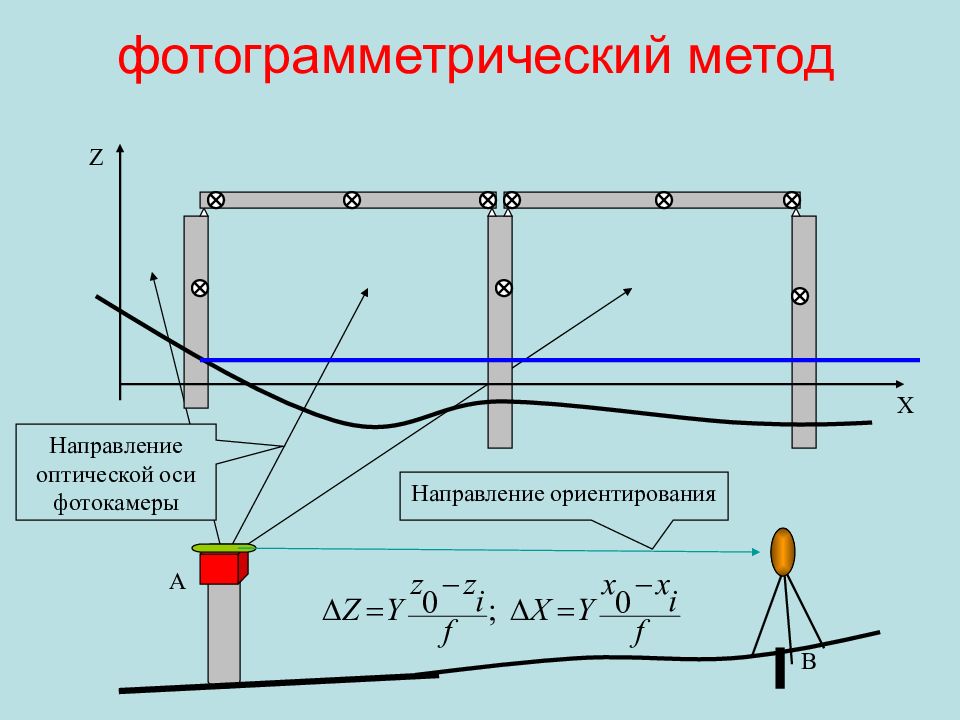
Слайд 111: фотограмметрический метод
Z X B A Направление оптической оси фотокамеры Направление ориентирования
Слайд 113
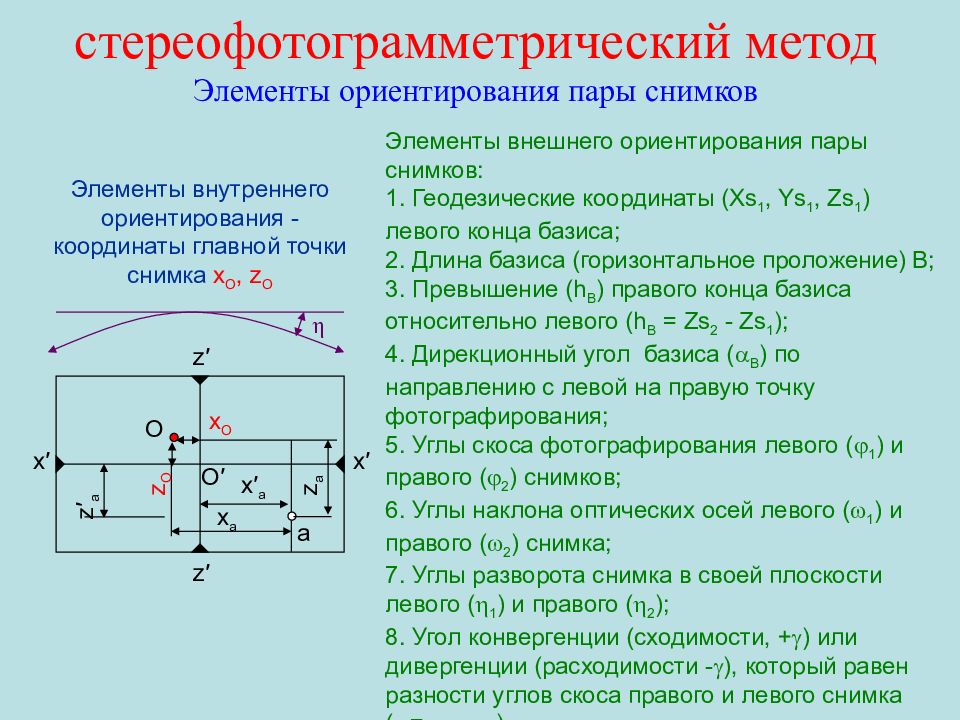
Элементы внутреннего ориентирования - координаты главной точки снимка x O, z O z ′ z′ x ′ x′ а О О ′ x O z O x ′ a z ′ a x a z a Элементы внешнего ориентирования пары снимков : 1. Геодезические координаты ( Xs 1, Ys 1, Zs 1 ) левого конца базиса; 2. Длина базиса (горизонтальное проложение) В; 3. Превышение ( h В ) правого конца базиса относительно левого ( h В = Zs 2 - Zs 1 ); 4. Дирекционный угол базиса ( В ) по направлению с левой на правую точку фотографирования; 5. Углы скоса фотографирования левого ( 1 ) и правого ( 2 ) снимков; 6. Углы наклона оптических осей левого ( 1 ) и правого ( 2 ) снимка; 7. Углы разворота снимка в своей плоскости левого ( 1 ) и правого ( 2 ); 8. Угол конвергенции (сходимости, + ) или дивергенции (расходимости - ), который равен разности углов скоса правого и левого снимка ( = 2 - 1 ). η стереофотограмметрический метод Элементы ориентирования пары снимков