Первый слайд презентации
Физические основы механики Лектор: Доцент НИЯУ МИФИ, к.ф.-м.н., Ольчак Андрей Станиславович Курс общей физики НИЯУ МИФИ
Слайд 2
Физические основы механики Кинематика материальной точки Курс общей физики НИЯУ МИФИ
Слайд 3
Кинематика. Основные понятия и величины. Предмет кинематики: Описание движения и связи между величинами, характеризующими это движение ( описание, но пока не объяснение !) Основные понятия и величины кинематики: Материальная точка – объект, размерами и структурой которого в данной задаче можно пренебречь Координаты ( x, y, z ) – определяют положение точки в пространстве Система отсчета = система координат + часы + тело отсчета Радиус-вектор материальной точки ( r ) Перемещение ( Δ r ) Пройденный путь ( S) Скорость ( v ) Ускорение ( a )
Слайд 4
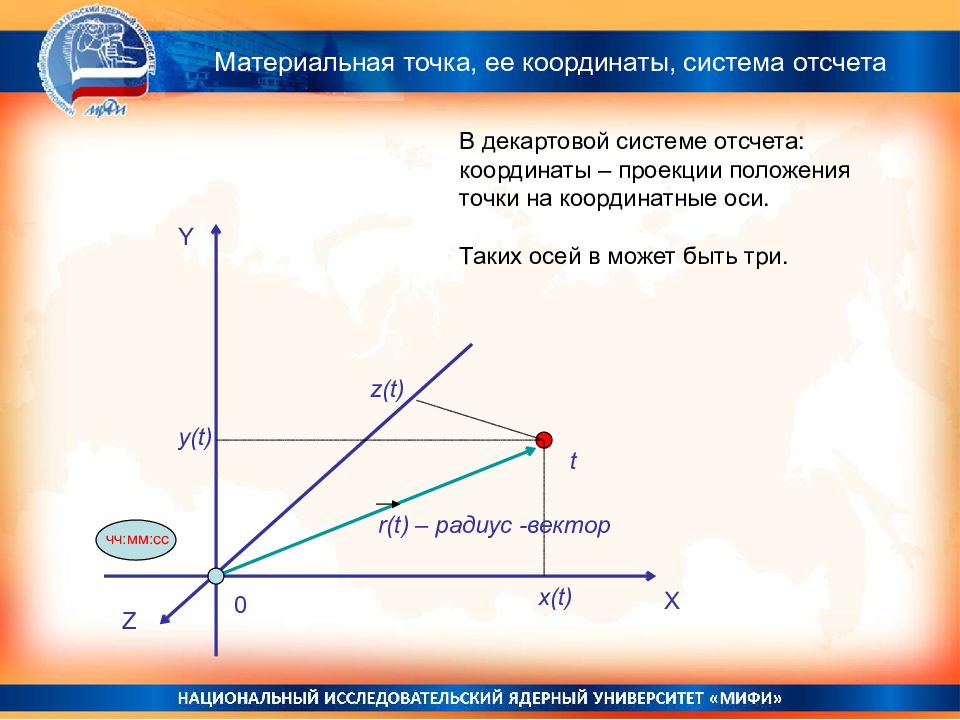
Материальная точка, ее координаты, система отсчета Y X Z z ( t) y(t) x(t) 0 чч:мм:сс t r ( t) – радиус -вектор В декартовой системе отсчета: координаты – проекции положения точки на координатные оси. Таких осей в может быть три.
Слайд 5
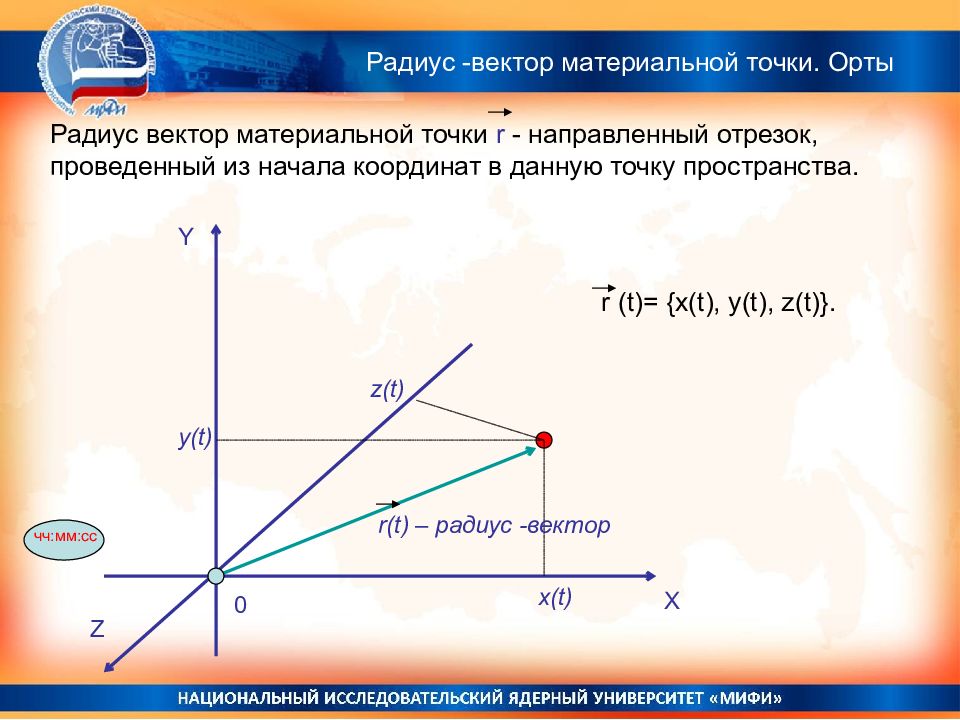
Радиус -вектор материальной точки. Орты Y X Z z ( t) y(t) x(t) 0 чч:мм:сс r ( t) – радиус -вектор Радиус вектор материальной точки r - направленный отрезок, проведенный из начала координат в данную точку пространства. r (t)= {x(t), y(t), z(t)}.
Слайд 6
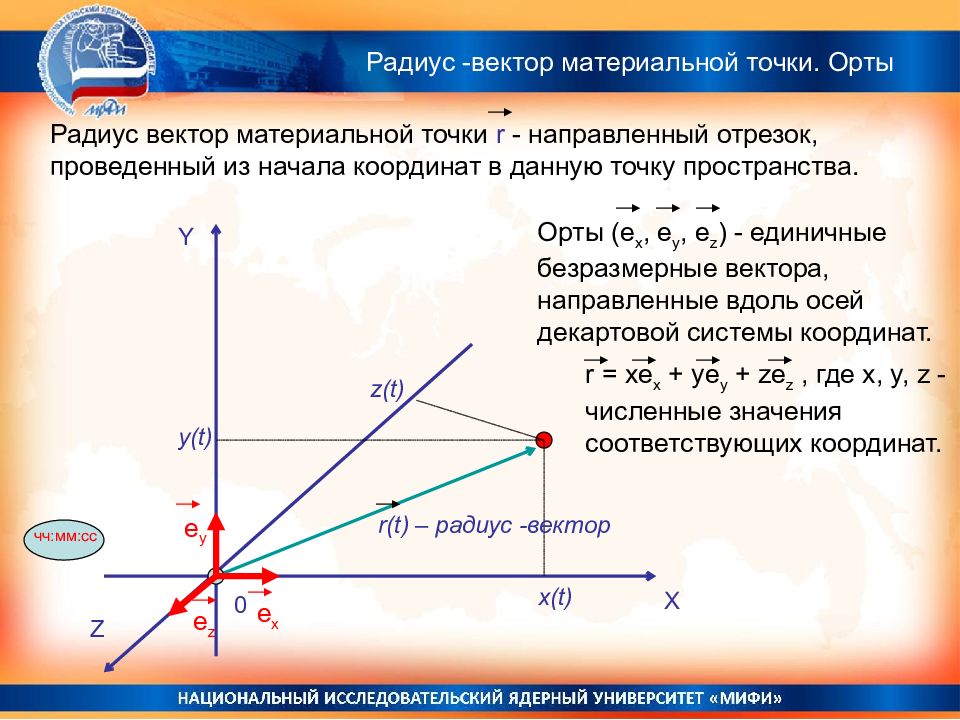
Y X Z z ( t) y(t) x(t) 0 чч:мм:сс r ( t) – радиус -вектор Радиус вектор материальной точки r - направленный отрезок, проведенный из начала координат в данную точку пространства. Орты (e x, e y, e z ) - единичные безразмерные вектора, направленные вдоль осей декартовой системы координат. e y e x e z r (t)= {x(t), y(t), z(t)}. Радиус -вектор материальной точки. Орты
Слайд 7
Y X Z z ( t) y(t) x(t) 0 чч:мм:сс r ( t) – радиус -вектор Радиус вектор материальной точки r - направленный отрезок, проведенный из начала координат в данную точку пространства. Орты (e x, e y, e z ) - единичные безразмерные вектора, направленные вдоль осей декартовой системы координат. e y e x e z r = xe x + ye y + ze z, где x, y, z - численные значения соответствующих координат. Радиус -вектор материальной точки. Орты
Слайд 8
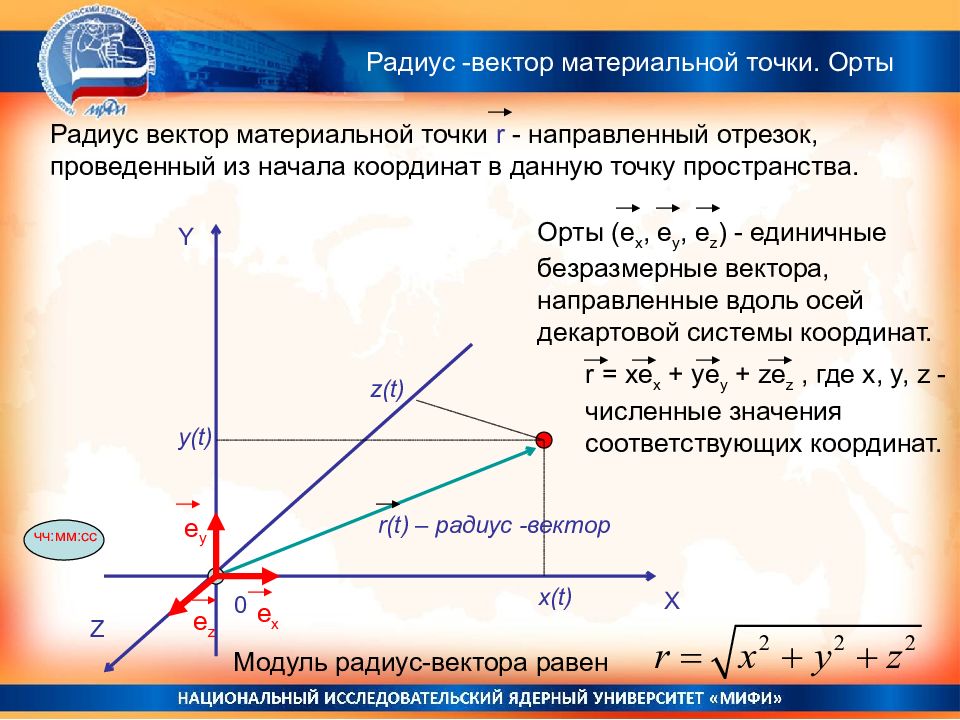
Y X Z z ( t) y(t) x(t) 0 чч:мм:сс r ( t) – радиус -вектор Радиус вектор материальной точки r - направленный отрезок, проведенный из начала координат в данную точку пространства. Орты (e x, e y, e z ) - единичные безразмерные вектора, направленные вдоль осей декартовой системы координат. e y e x e z r = xe x + ye y + ze z, где x, y, z - численные значения соответствующих координат. Модуль радиус-вектора равен Радиус -вектор материальной точки. Орты
Слайд 9
Перемещение, пройденный путь S X x(t) Δ r S Перемещение Δ r это: - приращение радиус-вектора r за некоторое время; - вектор, соединяющий начальное и конечное положение материальной точки Пройденный путь S – длина траектории движения точки Y X Z 0 чч:мм:сс r ( t) Δ r = r ( t+ Δ t) - r ( t) r ( t+ Δ t)
Слайд 10
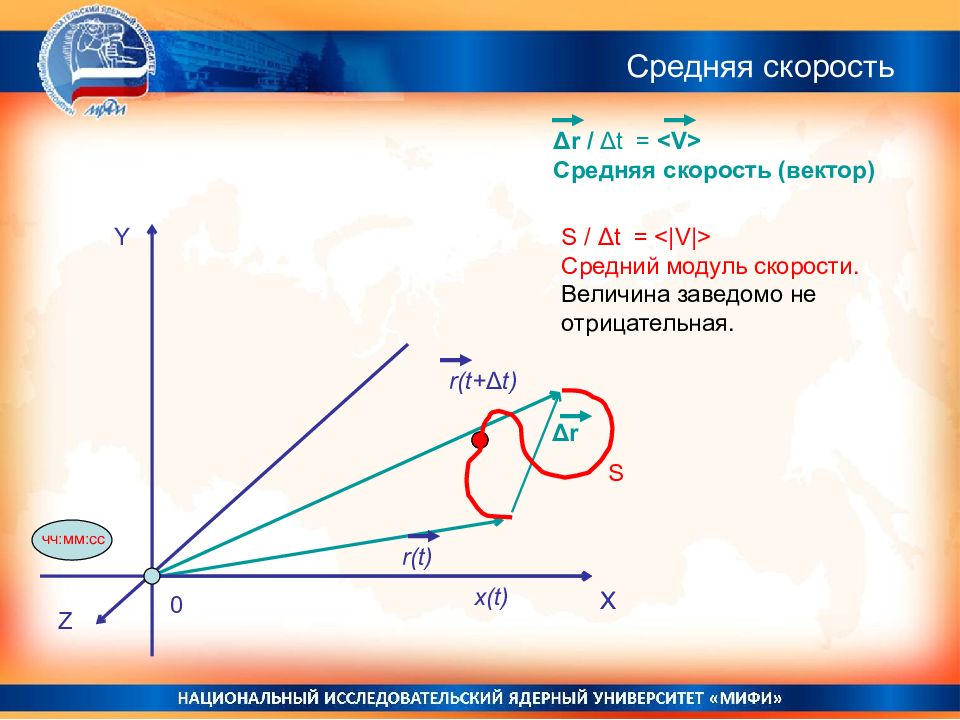
Средняя скорость Δ r / Δ t = <V> Средняя скорость (вектор) S / Δ t = <|V|> Средний модуль скорости. Величина заведомо не отрицательная. X x(t) Δ r S Y X Z 0 чч:мм:сс r ( t) r ( t+ Δ t)
Слайд 11
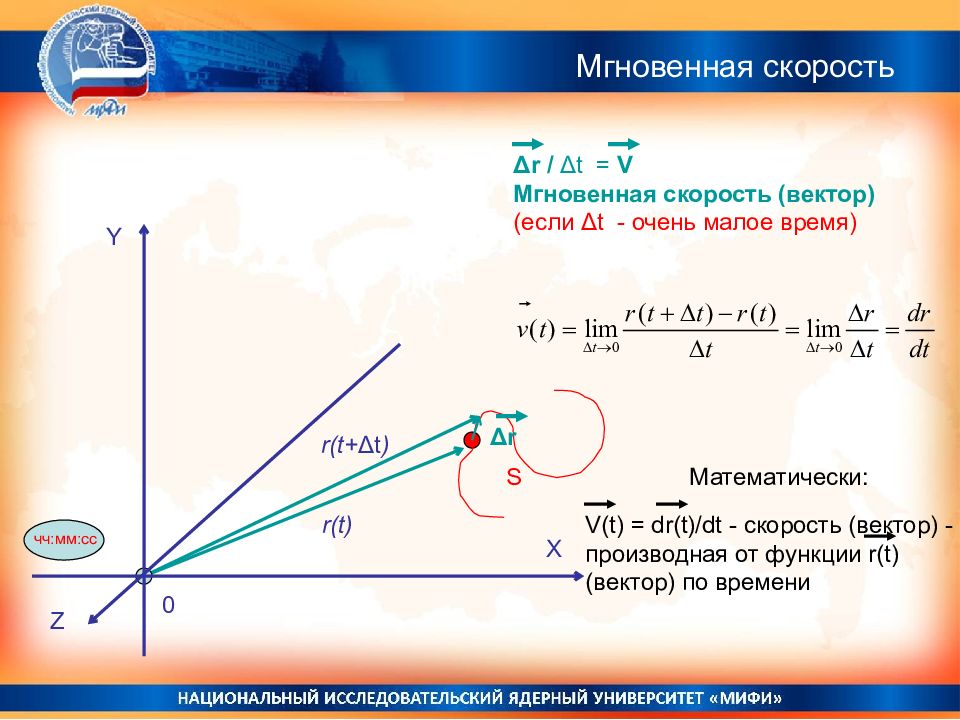
Y X Δ r S r ( t) Δ r / Δ t = V Мгновенная скорость (вектор) (если Δ t - очень малое время) r ( t + Δ t ) Z 0 чч:мм:сс Математически: V(t) = dr(t)/dt - скорость (вектор) - производная от функции r(t) (вектор) по времени Мгновенная скорость
Слайд 12
Y X z ( t) y(t) x(t) x(t + Δ t ) Δ r S r ( t) r ( t + Δ t ) Z 0 чч:мм:сс V x = dX(t)/dt V y = dY(t)/dt V z = dZ(t)/dt z ( t + Δ t ) y(t + Δ t ) 0 e y e x e z V(t) = dr(t)/dt = V x e x + V y e y + V z e z, где V x,V y,V z - численные значения координатных компонент мгновенной скорости, равные производным от соответствующих координат по времени: Мгновенная скорость в декартовой системе координат V(t) = dr(t)/dt - скорость производная от функции r(t) по времени Скорость, как вектор, раскладывается на координатные компоненты:
Слайд 13
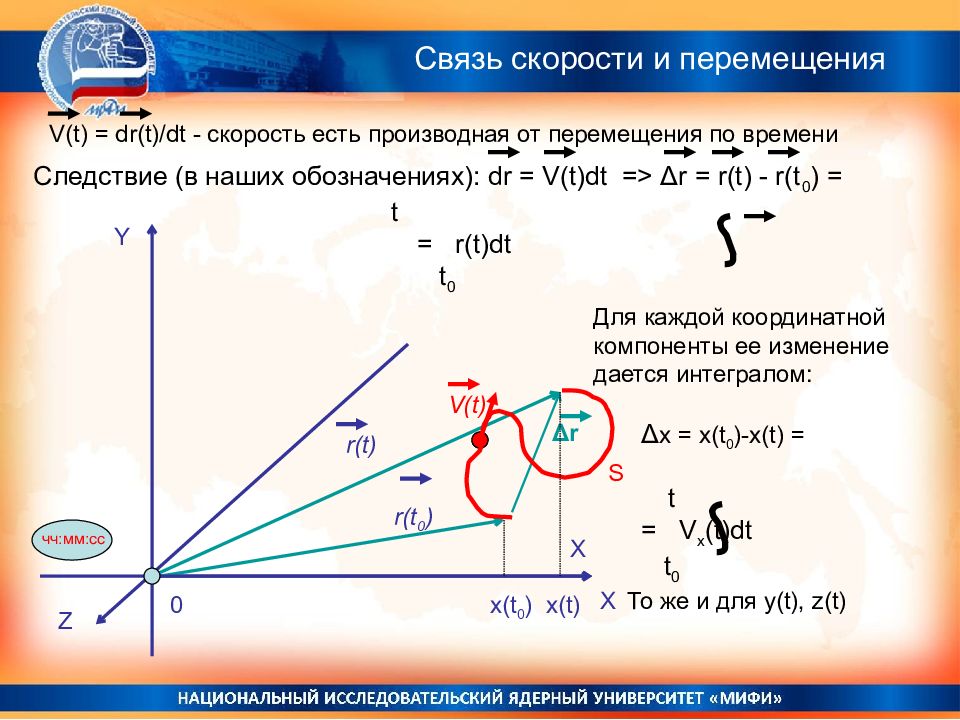
X Δ r S Y X Z 0 чч:мм:сс r ( t 0 ) r ( t) V ( t) Следствие (в наших обозначениях): dr = V(t)dt => Δ r = r(t) - r(t 0 ) = t = r(t)dt t 0 Для каждой координатной компоненты ее изменение дается интегралом: Δ x = x(t 0 )-x(t) = t = V x (t)dt t 0 То же и для y(t), z(t) х(t 0 ) x(t) Связь скорости и перемещения V(t) = dr(t)/dt - скорость есть производная от перемещения по времени
Слайд 14
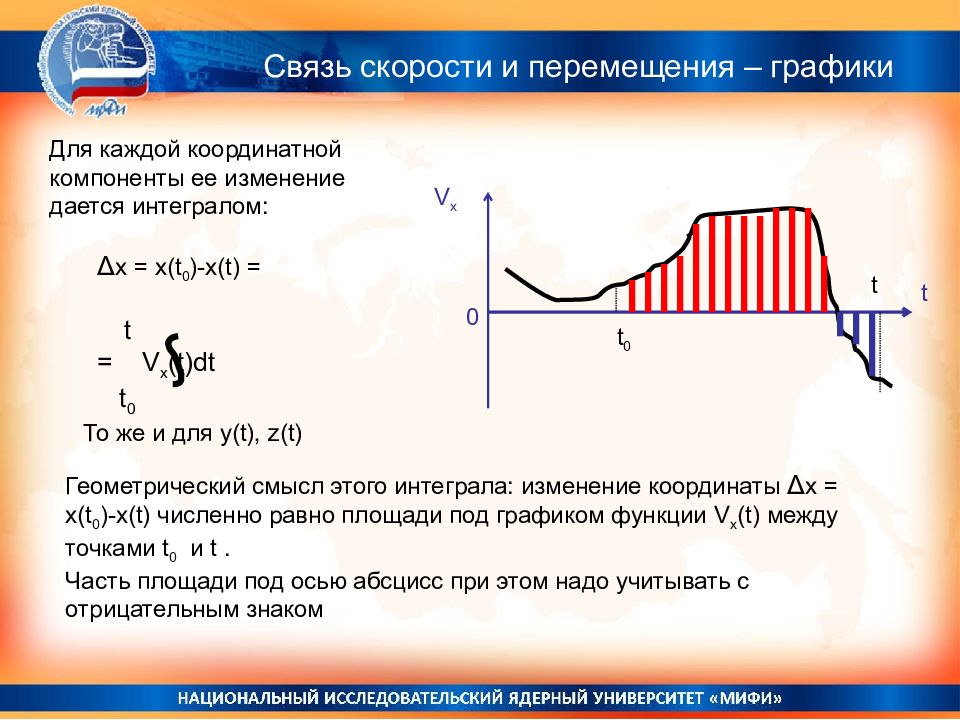
V х t 0 Для каждой координатной компоненты ее изменение дается интегралом: Δ x = x(t 0 )-x(t) = t = V x (t)dt t 0 То же и для y(t), z(t) Геометрический смысл этого интеграла: изменение координаты Δ x = x(t 0 )-x(t) численно равно площади под графиком функции V х (t) между точками t 0 и t. Часть площади под осью абсцисс при этом надо учитывать с отрицательным знаком t 0 t Связь скорости и перемещения – графики
Слайд 15
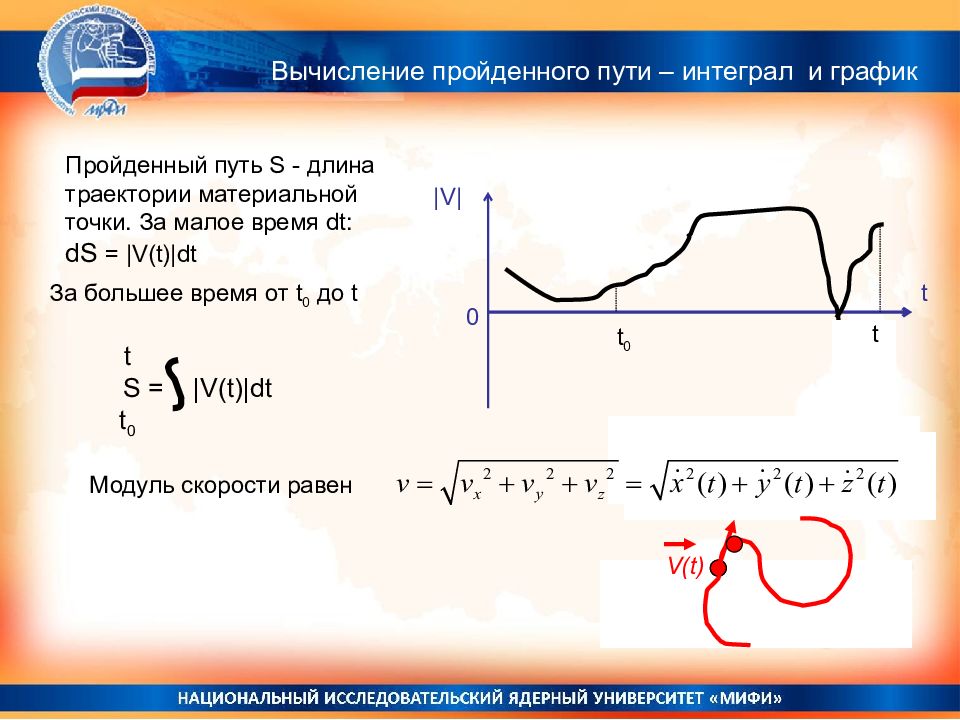
|V| t 0 За большее время от t 0 до t t S = |V(t)|dt t 0 t 0 t Пройденный путь S - длина траектории материальной точки. За малое время dt: dS = |V(t)|dt t Модуль скорости равен V ( t) Вычисление пройденного пути – интеграл и график
Слайд 16
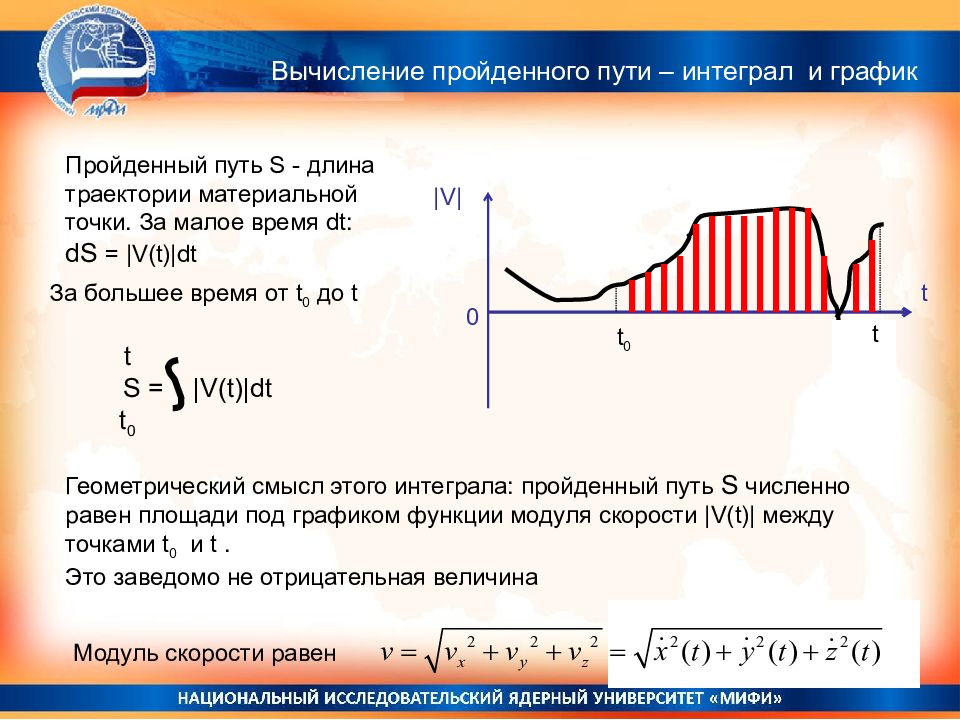
t 0 За большее время от t 0 до t t S = |V(t)|dt t 0 Геометрический смысл этого интеграла: пройденный путь S численно равен площади под графиком функции модуля скорости |V(t)| между точками t 0 и t. Это заведомо не отрицательная величина t 0 t Пройденный путь S - длина траектории материальной точки. За малое время dt: dS = |V(t)|dt t Модуль скорости равен |V| Вычисление пройденного пути – интеграл и график
Слайд 17
V(t) V(t+ Δ t ) V(t) V(t+ Δ t ) V(t+ Δ t ) - V(t) = Δ V Ускорением называется отношение приращения вектора скорости Δ V за некоторое время Δ t к величине этого времени. w = Δ V / Δ t Другими словами: ускорение это скорость изменения вектора скорости точки. Мгновенное ускорение: W (t) = d V (t)/dt = d 2 r(t)/dt 2 Математически ускорение - это первая производная от скорости V (t) и вторая производная от функции r(t) по времени Ускорение
Слайд 18
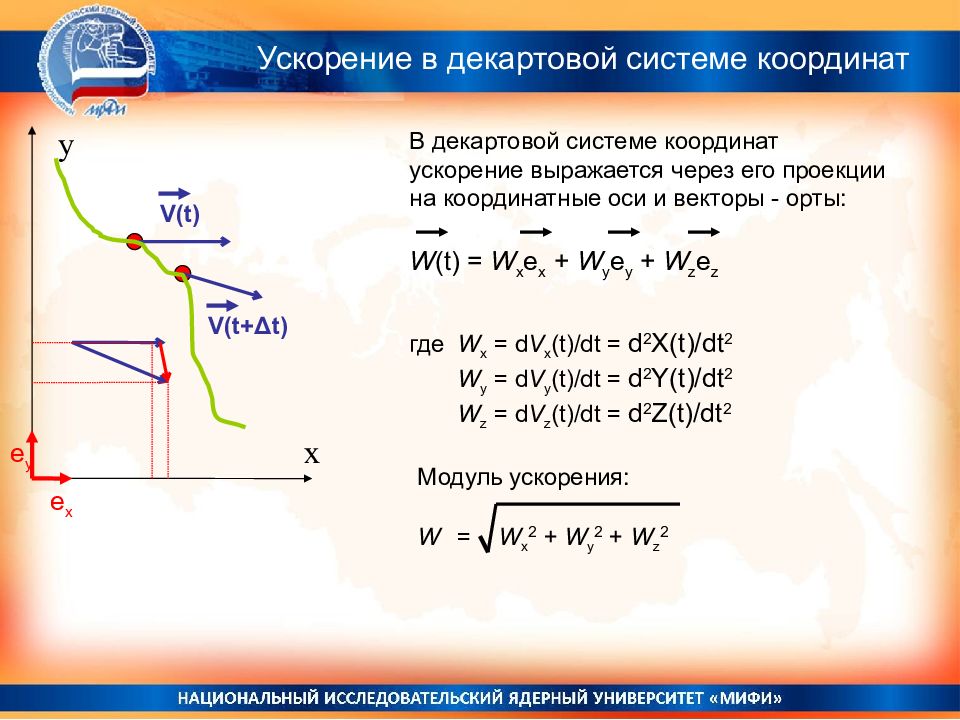
V(t) V(t+ Δ t ) x y В декартовой системе координат ускорение выражается через его проекции на координатные оси и векторы - орты: W (t) = W x e x + W y e y + W z e z e x e y где W x = d V x (t)/dt = d 2 X(t)/dt 2 W y = d V y (t)/dt = d 2 Y(t)/dt 2 W z = d V z (t)/dt = d 2 Z(t)/dt 2 Модуль ускорения: W = W x 2 + W y 2 + W z 2 Ускорение в декартовой системе координат
Слайд 19
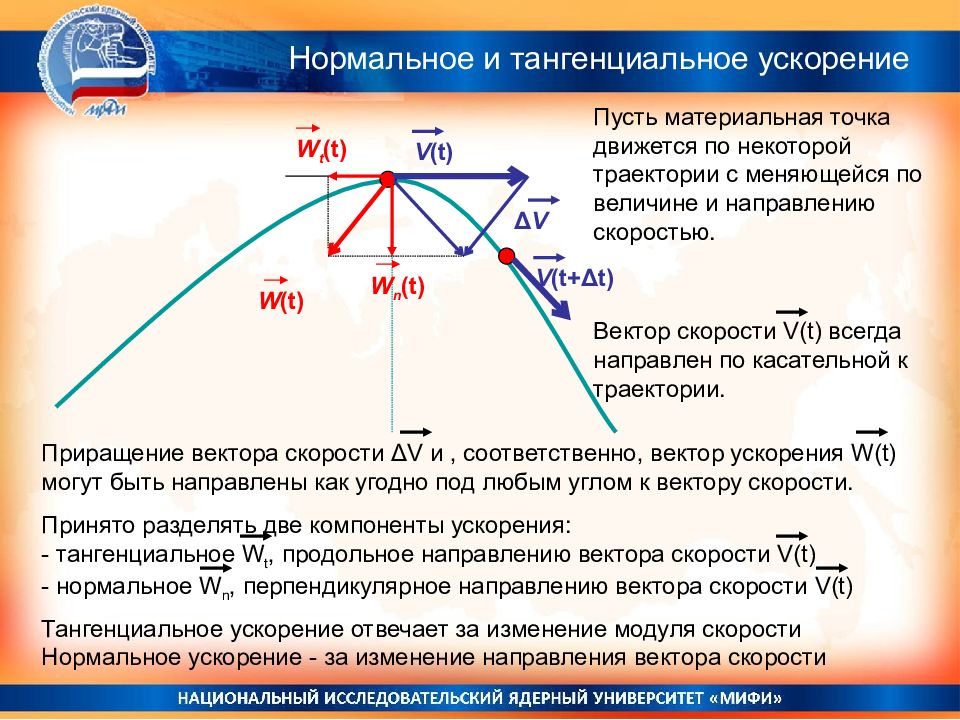
V (t) V (t+ Δ t ) W (t) W t (t) W n (t) Δ V Пусть материальная точка движется по некоторой траектории с меняющейся по величине и направлению скоростью. Вектор скорости V(t) всегда направлен по касательной к траектории. Приращение вектора скорости Δ V и, соответственно, вектор ускорения W(t) могут быть направлены как угодно под любым углом к вектору скорости. Принято разделять две компоненты ускорения: - тангенциальное W t, продольное направлению вектора скорости V(t) - нормальное W n, перпендикулярное направлению вектора скорости V(t) Тангенциальное ускорение отвечает за изменение модуля скорости Нормальное ускорение - за изменение направления вектора скорости Нормальное и тангенциальное ускорение
Слайд 20
V (t) W (t) W t (t) W n (t) Тангенциальное ускорение отвечает за изменение модуля скорости и равно: W t = d|V(t)|/dt Оно может быть отрицательным (модуль скорости убывает) или положительным (модуль скорости растет) Тангенциальное ускорение - это проекция вектора ускорения на направление вектора скорости. Эту проекцию можно найти с помощью скалярного произведения векторов ускорения и скорости: W t = (W,V)/V = W V cos(α) / V = Wcos(α) Проделаем некоторые математические преобразования (W,V) = ((dV/dt), V) = 1/2 d(V, V)/dt = 1/2 d(V 2 )/dt = V dV/dt => W t = dV/dt Тангенциальное ускорение
Слайд 21
V (t) W (t) W t (t) W n (t) Нормальное ускорение направлено перпендикулярно вектору скорости и отвечает за изменение направления вектора скорости. Для любой точки криволинейной траектории можно указать вписанную окружность, максимально близко совпадающую с траекторией вблизи данной точки. Радиус этой окружности R называется радиусом кривизны траектории в данной точке. R Из курса элементарной физики известно, что материальная точка, двигаясь по дуге окружности радиуса R, испытывает нормальное (перпендикулярное скорости) ускорение, равное по величине W n = V 2 /R Модуль полного ускорения будет равен: W = (dV/dt) 2 +(V 2 /R) 2 Эту формулу можно использовать для нахождения радиуса кривизны траектории в данной точке: R = V 2 / (dV/dt) 2 - (dV/dt) 2 Нормальное ускорение
Слайд 22
Абсолютно твердое тело: протяженный объект (система материальных точек) расстояния между которыми не изменяются в процессе движения Виды движения твердого тела 1. Поступательное движение 2. Вращение твердого тела вокруг неподвижной оси 3. Движение тела с одной закрепленной точкой 4. Плоское движение 5. Произвольное движение твердого тела Абсолютно твердое тело в кинематике
Слайд 23
При таком движении достаточно следить только за углом поворота тела по отношению к исходному положению. Все его точки движутся по дугам концентрических окружностям. Такое движение имеет всего 1 степень свободы. Для описания вращательного движения вводят понятие угловой скорости: ω = d φ/ dt [радиан / с] = [с -1 ] Линейная скорость материальной точки, отстоящей от оси вращения на расстояние R, связана с угловой простым соотношением: V = dr/dt = Rd φ/ dt = Rω = ωrsin(α) Движение твердого тела вокруг неподвижной оси
Слайд 24
Для описания вращательного движения вводят понятие угловой скорости: ω = d φ/ dt [с -1 ] В общем случае, при произвольном движении, угловую скорость следует рассматривать как вектор, направленный вдоль оси вращения - по правилу правого винта (в нашем примере вверх). По величине и направлен линейная скорость материальной точки, отстоящей от центра координат на радиус-вектор r, связана с угловой соотношением: V = [ω,r] = ( по модулю) ωrsin(α) = Rω Линейная скорость при вращательном движении всегда направлена по касательной к траектории движения (окружности). Такие вектора - связанные с направлением вращения - в математике называются псевдо-векторами Связь угловой и линейной скорости
Слайд 25
Для описания вращательного движения вводят понятие угловой скорости: ω = d φ/ dt [с -1 ] У гловую скорость рассматрива ю т как вектор, направленный вдоль оси вращения - по правилу правого винта V = [ω,r] = ( по модулю) ωrsin(α) = Rω 2. Линейная скорость при вращательном движении всегда направлена по касательной к траектории движения (окружности). 1. Конечное угловое перемещение – не вектор! Лекционные демонстрации
Слайд 26
Для описания неравномерного вращательного движения вводят понятие углового ускорения: β = dω / dt [радиан/с 2 ] = [с -2 ] Вектор углового ускорения продолен оси вращения, а вектор тангенциального ускорения, естественно, лежит в плоскости вращения точки. У гловое ускорение определяет тангенциальное линейное ускорение данной точки: W t = βR В векторном представлении тангенциальное линейное ускорение определяется векторным произведением : W t = [β, r] Полное линейное ускорение точки по модулю определяется ее тангенциальным и нормальным ускорениями: W = W t 2 + W n 2 = (βrsin (α)) 2 + (V 2 /R) 2 = R β 2 + ω 4 Движение твердого тела вокруг неподвижной оси
Слайд 27
Произвольное движение твердого тела Комбинация поступательного и вращательного движения без всяких ограничений. Возможно движение в трех пространственных направлениях, сочетаемое с вращением в трех плоскостях. При любом сложном движении скорость любой точки тела может быть представлена в виде V = V поступ + [ω,r]
Слайд 28
Физические основы механики Законы Ньютона Динамика. Виды сил. Курс общей физики НИЯУ МИФИ
Слайд 29
Первый закон Ньютона: Существуют такие системы отсчета, называемые инерциальными, где тела, на которые не действуют никакие силы (или действие разных сил скомпенсировано) либо покоятся, либо движутся равномерно и прямолинейно. Принцип относительности в механике: Все механические процессы протекают одинаково во всех инерциальных системах отсчета. Все инерциальные системы - равноправны. Принцип относительности. Первый закон Ньютона
Слайд 30
Инерциальная система отсчета не должна вращаться Инерциальная система отсчета не должна иметь ускорения относительно других инерциальных систем Систему, связанную с поверхностью Земли, можно считать условно инерциальной, если рассматривать движения небольшого масштаба, при которых вращением Земли и ее движением вокруг Солнца можно пренебречь Все системы, движущиеся относительно поверхности Земли равномерно и прямолинейно можно также рассматривать как условно инерциальные для движений малого масштаба Для движений космического масштаба в качестве условно инерциальных можно считать системы отсчета, связанные с Солнцем или далекими звездами. Инерциальные системы отсчета
Слайд 31
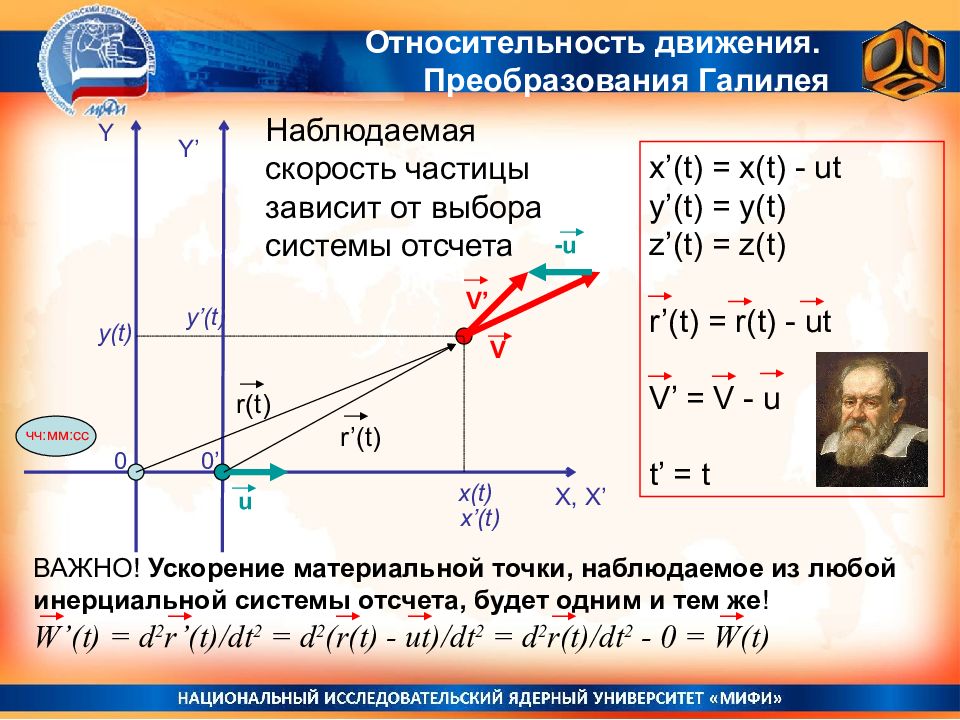
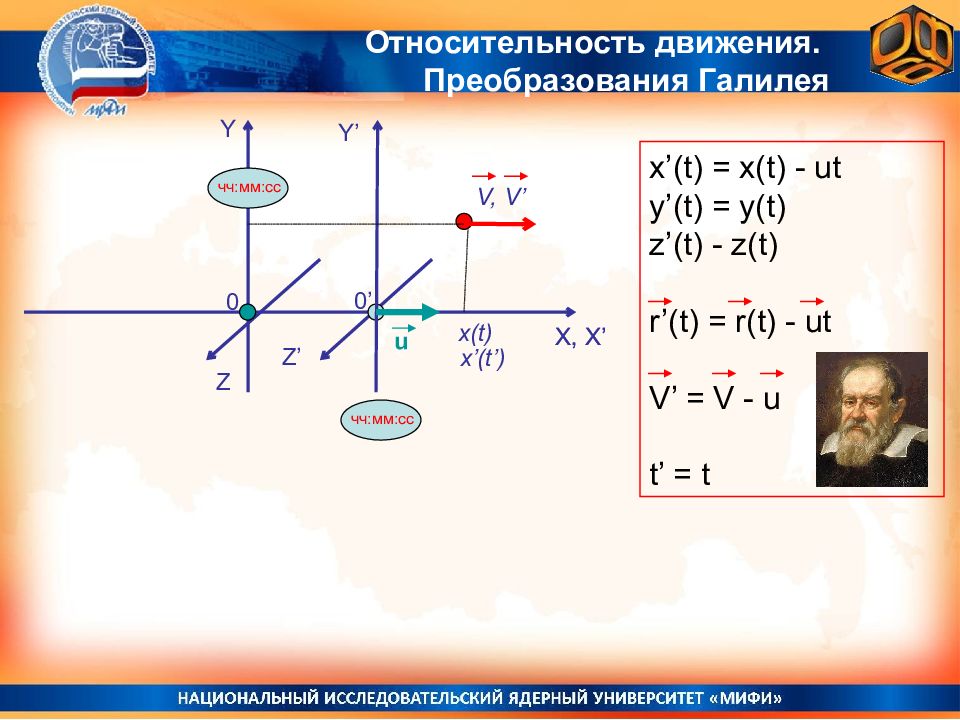
Относительность движения. Преобразования Галилея ВАЖНО! Ускорение материальной точки, наблюдаемое из любой инерциальной системы отсчета, будет одним и тем же ! W’(t) = d 2 r’(t)/dt 2 = d 2 (r(t) - ut )/dt 2 = d 2 r(t)/dt 2 - 0 = W(t) Y X, X’ y(t) x(t) 0 чч:мм:сс Y’ y’(t) 0’ x’(t) u V -u V’ r(t) r’(t) x’(t) = x(t) - ut y’(t) = y(t) z’(t) = z(t) r’(t) = r(t) - ut V’ = V - u t’ = t Наблюдаемая скорость частицы зависит от выбора системы отсчета
Слайд 32
Наблюдаемая скорость частицы зависит от выбора системы отсчета Ускорение материальной точки, наблюдаемое из любой инерциальной системы отсчета, будет одним и тем же Основное утверждение механики: Изменение скорости тела всегда вызывается воздействием на него других тел. Основные положения механики
Слайд 33
Наблюдаемое ускорение в инерциальных системах отсчета не зависит от конкретной системы отсчета Ускорение, с которым движутся тела в инерциальных системах отсчета, определяется действием на них какой-либо силы, или нескольких сил со стороны других тел, не компенсирующих друг друга, и равно: где m - масса тела => мера инерции тела, не зависящая от его движения. mW = m dV/dt = F 1 + F 2 + F 3 + … = ΣF i Ускорение. Второй закон Ньютона
Слайд 34
Другая формулировка второго закона Ньютона: Скорость изменения импульса материальной точки определяется суммой всех сил действующих на нее. Ускорение. Второй закон Ньютона mW = m dV/dt = d(mV)/dt = dP/dt = ΣF i
Слайд 35
Импульс силы Курс лекций по физике для 10-х классов. Лекция 7. Слайд 6 Изменение импульса за конечное время Δt определяется интегралом: Δ P = F (t) d t Δt Перепишем еще раз второй закон Ньютона для материальной точки - но чуть иначе: Здесь F - суммарная сила, действующая на точку. d P = F d t Произведение Fdt называют элементарным импульсом силы. Изменение импульса материальной точки за конечное время равно интегральному импульсу силы, действовавшей на нее.
Слайд 36
Силы возникают в результате взаимодействия материальных тел. При взаимодействии двух тел, сила F 12, с которой первое тело действует на второе, точно равна по величине и противоположна по направлению силе F 21, действующей со стороны второго тела на первое. F 12 F 21 m 2 m 1 P (вес) N (реакция опоры) F 12 = - F 21 P = - N Взаимодействие материальных тел Третий закон Ньютона
Слайд 37
Гравитационные силы. Гравитационные силы действуют между всеми телами, обладающими массой. Различают два случая: Притяжение малых тел большими вблизи их поверхности (сила тяжести) Гравитационные силы на космических расстояниях Силы электромагнитной природы Эти силы возникают при взаимодействии заряженных тел при контакте двух тел – силы связаны со взаимодействием электронных оболочек их атомов. В механике в разных задачах различают силы Электростатические силы (сила Кулона) Магнитные силы (силы Лоренца, Ампера) Трения и сопротивления среды Упругости и натяжения Реакция опоры и вес Виды сил в механике
Слайд 38
Гравитационные силы Сила тяжести вблизи поверхности Земли F = mg С ила тяжести почти не зависит от расстояния до поверхности (до тех пор, пока оно невелико) и направлена всегда в одну сторону (вниз, к центру притяжения) g =~ 9,8 м/с 2 - ускорение свободного падения. Ускорение свободного падения несильно зависит от географической широты, что связано с вращением Земли и ее не совсем сферической формой
Слайд 39
Гравитационные силы на космических расстояниях F 12 F 21 m 2 m 1 Гравитационные силы на космических расстояниях зависят от расстояния между центрами взаимодействующих тел ( центральные силы ) и равны ( четвертый Закон Ньютона ): R 12 R 12 - радиус-вектор, проведенный от центра первого тела к центру второго. R = | R 12 | - модуль вектора R 12, равный расстоянию между центрами взаимодействующих тел F 12 = - F 21 = - G m 1 m 2 R 12 / R 3 где G = 6.67х10 -11 н • м 2 / кг 2 - гравитационная постоянная. По абсолютной величине F 12 = F 21 = Gm 1 m 2 /R 2
Слайд 40
Гравитационные силы Ускорение свободного падения F -F m M R 12 =R+h F = GMm / (R + h) 2 если h << R, то F =~ GMm / R 2 = mg где g = G M / R 2 = ~ 9,8 м/с 2 - ускорение свободного падения M = ~ 6,0x10 24 кг - масса Земли R = ~ 6,4x10 6 м - радиус Земли G = ~ 6,67х10 -11 нм 2 / кг 2 - гравитационная постоянная R
Слайд 41
Вес. Реакция опоры P (вес) N (реакция опоры) P = - N = mg Вес - сила, с которой тело действует на опору или подвес | N | < mg ma n = mg - | N | mg V P = - N = mg - mV 2 /R < mg Если V 2 /R = g, то Р = 0 (!) Тело не давит на опору. Такое состояние называют невесомостью. mg (сила тяжести)
Слайд 42
Невесомость. Первая космическая скорость a n V R F = mg = ma n = mV 2 /R => N = P = 0 V 1 = (g R) 1/2 = (9,8 м /c 2 x 6,4x10 6 м) 1/2 = ~ 7,9 км/с - первая космическая скорость (скорость свободного полета спутника на низкой круговой околоземной орбите) Сам спутник и все, что внутри него пребывает в состоянии невесомости. Для высоких орбит ( высота сравнима с радиусом Земли или больше его): F = GMm / (R + Н) 2 < GMm /R 2 = mg V = ((R+H) F/m ) 1/2 = ( GM / (R + Н)) 1/2 < 7,9 км/с V R+Н
Слайд 43
Закон Кулона. Ш. Кулон 1785 г. Сила взаимодействия двух точечных неподвижных зарядов в пустоте пропорциональна величине каждого из зарядов, обратно пропорциональна квадрату расстояния между ними и направлена по прямой, соединяющей эти заряды
Слайд 44
Закон Кулона. Единицы измерения заряда. Курс лекций по физике для 10-х классов. Лекция 17. Слайд 13 Закон Кулона: F = kq 1 q 2 / R 2 где k - коэффициент пропорциональности, зависящий от выбора системы единиц. В системе СИ заряд измеряется в Кулонах. 1 Кулон численно равен количеству заряда, проходящего через сечение проводника за 1 секунду при токе 1 ампер. k = 1/4 πε 0 = 8,988 •10 9 н. м 2 /Кл 2 В системе СГСЭ коэффициент k = 1, а электрический заряд измеряется в т.н. единицах СГСЭ (статкулон, Франклин): Франклин — это такая величина электрического заряда, что два разноимённых заряда по 1 Фр, находящихся в вакууме на расстоянии 1 см, будут притягиваться друг к другу с силой 1 дина (10 -5 Ньютон) 1 Фр = г 1/2 см 3/2 с -1 = 0,33 нКл
Слайд 45
Сила Лоренца Сила Лоренца : Сила, действующая со стороны электромагнитного поля на движущийся заряд. q – величина заряда, V – скорость заряда E – напряженность электрического поля B – вектор магнитной индукции
Слайд 46
Силы упругости возникают при контакте двух тел и связаны с их деформацией, приводящей к изменению расстояний между молекулами и атомами, их составляющими. Деформацией называют изменение объема или формы тела. Такие силы, как вес, реакция опоры, натяжение нити при подвесе являются частными случаями сил упругости. В этих случаях достаточно ничтожно малой деформации, чтобы вызвать существенные силы. Поэтому величиной деформации в таких задачах пренебрегают. Силы упругости
Слайд 47
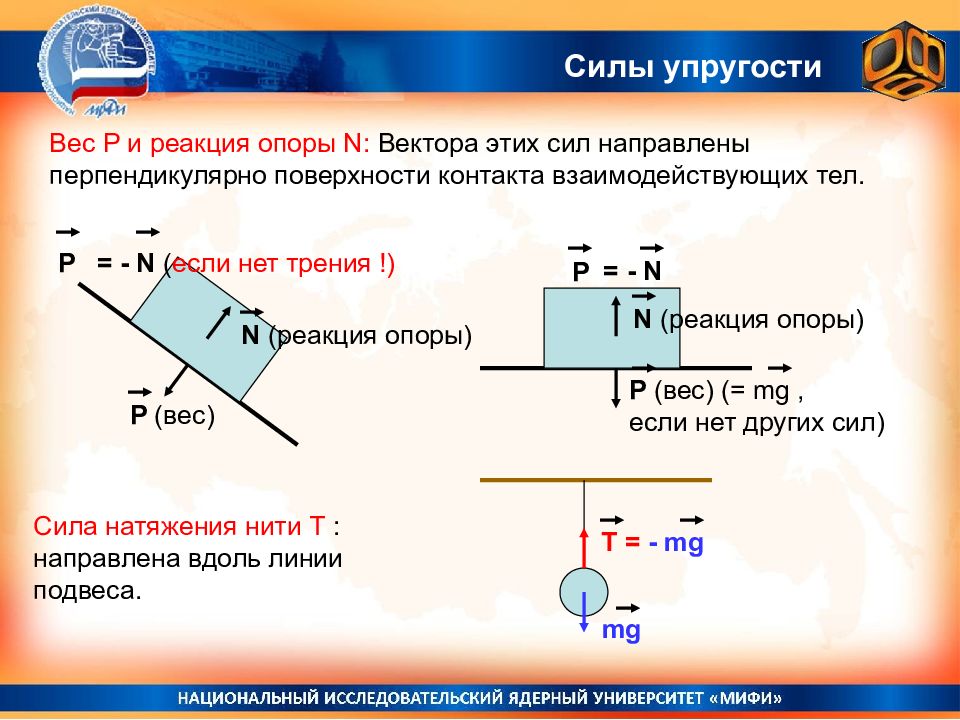
Вес P и реакция опоры N: Вектора этих сил направлены перпендикулярно поверхности контакта взаимодействующих тел. P (вес) (= mg, если нет других сил) N (реакция опоры) P = - N P (вес) N (реакция опоры) P = - N ( если нет трения !) Сила натяжения нити T : направлена вдоль линии подвеса. mg T = - mg Силы упругости
Слайд 48
В механике и технике используют специальные устройства, упругие свойства которых проявляются при заметных деформациях. Это пружины, эластичные шнуры, изгибающиеся пластины и т.п. F упр = - F F ΔX - изменение длины X Закон Гука: при упругой деформации сжатия или растяжения сила упругости прямо пропорциональна абсолютному значению изменения длины тела и направлена против деформации Важно:закон Гука справедлив, если деформация не очень велика Силы упругости. Закон Гука. F упр = - kΔX k - коэффициент упругости
Слайд 49
Всякое реальное тело под действием приложенных к нему сил изменяет свои размеры и форму, т.е. деформируется. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Сила упругости определяется законом Гука. Силы упругости. Модуль Юнга Для твердых тел (стержней) закон Гука принимает форму: Здесь коэффициент Е [н/м 2 ] называется модулем Юнга и характеризует прочность твердых тел. Для металлов он составляет 10 9 - 10 11 н/м 2 F упр = - kΔX
Слайд 50
Силы трения возникают при соприкосновении двух тел и действуют вдоль поверхности их соприкосновения. Силы трения связаны со взаимодействием электронных оболочек атомов соприкасающихся тел. В механике различают: трение покоя трение скольжения трение качения ... Отдельный случай - силы сопротивления движению твердых тел в газах и жидкостях (см. далее) Трение существует везде и всюду. Оно может быть полезным (например, помогая нам ходить и заставляя двигаться автомобили) или вредным (например, мешая скольжению в подшипниках) Силы трения
Слайд 51
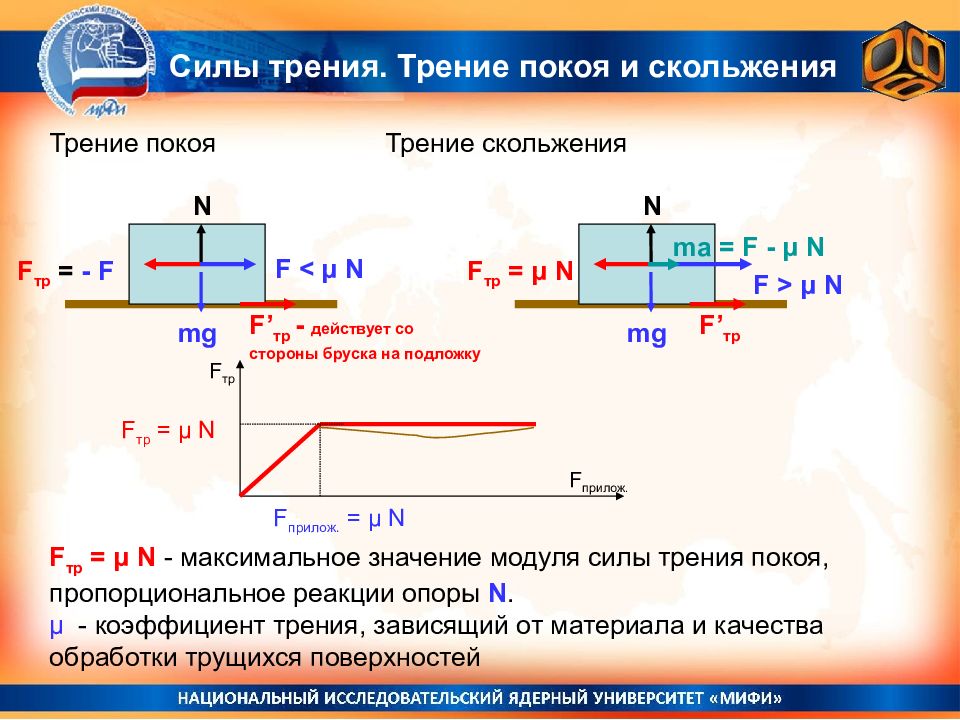
Трение покоя Трение скольжения Силы трения. Трение покоя и скольжения mg N F < μ N F тр = - F F’ тр - действует со стороны бруска на подложку mg N F > μ N F тр = μ N F’ тр ma = F - μ N F тр = μ N F тр F п рилож. F прилож. = μ N F тр = μ N - максимальное значение модуля силы трения покоя, пропорциональное реакции опоры N. μ - коэффициент трения, зависящий от материала и качества обработки трущихся поверхностей
Слайд 52
Физические основы механики Импульс. Работа. Энергия. Законы сохранения Дистанционный курс общей физики НИЯУ МИФИ
Слайд 53
Законы сохранения в физике Зако́ны сохране́ния — фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую физическую систему, не изменяются с течением времени.
Слайд 54: Внешние и внутренние силы. Замкнутая система
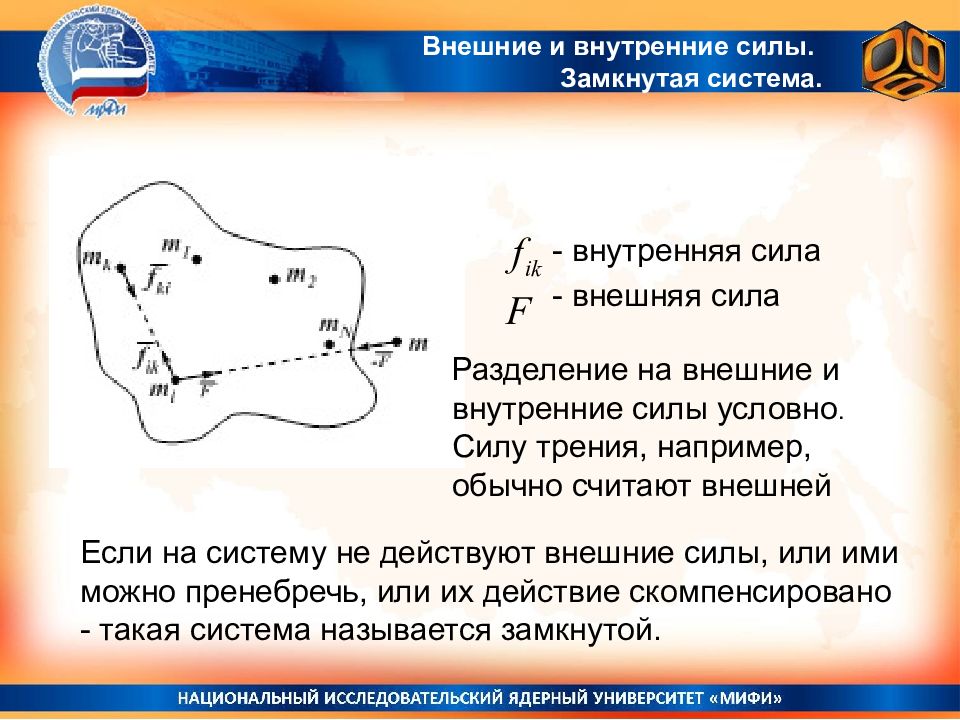
- внутренняя сила - внешняя сила Если на систему не действуют внешние силы, или ими можно пренебречь, или их действие скомпенсировано - такая система называется замкнутой. Разделение на внешние и внутренние силы условно. Силу трения, например, обычно считают внешней
Закон сохранения момента импульса Изотропия пространства Закон сохранения импульса Однородность пространства Закон сохранения энергии Однородность времени Законы сохранения, вытекающие из этих свойств Основные свойства пространства и времени Ландау Л.Д., Лифшиц Е.М. «Механика», гл.2
Слайд 57: Закон сохранения импульса для замкнутой системы частиц
Рассмотрим систему взаимодействующих материальных точек. Согласно второму и третьему законам Ньютона для любой пары взаимодействующих точек за любой промежуток времени выполняются условия: Δ P 1 = F 21 х Δ t F 12 F 21 m 2 m 1 m 3 m 4 m5 Δ P 2 = F 12 х Δ t = - F 12 х Δ t = - Δ P 1 Внутренние силы системы не меняют суммарный импульс системы. Он может измениться только под действием внешних сил. Закон сохранения импульса: если сумма внешних сил равна нулю (система замкнута) - суммарный импульс системы остается постоянным P сист = P 1 + P 2 + P 3 + … = Σ P i = Const Закон сохранения импульса для замкнутой системы частиц
Слайд 58
Элементарная работа силы. Работа силы на участке траектории от точки 1 до точки 2 Мгновенная мощность силы Определение работы по известной зависимости мощности от времени Средняя мощность силы Работа. Мощность.
Слайд 59: Консервативные и неконсервативные силы
Консервативными называются силы, работа которых не зависит от формы траектории, а зависит только от начального и конечного положений частицы. Работа не консервативных сил зависит от формы траектории. Работа консервативных сил на замкнутой траектории равна нулю
Слайд 60: Консервативные и неконсервативные силы
Работа консервативных сил не зависит от формы траектории, а зависит только от начального и конечного положений частицы. СЛЕДСТВИЕ: для консервативных сил можно ввести понятие потенциальной энергии, зависящей исключительно от координат точки в поле консервативной силы. Работа консервативной силы равна разности потенциальных энергий объекта в начальной и конечной точках траектории: А 12 = U 1 - U 2 Физический смысл имеет именно разность значений потенциальной энергии между разными точками. Абсолютное значение потенциальной энергии можно отсчитывать от любого уровня, какой удобен в той или иной задаче. Консервативные и неконсервативные силы.
Слайд 61: Работа силы тяжести
Однородная сила тяжести F = mg на малом участке траектории dr совершает элементарную работу dA = m(g, dr) = -mg dz F d r z dz На конечном участке траектории между точками 1 и 2 работа равна: z 1 z 2 Работа зависит только от начальной и конечной точек траектории. Сила тяжести - консервативная сила Потенциальная энергия силы тяжести: U = mgz. Отсчитывать вертикальную координату z можно от любого уровня, какой удобен в той или иной задаче.
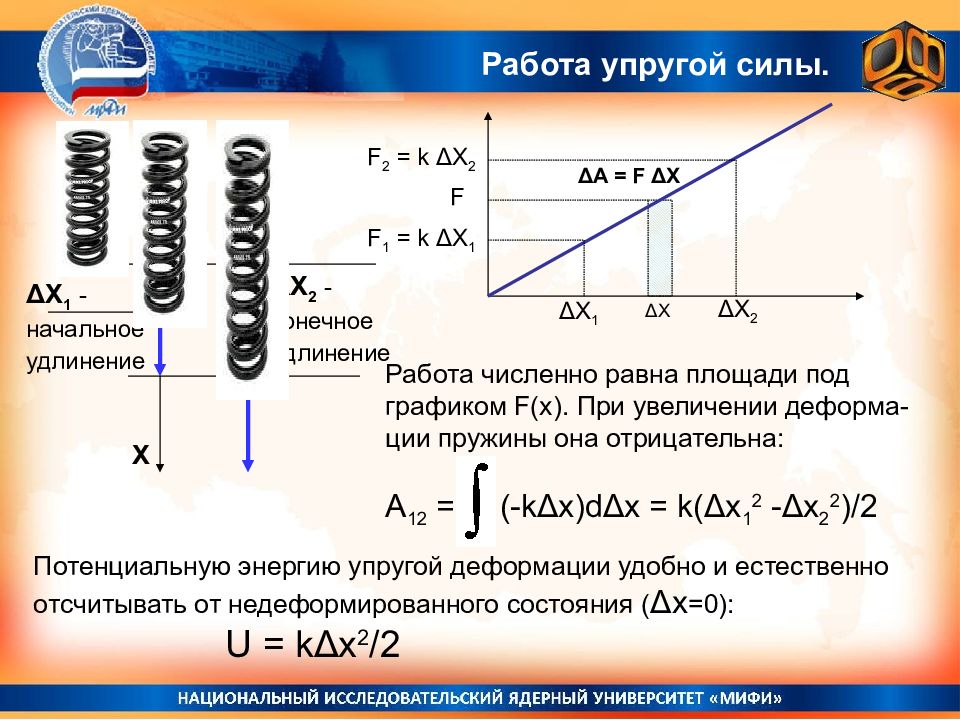
Слайд 62: Работа упругой силы
Потенциальную энергию упругой деформации удобно и естественно отсчитывать от недеформированного состояния ( Δx =0): U = kΔx 2 /2 X ΔX 1 - начальное удлинение ΔX 2 - конечное удлинение ΔX 1 ΔX 2 ΔX F ΔA = F ΔX F 2 = k ΔX 2 F 1 = k ΔX 1 Работа численно равна площади под графиком F(x). При увеличении деформа-ции пружины она отрицательна: A 12 = (-kΔx)dΔx = k(Δx 1 2 -Δx 2 2 )/2
Слайд 63: Работа центральной силы
Центральная сила - это сила, направленная от центра поля, модуль которой зависит только от расстояния до центра. ПРИМЕРЫ: сила Кулона, сила гравитации (на больших расстояниях) Работа центральной силы. Элементарная работа центральной силы Работа центральной силы при перемещении частицы из точки, находящейся на расстоянии r 1 от центра поля в точку, находящуюся на расстоянии r 2 равна Центральная сила консервативна, так как полученный интеграл зависит только от вида функции F(r) и пределов интегрирования.
Слайд 64: Работа гравитационной силы
Работа гравитационной силы при сближении тел с массами M и m от расстояния r 1 до расстояния r 2 положительна и равна: A 12 = (-GMm/r 2 )dr = GMm(r 2 -1 -r 1 -1 ) = U 1 - U 2 m M U гр = - GMm /r r 1 Потенциальная энергия гравитационного взаимодействия и определяется величинами масс взаимодействующих тел и расстоянием между ними: Потенциальную энергию гравитационного взаимодействия естественно считать равной нулю при бесконечном взаимоудалении тел, При сближении она уменьшается и становится отрицательной. r 2 Центральная сила - это сила, направленная от центра поля, модуль которой зависит только от расстояния до центра. ПРИМЕРЫ: сила Кулона, сила гравитации (на больших расстояниях)
Слайд 65: Работа силы Кулона
Работа силы Кулона при сближении зарядов Q и q от расстояния r 1 до расстояния r 2 равна: A 12 = (kQq/r 2 )dr = kQq(r 1 -1 -r 2 -1 ) = U 1 - U 2 q Q U КУЛ = kQq/r r 1 Потенциальная энергия кулоновского взаимодействия определяется величинами и знаками взаимодействующих зарядов и расстоянием между ними: Потенциальную энергию кулоновского взаимодействия естественно считать равной нулю при бесконечном взаимоудалении зарядов r 2 Центральная сила - это сила, направленная от центра поля, модуль которой зависит только от расстояния до центра. ПРИМЕРЫ: сила Кулона, сила гравитации (на больших расстояниях)
Слайд 66: Связь между потенциальной энергией и силой
Элементарная работа консервативной силы Из определения работы следует Полный дифференциал потенциальной энергии Для проекций консервативной силы на оси декартовой системы координат верны соотношения , Связь между потенциальной энергией и силой.
Слайд 67: Связь между потенциальной энергией и силой
Т.е. вектор консервативной силы равен градиенту потенциальной энергии, взятому с противоположным знаком. Консервативная сила, действующая на частицу всегда перпендикулярна к эквипотенциальным поверхностям и направлена в сторону убывания потенциальной энергии. Связь между потенциальной энергией и силой.
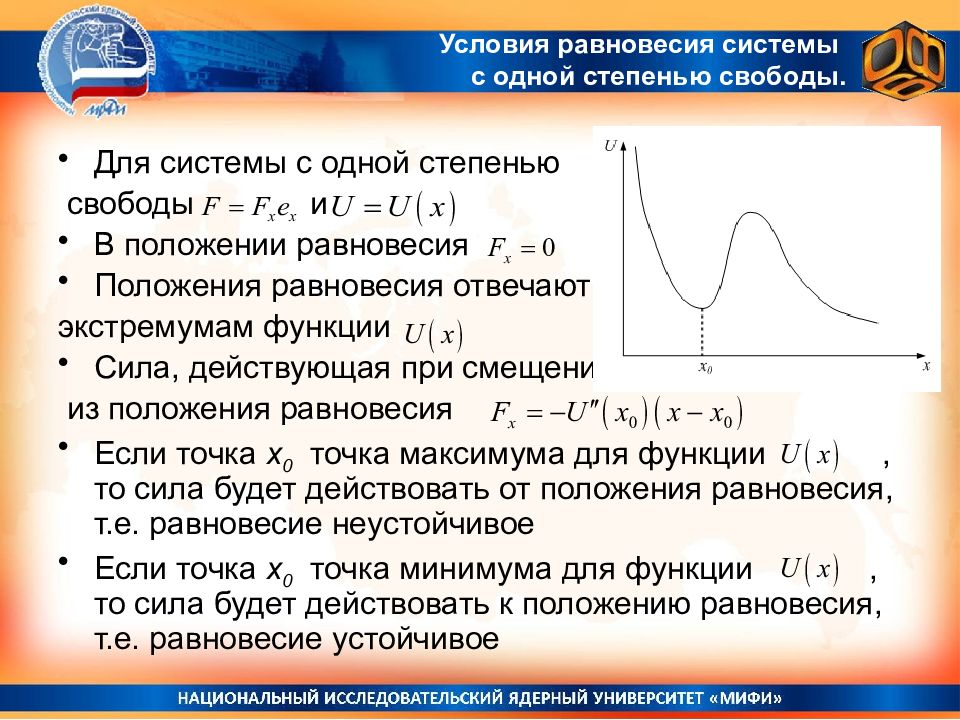
Слайд 68: Условия равновесия системы с одной степенью свободы
Для системы с одной степенью свободы и В положении равновесия Положения равновесия отвечают экстремумам функции Сила, действующая при смещении из положения равновесия Если точка x 0 точка максимума для функции, то сила будет действовать от положения равновесия, т.е. равновесие неустойчивое Если точка x 0 точка минимума для функции, то сила будет действовать к положению равновесия, т.е. равновесие устойчивое Условия равновесия системы с одной степенью свободы.
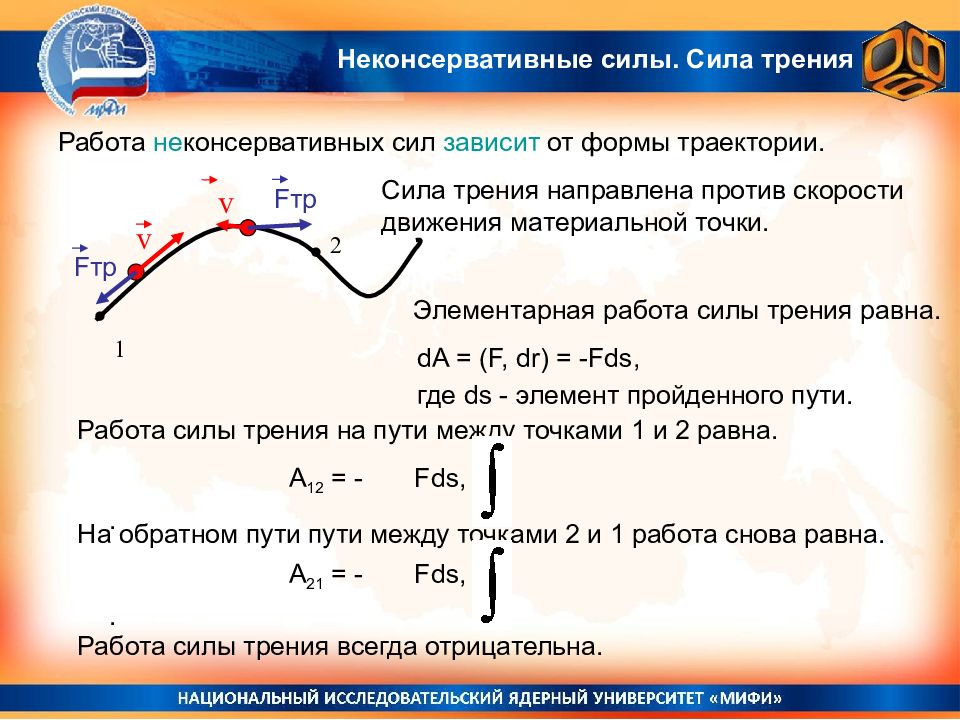
Слайд 69: Неконсервативные силы. Сила трения
Работа не консервативных сил зависит от формы траектории. v Fтр Сила трения направлена против скорости движения материальной точки. Элементарная работа силы трения равна. dA = (F, dr) = -Fds, где ds - элемент пройденного пути. Работа силы трения на пути между точками 1 и 2 равна. A 12 = - Fds, . 1 2 На обратном пути пути между точками 2 и 1 работа снова равна. A 21 = - Fds, . Работа силы трения всегда отрицательна. v Fтр
Слайд 70: Кинетическая энергия
Элементарную работу суммарной силы, действующей на материальную точку, можно представить в виде: Величину T = mV 2 /2 называют кинетической энергией материальной точки. Элементарная работа суммарной силы, действующей на материальную точку, равна дифференциалу ее кинетической энергии. Р абота суммарной силы, действующей на материальную точку, равна приращению ее кинетической энергии.
Слайд 71: Потенциальная энергия частицы во внешнем силовом поле
Работа консервативной силы не зависит от формы траектории , - потенциальная энергия точки в поле консервативной силы. Работа консервативной силы равна убыли потенциальной энергии Потенциальная энергия частицы во внешнем силовом поле.
Слайд 72: Полная механическая энергия частицы
Сумма кинетической и потенциальной энергий частицы есть полная механическая энергия Приращение полной механической энергии равно работе сторонних (неконсервативных) сил Если сторонние неконсервативные силы на частицу не действуют - ее полная механическая энергия сохраняется! (Закон сохранения энергии)
Слайд 73
Физические основы механики Импульс. Энергия. Система центра масс Дистанционный курс общей физики НИЯУ МИФИ
Слайд 74: Система центра масс
Как определить положение центра масс системы материальных точек? Рассмотрим несколько примеров. Две материальные точки (или две однородные сферы. Или 2 шара) - М 1 d 1 = M 2 d 2. d 1 d 2 М 1 М 2 y x 0 r 1 m 1 m 2 m 3 m 4 r 2 r 3 r 4 R Система материальных точек: R = Σ m i r i / Σ m i ВАЖНО: Центр масс может не совпадать ни с одним из тел системы
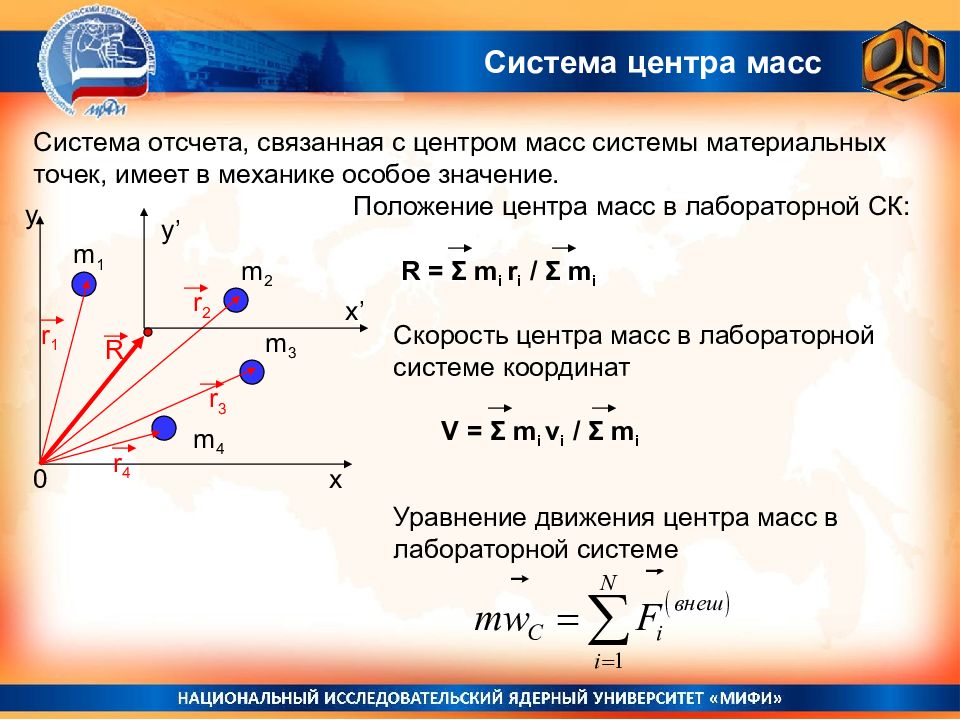
Слайд 75: Система центра масс
y x 0 r 1 m 1 m 2 m 3 m 4 r 2 r 3 r 4 R x’ y’ Система центра масс Система отсчета, связанная с центром масс системы материальных точек, имеет в механике особое значение. Положение центра масс в лабораторной СК: R = Σ m i r i / Σ m i Скорость центра масс в лабораторной системе координат V = Σ m i v i / Σ m i Уравнение движения центра масс в лабораторной системе
Слайд 76
Центр масс симметричных однородных тел. Для однородных симметричных тел - это их геометрический центр симметрии. Для однородного стержня - середина стержня. Для однородного диска или сферы - центр диска или сферы Центр масс твердого тела
Слайд 77: Центр масс твердого тела
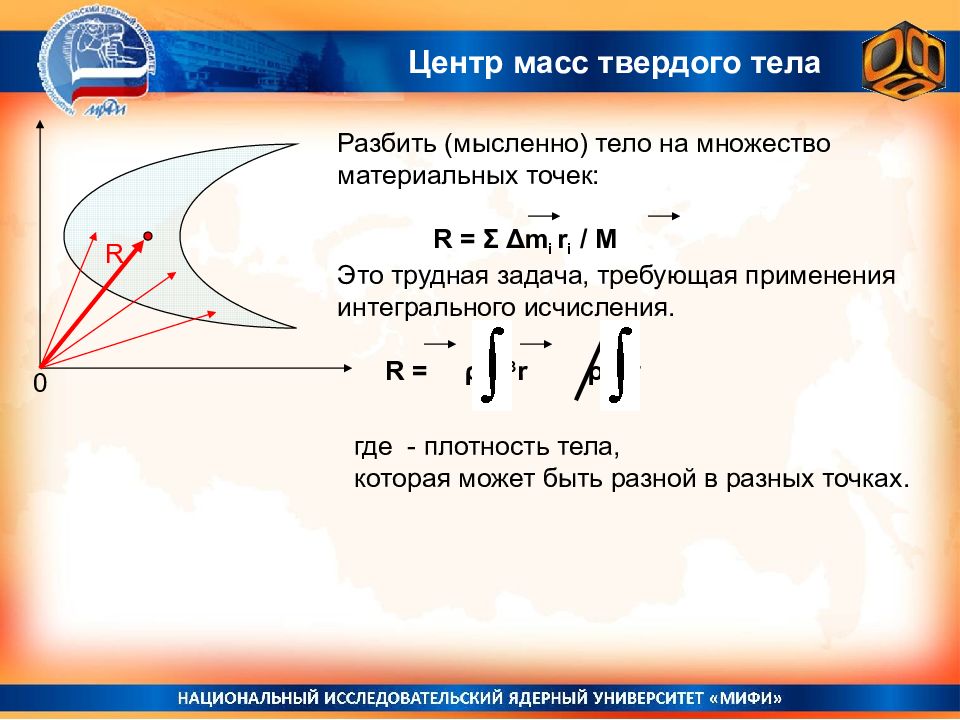
0 R Разбить (мысленно) тело на множество материальных точек: R = Σ Δm i r i / M Это трудная задача, требующая применения интегрального исчисления. R = ρrd 3 r ρd 3 r где - плотность тела, которая может быть разной в разных точках.
Слайд 79
- кинетическая энергия в ц - системе - полная масса системы - полный импульс в ц - системе, равный нулю - теорема Кенига Связь кинетической энергии системы частиц в ц–системе и в л–системе.
Слайд 80: Связь между потенциальной энергией и силой
Элементарная работа консервативной силы Из определения работы следует Полный дифференциал потенциальной энергии Для проекций консервативной силы на оси декартовой системы координат верны соотношения , Связь между потенциальной энергией и силой.
Слайд 81: Связь между потенциальной энергией и силой
Т.е. вектор консервативной силы равен градиенту потенциальной энергии, взятому с противоположным знаком. Консервативная сила, действующая на частицу всегда перпендикулярна к эквипотенциальным поверхностям и направлена в сторону убывания потенциальной энергии. Связь между потенциальной энергией и силой.
Слайд 82
Физические основы механики Закон сохранения момента импульса. Движение в центральном поле сил Дистанционный курс общей физики НИЯУ МИФИ
Слайд 83
Законы сохранения в физике Зако́ны сохране́ния — фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую физическую систему, не изменяются с течением времени.
Слайд 84: Связь законов сохранения со свойствами пространства и времени
Закон сохранения момента импульса Изотропность пространства Закон сохранения импульса Однородность пространства Закон сохранения энергии Однородность времени Законы сохранения, вытекающие из этих свойств Основные свойства пространства и времени Ландау Л.Д., Лифшиц Е.М. «Механика», гл.2
Слайд 85: Закон сохранения энергии для системы частиц
Для любых консервативных сил: A конс = U 1 - U 2 (убыль потенциальной энергии системы) На что может пойти работа консервативных сил? На увеличение (если А > 0) или уменьшение (А < 0) кинетической энергии (абсолютной скорости) тел системы: A конс = U 1 - U 2 = T 2 - T 1 Перепишем это равенство по другому: U 2 + T 2 = U 1 + T 1 = E = Сonst ЗСЭ : В замкнутой системе, где действуют только консервативные силы, механическая энергия (потенциальная плюс кинетическая) сохраняется. Закон сохранения энергии для системы частиц
Слайд 86
Моментом импульса частицы относительно точки называется векторное произведение радиус-вектора на импульс частицы: Длина перпендикуляра, опущенного из точки O на прямую, вдоль которой направлен импульс частицы называется плечом импульса относительно точки О Момент импульса. Плечо импульса
Слайд 87
Момент силы. Плечо силы. Моментом силы F относительно точки О, из которой проведен радиус-вектор r точки приложения силы называется псевдовектор : 1. Вектор N перпендикулярен векторам r и F, и образует с ними правую тройку. 2. Модуль момента силы можно представить в виде N = rF · sin α =l·F, где l=r·sin α – плечо силы относительно точки O ( длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила) 3. Точку приложения силы (в случае твердого тела) можно сдвигать вдоль линии действия силы : ни l ни N при этом не изменятся. Но величина и направление N зависят от выбора точки О
Слайд 88
Пара сил. Две равные по модулю противоположно направленные силы, не действующие вдоль одной прямой, называются парой сил. Расстояние между прямыми, вдоль которых действуют силы, называется плечом пары Суммарный момент сил, образующих пару, равен: Полученное выражение для N не зависит от точки O. Момент пары сил относительно любой точки будет одним и тем же. Вектор момента пары сил перпендикулярен к плоскости, в которой лежат силы и численно равен произведению модуля любой из сил на плечо. проведенный из точки приложения силы F 1 в точку приложения силы F 2
Слайд 89
Производная момента импульса по времени Производная по времени момента импульса частицы относительно некоторой точки равна моменту силы относительно той же точки.
Слайд 90
Момент импульса системы материальных точек Моментом импульса системы относительно точки называется векторная сумма моментов импульса частиц, входящих в систему:
Слайд 91
Закон сохранения момента импульса При отсутствии внешних сил Для замкнутой системы M постоянен Закон сохранения момента импульса : момент импульса замкнутой системы материальных точек остается постоянным. Момент импульса остается постоянным и для незамкнутой системы при условии, что суммарный момент внешних сил равен нулю.
Слайд 92
Движение в центральном поле сил Частица находится в центральном поле сил. По определению, направление силы, действующей на частицу в любой точке поля, проходит через центр поля, а модуль силы зависит только от расстояния до этого центра. Момент импульса частицы относительно центра будет сохраняться При движении частицы в центральном поле сил ее радиус-вектор остается все время в одной плоскости. В этой же плоскости лежит все время вектор p. Траектория частицы представляет собой плоскую кривую. M перпендикулярен к плоскости, образованной r и p M= const → плоскость фиксирована
Слайд 93
В центральном поле секториальная скорость частицы остается постоянной Движение в центральном поле сил
Слайд 94
Силы, обратно пропорциональные квадрату расстояния от центра Движение в центральном поле сил. ПРИМЕР
Слайд 95
Силы, обратно пропорциональные квадрату расстояния от центра Движение в центральном поле сил. ПРИМЕР Траектория частицы представляет собой коническое сечение, т.е. либо эллипс, либо параболу, либо гиперболу. α > 0 Гипербола. Если M z = 0 гипербола вырождается в прямую α < 0 Эллипс при E < 0, гипербола при E > 0, парабола при E = 0
Слайд 96
Силы, обратно пропорциональные квадрату расстояния от центра Движение в центральном поле сил. ПРИМЕР Траектория частицы представляет собой коническое сечение, т.е. либо эллипс, либо параболу, либо гиперболу. α > 0 Гипербола. Если M z = 0 гипербола вырождается в прямую α < 0 Эллипс при E < 0, гипербола при E > 0, парабола при E = 0
Слайд 97
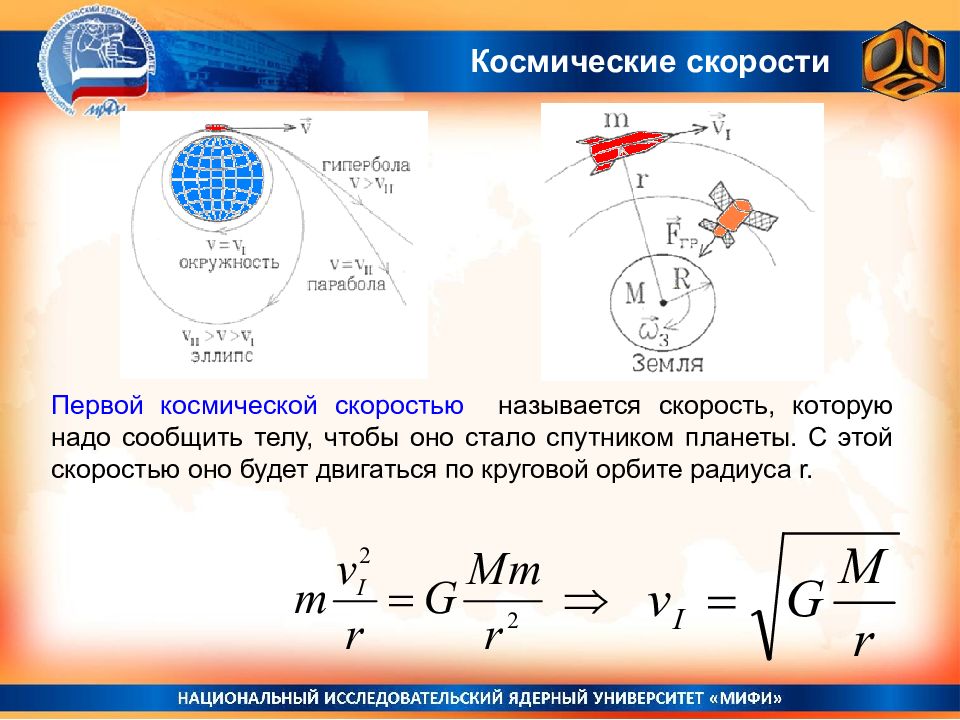
Космические скорости Первой космической скоростью называется скорость, которую надо сообщить телу, чтобы оно стало спутником планеты. С этой скоростью оно будет двигаться по круговой орбите радиуса r.
Слайд 98
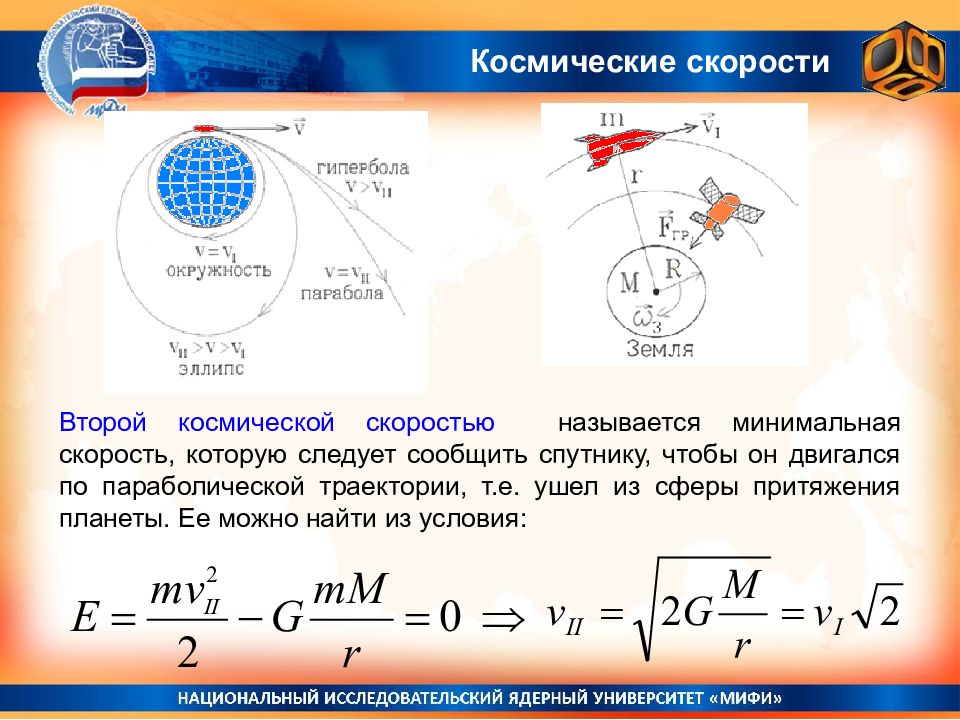
Космические скорости Второй космической скоростью называется минимальная скорость, которую следует сообщить спутнику, чтобы он двигался по параболической траектории, т.е. ушел из сферы притяжения планеты. Ее можно найти из условия:
Слайд 99
Физические основы механики Механика твердого тела Дистанционный курс общей физики НИЯУ МИФИ
Слайд 100
Движение центра масс твердого тела r i m i Уравнение движения для i-ой точки: m i w i = m i d 2 r i /dt 2 = f i + F i где f i - сумма всех внутренних сил, действующих на i-ую точку; F i - сумма всех внешних сил, действующих на i-ую точку r c Σm i w i = d 2 (Σm i r i )/dt 2 = Md 2 r c /dt 2 = Mw c = Σf i + ΣF i Центр масс твердого тела движется так же, как двигалась бы материальная точка равной массы под действием всех приложенных к телу внешних сил. При поступательном движении все остальные точки тела движутся параллельно центру масс..
Слайд 101
Момент импульса твердого тела при вращении вокруг неподвижной оси Момент импульса элементарной массы m i относительно оси OZ : M i = R i P i = R i ω z m i R i = ω z m i R i 2 Момент импульса всего тела массы М относительно оси OZ : M z = ω z Σm i R i 2 = ω z I z, где I z = Σm i R i 2 = >, момент инерции твердого тела относительно оси OZ Переходя от суммирования к интегрированию по объему тела, момент инерции можно записать в виде: I z = Σ m i R i 2 = ρ(r)r z 2 dV
Слайд 102
Уравнение движения для вращающегося твердого тела Это уравнение является аналогом второго закона Ньютона для поступательного движения. Подставим в него момент импульса, выраженный через момент инерции тела в проекции на ось вращения OZ : d(ω z I z )/dt = I z β z = ΣN iz Здесь β z - угловое ускорение вращающегося тела в проекции на ось вращения OZ ; ΣN iz - сумма проекций всех моментов внешних сил на ось вращения OZ. Это есть уравнение движения для твердого тела, вращающегося вокруг неподвижной оси
Слайд 103
Моменты инерции для некоторых симметричных тел Момент инерции твердого тела относительно оси вращения OZ можно представить в виде суммы или интеграла I z = Σ m i R i 2 = ρ(r)r z 2 dV Для отдельной элементарной массы m, (материальной точки) вращающейся на расстоянии R от оси, момент инерции очевидно равен I z = mR 2 Найдем далее моменты инерции для некоторых симметричных тел
Слайд 104
Моменты инерции для некоторых симметричных тел 1. Тонкое кольцо, вращающееся относительно оси, проходящей через его центр, перпендикулярно его плоскости. Каждая элементарная масса Δ m имеет момент инерции Δ I z = Δ mR 2 Очевидно, что все кольцо массы М имеет момент инерции I z = Σ Δ mR 2 = МR 2 ω Δm R 2. Тонкостенный цилиндр, вращающийся относительно оси симметрии Каждая элементарная масса Δ m имеет момент инерции Δ I z = Δ mR 2 Очевидно, что весь цилиндр массы М имеет момент инерции I z = Σ Δ mR 2 = МR 2 ω Δm R
Слайд 105
Моменты инерции для некоторых симметричных тел 3. Однородный цилиндр с плотностью вещества ρ, вращающийся вокруг оси симметрии. Возьмем вложенный тонкостенный цилиндр с массой d m = ρ L2πr dr Его момент инерции dI z = dmr 2 = ρL 2πr 3 dr ω R r = r+dr L Момент инерции всего цилиндра находим, интегрируя по всем тонкостенным цилиндрам с радиусами от 0 до R: I z = 2π L ρ r 3 dr = π L ρ R 4 /2 = = MR 2 /2 M = ρ L π R 2
Слайд 106
Моменты инерции для некоторых симметричных тел 4. Тонкостенная сфера массы М и радиуса R, вращаю- щаяся вокруг оси OZ, проходящей через ее центр. Разобьем сферу мысленно на множество тонких перпендикулярных оси OZ колец шириной Rdθ и с радиусами r = Rsinθ, зависящими от угла θ, под которым кольцо видно из центра сферы. ω, Z o R Каждое кольцо имеет момент инерции, равный dI z = dmR 2 sin 2 θ Массы колец пропорциональны их площадям поверхности: dm = М 2πR|sinθ| Rdθ / 4πR 2 = М|sinθ|dθ / 2 θ Интегрируя по всем кольцам (2 раза по dθ от 0 до π/2 ), находим: I z = MR 2 sin 3 θdθ = MR 2 (1 - cos 2 θ)d(-cosθ) = 2MR 2 /3 0 π/2 -1 0
Слайд 107
Моменты инерции для некоторых симметричных тел 5. Однородный шар с плотностью вещества ρ, вращающийся вокруг оси симметрии. Возьмем вложенную тонкостенную сферу с массой d m = ρ4 πr 2 dr Ее момент инерции dI z = 2dmr 2 /3= 8 π ρ r 4 dr/3 Момент инерции всего шара находим, интегрируя по всем тонкостенным сферам с радиусами от 0 до R: I z = (8/3) π ρ r 4 dr = 8 π ρ R 5 /15 = = 2MR 2 /5 M = ρ 4 π R 3 /3 ω, Z o R r - r+dr
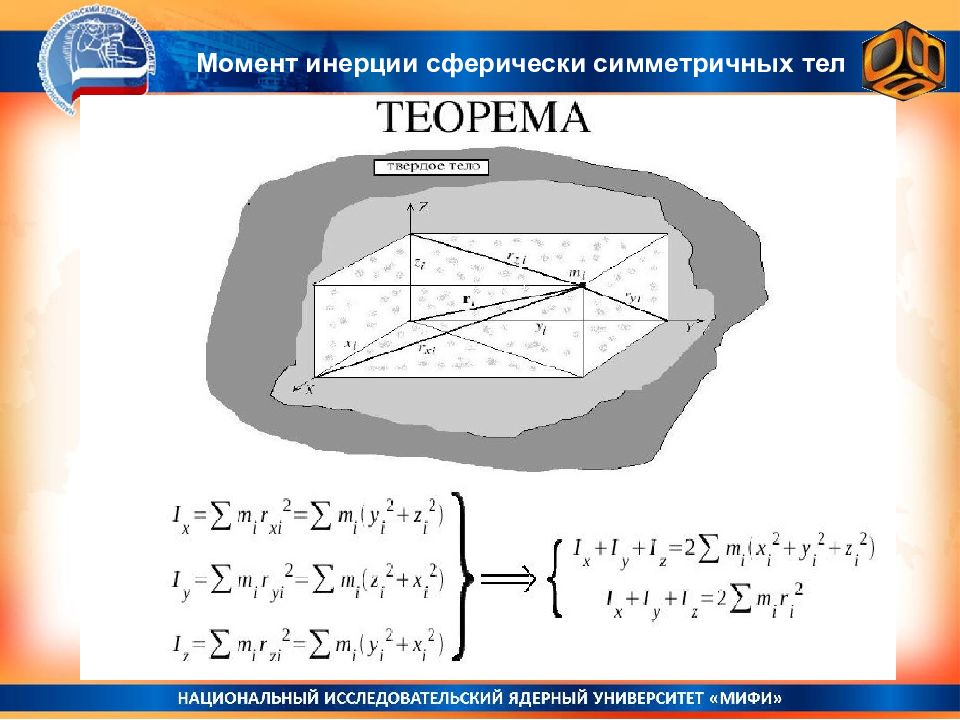
Слайд 109
Момент инерции сферически симметричных тел Пример использования теоремы z o R i Тонкостенная сфера массы М и радиуса R, вращаю- щаяся вокруг оси, проходящей через ее центр. y x Из сферической симметрии задачи следует: I x = I y = I z ; I x + I y + I z = 3I z ; С другой стороны, по теореме I x + I y + I z = 2Σ m i R i 2 = 2Σ m i R 2 = 2MR 2 Результат I x = I y = I z = 2MR 2 /3
Слайд 110
Моменты инерции для некоторых симметричных тел 6. Однородный тонкий стержень длины и массы М, вращающийся вокруг оси перпендикулярной ему и проходящей через конец стержня Разобьем мысленно стержень на элементарные массы d m i = Mdr/L Каждая элементарная масса имеет момент инерции dI z = dmr 2 = M r 2 dr/L Момент инерции всего стержня находим, интегрируя по всем элементарным массам с расстояниями до центра вращения от 0 до L : I z = (M/L) r 2 dr = ML 2 /3 ω r i dm i
Слайд 111
Теорема Штайнера o C m i R i Rc i a Пусть нам известен момент инерции тела массы М относительно оси, проходящей через центр масс С. Найдем его момент инерции относительно параллельной оси, проходящей через точку О, отстоящую от С на радиус - вектор а. I О = Σm i R i 2 = Σm i ( Rc i + a ) 2 = Σm i Rc i 2 + 2 a Σm i Rc i +(Σm i )a 2 Σm i Rc i 2 = I С ; 2 a Σm i Rc i = 0 ; (Σm i )a 2 = Ма 2 I О = I С + Ма 2 Момент инерции тела относительно произвольной оси равен его моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведению массы тела на квадрат расстояния между осями.
Слайд 113
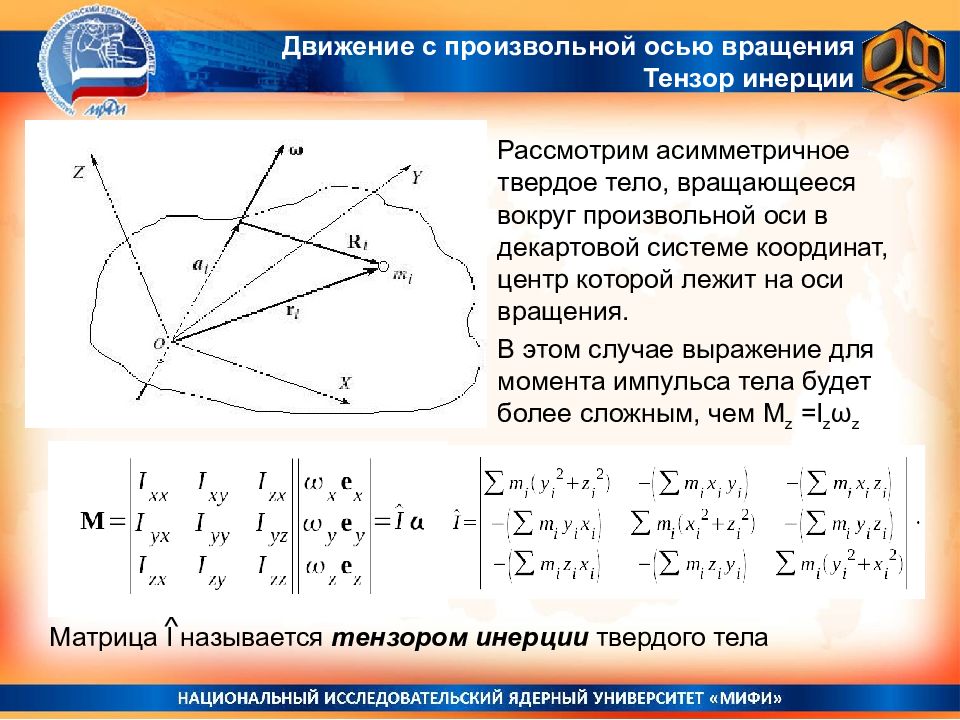
Рассмотрим асимметричное твердое тело, вращающееся вокруг произвольной оси в декартовой системе координат, центр которой лежит на оси вращения. Движение с произвольной осью вращения Тензор инерции В этом случае выражение для момента импульса тела будет более сложным, чем M z =I z ω z Матрица I называется тензором инерции твердого тела ^
Слайд 114
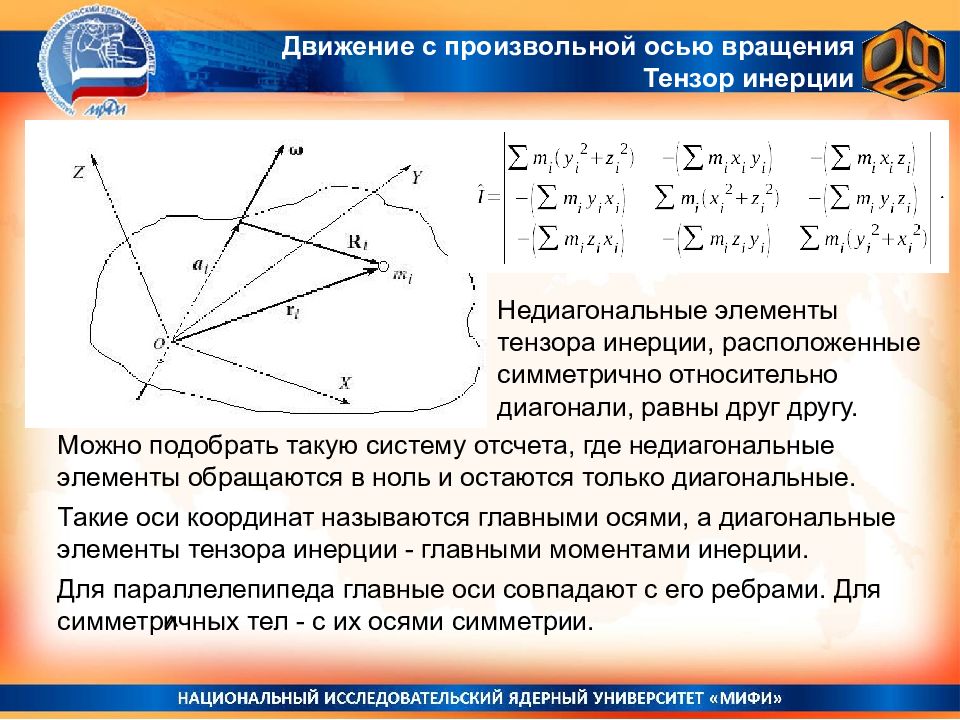
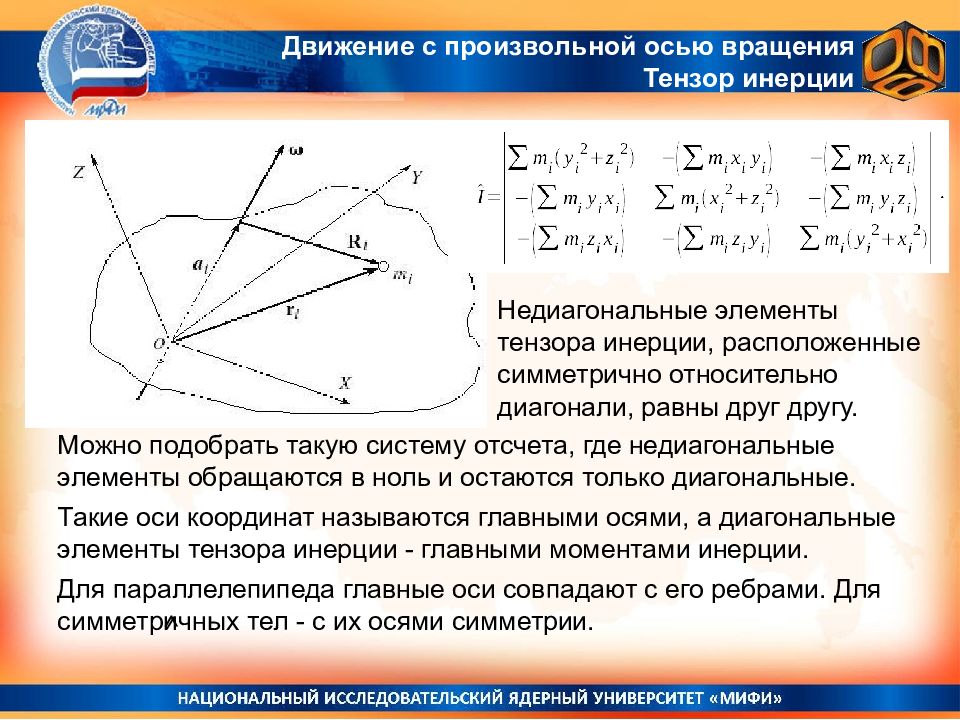
Движение с произвольной осью вращения Тензор инерции Недиагональные элементы тензора инерции, расположенные симметрично относительно диагонали, равны друг другу. ^ Можно подобрать такую систему отсчета, где недиагональные элементы обращаются в ноль и остаются только диагональные. Такие оси координат называются главными осями, а диагональные элементы тензора инерции - главными моментами инерции. Для параллелепипеда главные оси совпадают с его ребрами. Для симметричных тел - с их осями симметрии.
Слайд 115
Свободные оси вращения При вращении твердого тела вокруг закрепленной оси на оси могут возникать заметные нагрузки. Если убрать закрепление - тело может начать «кувыркаться». ^ Но если вращение происходит вокруг некоторых из главных осей - оно может продолжаться и после снятия закрепления. Пример: быстрое вращение стержня на подвесе остается устойчивым еще некоторое время, если снять нить с подвеса.
Слайд 116
Кинетическая энергия твердого тела при вращении вокруг неподвижной оси Окончательно для кинетической энергии находим: T = I z ω 2 /2 Кинетическая энергия твердого тела: T = Σm i v i 2 /2 Линейная скорость i-ой точки: v i = [ ω,r i ] ; v i = ω R i T = Σm i v i 2 /2 = ω 2 Σm i R i 2 /2 Σm i R i 2 = I z
Слайд 117
Работа внешних сил при вращении твердого тела вокруг неподвижной оси f i - равнодействующая всех внутренних сил, действующих на m i F i - равнодействующая всех внешних сил, действующих на m i f i + F i - равнодействующая всех сил, лежащая в плоскости вращения dA i = ( f i + F i ) dr i - элементарная работа всех сил; После циклической перестановки векторов: dA i = ( dφ [ f i,r i ]) +( dφ [ F i,r i ] ) Так как dr i = [ dφ,r i ] dA i = ( f i [ dφ,r i ]) +( F i [ dφ,r i ] ) Суммируем по всем элементарным массам: dA=ΣdA i = ( dφ, Σ [ f i,r i ]) +( dφ, Σ [ F i,r i ] )=( dφ, Σ N i внутр ) +( dφ, Σ N i внеш ) Окончательно: dA = ( dφ, Σ N i внеш ) = N Z внеш dφ При повороте на конечный угол: A = N Z внеш dφ
Слайд 118
Движение с произвольной осью вращения Тензор инерции Недиагональные элементы тензора инерции, расположенные симметрично относительно диагонали, равны друг другу. ^ Можно подобрать такую систему отсчета, где недиагональные элементы обращаются в ноль и остаются только диагональные. Такие оси координат называются главными осями, а диагональные элементы тензора инерции - главными моментами инерции. Для параллелепипеда главные оси совпадают с его ребрами. Для симметричных тел - с их осями симметрии.
Слайд 119
Движение с произвольной осью вращения Тензор инерции Свободно движущееся тело вращается вокруг оси, проходящей через центр масс тела ^ Среди осей, проходящих через центр масс тела, есть главные (как правило – оси симметрии тела), вращение вокруг которых может быть устойчиво. «Самые главные» оси те, вращение вокруг которых всегда устойчиво.
Слайд 121
Гироскопический эффект Гироскопический эффект Под действием силы F, приложенной к оси гироскопа в направлении линии В-В, ось гироскопа смещается в направлении момента этой силы, то есть в перпендикулярном силе F направлении ( вдоль линии D-D). Этот эффект называется гироскопическим эффектом
Слайд 122
Прецессия гироскопа Прецессия гироскопа – вращение оси гироскопа под действием приложенных к оси внешних сил. Определим угловую скорость прецессии волчка ω под действием силы тяжести Р, когда ω<<Ω 1)Угловая скорость прецессии 2) ω направлен против вектора силы Р ; 3) отсутствует инерция. Приближенная теория справедлива, когда ω<<Ω. 4) При ω ~Ω наряду с вращением наблюдаются колебания оси гироскопа (рис.б) - нутация
Слайд 123
Физические основы механики Неинерциальные системы отсчета. Курс общей физики НИЯУ МИФИ
Слайд 124
Неинерциальные системы отсчета (НеИСО) - движутся относительно инерциальных (ИСО) неравномерно и/или непрямолинейно. По мере усложнения описания мы рассмотрим три случая НеИСО НеИСО, движущиеся относительно ИСО неравномерно, но поступательно. НеИСО, вращающиеся относительно ИСО НеИСО, движущиеся относительно ИСО произвольным образом Неинерциальные системы отсчета (НеИСО)
Слайд 125
Второй закон Ньютона: а) ИСО: б)НеИСО: Поступательная сила инерции: НеИСО, движущиеся поступательно относительно ИСО
Слайд 126
Второй закон Ньютона: а) ИСО: б)НеИСО: НеИСО, движущиеся поступательно относительно ИСО
Слайд 127
По величине и направлеию линейная скорость материальной точки, отстоящей от центра координат на радиус-вектор r, связана с угловой соотношением : V = [ω,r] Связь угловой и линейной скорости Аналогично - линейная скорость конца вектора-орта е (любого), вращающегося относительно неподвижной системы отсчета с угловой скоростью ω связана с ней соотношением : V = [ω,е]
Слайд 128
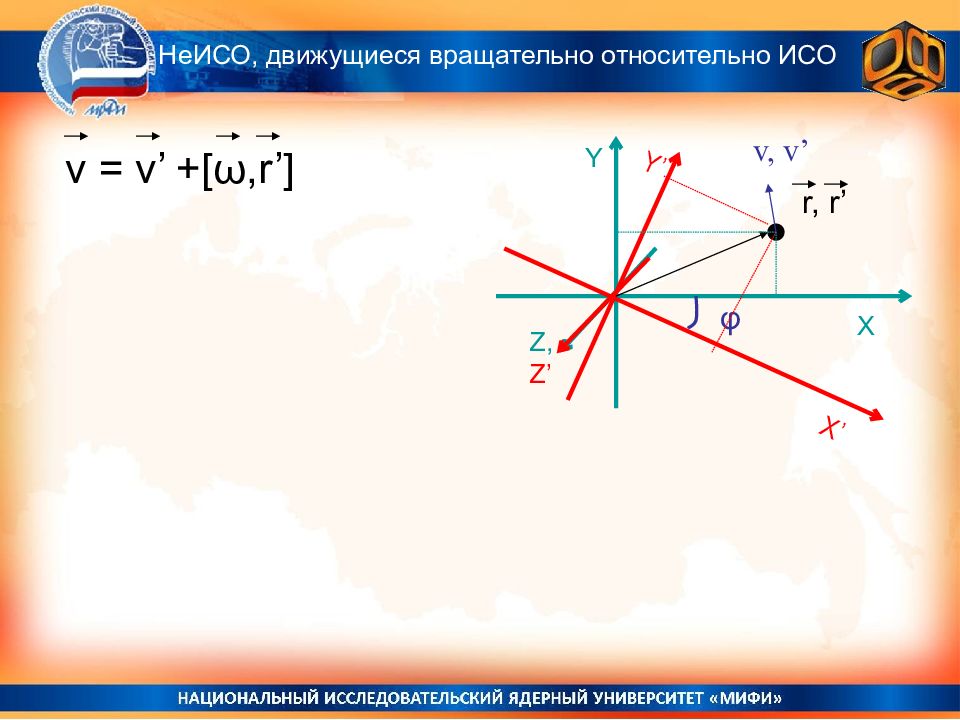
Y X Z, Z’ Y’ X’ φ r, r’ НеИСО, движущиеся вращательно относительно ИСО v, v’ v = v’ +[ ω,r’]
Слайд 129
НеИСО, движущиеся вращательно относительно ИСО v = v’ +[ ω,r’] dv/dt = w w = w’ +2[ ω,v’] + [ω,[ω,r’]] + [β,r’]
Слайд 130
НеИСО, движущаяся произвольно относительно ИСО w = w’ +2[ ω,v’] + [ω,[ω,r’]] + [β,r’] Мы никак не использовали тот факт, что вращение происходит вокруг оси OZ. То есть – эта формула справедлива для любого направления оси вращения! Более того –если добавить поступательную силу инерции – формула становится справедливой для любой произвольно движущейся системы отсчета! m w = m w’ + mw 0 +2 m [ ω,v’] +m[ω,[ω,r’]] + m[β,r’]
Слайд 131
НеИСО, движущаяся произвольно относительно ИСО m w = m w’ + mw 0 +2 m [ ω,v’] +m[ω,[ω,r’]] + m[β,r’] m w’ = F – (mw 0 +2 m [ ω,v’] +m[ω,[ω,r’]] + m[β,r’]) Итак, в ИСО 2-й закон Ньютона имеет вид: В силу соотношения в НеИСО, произвольно движущейся, 2-й закон Ньютона имеет вид: Разберем далее подробнее 4 разновидности сил инерции, которые приходится учитывать при работе с НеИСО
Слайд 132
Силы инерции в НеИСО Итак, в произвольно движущейся НеИСО 2-й закон Ньютона имеет вид: Сюда входят 4 силы инерции: m w’ = F – mw 0 - 2 m [ ω,v’] - m[ω,[ω,r’]] - m[β,r’] - mw 0 – поступательная сила инерции. Ее величина и направление понятны. - m[β,r’]– сила инерции, связанная с неравномерностью вращения НеИСО. На практике такие НеИСО почти не используются. - m[ω,[ω,r’]] – центробежная сила. - 2 m[ω,v’] – сила Кориолиса. О двух последних силах – центробежной и Кориолиса – поговорим подробнее
Слайд 133
Центробежная сила инерции - m[ω,[ω,r’]] – центробежная сила. Центробежная сила всегда направлена от оси вращения перпендикулярно ей и пропорциональна квадрату угловой скорости и расстоянию до оси вращения: m|[ω,[ω,r’]]| = mω 2 r ┴. Покажем это. Без потери общности будем считать, что ω направлена вдоль оси Z’ [ω,r’] = e x (ω y z-ω z y) + e y (ω z x – ω x z) + e z (ω x y – ω y x) = = - e x ω z y + e y ω z x = ω( e y x – e x y) [ω,[ω,r’]] = - e x ω 2 x - e y ω 2 y = -ω 2 ( e x x + e y y) = -ω 2 r ┴
Слайд 134
Центробежная сила инерции - m[ω,[ω,r’]] – центробежная сила. Центробежная сила всегда направлена от оси вращения перпендикулярно ей и пропорциональна квадрату угловой скорости и расстоянию до оси вращения: m|[ω,[ω,r’]]| = mω 2 r ┴. Второй закон Ньютона в НеИСО (пример на рисунке): F цб = - m[ω,[ω,r’]] = mω 2 r ┴.
Слайд 135
Сила Кориолиса - пример Сила Кориолиса перпендикулярна как угловой скорости вращения НеИСО, так и линейной скорости частицы. Она приводит (см. рисунок) к отклонению частицы от направления ее первоначальной скорости - 2 m[ω,v’] = 2 m[v’,ω] сила Кориолиса.
Слайд 136
Энергия материальной точки в НеИСО Рассмотрим особо случай равномерно вращающейся НеИСО, не имеющей поступательного ускорения. Для нее 2-й закон Ньютона имеет вид: m w’ = F + 2 m [ v’,ω] + mω 2 r ┴ v’ = v - [ ω,r] ; r’ = r Причем Сила Кориолиса перпендикулярна скорости и работы не совершает. Центробежная сила совершает работу и выглядит как потенциальная сила, которой можно приписать потенциальную энергию. Учитывая известную связь силы и потенциальной энергии F = - U, находим U цб = - mω 2 r 2 ┴ /2
Слайд 137
Энергия материальной точки в НеИСО Для энергии материальной точки в НеИСО можно записать: E ’ = U + mv’ 2 /2 - mω 2 r ┴ 2 /2 Причем v’ 2 = ( v – [ ω,r ]) 2 = v 2 – 2 v [ ω,r ] + [ ω, r ] 2 Заметим, что по свойствам векторного и скалярного произведений [ ω,r ] 2 = ( ω rsin( ω ^r )) 2 = ( ω r ┴ ) 2 ; ( v, [ ω,r] ) = ( [r,v], ω ) E ’ = U + mv 2 /2 – m ( [r,v], ω ) = Е 0 – (М, ω ) Подставляя v’ 2 в выражение для энергии замечаем, что центробежная энергия сокращается и остается Где E 0 = U + mv 2 /2 – полная энергия частицы в ИСО, М = [r,mv] – момент импульса частицы в ИСО
Слайд 139: Механика жидкостей и газов
Что мы знаем из школьного курса физики? 1) На тело, погруженное в газ или жидкость, действует сила Архимеда, направленная вверх и равная численно весу вытесненной телом жидкости или газа: F арх = ρ ж gV тела 2) На глубине Н под поверхностью жидкости ее давление равно: Р = ρ ж gН 3) На тело, движущееся в жидкости или газе, действует сила сопротивления, направленная против скорости тела (если тело имеет простую геометрическую форму) и тем большая, чем больше скорость. F сопр ~ v или v 2
Слайд 140: Механика несжимаемой жидкости
Основные понятия и определения dV v 1) Частица жидкости - малый объем ее dV, выделенный для рассмотрения. Аналог материальной точки. Малый объем - по сравнению с областью течения, но большой по сравнению с межмолекулярными расстояниями. 2) Для каждой частицы жидкости можно указать ее вектор скорости как функцию времени. 3) Совокупность векторов скорости для всех точек течения образует поле вектора скорости. 4) Если вектор скорости в каждой точке течения остается постоянным - течение называют стационарным. 5) Несжимаемая жидкость - такая жидкость, плотность которой ρ во всех точках течения постоянна и одинакова.
Слайд 141
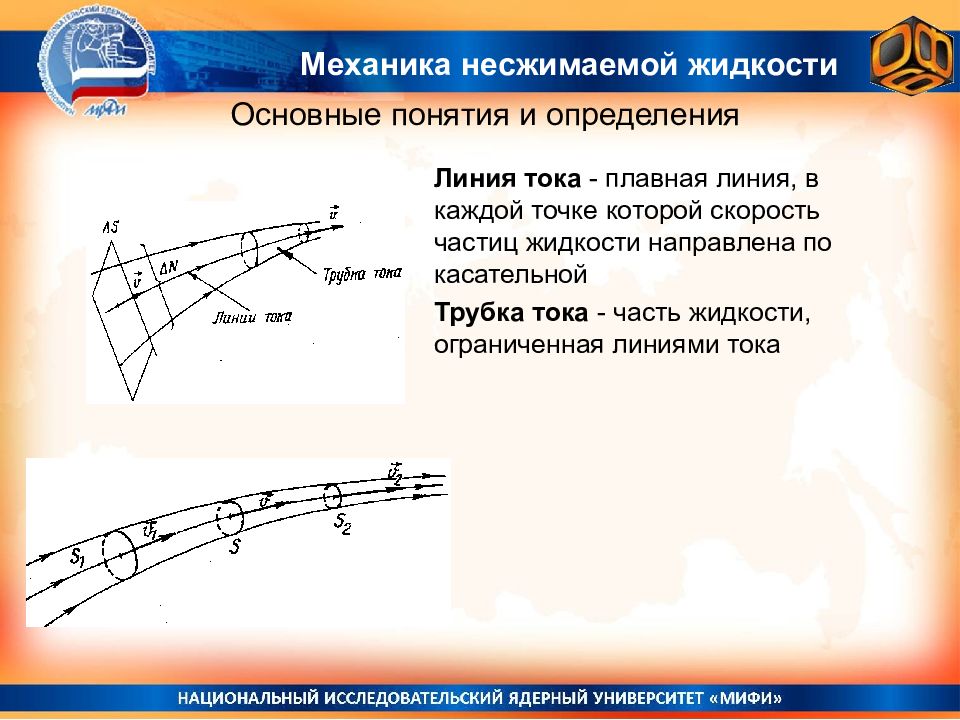
Линия тока - плавная линия, в каждой точке которой скорость частиц жидкости направлена по касательной Трубка тока - часть жидкости, ограниченная линиями тока Механика несжимаемой жидкости Основные понятия и определения
Слайд 142
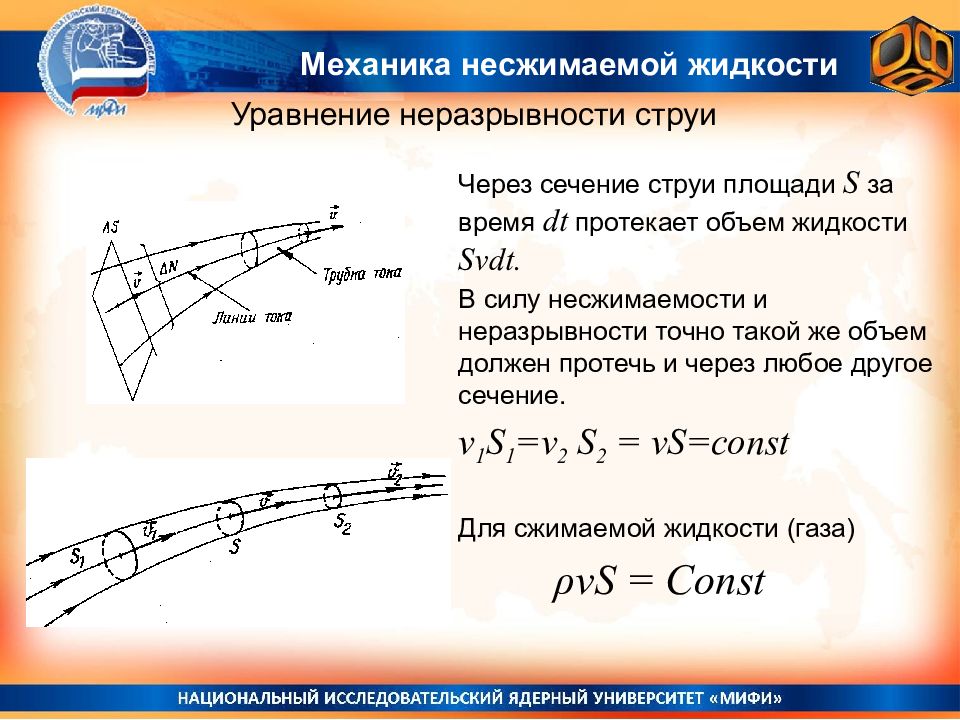
Через сечение струи площади S за время dt протекает объем жидкости Svdt. В силу несжимаемости и неразрывности точно такой же объем должен протечь и через любое другое сечение. v 1 S 1 =v 2 S 2 = vS=const Для сжимаемой жидкости (газа) ρvS = Const Механика несжимаемой жидкости Уравнение неразрывности струи
Слайд 143
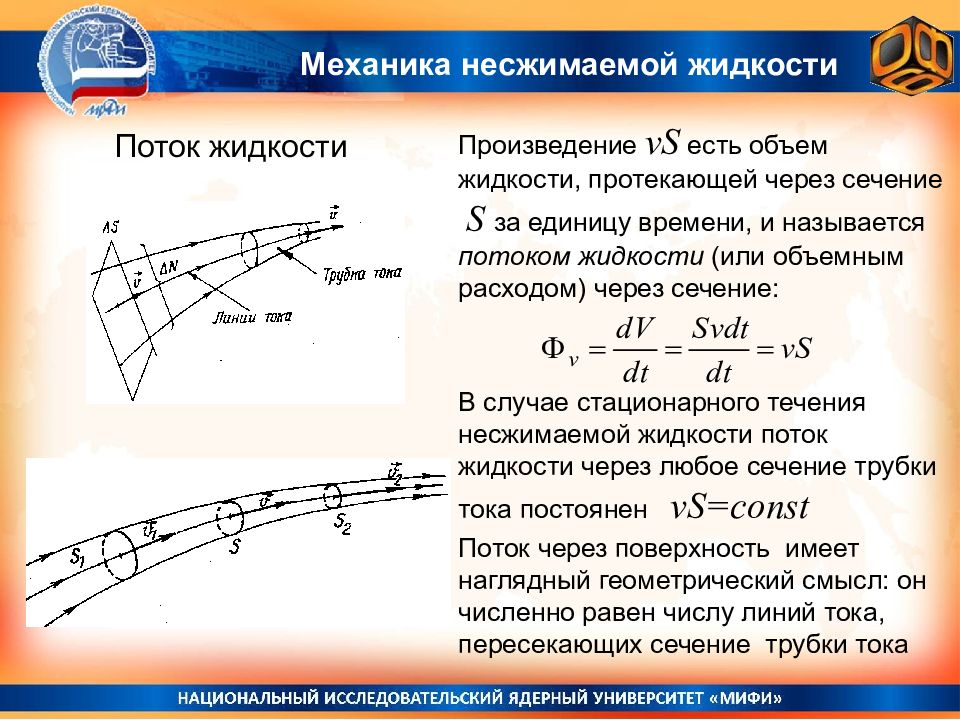
Механика несжимаемой жидкости Поток жидкости Произведение vS есть объем жидкости, протекающей через сечение S за единицу времени, и называется потоком жидкости (или объемным расходом) через сечение: В случае стационарного течения несжимаемой жидкости поток жидкости через любое сечение трубки тока постоянен vS=const Поток через поверхность имеет наглядный геометрический смысл: он численно равен числу линий тока, пересекающих сечение трубки тока
Слайд 144
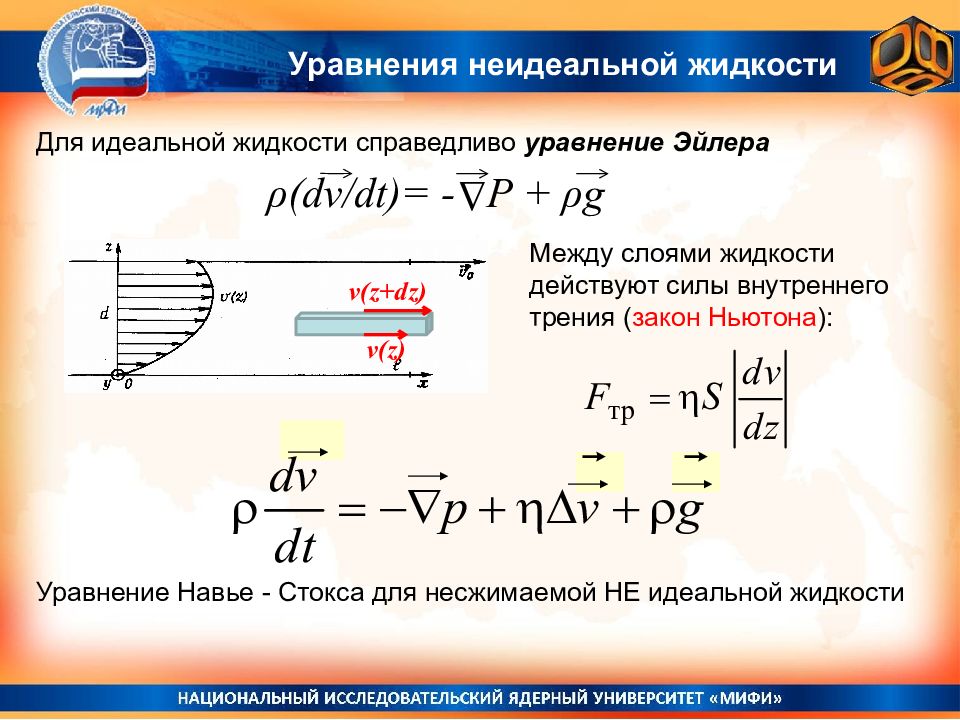
Уравнение идеальной жидкости dz dy dx P(x) P(x+dx) dF x = (P(x) – P(x+dx))dydz = - P’ x dxdydz dm(dv/dt)= - PdV + ρ gdV Δ Для идеальной жидкости справедливо уравнение Эйлера Жидкость, в которой отсутствуют силы трения, называют идеальной. Δ ρ (dv/dt)= - P + ρ g
Слайд 145
Уравнения идеальной жидкости Умножим уравнение Эйлера скалярно на dr = vdt : ; Для идеальной жидкости справедливо уравнение Эйлера ( dv / dt, vdt ) = ( dv,v ) = d(v 2 /2) ( P,dr ) = ( P’ x e x +P’ y e y + P’ z e z, dx e x +dy e y + dz e z ) = = P’ x dx + P’ y dy + P’ z dz = dP Δ (g, dr ) = - gdz = -d( gz ) d( ρ v 2 /2)= - dP – d( ρ gz) ρ v 2 /2 + P + ρ gz = Const = B; Уравнение Бернулли Δ ρ (dv/dt)= - P + ρ g
Слайд 146
Истечение жидкости из отверстия S s Задача: как быстро выльется вода из сосуда высоты h с основанием S через малое отверстие у дна площади s. РЕШЕНИЕ: Давление в верхнем (S) и нижнем (s) сечениях трубки тока одинаково и равно атмосферному. Следовательно: - скорость опускания свободной поверхности - скорость истечения из отверстия v = (2gh/(1 - s 2 /S 2 )) 1/2 => - формула Торричелли => =>
Слайд 147
Вязкость Между слоями жидкости действуют силы внутреннего трения ( закон Ньютона ): η – коэффициент динамической вязкости ; S – площадь слоя, на который действует сила; dv/dz = (v(z+dz) - v(z))/dz - скорость изменения скорости жидкости в направлении z. Как показывает опыт, закон Ньютона справедлив как для жидкостей, так и для газов
Слайд 148
Вязкость. Между слоями жидкости действуют силы внутреннего трения ( закон Ньютона ): Коэффициент вязкости η зависит от состава (химии) и агрегатного состояния (жидкость, газ) вещества. Единицы измерения коэффициента динамической вязкости в системе СИ: Па•с = кг/м•с ; 1 Пуаз = 0,1Па • с В некоторых случаях употребляется коэффициент кинематической вязкости: v = η/ρ. Его единица измерения в системе СИ: м 2 /с ; Устаревшая единица измерения Стокс : 1 Ст = 10 -4 м 2 /с
Слайд 149
Вязкость. Пример. F z v Между слоями жидкости действуют силы внутреннего трения ( закон Ньютона ): d С какой силой F надо тянуть верхнюю пластину, чтобы она двигалась со скоростью v относительно нижней? F = ηS(v/d) Коэффициент вязкости η зависит от состава (химии) и агрегатного состояния (жидкость, газ) вещества. Размерность коэффициента вязкости: Па•с = Н • с/м 2
Слайд 150
Уравнения неидеальной жидкости Для идеальной жидкости справедливо уравнение Эйлера Δ ρ (dv/dt)= - P + ρ g Уравнение Навье - Стокса для несжимаемой НЕ идеальной жидкости Между слоями жидкости действуют силы внутреннего трения ( закон Ньютона ): v(z+dz) v(z)
Слайд 151
Уравнения Навье - Стокса Основное уравнение Навье - Стокса для несжимаемой жидкости Уравнение неразрывности div v = δv x /δx + δv y /δy+ δv z /δz = 0 Δ = e x δ/δx + e y δ/δy + e z δ/δz Δ = δ 2 /δx 2 + δ 2 /δy 2 + δ 2 /δz 2 Оператор Гамильтона Оператор Лапласа Векторное поле скоростей v(r,t) = e x v x + e y v y + e z v z ρ - плотность жидкости ; η - коэффициент динамической вязкости р - давление; g - ускорение свободного падения; t - время
Слайд 152
Уравнения Навье - Стокса Основное уравнение Навье - Стокса для несжимаемой жидкости Уравнение неразрывности div v = δv x /δx + δv y /δy+ δv z /δz = 0 v = 0 например, на границах области тока - граничное условие v (r,t=0) = v 0 (r) - начальное условие ρ vS = Const Уравнение неразрывности струи (в пределах трубы или трубки тока)
Слайд 153
Плоское течение Уравнение Навье - Стокса для несжимаемой жидкости Пренебрегаем силой тяжести (течение в горизонтальном канале)
Слайд 154
Плоское течение Основные параметры плоского течения: ρ - плотность жидкости ; η - коэффициент динамической вязкости; v 0 – характерная скорость течения ; L - характерный линейный размер потока. Re= ρ v 0 L/ η – число Рейнольдса - безразмерная величина, характеризующая свойства течения Течения с одинаковыми числами Рейнольдса являются подобными.
Слайд 155
Плоское течение Re= ρ v 0 L/ η – число Рейнольдса Основные параметры плоского течения: ρ - плотность жидкости ; η - коэффициент динамической вязкости; v 0 – характерная скорость течения ; L - характерный линейный размер потока. Течения с одинаковыми числами Рейнольдса являются подобными. Re <~1 - вязкая жидкость, силы внутреннего трения играют важную роль по всему полю течения. Течение ламинарное. Re>>1 - силами внутреннего трения можно пренебречь (кроме пограничного слоя у границы твердого тела); жидкость является идеальной. Ламинарное течение Re >~10 3 - течение турбулентное.
Слайд 157
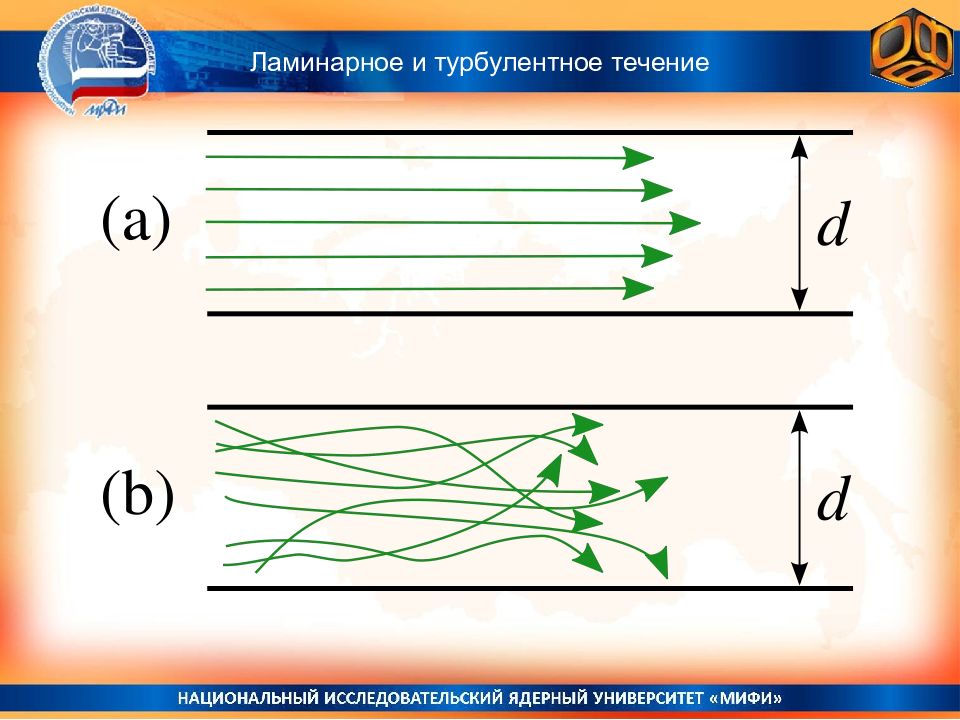
Ламинарное и турбулентное течения Ламинарное течение : Жидкость течет параллельным потоком. Течения устойчиво по отношению к малым возмущениям, которые при достаточно малых числах Re и благодаря силам вязкости быстро затухают Турбулентное течение : нерегулярное нестационарное хаотическое беспорядочное течение, в котором движение частицы складывается из движения вдоль трубы с некоторой усредненной скоростью и из беспорядочных пульсаций, колебаний и вращений. Течение теряет устойчивость по отношению к малым возмущениям, которые более не затухают, а усиливаясь, охватывают все большие и большие области течения при Re>Re кр ~ 10 3. Эта классификация относится как к жидкостям, так и к газам
Слайд 158
Движение тел в жидкости и газах Основной параметр = ρ v 0 l/ η Сопротивление движения (лобовое сопротивление): при Re < 1( вязкое обтекание): V T ~ l 3 - объем тела Для шара, например: - формула Стокса При Re >> 1( турбулентное обтекание) главную роль играет давление, а не вязкость: S П ~ l 2 - поперечное сечение тела тела Минимальный коэффициент пропорциональности ( ~0,04) характерен для тел каплевидной формы. Для шара этот коэффициент ~0,24
Слайд 159
Физические основы механики Механика больших скоростей Курс общей физики НИЯУ МИФИ
Слайд 160
Относительность движения. Преобразования Галилея Y’ X, X’ Z’ 0’ Y Z 0 u чч:мм:сс чч:мм:сс x’(t) = x(t) - ut y’(t) = y(t) z’(t) - z(t) r’(t) = r(t) - ut V’ = V - u t’ = t X, X’ x(t) x’(t’) V, V’
Слайд 161
x’(t) = x(t) - ut y’(t) = y(t) z’(t) - z(t) t’ = t V’ = V - u Преобразования Галилея в матричной форме x’ y’ z’ t’ ( ) Компактнее преобразования Галилея можно записать, опустив неменяющиеся координаты y и z = ( ) 1 0 0 -u 0 1 0 0 0 0 1 0 0 0 0 1 x y z t ( ) x’ t’ ( ) = 1 -u 0 1 ( ) x t ( ) x’(t) = x(t) – ut t’ = t Проблема преобразований Галилея : постоянство скорости света, независящей от системы отсчета, из которой ведется наблюдение.
Слайд 165
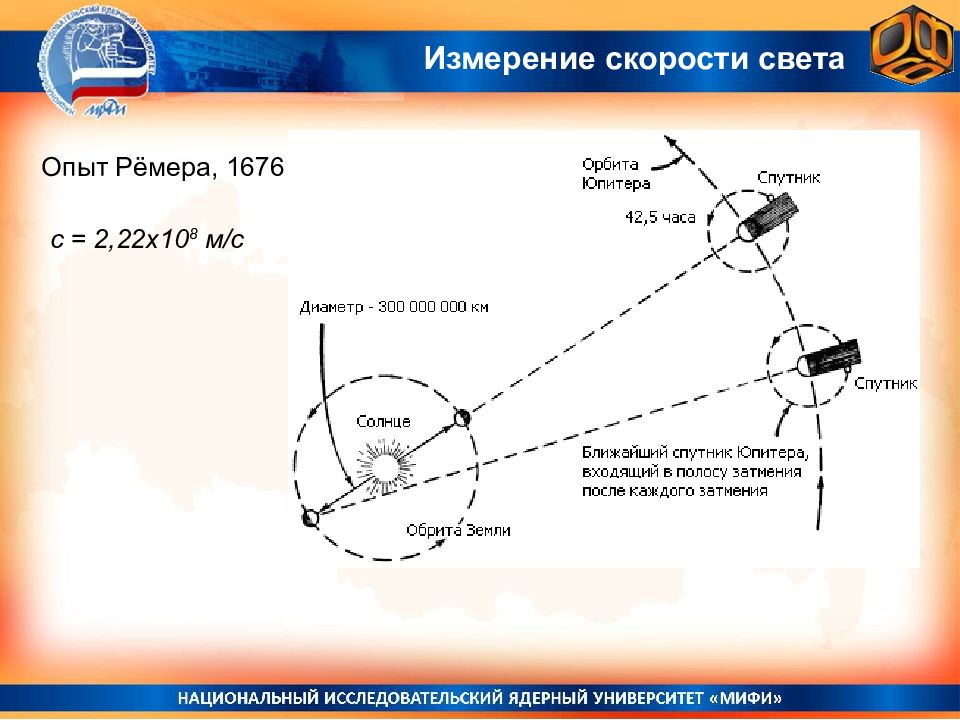
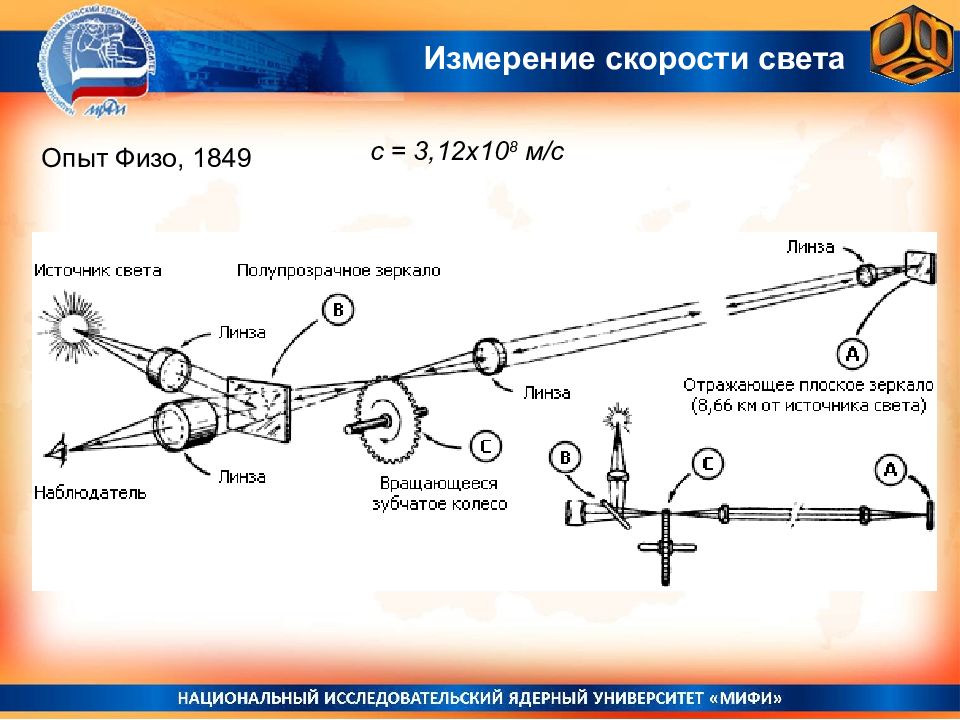
http://www.lightandmatter.com/html_books/6mr/ch01/ch01.html Опыт Майкельсона-Морли, 1887 Опыт Майкельсона-Морли и последующие опыты Миллера показали, что скорость света не зависит ни от направления движения Земли, ни от направления распространения света. А. Майкельсон Э. Морли Постоянство скорости света
Слайд 166
Опыт Майкельсона-Морли, последующие опыты Миллера, де-Ситтера, наблюдения двойных звезд показали, что скорость света не зависит ни от скорости источника, ни от скорости наблюдателя и всегда равна с = 3 х 10 8 м/с Точное значение скорости света в вакууме в системе СИ с 1983 года: с = 299 792 458 м/с Постоянство скорости света
Слайд 167
x’(t) = x(t) - vt t’ = t Преобразования Галилея и Лоренца Преобразования Галилея можно записать, опустив для простоты неменяющиеся координаты y и z x’ t’ ( ) = 1 - v 0 1 ( ) x t ( ) Проблема преобразований Галилея: постоянство скорости света, независящей от системы отсчета, из которой ведется наблюдение. Y X, X’ Z x(t) 0 Y’ Z’ 0’ x’(t’) v В электродинамике, в применении к векторам напряженности электрического поля и магнитной индукции, известны похожие по форме преобразования Лоренца, содержащие скорость света (скорость распространения электромагнитных волн в вакууме) явно. ( ) = ( ) ( ) γ -γv -γv/c 2 γ Х. А. Лоренц = γ ( ) ( 1 -v -v/c 2 1 )
Слайд 168
Преобразования Лоренца - Идея Эйнштейна - Пуанкаре Идея Эйнштейна и Пуанкаре: применить преобразования Лоренца к механике. Y X, X’ Z x(t) 0 Y’ Z’ 0’ x’(t’) v ( ) = γ ( ) ( ) 1 -v -v/c 2 1 x’ t’ x t Важно, что при v<<c = > γ ~= 1, v/c 2 ->0 и преобразования Лоренца превращаются в преобразования Галилея. При v>c преобразования Лоренца теряют физический смысл, что означает, что величина с является предельной скоростью движения, достижимой в механике Моменты совершения событий, измеряемые по часам в разных системах отсчета, могут быть разными(!). Тот факт, что время и координаты выражаются друг через друга означает их неразрывную связь. В дальнейшем мы будем использовать термин пространство-время.
Слайд 169
Идея Эйнштейна и Пуанкаре: применить преобразования Лоренца к механике. Y X, X’ Z x(t) 0 Y’ Z’ 0’ x’(t’) v ( ) = γ ( ) ( ) 1 -v -v/c 2 1 x’ t’ x t Постулаты СТО: 1) Все законы природы во всех ИСО одинаковы (И. Ньютон). 2) Максимальная скорость распространения взаимодействий (скорость света в вакууме) одинакова во всех направлениях и не зависит от скоростей источника и приемника (А. Эйнштейн) А. Эйнштейн Постулаты СТО Был этот мир глубокой тьмой окутан. Да будет свет! И вот явился Ньютон. Эпиграмма XVIII века Но сатана недолго ждал реванша. Пришёл Эйнштейн – и стало всё как раньше. Эпиграмма XX века
Слайд 170
Идея Эйнштейна и Пуанкаре: применить преобразования Лоренца к механике. Y X, X’ Z x(t) 0 Y’ Z’ 0’ x’(t’) v ( ) = γ ( ) ( ) 1 -v -v/c 2 1 x’ t’ x t Постулаты СТО: 1) Все законы природы во всех ИСО одинаковы (И. Ньютон). 2) Максимальная скорость распространения взаимодействий (скорость света в вакууме) одинакова во всех направлениях и не зависит от скоростей источника и приемника (А. Эйнштейн) Постулаты СТО На самом деле: вывести преобразования Лоренца для механики и показать неизбежность существования предельной скорости для любого движения можно и не прибегая к прямому постулированию существования такой скорости. Попробуем показать это
Слайд 171
Будем исходить из того, что по форме искомые преобразования должны иметь матричную форму, похожую на известные преобразования Галилея и Лоренца. Y X, X’ Z x(t) 0 Y’ Z’ 0’ x’(t’) v ( ) = ( ) ( ) α(v) β(v) γ(v) δ(v) x’ t’ x t Вывод преобразований Лоренца для механики Функции α(v), β(v), γ(v), δ(v) бу дем считать пока неизвестными. Попробуем установить их вид исходя из естественных требований: 1) При малых скоростях преобразования должны превращаться в преобразования Галилея ( α(v) = 1, β(v) = -v, γ(v) = 0, δ(v) = 1) 2) Преобразования должны отвечать принципам симметрии и изотропии пространства-времени 3) Для каждого преобразования должно существовать аналогичное по форме и обратное ему 4) Преобразования не должны приводить к нарушению принципа причинности
Слайд 172
Y X, X’ Z x(t) 0 Y’ Z’ 0’ x’(t’) v ( ) = ( ) ( ) α(v) β(v) γ(v) δ(v) x’ t’ x t Вывод преобразований Лоренца для механики 1) Преобразования не должны давать качественно разные результаты в зависимости от направления скорости - из этого следует, функции α(v), β(v), γ(v), δ(v) могут быть или четными, или нечетными. ( ) = ( ) ( ) α(v) -vb(v) vk(v) δ(v) x’ t’ x t Учитывая необходимость соответствия преобразованиям Галилея ( α(v) = 1, β(v) = -v, γ(v) = 0, δ(v) = 1) делаем первый вывод : α(v), δ(v) - функции четные β(v) = -vb(v), γ(v) = vk(v), где b(v), k(v) - функции четные
Слайд 173
Y X, X’ Z x(t) 0 Y’ Z’ 0’ x’(t’) v Вывод преобразований Лоренца для механики 2) Проследим из системы К за движением центра отсчета системы К ’. По определению: x’ =0; х = Vt ( ) = ( ) ( ) α(v) -vb(v) vk(v) δ(v) x’ t’ x t В частности: 0 = ( V α(v) - Vb(v))t Следствие: α(v) = b(v) ( ) = ( ) ( ) α(v) -vb(v) vk(v) δ(v) 0 t’ Vt t ( ) = ( ) ( ) α(v) -vα(v) vk(v) δ(v) x’ t’ x t
Слайд 174
Y X, X’ Z x(t) 0 Y’ Z’ 0’ x’(t’) v Вывод преобразований Лоренца для механики ) 1 0 0 1 -> α(v) = δ(v); k(v) = K(v)α(v) α 2 (v) = (1 + Kv 2 ) -1 = ( α 2 (v) + v 2 α(v)k(v) = 1 - v α 2 (v) + v α(v)δ(v) = 0 - v α(v)k(v) + v δ(v)k(v) = 0 δ 2 (v) + v 2 α(v)k(v) = 1 3) Если к вектору (x’, t’) применить преобразование перехода к системе, движущейся со скоростью - v, должен получиться вектор (x, t) - то есть, мы возвращаемся в исходную систему. ( ) α(v) vα(v) -vk(v) δ(v) ( ) α(v) -vα(v) vk(v) δ(v) ( ) = ( ) ( ) α(v) -vα(v) vk(v) δ(v) x’ t’ x t
Слайд 175
Y X, X’, X’’ Z 0 Y’ Z’ 0’ v 1 Вывод преобразований Лоренца для механики 4) Рассмотрим теперь 2-этапный переход: 1: из K в K’ (скорость ее отн. K равна V 1 ) 2: из K’ в K’’ (скорость ее отн. K’ равна V 2 ) Этот же переход должен быть возможен и в один этап: из K в K’’ (скорость ее отн. K равна V 3 ). ВАЖНО: мы не требуем, чтобы V 3 = V 1 + V 2 ( ) = α(v) ( ) ( ) 1 -v vK(v) 1 x’ t’ x t Y’’ Z’’ 0’’ v 2 v 3 α(v 1 ) ( ) 1 -v 1 v 1 K 1 1 α(v 1 )α(v 2 )(1 - v 1 v 2 K 2 ) = α(v 3 ) α(v 1 )α(v 2 )(1 - v 1 v 2 K 1 ) = α(v 3 ) - α(v 1 )α(v 2 )(v 1 + v 2 ) = - v 3 α(v 3 ) α(v 1 )α(v 2 )(K 1 v 1 + K 2 v 2 ) = - v 3 K 3 α(v 3 ) α(v 2 ) ( ) 1 -v 2 v 2 K 2 1 = α(v 3 ) ( ) 1 -v 3 v 3 K 3 1 α(v) = (1 + Kv 2 ) -1/2 Следствия: K 1 = K 2 = K 3 = K = Const α(v) = (1 + Kv 2 ) -1/2 v 3 = (v 1 + v 2 )/(1 - Kv 1 v 2 )
Слайд 176
Y X, X’, Z 0 Y’ Z’ 0’ v Вывод преобразований Лоренца для механики ( ) = α(v) ( ) ( ) 1 -v vK 1 x’ t’ x t Y’’ α(v) = (1 + Kv 2 ) -1/2 Итак, получаем: Константа К имеет размерность [c 2 /м 2 ]. Определить ее можно только экспериментально. Рассмотрим несколько возможностей: 1) К = 0 => α(v) = 1 => получаем преобразования Галилея
Слайд 177
Y X, X’, Z 0 Y’ Z’ 0’ v Вывод преобразований Лоренца для механики ( ) = α(v) ( ) ( ) 1 -v vK 1 x’ t’ x t Y’’ α(v) = (1 + Kv 2 ) -1/2 Итак, получаем: Константа К имеет размерность [c 2 /м 2 ]. Определить ее можно только экспериментально. Рассмотрим несколько возможностей: 2) K < 0 => переобозначим K = -(1/с 2 ), где с - постоянная с размерностью скорости. Получим преобразования Лоренца со всеми вытекающими следствиями. Постоянная с имеет смысл максимально возможной скорости перемещения. Опыт показывает, что она равна скорости света в вакууме. При v<<c опять получаем преобразования Галилея (приближенно)
Слайд 178
Вывод преобразований Лоренца для механики ( ) = α(v) ( ) ( ) 1 -v vK 1 x’ t’ x t α(v) = (1 + Kv 2 ) -1/2 Итак, получаем: Константа К имеет размерность [c 2 /м 2 ]. Определить ее можно только экспериментально. Для полноты, рассмотрим и третью возможность: K > 0 При малых скоростях Kv 2 << 1 получаются опять преобразования Галилея. При этом никаких ограничений на скорости нет. НО! Закон сложения скоростей: v 3 = (v 1 + v 2 )/(1 - Kv 1 v 2 ) в случае Kv 1 v 2 >1 чреват нарушением причинности! Остается единственный вариант - преобразования Лоренца Y X, X’, Z 0 Y’ Z’ 0’ v 1
Слайд 179
Преобразования Лоренца для механики ( ) = γ (v ) ( ) ( ) 1 -v -v /с 2 1 x’ t’ x t v 3 = (v 1 + v 2 )/(1 + v 1 v 2 /с 2 ) < c Итак, в механике при больших скоростях движения следует применять преобразования Лоренца: Y X, X’, X’’ Z 0 Y’ Z’ 0’ v 1 Y’’ Z’’ 0’’ v 2 v 3 При малых скоростях движения V<<C преобразования Лоренца совпадают с преобразованиями Галилея: ( ) = ( ) ( ) 1 -v 0 1 x’ t’ x t v 3 = v 1 + v 2
Слайд 180
Преобразования Лоренца для механики ( ) = γ (v ) ( ) ( ) 1 -v -v /с 2 1 x’ t’ x t v 3 = (v 1 + v 2 )/(1 + v 1 v 2 /с 2 ) < c Итак, в механике при больших скоростях движения следует применять преобразования Лоренца: Y X, X’, X’’ Z 0 Y’ Z’ 0’ v 1 Y’’ Z’’ 0’’ v 2 v 3 СЛЕДСТВИЕ («постулат» Эйнштейна): существует максимально возможная скорость движения или распространения взаимодействий, которая одинакова во всех направлениях, не зависит от скоростей источника и приемника и совпадает со скоростью света в вакууме С = 299,8 тысяч километров в секунду
Слайд 181
Y Z 0 Y’ Z’ 0’ V Преобразования для скоростей Y’’ v1 Относительная скорость двух частиц v2 x’ = γ (v) (x - Vt) y’ = y z’ = z t’ = γ (v)(t - xV/c 2 ) x = γ (v) (x’ + Vt) y = y’ z = z’ t = γ (v)(t’ + x’/V/c 2 ) γ (v) = (1 - v 2 /с 2 ) -1/2
Слайд 182
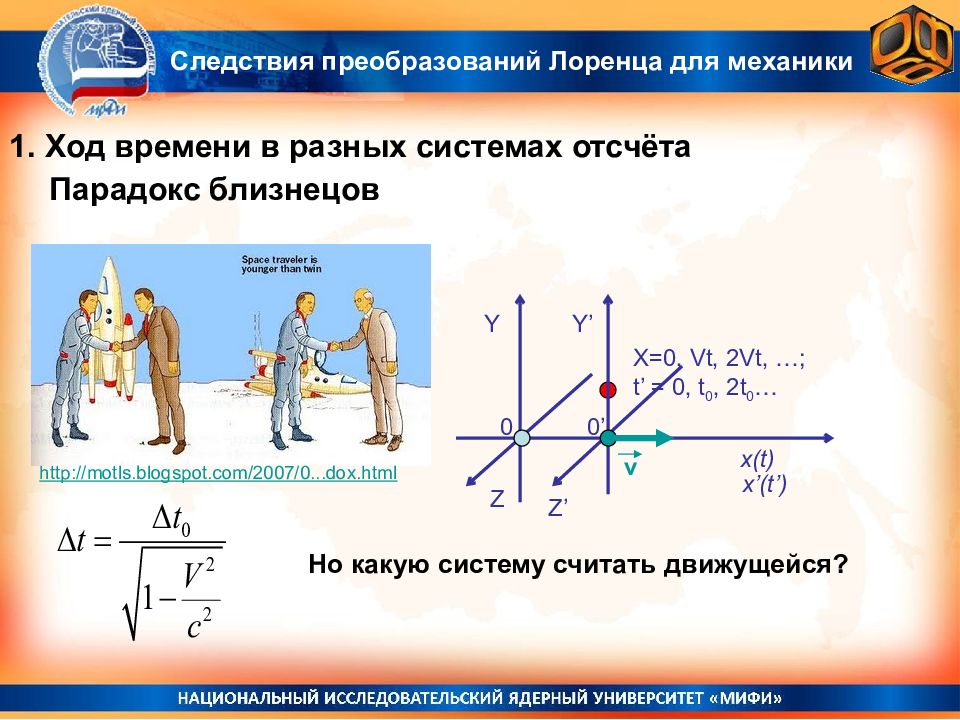
Следствия преобразований Лоренца для механики ( ) = γ ( v) ( ) ( ) 1 -v -v /с 2 1 x’ t’ x t t’ = γ (v)(t - xv/с 2 ) t 0 = γ (v)(t – v 2 t /с 2 ) = t / γ (v) t = γ (v) t 0 > t 0 Y X=0, Vt, 2Vt, …; t’ = 0, t 0, 2t 0 … Z x(t) 0 Y’ Z’ 0’ x’(t’) v В движущейся системе отсчета время течет медленнее. Но какую систему считать движущейся? 1. Ход времени в разных системах отсчёта
Слайд 183
http://motls.blogspot.com/2007/0...dox.html Парадокс близнецов Следствия преобразований Лоренца для механики Y X=0, Vt, 2Vt, …; t’ = 0, t 0, 2t 0 … Z x(t) 0 Y’ Z’ 0’ x’(t’) v Но какую систему считать движущейся? 1. Ход времени в разных системах отсчёта
Слайд 184
2. Неодновременность событий в разных системах отсчёта Следствия преобразований Лоренца для механики ( ) = γ ( v) ( ) ( ) 1 -v -v /с 2 1 x’ t’ x t t 1 ’ = γ (v)t Y X=0, t = t X’ = -vt’, t 1 ’ = ? Z x(t) 0 Y’ Z’ 0’ x’(t’) v X= vt, t = t X’=0, t 2 ’ = ? t 2 ’ = γ (v)(t – v 2 t /с 2 ) = t/ γ (v) < t 1 ’ Если в одной системе отсчета два события кажутся одновременными – в другой они могут показаться произошедшими в разные моменты времени
Слайд 185
3. Кажущееся сокращение длины движущегося тела Следствия преобразований Лоренца для механики ( ) = γ ( v) ( ) ( ) 1 -v -v /с 2 1 x’ t’ x t x 2 ’ = γ (v) x 2 = l Y Z,Z’ x(t) 0 Y’ 0’ x’(t’) v t’ = 0 X 1 ’=0, Х 2 ’ = l Движущееся с большой скоростью тело кажется неподвижному наблюдателю короче, чем оно есть t = 0 X 1 =0, Х 2 = ? x 2 = x 2 ’ / γ (v) < l
Слайд 186
Относительная скорость двух частиц Следствия преобразований Лоренца для механики 4. Удивительное сложение скоростей ( ) = γ ( v) ( ) ( ) 1 -v -v /с 2 1 x’ t’ x t v 3 = (v 1 + v 2 )/(1 + v 1 v 2 /с 2 ) < c Y Z 0 Y’ Z’ 0’ v 1 Y’’ Z’’ 0’’ v 2 v 3 Y Z 0 Y’ Z’ 0’ V Y’’ v 1 v 2 c v 1 + c v 2 < c 2 + v 1 v 2 0 < c 2 -cv 1 –cv 2 + v 1 v 2 =(c-v 1 )(c–v 2 ) >0 ПРИМЕР: v 1 = 0,9c; v 2 = 0,9c V rel = (0,9c+0,9c)/(1+0,9 * 0,9)= =1,8 c/ 1,81 = 0,995c
Слайд 187
Экспериментальные подтверждения специальной теории относительности Эксперимент Хафеле (J.C. Hafele) и Китинга (Richard E. Keating), октябрь 1971 Разность показаний путешествовавших и остававшихся на месте часов, наносекунды предсказанная измеренная гравитационный вклад ( общая теория относительности ) кинематический вклад (специальная теория относительности) Всего на восток 144 ± 14 −184 ± 18 −40 ± 23 −59 ± 10 на запад 179 ± 18 96 ± 10 275 ± 21 273 ± 7
Слайд 188
где Точечные события: Интервал инвариант преобразований Лоренца, т.е. Инварианты преобразований Лоренца. Интервал. Y Z,Z’ x(t) 0 Y’ 0’ x’(t’) v t = 0, x=0 t’=0, x’=0 x=r, t = t x’= γ (r-vt) t’= γ (t-vr/c 2 ) s 12 = c 2 t 2 – r 2 = c 2 γ 2 (t-vr/c 2 ) 2 – γ 2 (r-vt) 2 = ( ) = γ ( v) ( ) ( ) 1 -v -v /с 2 1 x’ t’ x t = γ 2 ((ct-vr/c) 2 – (r-vt) 2 ) = = γ 2 (c 2 t 2 -2vrt +v 2 r 2 /c 2 – r 2 +2rvt-v 2 t 2 ) = = c 2 t 2 – r 2
Слайд 189
Классификация интервалов Пространственноподобный интервал Времениподобный интервал Светоподобный (нулевой) интервал Инварианты преобразований Лоренца. Интервал. =ct x s 2 >0 s 2 >0 s 2 <0 s 2 <0 I II III IV O s 2 = 2 x 2 I абсолютное будущее II абсолютное прошедшее III, IV абсолютно удалённое
Слайд 190
В 4-х мерной СТО интервалы (а также модули любых 4-х мерных векторов) должны быть ковариантны относительно преобразований Лоренца (их модули не должны зависеть от выбора системы отсчета). 4-интервал содержит временные и координатные переменные. Сохранение энергии в механике связано с однородностью времени. Сохранение импульса - с однородностью пространства. Естественно предположить, что энергия и импульс должны образовывать в релятивистской механике 4-вектор, ковариантный относительно преобразований Лоренца. Ковариантность законов природы относительно преобразований Лоренца τ = ct
Слайд 191
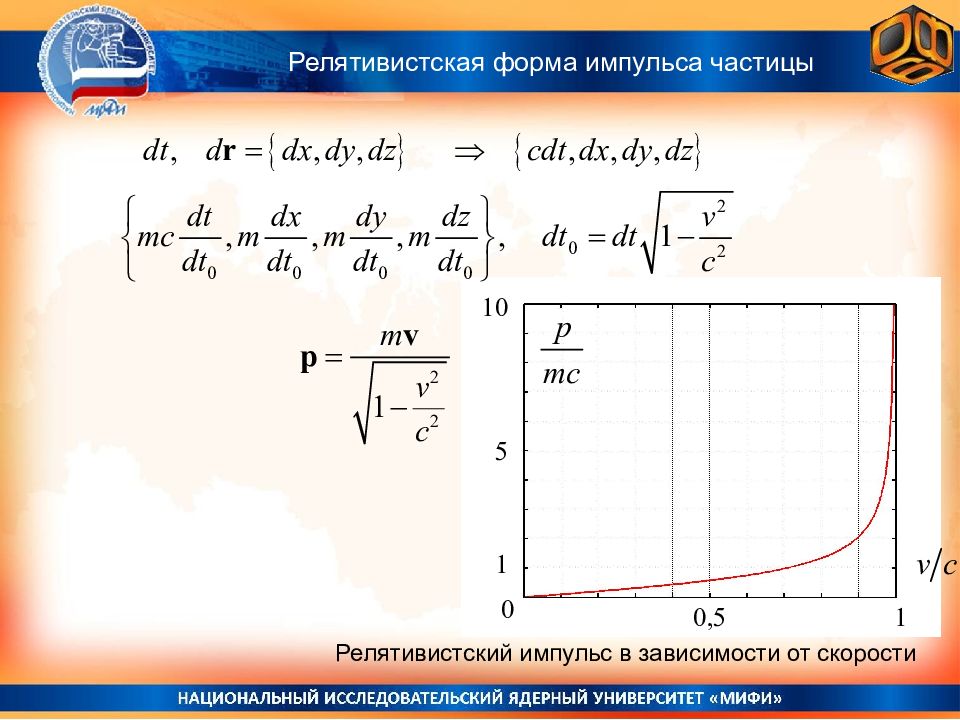
Релятивистская форма импульса частицы 0 1 10 0,5 5 1 Релятивистский импульс в зависимости от скорости
Слайд 192
Релятивистская форма энергии частицы Первая компонента 4-вектора имеет смысл энергии частицы, деленной на скорость света. Остальные три- вектор импульса. Модуль 4-вектора энергии-импульса инвариантен относительно выбора системы координат: ( E/c) 2 - p 2 = m 2 c 2 /(1-v 2 /c 2 ) - m 2 v 2 /(1 - v 2 /c 2 ) = m 2 c 2 = inv E 2 – p 2 c 2 = (mc 2 ) 2 = inv (E 2 – p 2 c 2 ) 1/2 = mc 2 = inv
Слайд 193
Релятивистская форма энергии частицы Первая компонента 4-вектора имеет смысл энергии частицы, деленной на скорость света. Остальные три- вектор импульса. Модуль 4-вектора энергии-импульса инвариантен относительно выбора системы координат: ВАЖНО: при v = 0 энергия частицы E = mc 2 Это энергия покоя частицы, не связанная ни с ее движением, ни со взаимодействием с другими частицами. (E 2 – p 2 c 2 ) 1/2 = mc 2 = inv
Слайд 194
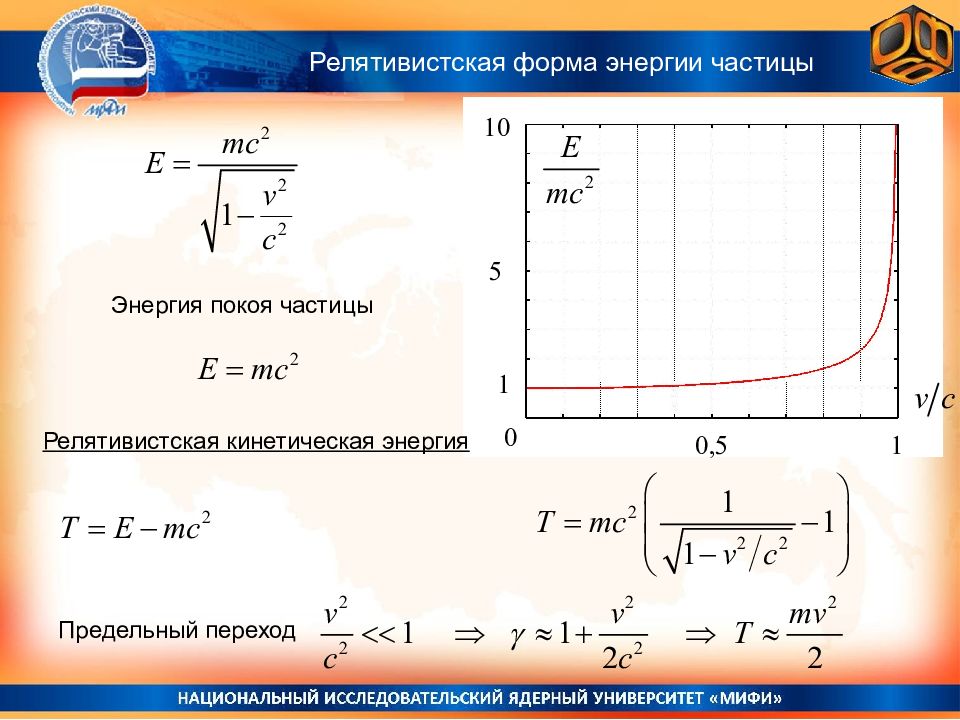
10 5 0 1 0,5 1 Энергия покоя частицы Релятивистская кинетическая энергия Предельный переход Релятивистская форма энергии частицы
Слайд 195
Инварианты преобразований Лоренца Собственная длина l 0. Собственный промежуток времени t 0. Интервал s 12. Масса m. Квадрат четыре-вектора энергии- импульса E 2 p 2 c 2 = m 2 c 4. Релятивистские формулы для энергии и импульса переходят в формулы классической механики при. Формула находит экспериментальное подтверждение при распадах ядер, процессах аннигиляции электрона и позитрона и других реакциях с участием элементарных частиц.
Слайд 196
Скорость центра инерции В релятивистской механике не выполняется закон сложения масс. Система невзаимодействующих частиц Энергия покоящейся изолированной системы включает в себя энергии покоя и кинетические энергии всех частиц, а также энергию взаимодействия частиц друг с другом. Системы частиц в СТО
Слайд 197
Скорость центра инерции В релятивистской механике не выполняется закон сложения масс. Система взаимодействующих частиц ( силы притяжения) Энергия покоящейся изолированной системы включает в себя энергии покоя и кинетические энергии всех частиц, а также энергию взаимодействия частиц друг с другом. Системы частиц в СТО -U <
Слайд 198
Удельная энергия связи ядер элементов Энергия связи ядра: Дефект масс Ядро неустойчиво, если Ядро устойчиво, если
Слайд 199
Частицы с нулевой массой Фотон элементарная частица, квант электромагнитного излучения. Фотон (гамма квант) всегда движется со скоростью света. Лазерный луч E 2 – pc 2 = (mc 2 ) 2 = 0
Слайд 200
Рождение массы из энергии Образование электрон-позитронных пар Порог реакции соответствует тому, что электрон и позитрон после реакции покоятся в системе центра масс
Слайд 201
Релятивистское уравнение второго закона Ньютона F = m( a + v( v,a ) /c 2 ) / (1 – v 2 /c 2 ) 3/2
Слайд 202
1. Эквивалентности инертной и гравитационной массы. Если инертная и гравитационная массы равны, то невозможно отличить какая сила действует на данное тело гравитационная или сила инерции. Три функции массы Что такое масса?: Мера инерции тела: F = Ma – классическая механика Ньютона 2. Гравитационный заряд: F = GMm/r 2 – теория гравитации Ньютона 3. Мера внутренней энергии: E = Mc 2 – релятивистская механика Эйнштейна 2. Эквивалентность массы и энергии. Если масса есть мера внутренней энергии, то гравитация должна действовать на все виды энергии (в частности – на электромагнитное излучение).
Слайд 203
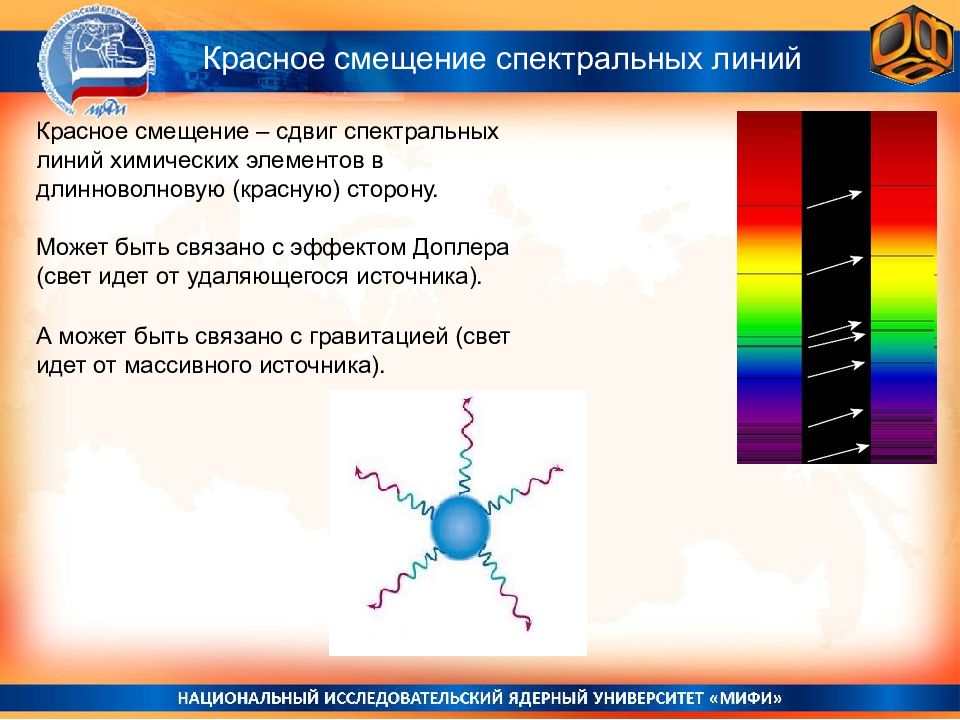
Экспериментальные подтверждения ОТО 2. Гравитационное красное смещение частоты спектральных линий (работа сил гравитации меняет энергию фотонов) 1. Искривление светового луча в гравитационном поле Гравитация в ОТО - геометрический эффект проявление искривления пространства-времени. В искривленном пространстве-времени частицы движутся по кратчайшим траекториям. Элементы общей теории относительности 3. Не-замкнутость планетных траекторий 4. Расширение Вселенной, существование «черных дыр» и др… ОТО опубликована А. Эйнштейном в 1915-16 г.г.
Слайд 204
Измерения, проведенные группой А.С. Эддингтона во время солнечного затмения 1919 года, подтвердили предсказание теории относительности. Современные наблюдения внеземных точечных радиоисточников (1980 г.) подтверждают формулу с точностью до 6 %. Теория Эйнштейна по сравнению с теорией Ньютона предсказывает вдвое больший угол отклонения луча Искривление светового луча в гравитационном поле
Слайд 205
Прецессия перигелия Меркурия В движении планет солнечной системы можно обнаружить влияние теории Эйнштейна.
Слайд 206
Прецессия перигелия Меркурия В движении планет солнечной системы можно обнаружить влияние теории Эйнштейна. Изменённая величина поля не будет соответствовать точно соответствовать закону Следствие: реальные орбиты планет не замкнуты. F = GMm/r 2
Слайд 207
http://scienceblogs.com/startswi...ytwidget Прецессия перигелия Меркурия Смещение перигелия за 100 лет Планета Эксперимент Теория Меркурий 43,11 0,45 43,0 Венера 8,4 4,8 8,6 Икарус 9,8 8 10,3 Земля 5 1,2 3,8 В движении планет солнечной системы можно обнаружить влияние теории Эйнштейна. Изменённая величина поля не будет соответствовать точно соответствовать закону Следствие: реальные орбиты планет не замкнуты. F = GMm/r 2
Слайд 208
Рентгеновский телескоп Chandra "заснял" массивную черную дыру, которая находится в центре нашей галактики. На иллюстрации помечено место расположения источника рентгеновского излучения, которое ассоциируется именно с массивной черной дырой. http://chandra.harvard.edu/photo/2003/0203long/ Вторая космическая скорость вблизи чёрной дыры превосходит скорость света, поэтому ни один материальный объект не может преодолеть силу гравитационного притяжения чёрной дыры. Чёрные дыры Гравитационный радиус Солнца r g = 3 км.
Слайд 209
Красное смещение спектральных линий Красное смещение – сдвиг спектральных линий химических элементов в длинноволновую (красную) сторону. Может быть связано с эффектом Доплера (свет идет от удаляющегося источника). А может быть связано с гравитацией (свет идет от массивного источника).
Последний слайд презентации: Физические основы механики Лектор: Доцент НИЯУ МИФИ, к.ф.-м.н., Ольчак Андрей
Флуктуации космического микроволнового реликтового излучения после удаления дипольного и галактического излучения. Данные получены с помощью дифференциального радиоволнового радиометра, установленного на спутнике COBE, запущенного в 1989 г. NASA. Вселенная