Первый слайд презентации
Уральский государственный технический университет - УПИ Кафедра “ Инженерная графика ” НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ автор Кириллова Татьяна Ивановна доцент
Слайд 2
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ занимается построением изображений и изучением пространственных объектов по их изображениям графическими методами
Слайд 3
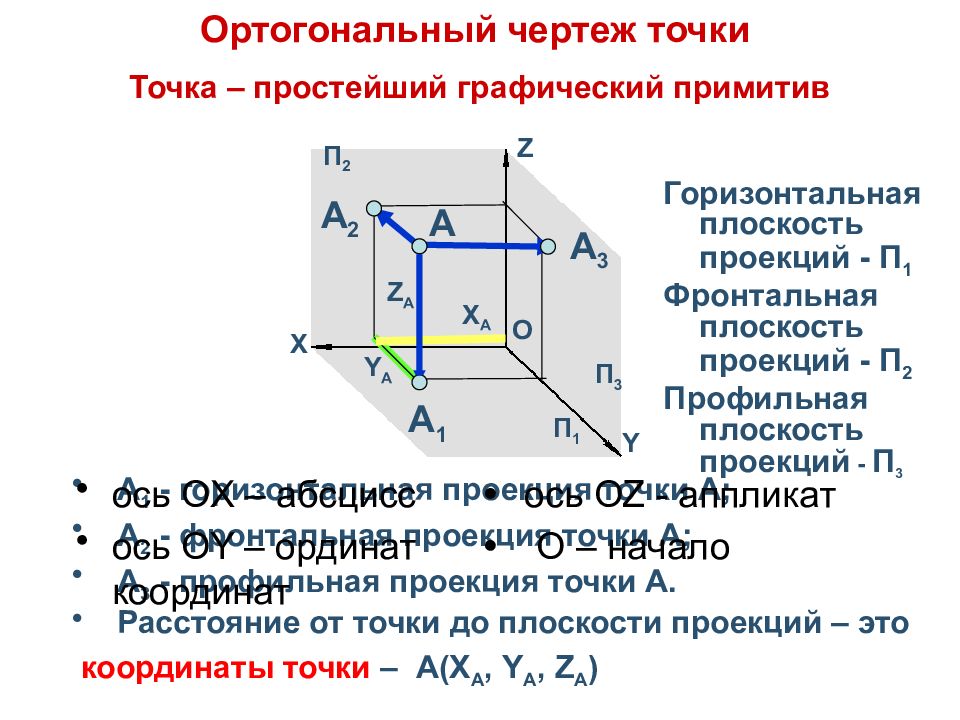
А 1 - горизонтальная проекция точки А ; А 2 - фронтальная проекция точки А ; А 3 - профильная проекция точки А. Расстояние от точки до плоскости проекций – это координаты точки – А( X А, Y А, Z А ) X Y O П 1 П 3 П 2 X A Z А А 1 А 2 А 3 Y A Z A Ортогональный чертеж точки Точка – простейший графический примитив ось О X – абсцисс • ось О Z - аппликат ось О Y – ординат • О – начало координат Горизонтальная плоскость проекций - П 1 Фронтальная плоскость проекций - П 2 Профильная плоскость проекций - П 3
Слайд 4: ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ - ЭПЮР
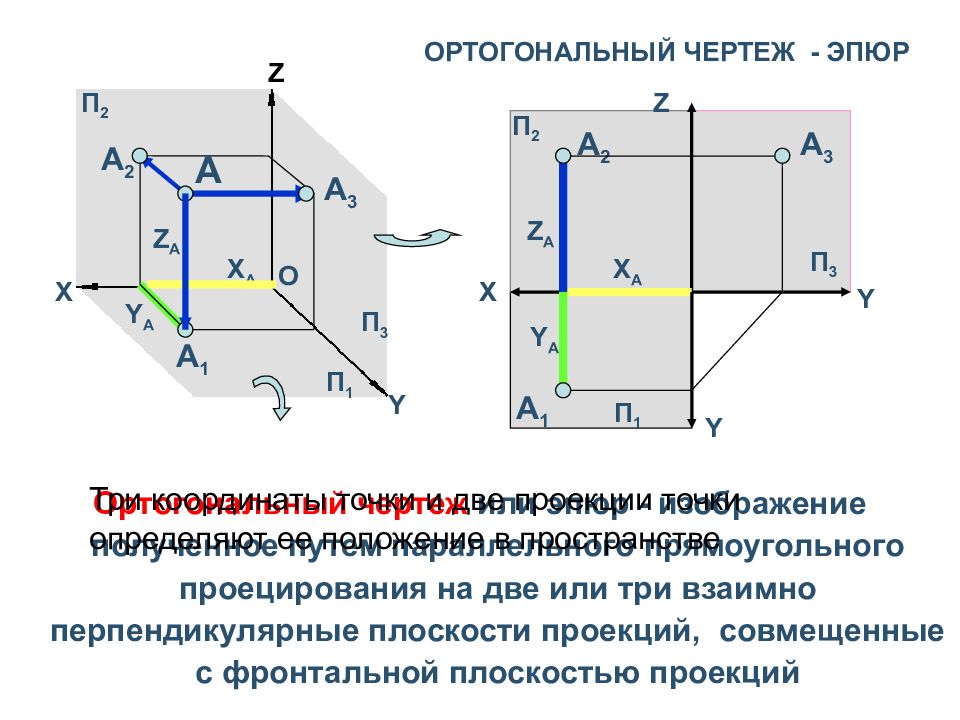
Ортогональный чертеж или эпюр - изображение полученное путем параллельного прямоугольного проецирования на две или три взаимно перпендикулярные плоскости проекций, совмещенные с фронтальной плоскостью проекций Z Y Y X П 3 П 1 П 2 X A А 2 А 3 Y A Z A X Y O П 1 П 3 П 2 X A Z А А 1 А 2 А 3 Y A Z A А 1 Три координаты точки и две проекции точки определяют ее положение в пространстве
Слайд 5
ВИДЫ ПРЯМЫХ ЛИНИЙ Прямые частного положения Прямые общего положения Ортогональный чертеж прямой линии
Слайд 6
Прямые частного положения : • ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ – прямые перпендикулярные плоскостям проекций • ЛИНИИ УРОВНЯ – прямые параллельные плоскостям проекций ;
Слайд 7: 1. Проецирующие прямые
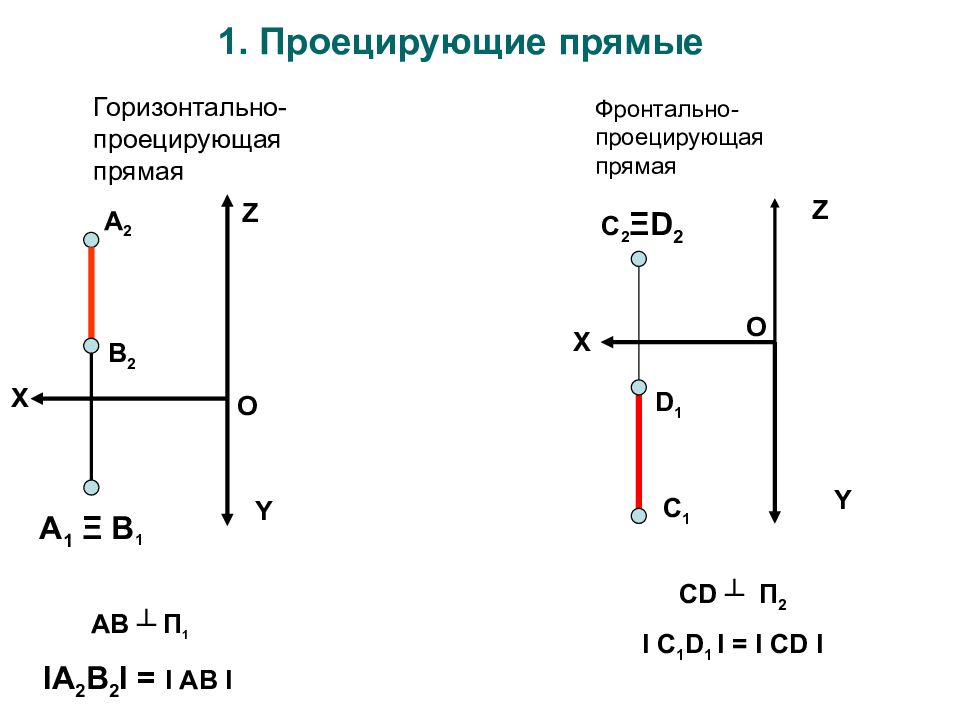
Z X Y А 1 Ξ B 1 B 2 А 2 О AB ┴ П 1 I А 2 В 2 I = I АВ I Горизонтально-проецирующая прямая Фронтально-проецирующая прямая X C 1 C 2 Ξ D 2 D 1 О Z Y CD ┴ П 2 I C 1 D 1 I = I CD I
Слайд 8: 2. Прямые уровня
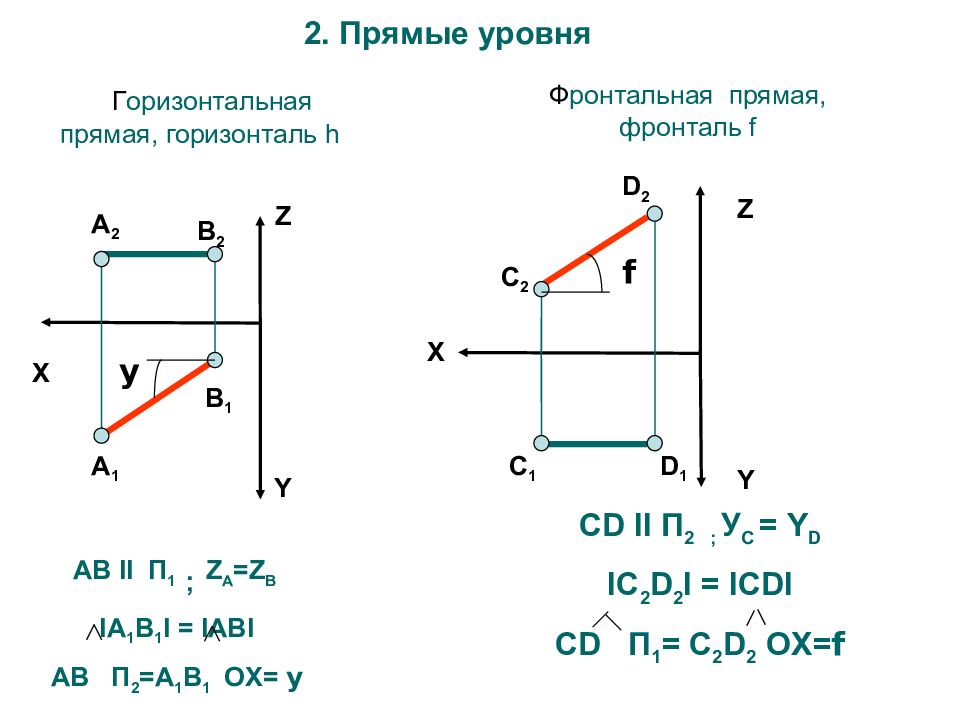
Г оризонтальная прямая, горизонталь h X Z Y А 2 А 1 В 2 В 1 A В II П 1 ; Z А = Z B I А 1 В 1 I = I АВ I АВ П 2 = А 1 В 1 OX= y y Ф ронтальная прямая, фронталь f X Z Y C 2 C 1 D 2 D 1 f CD II П 2 ; У С = Y D I С 2 D 2 I = ICDI CD П 1 = С 2 D 2 OX = f
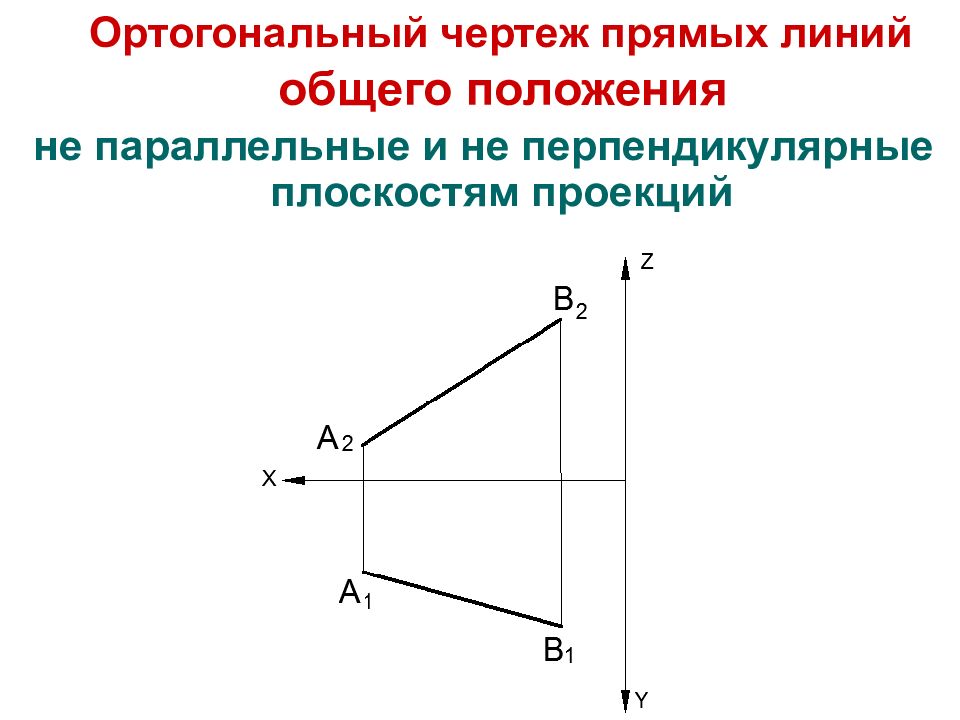
Слайд 9: Ортогональный чертеж прямых линий общего положения
не параллельные и не перпендикулярные плоскостям проекций
Слайд 10: ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ ПЛОСКОСТИ
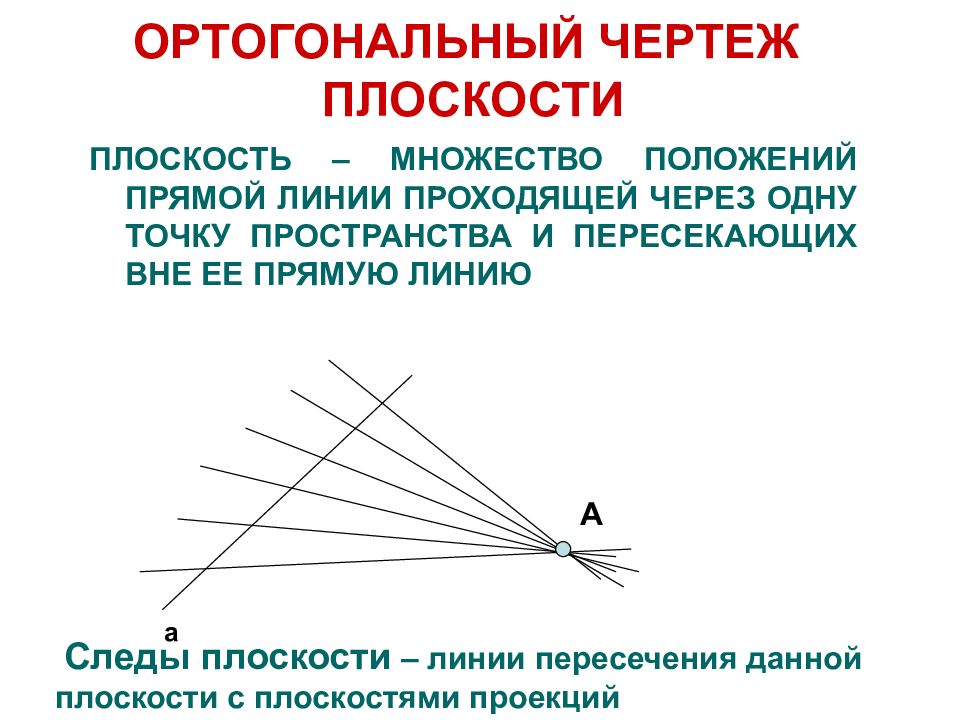
ПЛОСКОСТЬ – МНОЖЕСТВО ПОЛОЖЕНИЙ ПРЯМОЙ ЛИНИИ ПРОХОДЯЩЕЙ ЧЕРЕЗ ОДНУ ТОЧКУ ПРОСТРАНСТВА И ПЕРЕСЕКАЮЩИХ ВНЕ ЕЕ ПРЯМУЮ ЛИНИЮ A a Следы плоскости – линии пересечения данной плоскости с плоскостями проекций
Слайд 11: ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
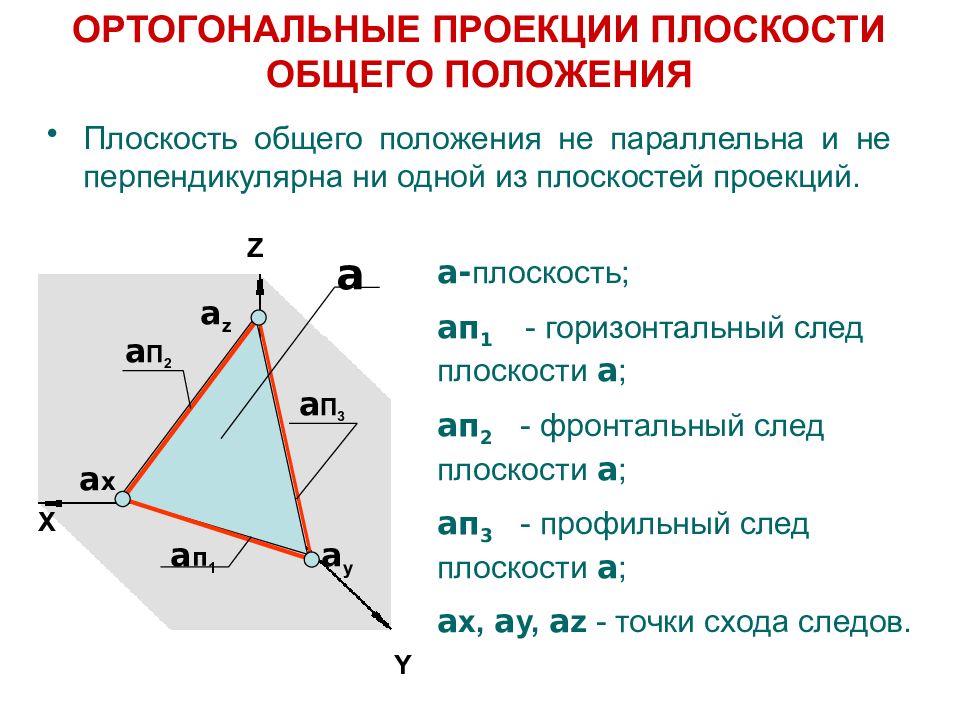
Y Z X a п 1 a П 3 a П 2 a x a y a z a a- плоскость ; a п 1 - горизонтальный след плоскости a ; a п 2 - фронтальный след плоскости a ; a п 3 - профильный след плоскости a ; a x, a y, a z - точки схода следов. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Слайд 12: Плоскости частного положения
ПЛОСКОСТИ УРОВНЯ плоскости параллельные плоскостям проекций – ПЛОСКОСТИ ПРОЕЦИРУЮЩИЕ плоскости перпендикулярные плоскостям проекций – Плоскости частного положения
Слайд 13
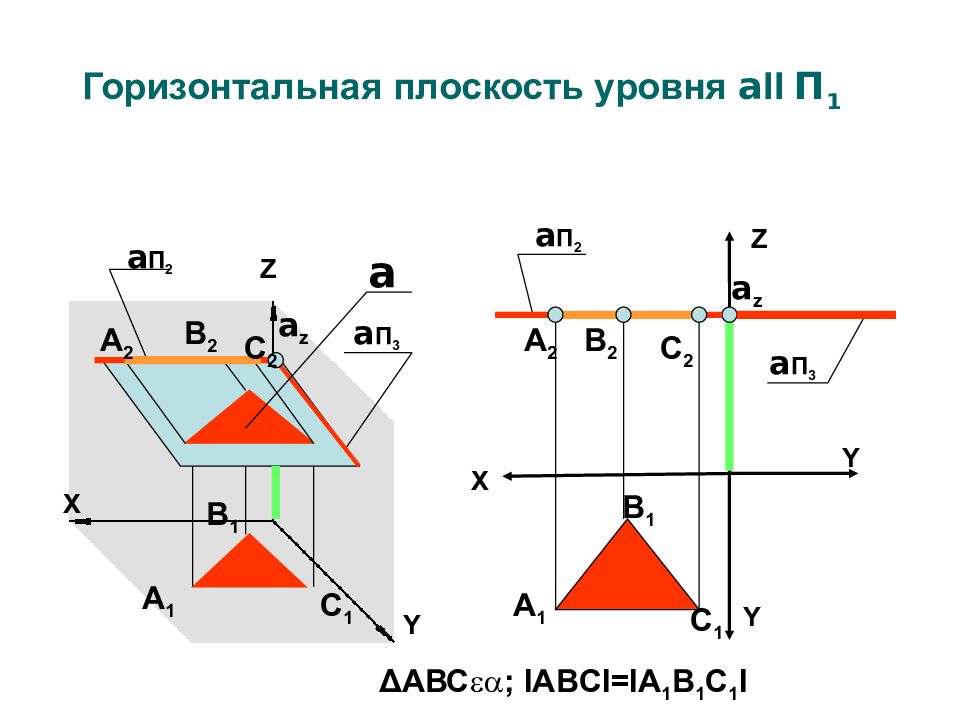
Горизонтальная плоскость уровня a II П 1 Z X Y Y a П 2 a П 3 a z Y Z X a П 3 a П 2 a z a А 1 В 1 С 1 А 2 В 2 С 2 А 1 С 1 В 1 А 2 В 2 С 2 Δ АВС ; IABCI=IA 1 B 1 C 1 I
Слайд 14
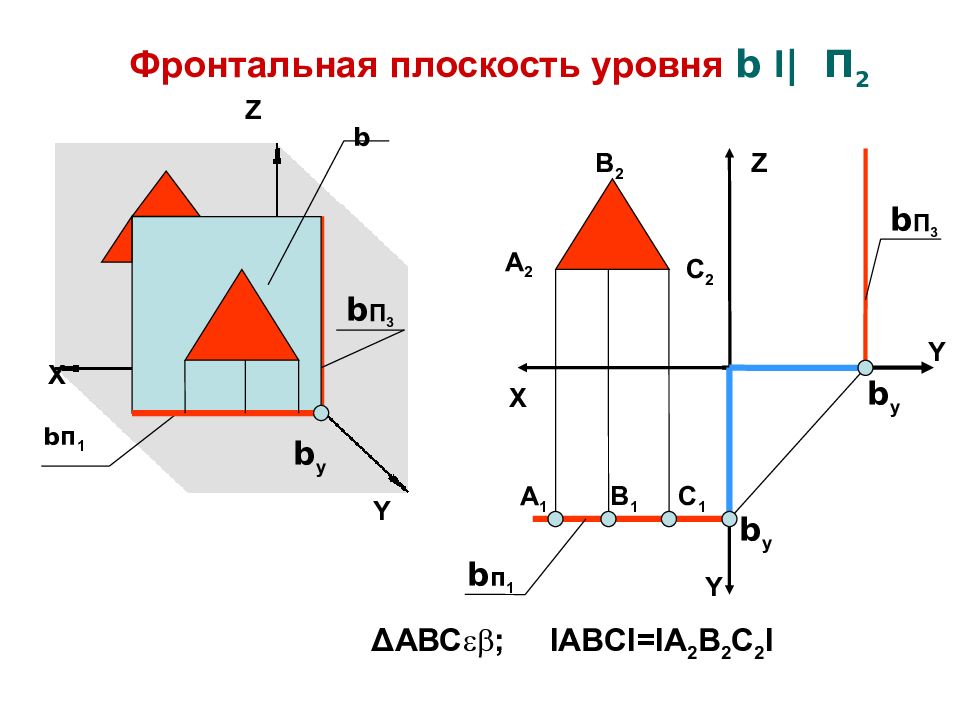
Z X Y Y b п 1 b П 3 b y Y Z X b п 1 b П 3 b y b y Фронтальная плоскость уровня b I | П 2 А 1 В 1 С 1 С 2 В 2 А 2 b Δ АВС ; IABCI=IA 2 B 2 C 2 I
Слайд 15
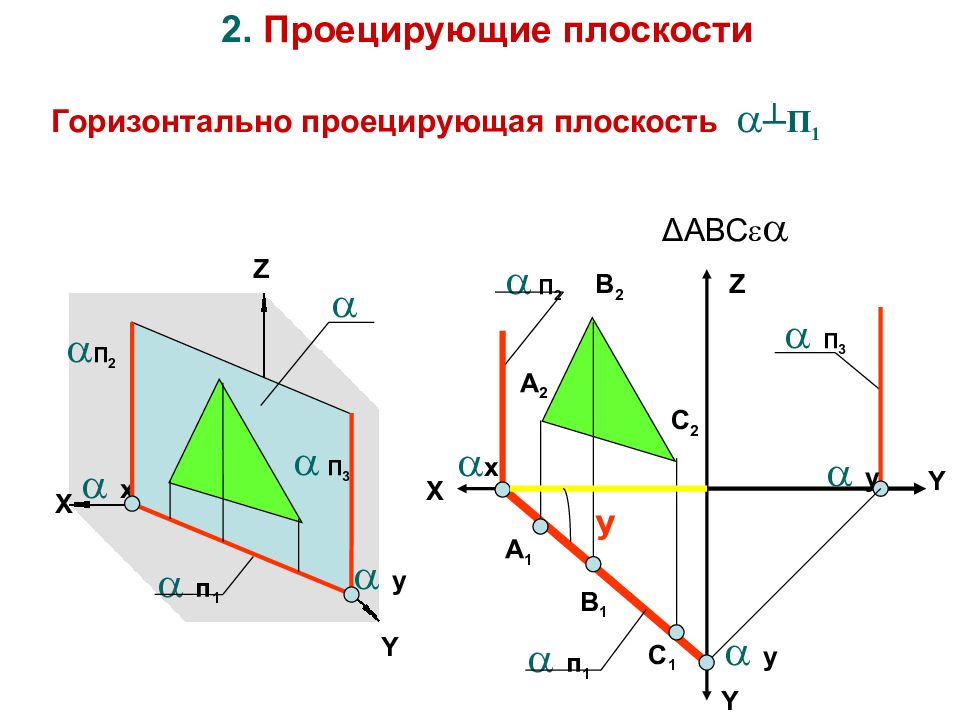
2. Проецирующие плоскости Горизонтально проецирующая плоскость ┴ П 1 X Y Y П 2 П 3 Z X п 1 П 2 x x Z п 1 П 3 Y y y y y А 1 В 1 С 1 А 2 В 2 С 2 Δ АВС
Слайд 16
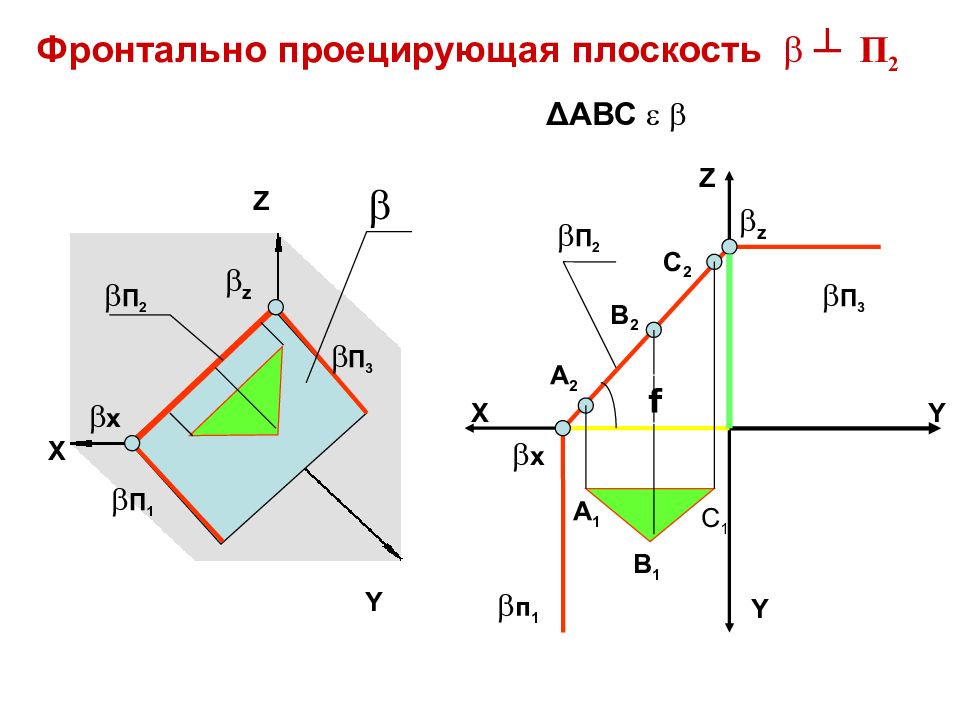
Фронтально проецирующая плоскость ┴ П 2 Z X Y Y П 2 п 1 x Y Z X П 2 z П 3 П 1 П 3 z x А 2 В 2 С 2 А 1 В 1 С 1 f Δ АВС
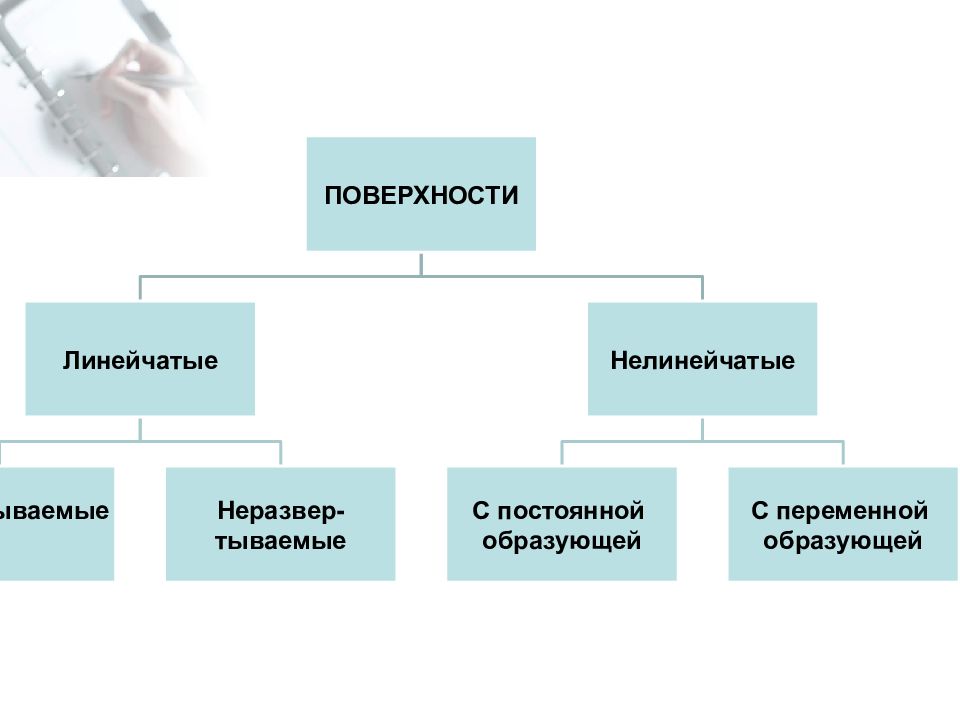
Слайд 18: ПОВЕРХНОСТИ
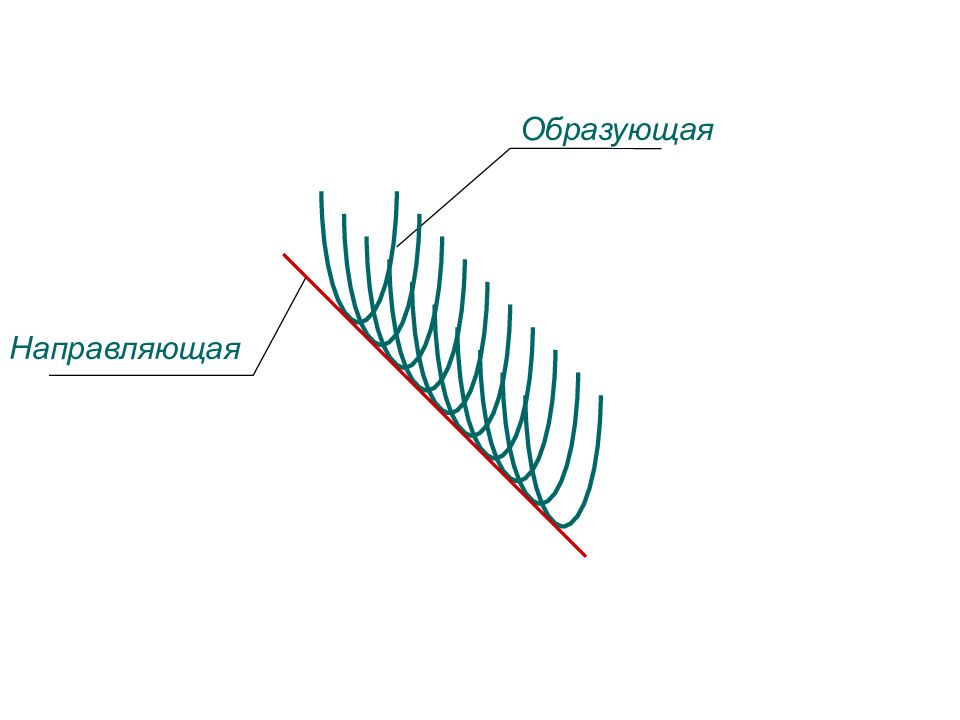
ПОВЕРХНОСТЬ МНОЖЕСТВО ПОЛОЖЕНИЙ ЛИНИИ ПЕРЕМЕЩАЮЩЕЙСЯ В ПРОСТРАНСТВЕ ПО ОПРЕДЕЛЕННОМУ ЗАКОНУ ЛИНИЯ ПЕРЕМЕЩАЮЩАЯСЯ В ПРОСТРАНСТВЕ - ОБРАЗУЮЩАЯ ЛИНИЯ ПО КОТОРОЙ ПРОИСХОДИТ ПЕРЕМЕЩЕНИЕ - НАПРАВЛЯЮЩАЯ
Слайд 20: ОЧЕРК ПОВЕРХНОСТИ
Очерк поверхности при ортогональном проецировании – это границы проекций поверхности или следы проецирующей поверхности, огибающей заданную поверхность, на плоскостях проекций Графический способ задания поверхности
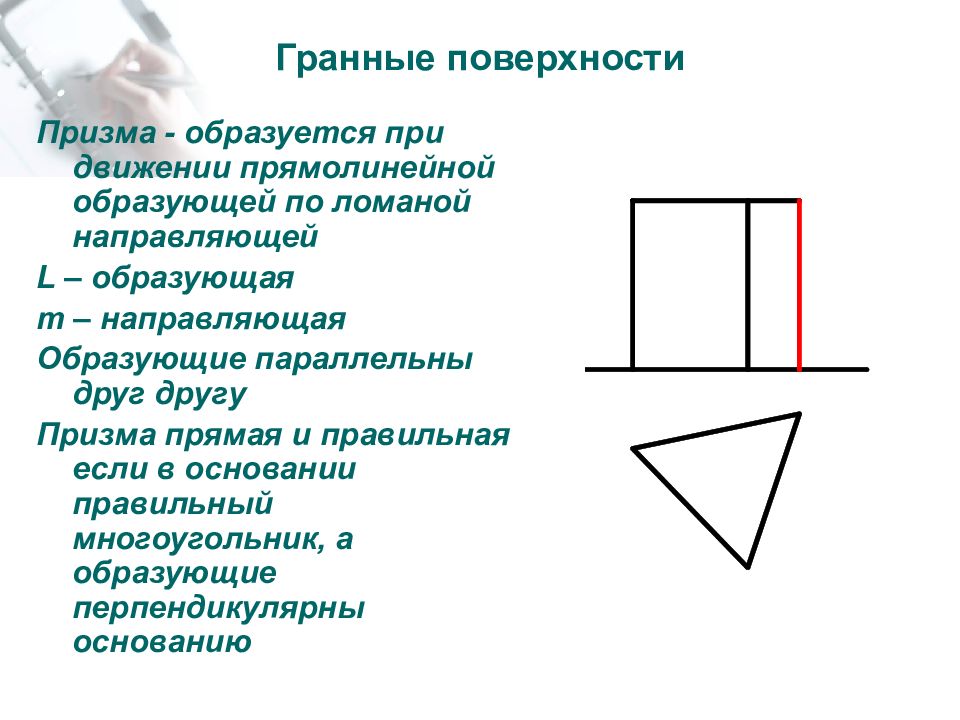
Слайд 24: Гранные поверхности
Призма - образуется при движении прямолинейной образующей по ломаной направляющей L – образующая m – направляющая Образующие параллельны друг другу Призма прямая и правильная если в основании правильный многоугольник, а образующие перпендикулярны основанию L 2 m 1
Слайд 25
Пирамида – образуется при движении прямолинейной образующей по ломаной направляющей. Все образую щие имеют общую точку – вершину пирамиды L – образующая m - направляющая Пирамида прямая и правильная, если в основании правильный многоугольник, а высота перпендикулярна основанию L 2 m 1 m 2 L 1
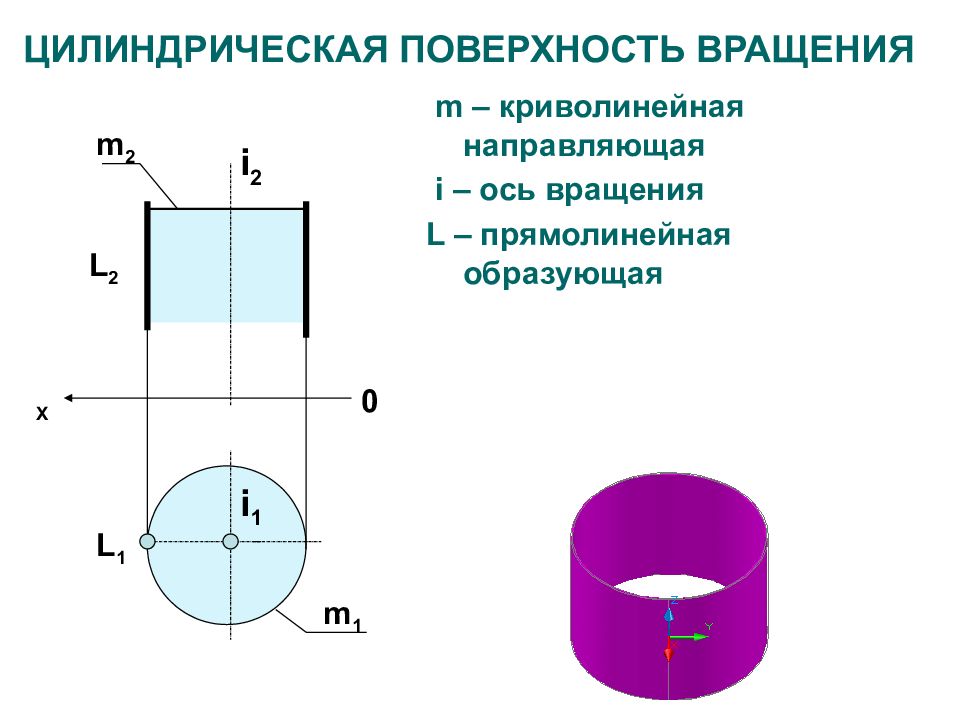
Слайд 26: ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ
L 2 i 2 i 1 L 1 m – криволинейная направляющая i – ось вращения L – прямолинейная образующая m 1 m 2 X 0
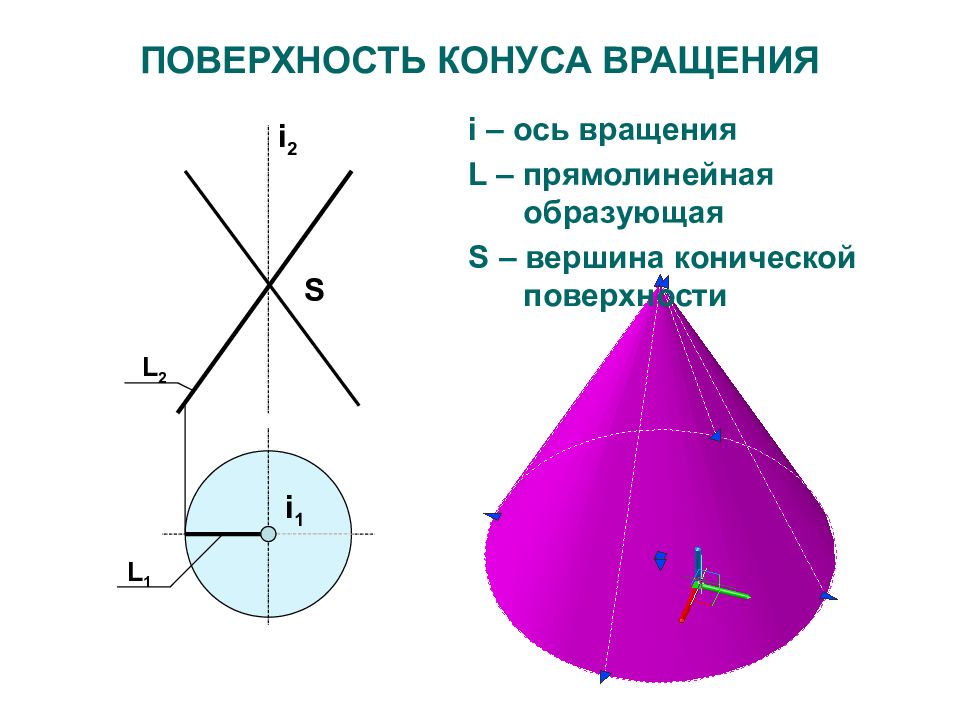
Слайд 27: ПОВЕРХНОСТЬ КОНУСА ВРАЩЕНИЯ
i – ось вращения L – прямолинейная образующая S – вершина конической поверхности L 2 L 1 i 2 i 1 S
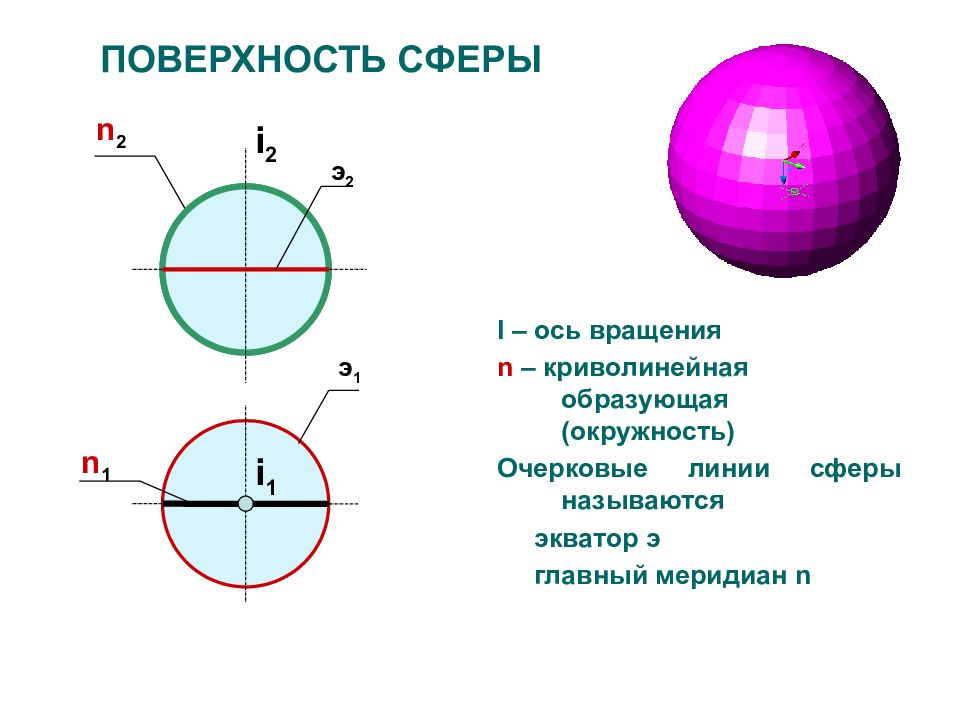
Слайд 28: ПОВЕРХНОСТЬ C ФЕРЫ
I – ось вращения n – криволинейная образующая (окружность) Очерковые линии сферы называются экватор э главный меридиан n n 2 n 1 i 2 i 1 э 2 э 1
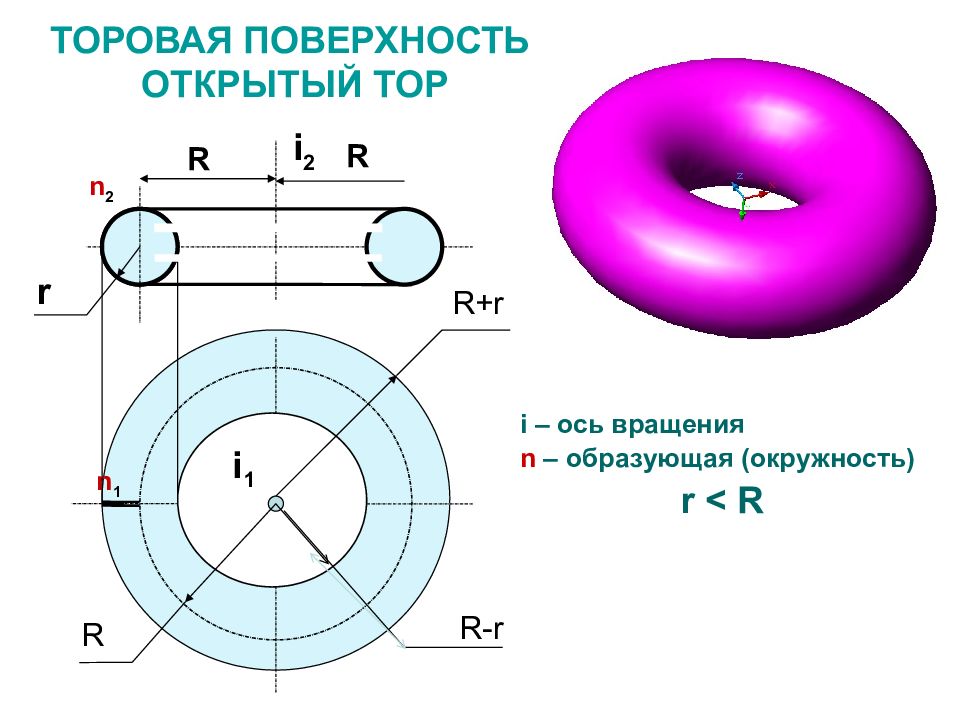
Слайд 29: ТОРОВАЯ ПОВЕРХНОСТЬ ОТКРЫТЫЙ ТОР
i – ось вращения n – образующая (окружность) r < R i 2 n 2 n 1 r R R-r R+r R I 1 i 1 R
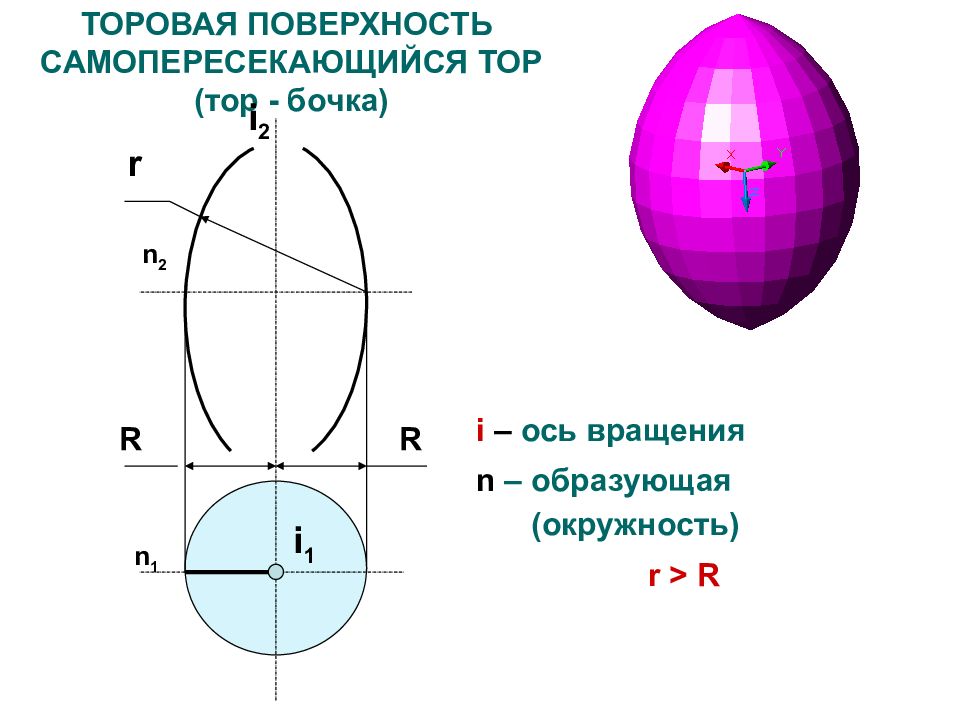
Слайд 30: ТОРОВАЯ ПОВЕРХНОСТЬ САМОПЕРЕСЕКАЮЩИЙСЯ ТОР (тор - бочка)
i – ось вращения n – образующая (окружность) r > R R r i 2 n 2 n 1 i 1 R
Слайд 31: СЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
- это линия пересечения поверхности и плоскости или совокупность точек одновременно принадлежащих поверхности и плоскости
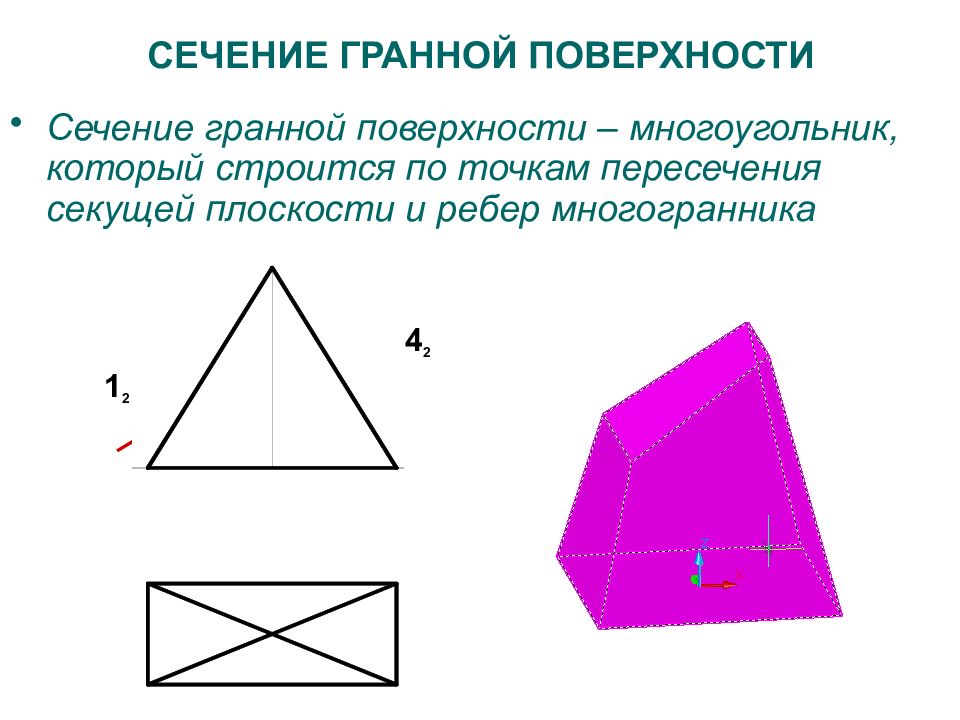
Слайд 32: СЕЧЕНИЕ ГРАННОЙ ПОВЕРХНОСТИ
Сечение гранной поверхности – многоугольник, который строится по точкам пересечения секущей плоскости и ребер многогранника 1 2 Ξ 2 2 3 2 Ξ 4 2 1 1 2 1 4 1 3 1
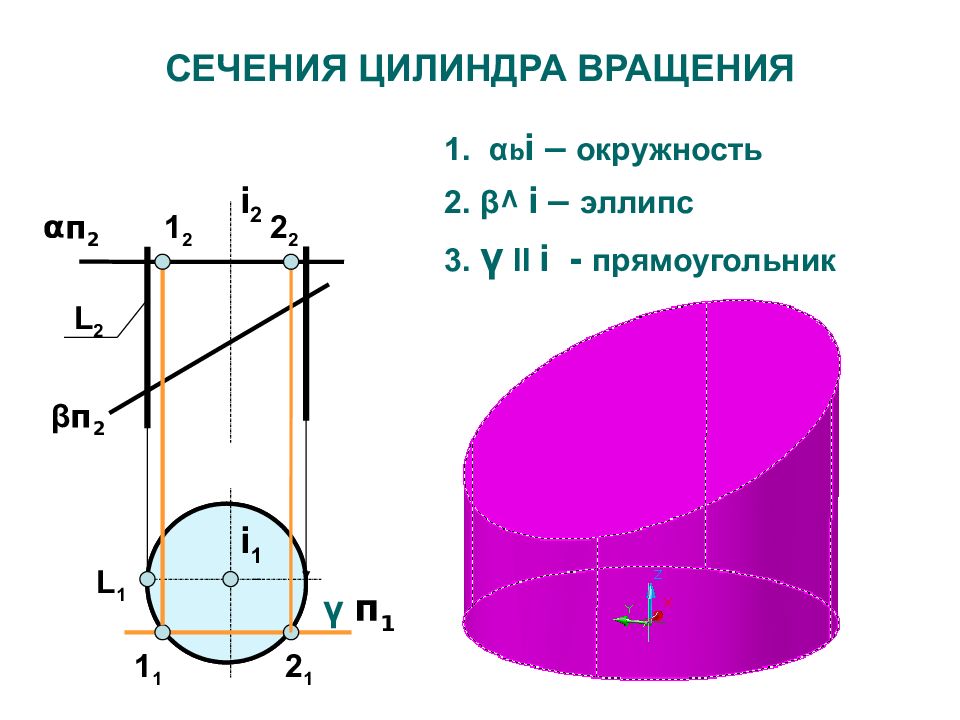
Слайд 33: СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
1. α b i – окружность 2. β ^ i – эллипс 3. γ ll i - прямоугольник L 2 i 2 i 1 L 1 α п 2 β п 2 γ п 1 1 1 2 1 1 2 2 2
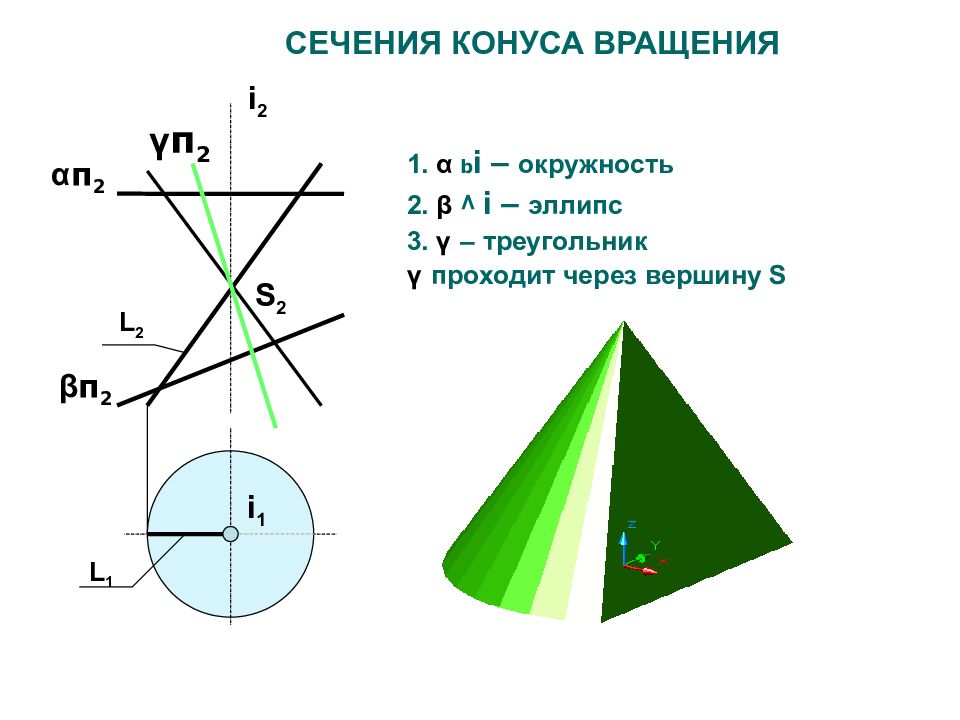
Слайд 34: СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ
1. α b i – окружность 2. β ^ i – эллипс 3. γ – треугольник γ проходит через вершину S L 2 L 1 i 2 i 1 S 2 α п 2 β п 2 γ п 2
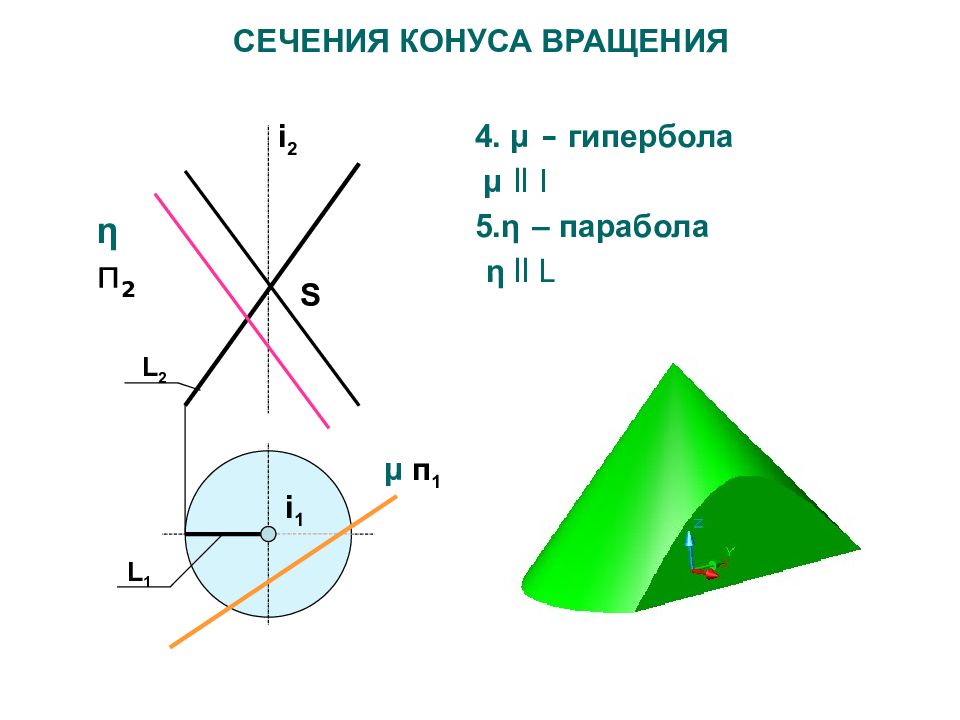
Слайд 35: СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ
4. μ – гипербола μ ll I 5. η – парабола η ll L L 2 L 1 i 2 i 1 S СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ μ п 1 η п 2
Слайд 36: СЕЧЕНИЯ СФЕРЫ
Сечение сферы плоскостью – окружность, которая может проецироваться как : прямая линия окружность эллипс
Слайд 48
Линия пересечения поверхностей - совокупность точек одновременно принадлежащих двум пересекающимся поверхностям Характер линии пересечения зависит от вида поверхностей Линия пересечения многогранников ломаная линия
Слайд 49
Линия пересечения многогранника и поверхности вращения - сочетание плоских кривых линий (парабола, гипербола, эллипс и т.д.) Линия пересечение двух поверхностей второго порядка - пространственная кривая линия
Слайд 50
Алгоритм решения задач 1. Анализ заданных поверхностей - Определить заданные поверхности Определить наличие проецирующей поверхности (цилиндр и призма) На плоскости проекций, к которой проецирующая поверхность перпендикулярна, проекция линии пересечения совпадает с очерком проецирующей поверхности
Слайд 51
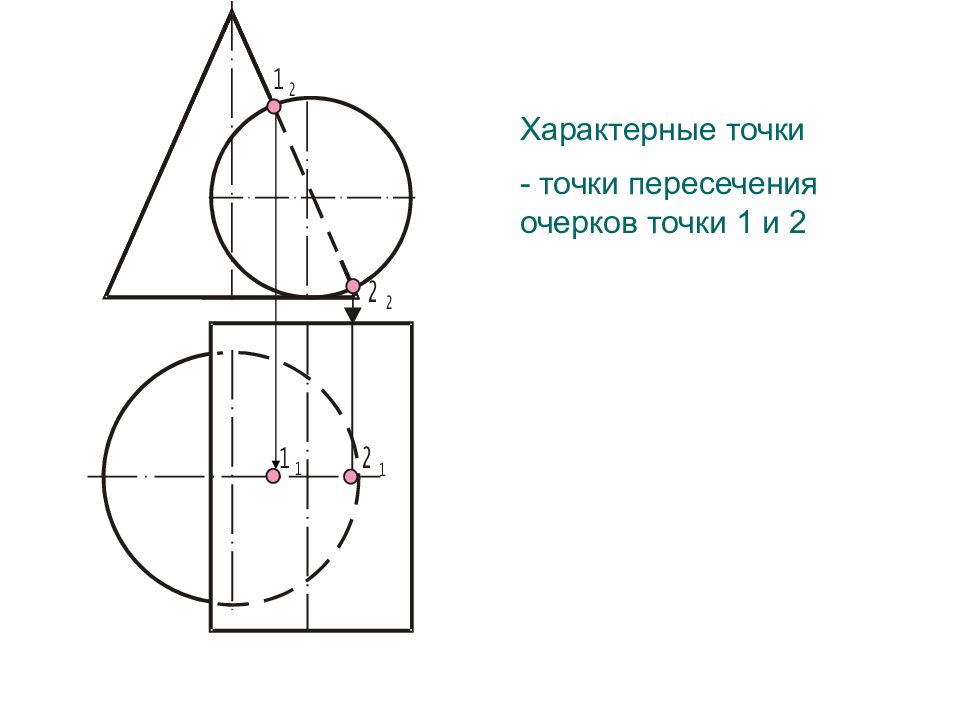
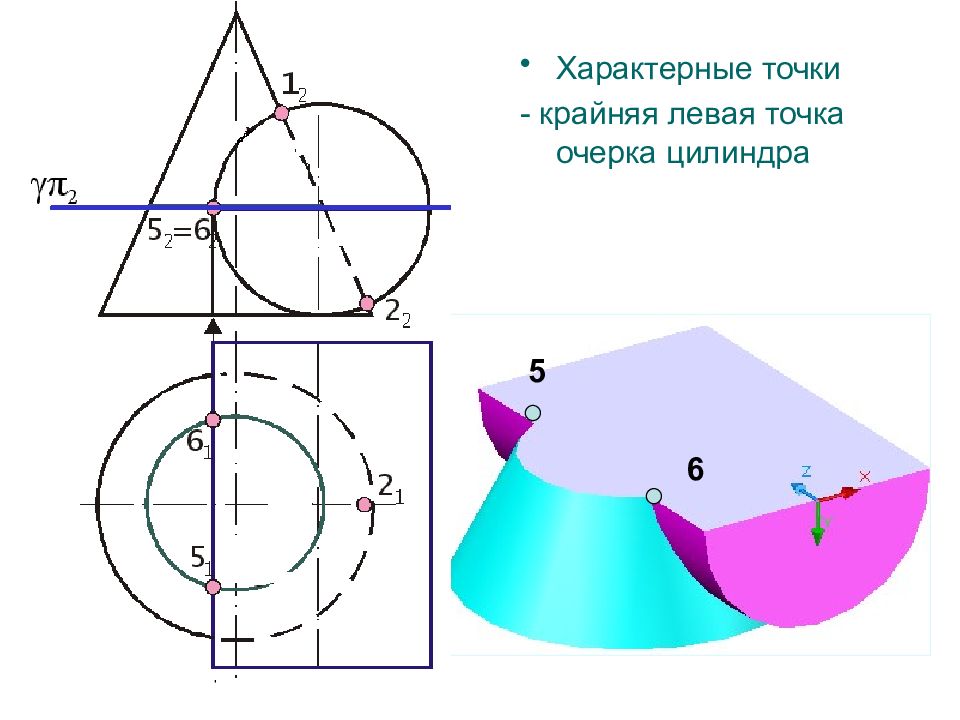
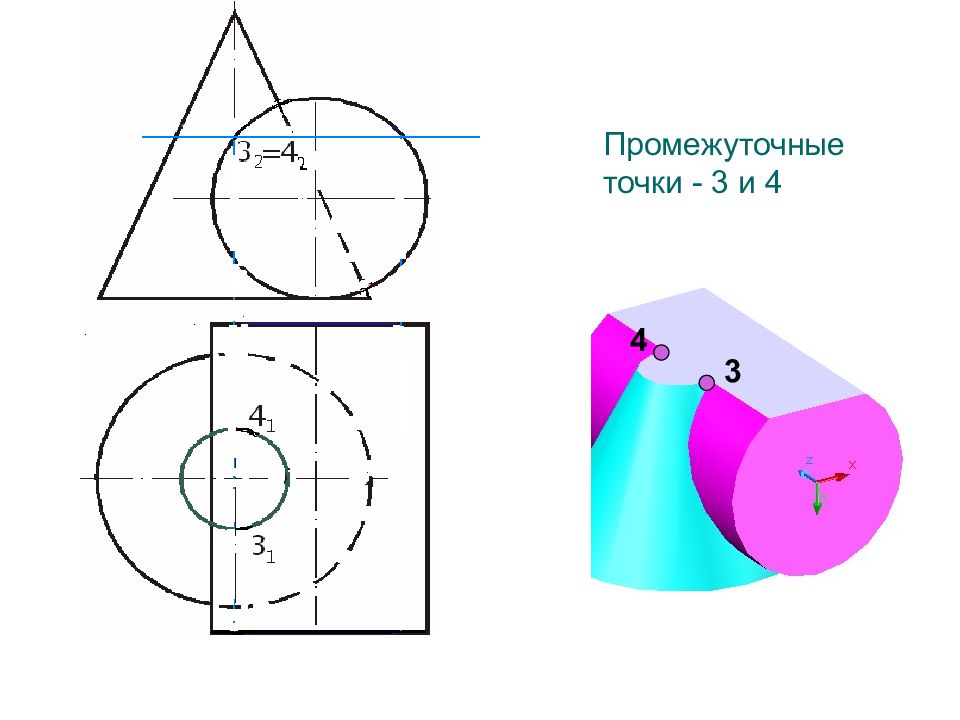
2. Определить характерные точки линии пересечения точки пересечения очерков поверхностей высшие и низшие, правые и левые точки поверхностей наиболее удаленные и приближенные к плоскостям проекций точки точки принадлежащие очерковым линиям поверхностей ВЫБОР СПОСОБА РЕШЕНИЯ ЗАДАЧИ : - вспомогательные секущие плоскости вспомогательные секущие концентрические сферы
Слайд 52: Способ вспомогательных секущих плоскостей
1. Провести вспомогательную секущую плоскость частного положения. В сечении поверхностей должны получаться простые геометрические фигуры – окружности, треугольники, прямоугольники. 2. Построить сечения заданных поверхностей вспомогательной секущей плоскостью. 3. Определить точки пересечения построенных сечений. Это искомые точки линии пересечения поверхностей. Повторение пунктов 1, 2, 3 – n раз
Слайд 53
4. Соединить линией, полученные точки пересечения. 5. Определить видимость линии пересечения и очерковых линий заданных поверхностей.
Слайд 54
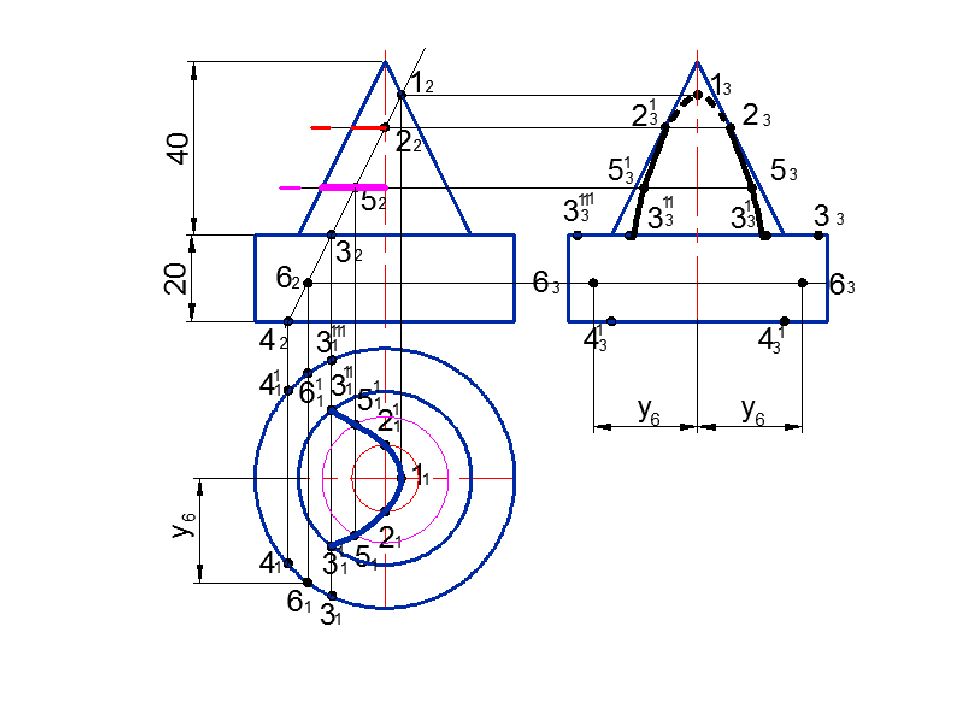
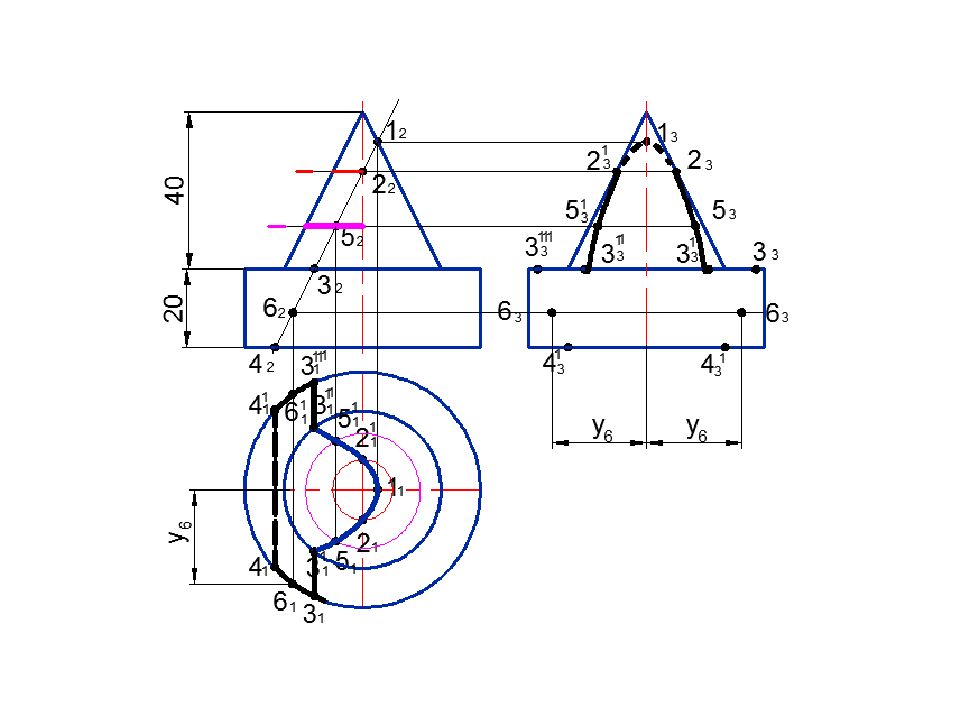
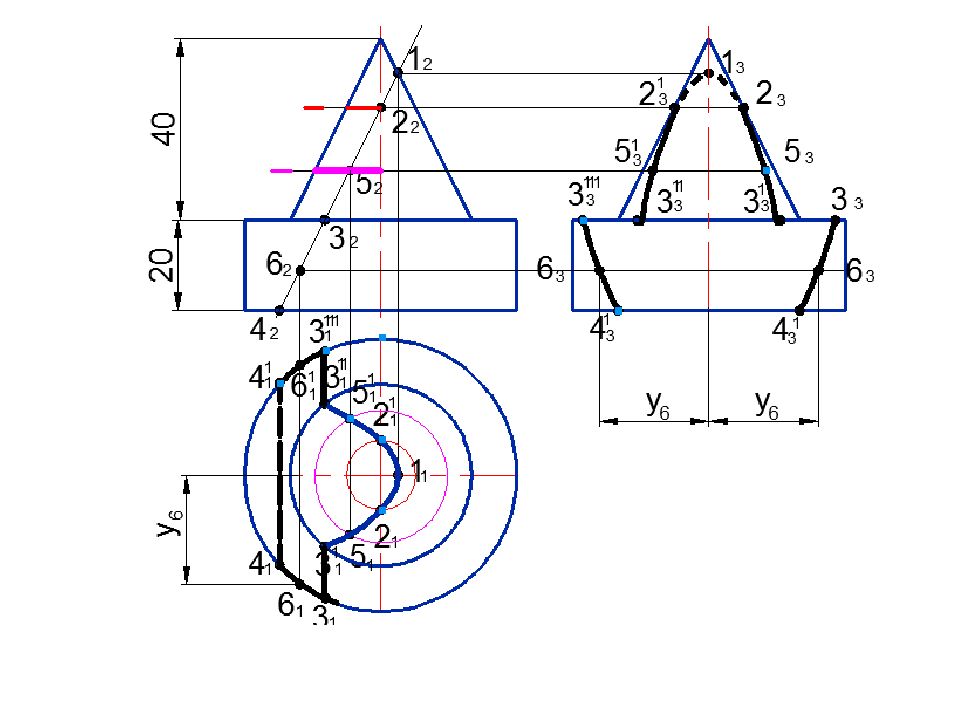
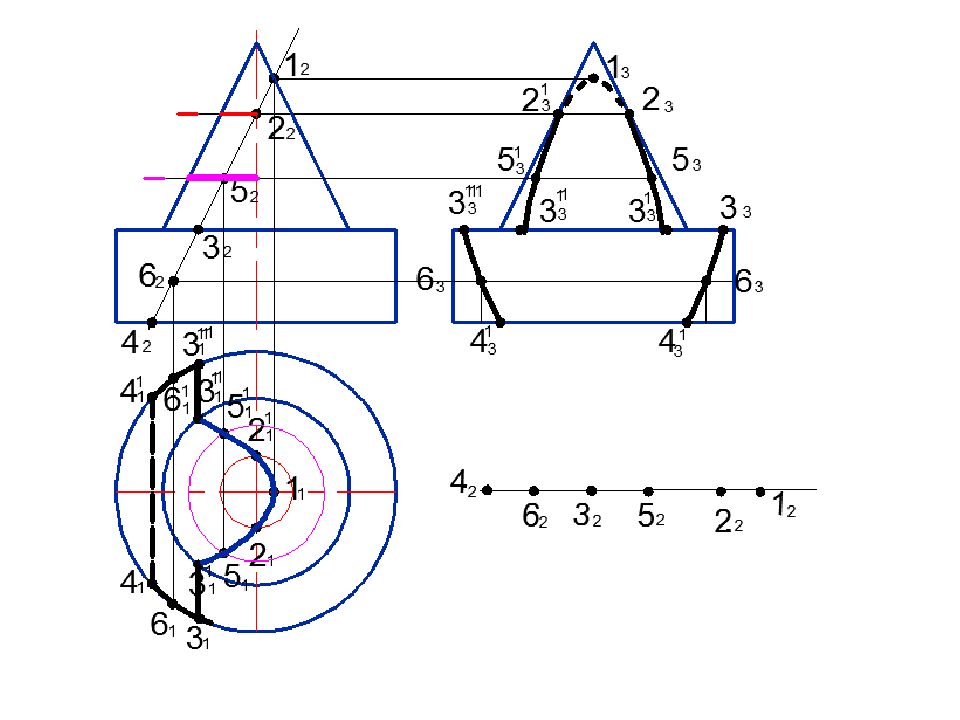
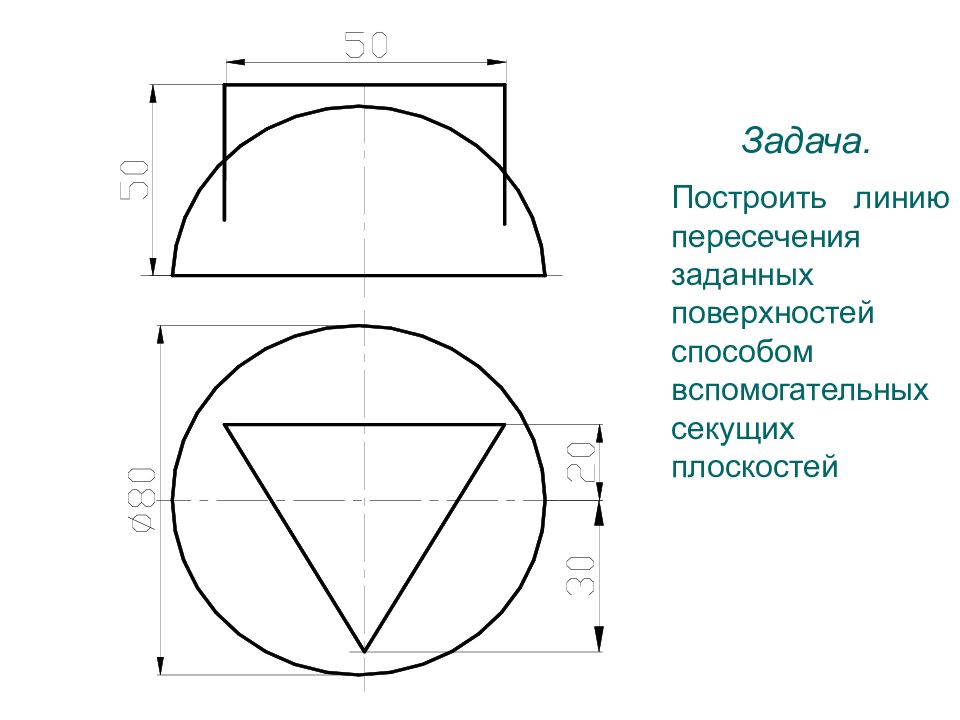
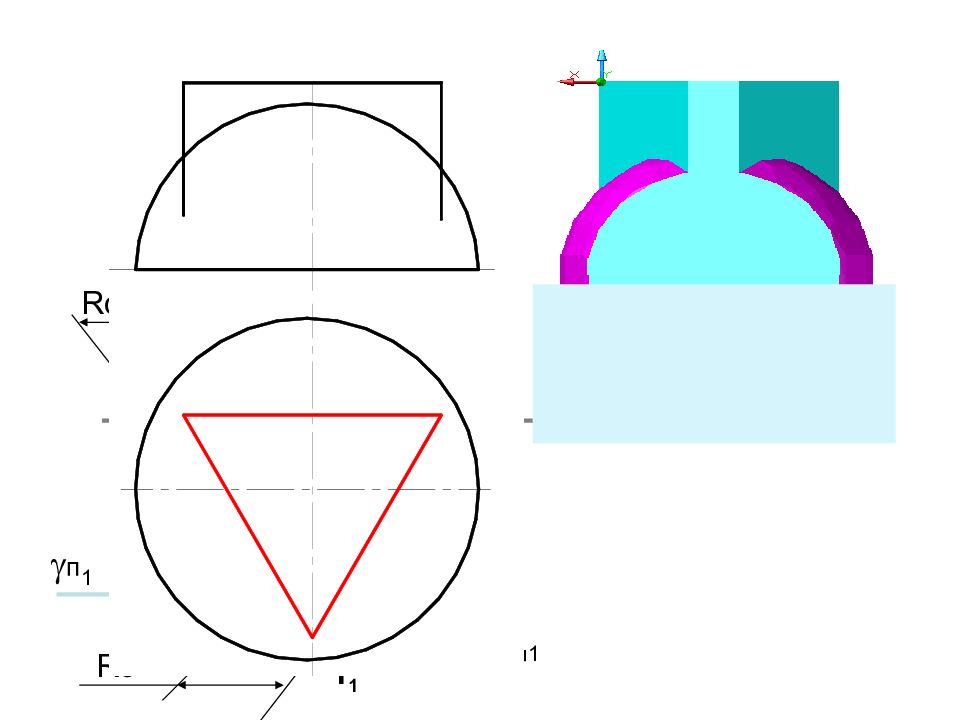
Задача. Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей
Слайд 56
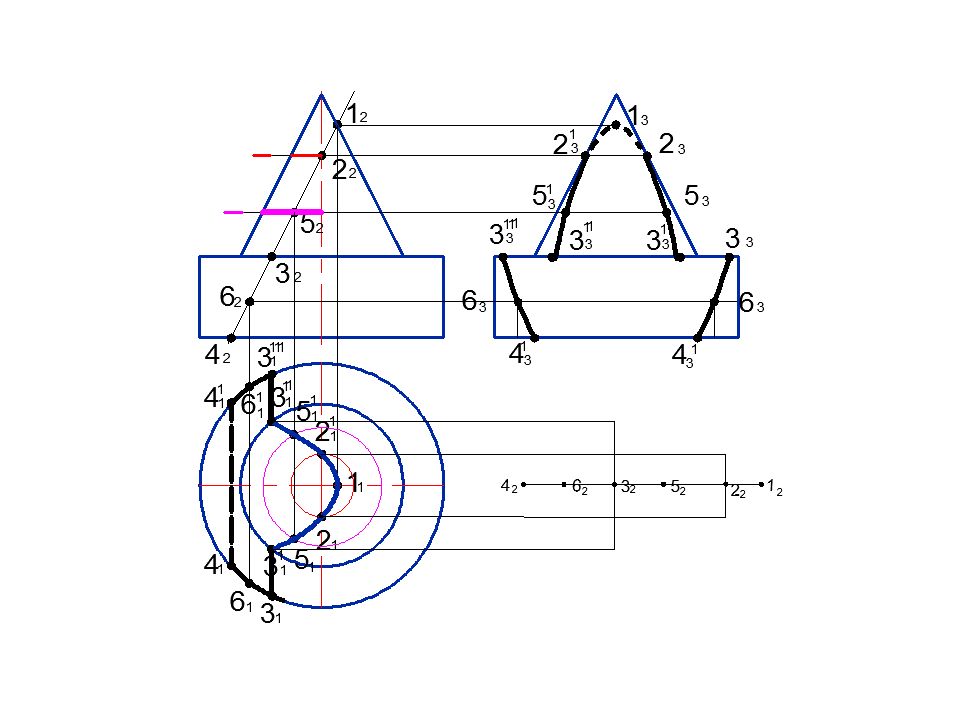
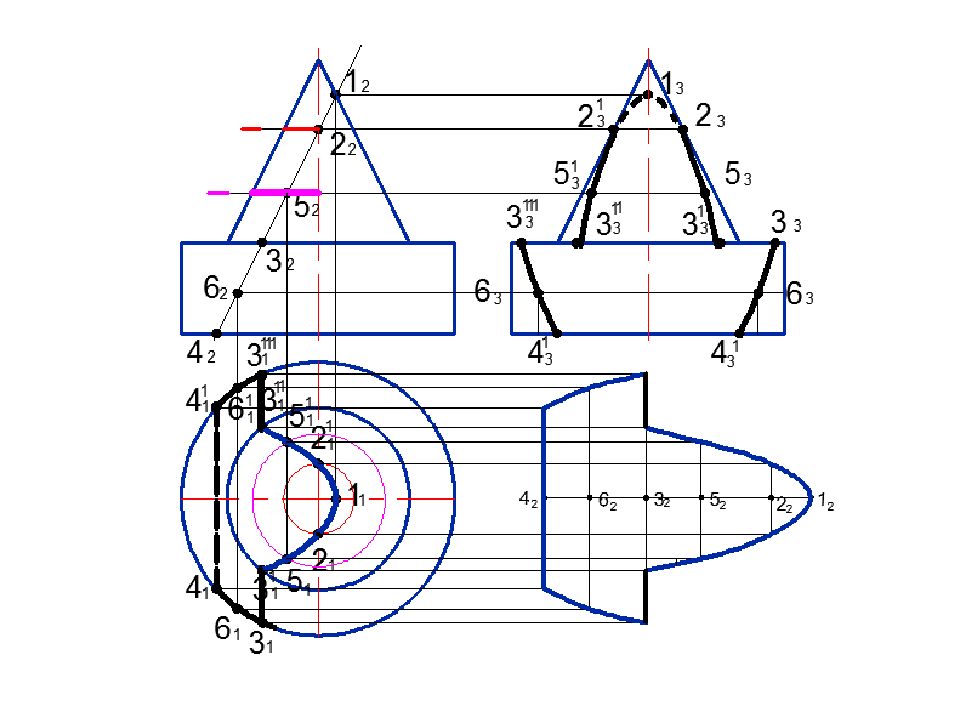
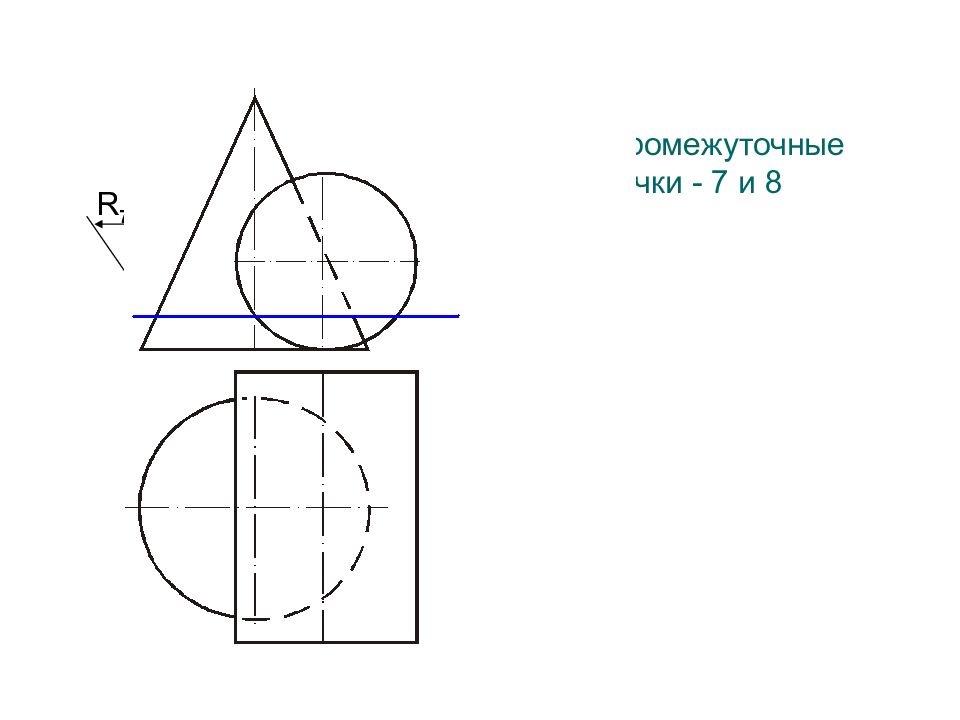
п1 Rc 4 1 5 2 4 2 5 1 3 2 2 2 3 1 2 1 b п1 Rc 1 1 1 2 п 1 7 1 6 1 7 2 6 2 0 1 0 2
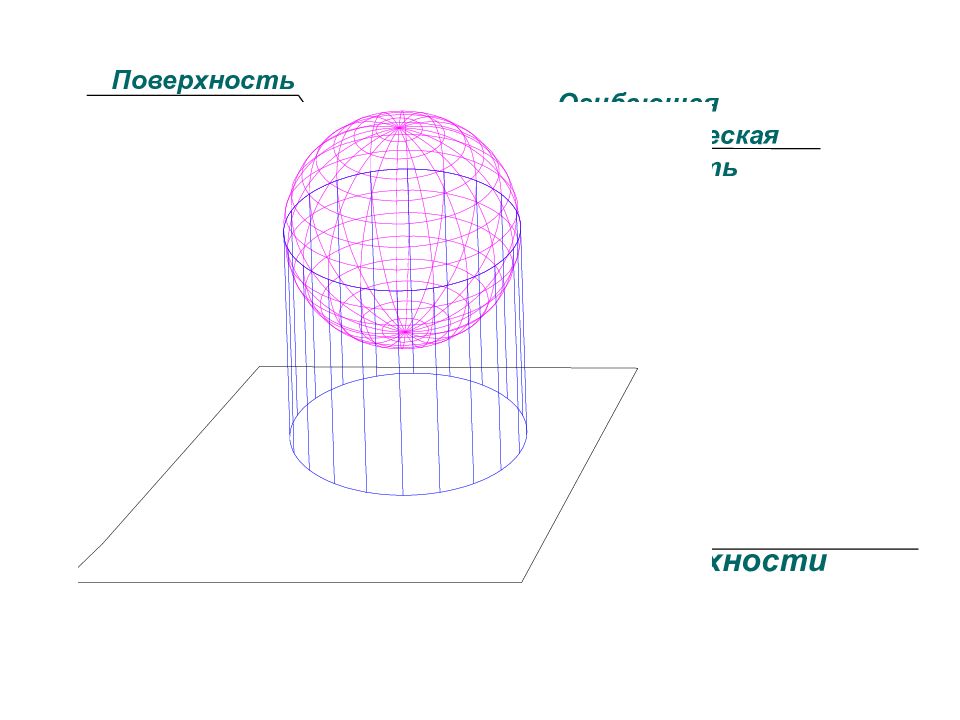
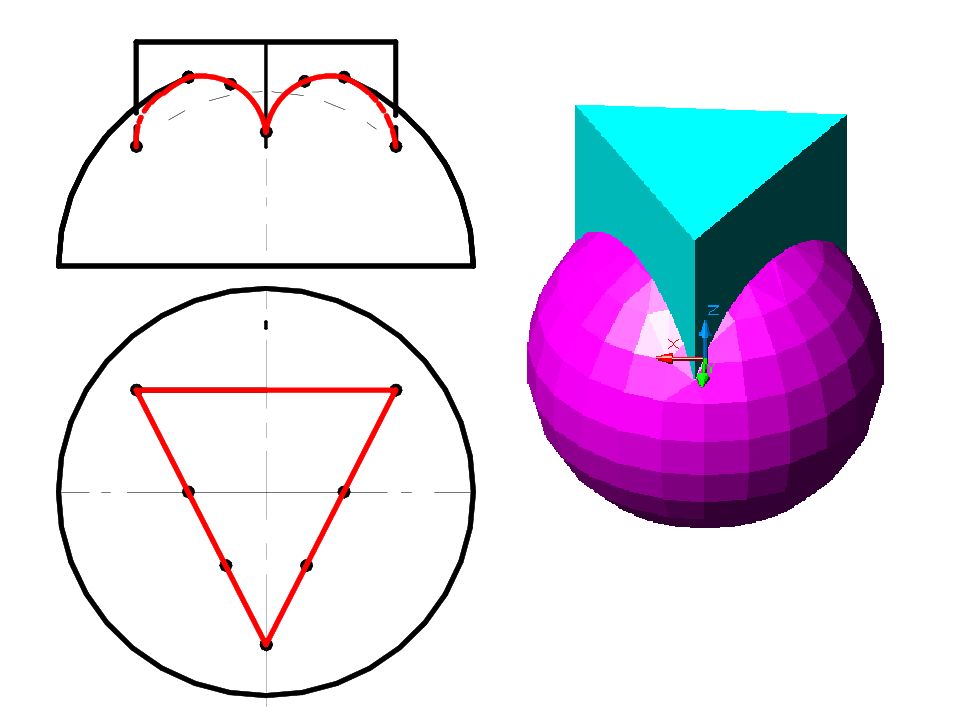
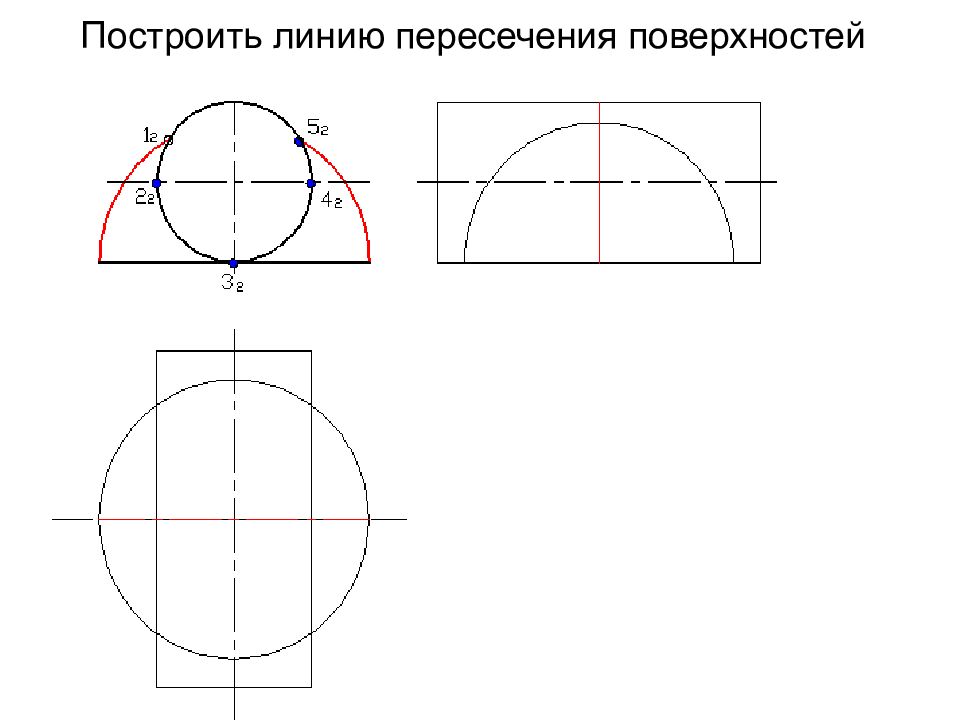
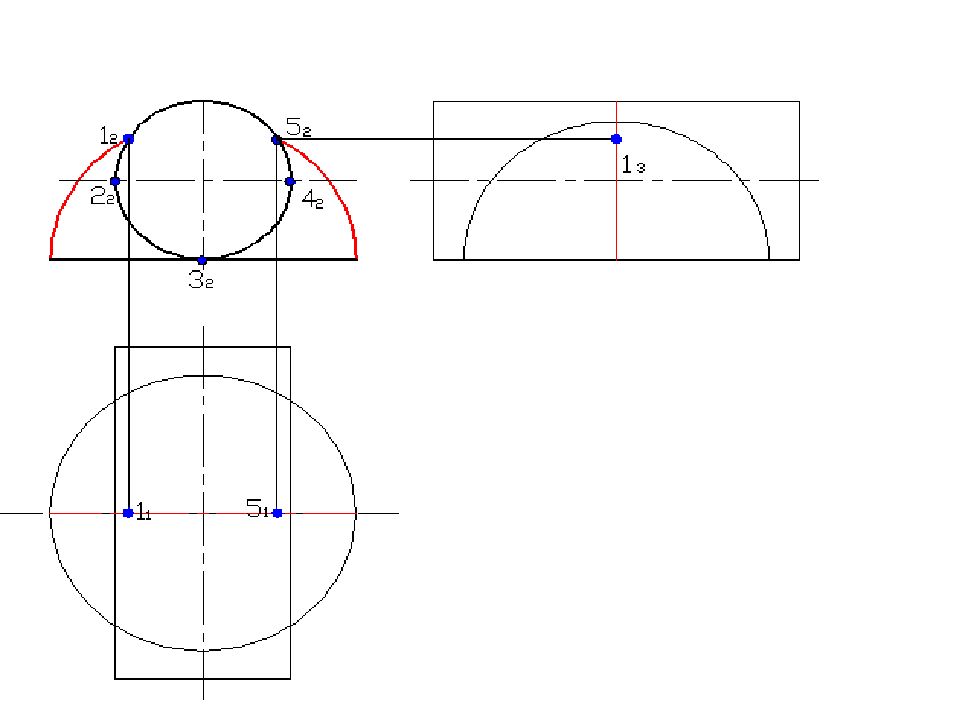
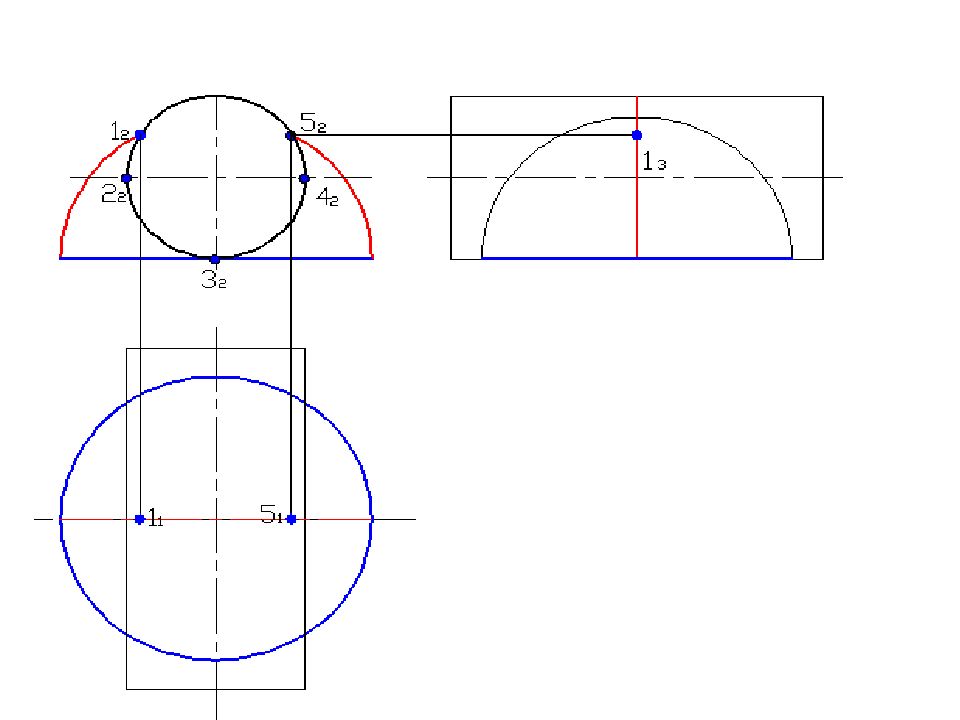
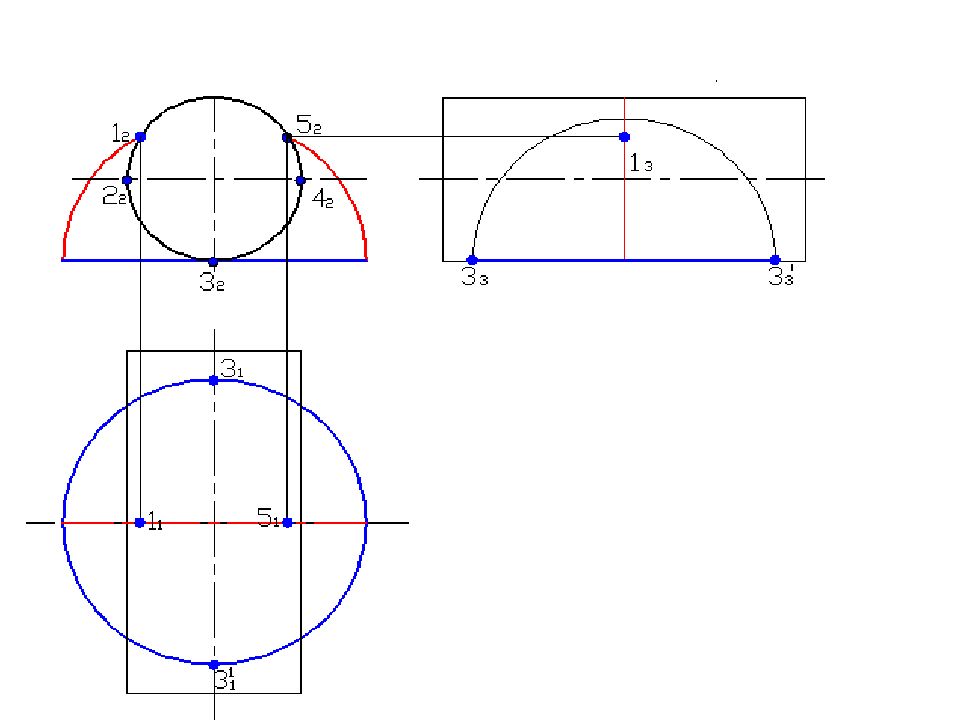
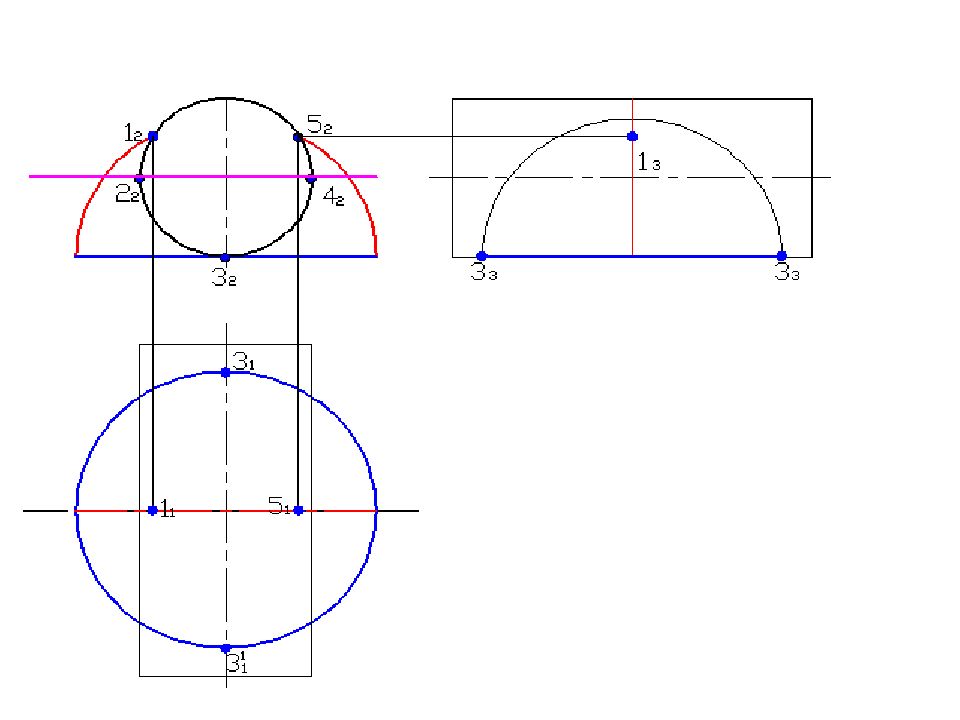
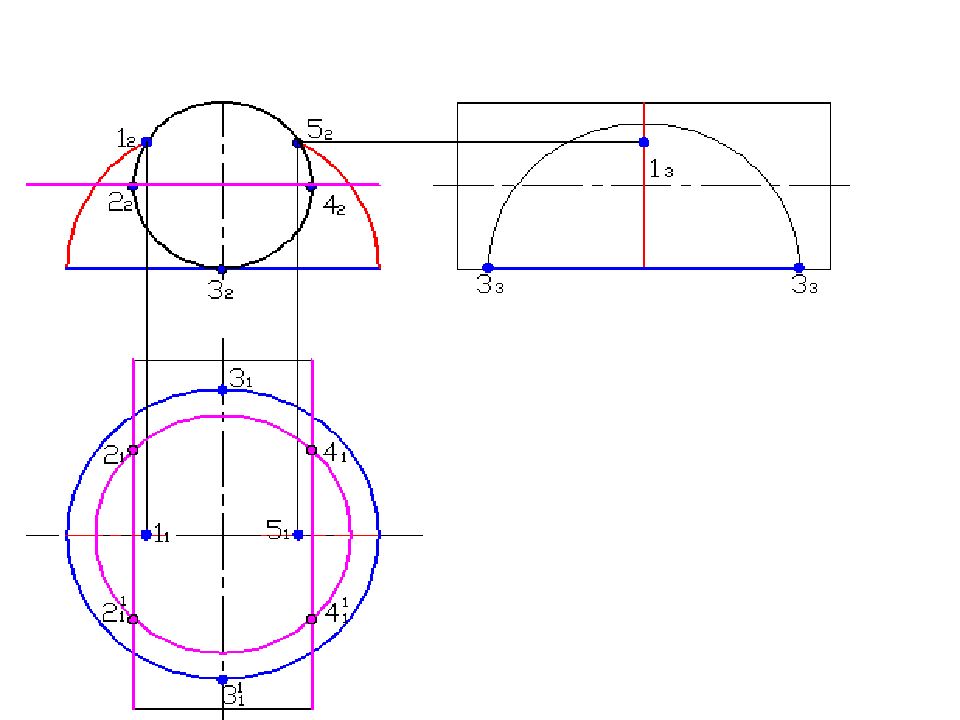
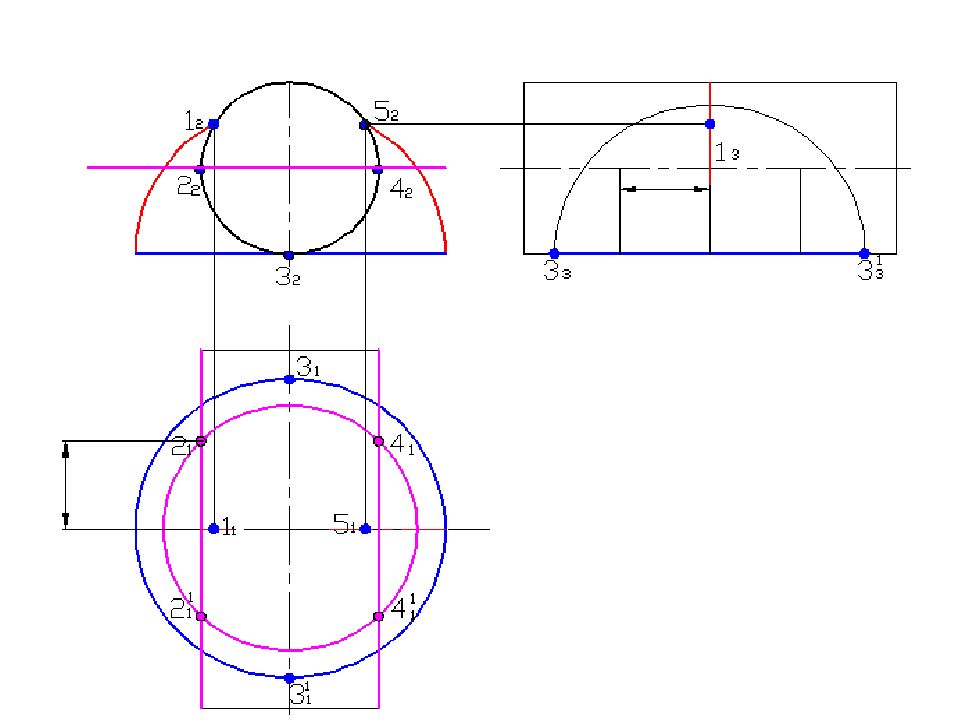
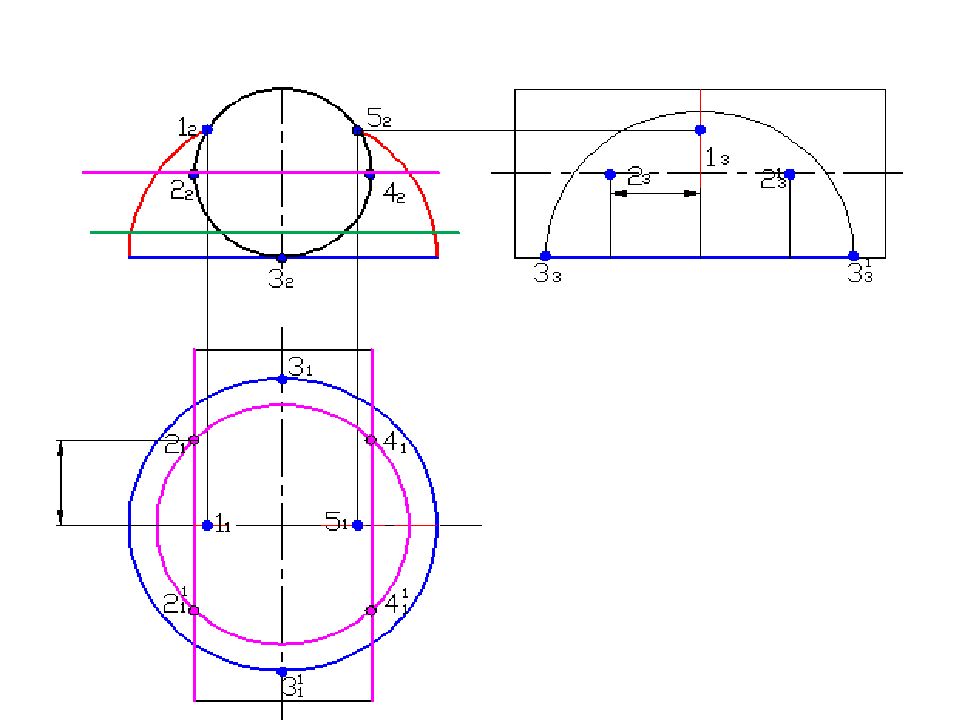
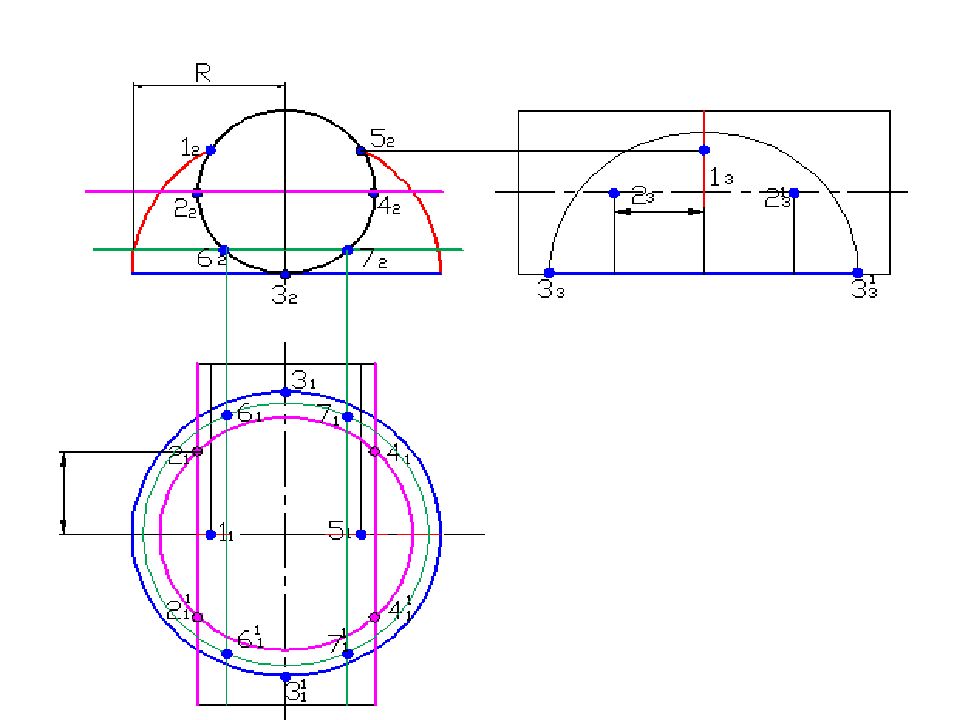
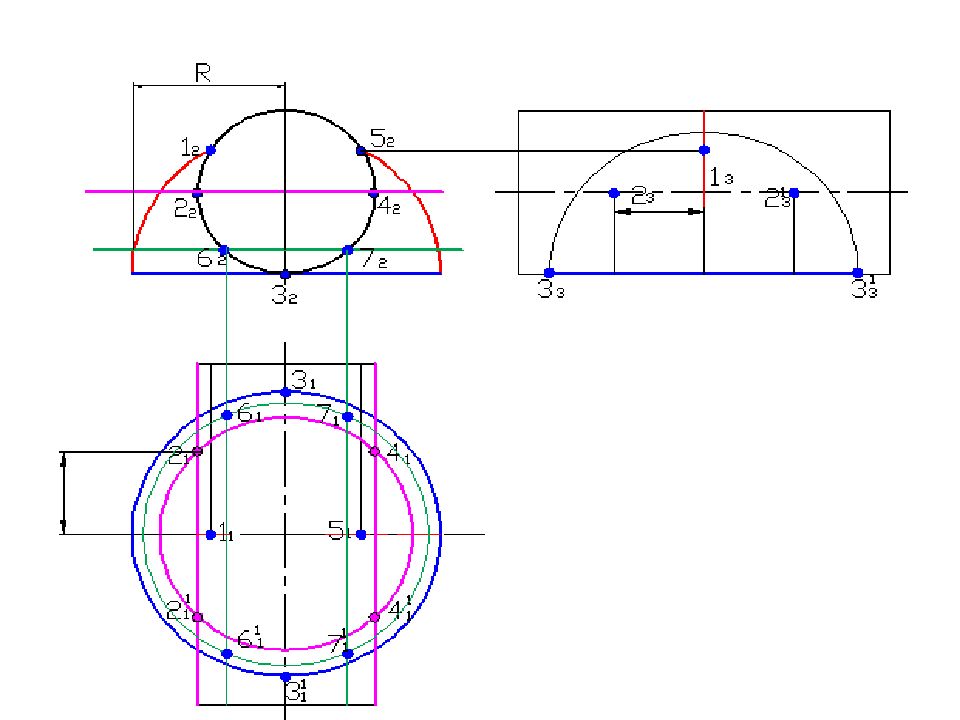
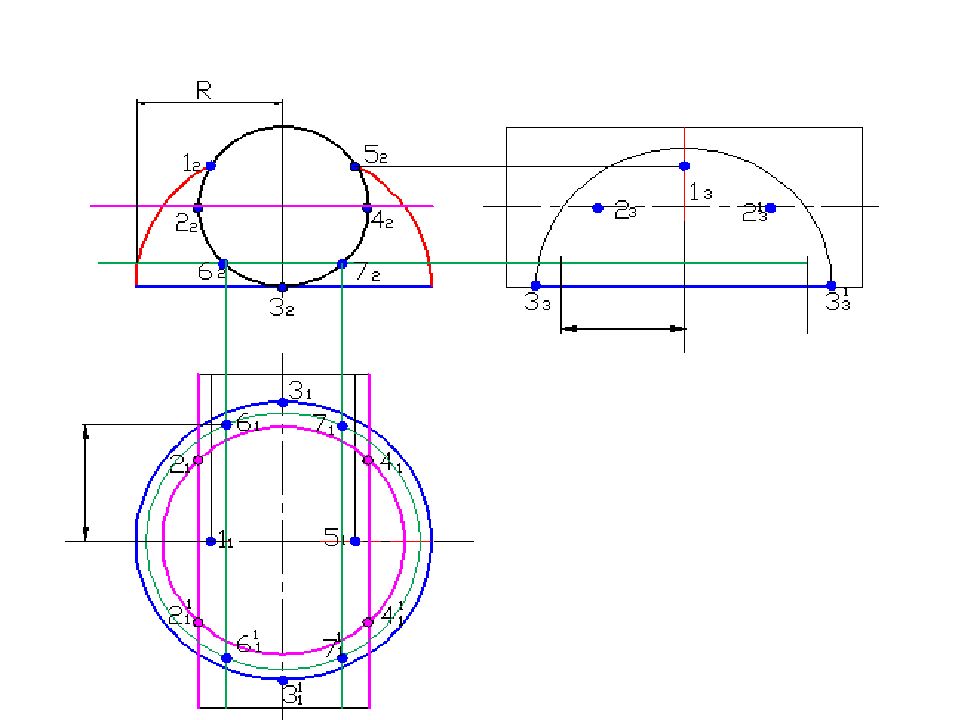
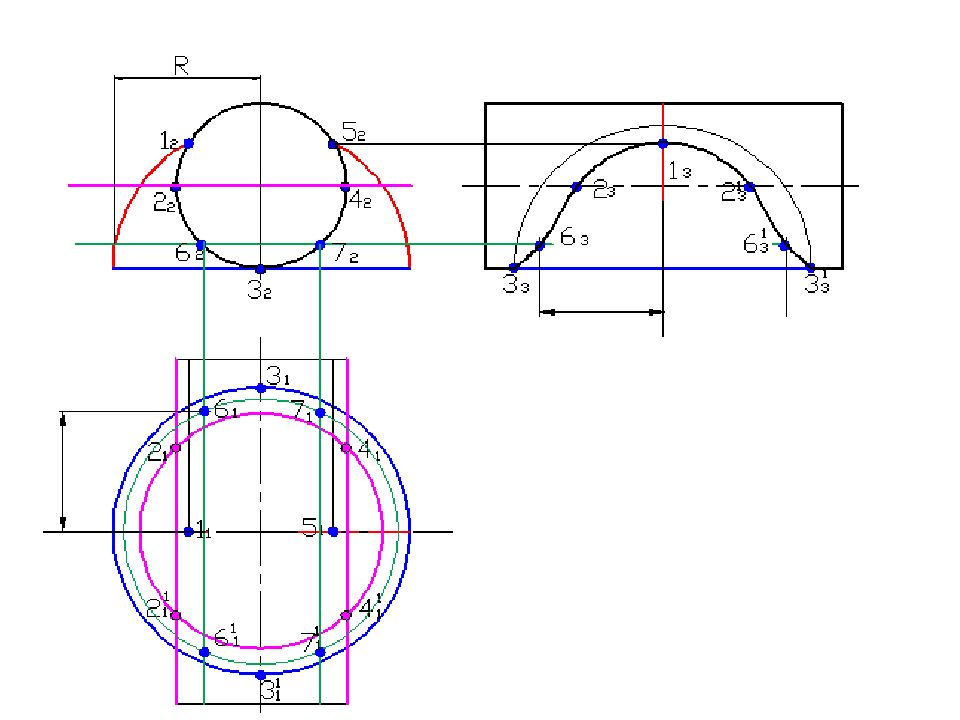
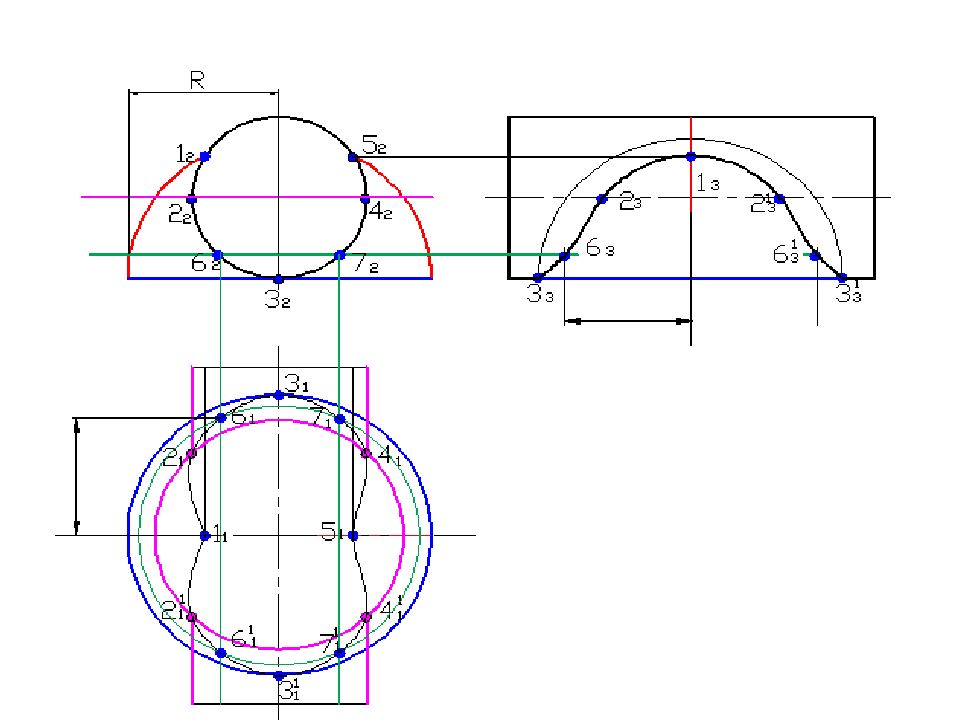
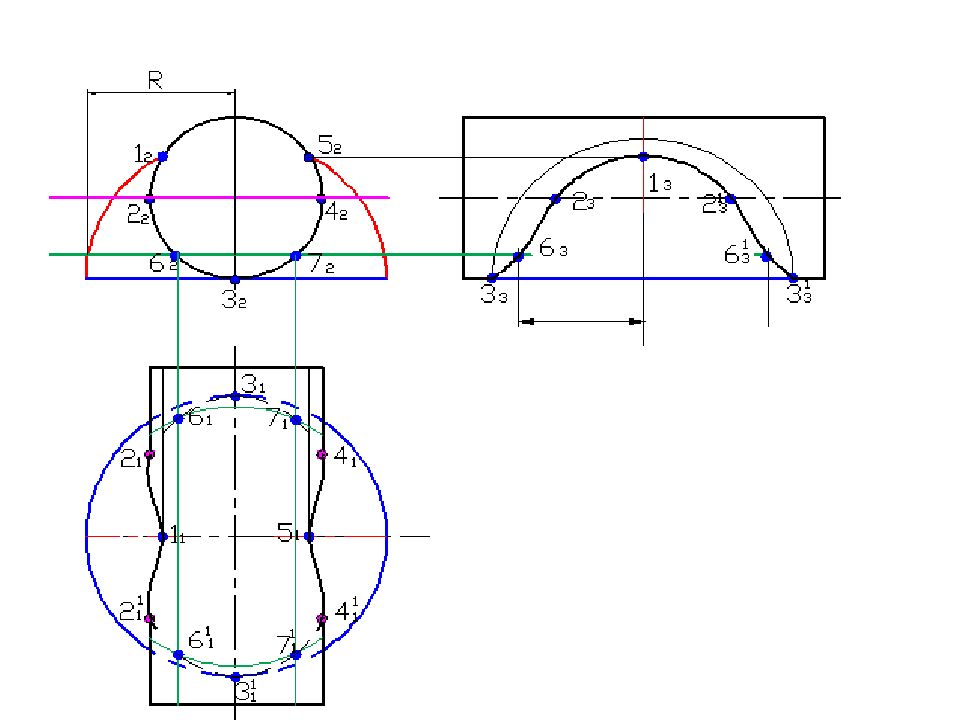
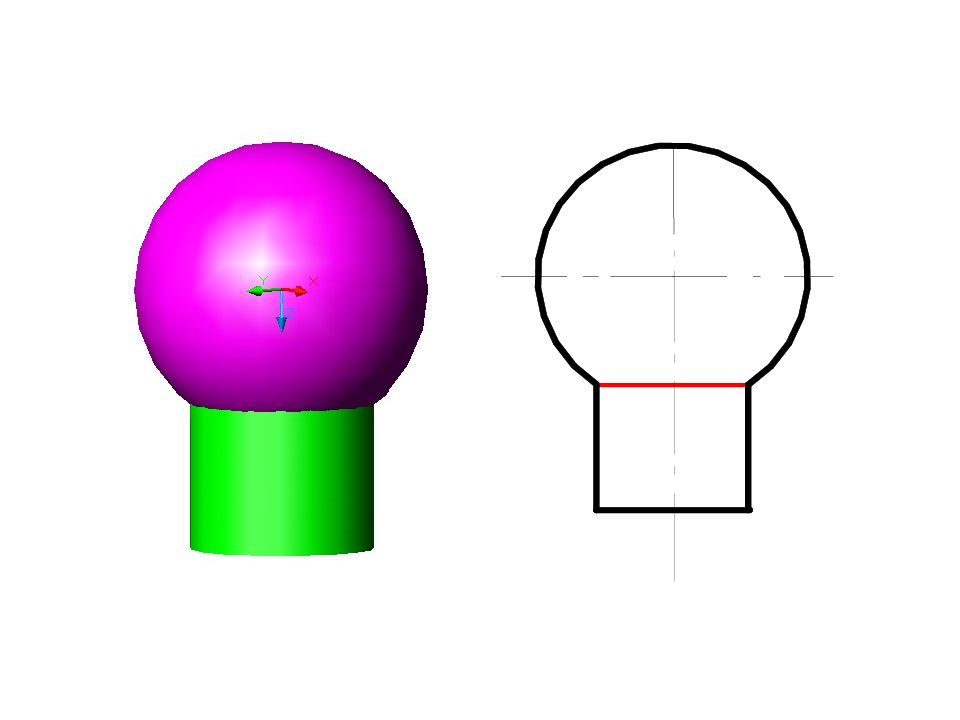
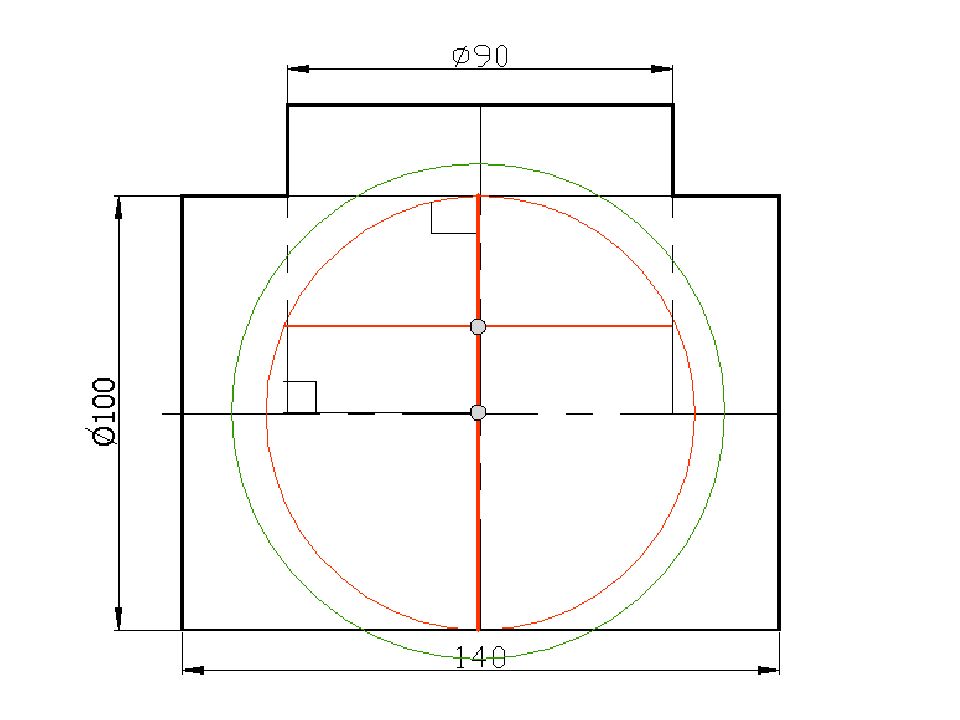
Слайд 58: Построить линию пересечения поверхностей
Полусфера диаметром 90 мм Цилиндр диаметром 50 мм
Слайд 73
ОСНОВНОЙ ПРИНЦИП СФЕРА С ПОВЕРХНОСТЯМИ ВРАЩЕНИЯ, ОСИ КОТОРЫХ ПРОХОДЯТ ЧЕРЕЗ ЦЕНТР СФЕРЫ, ПЕРЕСЕКАЕТСЯ ПО ОКРУЖНОСТЯМ, ПЛОСКОСТИ КОТОРЫХ ПЕРПЕНДИКУЛЯРНЫ ОСИ ВРАЩЕНИЯ ПОВЕРХНОСТИ
Слайд 75
СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР 1. ПЕРЕСЕКАЮТСЯ ПОВЕРХНОСТИ ВРАЩЕНИЯ ОСИ ВРАЩЕНИЯ ПОВЕРХНОСТЕЙ ПЕРЕСЕКАЮТСЯ ПОВЕРХНОСТИ ИМЕЮТ ОБЩУЮ ПЛОСКОСТЬ СИММЕТРИИ
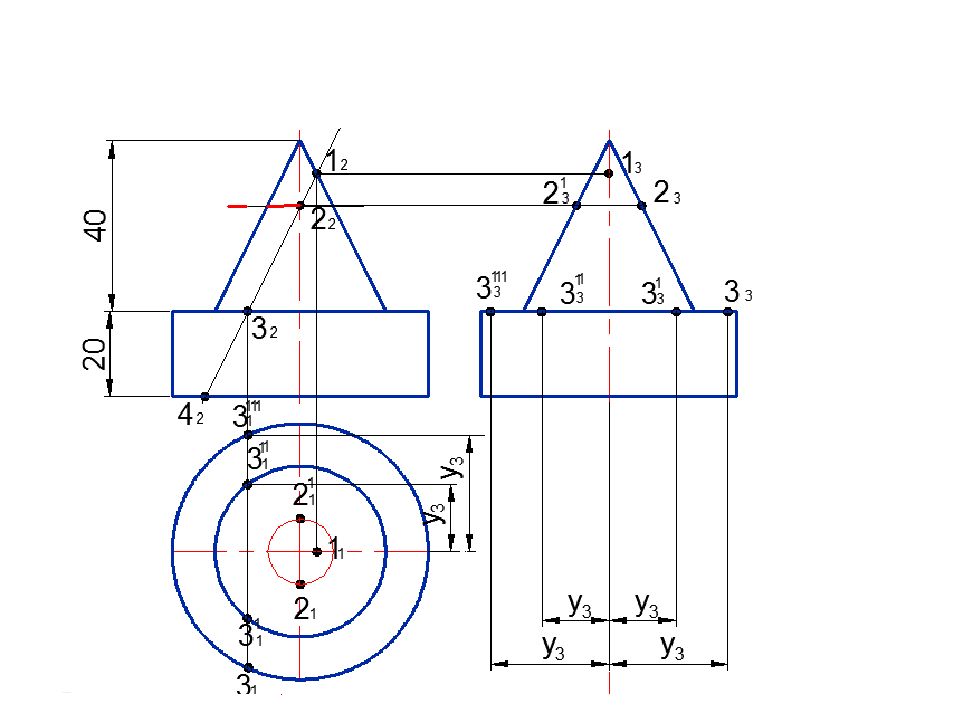
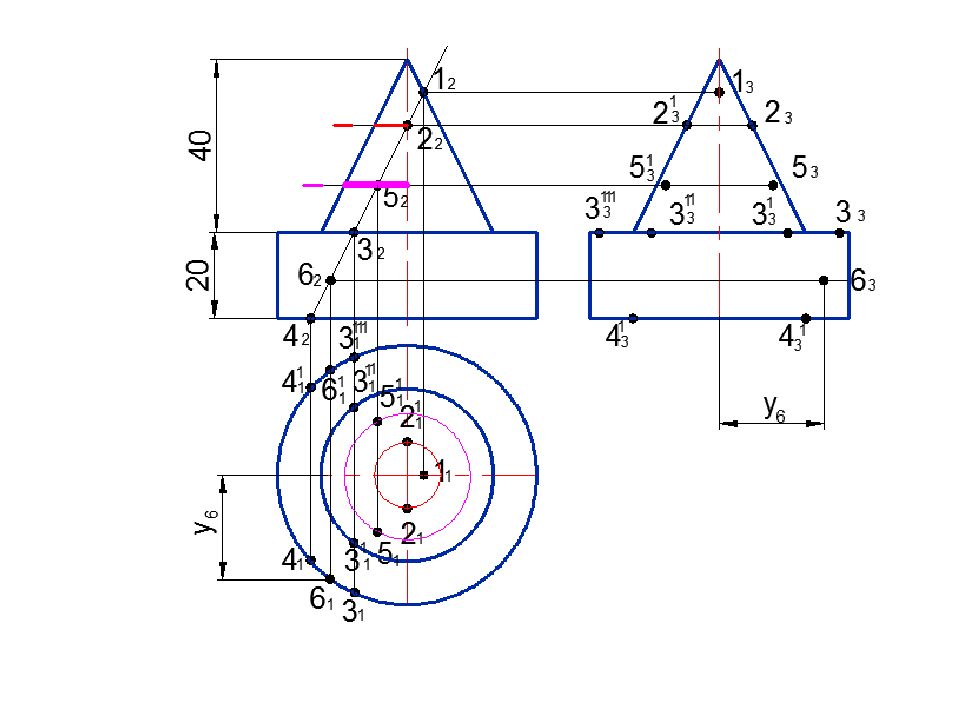
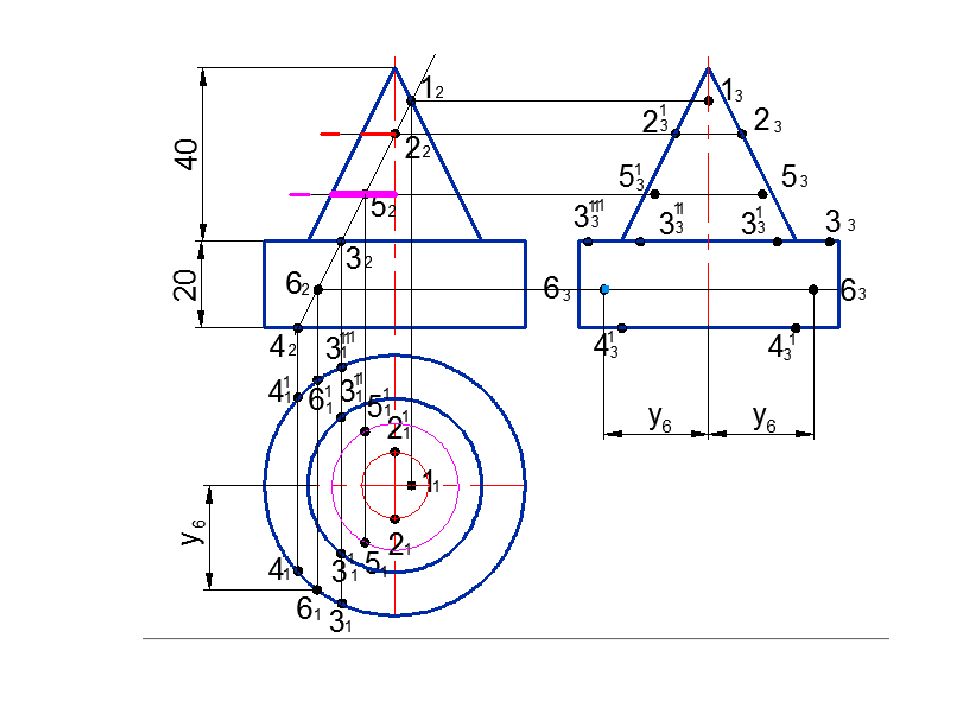
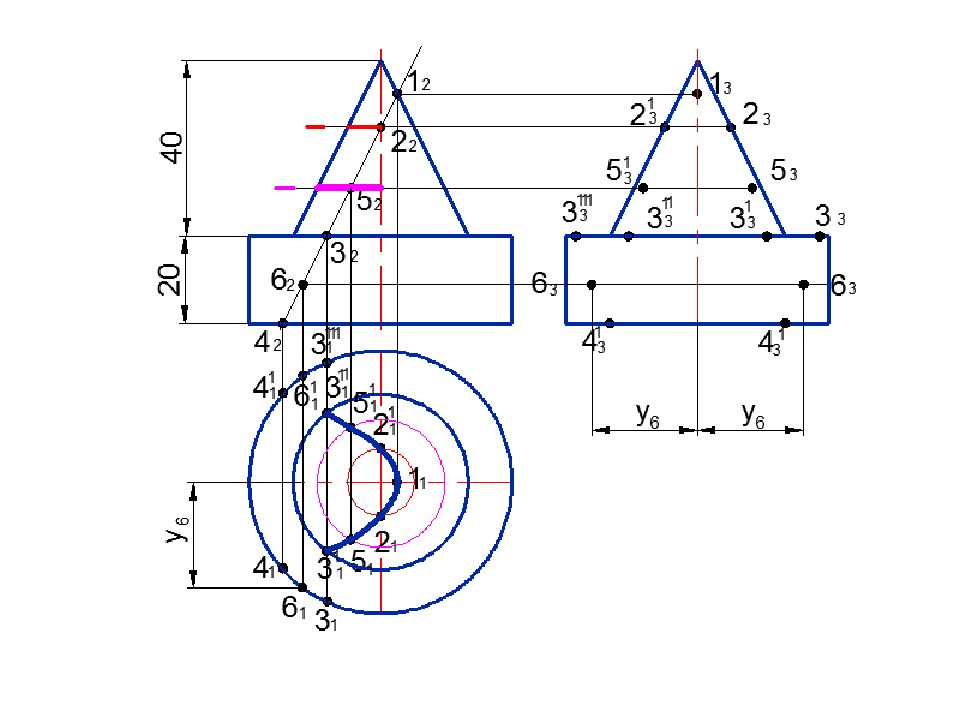
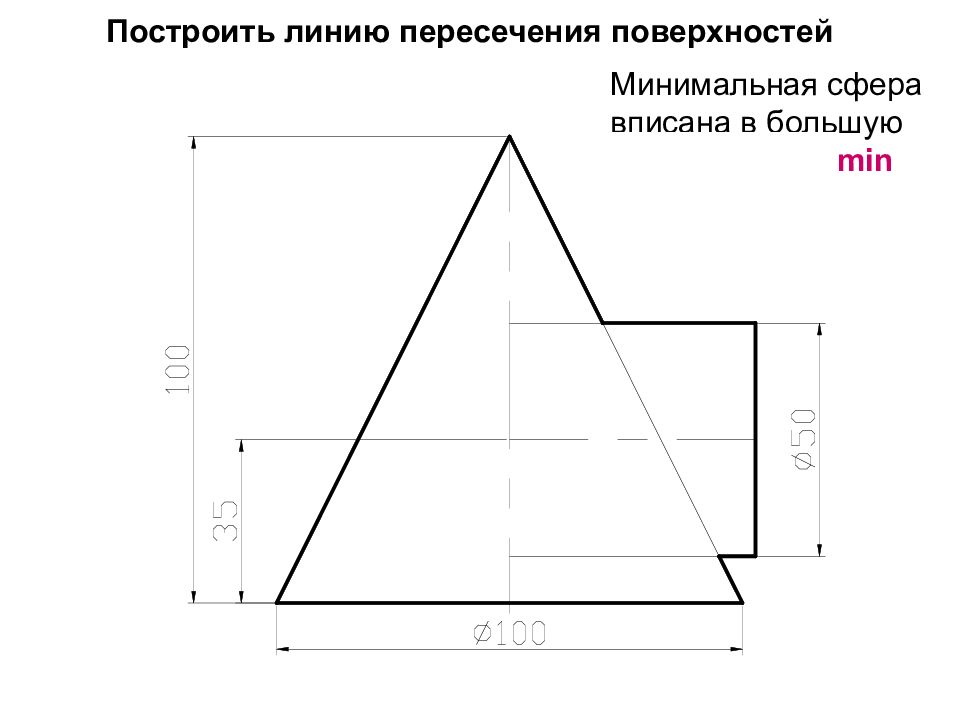
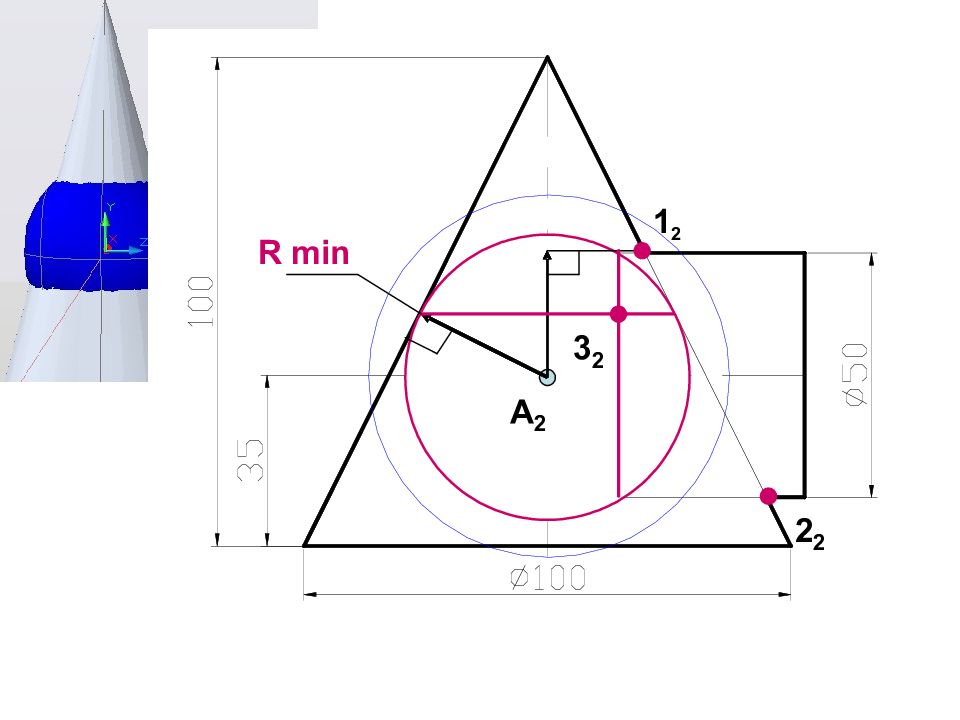
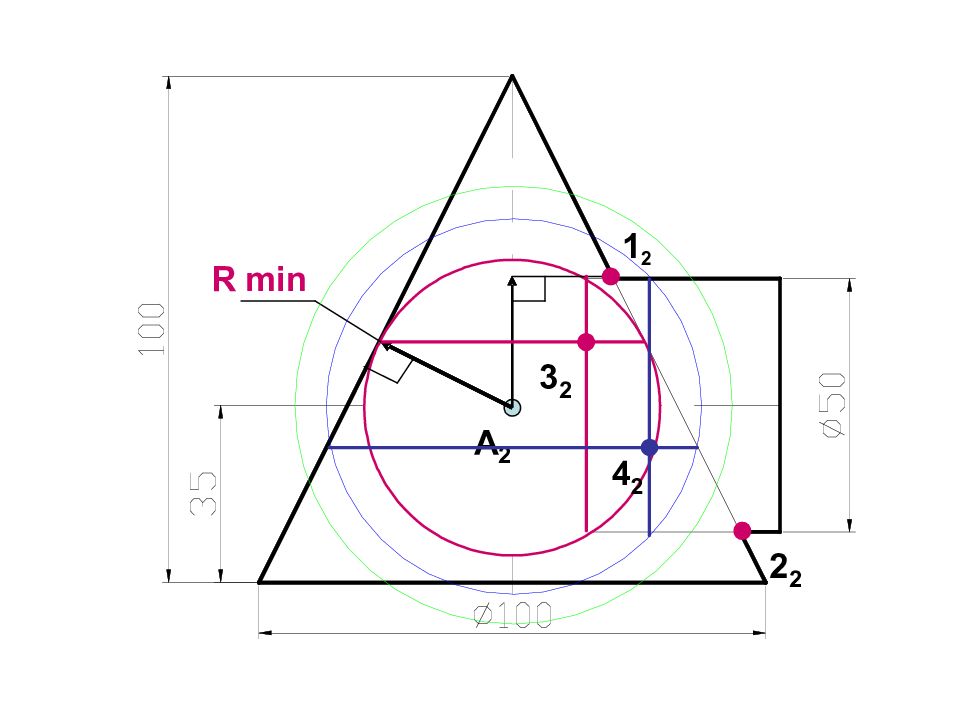
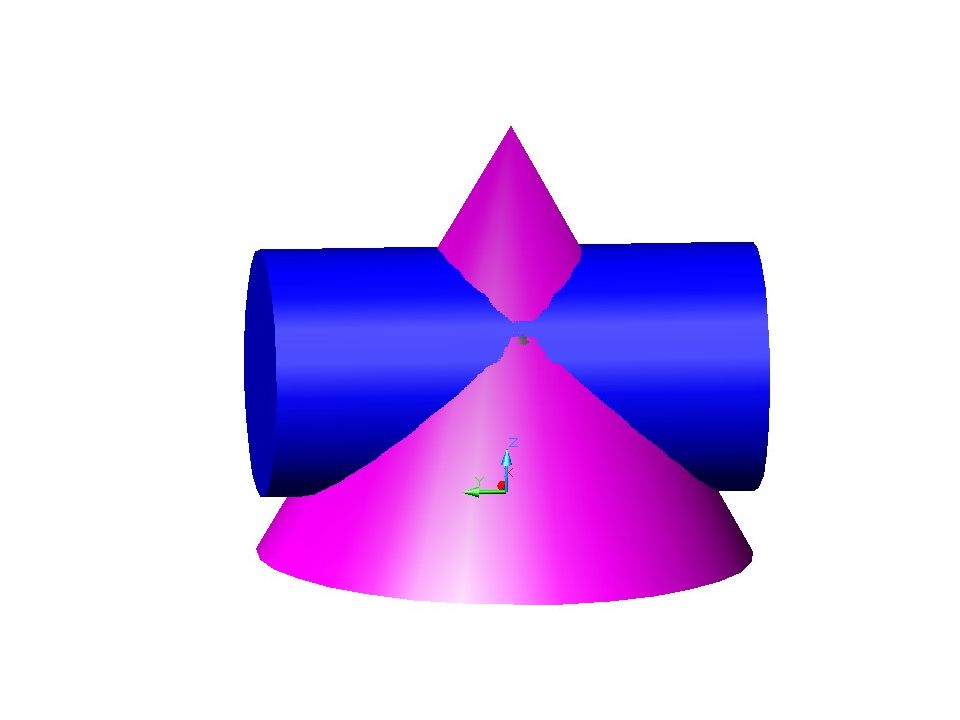
Слайд 76: Построить линию пересечения поверхностей
А 2 Минимальная сфера вписана в большую поверхность R min R min 3 2 1 2 2 2 Rmax
Слайд 80
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА ОПИСАННЫЕ ИЛИ ВПИСАННЫЕ В ДРУГУЮ ПОВЕРХНОСТЬ 2- го ПОРЯДКА, ПЕРЕСЕКАЮТСЯ ПО ДВУМ КРИВЫМ ВТОРОГО ПОРЯДКА, ПЛОСКОСТИ КОТОРЫХ ПРОХОДЯТ ЧЕРЕЗ ПРЯМУЮ, СОЕДИНЯЮЩУЮ ТОЧКИ ПЕРЕСЕЧЕНИЯ ЛИНИЙ КАСАНИЯ
Слайд 87
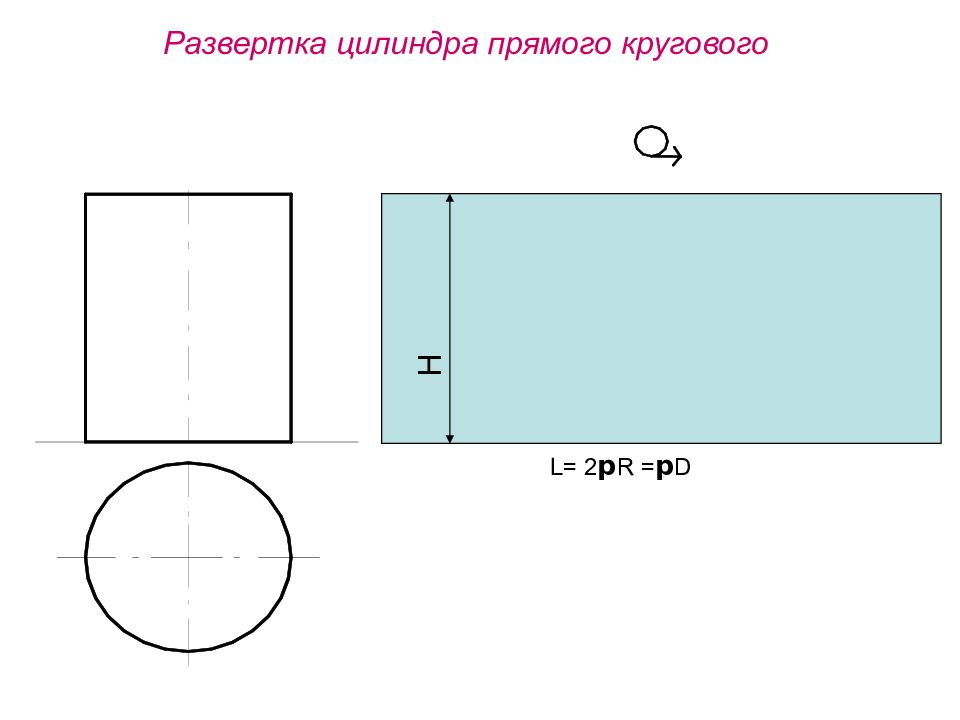
РАЗВЕРТКА ПОВЕРХНОСТИ – ЭТО ПЛОСКАЯ ФИГУРА, КОТОРАЯ ПОЛУЧАЕТСЯ СОВМЕЩЕНИЕМ ВСЕЙ БОКОВОЙ ПОВЕРХНОСТИ ОБЪЕКТА С ПЛОСКОСТЬЮ
Слайд 89
1. ТОЧНЫЕ – ПОСТРОЕННЫЕ ГРАФОАНАЛИТИЧЕСКИМ СПОСОБОМ 2. ПРИБЛИЖЕННЫЕ – ВЫПОЛНЕННЫЕ СПОСОБОМ АППРОКСИМАЦИИ РАЗВЕРТКИ РАЗВЕРТЫВАЕМЫХ ПОВЕРХНОСТЕЙ (ЦИЛИНДРЫ, КОНУСЫ) 3. УСЛОВНЫЕ – РАЗВЕРТКИ НЕРАЗВЕРТЫВАЕМЫХ ПОВЕРХНОСТЕЙ (СФЕРА, ТОР)
Слайд 90: СПОСОБЫ ПОСТРОЕНИЯ РАЗВЕРТОК ПОВЕРХНОСТЕЙ
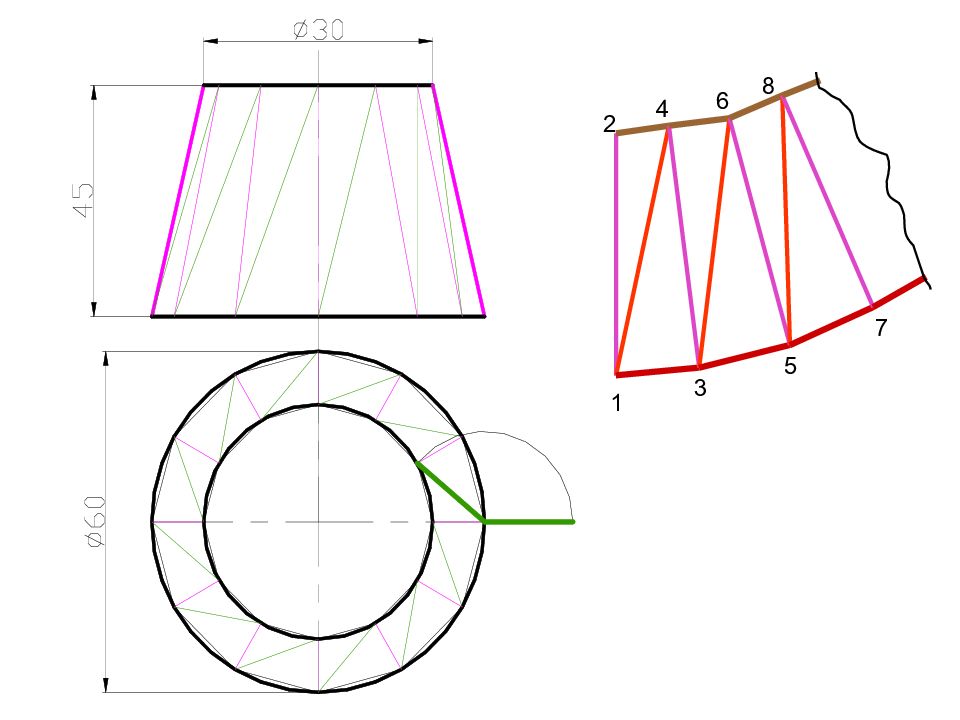
АППРОКСИМАЦИЯ – ЗАМЕНА СЛОЖНОЙ ПОВЕРХНОСТИ ПРОСТОЙ, ВПИСАННОЙ ИЛИ ОПИСАННОЙ МНОГОГРАННОЙ ПОВЕРХНОСТЬЮ 1. СПОСОБ НОРМАЛЬНОГО СЕЧЕНИЯ 2. СПОСОБ РАСКАТКИ 3. СПОСОБ ТРИАНГУЛЯЦИИ
Слайд 91: АППРОКСИМАЦИЯ
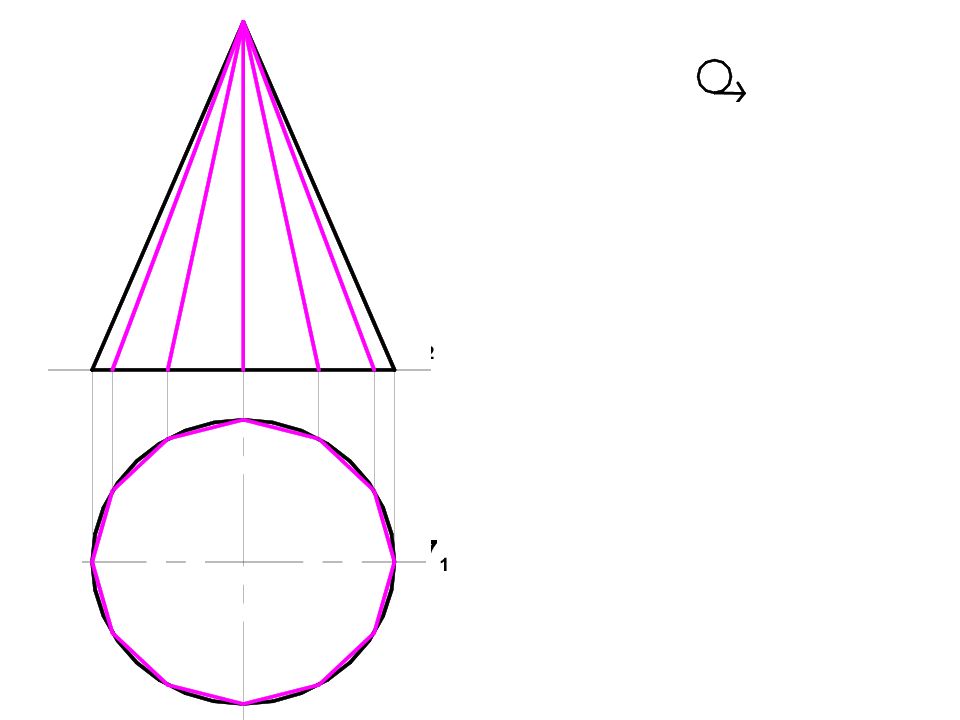
В КРУГОВОЕ ОСНОВАНИЕ ВПИСЫВАЮТ ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК, ЧЕРЕЗ ВЕРШИНЫ МНОГОУГОЛЬНИКА ПРОВОДЯТ РЕБРА ПРИЗМЫ ИЛИ ПИРАМИДЫ
Слайд 92: Способ нормального сечения
Нормальное сечение - это сечение поверхности плоскостью перпендикулярной оси вращения или высоте поверхности
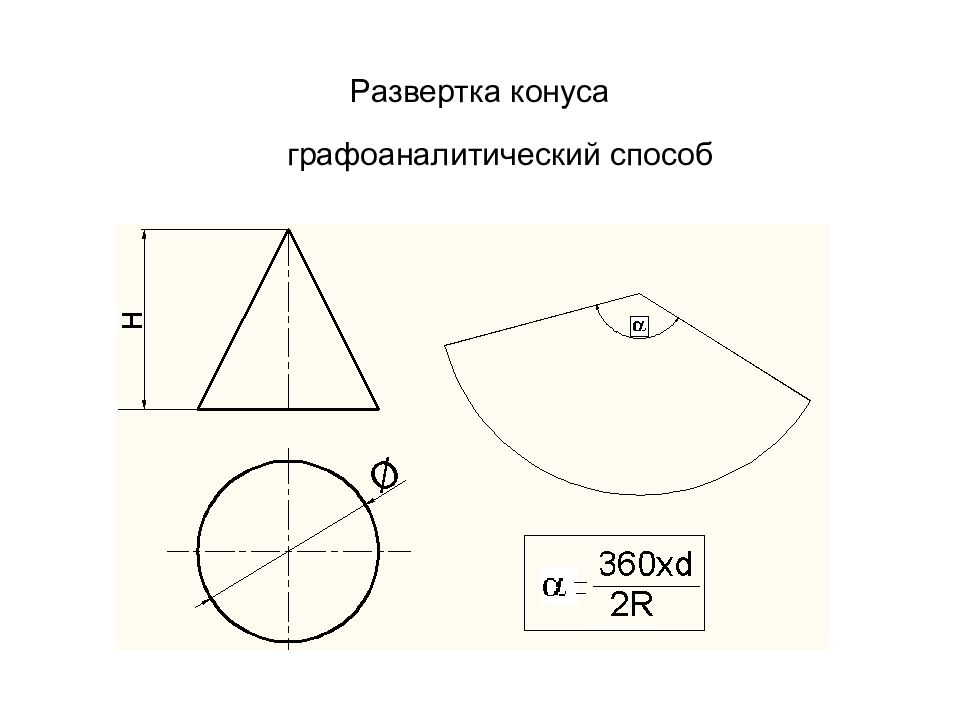
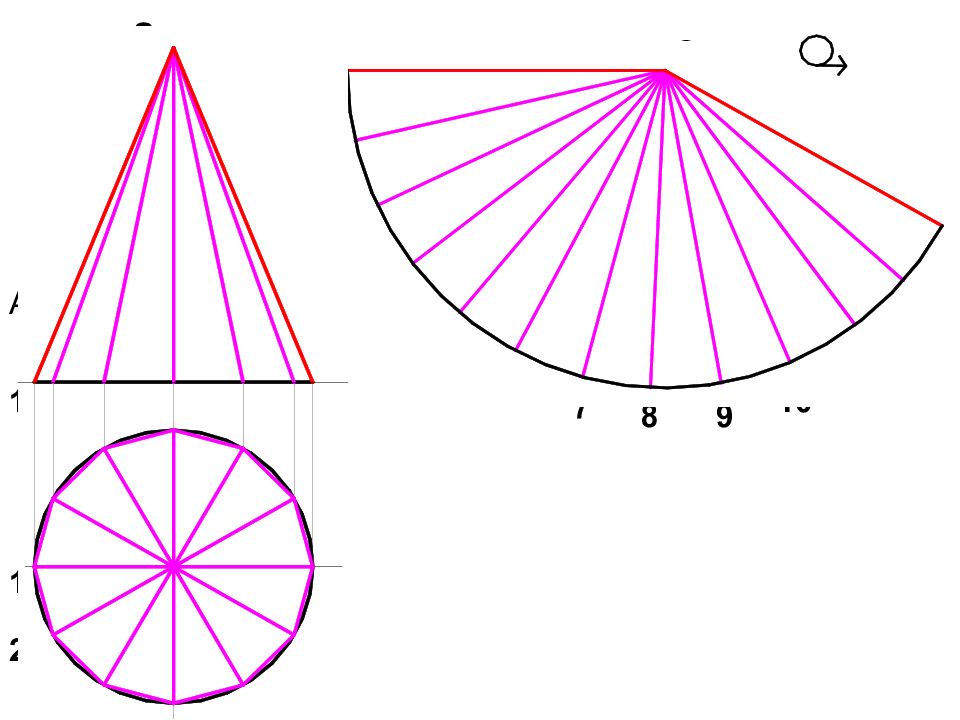
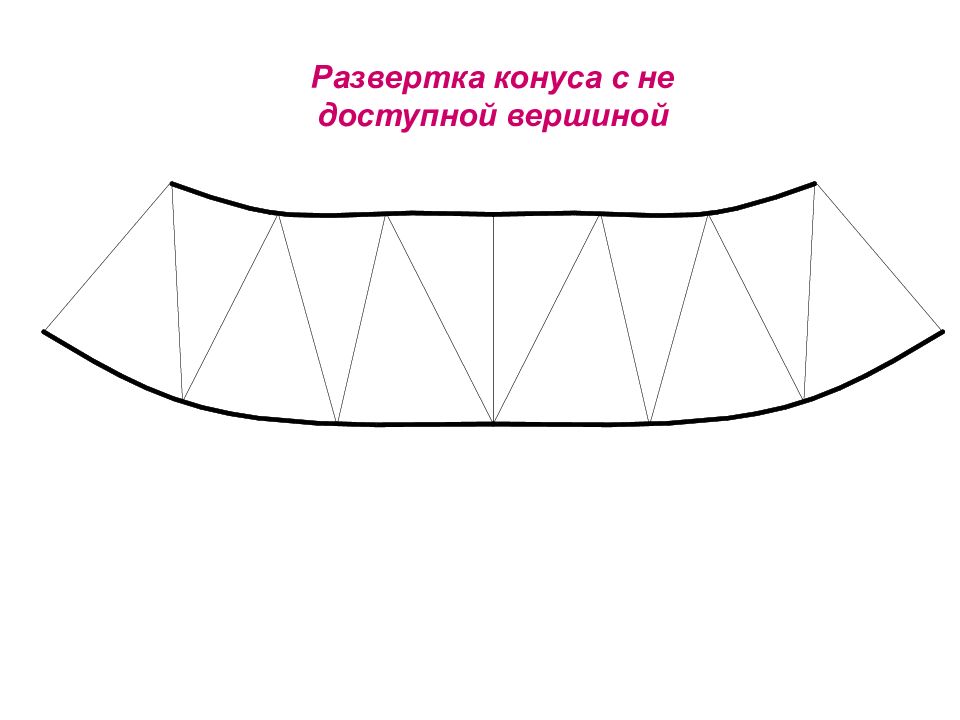
Слайд 94: Развертка конуса прямого кругового
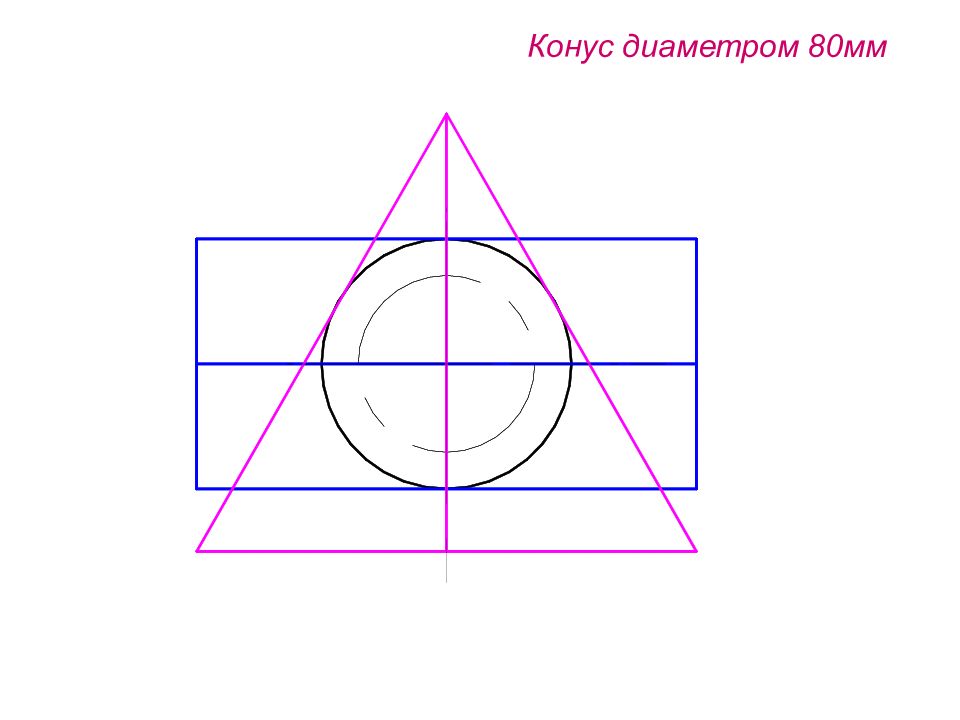
Конус : Диаметр 40 мм Высота 60 мм S 2 S 1
Слайд 96
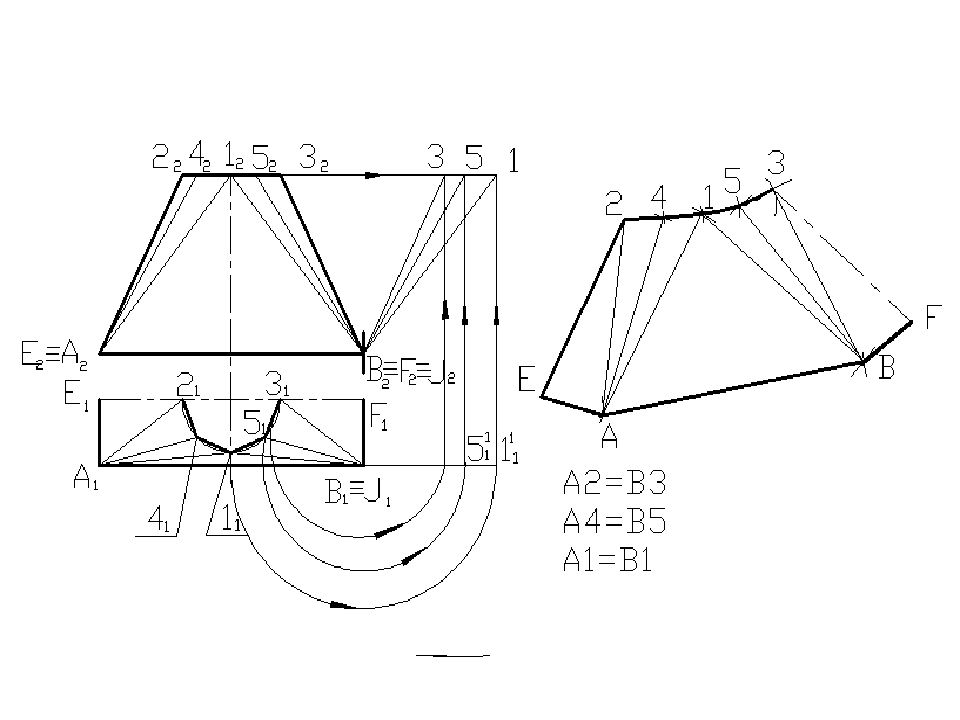
1 1 2 1 3 1 4 1 5 1 6 1 7 1 1 2 3 4 5 6 7 8 9 10 11 12 1 s 2 s 1 s А 2 в 2 С 2 D 2 E 2 F 2 K 2 В 1 A В С D E F K A 1 2 7 2
Слайд 98
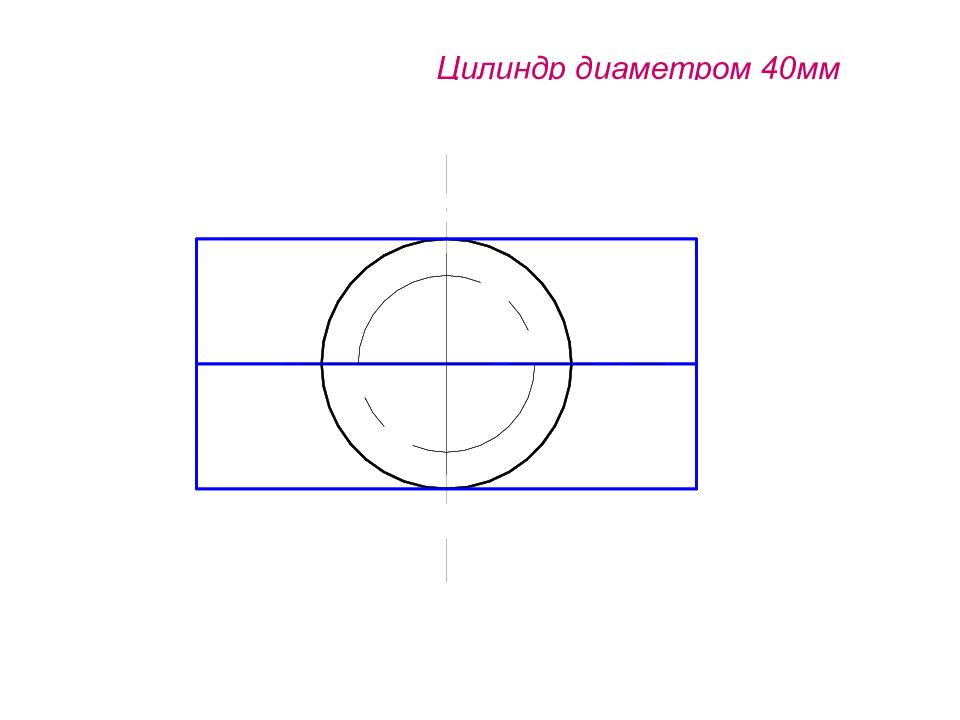
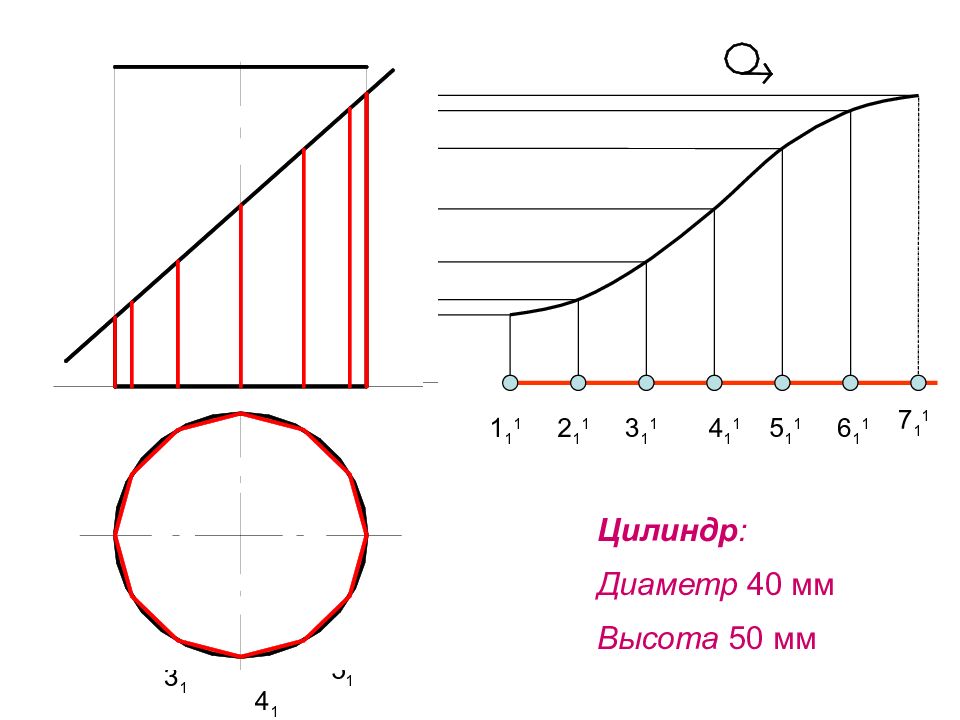
1 1 2 1 4 1 5 1 6 1 7 1 3 1 3 1 1 4 1 1 2 1 1 1 1 1 6 1 1 7 1 1 5 1 1 Цилиндр : Диаметр 40 мм Высота 50 мм
Слайд 100
1 1 2 2 1 2 2 1 2 1 4 2 3 1 5 2 3 2 5 1 4 1 6 1 6 2 3 4 6 5 8 8 2 7 2 8 1 7 1 7
Слайд 103
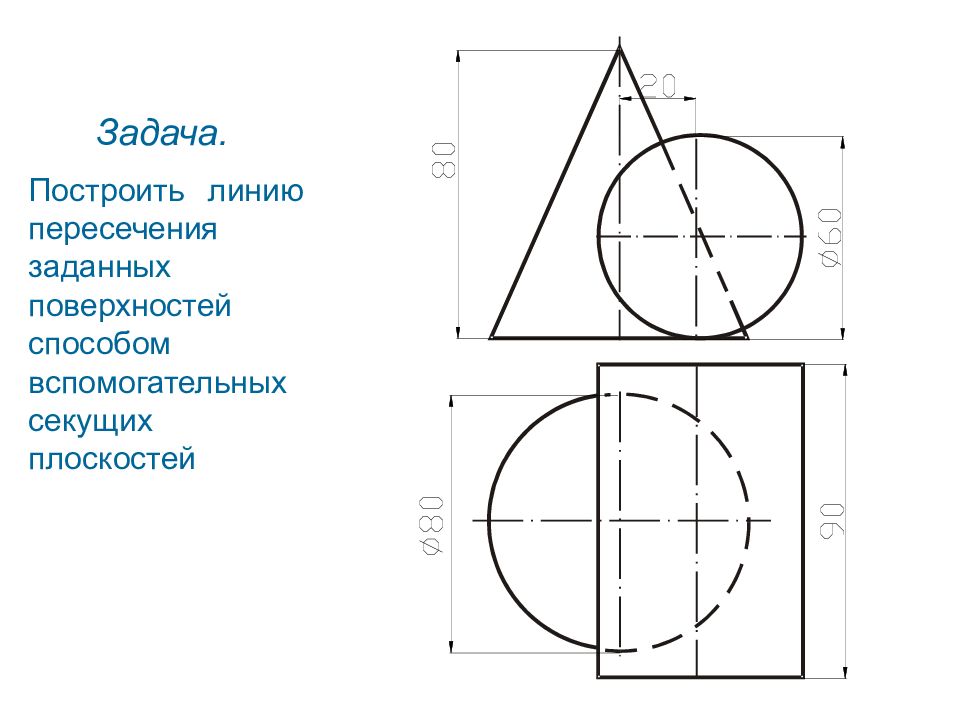
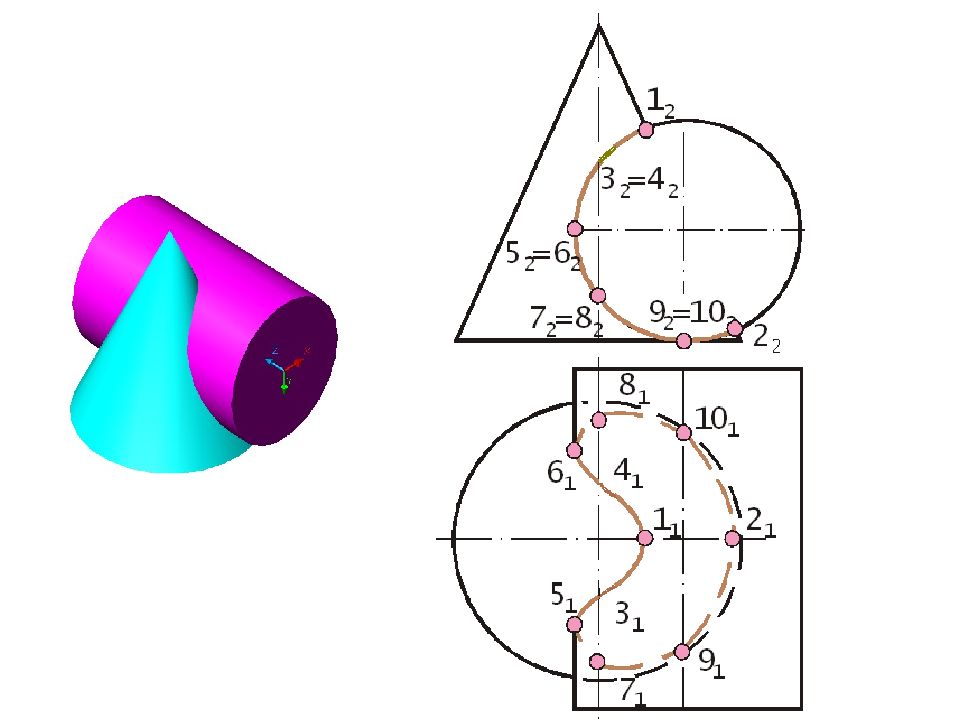
Задача. Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей 30
Слайд 105
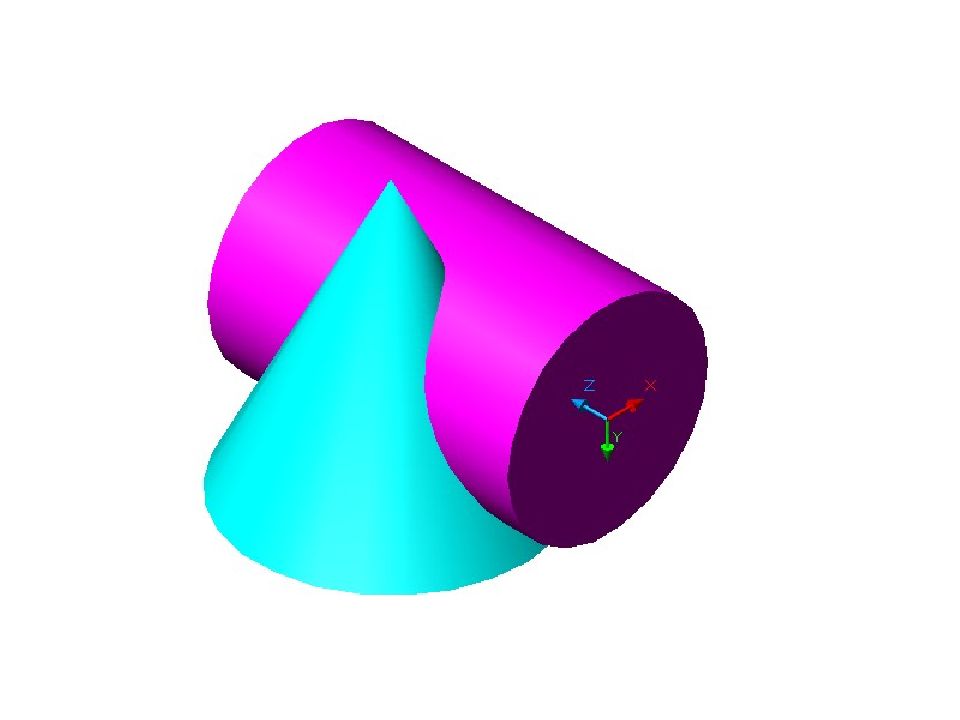
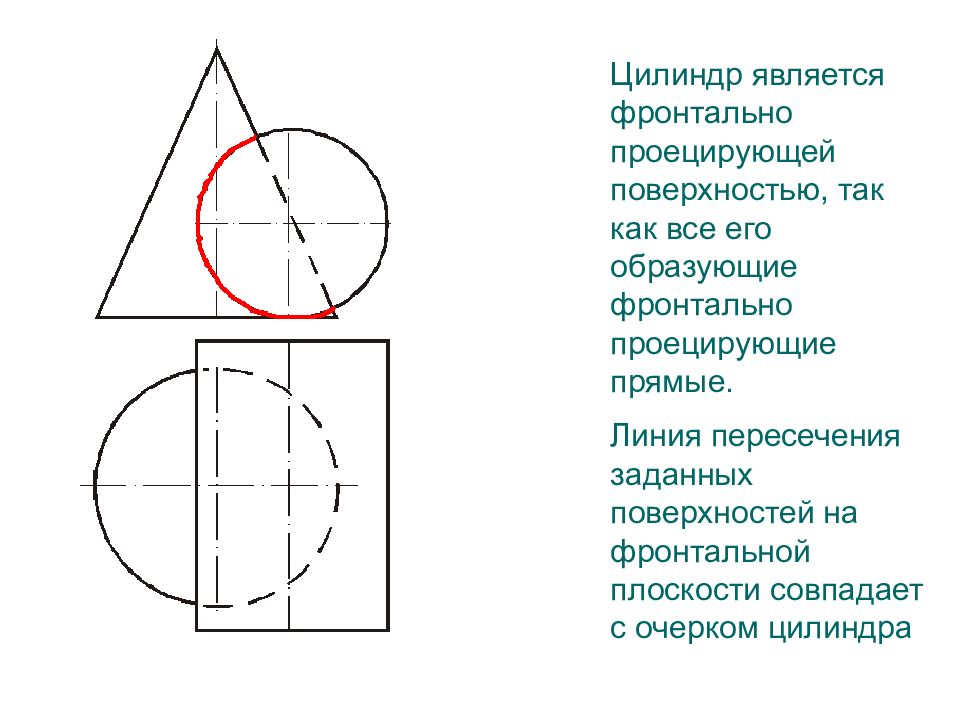
Цилиндр является фронтально проецирующей поверхностью, так как все его образующие фронтально проецирующие прямые. Линия пересечения заданных поверхностей на фронтальной плоскости совпадает с очерком цилиндра
Слайд 107
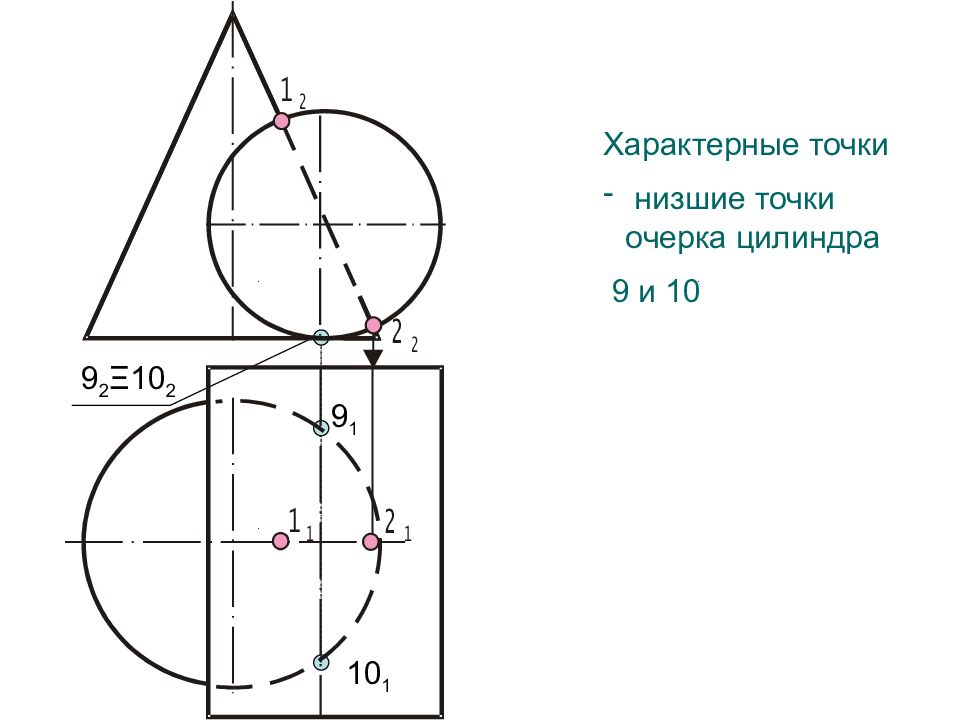
Характерные точки низшие точки очерка цилиндра 9 и 10 9 2 Ξ 10 2 9 1 10 1
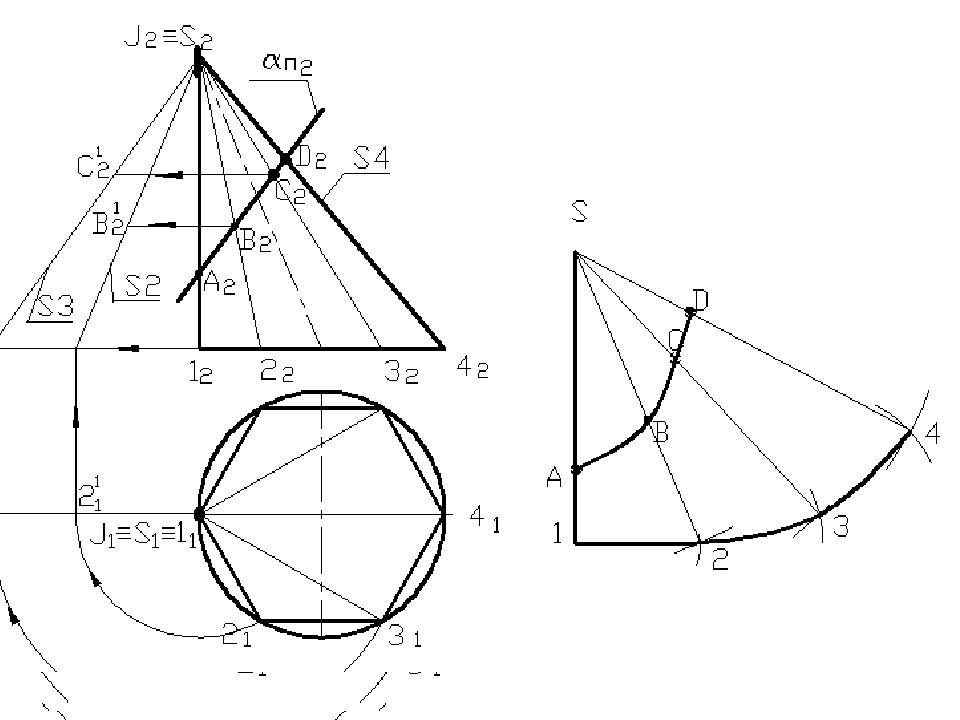
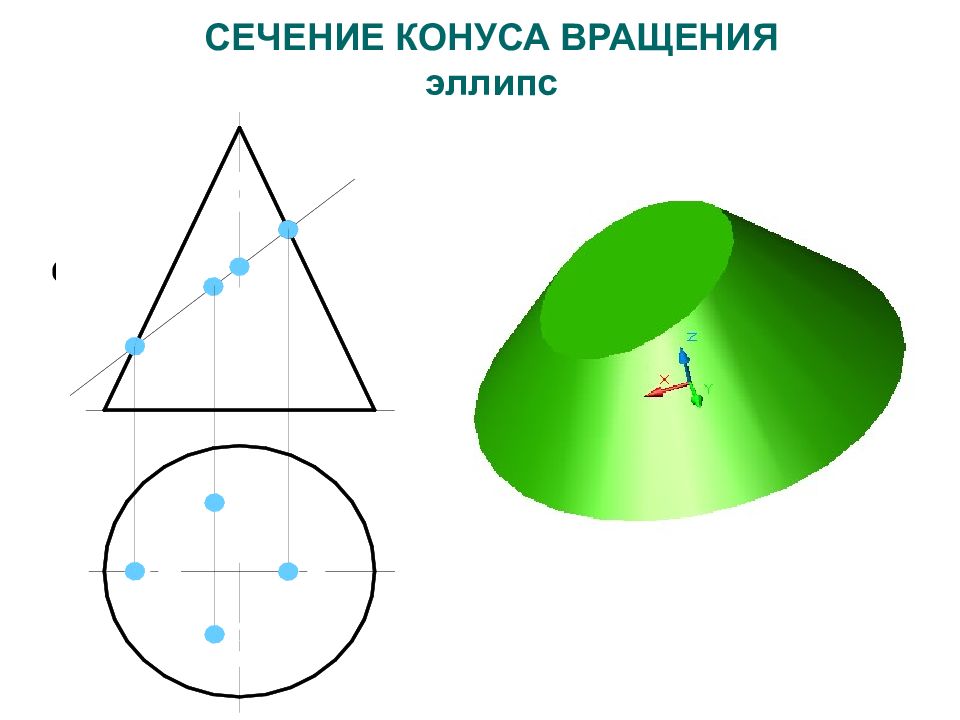
Слайд 116: СЕЧЕНИЕ КОНУСА ВРАЩЕНИЯ эллипс
2 2 1 2 3 2 1 1 2 1 α п2 R к 3 1 1 3 1 R к 4 1 4 1 1 4 2 1 2 3 1 1 3 1 2 1 1 2 2 2 3 2
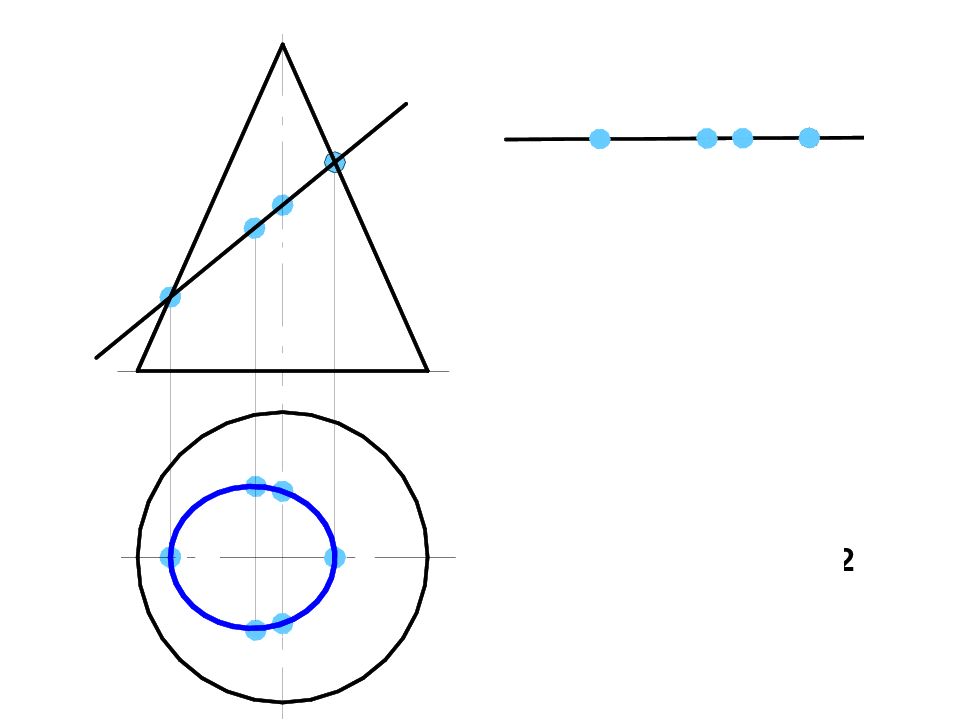
Слайд 117
1 2 1 1 4 2 3 2 2 2 2 1 4 1 4 1 1 3 1 1 3 1 1 2 1 3 2 1 4 2 1 2 2 1 1 2 3 1 3 4 1 4
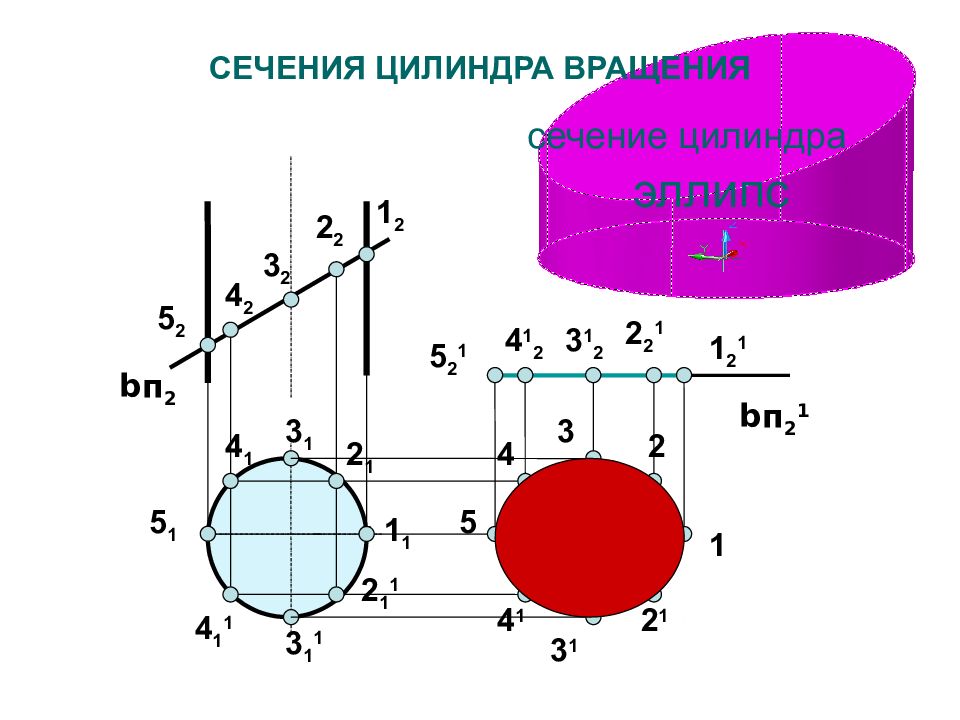
Слайд 118: СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
сечение цилиндра эллипс СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ b п 2 1 1 2 1 2 1 1 1 1 2 2 1 1 2 2 1 2 1 2 2 2 1 3 2 3 3 1 3 1 1 3 1 2 3 1 4 1 1 4 2 4 1 4 1 2 4 1 4 5 1 5 5 2 1 5 2 b п 2
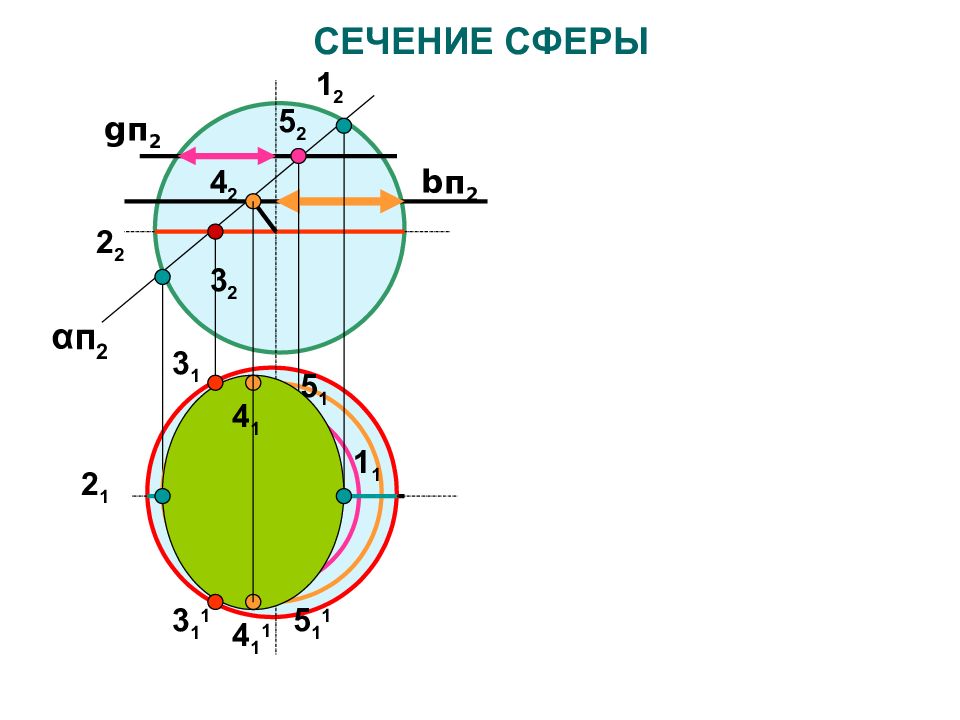
Слайд 119: СЕЧЕНИЕ СФЕРЫ
α п 2 1 2 1 1 2 2 2 1 3 2 3 1 3 1 1 4 2 b п 2 4 1 1 4 1 g п 2 5 2 5 1 5 1 1