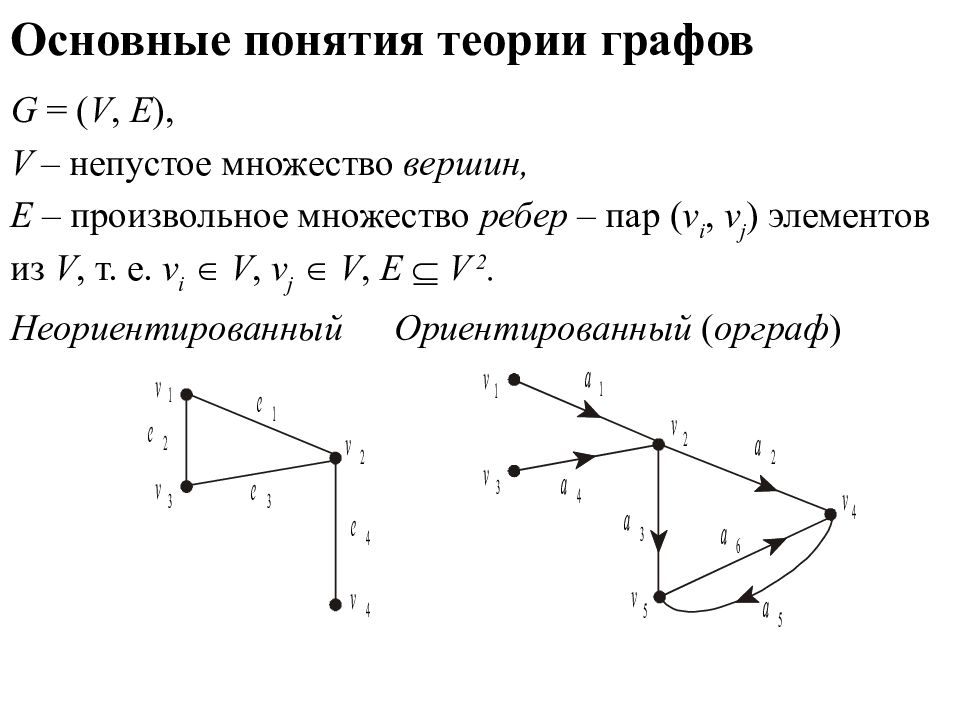
Тема лекции : Интерполяция, экстраполяция, аппроксимация
Интерполяция — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Экстраполяция — особый тип аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не между заданными значениями. Аппроксимация — научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми.
ИНТЕРПОЛЯЦИЯ оригинал увеличенный участок интерполяция
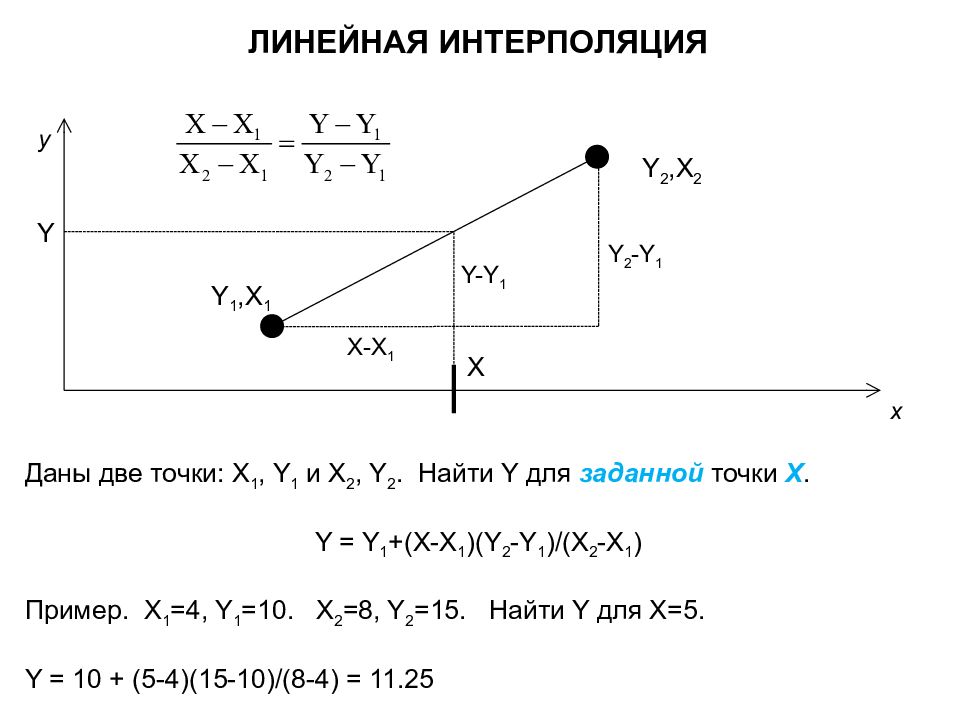
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ Даны две точки: X 1, Y 1 и X 2, Y 2. Найти Y для заданной точки X. Y = Y 1 +(X-X 1 )(Y 2 -Y 1 )/(X 2 -X 1 ) Пример. X 1 =4, Y 1 =10. X 2 =8, Y 2 =15. Найти Y для X=5. Y = 10 + (5-4)(15-10)/(8-4) = 11.25 y x Y 2,X 2 X Y Y 1,X 1 Y-Y 1 X-X 1 Y 2 -Y 1
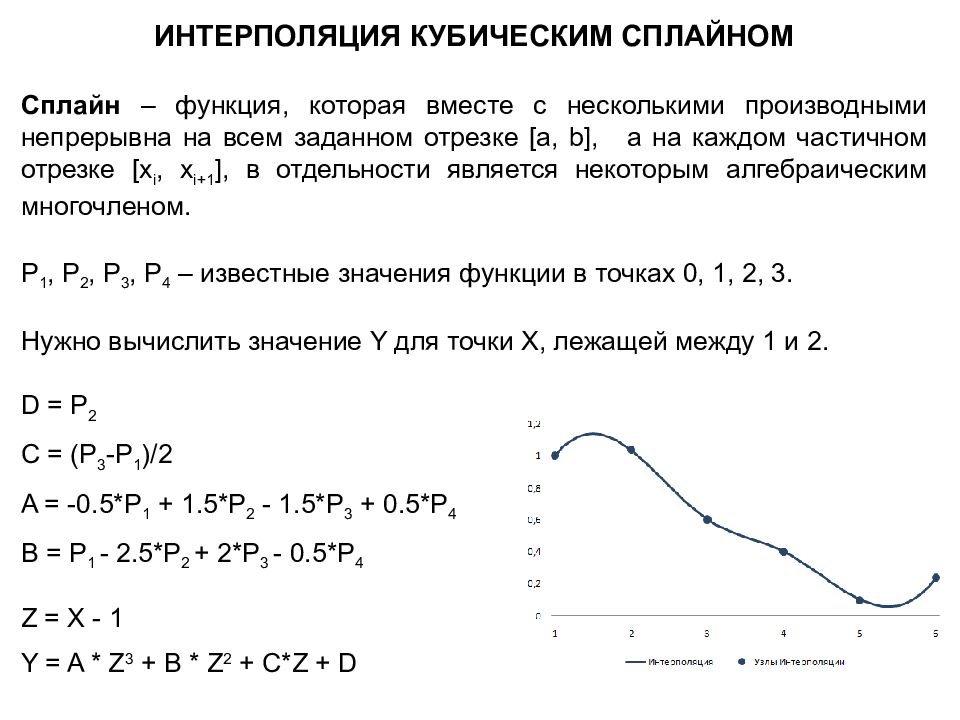
ИНТЕРПОЛЯЦИЯ КУБИЧЕСКИМ СПЛАЙНОМ Сплайн – функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [a, b], а на каждом частичном отрезке [x i, x i+1 ], в отдельности является некоторым алгебраическим многочленом. P 1, P 2, P 3, P 4 – известные значения функции в точках 0, 1, 2, 3. Нужно вычислить значение Y для точки X, лежащей между 1 и 2. D = P 2 C = (P 3 -P 1 )/2 A = -0.5* P 1 + 1.5* P 2 - 1.5* P 3 + 0.5* P 4 B = P 1 - 2.5*P 2 + 2*P 3 - 0.5*P 4 Z = X - 1 Y = A * Z 3 + B * Z 2 + C*Z + D
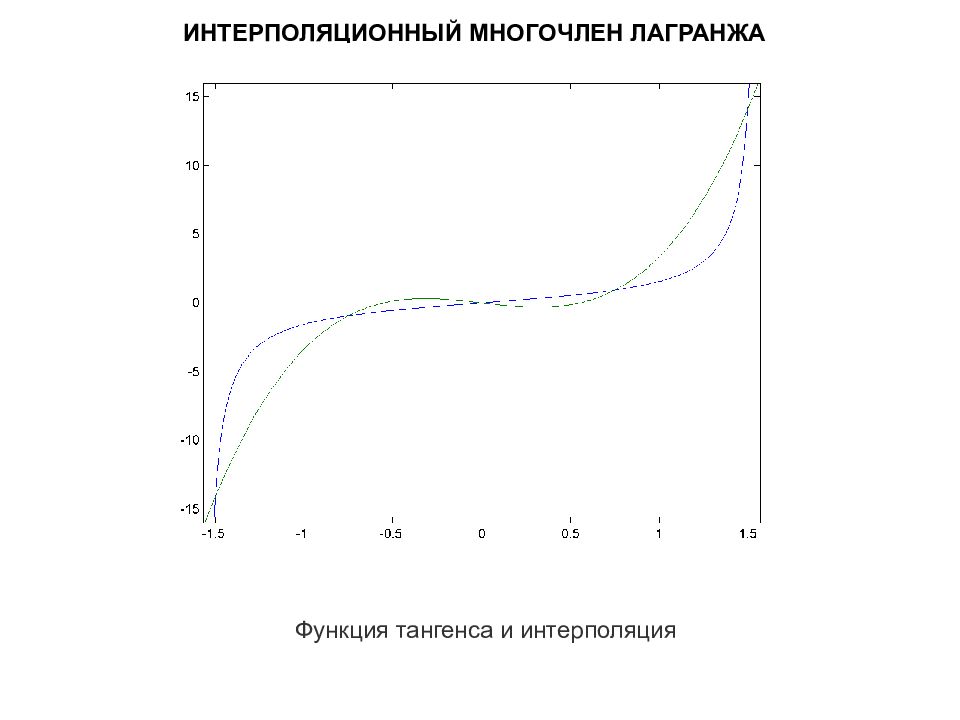
ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН ЛАГРАНЖА Интерполяционный многочлен Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n+1 пар чисел (x0, y0), (x1, y1),…, (xn, yn), где все xj различны, существует единственный многочлен L(x) степени не более n, для которого L(x j ) = y j. Лагранж предложил способ вычисления таких многочленов: где базисные полиномы определяются по формуле:
ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН ЛАГРАНЖА ПРИМЕР. Найдем формулу интерполяции для f(x) = tan( x ) имеющей следующие значения:
ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН ЛАГРАНЖА Функция тангенса и интерполяция
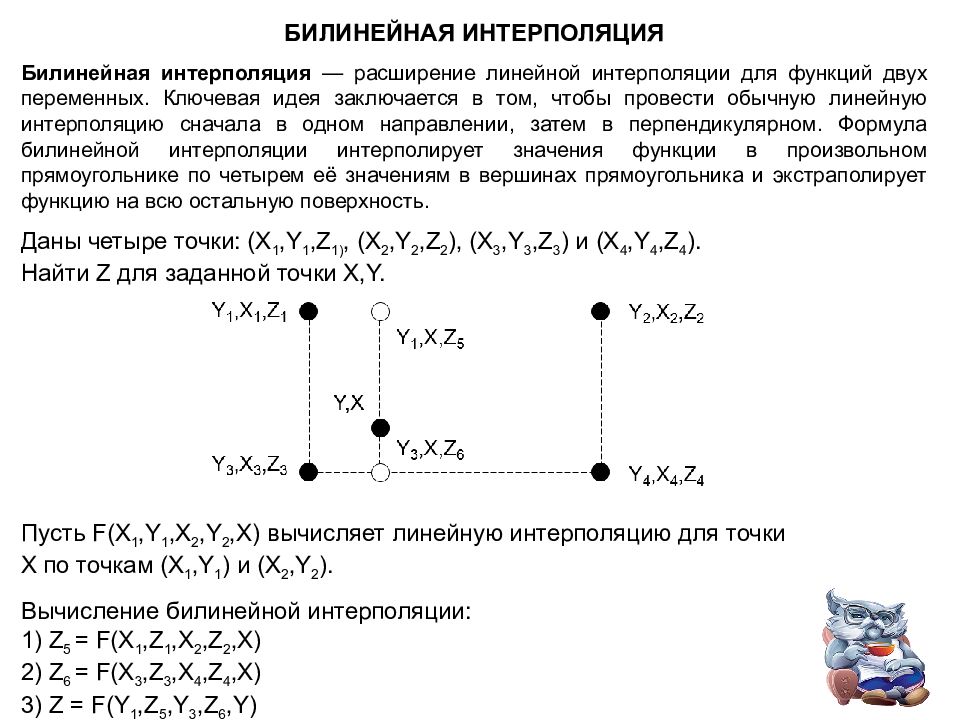
БИЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ Билинейная интерполяция — расширение линейной интерполяции для функций двух переменных. Ключевая идея заключается в том, чтобы провести обычную линейную интерполяцию сначала в одном направлении, затем в перпендикулярном. Формула билинейной интерполяции интерполирует значения функции в произвольном прямоугольнике по четырем её значениям в вершинах прямоугольника и экстраполирует функцию на всю остальную поверхность. Даны четыре точки: (X 1,Y 1,Z 1), (X 2,Y 2,Z 2 ), (X 3,Y 3,Z 3 ) и (X 4,Y 4,Z 4 ). Найти Z для заданной точки X,Y. Пусть F(X 1,Y 1,X 2,Y 2,X) вычисляет линейную интерполяцию для точки X по точкам (X 1,Y 1 ) и (X 2,Y 2 ). Вычисление билинейной интерполяции: 1) Z 5 = F(X 1,Z 1,X 2,Z 2,X) 2) Z 6 = F(X 3,Z 3,X 4,Z 4,X) 3) Z = F(Y 1,Z 5,Y 3,Z 6,Y)
ЭКСТРАПОЛЯЦИЯ ЭКСТРАПОЛЯЦИЯ — определение будущих, ожидаемых значений величин, показателей на основе имеющихся данных о тенденциях их изменений в прошлые периоды. Математически сводится к продолжению кривой. Методы экстраполяции во многих случаях сходны с методами интерполяции. Применение. Общее значение — распространение выводов, полученных из наблюдения над одной частью явления, на другую его часть. В маркетинге — распространение выявленных закономерностей развития изучаемого предмета на будущее. В статистике — распространение установленных в прошлом тенденций на будущий период (экстраполяция во времени применяется для перспективных расчетов населения); распространение выборочных данных на другую часть совокупности, не подвергнутую наблюдению.
АППРОКСИМАЦИЯ Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа. Аппроксимацией (приближением) функции f(x) называется нахождение такой функции ( аппроксимирующей функции ) g(x), которая была бы близка заданной. Критерии близости функций могут быть различные. В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной. В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Метод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Суть метода наименьших квадратов (МНК). Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Дана таблица исходных данных. Используя метод наименьших квадратов, аппроксимировать эти данные какой либо зависимостью, например линейной y=ax+b ( коэффициенты a, b - неизвестные ). Находим частные производные функции по приведенной формуле F(a,b) по переменным а и b, приравниваем эти производные к нулю.
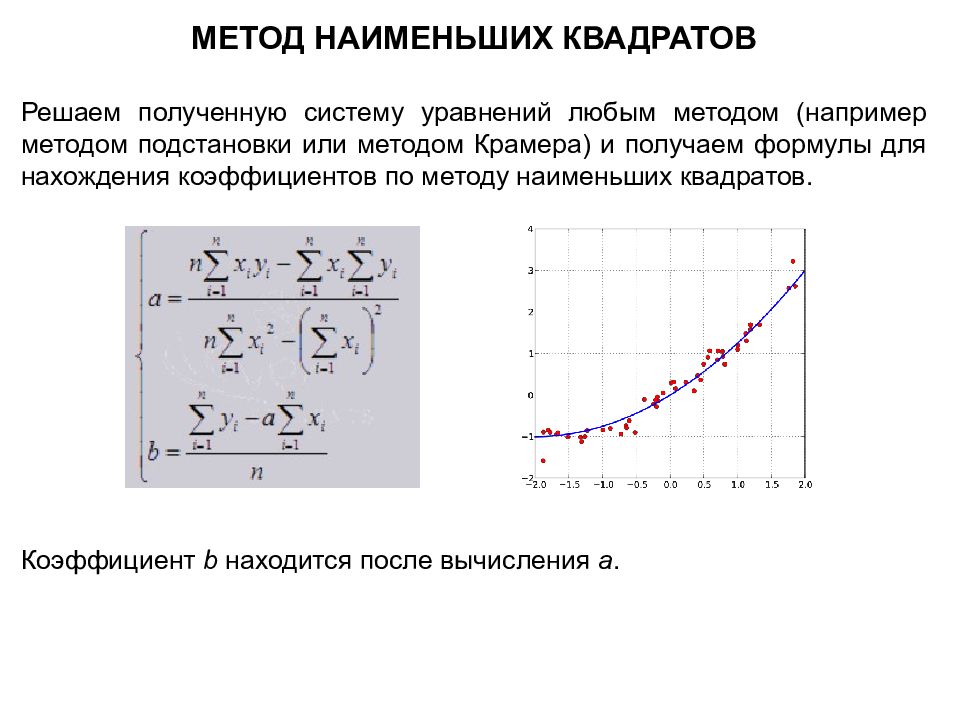
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Решаем полученную систему уравнений любым методом (например методом подстановки или методом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов. Коэффициент b находится после вычисления a.
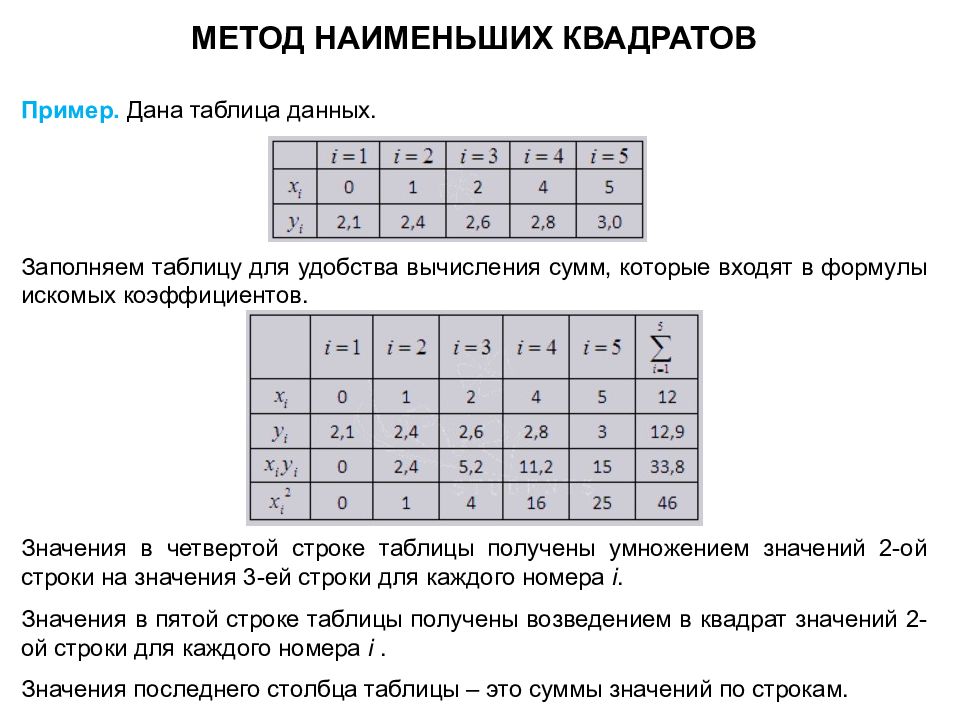
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Пример. Дана таблица данных. Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов. Значения в четвертой строке таблицы получены умножением значений 2-ой строки на значения 3-ей строки для каждого номера i. Значения в пятой строке таблицы получены возведением в квадрат значений 2-ой строки для каждого номера i . Значения последнего столбца таблицы – это суммы значений по строкам.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Используем формулы метода наименьших квадратов для нахождения коэффициентов а и b. Подставляем в них соответствующие значения из последнего столбца таблицы Следовательно, y = 0.165 * X + 2.184 - искомая аппроксимирующая прямая.
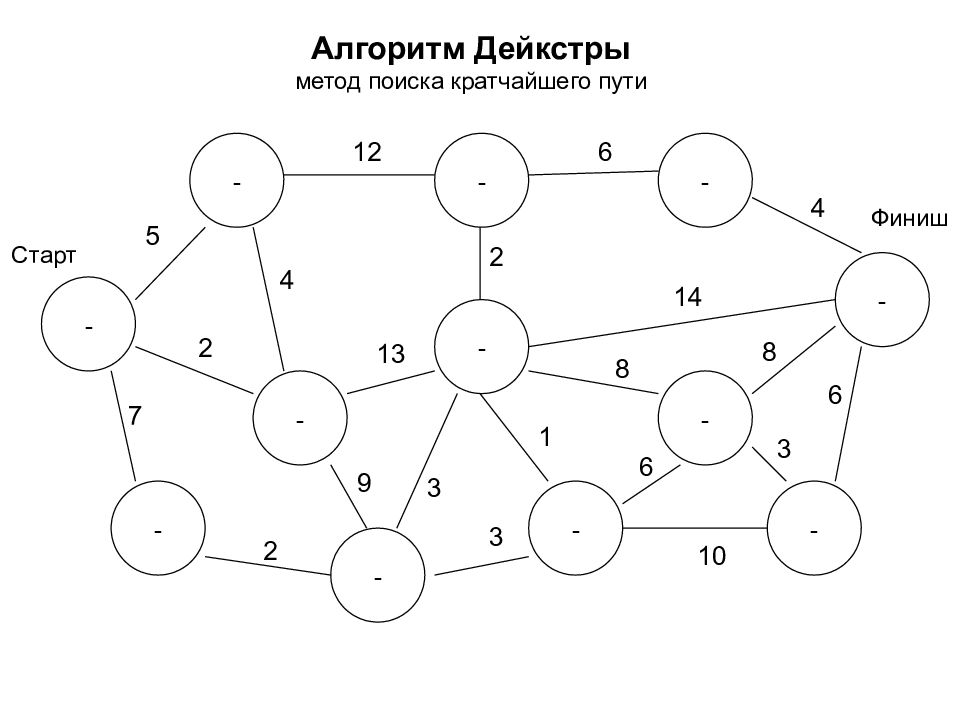
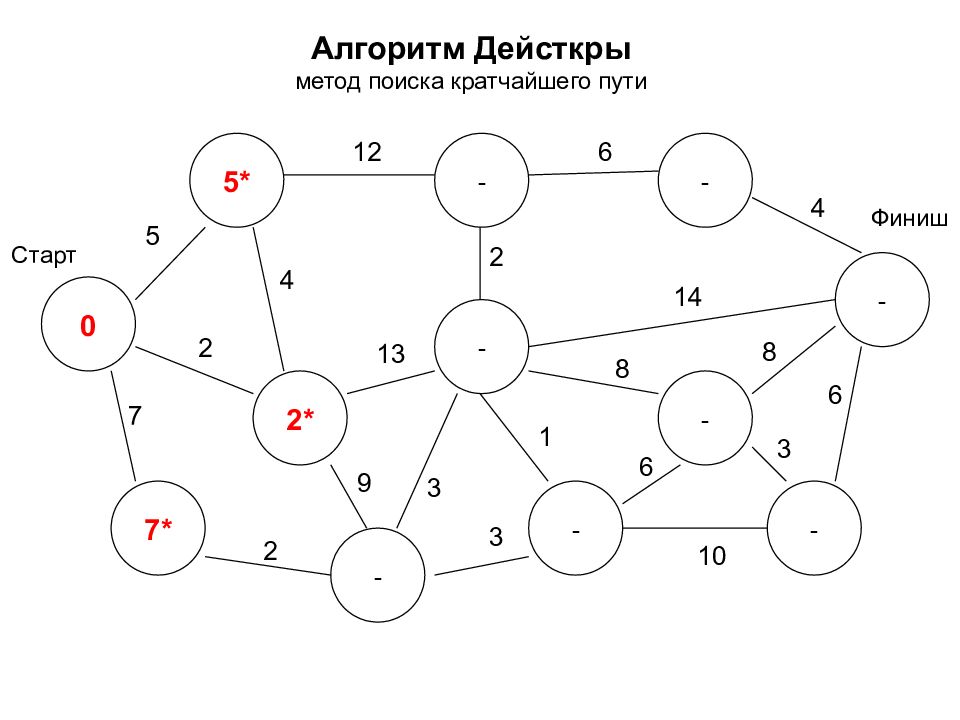
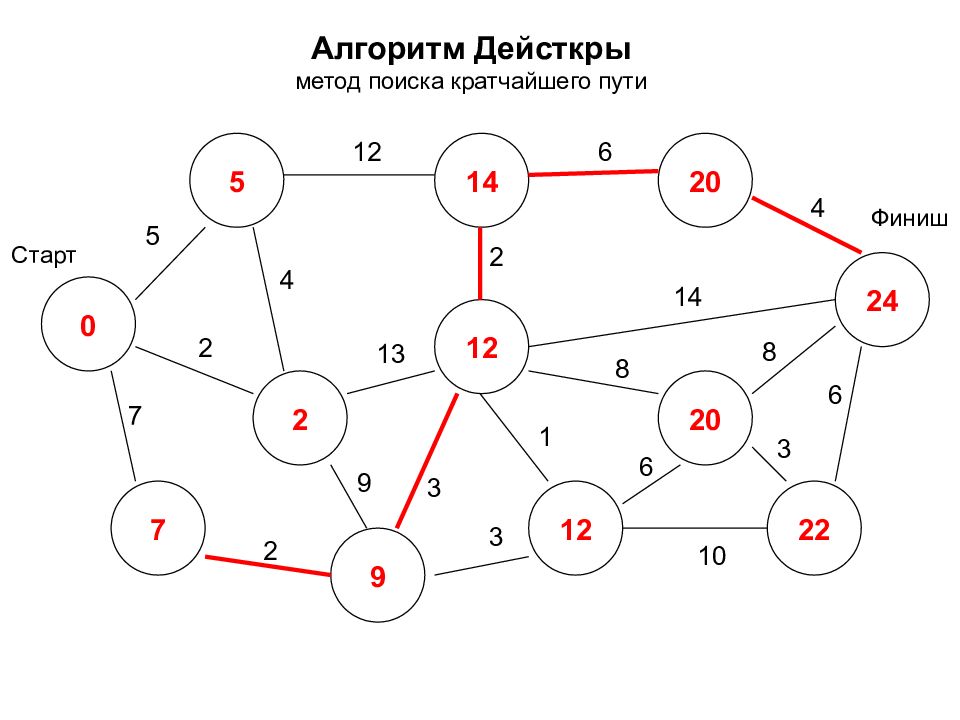
Алгоритм Дейкстры метод поиска кратчайшего пути - - - - - - - - - - - - Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
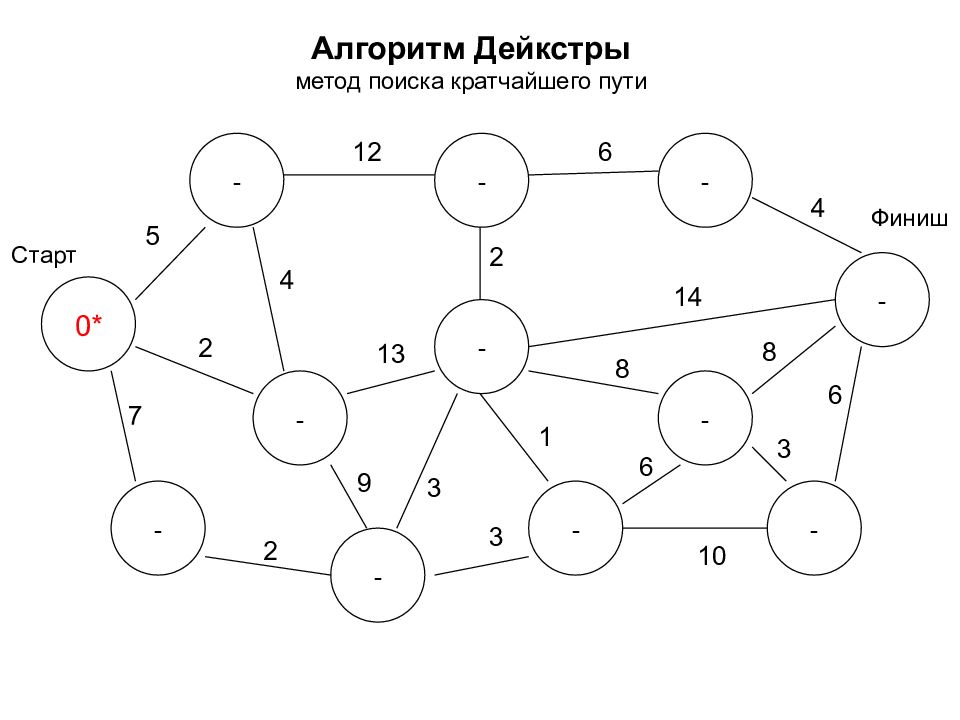
Алгоритм Дейкстры метод поиска кратчайшего пути 0* - - - - - - - - - - - Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2* 7* 5* - - - - - - - - Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
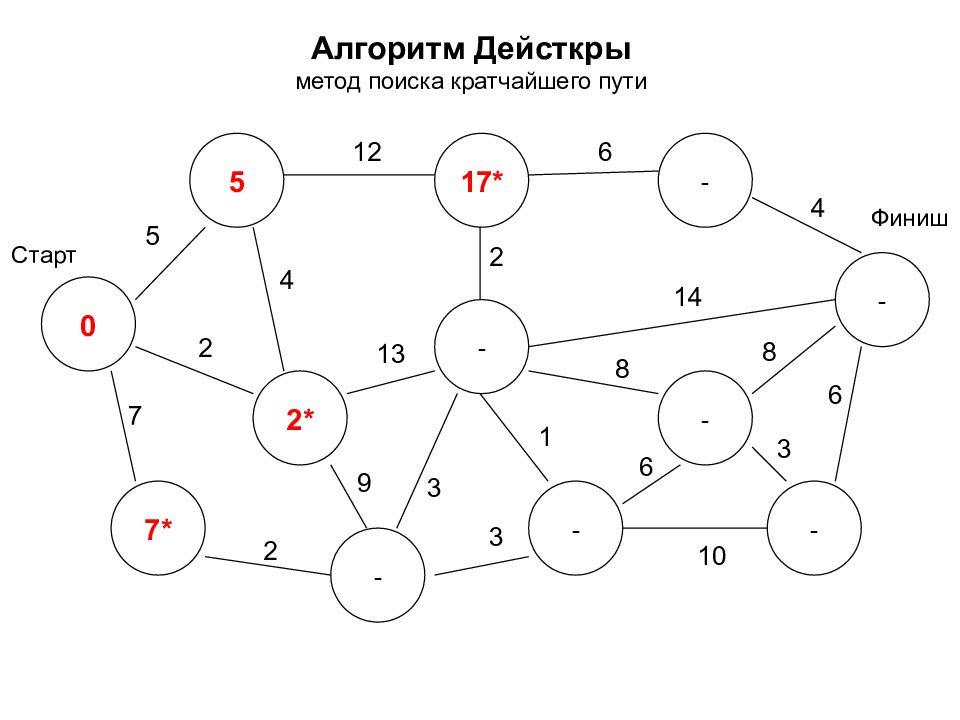
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2* 7* 5 17* - - - - - - - Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
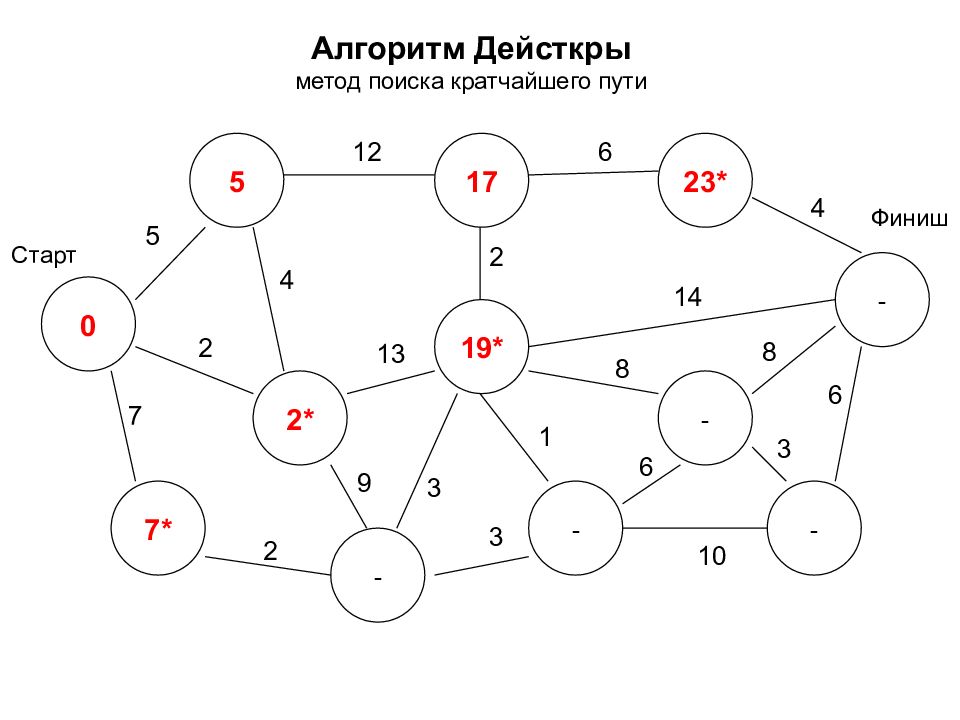
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2* 7* 5 17 - - 19* - - 23* - Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
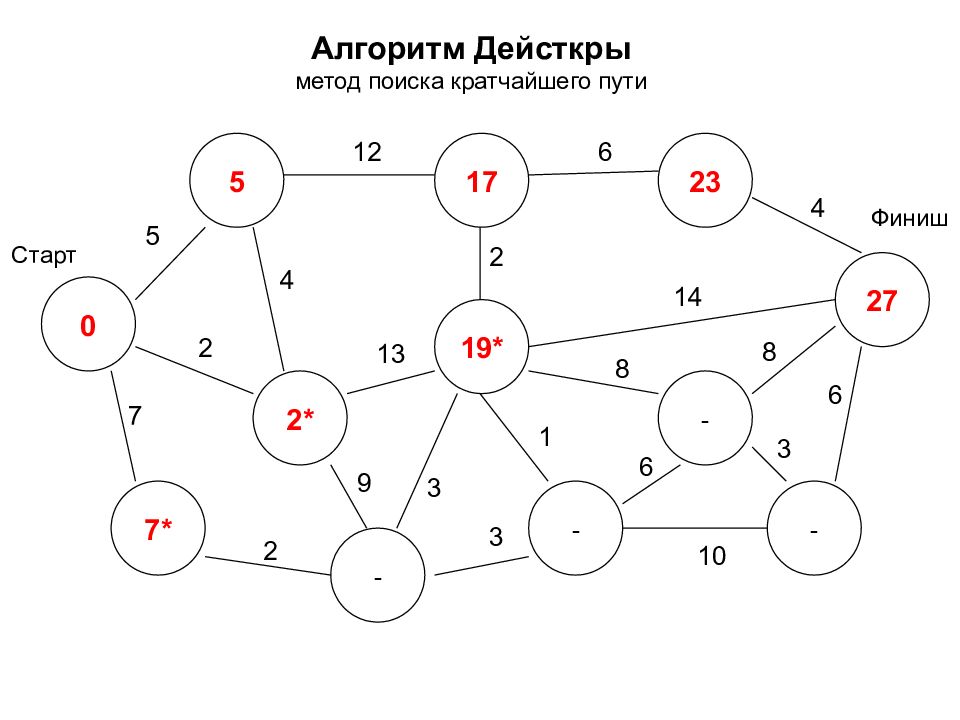
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2* 7* 5 17 - 27 19* - - 23 - Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
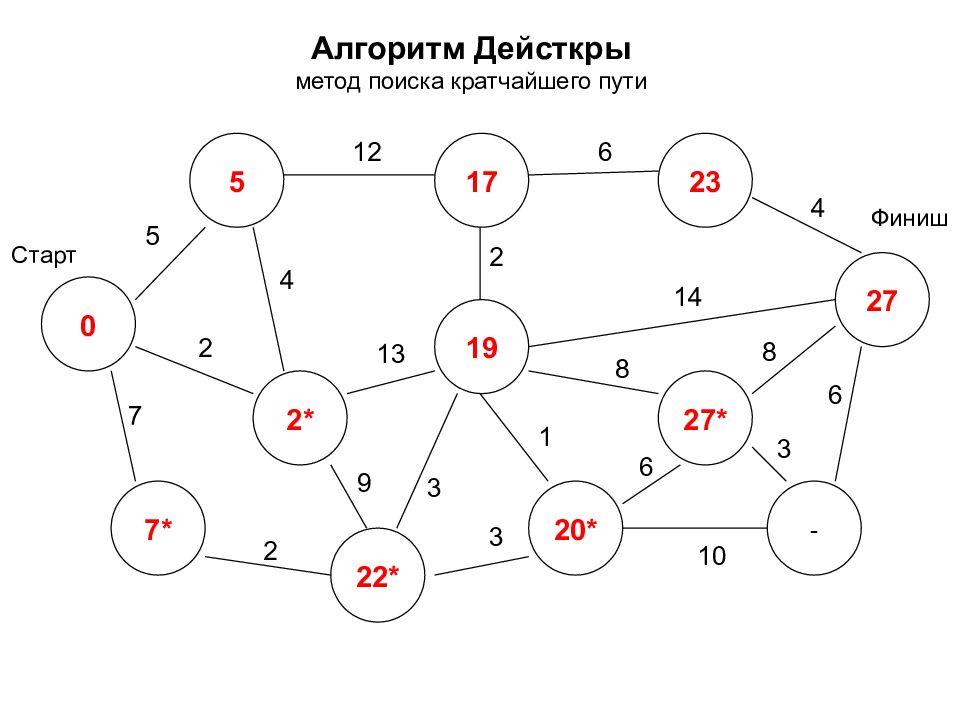
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2* 7* 5 17 20* 27 19 27* - 23 22* Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
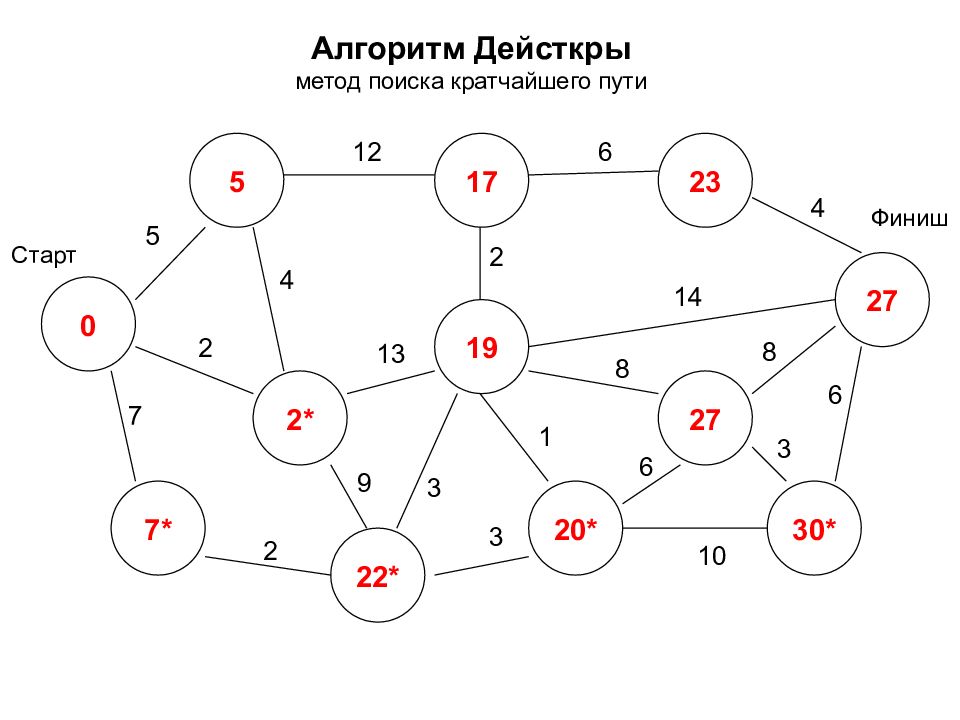
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2* 7* 5 17 20* 27 19 27 30* 23 22* Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
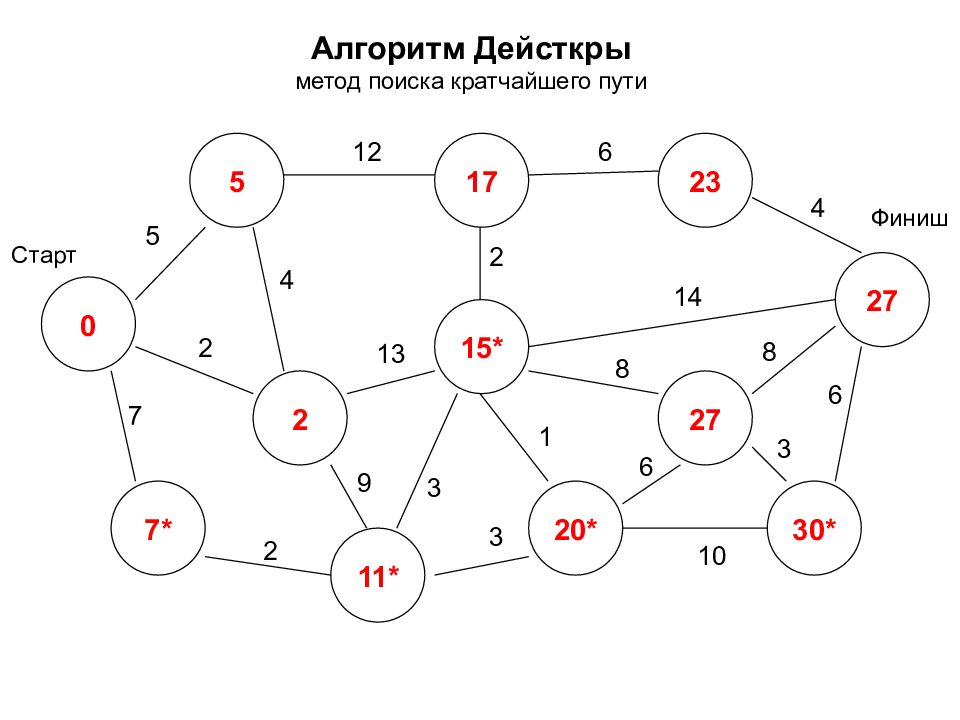
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7* 5 17 20* 27 15* 27 30* 23 11* Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
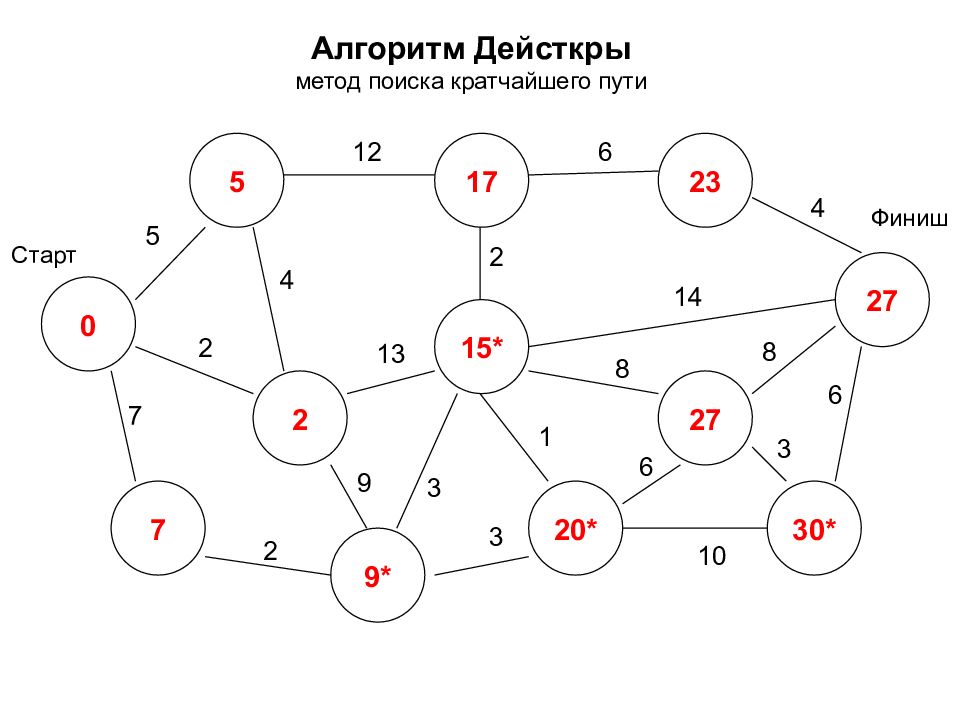
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 17 20* 27 15* 27 30* 23 9* Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
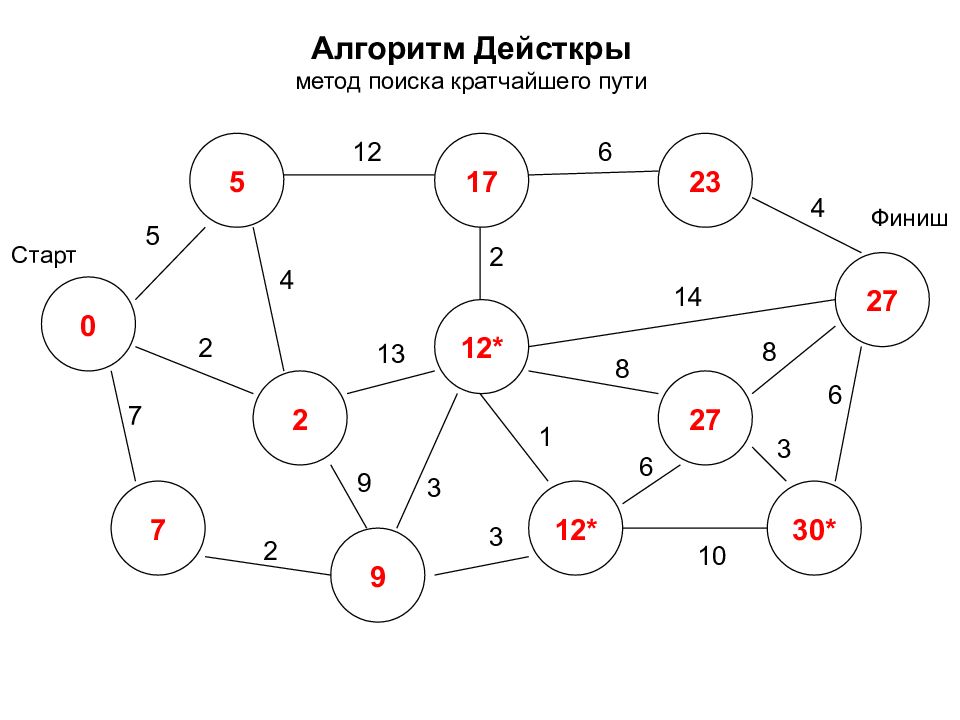
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 17 12* 27 12* 27 30* 23 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
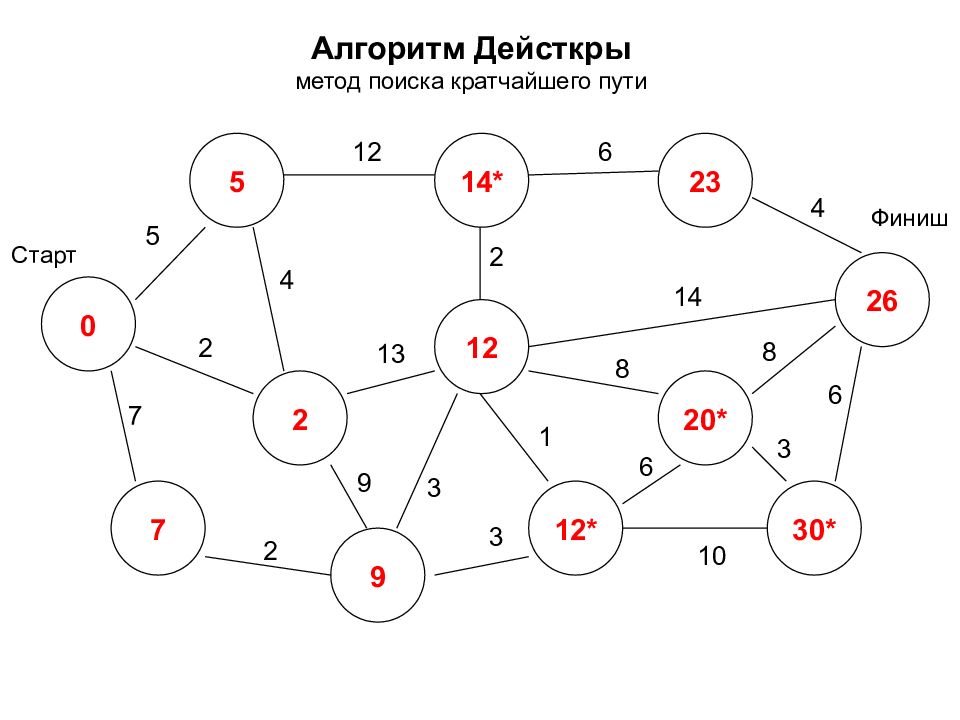
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14* 12* 26 12 20* 30* 23 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
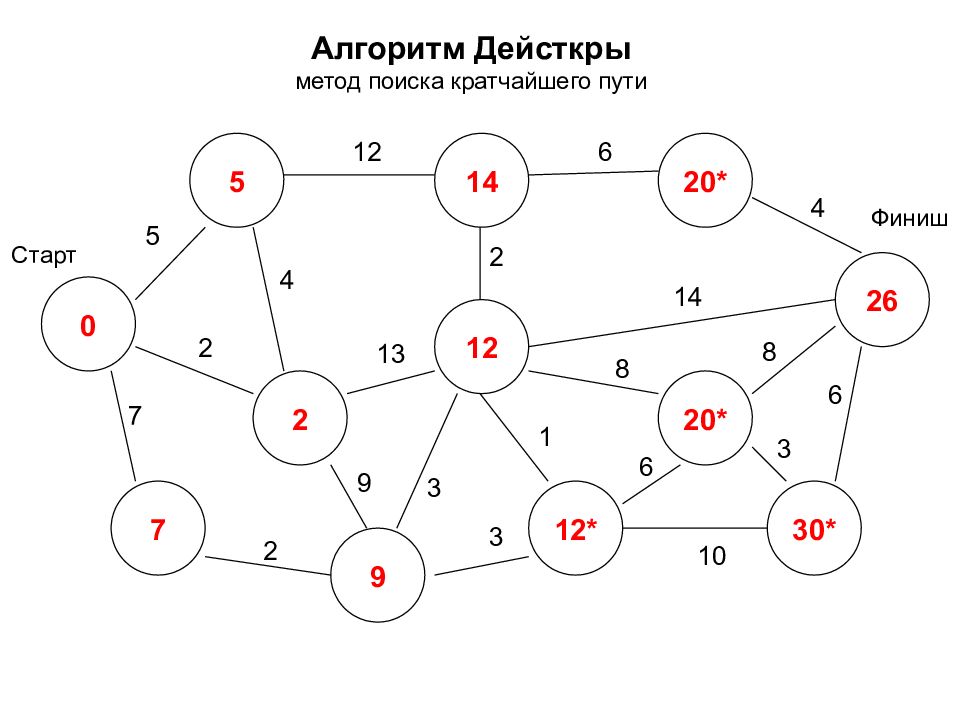
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12* 26 12 20* 30* 20* 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
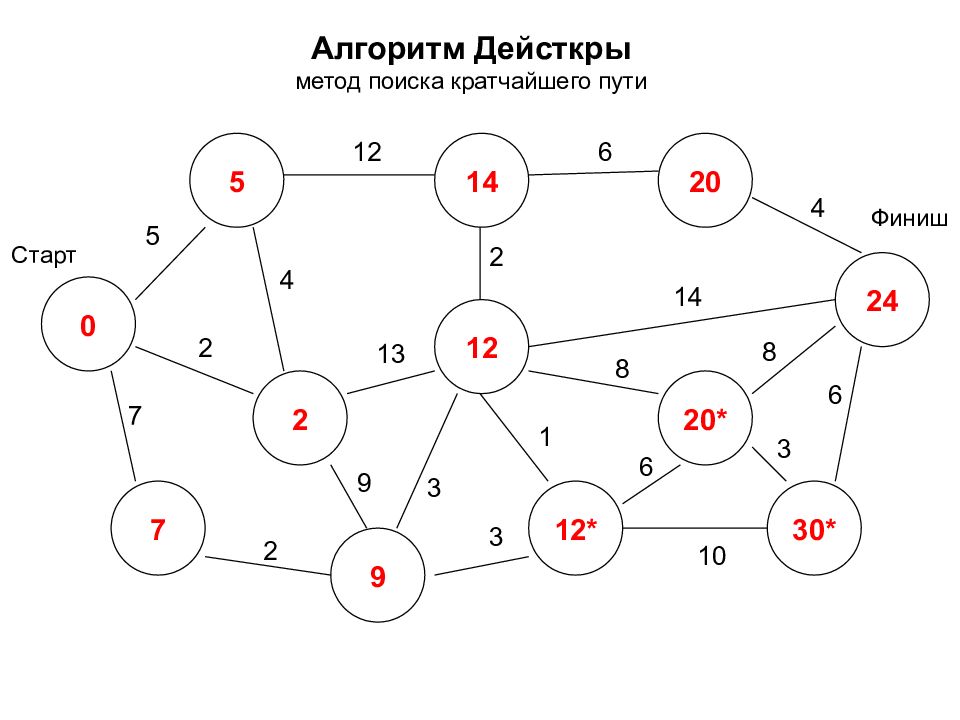
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12* 24 12 20* 30* 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12* 24 12 20 23* 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
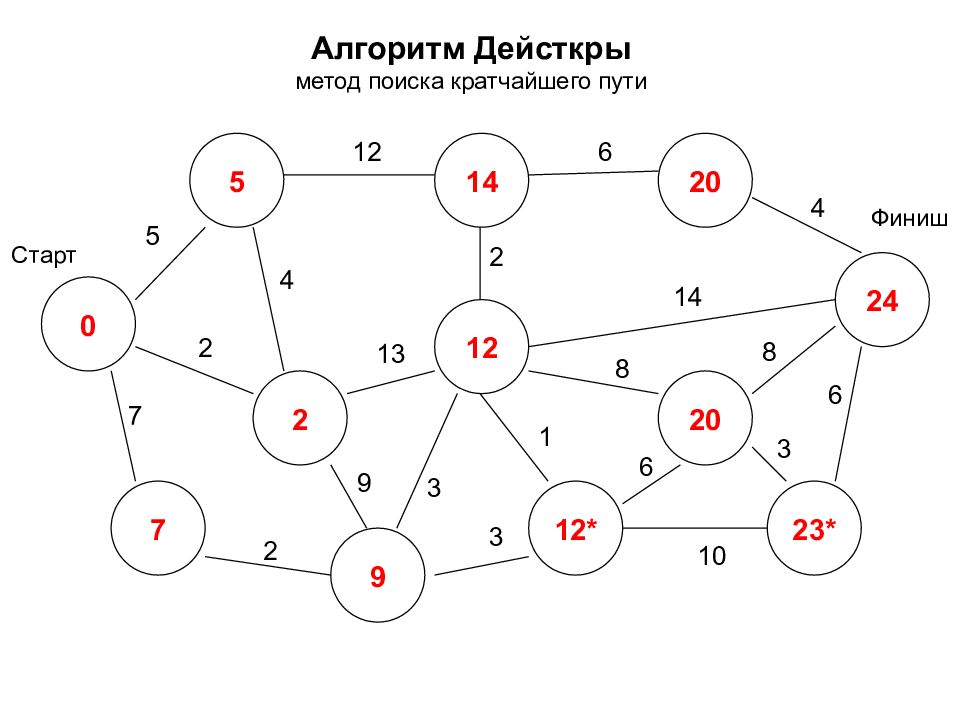
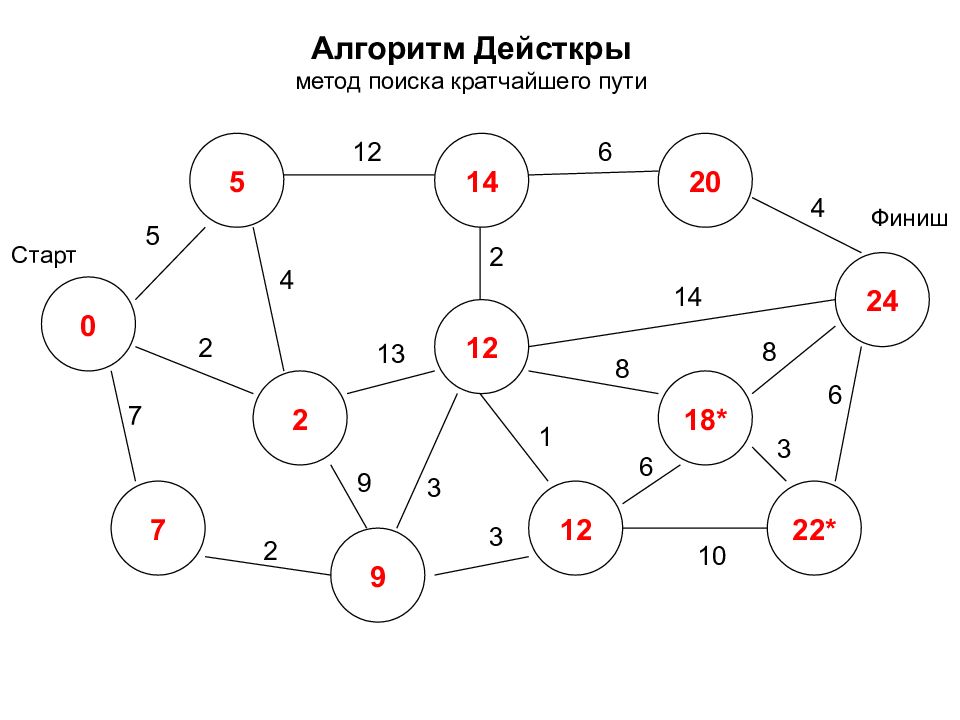
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12 24 12 18* 22* 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
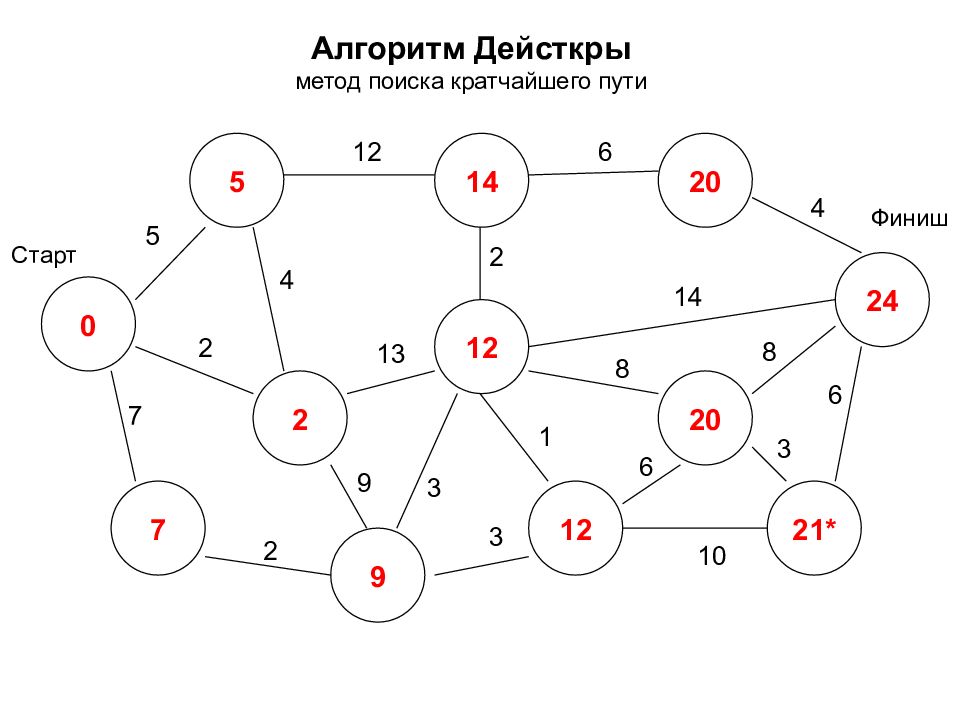
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12 24 12 20 2 1* 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12 24 12 20 2 2 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12 24 12 20 22 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12 24 12 20 22 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12 24 12 20 22 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12 24 12 20 22 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12 24 12 20 22 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
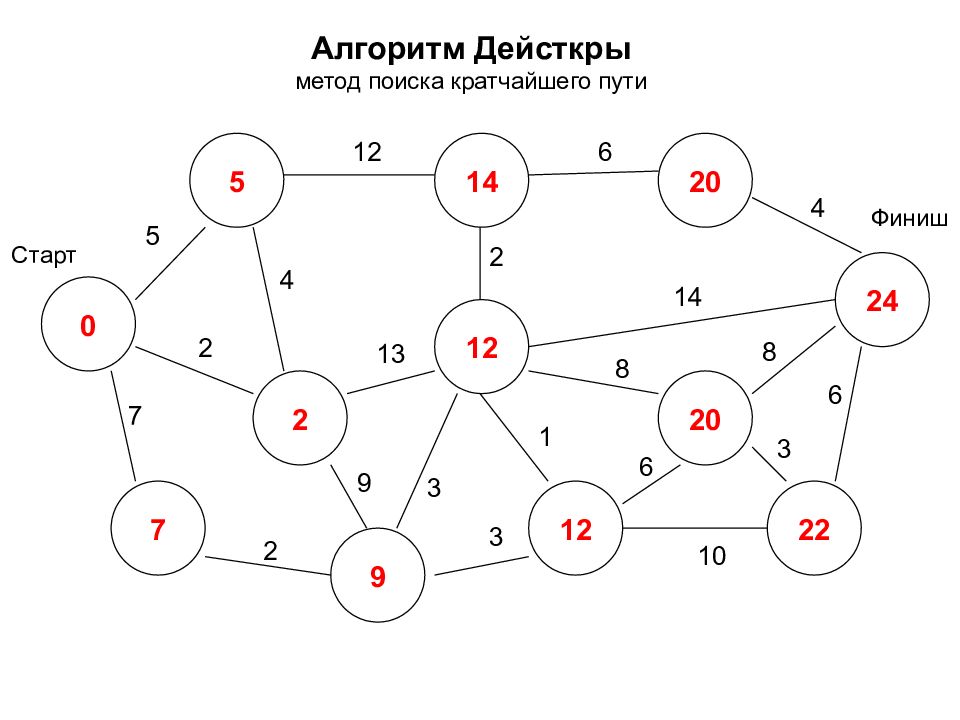
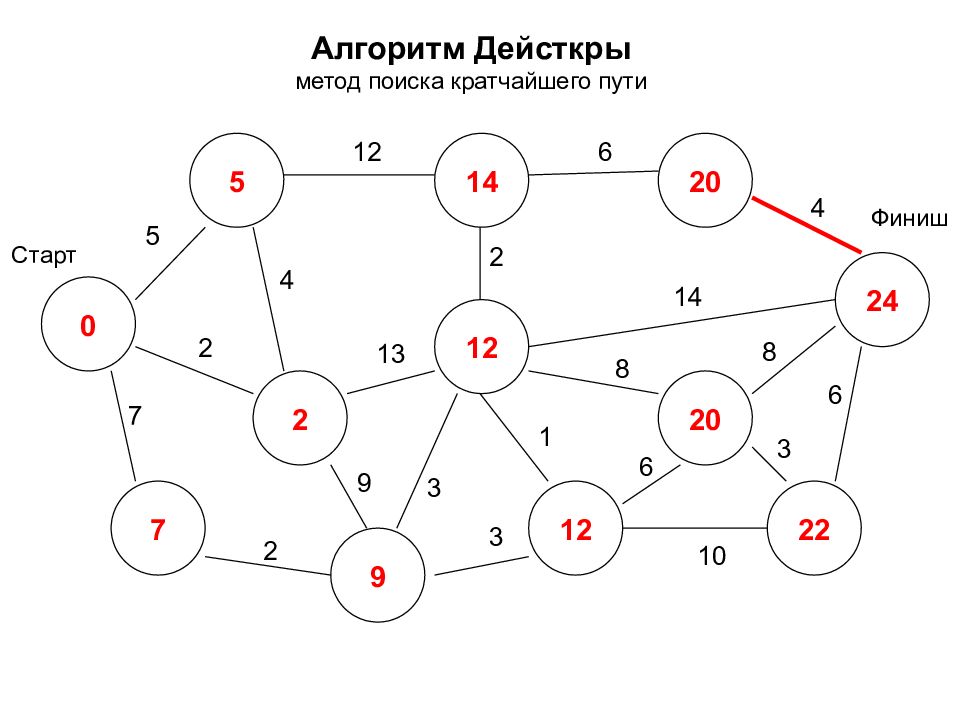
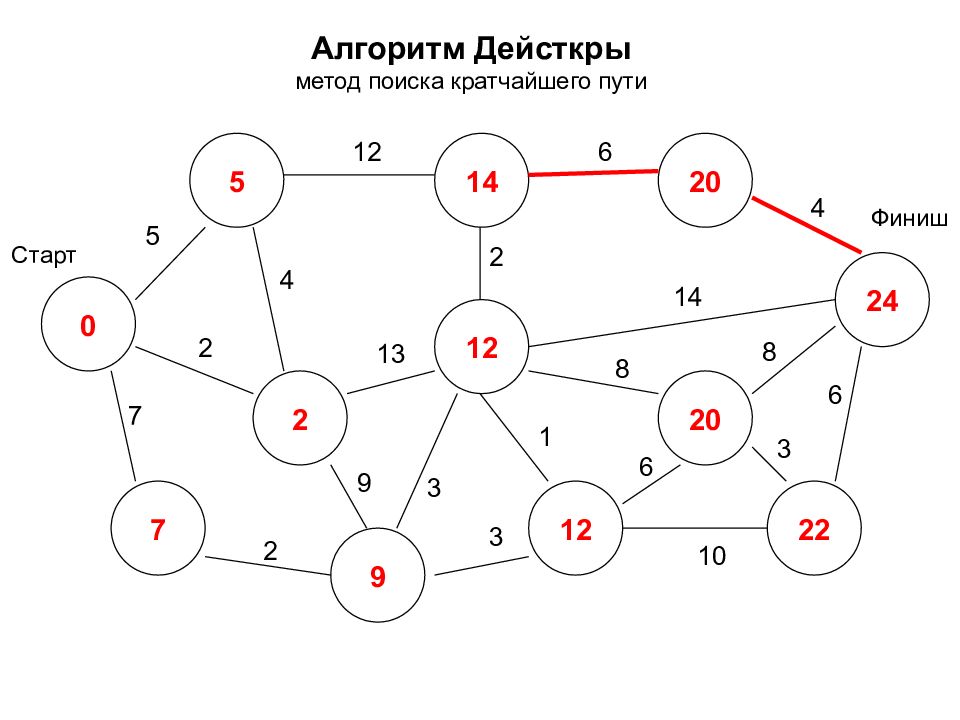
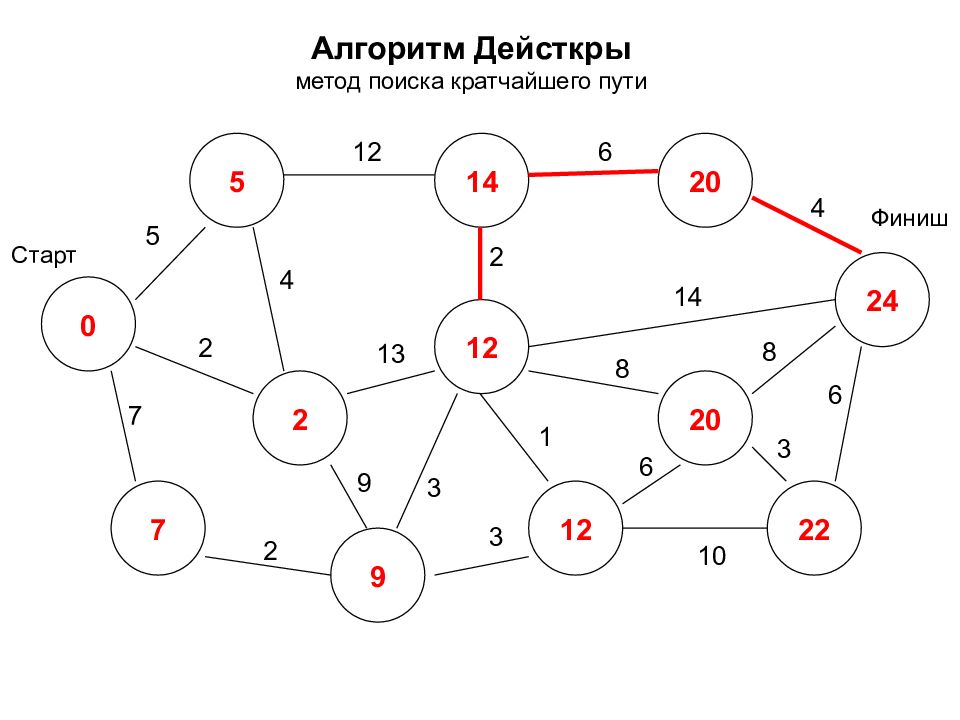
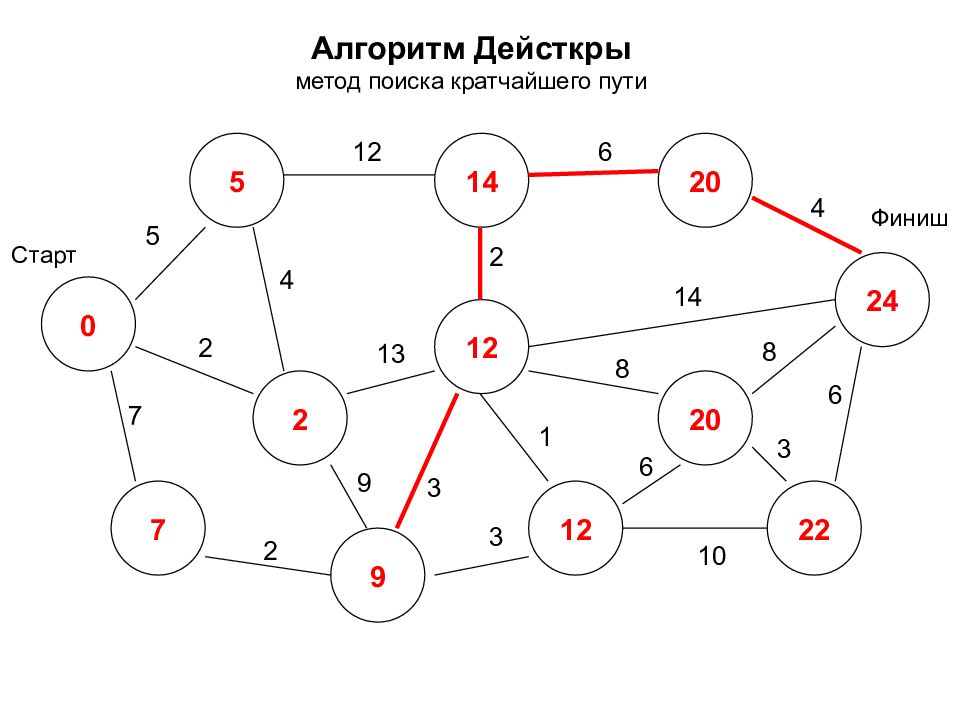
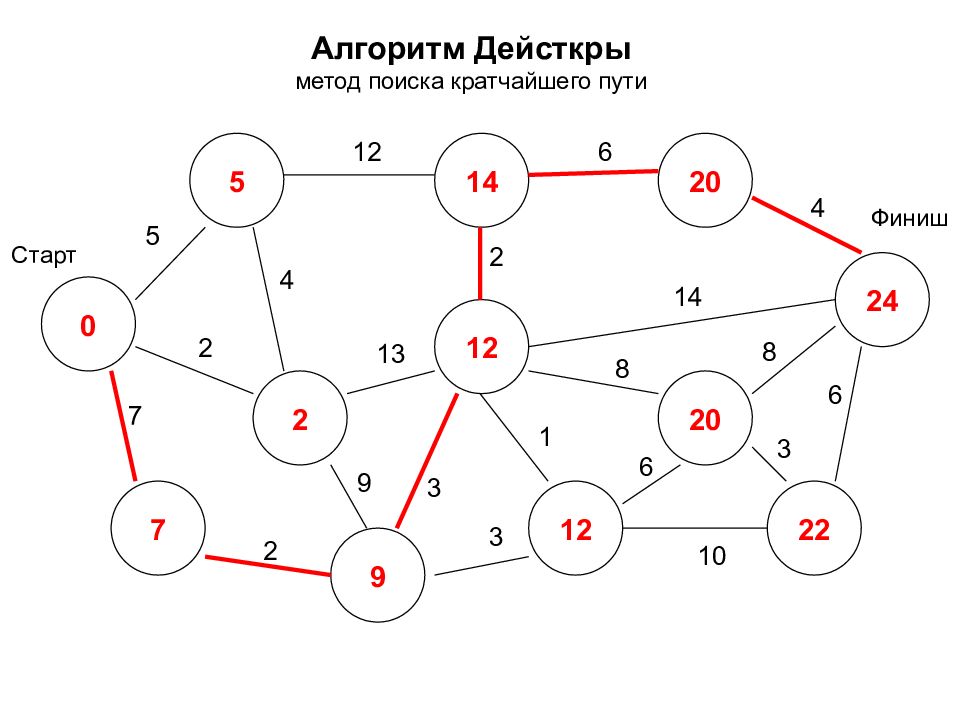
Алгоритм Дейсткры метод поиска кратчайшего пути 0 2 7 5 14 12 24 12 20 22 20 9 Старт Финиш 5 7 2 2 12 3 9 4 2 6 4 14 8 8 3 6 1 3 10 6 13
