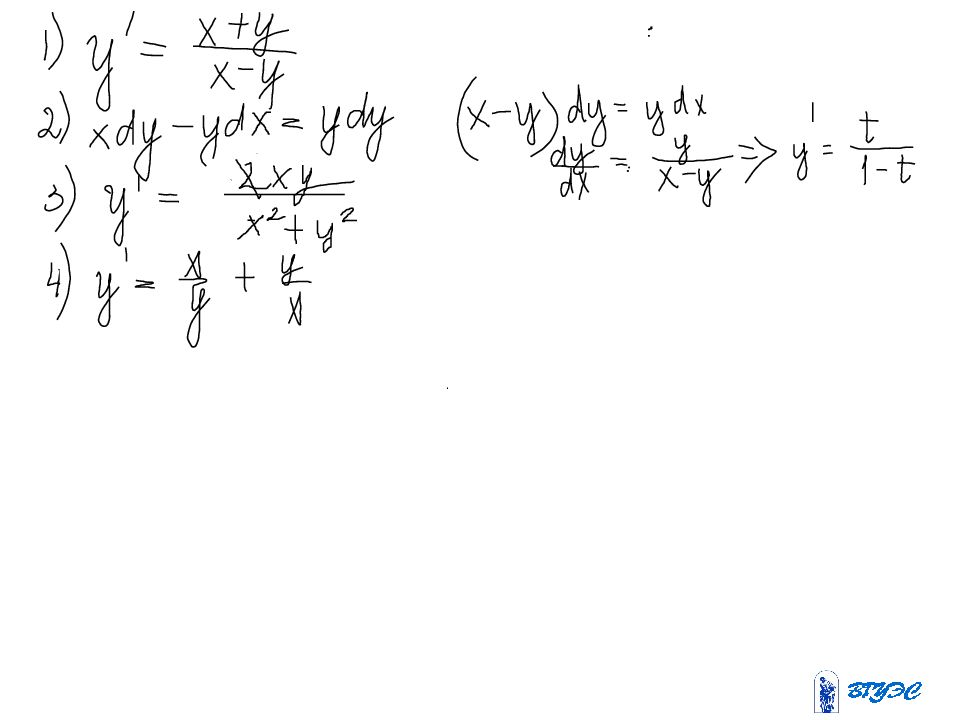Смысл там, где змеи интеграла. Меж цифр и букв, меж d и f ! В.Брюсов Дифференцирование – это технология, тогда как интегрирование всегда было искусством.
При изучении явлений природы, решении многих задач физики и техники, химии и биологии, других наук не всегда удается непосредственно установить прямую зависимость между величинами, описывающими тот или иной процесс. Однако в большинстве случаев можно установить связь между величинами (функциями) и скоростями их изменения относительно других (независимых) переменных величин, т.е. найти уравнения, в которых неизвестные функции входят под знак производной. Эти уравнения называют дифференциальными.
Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f(x) и её производных (или дифференциалов ): Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала). Пример: y (4) – y + x = 0 - уравнение четвёртого порядка. Уравнение второго порядка: Функция y ( x ) называется решением (или интегралом) дифференциального уравнения если при подстановке ее в уравнение обращает его в тождество.
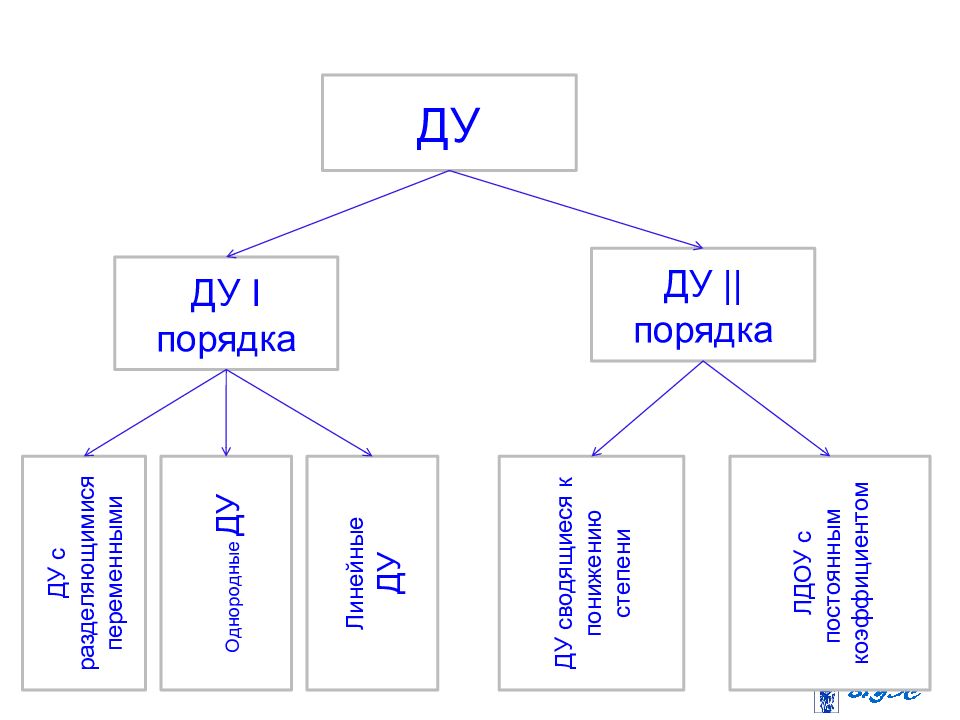
ДУ с разделяющимися переменными ДУ ДУ I порядка ДУ || порядка Однородные ДУ ДУ сводящиеся к понижению степени ЛДОУ с постоянным коэффициентом Линейные ДУ
ОДУ первого порядка Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида: где x - независимая переменная, y(x) - неизвестная функция Общее решение: Пример : общее решение:
Функциональное уравнение F ( x, y, y ) = 0 или y = f ( x, y ), связывающее между собой независимую переменную, искомую функцию y(x) и ее производную y (x) ( или дифференциал d(y)), называется дифференциальным уравнением первого порядка.
Простейшим примером дифференциального уравнения является уравнение где f ( x ) – известная функция, а y = y ( x ) – искомая функция независимого переменного x. Решения этого уравнения называют первообразными функциями для функции f ( x ). Например, решениями дифференциального уравнения являются функции С – произвольная постоянная, причем других решений это уравнение не имеет.
Дифференциал Дифференциал функции (differential) есть главная (линейная) часть приращения функции, равная произведению производной на приращение аргумента: dy = f ′( x ) ⋅Δ x Или dy = f ′( x ) ⋅ dx Если x – независимая переменная, то Δ x = dx Дифференциал Δ y = f ′( x ) ⋅Δ x +α (Δ x ) ⋅Δ x
Различие между дифференциалом производной функции: Для любой функции y = f(x) производная y ´ зависит только от одной переменной x, тогда как её дифференциал dy зависит от двух переменных x и Δ x.
Переменная величина z называется функцией двух переменных x; y, если каждой паре допустимых значений x и y соответствует единственное значение z. Записывают так: z = f(x, у ) Понятие о частных производных Частной производной функции z по переменной x называется производная, вычисленная в предположении, что y – const. Обозначается: Аналогично: частная производная по y, вычисленная в предположении, что х – const. Выражение называется полным дифференциалом функции z
Вычислить частные производные от функции: постоянная постоянная постоянные постоянная
Большое количество задач, приводящих к дифференциальным уравнениям, дает механика. Классической задачей динамики точки является задача отыскания закона движения материальной точки, если известны действующие силы. В этом случае второй закон Ньютона приводит к дифференциальному уравнению. В зависимости от действующих сил получаются уравнения самых различных типов. Рассмотрим наиболее простую из задач этого типа.
Задача4. Материальная точка массы m (г) свободно падает под действием силы тяжести. Найти закон движения точки без учёта сопротивления воздуха. Решение. Возьмем вертикальную ось, направленную вниз, с выбранной на ней точкой отсчёта О. Положение материальной точки определяется координатой ОМ= s, изменяющейся в зависимости от времени t (Рисунок 4) Запишем второй основной закон динамики в виде s s 0 О М Рисунок 4 где m – масса, а - ускорение точки и F – действующая сила. По предположению, на точку действует только сила тяжести, так что где g – ускорение силы тяжести. Ускорение а есть вторая производная от пути по времени, и мы получаем: или (18)
Равенство (18) представляет собой дифференциальное уравнение, содержащее вторую производную неизвестной функции s = s ( t ). Так как эта вторая производная оказывается здесь известной функцией от аргумента (даже просто постоянной величиной), то искомую функцию легко получить, произведя дважды интегрирование по t. Последовательно находим (19) (20) Равенство (20) дает искомый закон движения, однако, как и в предыдущих задачах, оно содержит постоянные интегрирования, в данном случае – два. Их можно определить, зная начальное положение и начальную скорость точки. Пусть в начальный момент ( t =0) скорость точки равна, а ее расстояние от точки отсчета О равно s 0. Так как выражает скорость, то из (19) получаем, а из (20) -, и закон движения приобретает вид Таким образом, получили известную формулу пути, пройденного точкой при равномерно ускоренном движении.
Решением (интегралом) уравнения первого порядка называется всякая функция y = ( x ), которая, будучи подставлена в уравнение вместе со своей производной y = ( x ), обращает его в тождество относительно x.
Общим решением дифференциального уравнения первого порядка называется такая функция y = ( x, C ), которая при любом значении параметра C является решением этого дифференциального уравнения. Уравнение Ф( x, y, C ) =0, определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
Если уравнение 1-го порядка разрешить относительно производной, то оно может быть представлено в виде Его общее решение геометрически представляет собой семейство интегральных кривых, т. е. совокупность линий, соответствующих различным значениям постоянной C.
Задача отыскания решения дифференциального уравнения, удовлетворяющего начальному условию при,называется задачей Коши для уравнения 1-го порядка. Геометрически это означает: найти интегральную кривую дифференциального уравнения, проходящую через данную точку.
График решения дифференциального уравнения называется интегральной кривой. С геометрической точки зрения, общее решение ДУ первого порядка есть семейство интегральных кривых на плоскости XOY Например, общее решение ДУ есть семейство парабол : x y 0 Частное решение - одна кривая из этого семейства, проходящая через точку М(х 0 ; у 0 ) Частное решение, удовлетворяющее начальному условию: у(1) = 2 - это одна парабола, проходящая через точку М(1, 2) с уравнением: Задача отыскания частного решения ДУ, удовлетворяющего заданному начальному условию называется задачей Коши.
Дифференциальное уравнение называется уравнением с разделенными переменными. Дифференциальное уравнение 1-го порядка называется уравнением с разделяющимися переменными, если оно имеет вид: . Для решения уравнения делят обе его части на произведение функций, а затем интегрируют.
Выражают производную функции через дифференциалы dx и dy. Члены с одинаковыми дифференциалами переносят в одну сторону равенства и выносят дифференциал за скобку. Разделяют переменные. Интегрируют обе части равенства и находят общее решение. Если заданы начальные условия, то находят частное решение.
Разделим переменные в уравнении Интегрируем: Имеем:
Характерное свойство дифференциальных уравнений – иметь бесконечное множество решений. В этом смысле приведенный выше пример типичен. Поэтому, решив дифференциальное уравнение, описывающее эволюцию некоторого процесса, нельзя одновременно найти зависимость между величинами, характеризующими данный процесс. Чтобы выделить из бесконечного множества зависимостей ту, которая описывает именно этот процесс, надо иметь дополнительную информацию, например знать начальное состояние процесса. Без этого дополнительного условия задача недоопределенна.
Дифференциальное уравнение первого порядка называется однородным, если его можно привести к виду y = или к виду где и – однородные функции одного порядка.
Функция z=f(x,y) называется однородной порядка k, если при умножении ее аргументов на t получаем: Если k=0, то имеем функцию нулевого порядка. Например, функция нулевого порядка.
1) Разрешить уравнение относительно производной 2) Ввести новую переменную y = tx 3) Вычислить 4) Подставить y и в уравнение 5) Получить ДУ с разделяющимися переменными и решать по схеме
Разрешим уравнение относительно производной : Разделив числитель и знаменатель дроби на, имеем:
Интегрируем: Исключая вспомогательную функцию и, окончательно получим: или
1 вариант 2 вариант
Дифференциальное уравнение первого порядка называется линейным, если оно содержит и в первой степени, т.е. имеет вид . Решают такое уравнение с помощью подстановки y = u∙v, где u и v -вспомогательные неизвестные функции, которые находят, подставляя в уравнение вспомогательные функции и на одну из функций налагают определенные условия.
ДУ первого порядка называется линейным, если неизвестная функция y ( x ) и её производная входят в уравнение в первой степени: здесь p ( x ), q ( x ) - непрерывные функции. Пример :
Для решения уравнения представим y ( x ) в виде произведения двух новых неизвестных функций u(x) и v(x) : y(x) = u(x)v(x). Тогда и уравнение приводится к виду : или Это уравнение решаем в два этапа: сначала находим функцию v ( x ) как частное решение уравнения с разделяющимися переменными : затем находим u ( x ) из уравнения :
Пример : Решение: и общее решение уравнения .
Для нахождения частного решения, соответствующего начальным условиям (задача Коши), подставим в общее решение Решение задачи:
Задание : К какому типу относятся дифференциальные уравнения:
Уравнением Бернулли называется уравнение 1-го порядка, имеющее вид , где и Его, как и линейное уравнение решают с помощью подстановки
Линейное уравнение решим с помощью подстановки y = uv, где u и v - вспомогательные неизвестные функции. Приравняем к нулю выражение в скобках: Тогда Найдем v : Реш
Некоторые типы уравнений, допускающие понижение порядка Уравнение вида решается последовательным n -кратным интегрированием. Переобозначив постояные, общее решение запишем в виде : y = cos x + C 1 x 3 + C 2 x 2 + C 3 x + C 4. Пример :
Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные. Порядок уравнения вида F(x, y (k), y (k+1), y (k+2 ), …,y (n) ) = 0, не содержащего функции y(x) и (k – 1) младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z(x) = y (k) (x). Тогда уравнение примет вид т.е. будет уравнением (n – k) -го порядка. После нахождения z (x) последовательным интегрированием решается уравнение y (k) (x)= z(x).
Пример: Понизить порядок уравнения: Младшая производная, входящая в явной форме в уравнения, - вторая, поэтому делаем замену искомой функции: Тогда и уравнение примет вид :
Уравнение, содержащее производную или дифференциалы второго порядка, называется дифференциальным уравнением второго порядка. Простейшее из этих уравнений имеет вид:
Решается двукратным интегрированием: Получено общее решение:
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида: где p и q – постоянные величины, а f(x) – непрерывная функция. Уравнение, правая часть которого равна нулю, называется однородным:
Теорема 1: Если y=y 1 решение однородного уравнения, то y= а y 1, где а – постоянный множитель, также будет решением этого уравнения. Теорема 2: Если y=y 1 и y=y 2 - решения однородного уравнения, то сумма у=у 1 +у 2 также решение этого уравнения. Решения y=y 1 и y=y 2 - частные. Частные решения могут быть линейно зависимые и линейно независимые.
Два частных решения однородного уравнения называются линейно зависимыми, если одно из них может быть получено умножением другого на какой-нибудь постоянный множитель; в противном случае частные решения называются линейно независимыми. Пример: Частные решения: - линейно независимые решения.
Теорема 3: Если линейно независимые частные решения однородного уравнения, то общее решение будет: где С 1 и С 2 – произвольные постоянные величины
Частными линейно независимыми решениями являются функции вида: где k постоянное число, которое нужно найти для того или иного линейного дифференциального уравнения второго порядка. Если - частное решение однородного уравнения, то оно должно удовлетворять этому уравнению при некотором значении k. Чтобы найти это значение k, продифференцируем функцию
Подставим в однородное уравнение вместо и их значения, получим: или:
Уравнение называют характеристическим уравнением линейного дифференциального однородного уравнения второго порядка. Для составления характеристического уравнения достаточно в однородном уравнении вместо : написать соответственно:
характеристическое уравнение D = корни Общее решение уравнения D Y = C 1 + C 2 D=0 K 1 =K 2 =K Y = C 1 + C 2 x D<0 K 1,2 = Y =
Решить уравнение: Составим характеристическое уравнение: Откуда: Линейно независимые частные решения: Общее решение:
Решить уравнение: Составим характеристическое уравнение: Тогда частные решения: Общее решение:
Решить уравнение: Составим характеристическое уравнение: Частные решения: Общее решение:
Показать, что функция где С 1 и С 2 – произвольные постоянные, является общим решением уравнения: Найти частные решения уравнений: При решить уравнение: При решить уравнение: 3. При решить уравнение:
