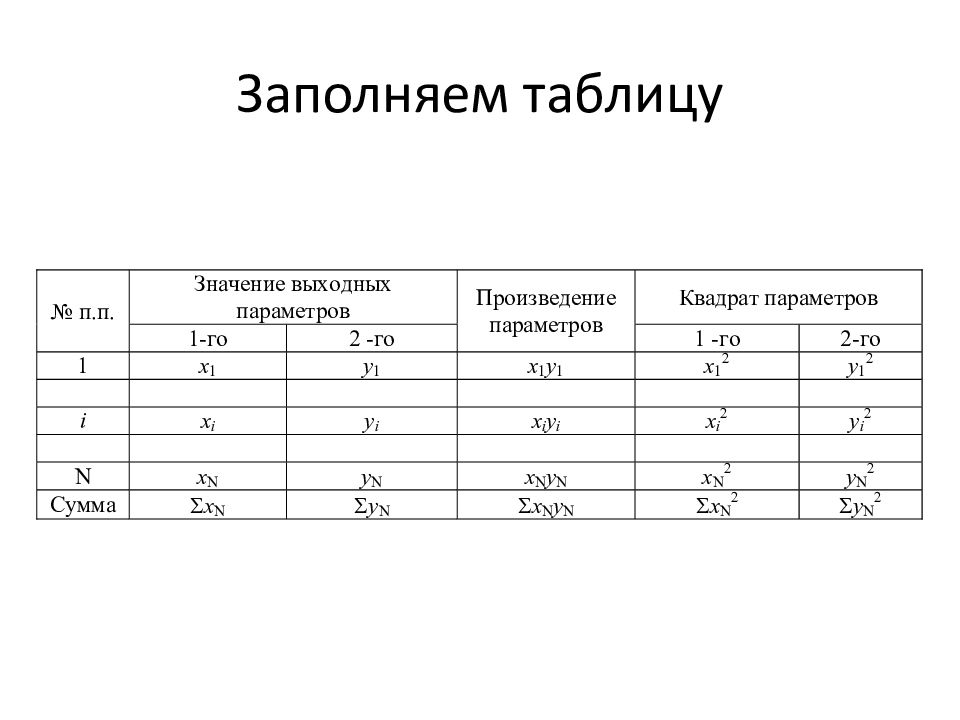
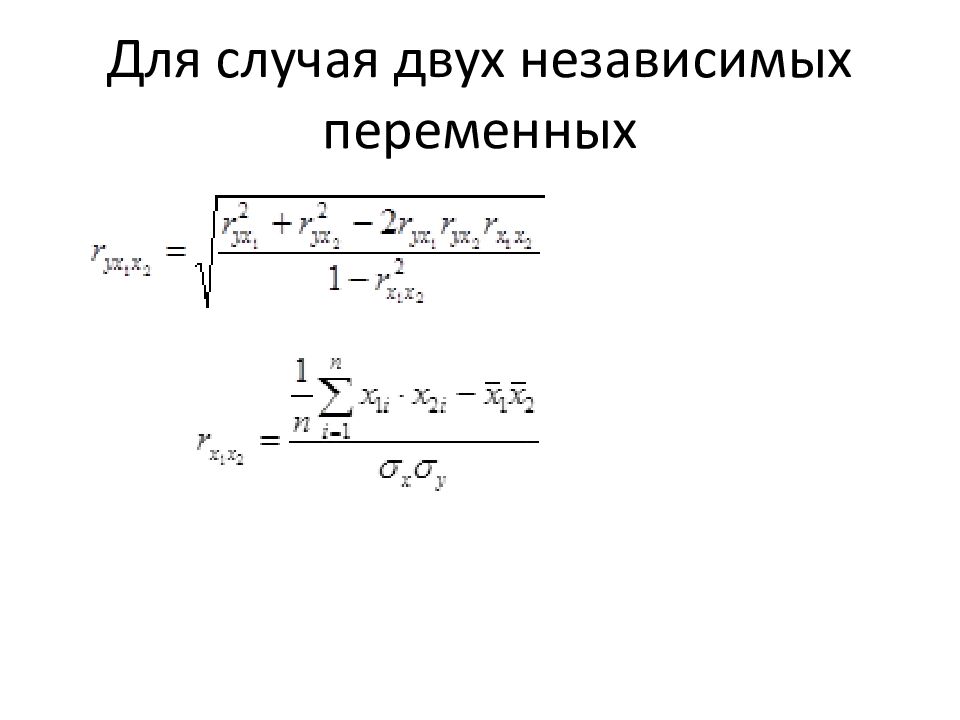
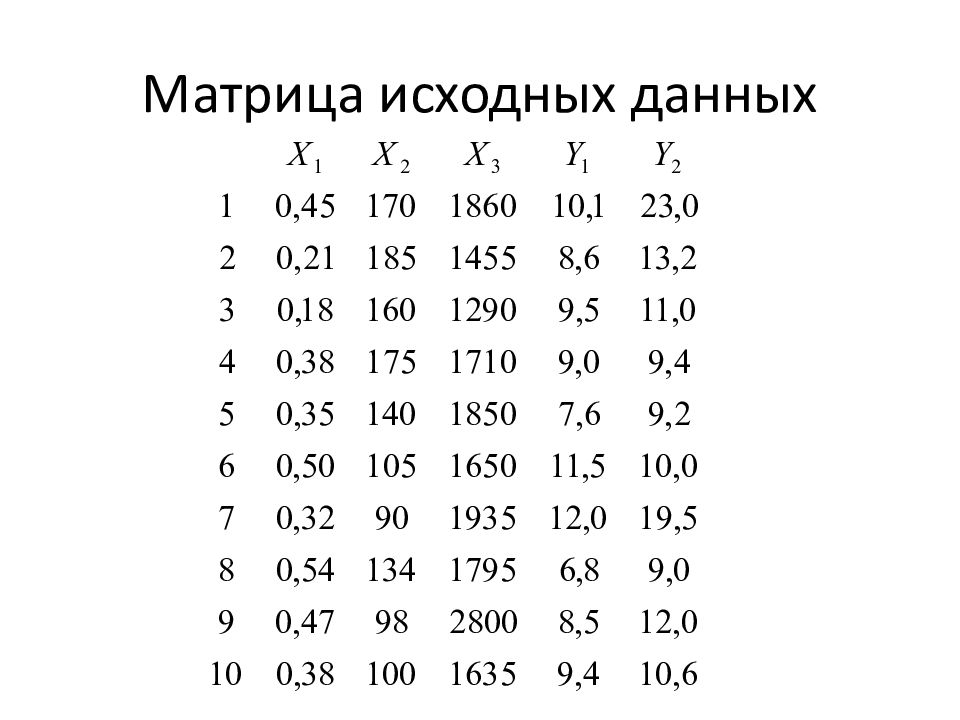
Слайд 2: Корреляционный анализ
Он используется для установления статистических связей между параметрами оптимизации. Для множества объектов матрицу парных корреляций R получают в ходе следующих преобразований матриц: где Z – матрица стандартных значений, а ее элементы получают:
Слайд 3: Элементы матрицы коэффициентов
получают по данным матрицы частных корреляций. Коэффициент множественной корреляции R o представляет собой численную характеристику силы связей отклика со всеми факторами.
Слайд 4: Парная корреляция
Корреляционный анализ – метод установления статистических связей между выходными параметрами сложной системы. Коэффициент парной корреляции является мерой тесноты линейной связи между двумя случайными величинами. В общем случае его величина меняется от 0 до 1. Если коэффициент = 0, то связь отсутствует, а если 1, то связь линейная.
Слайд 6: Упрощение расчетов
Слайд 8: Статистическая значимость коэффициента
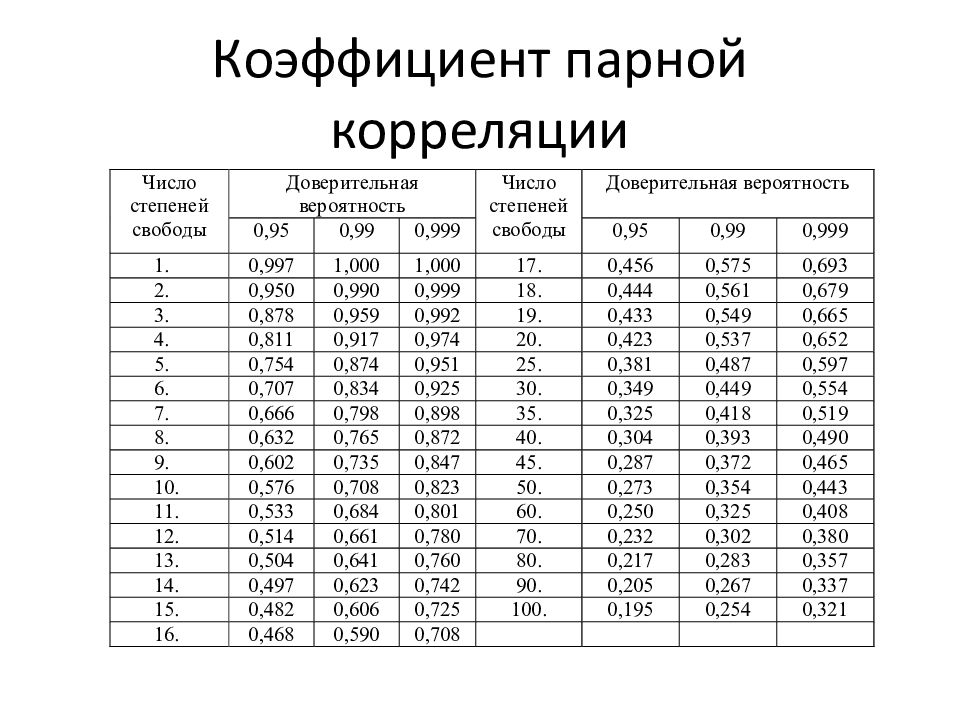
Для этого по выбранному уровню доверительной вероятности (для обычных технических расчетов принимается равной 0,95 или 0,99) и числу степеней свободы f = N -2 определяется критическое значение коэффициента парной корреляции ( r кр ). Выбор значений r кр производится по таблице, имеющейся в приложении. В случае, если абсолютная величина коэффициента парной корреляции не меньше критического, то линейная связь между параметрами считается статистически значимой. В противном случае линейная связь статистически не значима и, следовательно, необходимо переходить более сложным математическим зависимостям.
Слайд 9: Построение уравнения регрессии
Линейное уравнение регрессии имеет вид: Коэффициенты уравнения регрессии можно рассчитать по следующим формулам (за х и у можно принять ту или другую величину):
Слайд 10: Анализ полученных результатов
После установления статистически значимой линейной связи необходимо определить параметр, который будет определяться экспериментально, и по которому будет осуществляться оптимизация технологического процесса. Оценку линейных связей параметров необходимо осуществлять с учетом абсолютного значения коэффициента парной корреляции. При прочих равных условиях предпочтение отдается тем параметрам, для которых метод определения более прост или позволяет проводить измерения с высокой точностью. Для упрощения анализ полученных результатов регрессионное уравнение может быть представлено в графическом виде.
Слайд 13: Множественная корреляция
На практике, весьма часто, приходиться анализировать связь между зависимой переменной у и группой факторов х 1 ; х 2 ;....... х l. Для оценки используют: а) коэффициент множественной корреляции. б) коэффициент парциальной корреляции
Слайд 14: Коэффициент множественной корреляции
выражает степень связи между у и всей группой независимых переменных R – матрица парных корреляций R 11 – алгебраическое дополнение определителя R к элементу r yy. Для l – независимых переменных и n измеренных значений у:
Слайд 16: Коэффициент парциальной корреляции
позволяет оценить влияние на у каждой из независимых переменных последовательно алгебраические дополнения к элементам Для частных случаев можно воспользоваться формулами Другие коэффициенты получают циклической перестановкой индексов
Слайд 17: Оценка статистической значимости гипотезы
Если ( х 1.....х l ) – факторы, а ( у 1........у n ) – опыты на точках, то: где это число степеней свободы. При наличии линейной связи проводят проверку по критерию Фишера: Можно пользоваться корреляционным отношением: где m – количество измерений на одну точку
Слайд 18: Пример:
При анализе связи σ в (у) размеры частиц η – фазы (х 1 ) и межчастичным расстоянием (х 2 ) после 5 режимов обработки при испытании трех образцов получено: n =15 1 = числу свободных переменных = l. 2 = 15-2-1=12 Парциальные корреляции: Вывод: по коэффициенту множественной корреляции оба параметра оказывают влияние на прочностные свойства. По парциальной корреляции влияет только межчастичное расстояние.
Слайд 20: Сущность и теоретические основы метода
Метод канонических корреляций относится к статистическим методам анализа связей между массовыми явлениями и процессами. Если рассматривается зависимость между одним результативным показателем Y и одним фактором X, то речь идет о парной корреляции. Когда имеется несколько переменных X и одна переменная У, проводится множественный корреляционный анализ для установления и измерения степени связи между переменными. Каноническая корреляция — это распространение парной корреляции на случай, когда имеется несколько результативных показателей Y и несколько факторов X. Основная цель применения этого метода состоит прежде всего в поиске максимальных корреляционных связей между группами исходных переменных: показателями-факторами и результативными качественными показателями. Кроме того, метод канонических корреляций дает возможность сократить объем исходных данных за счет отсева малозначимых факторов.
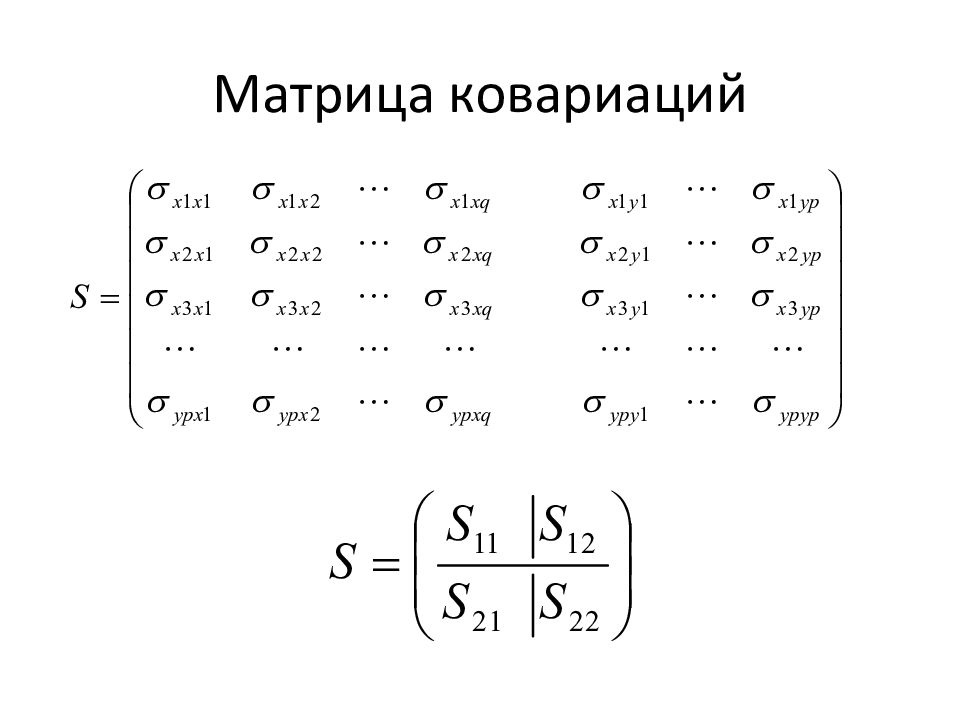
Слайд 21: Матрица значений исходных переменных
Х 1, Х 2, X g — переменные факторы; У 1, Y 2, Y p — результативные показатели. Так как на практике количество факторов значительно превосходит количество результативных показателей, то будем предполагать, что р < g. Каноническая корреляция — это корреляция между новыми компонентами (каноническими переменными) U и V:
Слайд 22: Подготовка информации и вычисления канонических корреляций
По аналогии с парной корреляцией теснота связи между каноническими переменными будет определятся каноническими коэффициентами: cov - некоторое число Е – математическое ожидание величины. P ij – совместная вероятность х и у. var – дисперсия случайной величины (вспомним 2 случая среднеквадратических отклонения). var (х) = 0.
Слайд 23: Вычисление канонических коэффициентов корреляции
S 12, S 21 – матрица взаимодействия х и у (размерность). ( S 12 – g x p и S 21 – p x g ) S 21 – результат транспонирования S12. S 11 – ковариационная матрица исходных переменных, ее размер g x g. S 22 – ковариантная матрица у, p x p.
Слайд 24: Решение задачи
необходимо решить уравнения: U, V – векторы канонических переменных. X, Y – матрицы исходных значений. А, В – векторы коэффициентов. Если предположить, что средние значения канонических переменных U и V равны нулю, а их дисперсии равны единице, r Для упрощения расчетов, считаем, что каждая из переменных имеет единичную дисперсию и нулевое математическое ожидание, следовательно знаменатель этого выражения = 1.
Слайд 25: Находим максимальный коэффициент корреляции
воспользуемся способом множителей Лагранжа для нахождения условного экстремума ( λ – множитель Лагранжа), продифференцируем функцию Лагранжа по компонентам векторов А и В и приравняем их к нулю, получим систему: Домножим полученные выражения на λ и обратную матрицу соответсвенно, получим: Умножив обе части на, получим Рассуждая аналогично
Слайд 26: Решение последнего уравнения
Чтобы решить уравнение, необходимо найти характеристи-ческие корни и характеристические векторы. Из предположения, что р < g, вытекает, что размерность вектора В меньше размерности вектора А. Можно определить вектор А из 1 уравнения системы: Для того чтобы найти компоненты вектора А, необходимо определить векторы В и . Значения 2 находятся как собственные значения матрицы С: Можно показать, что = r 1 1 = r
Слайд 27: Расчет канонических корреляций 3 фактора 2 параметра оптимизации
Пример
Слайд 31: Вспомогательные матрицы
Для определения собственных значений найдем матицу С Т.к. эта матрица имеет размер 2 х 2, то она будет иметь два собственных значения, и два собственных вектора.
Слайд 32: Вспомогательные матрицы
Для определения собственных значений найдем матицу С Т.к. эта матрица имеет размер 2 х 2, то она будет иметь два собственных значения, и два собственных вектора.
Слайд 34: Канонические переменные
И так максимальный коэффициент канонической корреляции 0,71.
Слайд 35: Проверка статистической значимости
Проверку статистической значимости коэффициентов проводят по критерию Бартлета: И для данного числа степеней свободы сравнивают с табличными: для числа степеней свободы ( p -1)( g -1)=2, и уровня значимости 0,95.
Слайд 36: Получение реальных коэффициентов
Для того чтобы получить коэффициенты, относящиеся к исходным данным, необходимо помнить, что мы все дисперсии приравняли к 1 => Т.о., все остальные коэффициенты будут равны: a2=0.03004 a3=0.0021 b1=-0.7147 b 2=0.1764 Уравнение канонических корреляций будет выглядеть следующим образом: U1=0, 9553 x1+ 0,0 304 x2+0, 0021 x3 V 1=-0,7147 y 1+0,176 y 2 В том случае, если нельзя ограничиться одним выходным параметром, то необходимо перейти к обобщенному параметру оптимизации.
Последний слайд презентации: Корреляционный анализ: Выводы
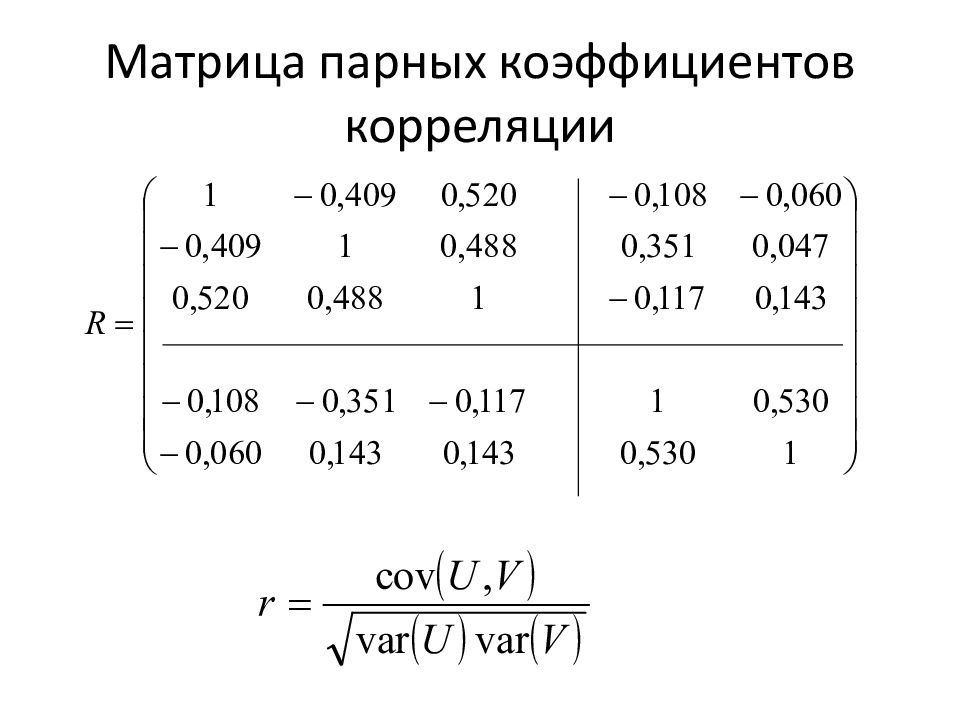
Максимальный коэффициент корреляции 0,701, что означает наличии тесной связи между факторами. Сами факторы Y тесно связаны между собой (их корреляция 0,53), также высокую сязь имеют факторы Х1 и Х3 (0,52) Второй коэффициент корреляции не велик и говорит о том, что другие линейные комбинации маловероятны. В обеих линейных комбинациях наиболее значима величина Х3, коэффициенты при других величинах существенно меняются по величине и меняют знак, т.е. достоверно только влияние фактора Х3. Для уточнения результатов следует повторить расчеты для других сочетаний факторных и результативных переменных, можно отбрасывать одну из переменных, и рассчитывать новые коэффициенты. В случае определения канонических корреляций нет необходимости добиваться независимости исходных переменных.