Эконометрика Тема 4
Элементы линейной алгебры Классическая нормальная линейная модель множественной регрессии Оценка параметров классической регрессионной модели методом наименьших квадратов Ковариационная матрица и ее выборочная оценка Определение доверительных интервалов для коэффициентов и функции регрессии Оценка значимости множественной регрессии. Коэффициент множественной детерминации и скорректированный коэффициент множественной детерминации 2
1. Элементы линейной алгебры 3 Матрицей размера (m * n) или mn - м атрицей называется таблица чисел, содержащая m строк и n столбцов:
1. Элементы линейной алгебры 4 Виды матриц (1): - вектор-строка размера n - вектор-столбец размера m - квадратная матрица n- го порядка
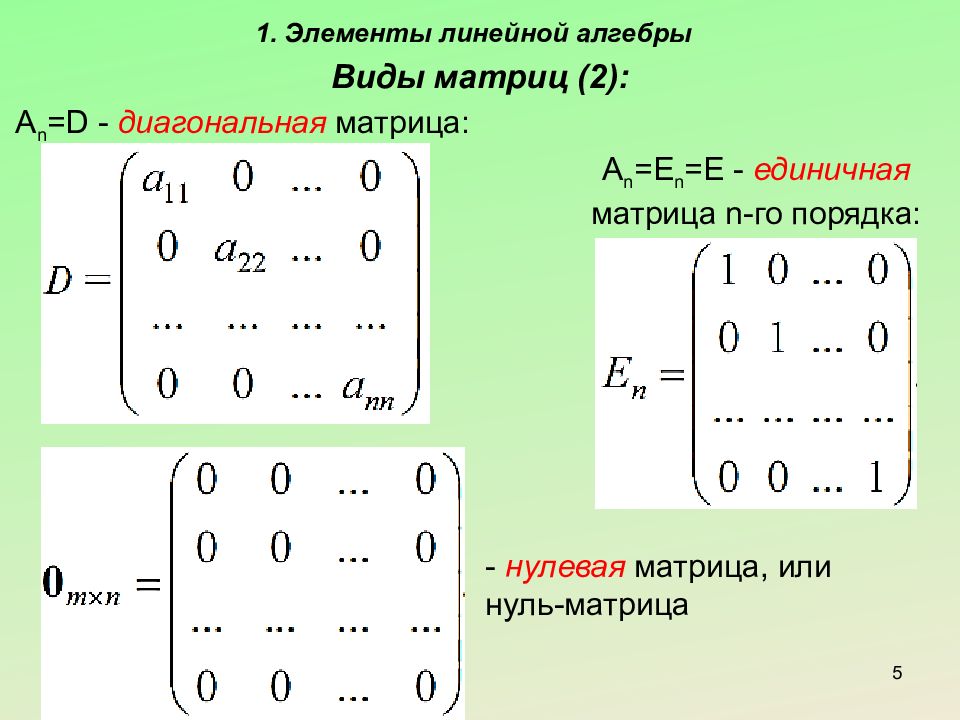
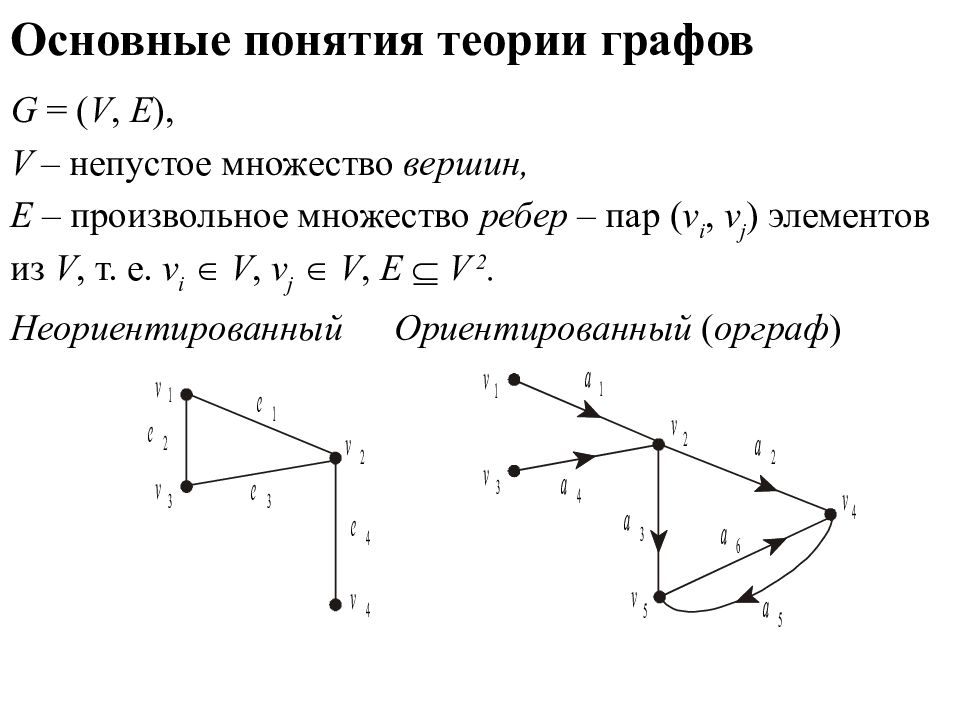
1. Элементы линейной алгебры 5 Виды матриц (2): A n =D - диагональная матрица: A n =E n = E - единичная матрица n- го порядка : - нулевая матрица, или нуль-матрица
1. Элементы линейной алгебры 6 Операции над матрицами (1): 1. Равенство матриц: 2. Произведение матрицы на число: 3. Сумма двух матриц:
1. Элементы линейной алгебры 7 Операции над матрицами (2): 4. Произведение двух матриц: 5. Транспонирование матриц:
1. Элементы линейной алгебры 8 Операции над матрицами (3): 6. Свойства операции транспонирования: - квадратные матрицы соответственно m- го и n- го порядков: - квадратная матрица 1-го порядка (т.е. число) - квадратная матрица n -го порядка
1. Элементы линейной алгебры 9 Определители квадратной матрицы 1-го, 2-го и 3-го порядков:
1. Элементы линейной алгебры 10 Определитель квадратной матрицы n- го порядка может быть вычислен с помощью разложения по элементам строки или столбца ( теорема Лапласа):
1. Элементы линейной алгебры 11 Свойства определителя:
1. Элементы линейной алгебры 12 Следом квадратной матрицы A n- го порядка) называется сумма ее диагональных элементов: Свойства следа матриц:
1. Элементы линейной алгебры 13 Матрица А называется невырожденной (неособенной), если. При матрица А – вырожденная (особенная). Матрица А -1 называется обратной по отношению к квадратной матрице А, если Для существования обратной матрицы А - необходимо и достаточно, чтобы матрица А была невырожденной Обратную матрицу можно рассчитать как:
1. Элементы линейной алгебры 14 Свойства обратной матрицы:
1. Элементы линейной алгебры 15 Рангом матрицы А ( rang A или r (A)) называется наивысший порядок ее миноров, отличных от нуля. Свойства ранга матрицы:
1. Элементы линейной алгебры 16 Пусть строки матрицы А: Строка е называется линейной комбинацией строк e 1, e 2 …, e m матрицы, если (*) (равенство (*) понимается в смысле поэлементного сложения строк, т. е. равенству (*) соответствует n равенств для элементов строк с номерами 1,2,..., n ) (**)
1. Элементы линейной алгебры 17 Если равенство (**) выполняется тогда и только тогда, когда, то строки матрицы называются линейно независимыми. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки (столбцы).
1. Элементы линейной алгебры 18 Система m линейных уравнений с n переменными имеет вид: или в матричной форме: (***)
1. Элементы линейной алгебры 19 где Если число уравнений равно числу переменных (m = n), и квадратная матрица А – невырожденная ( ), то система (***) имеет единственное решение:
1. Элементы линейной алгебры 20 Также решение системы (***), т.е. переменные x 1, x 2, …, x n при m=n может быть найдено по формулам Крамера : где - определитель матрицы А; - определитель матрицы A j, получаемой из матрицы А заменой j- го столбца столбцом свободных членов. Система линейных однородных уравнений, т. е. система АХ = 0 с нулевыми свободными членами, имеет ненулевое решение тогда и только тогда, когда матрица А – вырожденная (т.е. det A = 0).
1. Элементы линейной алгебры 21 n-мерны й вектор - упорядоченная совокупность n действительных чисел, записываемых в виде х = (х 1, х 2,…, x n ), где х i - i-я компонента вектора х Операции над векторами: Векторным (линейным) пространством называется множество векторов ( элементов) с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие следующим свойствам:
1. Элементы линейной алгебры 22 Понятие линейной комбинации, линейной зависимости и независимости векторов e 1, e 2,…, e m аналогичны соответствующим понятиям для строк матрицы e 1, e 2,…, e m. Линейное пространство R n называется n-мерным, если в нем существует n линейно независимых векторов, а любые из (n+1 ) векторов уже являются зависимыми. Иначе, размерность пространства - это максимальное число содержащихся в нем линейно независимых векторов, т. е. dim ( R n ) = n.
1. Элементы линейной алгебры 23 Совокупность n линейно независимых векторов n-мерного пространства R n называется базисом. Скалярным произведением двух векторов х = (x 1, x 2,…, x n ) и y = (y 1, y 2,…, y n ) называется число: Евклидовым пространством называется векторное ( линейное ) пространство, в котором задано скалярное произведение векторов, удовлетворяющее следующим свойствам:
1. Элементы линейной алгебры 24 Длиной (нормой) вектора х в евклидовом пространстве называется корень квадратный из его скалярного квадрата : Два вектора называются ортогональными, если их скалярное произведение равно нулю. Векторы e 1, e 2,…, e n n-мерного евклидова пространства образуют ортонормированный базис, или ортонормированную систему векторов, если эти векторы попарно ортогональны и длина каждого из них равна 1, т.е. если:
1. Элементы линейной алгебры 25 Вектор называется собственным вектором квадратной матрицы А, если найдется такое число, что Число называется собственным значением (собственным числом ) матрицы А, соответствующим вектору х. Для существования ненулевого решения уравнения необходимо и достаточно, чтобы Определитель - характеристический многочлен матрицы А, а уравнение - характеристическое уравнение матрицы А. Разным собственным значениям матрицы соответствуют линейно независимые собственные векторы.
1. Элементы линейной алгебры 26 Квадратная матрица А называется симметричной, если Симметричная матрица А n- го порядка называется положительно ( неотрицательно) определенной, если для любого ненулевого вектора выполняется неравенство: Квадратная матрица С называется ортогональной, если Симметричная матрица А называется идемпотентной, если она совпадает со своим квадратом:
2. Классическая нормальная линейная модель множественной регрессии 27 Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. Классическая нормальная линейная модель множественной регрессии: где y i – i -е наблюдение зависимой переменной; x i1, x i2, …, x ip – i -е наблюдения объясняющих переменных x 1, x 2, …, x p p – количество объясняющих переменных; e i – i - е возмущение (****)
3. Основные положения регрессионного анализа. Оценка параметров парной регрессионной модели. Теорема Гаусса—Маркова. 28 Предпосылки модели (****): В модели (****) возмущение ( или y i ) – величина случайная, а x i - величины неслучайные; 2) Математическое ожидание возмущения равно нулю: ; 3) Дисперсия возмущения ( или y i ) постоянна для любого i: или ; 4) Возмущения и (или переменные y i и y j ) не коррелированы: ; 5) Возмущение ( или зависимая переменная y i ) есть нормально распределенная случайная величина; 6) Н евырожденность матрицы ( независимость столбцов) значений объясняющих переменных.
2. Классическая нормальная линейная модель множественной регрессии 29 Модель (****) в матричной форме: где - вектор значений зависимой переменной размера n матрица значений объясняющих переменных размера n * ( p+1 ), p – количество объясняющих переменных - вектор параметров размера ( p+1) - вектор возмущений (случайных ошибок, остатков) размера n
2. Классическая нормальная линейная модель множественной регрессии 30 Оценка модели (****) по выборке: где
3. Оценка параметров классической регрессионной модели методом наименьших квадратов 31 Оценка параметров классической модели множественной линейной регрессии производится методом наименьших квадратов (МНК) аналогично оценке параметров модели парной линейной регрессии (вопросы 2-3 темы 3), но в матричной форме: Теорема Гаусса—Маркова для множественной регрессии: При выполнении предпосылок 1)-6) множественного регрессионного анализа оценка МНК является наиболее эффективной, т. е. обладает наименьшей дисперсией в классе линейных несмещенных оценок ( Best Linear Unbiased Estimator или BLUE)
3. Оценка параметров классической регрессионной модели методом наименьших квадратов 32 Стандартизированные коэффициенты регрессии (бета-коэффициенты) и коэффициенты эластичности:
4. Ковариационная матрица и ее выборочная оценка 33 Вариации оценок параметров будут определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают ковариационную матрицу вектора оценок параметров,являющуюся матричным аналогом дисперсии одной переменной: - где элементы - ковариации оценок параметров и.
4. Ковариационная матрица и ее выборочная оценка 34 Оценка ковариационной матрицы вектора оценок параметров: где - дисперсия возмущения постоянная для любого i. При этом несмещенная оценка - выборочная остаточная дисперсия :
5. Определение доверительных интервалов для коэффициентов и функции регрессии 35 Оценка значимости коэффициента множественной регрессии b j : Проводится аналогично оценке значимости коэффициентов парной линейной регрессии: е сли , то гипотеза отвергается на уровне значимости При этом с реднее квадратическое отклонение коэффициента регрессии : Табличное значение t-критерия Стьюдента для уровня значимости при числе степеней свободы k = n – p – 1:
5. Определение доверительных интервалов для коэффициентов и функции регрессии 36 Доверительный интервал для параметра : (трактовка аналогична случаю парной линейной регрессии) Доверительный интервал для : где групповая средняя, определяемая по уравнению регрессии; - стандартная ошибка
6. Оценка значимости множественной регрессии. 37 Оценка значимости уравнения множественной регрессии: Проводится аналогично оценке значимости уравнения парной линейной регрессии: Уравнение множественной регрессии значимо (т.е. гипотеза отвергается ), если: где Q e =, Q R =, - табличное значение F- критерия Фишера - Снедекора
7. Коэффициент множественной детерминации и скорректированный коэффициент множественной детерминации 38 Коэффициент детерминации показывает долю вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющих переменных: Чем ближе R 2 к единице, тем лучше регрессия описывает зависимость между объясняющими и зависимой переменными.
7. Коэффициент множественной детерминации и скорректированный коэффициент множественной детерминации 39 Недостаток коэффициента детерминации – его увеличение при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. Поэтому для множественной регрессии предпочтительнее использовать скорректированный коэффициент детерминации:
32 Элементы линейной алгебры Классическая нормальная линейная модель множественной регрессии Оценка параметров классической регрессионной модели методом наименьших квадратов Ковариационная матрица и ее выборочная оценка Определение доверительных интервалов для коэффициентов и функции регрессии Оценка значимости множественной регрессии. Коэффициент множественной детерминации и скорректированный коэффициент множественной детерминации
