Теория вероятностей – математическая наука, которая позволяет по вероятности одних случайных событий находить вероятности других случайных событий, связанных каким-либо образом между собой. 2
Слайд 3: Элементарные события и вероятность
Исход опыта - результат любого проводимого опыта (эксперимента). Событие - исход или группа исходов, удовлетворяющих определённым требованиям. 3
Слайд 4: События
Достоверное событие – это такое событие, которое всегда происходит в рассматриваемом эксперименте. Невозможное событие – это такое событие, которое никогда не может наступить в рассматриваемом эксперименте. Случайное событие - событие, которое при воспроизведении опыта может наступить, а может и не наступить. 4
Слайд 5: Вероятность события
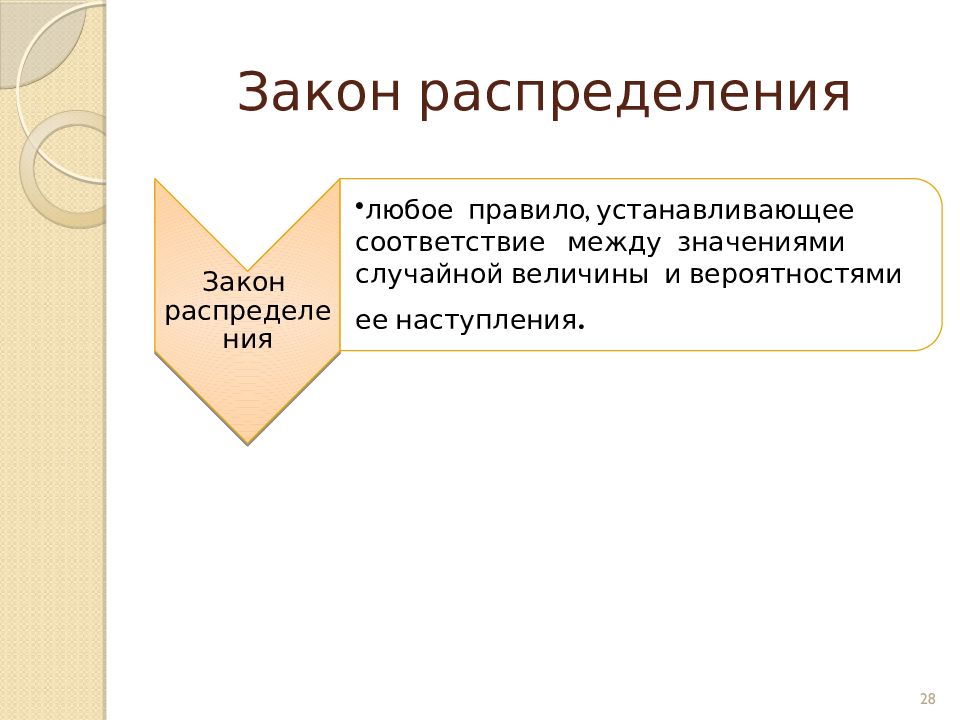
Вероятность события - численная мера степени объективной возможности этого события. 0 ≤ P(A) ≤ 1 Полная группа событий – это несколько возможных событий, одно из которых обязательно должно произойти в результате опыта. 5
Слайд 6: События
Несовместные события – это события, которые не могут появиться вместе. Равновероятные события – события, вероятности которых равны между собой. 6
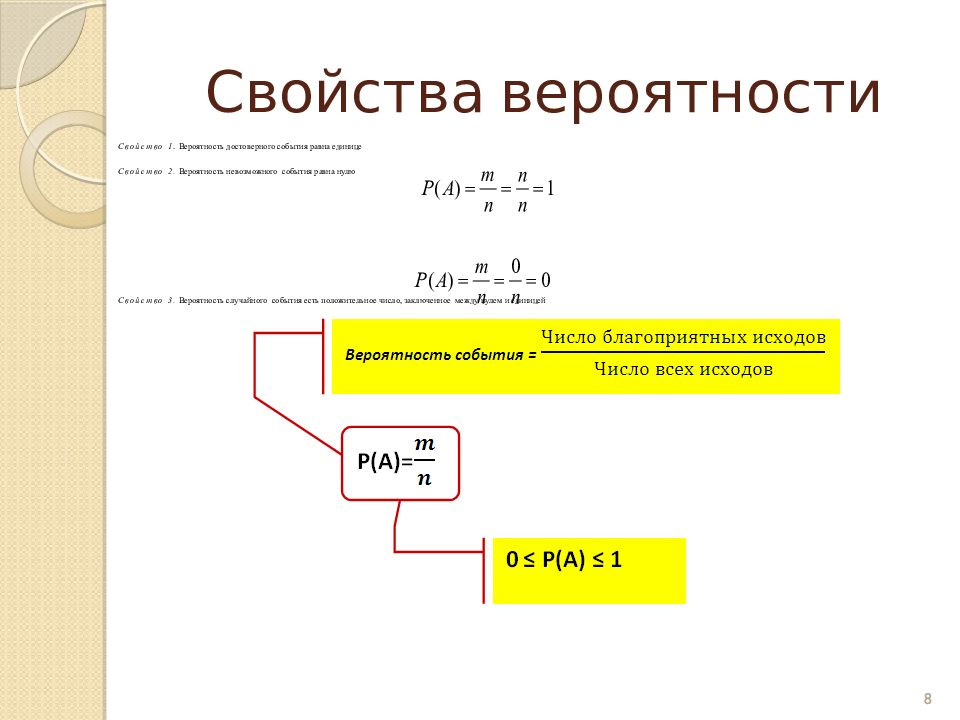
Вероятность события А - отношение благоприятного числа исходов опыта к общему числу всех равновозможных несовместных элементарных исходов 7 где m – благоприятное число исходов опыта, n – общее число исходов опыта.
Слайд 8
8 Свойства вероятности Свойство 1. Вероятность достоверного события равна единице Свойство 2. Вероятность невозможного события равна нулю Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей 8
Слайд 9: Статистическая вероятность
Относительная частота события А (статистическая вероятность) серии одинаковых опытов - отношение числа опытов, в которых появилось событие А, к общему числу фактически произведённых опытов. 9 где m – число появлений события А, n – число опытов в серии.
Слайд 10: Комбинаторика
Комбинаторика изучает количество комбинаций, которое можно составить из элементов, заданного конечного множества, в определенных условиях. 10
Слайд 11: Перестановка
Перестановка - это комбинация, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. где. 11
Слайд 12: Пример 1
Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз? Решение. Искомое число трехзначных чисел 12
Слайд 13: Размещение
Размещение - это комбинация, составленные из n различных элементов по m элементов, которые отличаются либо составом, либо их порядком. 13
Слайд 14: Пример 2
Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? Решение. Искомое число сигналов 14
Слайд 15: Сочетание
Сочетание - это комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. 15
Слайд 16: Пример 3
Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей 2? Решение. Искомое число сигналов 16
Слайд 17: Основные правила комбинаторики
Правило суммы. Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран п способами, то выбрать либо А, либо В можно т + п способами. Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать п способами, то пара объектов (А, В) в указанном порядке может быть выбрана тп способами. 17
Слайд 18: Пример 4
В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных. Решение. Общее число исходов испытания равно числу способов Число благоприятствующих событию Искомая вероятность 18
Слайд 19: Теорема сложения вероятностей
19 Теорема. Вероятность появления одного из двух совместных событий, безразлично какого, равна сумме вероятностей этих событий без учета вероятности их совместного появления:
Слайд 20
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р(А + В) = Р(А) + Р(В). Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р (А 1 + А 2 +... + А n ) = Р (А 1 ) + Р (А 2 ) +...+Р (А n ) 20
Слайд 21: Пример
Найти вероятность того, что наудачу взятое двухзначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно. Решение. Пусть А - наудачу взятое двузначное число кратно 2, а В - это число кратно 5. А и В - события совместные. Двузначные числа - это 10, 11,...,98, 99. (Всего их 90). Очевидно, 45 из них кратны 2 (событие А), 18 кратны 5 (событие В) и, наконец 9 кратны и 2, и 5 одновременно (события А и В). По классическому определению вероятности: Р(А) = 45/90= 0,5; Р(В) = 18/90 = 0,2; Р(АВ) = 9/90 и следовательно: Р(А + В) = 0,5 + 0,2 - 0,1 = 0,6. 21
Слайд 22: Теорема произведения вероятностей
Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило : Р(АВ ) = Р(А)Р A (В ). Для независимых событий теорема умножения имеет вид Р (АВ) = Р (А) Р ( В ). 22
Слайд 23: Пример 1
У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков – конусный, а второй – эллиптический. Решение. Вероятность того, что первый валик окажется конусным (событие А), Р (А) = 3/10. Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик — конусный, т. е. условная вероятность Р А (В) = 7/9. По теореме умножения, искомая вероятность Р (АВ) = Р (А) Р А ( В ) = (3/10) • (7/9) = 7/30. Заметим, что, сохранив обозначения, легко найдем: Р (В) =7/10, Р В (А) =3/9, Р (В)Р В (А) = 7/30, что наглядно иллюстрирует справедливость равенства Р (А) Р А (В) = Р (В) Р В (А). 23
Слайд 24: Формула Бернулли
Задача. Вычислить вероятность того, что при n испытаниях событие А осуществится ровно k раз и, не осуществится n – k раз. Формула Бернулли или 24
Слайд 25: Пример
Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равно P=0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течении 4 суток не превысит нормы. Решение Вероятность нормального расхода электроэнергии постоянна и равна P=0,75. Следовательно, вероятность перерасхода также постоянна и равна q=1-P =0,25. Искомая вероятность по формуле Бернулли равна 25
Слайд 31: Пример
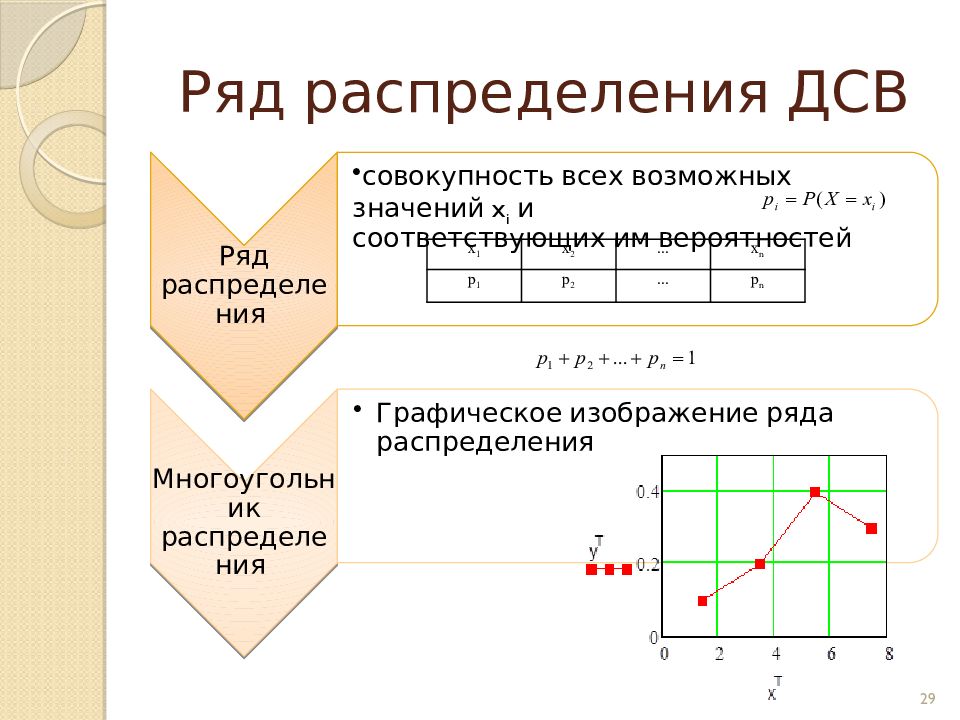
Из партии, содержащей 100 изделий, среди которых имеются 10 дефектных, выбраны случайным образом пять изделий для проверки их качества. Построить ряд распределений случайного числа X дефектных изделий, содержащихся в выборке. Решение. Так как в выборке число дефектных изделий может быть любым целым числом в пределах от 0 до 5 включительно, то возможные значения x i случайной величины X равны: . Вероятность Р(Х = k ) того, что в выборке окажется ровно k ( k =0, 1, 2, 3, 4, 5) дефектных изделий, равна Используя для проверки равенство, убеждаемся, что расчеты и округление произведены правильно (см. таблицу). 31 x i 0 1 2 3 4 5 p i. 0,583 0,3401 0,070 0,007 0 0
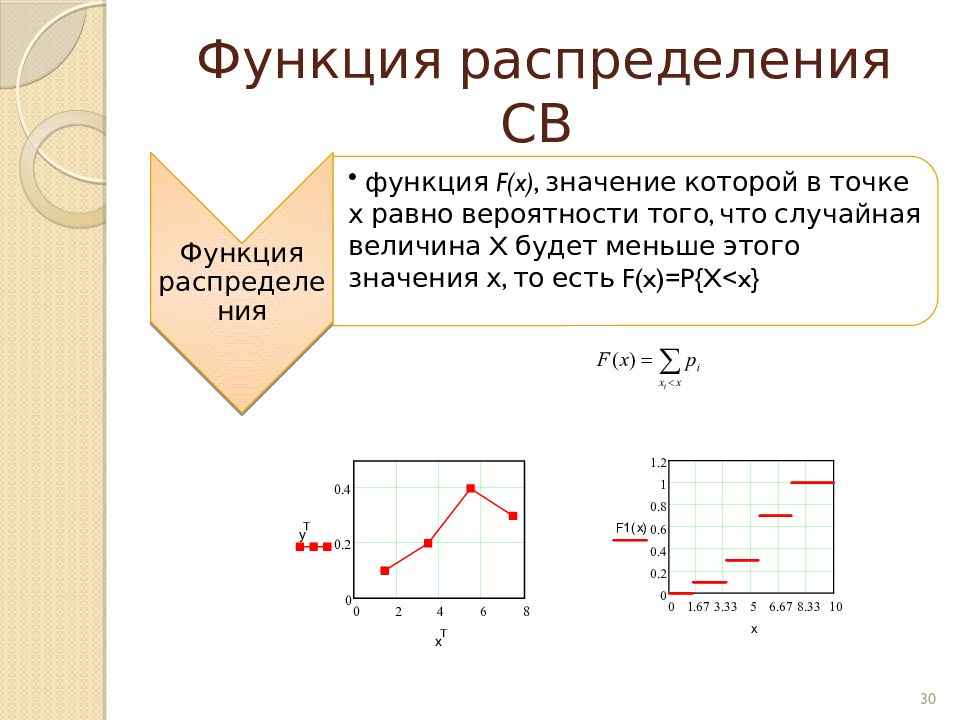
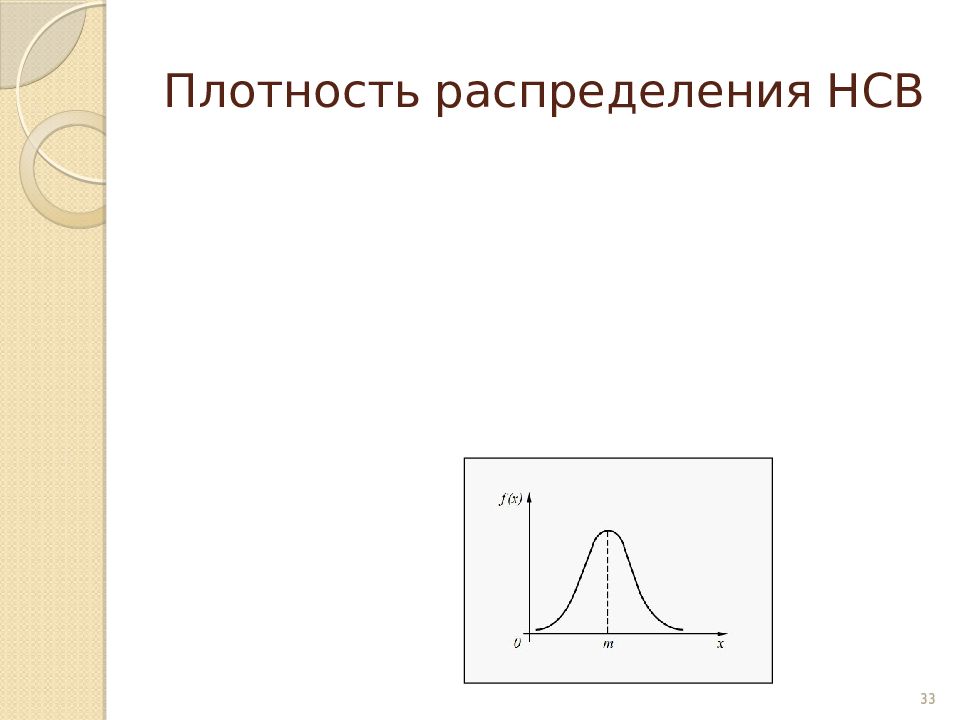
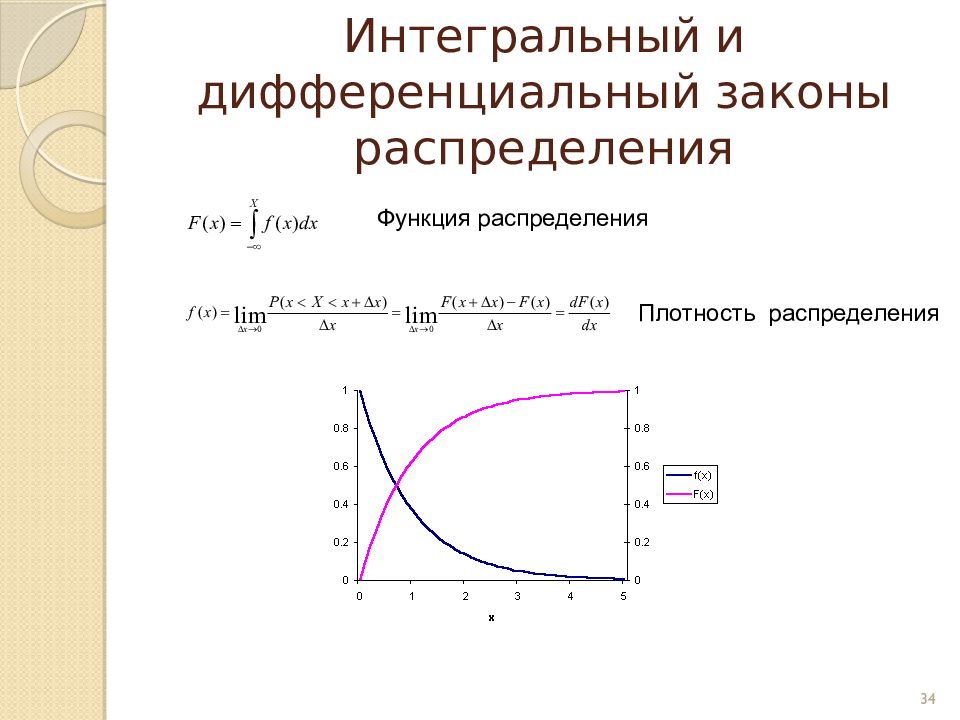
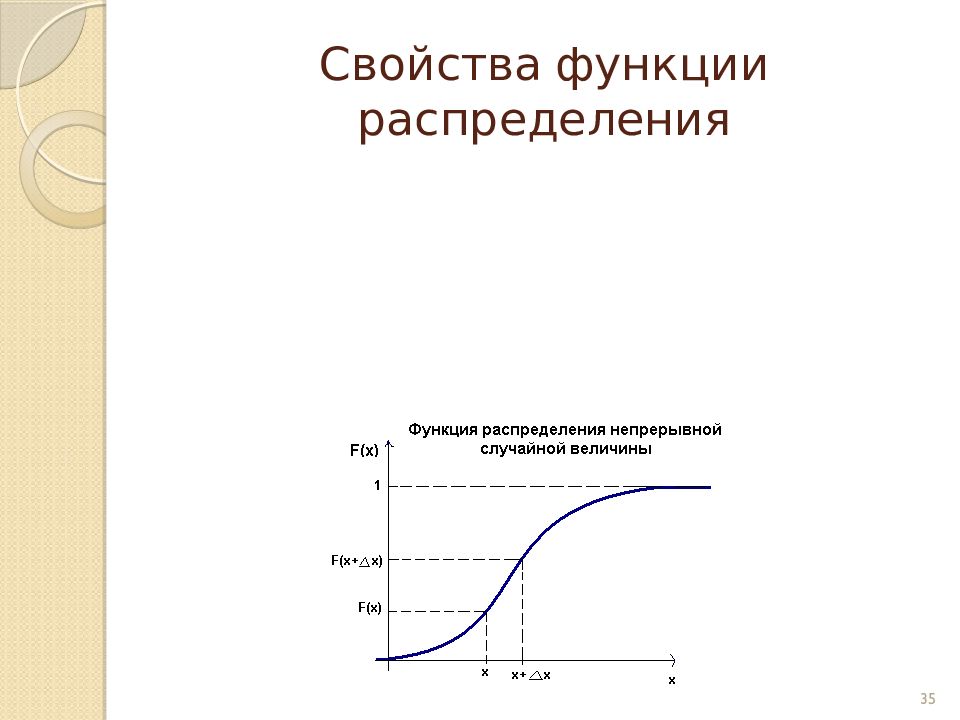
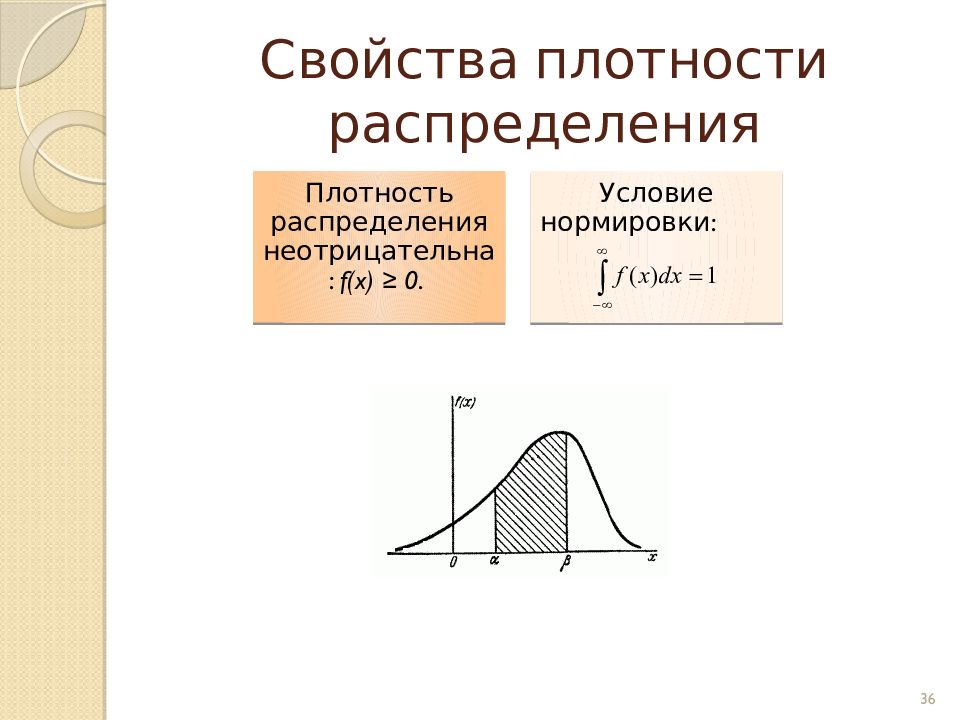
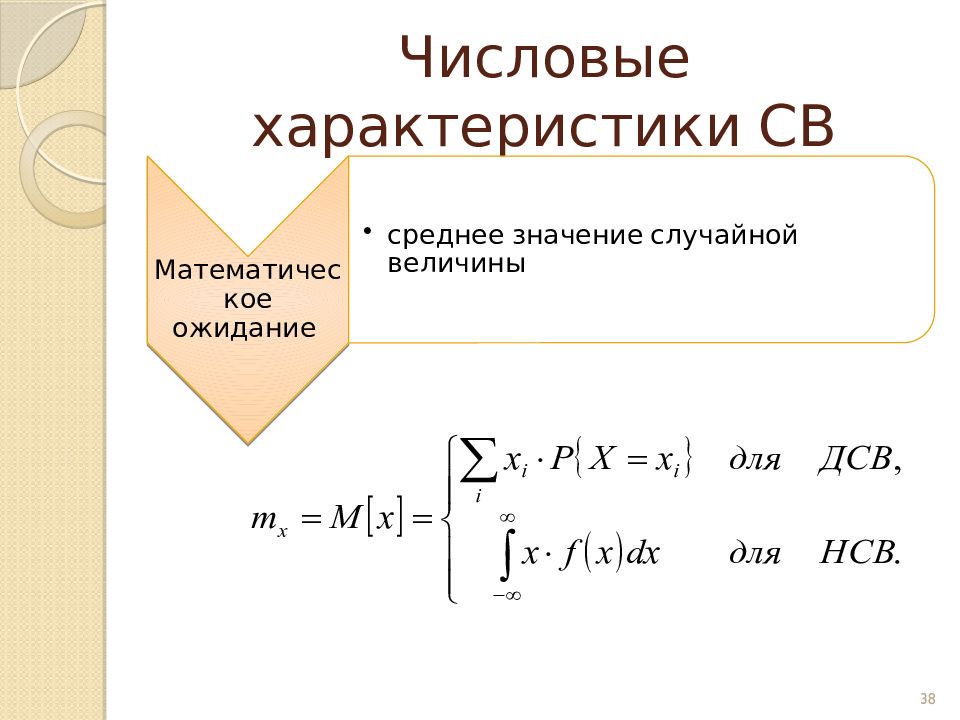
Слайд 34: Интегральный и дифференциальный законы распределения
Функция распределения Плотность распределения 34
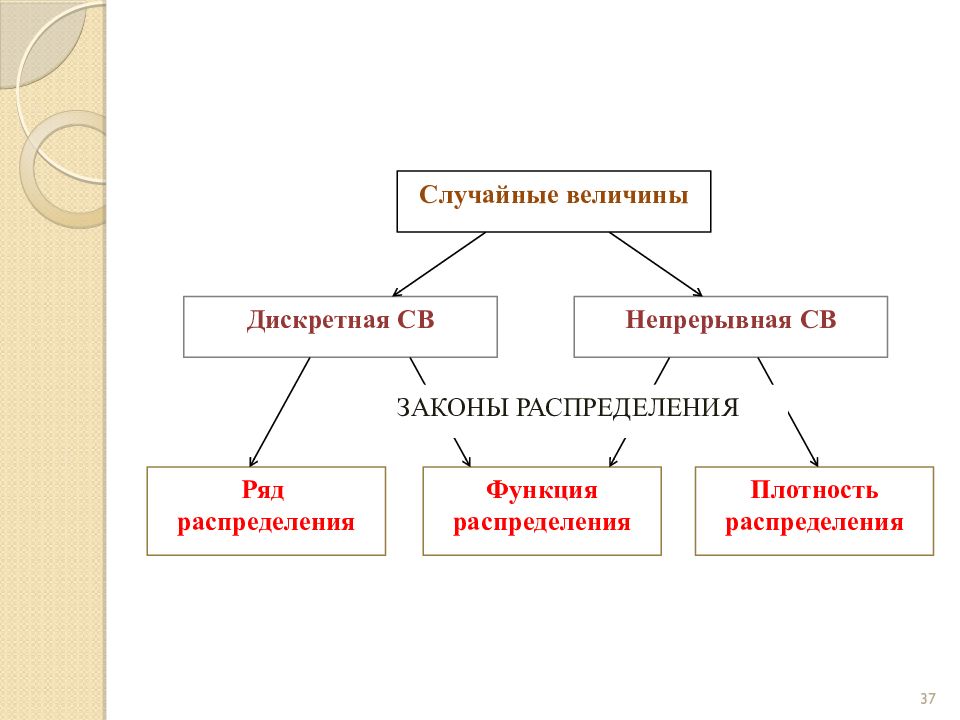
Слайд 37
37 Случайные величины Дискретная СВ Непрерывная СВ Ряд распределения Функция распределения Плотность распределения ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
Слайд 44: Пример 1
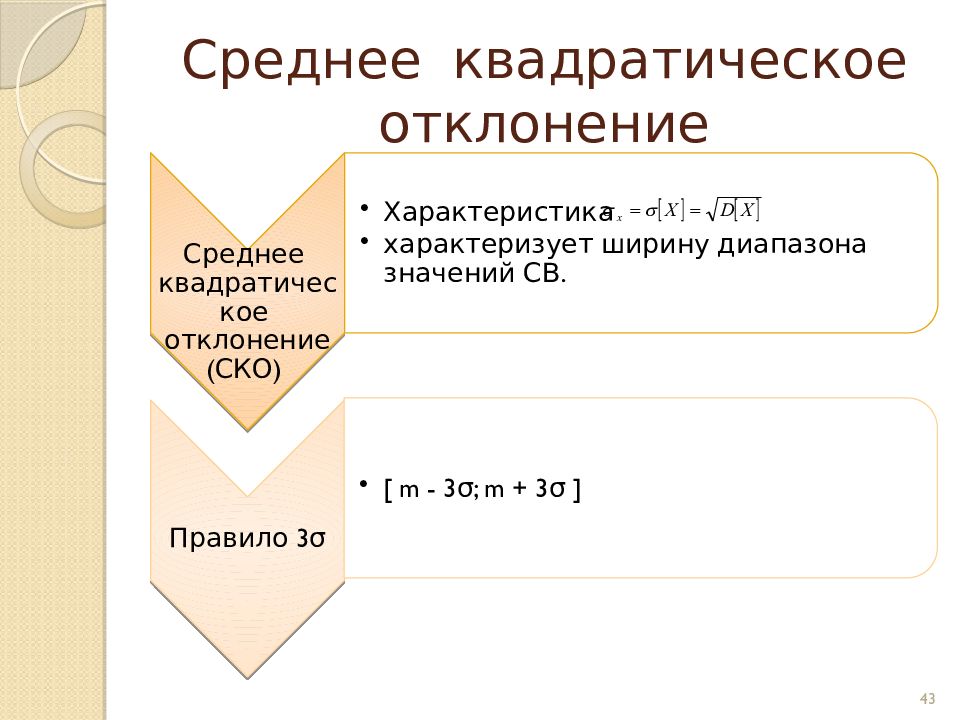
Из партии численностью 25 изделий, среди которых имеется шесть нестандартных, случайным образом выбраны три изделия. Найти математическое ожидание и среднее квадратическое отклонение нестандартных изделий, содержащихся в выборке. Решение. По условию задачи CB X принимает следующие значения: x1=0; x2=1; x3=2; x4=3. Вероятность того, что в этой выборке окажется ровно i (i = 0, 1, 2, 3) нестандартных изделий, вычисляется по формуле 44 x i 1 2 3 4 p i. 0, 41 0, 43 0, 11 0,0 05
Слайд 46: Некоторые частные законы распределения СВ
Законы распределения дискретных случайных величин Законы распределения непрерывных случайных величин Некоторые частные законы распределения СВ 46
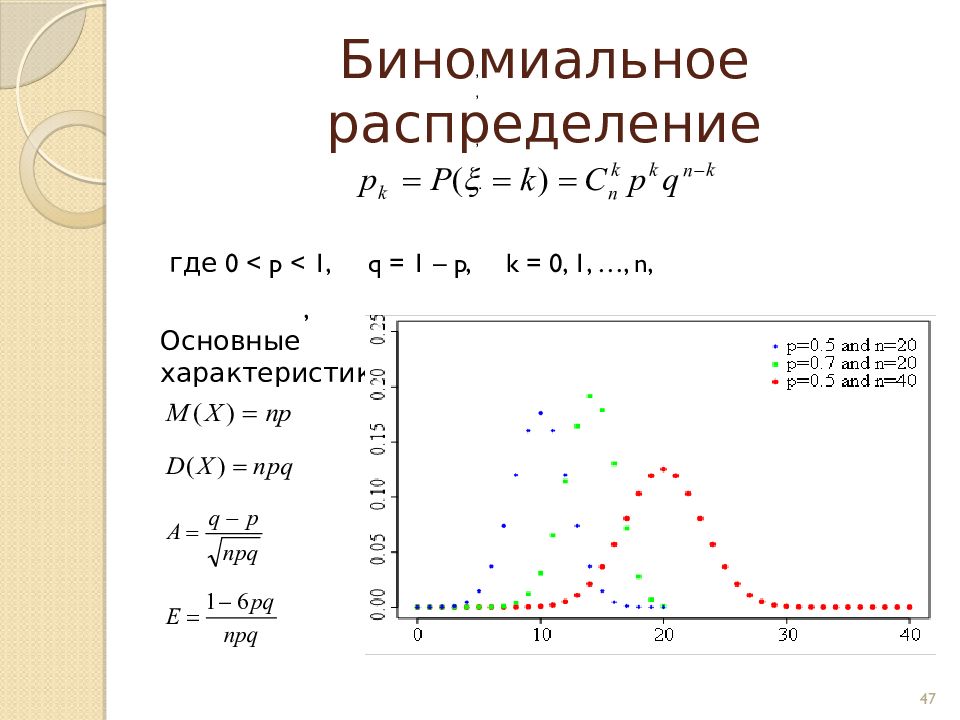
Слайд 47: Биномиальное распределение
47 где 0 < p < 1, q = 1 – p, k = 0, 1, …, n, , Основные характеристики : , , , .
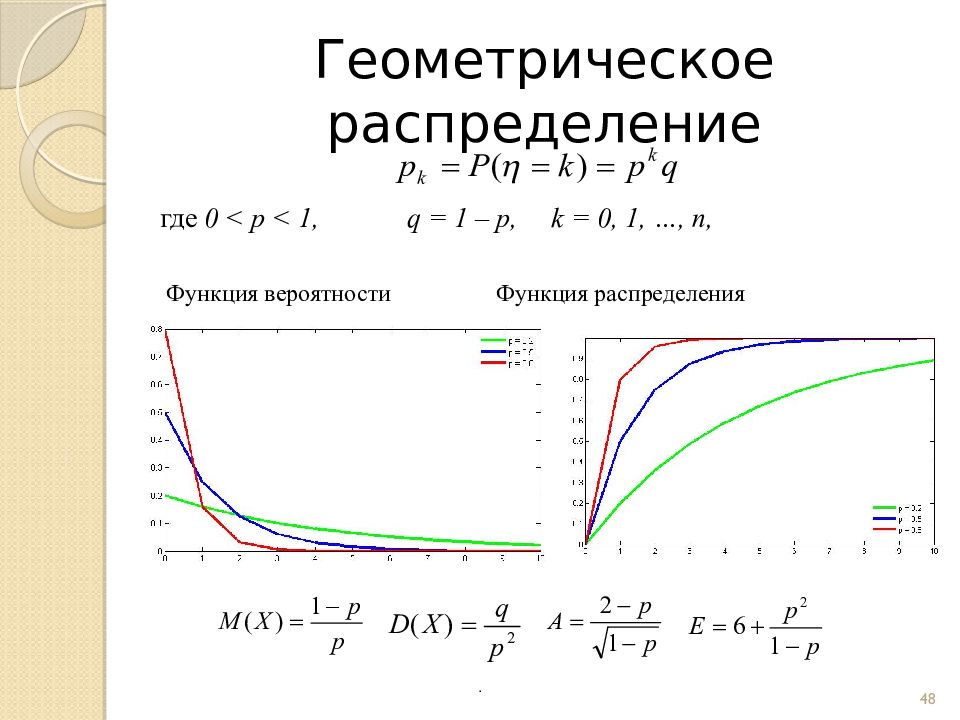
Слайд 48: Геометрическое распределение
где 0 < p < 1, q = 1 – p, k = 0, 1, …, n, Функция вероятности Функция распределения Основные характеристики 48 .
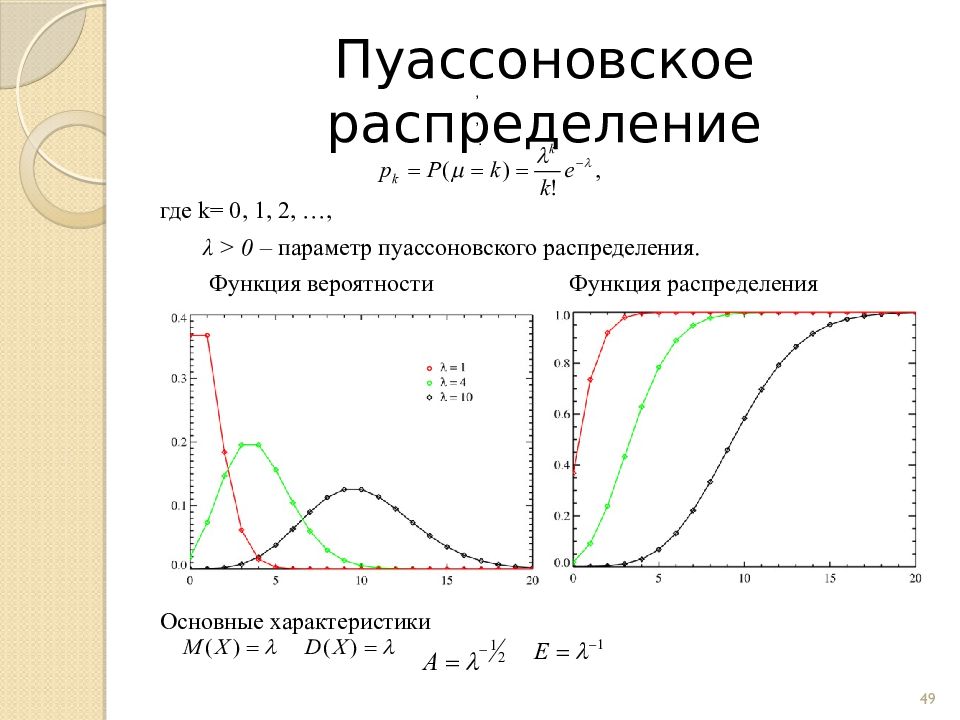
Слайд 49: Пуассоновское распределение
где k = 0, 1, 2, …, λ > 0 – параметр пуассоновского распределения. Функция вероятности Функция распределения Основные характеристики 49 , , , .
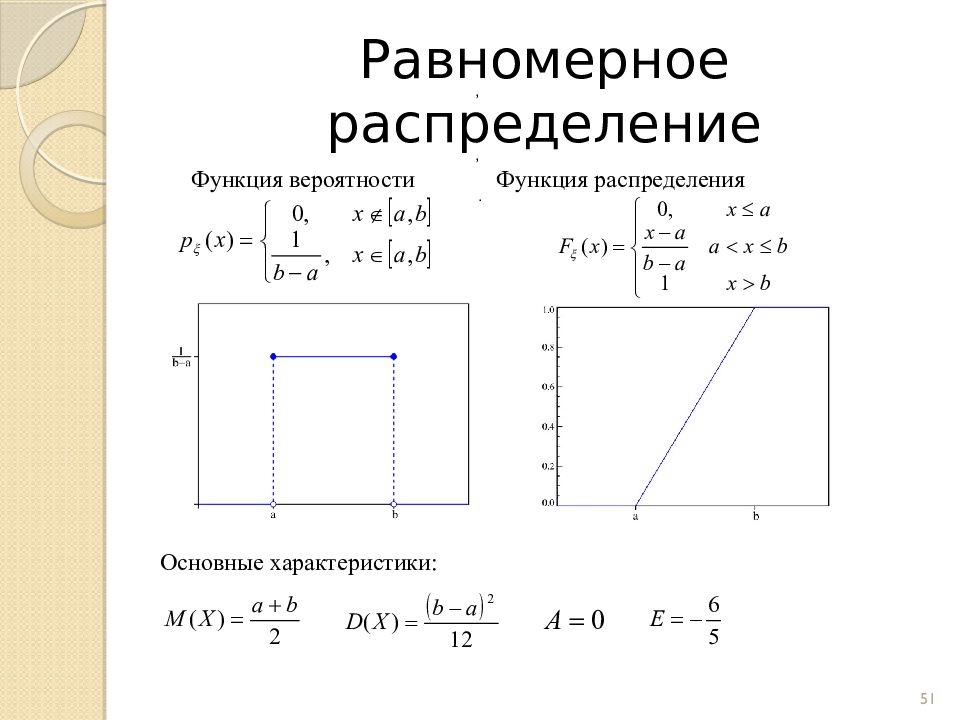
Слайд 51: Равномерное распределение
Функция вероятности Функция распределения Основные характеристики: 51 , , , .
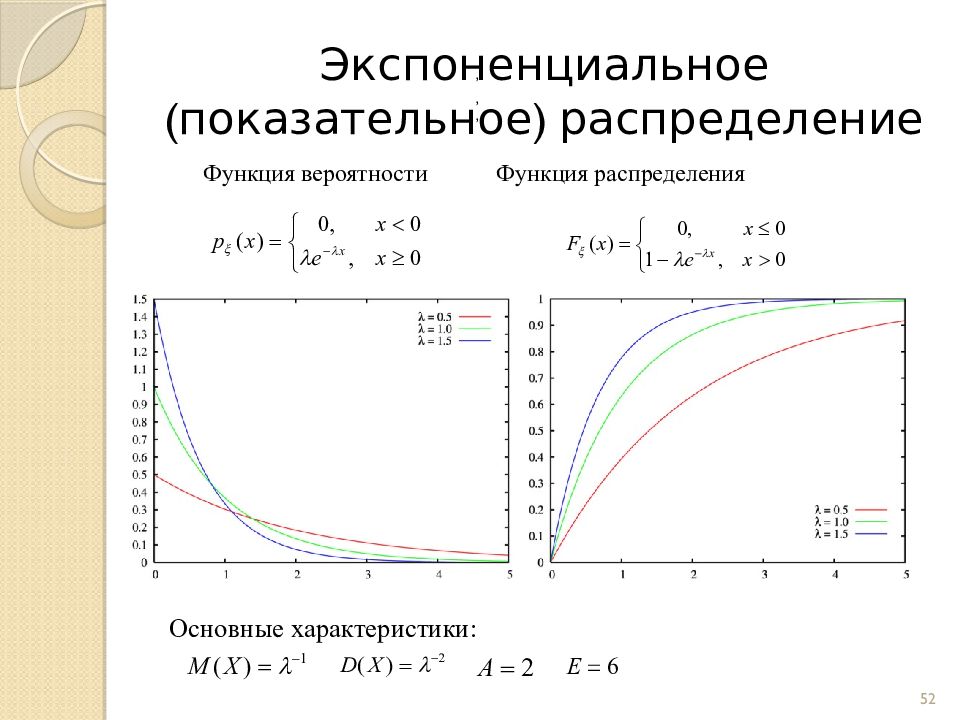
Слайд 52: Экспоненциальное (показательное) распределение
Функция вероятности Функция распределения Основные характеристики: Основные характеристики: 52 , , ,
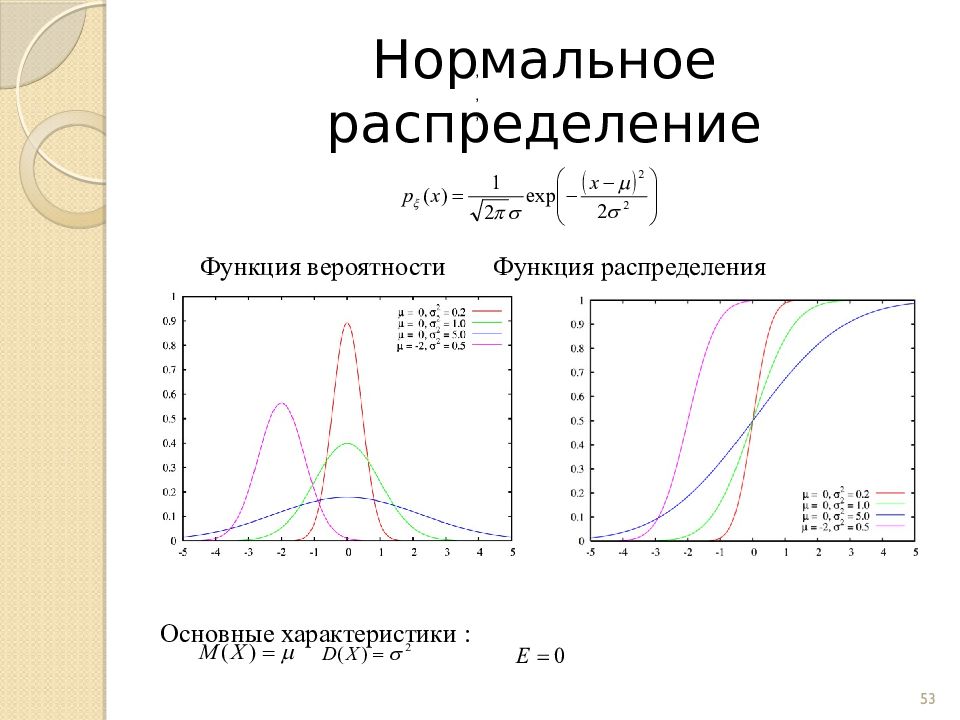
Слайд 53: Нормальное распределение
Функция вероятности Функция распределения Основные характеристики : 53 , , , .
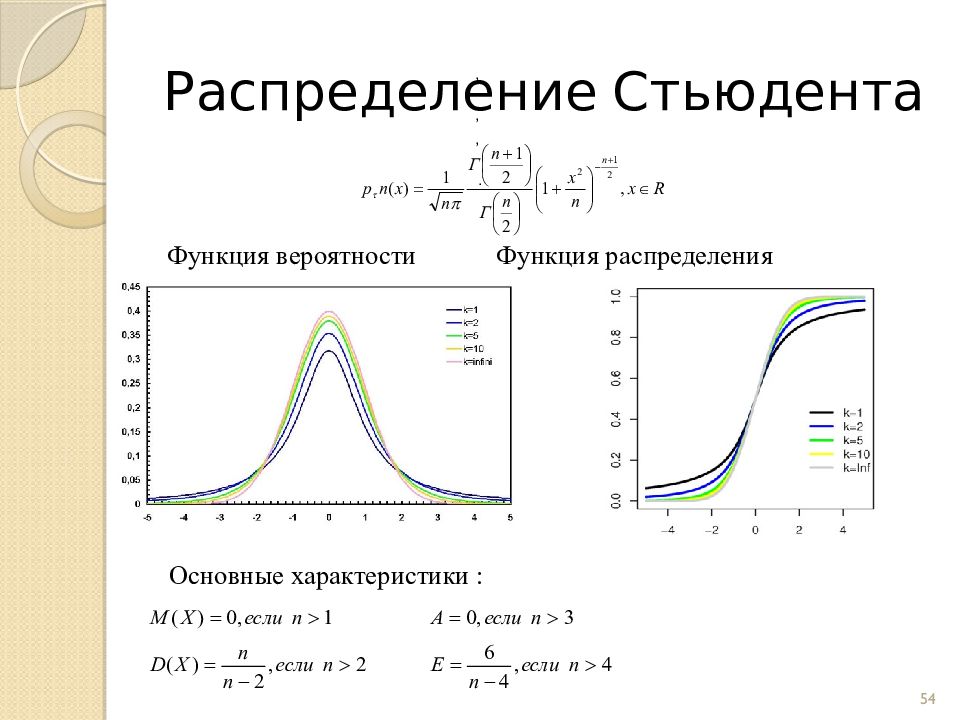
Слайд 54: Распределение Стьюдента
Функция вероятности Функция распределения Основные характеристики : Основные характеристики : 54 , , , .
Слайд 56: Задачи математической статистики
Первая задача — указать способы сбора и группировки статистических сведений. (описательная статистика) Вторая задача — разработать методы анализа статистических данных: а) оценка неизвестных параметров распределения (теорию оценивания) б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен (теория проверки гипотез). Задачи математической статистики 56
Слайд 58: Выборочная и генеральная совокупности
58 Выборочная и генеральная совокупности
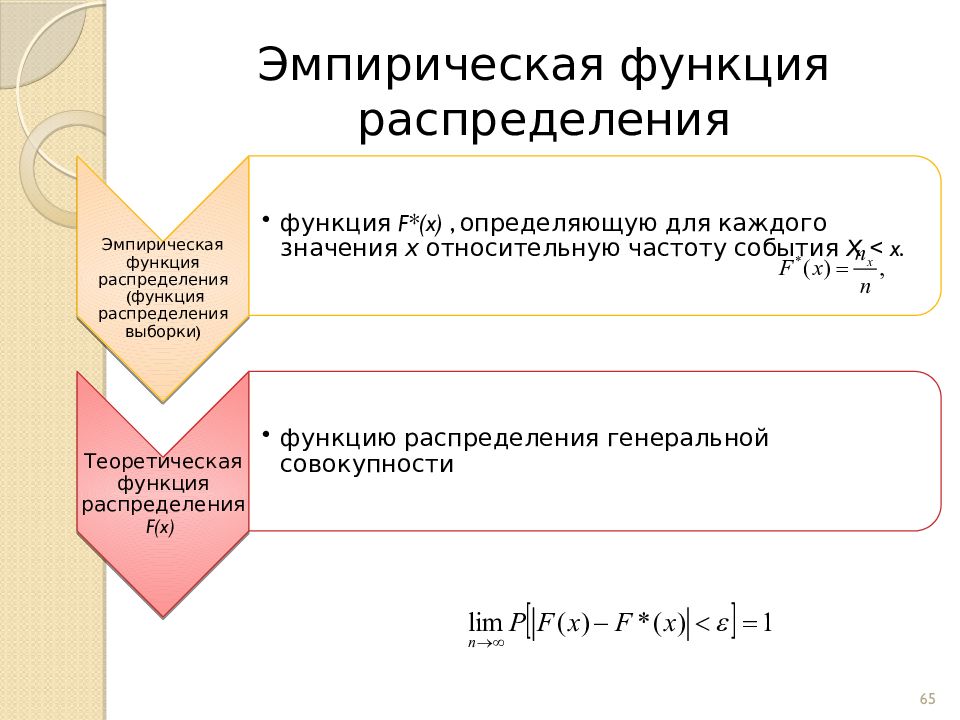
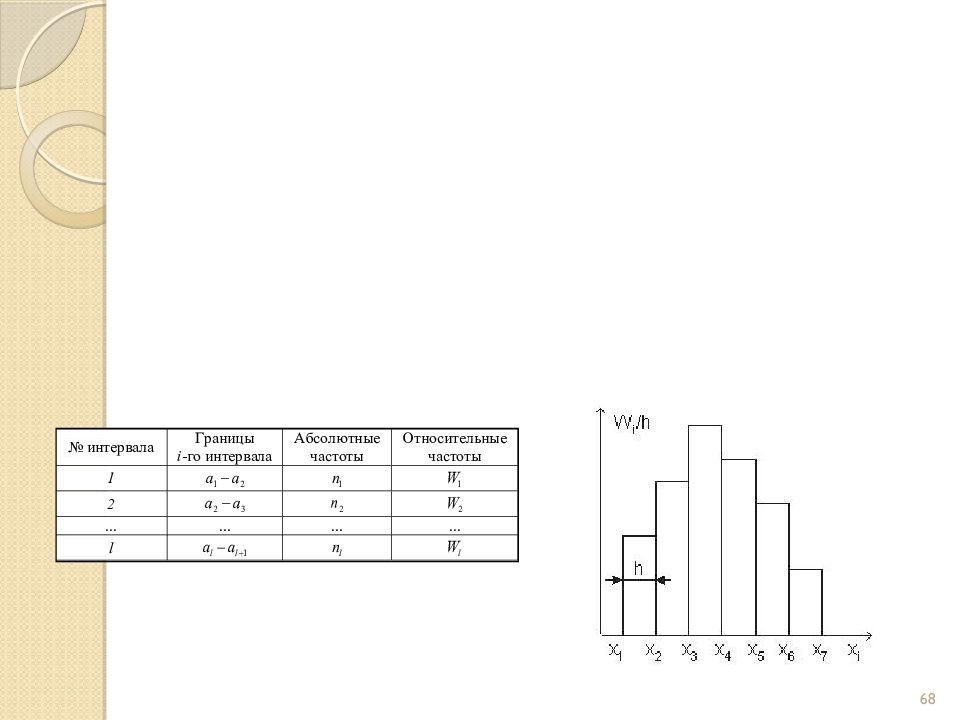
Слайд 62: Статистическое распределение выборки
62 Статистическое распределение выборки x i x 1 x 2 … x l n i n 1 n 2 … n l W i W 1 W 2 … W l
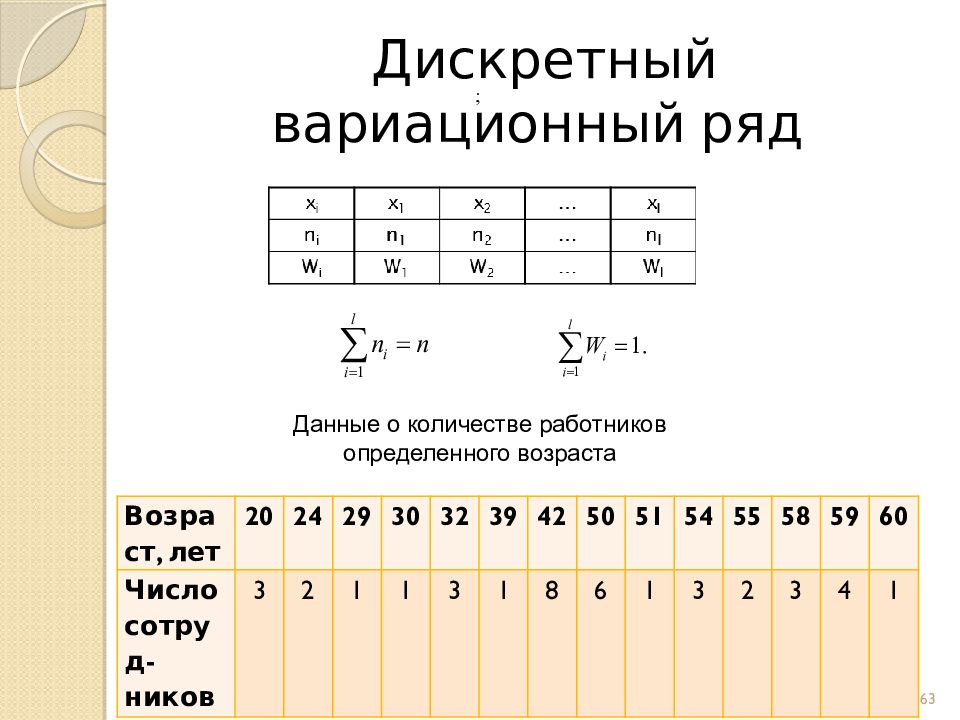
Слайд 63: Дискретный вариационный ряд
; Возраст, лет 20 24 29 30 32 39 42 50 51 54 55 58 59 60 Число сотруд - ников 3 2 1 1 3 1 8 6 1 3 2 3 4 1 Данные о количестве работников определенного возраста 63
Слайд 64: Интервальный вариационный ряд
x min и x max Формула Стэрджеса : Интервальный вариационный ряд 64
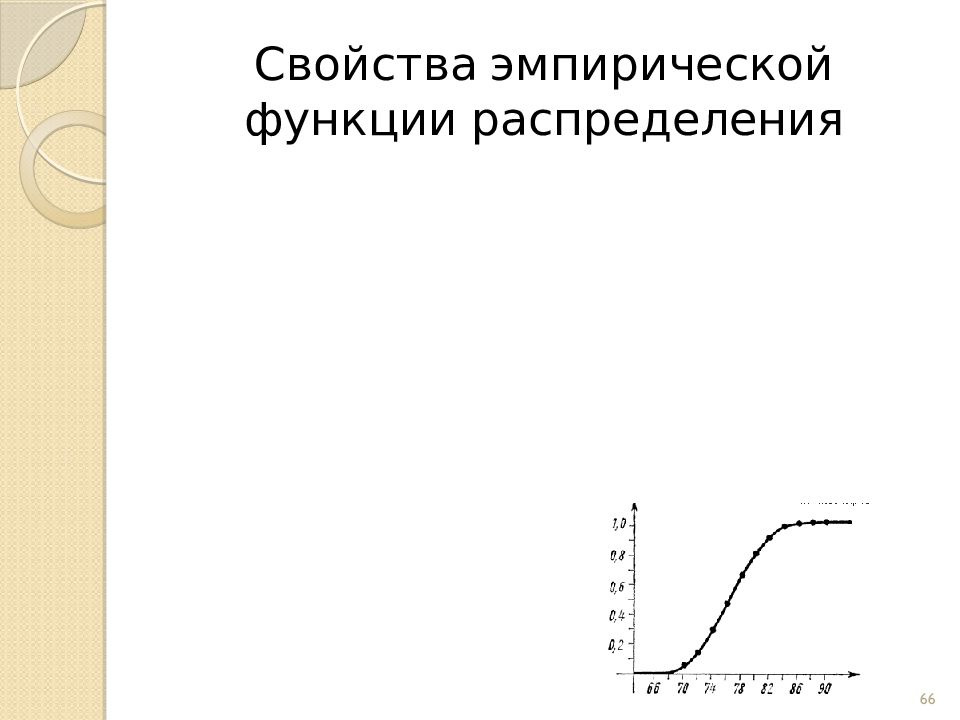
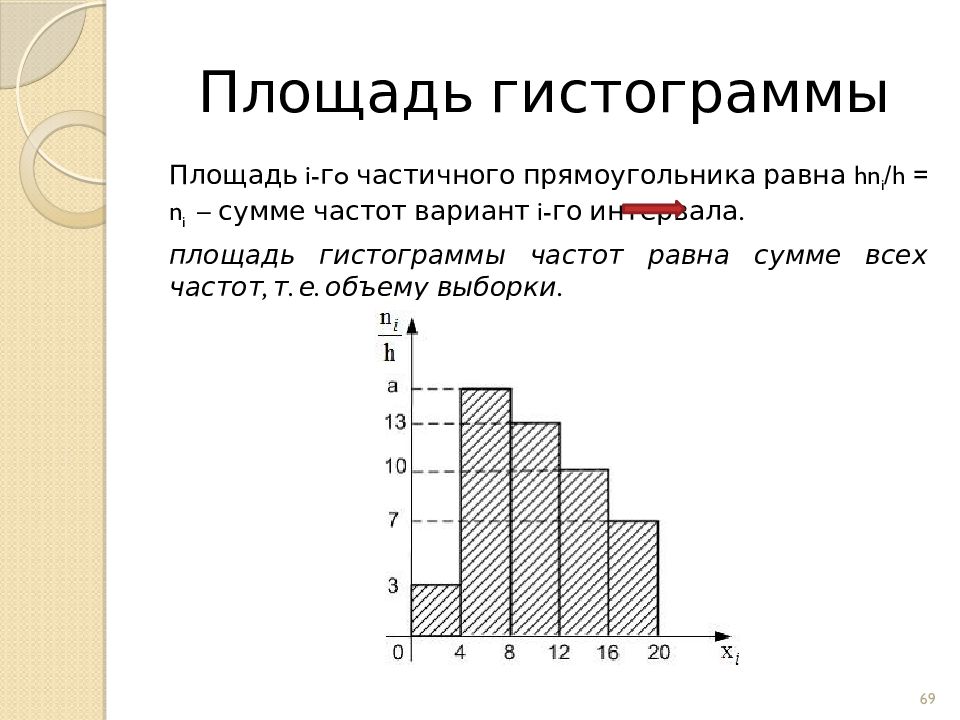
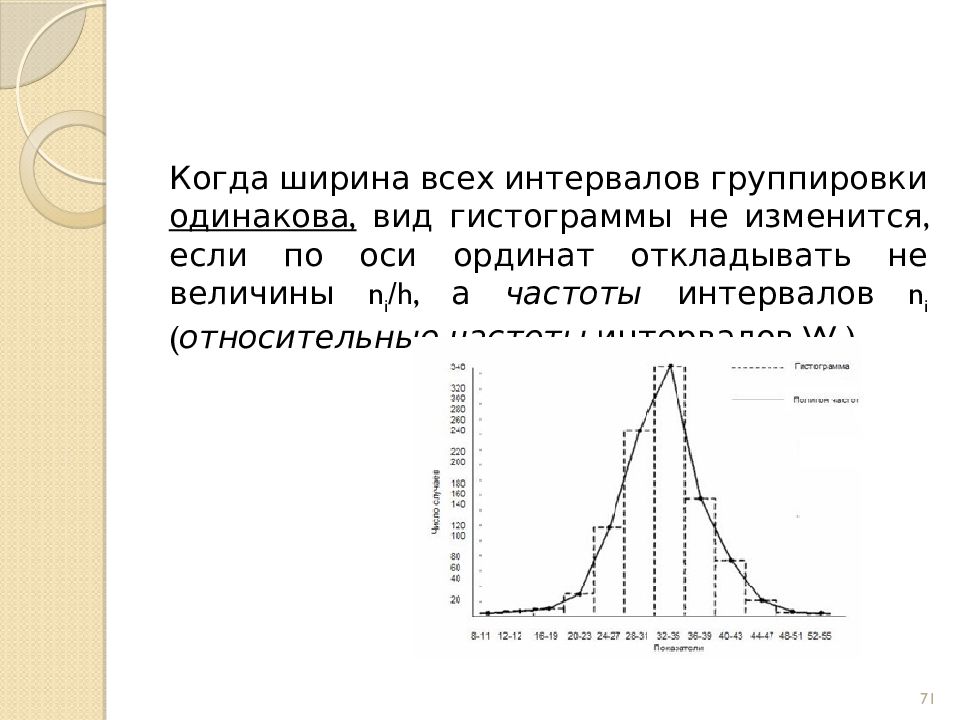
Слайд 69: Площадь гистограммы
Площадь i-гo частичного прямоугольника равна h n i /h = n i – сумме частот вариант i -го интервала. площадь гистограммы частот равна сумме всех частот, т. е. объему выборки. 69 Площадь гистограммы
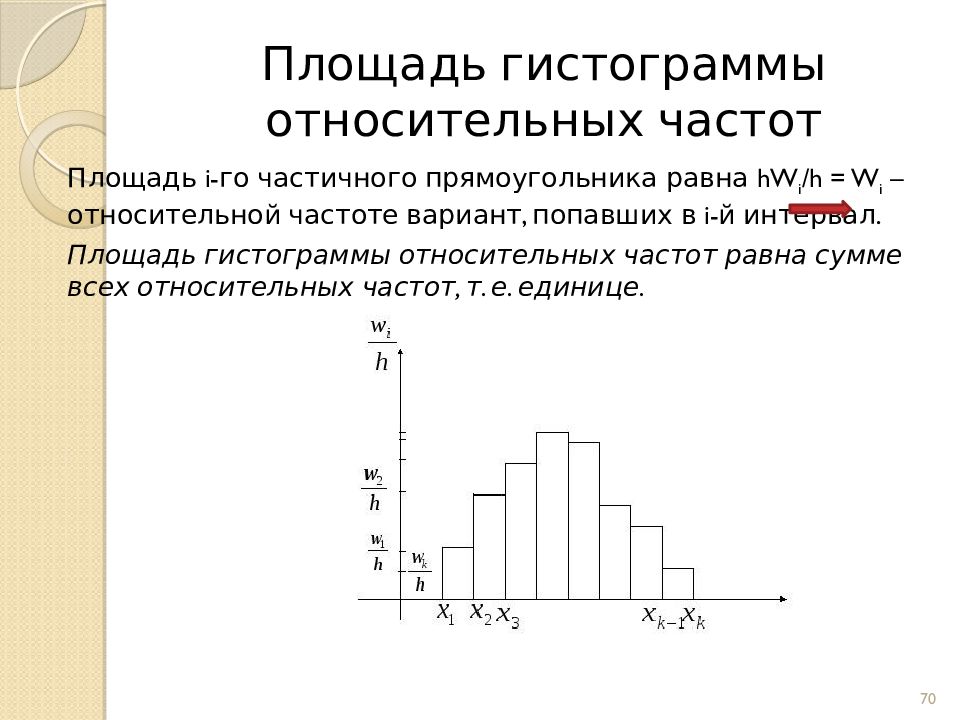
Слайд 70: Площадь гистограммы относительных частот
Площадь i-го частичного прямоугольника равна hW i /h = W i – относительной частоте вариант, попавших в i -й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице. Площадь гистограммы относительных частот 70